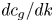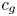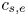1. Introduction
Whistler-mode chorus (WMC) waves play a significant role in determining energetic electron dynamics within terrestrial and magnetospheric plasmas (Horne et al. Reference Horne, Thorne, Shprits, Meredith, Glauert, Smith, Kanekal, Baker, Engebretson and Posch2005; Thorne et al. Reference Thorne, Ni, Tao, Horne and Meredith2010; Artemyev et al. Reference Artemyev, Agapitov, Mourenas, Krasnoselskikh, Shastun and Mozer2016; Woodfield et al. Reference Woodfield, Glauert, Menietti, Averkamp, Horne and Shprits2019). The WMC are one particular manifestation of the so-called ‘whistler-mode’ electromagnetic/plasma wave (Stix Reference Stix1992), and are particularly noteworthy for their role in rapid electron energisation and pitch-angle scattering (Bortnik, Thorne & Inan Reference Bortnik, Thorne and Inan2008; Omura, Katoh & Summers Reference Omura, Katoh and Summers2008; Albert Reference Albert2010; Artemyev et al. Reference Artemyev, Neishtadt, Vasiliev and Mourenas2018; Zhang et al. Reference Zhang, Artemyev, Angelopoulos, Tsai, Wilkins, Kasahara, Mourenas, Yokota, Keika and Hori2022). Discussions of the role of WMC as one driver among many (within the general context of energetic charged particle dynamics in the inner magnetosphere) can be found in, for example, Green & Kivelson (Reference Green and Kivelson2004), Thorne (Reference Thorne2010), Bortnik et al. (Reference Bortnik, Thorne, Li and Tao2016), Li & Hudson (Reference Li and Hudson2019) and Lejosne et al. (Reference Lejosne, Allison, Blum, Drozdov, Hartinger, Hudson, Jaynes, Ozeke, Roussos and Zhao2022). In perhaps overly simplistic terms, one can consider two main and contrasting challenges to achieving a full understanding of the role of WMC in magnetospheric plasma dynamics. While they are somewhat contrasting, both of these challenges are fundamentally united by the critical role that is played by wave–particle interactions (Brice Reference Brice1964; Kennel & Petschek Reference Kennel and Petschek1966; Tsurutani & Lakhina Reference Tsurutani and Lakhina1997; Summers, Thorne & Xiao Reference Summers, Thorne and Xiao1998).
One challenge, the ‘test-particle’ case, is to determine the direct impact of WMC on electrons that would otherwise evolve adiabatically as a geomagnetically trapped particle (Shklyar & Matsumoto Reference Shklyar and Matsumoto2009; Albert et al. Reference Albert, Artemyev, Li, Gan and Ma2022b). One of the most impressive manifestations of this approach (‘wave effects on particles only’) is the application of the resonant diffusion limit of the quasilinear theory (e.g. Kennel & Engelmann Reference Kennel and Engelmann1966; Summers Reference Summers2005; Allanson et al. Reference Allanson, Elsden, Watt and Neukirch2022) to global-scale numerical modelling of the terrestrial and planetary radiation belt populations using Fokker–Planck radiation-belt models (e.g. Li et al. Reference Li, Thorne, Ma, Ni, Bortnik, Baker, Spence, Reeves, Kanekal and Green2014; Glauert, Horne & Meredith Reference Glauert, Horne and Meredith2018; Wang et al. Reference Wang, Shprits, Zhelavskaya, Effenberger, Castillo, Drozdov, Aseev and Cervantes2020; Allison et al. Reference Allison, Shprits, Zhelavskaya, Wang and Smirnov2021). One of the numerous outstanding problems in this area is to understand and incorporate the role of so-called ‘nonlinear wave–particle interactions’ (Artemyev et al. Reference Artemyev, Neishtadt, Vasiliev, Zhang, Mourenas and Vainchtein2021, Reference Artemyev, Mourenas, Zhang and Vainchtein2022), with WMC playing a very important role.
Another challenge, the ‘self-consistent case’, is to instead try to solve for one or more of the generation, interaction and subsequent evolution of the WMC wave modes, as a function of, for example, a given initial plasma condition, and perhaps with some external driving or particle sources/injections. Studies of this nature try to understand the evolution of both the wave amplitude (i.e. amplitude amplification and modulation) and the structure in frequency space (i.e. either rising or falling tones, or even more exotic forms such as ‘hooks’). We should point out that the most general definition of WMC includes a variety of spectral forms, including comparatively structureless emissions (sometimes known as ‘hiss-like chorus’; e.g. see Tsurutani & Smith (Reference Tsurutani and Smith1974), Li et al. (Reference Li, Thorne, Bortnik, Tao and Angelopoulos2012), Tsurutani, Lakhina & Verkhoglyadova (Reference Tsurutani, Lakhina and Verkhoglyadova2013), Gao et al. (Reference Gao, Li, Thorne, Bortnik, Angelopoulos, Lu, Tao and Wang2014) and Shumko et al. (Reference Shumko, Turner, O'Brien, Claudepierre, Sample, Hartley, Fennel, Blake, Gkioulidou and Mitchell2018)), as well as the more well known and coherent/structured/‘chirping’ rising and falling tones (Burtis & Helliwell Reference Burtis and Helliwell1976; Koons & Roeder Reference Koons and Roeder1990; Li et al. Reference Li, Thorne, Bortnik, Shprits, Nishimura, Angelopoulos, Chaston, Le Contel and Bonnell2011, Reference Li, Thorne, Bortnik, Tao and Angelopoulos2012; Santolík et al. Reference Santolík, Kletzing, Kurth, Hospodarsky and Bounds2014; Taubenschuss et al. Reference Taubenschuss, Khotyaintsev, Santolík, Vaivads, Cully, Contel and Angelopoulos2014; Teng, Tao & Li Reference Teng, Tao and Li2019). Approaches of this kind usually necessitate some form of ‘self-consistent approach’, in which one ultimately solves some variation of the Vlasov–Maxwell system (Schindler Reference Schindler2007) given a number of constraints. Therefore, one is likely solving first for the influence of unstable particle distributions on waves (Gary Reference Gary1993), and possibly also for subsequent resulting turbulence induced by wave–particle interactions and/or wave–wave interactions (Kadomtsev Reference Kadomtsev1965; Sagdeev & Galeev Reference Sagdeev and Galeev1969).
A number of important open questions remain regarding both of these challenges, and of course the separation into these two contrasting approaches (which for the purposes of this discussion have been crudely polarised as ‘wave effect on particle only’ and ‘wave evolution only’) is an approximation to the complex, dynamic and networked energy pathways of the inner magnetospheric plasma (Jaynes et al. Reference Jaynes, Baker, Singer, Rodriguez, Loto'aniu, Ali, Elkington, Li, Kanekal and Claudepierre2015; Li & Hudson Reference Li and Hudson2019; Ripoll et al. Reference Ripoll, Claudepierre, Ukhorskiy, Colpitts, Li, Fennell and Crabtree2020; Koskinen & Kilpua Reference Koskinen and Kilpua2022). Many works that consider the ‘test-particle’ and ‘self-consistent’ problems consider the fundamental role played by cyclotron resonant interactions (e.g. see Albert, Tao & Bortnik (Reference Albert, Tao and Bortnik2012) and Omura-2021, respectively). In terms of the ‘test-particle’ approach, it is well known that high-amplitude chorus (and indeed other mode) waves can interact with electrons via cyclotron resonance and instigate particle transport that can be described either via quasilinear diffusion coefficients if the background field inhomogeneity is sufficiently large (Albert Reference Albert2010), or else via more complicated descriptions (e.g. see Artemyev et al. Reference Artemyev, Neishtadt, Vasiliev, Zhang, Mourenas and Vainchtein2021; Albert et al. Reference Albert, Artemyev, Li, Gan and Ma2022b, Reference Albert, Artemyev, Li, Gan and Ma2022a; Artemyev et al. Reference Artemyev, Mourenas, Zhang and Vainchtein2022; Bortnik et al. Reference Bortnik, Albert, Artemyev, Li, Jun, Grach and Demekhov2022). In this work we specifically consider the role of the ponderomotive force, and, furthermore, consider influences of both waves on particles, and particles on waves, i.e. a version of the ‘self-consistent’ approach.
There have been a number of thorough recent reviews and discussions of WMC generation and evolution (Gołkowski, Harid & Hosseini Reference Gołkowski, Harid and Hosseini2019; Tao et al. Reference Tao, Zonca, Chen and Wu2020; Omura Reference Omura2021; Tao, Zonca & Chen Reference Tao, Zonca and Chen2021; Zonca, Tao & Chen Reference Zonca, Tao and Chen2021) and so we do not do a complete literature review, instead directing the reader to those references and therein. It suffices to say that the inhomogeneity of the background magnetic field is frequently invoked to play a key role in the chirping mechanism for WMC (Helliwell Reference Helliwell1967; Sudan & Ott Reference Sudan and Ott1971; Nunn Reference Nunn1974; Vomvoridis, Crystal & Denavit Reference Vomvoridis, Crystal and Denavit1982; Trakhtengerts Reference Trakhtengerts1995; Omura et al. Reference Omura, Katoh and Summers2008; Tao et al. Reference Tao, Zonca and Chen2021), facilitating resonant particle trapping, bunching and the formation of ‘resonant currents.’ However there are some proposed mechanisms that do not rely upon the inhomogeneous background to drive the chirping behaviour (Zonca et al. Reference Zonca, Tao and Chen2021; Zonca, Tao & Chen Reference Zonca, Tao and Chen2022), and in particular, we note recent particle-in-cell numerical experiments that demonstrate chirping behaviour within the context of a uniform background magnetic field (Wu et al. (Reference Wu, Tao, Zonca, Chen and Wang2020)). The most significant contribution of this work is to demonstrate the key role that the ponderomotive force, identified in previous theoretical studies of nonlinear WMC evolution (Ganguli et al. Reference Ganguli, Rudakov, Scales, Wang and Mithaiwala2010; Crabtree et al. Reference Crabtree, Rudakov, Ganguli, Mithaiwala, Galinsky and Shevchenko2012; Krafft & Volokitin Reference Krafft and Volokitin2018), plays in driving chirping behaviour in WMC within the context of a homogeneous background field. This phenomenon could now be considered in addition to other aforementioned mechanisms.
In this paper we simultaneously consider the role of wave–particle interactions both on the evolution of WMC and on the particle populations themselves due to ponderomotive forces. We will do so via the theory of modulations and weakly nonlinear theories, through which the evolution of the wave amplitude is coupled to the variations of number density, to observe how the interplay between the two manifests at the onset of nonlinear effects. Ultimately this will build upon the ideas introduced in previous theoretical treatments, and crucially those introduced by Omura et al. (Reference Omura, Katoh and Summers2008) and Omura (Reference Omura2021), which investigated the evolution of WMC given a background particle population, now accounting for the simultaneous evolution of these species alongside the wave motion. However, we reiterate that the derivations presented in this work are limited to the case in which the background magnetic field is infinite and uniform. Therefore, in the context of, for example, the Earth's radiation belts, this implies that the analysis applies close to the geomagnetic equator.
The approach that we take is facilitated by several observations. The first is that coherent WMC waves are known to be narrow banded, with the bandwidth being approximately $10\,\%$![]() of the local gyrofrequency (Santolík et al. Reference Santolík, Gurnett, Pickett, Parrot and Cornilleau-Wehrlin2003; Santolik et al. Reference Santolik, Macusova, Titova, Kozelov, Gurnett, Pickett, Trakhtengerts and Demekhov2008), meaning that one may restrict the study of the dynamics to a single wave mode. Further, the asymptotic picture is simplified further by the observation that the majority of nonlinear generation processes and amplification events occur near-equatorially in the magnetosphere and are confined to very limited latitudes (LeDocq, Gurnett & Hospodarsky Reference LeDocq, Gurnett and Hospodarsky1998; Lauben et al. Reference Lauben, Inan, Bell and Gurnett2002; Meredith et al. Reference Meredith, Horne, Shen, Li and Bortnik2020), meaning it is not unreasonable to restrict ourselves to a fluid system in Cartesian coordinates without latitude considerations and that we are within the remit of weak curvilinear magnetic field effects. Finally, by considering the field-aligned case so that the wavevector ${\boldsymbol k}$
of the local gyrofrequency (Santolík et al. Reference Santolík, Gurnett, Pickett, Parrot and Cornilleau-Wehrlin2003; Santolik et al. Reference Santolik, Macusova, Titova, Kozelov, Gurnett, Pickett, Trakhtengerts and Demekhov2008), meaning that one may restrict the study of the dynamics to a single wave mode. Further, the asymptotic picture is simplified further by the observation that the majority of nonlinear generation processes and amplification events occur near-equatorially in the magnetosphere and are confined to very limited latitudes (LeDocq, Gurnett & Hospodarsky Reference LeDocq, Gurnett and Hospodarsky1998; Lauben et al. Reference Lauben, Inan, Bell and Gurnett2002; Meredith et al. Reference Meredith, Horne, Shen, Li and Bortnik2020), meaning it is not unreasonable to restrict ourselves to a fluid system in Cartesian coordinates without latitude considerations and that we are within the remit of weak curvilinear magnetic field effects. Finally, by considering the field-aligned case so that the wavevector ${\boldsymbol k}$![]() is parallel to the background field, i.e. ${\boldsymbol k} \parallel {\boldsymbol B}_0$
is parallel to the background field, i.e. ${\boldsymbol k} \parallel {\boldsymbol B}_0$![]() ) the reduction procedure is much more straightforward owing to the fact that the Lorentz force due to the wave vanishes. This is because the field-aligned case leads to the wave and the velocity field also being parallel to one another and so for the wave (i.e. perturbed) portion of the motion one has ${\boldsymbol v}\times {\boldsymbol B}={\boldsymbol 0}.$
) the reduction procedure is much more straightforward owing to the fact that the Lorentz force due to the wave vanishes. This is because the field-aligned case leads to the wave and the velocity field also being parallel to one another and so for the wave (i.e. perturbed) portion of the motion one has ${\boldsymbol v}\times {\boldsymbol B}={\boldsymbol 0}.$![]() As a result, the Lorentz force does not generate anything beyond linear terms in an asymptotic theory. A consequence of this is that higher harmonics, that is non-zero integer frequency multiples of the carrier wave (e.g. $\pm 2 \omega, \pm 3 \omega, \ldots$
As a result, the Lorentz force does not generate anything beyond linear terms in an asymptotic theory. A consequence of this is that higher harmonics, that is non-zero integer frequency multiples of the carrier wave (e.g. $\pm 2 \omega, \pm 3 \omega, \ldots$![]() ), do not contribute to the wave motion. Instead, the wave evolution consists of simply the carrier wave interacting with the particle populations, and it is solely the wave–particle interaction via the ponderomotive forces that drives the nonlinearity observed in the wave's evolution.
), do not contribute to the wave motion. Instead, the wave evolution consists of simply the carrier wave interacting with the particle populations, and it is solely the wave–particle interaction via the ponderomotive forces that drives the nonlinearity observed in the wave's evolution.
With these simplifying factors considered, we are able to explore the emergence of wave packets in WMC using two main nonlinear approaches. The first of these is via classical modulation theory (Whitham Reference Whitham2011), which postulates that the parameters of the wave such as the amplitude, frequency and wavenumber all evolve slowly over the course of many wave periods in a similar fashion to classical Wentzel–Kramers–Brillouin (WKB) theory. Such approaches have been successfully used within space plasmas (Mjølhus Reference Mjølhus1976; Gribben & Parkes Reference Gribben and Parkes1977; Mjølhus & Wyller Reference Mjølhus and Wyller1986; Eliasson & Shukla Reference Eliasson and Shukla2005; Omura et al. Reference Omura, Katoh and Summers2008; Tracy et al. Reference Tracy, Brizard, Richardson and Kaufman2014; Omura Reference Omura2021), with the closest related work to this paper considering WMC to deduce the modulation stability of these waves (Tam Reference Tam1969), but with wave–particle interactions not fully accounted for and by use of a simplified version of the dispersion relation. When a similar approach is also utilised for the electron velocity and number density with ponderomotive effects accounted for, we obtain our first insight into the ponderomotive-driven wave–particle interactions influencing WMC modulation. It is these interactions that are influencing the emergence of wave packets through electron-acoustic effects. Ultimately this builds upon the ideas introduced in theoretical treatments of the second approach, crucially those introduced by Omura et al. (Reference Omura, Katoh and Summers2008) and Omura (Reference Omura2021) which investigated the evolution of WMC given a background particle population, and now account for the simultaneous evolution of these species alongside the wave motion.
The second approach is to undertake a formal multiple-scales analysis to derive a direct evolution equation for the spatiotemporal evolution of WMC amplitude, taking the form of the nonlinear Schrödinger (NLS) equation. This equation has emerged from heuristic arguments in prior works (Karpman & Washimi Reference Karpman and Washimi1977; Stenflo, Yu & Shukla Reference Stenflo, Yu and Shukla1986), with the key work of Krafft & Volokitin (Reference Krafft and Volokitin2018) highlighting its emergence within a wave–particle interaction framework. However, one of the results of this paper is to demonstrate that a formal asymptotic procedure reveals that one should be cautious using such approaches due to an inconsistency that emerges in the induction equation, which is overlooked in previous approaches. As a consequence it highlights that the motion of ions, and not just a population that ensures neutrality, must necessarily be considered to resolve this inconsistency, and in doing so we find that these wave–particle interactions are augmented. Our paper demonstrates that although some of the qualitative conclusions of Krafft & Volokitin (Reference Krafft and Volokitin2018) are the same, namely that the group velocity dispersion (by which we mean ${dc_g}/{dk}$![]() ) plays a role in the formation of solitons, the ion number fraction plays a critical role in whether WMC elements are to be observed. Therefore, one of the main conclusions of this work is the statement that ion motion cannot be neglected in such problems.
) plays a role in the formation of solitons, the ion number fraction plays a critical role in whether WMC elements are to be observed. Therefore, one of the main conclusions of this work is the statement that ion motion cannot be neglected in such problems.
With the understanding that arises from the above theoretical approaches, we are then able to augment these ideas within this paper by capturing WMC chirp, the mechanism behind rising and falling tones and one of the most intriguing features of WMC. This phenomenon presents itself as a significant repetitive sweep of the dominant frequency peak of the wave. It is known that the NLS equation does not admit such behaviours and requires higher-order effects to be introduced to account for this behaviour. This is precisely what we obtain as part of this work, extending the multiple-scales analysis we demonstrate from a formal perspective that this process arises from the wave–particle interactions. A surprising consequence of this is that the extended model may provide an explanation for the observed band gap in WMC waves at half the gyrofrequency (Li et al. Reference Li, Bortnik, Thorne and Angelopoulos2011; Fu et al. Reference Fu, Cowee, Friedel, Funsten, Gary, Hospodarsky, Kletzing, Kurth, Larsen and Liu2014; Gao et al. Reference Gao, Chen, Li, Lu and Wang2019; Chen et al. Reference Chen, Gao, Lu, Fan, Ke, Wang and Wang2022) as the terms responsible for frequency variations vanish at precisely this frequency. As such, the theory suggests that sweep rates decrease for waves that approach the band gap before arresting completely. Overall, this analysis provides expressions for the sweep rate of a single WMC element, which demonstrates that within isolation a WMC element/wave packet cannot produce a net change in the frequency of the wave. Instead, it suggests that the chirping behaviour observed originates from the interaction of several WMC elements, which we corroborate with numerical experiments. These produce repetitive WMC tones, and the space–time series demonstrates that their interaction also generates pulsations in the wave envelope which manifest in the particle dynamics as amplifications in the energy density. This, we speculate, may shed light on which stage of their propagation WMC might be energising the electron populations they trap during transit.
The outline of this paper is as follows. We begin with a review of the modulation instability of parallel propagating WMC in § 2, a process entirely driven by the ponderomotive wave–particle interactions, outlining where such waves become unstable and form subpacket structures. Subsequently, we derive evolution equations for the wave envelope of WMC in § 3, leading to a NLS equation and revealing that ions play a crucial role in the envelope dynamics and alter the expected modulational stability transition. Owing to a lack of chirping behaviour, we add correction terms to the NLS that capture such effects in § 4, leading to explicit expressions for chirping within a single element. Finally, we use numerical simulations of this model in § 5 to demonstrate how the interactions between wave packets is the main driver of the chirping seen within the mission data. Concluding remarks are given in § 6.
2. Review: modulation instability of whistler mode waves in electron-only plasmas
To understand the formation of WMC wave packets, we must first analyse the necessary conditions that permit their formation. This is done from the viewpoint of modulation instability, the process under which uniform wave trains destabilise and undergo amplitude modulations, ultimately to form several wave elements as wave energy clusters within packets (Ablowitz & Segur Reference Ablowitz and Segur1981; Chen et al. Reference Chen1984; Billingham & King Reference Billingham and King2000; Treumann & Baumjohann Reference Treumann and Baumjohann2001; Whitham Reference Whitham2011). The approach to identify this instability is to derive quasilinear modulation equations governing the slow evolution of waves, typically amplitude and wavenumber, and determine when this system possesses complex eigenvalues. Quasilinear modulation equations have been derived previously for the wave without particle interaction effects, with notable works relevant to our approach including Tam (Reference Tam1969), Omura et al. (Reference Omura, Katoh and Summers2008) and Omura (Reference Omura2021), but a key extension of this work will be to introduce modulation equations governing the electron number density and parallel velocity. Such effects make a significant difference to the stability transition of the wave and thus it is pertinent to include such evolution simultaneously with the electromagnetic wave.
Throughout this paper, we will be considering collisonless, warm, isothermal plasmas from a fluid description. In the first instance, we will be considering a non-relativistic plasma purely comprising of electrons, neglecting any ion influences for the moment but we note these will be accounted for in later sections. The non-relativistic assumption applies to the fluid velocities $v\ll c$![]() (with $v$
(with $v$![]() the magnitude of the velocity of a given fluid bulk motion), as is standard practice in such domains (Omura Reference Omura2021). Furthermore, the mathematics that follows in this paper that does consider individual particle/kinetic quantities (e.g. the gyrofrequency $\varOmega = |q|B_0/m$
the magnitude of the velocity of a given fluid bulk motion), as is standard practice in such domains (Omura Reference Omura2021). Furthermore, the mathematics that follows in this paper that does consider individual particle/kinetic quantities (e.g. the gyrofrequency $\varOmega = |q|B_0/m$![]() ) does assume non-relativistic particle velocities. This is valid for the non-relativistic particle energies that we consider, for example, electron energies $\le$
) does assume non-relativistic particle velocities. This is valid for the non-relativistic particle energies that we consider, for example, electron energies $\le$![]() 511 keV. Thus, we will be concerned with the following equations of motion:
511 keV. Thus, we will be concerned with the following equations of motion:
In the above, ${\boldsymbol B}$![]() and ${\boldsymbol E}$
and ${\boldsymbol E}$![]() represent the magnetic field and electric field, respectively. The electron velocity field and electron number density, ${\boldsymbol {V}}_e$
represent the magnetic field and electric field, respectively. The electron velocity field and electron number density, ${\boldsymbol {V}}_e$![]() and $n$
and $n$![]() , respectively, are fluid quantities generated from the first two moments of a given distribution function (Chen et al. Reference Chen1984; Baumjohann & Treumann Reference Baumjohann and Treumann2012),
, respectively, are fluid quantities generated from the first two moments of a given distribution function (Chen et al. Reference Chen1984; Baumjohann & Treumann Reference Baumjohann and Treumann2012),
The parameters $q = -e$![]() and $m$
and $m$![]() represent the charge and mass of an electron, $\mu _0$
represent the charge and mass of an electron, $\mu _0$![]() is the magnetic permittivity constant, $c$
is the magnetic permittivity constant, $c$![]() is the speed of light and $c_s^2 = k_BT/m$
is the speed of light and $c_s^2 = k_BT/m$![]() is the speed of sound for the purely electron plasma. The presence of this sound speed, and by virtue the $\boldsymbol {\nabla } n$
is the speed of sound for the purely electron plasma. The presence of this sound speed, and by virtue the $\boldsymbol {\nabla } n$![]() term in the momentum equation, are the result of the warm plasma and isothermal assumptions where $T$
term in the momentum equation, are the result of the warm plasma and isothermal assumptions where $T$![]() is finite (Chen et al. Reference Chen1984). Such terms would be neglected within the cold plasma regime where $T\to 0$
is finite (Chen et al. Reference Chen1984). Such terms would be neglected within the cold plasma regime where $T\to 0$![]() , whereas hot plasmas would be more accurately treated via a kinetic (Vlasov) approach rather than the fluid description of this paper (Chen et al. Reference Chen1984; Baumjohann & Treumann Reference Baumjohann and Treumann2012). The ponderomotive force ${\boldsymbol F}_P$
, whereas hot plasmas would be more accurately treated via a kinetic (Vlasov) approach rather than the fluid description of this paper (Chen et al. Reference Chen1984; Baumjohann & Treumann Reference Baumjohann and Treumann2012). The ponderomotive force ${\boldsymbol F}_P$![]() acting on each electron is given by (see, e.g. Lamb & Morales Reference Lamb and Morales1983; Nicholson Reference Nicholson1983; Chen et al. Reference Chen1984)
acting on each electron is given by (see, e.g. Lamb & Morales Reference Lamb and Morales1983; Nicholson Reference Nicholson1983; Chen et al. Reference Chen1984)
where $\omega _{pe}$![]() is the electron plasma frequency and $\omega$
is the electron plasma frequency and $\omega$![]() is the frequency of the electromagnetic wave. In essence, this force determines the mean drift of electrons over rapid gyrofrequency oscillations due to amplitude modulations emerging within the monochromatic wave train. There are a number of choices one can make for this force depending on the plasma environment (Treumann & Baumjohann Reference Treumann and Baumjohann1997; Krafft & Volokitin Reference Krafft and Volokitin2018), but in this body of work we consider the simplest such force corresponding to the lowest-order ponderomotive effect. This is to illustrate that the presence of such a force, even in its most rudimentary form, is crucial for wave–particle interactions and as a consequence the formation of chorus wave packets and elements.
is the frequency of the electromagnetic wave. In essence, this force determines the mean drift of electrons over rapid gyrofrequency oscillations due to amplitude modulations emerging within the monochromatic wave train. There are a number of choices one can make for this force depending on the plasma environment (Treumann & Baumjohann Reference Treumann and Baumjohann1997; Krafft & Volokitin Reference Krafft and Volokitin2018), but in this body of work we consider the simplest such force corresponding to the lowest-order ponderomotive effect. This is to illustrate that the presence of such a force, even in its most rudimentary form, is crucial for wave–particle interactions and as a consequence the formation of chorus wave packets and elements.
The framework in which this will be achieved is through the use of WKB theory, or equivalently Whitham modulation theory. The starting point for this will be to consider the following Stokes wave ansatz for a wave–particle solution, representing a parallel propagating right polarised wave in the presence of a uniform magnetic field with strength $B_0$![]() :
:

where $z$![]() is in the direction of $\hat {\boldsymbol {z}}$
is in the direction of $\hat {\boldsymbol {z}}$![]() . The parameters $v_{\|}$
. The parameters $v_{\|}$![]() and $n_0$
and $n_0$![]() represent the constant parallel velocity and reference electron number density, respectively.Footnote 1 The constants $\alpha _1, \alpha _2$
represent the constant parallel velocity and reference electron number density, respectively.Footnote 1 The constants $\alpha _1, \alpha _2$![]() characterising the wave modes of the electric and electron velocity, respectively, can be found as part of the linear theory and are explicitly given by
characterising the wave modes of the electric and electron velocity, respectively, can be found as part of the linear theory and are explicitly given by
as detailed in the Appendix (A), where $\varOmega _e = eB_0/m$![]() is the electron charge with $e$
is the electron charge with $e$![]() being the elementary electron charge. The wave amplitude $B_W$
being the elementary electron charge. The wave amplitude $B_W$![]() , mean velocity perturbation $V$
, mean velocity perturbation $V$![]() and number density perturbation $N$
and number density perturbation $N$![]() are initially assumed to be constant but small, so that $|B_W|/B_0\ll 1$
are initially assumed to be constant but small, so that $|B_W|/B_0\ll 1$![]() . Typically one is able to characterise this smallness by comparing linear and leading-order nonlinear terms, which for WMC is achieved by comparing the convective term with the Lorentz force in the momentum equation,
. Typically one is able to characterise this smallness by comparing linear and leading-order nonlinear terms, which for WMC is achieved by comparing the convective term with the Lorentz force in the momentum equation,
where $\phi$![]() is the wave normal angle, that is the angle between the wave and background magnetic field. It follows that this ordering of magnitude is trivially satisfied for any choice of the system parameters for parallel propagating WMC. Thus, there is considerable freedom regarding the magnitude of waves this theory can consider, but must still be small enough to separate linear and nonlinear scales. The expansion procedure requires that $N, V = O(|B_W|^2)$
is the wave normal angle, that is the angle between the wave and background magnetic field. It follows that this ordering of magnitude is trivially satisfied for any choice of the system parameters for parallel propagating WMC. Thus, there is considerable freedom regarding the magnitude of waves this theory can consider, but must still be small enough to separate linear and nonlinear scales. The expansion procedure requires that $N, V = O(|B_W|^2)$![]() , owing to the fact that these oscillation-free terms must balance the oscillation-free terms generated by the ponderomotive force.
, owing to the fact that these oscillation-free terms must balance the oscillation-free terms generated by the ponderomotive force.
The approach is to substitute this ansatz into the governing equations (2.1) and consider terms up to $O(|B_W|^3)$![]() . The details of this calculation can be found within the Appendix (A), but we summarise the key elements of the approach here. The carrier wave terms, when substituted into the governing equations, generate the dispersion relation
. The details of this calculation can be found within the Appendix (A), but we summarise the key elements of the approach here. The carrier wave terms, when substituted into the governing equations, generate the dispersion relation
which vanishes whenever the frequency $\omega = \omega _0(k,v_{\|})$![]() satisfies the typical whistler-mode dispersion curve
satisfies the typical whistler-mode dispersion curve
The presence of the electron velocity within this dispersion relation is a natural consequence of the ansatz, rather than a particular assumption within our fluid approach, and acts like a Doppler shift on the plasma response portion of the dispersion curve. Typically this velocity is ignored within cold non-relativistic plasma fluid theory, which is permissible as $|v_{\|}|\ll c$![]() , as it adds no new physics to the linear wave motion. It is known to have consequences on the nonlinear portion of the motion due to bulk effects (Krafft & Volokitin Reference Krafft and Volokitin2018), as we shall see within our analyses. We will make use of the fact we can neglect the particular value of $v_{\|}$
, as it adds no new physics to the linear wave motion. It is known to have consequences on the nonlinear portion of the motion due to bulk effects (Krafft & Volokitin Reference Krafft and Volokitin2018), as we shall see within our analyses. We will make use of the fact we can neglect the particular value of $v_{\|}$![]() when evaluating later coefficients within the theory of this paper, as the choice of velocity does not meaningfully impact the results of this paper. The theory here may proceed so long as one avoids the choice that leads to the first cyclotron resonance,
when evaluating later coefficients within the theory of this paper, as the choice of velocity does not meaningfully impact the results of this paper. The theory here may proceed so long as one avoids the choice that leads to the first cyclotron resonance,
where alternative treatments are required (Omura et al. Reference Omura, Katoh and Summers2008; Omura Reference Omura2021). By continuing the analysis to higher powers of the amplitude to include amplitude-dependent weakly nonlinear effects, one finds the result

which can be used to extract the nonlinear dispersion relations

These are denoted as nonlinear dispersion relations due to the presence of the wave amplitude, mean velocity and number density variation as corrections to the linear dispersion. To complete our analysis here, we demonstrate the above system can be cast in variational form, to make the subsequent analysis closer to classical wave modulation theory (Whitham Reference Whitham2011). This is done by introducing
with the factor non-vanishing for whistler waves, allowing the system can be written as

The above system of equations is generated by the $\mathscr {B}$![]() and $N$
and $N$![]() variations of Lagrangian density
variations of Lagrangian density

This Lagrangian can be thought of as that which is averaged over one period of the whistler mode wave. It is from this Lagrangian density that we will derive the conditions for the whistler wave to undergo a modulational instability, associated with wave packet generation. Ultimately this will signpost this criterion in the electron case, which we will develop within the more applicable but involved ion–electron plasma case.
2.1. Modulation instability
We may now study the Lagrangian (2.17) to determine when the parallel whistler wave is expected to be stable and remain close to monochromatic. If it is not, it is expected to form packets (also known as elements) and as a result generate larger amplitude events. We do so by appealing to Whitham modulation theory (Whitham Reference Whitham1970, Reference Whitham2011) which has in the past been utilised in plasma contexts for the same purpose (see Mjølhus (Reference Mjølhus1976), Gribben & Parkes (Reference Gribben and Parkes1977) and Mjølhus & Wyller (Reference Mjølhus and Wyller1986) for some key examples). Notably we will be augmenting the existing literature on plasma modulations to account for wave–particle interaction effects, requiring the consideration of an additional phase for the background velocity. The crux of the approach is to introduce the ‘rapid’ wave phase and velocity potential,
This allows the wave parameters $k, \omega, v_{\|}$![]() and $\gamma$
and $\gamma$![]() to vary slowly in space and time,
to vary slowly in space and time,
where subscripts denote partial derivatives with respect to the subscripted variable. This admits the phase consistency conditions
We can replace $\omega$![]() and $\gamma$
and $\gamma$![]() using (2.14) to obtain the first two modulation equations
using (2.14) to obtain the first two modulation equations

The first of these equations is referred to as the conservation of waves, whereas the second is the classical conservation of momentum for the plasma in the presence of the wave. The subsequent two equations, which close the system, come from taking the $\varTheta$![]() and $\varPhi$
and $\varPhi$![]() variations of $\mathscr {L}$
variations of $\mathscr {L}$![]() , which when simplified give
, which when simplified give

These equations represent the conservation of wave action and the conservation of mass, respectively. Thus, the complete modulation system is given by


Before proceeding, it is worth noting the connection between the system derived here and that of the system considered (Omura et al. Reference Omura, Katoh and Summers2008; Omura Reference Omura2021). When the electron fluid responses are neglected (so that $N, \gamma, v_{\|} = 0$![]() ) the system (2.23) reduces to a form that is identical to that of Omura when hot electron and magnetic curvature effects are neglected, consistent with the warm plasma and uniform field assumptions of this paper. Thus, the theory here could be used to extend parts of Omura's quasilinear wave analysis to account for higher-order nonlinear effects and the inherent wave–particle interactions due to ponderomotive effects, essentially taking the form of perturbations to the cold plasma distribution function. However, the aforementioned assumptions of this paper do not permit the formation of the phase space holes necessary to support the formation of rising tones within Omura's work. Instead, the formulation of this paper is a more local, fluid driven analysis focussing on a constant average electron velocity instead of a hot electron distribution. As a consequence, the mechanism which generates rising tones within this paper is of a different nature than that of Omura, but still rooted within wave–particle interactions, and is the subject of later sections within this paper.
) the system (2.23) reduces to a form that is identical to that of Omura when hot electron and magnetic curvature effects are neglected, consistent with the warm plasma and uniform field assumptions of this paper. Thus, the theory here could be used to extend parts of Omura's quasilinear wave analysis to account for higher-order nonlinear effects and the inherent wave–particle interactions due to ponderomotive effects, essentially taking the form of perturbations to the cold plasma distribution function. However, the aforementioned assumptions of this paper do not permit the formation of the phase space holes necessary to support the formation of rising tones within Omura's work. Instead, the formulation of this paper is a more local, fluid driven analysis focussing on a constant average electron velocity instead of a hot electron distribution. As a consequence, the mechanism which generates rising tones within this paper is of a different nature than that of Omura, but still rooted within wave–particle interactions, and is the subject of later sections within this paper.
The four equations in (2.23) can then be written in quasilinear form (Whitham Reference Whitham2011),

This quasilinear system of equations encapsulates the wave–particle interactions for a single wave – the second equation determines how the wave amplitude is modified by the presence of variations to the number density, whilst simultaneously the fourth equation describes how the local number density is altered due to the wave. The remaining equations, the first and third, dictate how the local frequencies and velocity field responds to the wave–particle interaction, respectively, and thus alter the properties of the wave propagation.
These modulation equations for the wave parameters can now be analysed for their stability, which is achieved by investigating small perturbations to some fixed state. We take this constant state to be ${\boldsymbol U}_0 = (k_0,\mathscr {B}_0,0,N_0)$![]() , noting that the choice of velocity does not meaningfully impact the results that follow. By considering perturbations of the form ${\boldsymbol U}={\boldsymbol U}_0+\delta \hat {U} \textrm {e}^{\textrm {i}(Z-CT)}$
, noting that the choice of velocity does not meaningfully impact the results that follow. By considering perturbations of the form ${\boldsymbol U}={\boldsymbol U}_0+\delta \hat {U} \textrm {e}^{\textrm {i}(Z-CT)}$![]() , then the leading-order perturbation is governed by the eigenvalue problem
, then the leading-order perturbation is governed by the eigenvalue problem
The resulting eigenvalues $C$![]() ultimately determine the stability of this system – if they are all real the constant state ${\boldsymbol U}_0$
ultimately determine the stability of this system – if they are all real the constant state ${\boldsymbol U}_0$![]() is stable and the monochromatic wave perseveres; however, when any of these eigenvalues is complex (occurring in complex conjugate pairs) there is an exponentially growing mode that causes the perturbation to rapidly diverge from the monochromatic wave state (Whitham Reference Whitham2011). The emergence of these complex eigenvalues is more commonly referred to as a modulational instability. The characteristic polynomial for this problem admits four roots in general, which can be categorised by their values as $\mathscr {B}_0\,N_0 \to 0$
is stable and the monochromatic wave perseveres; however, when any of these eigenvalues is complex (occurring in complex conjugate pairs) there is an exponentially growing mode that causes the perturbation to rapidly diverge from the monochromatic wave state (Whitham Reference Whitham2011). The emergence of these complex eigenvalues is more commonly referred to as a modulational instability. The characteristic polynomial for this problem admits four roots in general, which can be categorised by their values as $\mathscr {B}_0\,N_0 \to 0$![]() :
:
We focus on the latter set of roots, as it transpires that the eigenvalues associated with the sound speed can be shown to be real but those associated with the group velocity can become complex. This is typical of problems involving waves coupled to a mean field, where it is the wave mode driving the instability(Bridges & Ratliff Reference Bridges and Ratliff2022; Tam Reference Tam1970), and so is not unexpected here either. For this problem, these latter roots can be expanded in powers of $\mathscr {B}_0$![]() and $N_0$
and $N_0$![]() , again assumed small, to give
, again assumed small, to give
where the effective nonlinear frequency correction $\omega _2$![]() is given by
is given by

It is clear that these eigenvalues are complex whenever $\omega _0''\omega _2<0$![]() . To determine when this occurs more readily, we introduce the non-dimensionalscalings
. To determine when this occurs more readily, we introduce the non-dimensionalscalings
giving

The only sign changes that happen within the whistler wave interval $0< W<1$![]() are the roots of $\omega _0''$
are the roots of $\omega _0''$![]() ,
,
which for large $\alpha$![]() typical in the earth's radiation belts approaches $W = \tfrac {1}{4}$
typical in the earth's radiation belts approaches $W = \tfrac {1}{4}$![]() , a quarter of the gyrofrequency. The other sign change is due to the factor $V^2-\nu ^2$
, a quarter of the gyrofrequency. The other sign change is due to the factor $V^2-\nu ^2$![]() passing through zero, which occurs when the whistler wave's group velocity goes from subsonic ($c_g< c_s$
passing through zero, which occurs when the whistler wave's group velocity goes from subsonic ($c_g< c_s$![]() ) to supersonic ($c_g>c_s$
) to supersonic ($c_g>c_s$![]() ). Thus, we have the following criterion for the modulation stability of whistler waves:
). Thus, we have the following criterion for the modulation stability of whistler waves:

This information is summarised in figure 1. It should be noted there are cases where $|V|\sim \nu$![]() where the story is partially more complex and introduces a further stability boundary, but this is not generic and will not be discussed in detail here. As the speed of sound scales linearly with temperature within the setting considered, we can infer that the supersonic case is more prevalent in cold plasmas, with the subsonic case being expected in warmer plasmas. However, some caution should be noted here as the isothermal approximation is known to be poorer for warmer plasmas (Li et al. Reference Li, Thorne, Nishimura, Bortnik, Angelopoulos, McFadden, Larson, Bonnell, Le Contel and Roux2010; Chen et al. Reference Chen, Li, Bortnik and Thorne2012; Gao et al. Reference Gao, Li, Thorne, Bortnik, Angelopoulos, Lu, Tao and Wang2014), so a more technical theory to confidently conclude anything regarding this limit.
where the story is partially more complex and introduces a further stability boundary, but this is not generic and will not be discussed in detail here. As the speed of sound scales linearly with temperature within the setting considered, we can infer that the supersonic case is more prevalent in cold plasmas, with the subsonic case being expected in warmer plasmas. However, some caution should be noted here as the isothermal approximation is known to be poorer for warmer plasmas (Li et al. Reference Li, Thorne, Nishimura, Bortnik, Angelopoulos, McFadden, Larson, Bonnell, Le Contel and Roux2010; Chen et al. Reference Chen, Li, Bortnik and Thorne2012; Gao et al. Reference Gao, Li, Thorne, Bortnik, Angelopoulos, Lu, Tao and Wang2014), so a more technical theory to confidently conclude anything regarding this limit.

Figure 1. Signs of the right-hand side term in blue and instability in red for parallel propagating whistler waves for subsonic (a) and supersonic (b) waves. The dashed line marks the asymptote $\omega = {\varOmega _e}/{4}$![]() .
.
In summary, we have used classical modulation theory to explore the stability of monochromatic WMC waves with the additional consideration of the particle effects. A criterion for modulation instability, associated with the formation of wave packets, is deduced by exploring the nature of the eigenvalues of the $4\times 4$![]() quasilinear system (2.24), revealing both the group velocity dispersion $\omega _0''$
quasilinear system (2.24), revealing both the group velocity dispersion $\omega _0''$![]() and the difference between the squares of the group and sound speed $c_g^2-c_s^2$
and the difference between the squares of the group and sound speed $c_g^2-c_s^2$![]() . This identifies where one should look for the subelement structures typical of WMC waves, and the analysis of their evolution forms the remainder of this paper. To do so we will rely on the classical perturbative approach for the evolution of the wave envelope which we derive in the next section.
. This identifies where one should look for the subelement structures typical of WMC waves, and the analysis of their evolution forms the remainder of this paper. To do so we will rely on the classical perturbative approach for the evolution of the wave envelope which we derive in the next section.
3. Ion effects and packet generation
The classical Whitham modulation approach of the previous section grants us insight into the criteria necessary for WMC waves to develop into packets. It is the case, however, that to formally derive an equation for the spatiotemporal evolution of these packets one must also include the effects of ions within the analysis. It is not a priori obvious that this is necessary, especially as their role is greatly overshadowed by effects due to electron motion, but this analysis will highlight those ionic features, particularly the number fraction of ions present in the plasma, which have a crucial role in the modulation stability of WMC.
With ion motions included, we will consider the two-fluid plasma description (Baumjohann & Treumann Reference Baumjohann and Treumann2012) with the assumption of isothermality for each particle species. This gives the system of equations
where the subscripts $i, e$![]() denote fields and quantities which describe the ion and electron populations, respectively. The ponderomotive forces for each species will be taken as
denote fields and quantities which describe the ion and electron populations, respectively. The ponderomotive forces for each species will be taken as
The ponderomotive force for the ion equation is of the same form as the electron, which can be obtained by following the derivation in Chen et al. (Reference Chen1984). As in the purely electron case, alternate forms of this force may be supplied instead but this primary form of the ponderomotive force captures the essence of the wave–particle interaction. For the spatiotemporal analysis, we will undertake a formal weakly nonlinear analysis in the small parameter $\varepsilon \ll 1$![]() . This parameter is a characterisation of the wave amplitude, which in turn determines the strength of the nonlinear effects. Following typical amplitude equation approaches, we postulate the following expansions:
. This parameter is a characterisation of the wave amplitude, which in turn determines the strength of the nonlinear effects. Following typical amplitude equation approaches, we postulate the following expansions:

where the slow variables $Z$![]() and $T$
and $T$![]() , encoding two time scales, are defined as
, encoding two time scales, are defined as
whose scalings are chosen so that the terms of the derived evolution equation are all of the same order in $\varepsilon$![]() . The smallness of the parameter $\varepsilon$
. The smallness of the parameter $\varepsilon$![]() is once again determined by the separation between linear and nonlinear scales, and following a similar calculation as that in § 2, one finds that $\varepsilon$
is once again determined by the separation between linear and nonlinear scales, and following a similar calculation as that in § 2, one finds that $\varepsilon$![]() must satisfy the ordering
must satisfy the ordering
which for field-aligned WMC with a velocity parallel to the magnetic field is automatic, as $\sin \phi =0$![]() . Such scalings are typical within weakly nonlinear theories describing spatiotemporal amplitude evolution and ultimately indicate that the evolution equation for the amplitude is of NLS type. Indeed, substitution of the above expansions into the governing equations and solving the resulting problems at each order of $\varepsilon$
. Such scalings are typical within weakly nonlinear theories describing spatiotemporal amplitude evolution and ultimately indicate that the evolution equation for the amplitude is of NLS type. Indeed, substitution of the above expansions into the governing equations and solving the resulting problems at each order of $\varepsilon$![]() confirm this, as we will outline below.
confirm this, as we will outline below.
At leading order, $O(\varepsilon )$![]() , we find that $\omega,k$
, we find that $\omega,k$![]() satisfy the relation
satisfy the relation

which has a root corresponding to the whistler dispersion relation

Waves along this dispersion branch require that
The next order of the analysis generates both first-harmonic and zero-harmonic terms. The former of these may be solved to show that $\beta _1 = 0$![]() and
and

The first of the zero-harmonic (i.e. oscillation-free) problems arises from (3.2) and is simply
This is to say that the parallel propagating wave does not induce an additional current at this order of the analysis. The second arises from (3.7) and gives that
which is equivalent to quasineutrality holding in the presence of slow deviations. This allows one to write the electron number density variations according to
where $\mathcal {Z}_c$![]() is the ion charge number. Both of the conditions (3.16) and (3.17) highlight the importance of ionic effects, as without the ionic contribution this equation would necessarily yield that $N_e, V_e$
is the ion charge number. Both of the conditions (3.16) and (3.17) highlight the importance of ionic effects, as without the ionic contribution this equation would necessarily yield that $N_e, V_e$![]() must vanish and lead to no nonlinear effects emerging from the weakly nonlinear analysis. Thus,this order makes it clear that ionic effects must be included in the study of the multiple scale WMC evolution and should not be neglected.
must vanish and lead to no nonlinear effects emerging from the weakly nonlinear analysis. Thus,this order makes it clear that ionic effects must be included in the study of the multiple scale WMC evolution and should not be neglected.
The problem at $O(\varepsilon ^3)$![]() is where the analysis terminates, and only the first harmonic and zero-harmonic terms need to be considered to develop the evolution equation that results here. The zero-harmonic terms are more involved at this order, and these read
is where the analysis terminates, and only the first harmonic and zero-harmonic terms need to be considered to develop the evolution equation that results here. The zero-harmonic terms are more involved at this order, and these read

where primes denote derivatives with respect to $Z$![]() . We may use equation (3.16) to show that, if we add $q_e$
. We may use equation (3.16) to show that, if we add $q_e$![]() times the first equation of (3.19) to $q_i$
times the first equation of (3.19) to $q_i$![]() times the second of (3.19), we necessarily have that
times the second of (3.19), we necessarily have that
From (3.17) we can see that it follows that this constant is zero. We will recast the system (3.19) by taking the third equation of (3.19) and subtracting ${q_i}/{q_e} = -\mathcal {Z}_c$![]() times the fourth. Overall, this gives that
times the fourth. Overall, this gives that

This system of equations can be inverted to show that the modulation of the mean particle quantities are related to the carrier wave by

The arbitrary functions resulting from the integration have been ignored here, as these simply correspond to a shift in the frequency of the carrier wave which evolves much more slowly than the envelope.
At $O(\varepsilon ^3)$![]() , we require that all terms proportional to the first harmonic vanish, else the analysis will generate secular terms. It can be shown that in order to do so, the amplitude $B_W$
, we require that all terms proportional to the first harmonic vanish, else the analysis will generate secular terms. It can be shown that in order to do so, the amplitude $B_W$![]() must satisfy the following NLS equation:
must satisfy the following NLS equation:
where the nonlinear frequency correction $\varGamma$![]() is given by
is given by

We conclude our formal derivation with a few marks about the validity and limitations of the above model. Primarily we expect the NLS equation above to be a good representation whenever the variations in the wave amplitude occur over scales much larger than the wave period, which is to say that the model is representative whenever the typical packet contains many waves. Observation from the Van Allen Probes and THEMIS mission support this being typical of WMC (Zhang et al. Reference Zhang, Mourenas, Artemyev, Angelopoulos, Bortnik, Thorne, Kurth, Kletzing and Hospodarsky2019; Artemyev et al. Reference Artemyev, Mourenas, Zhang and Vainchtein2022). It is also known that such envelope models are valid for evolution times up to $O(\varepsilon ^{-2})$![]() , so one can expect much longer predictions for lower amplitude packets. However, nonlinear events in WMC typically happen on scales of less than a second (Santolik et al. Reference Santolik, Macusova, Titova, Kozelov, Gurnett, Pickett, Trakhtengerts and Demekhov2008), with the most repetitive emissions taking place within windows of several seconds (Gao et al. Reference Gao, Chen, Lu, Chen, Chen and Wang2022), suggesting that these events lie within the time span of model validity. Finally a consequence of the scalings of the moving coordinate we have a narrow spectrum requirement of $|k-\delta k|, |\omega - \delta \omega | \sim O(\varepsilon )$
, so one can expect much longer predictions for lower amplitude packets. However, nonlinear events in WMC typically happen on scales of less than a second (Santolik et al. Reference Santolik, Macusova, Titova, Kozelov, Gurnett, Pickett, Trakhtengerts and Demekhov2008), with the most repetitive emissions taking place within windows of several seconds (Gao et al. Reference Gao, Chen, Lu, Chen, Chen and Wang2022), suggesting that these events lie within the time span of model validity. Finally a consequence of the scalings of the moving coordinate we have a narrow spectrum requirement of $|k-\delta k|, |\omega - \delta \omega | \sim O(\varepsilon )$![]() , where $\delta k, \delta \omega$
, where $\delta k, \delta \omega$![]() represent the wavenumber and frequency associated with the amplitude $B_W$
represent the wavenumber and frequency associated with the amplitude $B_W$![]() , a constraint that mission data suggests WMC satisfies (Santolík et al. Reference Santolík, Gurnett, Pickett, Parrot and Cornilleau-Wehrlin2003; Santolik et al. Reference Santolik, Macusova, Titova, Kozelov, Gurnett, Pickett, Trakhtengerts and Demekhov2008).
, a constraint that mission data suggests WMC satisfies (Santolík et al. Reference Santolík, Gurnett, Pickett, Parrot and Cornilleau-Wehrlin2003; Santolik et al. Reference Santolik, Macusova, Titova, Kozelov, Gurnett, Pickett, Trakhtengerts and Demekhov2008).
3.1. Influence of ions on modulation stability
In order to analyse the modulation instability of whistler mode waves, we will again non-dimensionalise the wave quantities according to (2.29a–e), and introduce the further non-dimensionalisations
Additionally, to simplify the analysis in the first instance, we will choose that $v_{\|} = u_{\|} = 0$![]() . We note that the parameter $r$
. We note that the parameter $r$![]() is typically small, with its largest value occurring for hydrogen ions where it takes the value $r = \tfrac {1}{1836}$
is typically small, with its largest value occurring for hydrogen ions where it takes the value $r = \tfrac {1}{1836}$![]() . Thus, we treat $r \ll 1$
. Thus, we treat $r \ll 1$![]() . This simplifies the coefficients of the NLS (3.23) to
. This simplifies the coefficients of the NLS (3.23) to

In addition, our perturbations to the electron number $N_i$![]() and their velocity characterised by $\alpha _4, V_i$
and their velocity characterised by $\alpha _4, V_i$![]() become, in this limit,
become, in this limit,

It becomes clear that although the vast majority of effects due to ions characterised by $r$![]() vanish, save for the zero harmonic/bulk variations, more or less recovering the modulation instability criterion of the electron-only plasma presented in § 2.1. There is, however, a non-negligible ion effect that is crucial in the expression for $\varDelta$
vanish, save for the zero harmonic/bulk variations, more or less recovering the modulation instability criterion of the electron-only plasma presented in § 2.1. There is, however, a non-negligible ion effect that is crucial in the expression for $\varDelta$![]() associated with the subsonic to supersonic wave transition. The remaining expression involving the ion number density now controls one of the stability boundaries for the whistler waves, as was demonstrated in § 2. This expression indicates that the proportion of ions present in the plasma directly alter this boundary, and so the supersonic and subsonic regimes are altered to transition at ratios that can be much lower than unity; this is since
associated with the subsonic to supersonic wave transition. The remaining expression involving the ion number density now controls one of the stability boundaries for the whistler waves, as was demonstrated in § 2. This expression indicates that the proportion of ions present in the plasma directly alter this boundary, and so the supersonic and subsonic regimes are altered to transition at ratios that can be much lower than unity; this is since
Further, in the limit as $\eta _i\to 0$![]() where the electron fluid (i.e. static electrons) description is expected to be employed, one finds that the sound speed term is eliminated and only the supersonic case is operational, suggesting that parallel WMC would only rise in tone and parallel falling tones are expected to be non-existent in this regime. This is in strong agreement with the mission data on parallel WMC waves, where rising tones are closely aligned with the magnetic field whereas falling tones are to be expected nearly orthogonal to it (Taubenschuss et al. Reference Taubenschuss, Khotyaintsev, Santolík, Vaivads, Cully, Contel and Angelopoulos2014; Teng et al. Reference Teng, Tao and Li2019). We make this inference primarily based on the location of the region within which the wave is stable; however, dynamically speaking we do not have a term which dictates the movement of the main spectral peak in frequency space. The NLS will need to be extended in order to accommodate such terms and test part of this hypothesis, which is precisely the aim of the next section of our analysis.
where the electron fluid (i.e. static electrons) description is expected to be employed, one finds that the sound speed term is eliminated and only the supersonic case is operational, suggesting that parallel WMC would only rise in tone and parallel falling tones are expected to be non-existent in this regime. This is in strong agreement with the mission data on parallel WMC waves, where rising tones are closely aligned with the magnetic field whereas falling tones are to be expected nearly orthogonal to it (Taubenschuss et al. Reference Taubenschuss, Khotyaintsev, Santolík, Vaivads, Cully, Contel and Angelopoulos2014; Teng et al. Reference Teng, Tao and Li2019). We make this inference primarily based on the location of the region within which the wave is stable; however, dynamically speaking we do not have a term which dictates the movement of the main spectral peak in frequency space. The NLS will need to be extended in order to accommodate such terms and test part of this hypothesis, which is precisely the aim of the next section of our analysis.
4. Spectral asymmetry and the emergence of chirp
It is known that NLS models do not admit chirping behaviour for monochromatic waves or wave packets (see, for example, the standard textbooks Ablowitz & Segur (Reference Ablowitz and Segur1981), Agrawal (Reference Agrawal2000) and Billingham & King (Reference Billingham and King2000) on the subject). This owes to the fact that the growth of sidebands due to modulation instability are symmetric and thus it has no preferred spectral shift. This limits the effect of the NLS solutions on the original carrier wave to simply a constant, time-independent frequency shift. To break this spectral symmetry, it is necessary to appeal to higher-order effects within the weakly nonlinear theory that induce self-frequency shifting as has been explored in optics (Palacios et al. Reference Palacios, Guinea, Fernandez-Diaz and Crespo1999; Goyal et al. Reference Goyal, Gupta, Kumar and Raju2011; Triki et al. Reference Triki, Porsezian, Choudhuri and Dinda2016, Reference Triki, Sun, Biswas, Zhou, Yıldırım, Zhong and Alshehri2022).
We return our discussion to the approach outlined in § 3. To obtain these higher-order effects, it is necessary to analyse the contributions from the first-harmonic terms at $O(\varepsilon )$![]() . The terms these generate are then included into the NLS equation (3.23) and treated as correction terms (as these are, strictly speaking, of a lower order than the original terms). The result of doing this for parallel propagating whistlers is the modified NLS equation
. The terms these generate are then included into the NLS equation (3.23) and treated as correction terms (as these are, strictly speaking, of a lower order than the original terms). The result of doing this for parallel propagating whistlers is the modified NLS equation
where the additional nonlinear correction has coefficient

We now demonstrate how this additional term alters the growth of sidebands due to a modulation instability. This may be investigated by perturbing the Stokes wave solution, an exact monochromatic wave train solution to this amplitude equation, by
for Stokes wave amplitude $A$![]() , sideband wavenumber $\delta k$
, sideband wavenumber $\delta k$![]() and $P$
and $P$![]() is a perturbation assumed small enough that quadratic terms in it are negligible. Upon substitution, it can be shown that the perturbation $P$
is a perturbation assumed small enough that quadratic terms in it are negligible. Upon substitution, it can be shown that the perturbation $P$![]() admits the linear spectrum
admits the linear spectrum
and thus there is a band of spectral wavenumbers $\kappa$![]() which generates perturbations that grow in time whenever
which generates perturbations that grow in time whenever
We can see that the modulation criterion $\omega _0''\varGamma <0$![]() may persist if the bracketed expression is positive. This is ensured even if $\delta k>0$
may persist if the bracketed expression is positive. This is ensured even if $\delta k>0$![]() as for parameter ranges operational in the magnetosphere one has $\varepsilon Q/\varGamma \ll 1$
as for parameter ranges operational in the magnetosphere one has $\varepsilon Q/\varGamma \ll 1$![]() , and so $\delta k$
, and so $\delta k$![]() must be significantly large in order to do so which would violate the assumptions used to derive (4.1). Thus, the modulational instability has exactly the same thresholds as the NLS equation. The asymmetry in the wavenumber spectrum can then be determined by studying the maximum growth rate for the perturbed Stokes wave. This can be calculated as
must be significantly large in order to do so which would violate the assumptions used to derive (4.1). Thus, the modulational instability has exactly the same thresholds as the NLS equation. The asymmetry in the wavenumber spectrum can then be determined by studying the maximum growth rate for the perturbed Stokes wave. This can be calculated as

It is apparent now that the sideband wavenumber $\delta k$![]() introduces bias to one side of the spectrum via this higher-order term characterised by $Q$
introduces bias to one side of the spectrum via this higher-order term characterised by $Q$![]() . This is determined by the sign of $Q$
. This is determined by the sign of $Q$![]() , which like $\varGamma$
, which like $\varGamma$![]() is determined by the factor $\varDelta$
is determined by the factor $\varDelta$![]() . Thus, terms with a lower sideband wavenumber will grow at a faster rate than their upper sideband counterpart. What happens subsequently cannot be inferred by this linear stability analysis, and requires further nonlinear approaches that we will not consider here.
. Thus, terms with a lower sideband wavenumber will grow at a faster rate than their upper sideband counterpart. What happens subsequently cannot be inferred by this linear stability analysis, and requires further nonlinear approaches that we will not consider here.
This observation is the first hint that this higher-order term will be the driver of the chirping behaviour that we seek to understand. We will continue to explore this extended NLS equation from the perspective of nonlinear wave packets, the structures observed within WMC waves that ultimately generate the rising and falling tones we are interested in understanding. These structures will be derived and explored analytically and numerically in later parts of this section to explore how these may encourage a similar spectral asymmetry in WMC waves.
4.1. Emergence of the band gap
Of significant note within this weakly nonlinear theory, when accounting for the higher-order terms, is that the classical band gap at half the gyrofrequency is a natural consequence. We can identify this by using the non-dimensionalisations (2.29a–e) and (3.25), where $r \ll 1$![]() , to simplify the coefficient of the term responsible for chirping to
, to simplify the coefficient of the term responsible for chirping to
In this limit there is clearly a root of $Q$![]() at $W = \tfrac {1}{2}$
at $W = \tfrac {1}{2}$![]() , namely $\omega = \varOmega _e/2$
, namely $\omega = \varOmega _e/2$![]() , which is at the typical band-gap for WMC waves. The only other sign change of $Q$
, which is at the typical band-gap for WMC waves. The only other sign change of $Q$![]() is determined by $\varDelta$
is determined by $\varDelta$![]() (which ultimately leads to a breakdown of the weakly nonlinear theory as a whole) as the remaining factors result in a positive definite quantity in the lower band WMC range $0< W\leq \tfrac {1}{2}$
(which ultimately leads to a breakdown of the weakly nonlinear theory as a whole) as the remaining factors result in a positive definite quantity in the lower band WMC range $0< W\leq \tfrac {1}{2}$![]() .
.
This observation of this root of $Q$![]() at $W=\tfrac {1}{2}$
at $W=\tfrac {1}{2}$![]() is an important one. It demonstrates that at half the gyrofrequency the amplitude evolution equations once again reduce to the NLS equation, so the wave mode neither biases a rise or fall in the frequency. Thus, there is no emergent sweep rate for waves at this frequency, and it is clear that waves with frequencies close to this band gap will have very weak sweep rates too. Overall, this observation suggests that a WMC element that rises or falls in frequency will have its sweep rate continuously reduced as its spectral peak approaches this band gap until the wave becomes incoherent or its energy is exchanged with another wave of a different frequency.
is an important one. It demonstrates that at half the gyrofrequency the amplitude evolution equations once again reduce to the NLS equation, so the wave mode neither biases a rise or fall in the frequency. Thus, there is no emergent sweep rate for waves at this frequency, and it is clear that waves with frequencies close to this band gap will have very weak sweep rates too. Overall, this observation suggests that a WMC element that rises or falls in frequency will have its sweep rate continuously reduced as its spectral peak approaches this band gap until the wave becomes incoherent or its energy is exchanged with another wave of a different frequency.
Unfortunately, the narrow-band picture of the nonlinear theory is insufficient to fully test this hypothesis. For energy exchanges between different frequencies and how the wave responds, a multimode interaction system is required in the spirit of either a coupled NLS/Manakov system (Manakov Reference Manakov1974; Kourakis, Shukla & Morfill Reference Kourakis, Shukla and Morfill2005b,Reference Kourakis, Shukla and Morfilla; Baronio et al. Reference Baronio, Degasperis, Conforti and Wabnitz2012) or a Zakharov/wave turbulence model (Galtier et al. Reference Galtier, Nazarenko, Newell and Pouquet2000; Newell & Rumpf Reference Newell and Rumpf2011; David & Galtier Reference David and Galtier2022), both much more complex dynamical models. Therefore, a full validation of this continual sweep rate reduction postulation is reserved for later study. We, however, note that the former of these extensions is essentially a coupled system of NLS-like equations and will retain many of the coefficients derived in this paper, and thus the argument regarding an arrested sweep rate in the proximity of the band gap we hypothesise to hold true.
4.2. Wave packets with chirp
Now that we have a modification to the NLS, as well as some insight into how chirp might come about for sidebands, let us formally derive a solution for a chorus element that undergoes chirping. To do so, we follow Dias & Iooss (Reference Dias and Iooss1993) and consider a solution of (4.1) of the form
which is formed of three parts – the amplitude function $R$![]() , the sideband wave component represented by the second term and a phase function $\phi$
, the sideband wave component represented by the second term and a phase function $\phi$![]() , which will ultimately be the source of chirp. This is because the local frequency of this solution can be defined as the negative of time derivative of the total phase function,
, which will ultimately be the source of chirp. This is because the local frequency of this solution can be defined as the negative of time derivative of the total phase function,
From this one may identify a sweep rate, defined as the rate of change of the frequency in time,
Our aim is to relate this sweep rate with properties of the wave packet solution to determine the resulting frequency change, which is achieved though substitution of this ansatz into (4.1) and solve the resulting ordinary differential equations (ODEs).
Starting with our guess at a solution, and splitting the resultant system into real and imaginary parts, we have the equations
We start by taking the second equation, (4.12), and multiplying by $R$![]() , which makes it an exact derivative. Integrating gives
, which makes it an exact derivative. Integrating gives
for some constant $I$![]() . It will be convenient herein to introduce $U = R^2>0$
. It will be convenient herein to introduce $U = R^2>0$![]() , and note that for solitary wave packets one must have that $U,U'$
, and note that for solitary wave packets one must have that $U,U'$![]() and $U''$
and $U''$![]() tend to zero as $\xi \to \pm \infty$
tend to zero as $\xi \to \pm \infty$![]() . This yields that $I=0$
. This yields that $I=0$![]() and allows one to manipulate (4.13) to show that the sweep rate $\mathscr {S}$
and allows one to manipulate (4.13) to show that the sweep rate $\mathscr {S}$![]() is
is
In modulationally unstable regions, this prefactor is negative, meaning that a positive sweep rate occurs when $U'>0$![]() , i.e. at points where the envelope of an element is increasing.
, i.e. at points where the envelope of an element is increasing.
We conclude the discussion here with an exact solution describing the envelope of a single whistler packet/element. To do so, we note that we can set $\nu = 0$![]() to simplify the analysis, and it can be reintroduced under suitable mappings. In this case, we get a quartic potential,
to simplify the analysis, and it can be reintroduced under suitable mappings. In this case, we get a quartic potential,
with
A homoclinic connection (that is a trajectory that begins and terminates at the same fixed point) within this system, corresponding to a solitary wave solution is only possible so long as there is an interval for which $\mathscr {V}(U)>0$![]() . As $B_4>0$
. As $B_4>0$![]() , we need $B_2<0$
, we need $B_2<0$![]() and so
and so
Since $\sigma$![]() is a free real-valued parameter, this is always possible to satisfy. Following Kamchatnov et al. (Reference Kamchatnov, Kuo, Lin, Horng, Gou, Clift, El and Grimshaw2012) let us factorise this ODE as follows:
is a free real-valued parameter, this is always possible to satisfy. Following Kamchatnov et al. (Reference Kamchatnov, Kuo, Lin, Horng, Gou, Clift, El and Grimshaw2012) let us factorise this ODE as follows:
where the roots are given by

The negative subscript denotes the negative root, and plus the positive root, so that $U_-<0< U_+$![]() . Thus, the expression in (4.18) under the square root is positive in the interval $U_-< U< U_+$
. Thus, the expression in (4.18) under the square root is positive in the interval $U_-< U< U_+$![]() , but as $U = R^2>0$
, but as $U = R^2>0$![]() the only interval of interest to us will be $0\leq U< U_+$
the only interval of interest to us will be $0\leq U< U_+$![]() . The solution to this ODE is of the form of a Gardner/extended Korteweg–de Vries soliton (Grimshaw et al. Reference Grimshaw, Pelinovsky, Talipova and Kurkina2010; Kamchatnov et al. Reference Kamchatnov, Kuo, Lin, Horng, Gou, Clift, El and Grimshaw2012),
. The solution to this ODE is of the form of a Gardner/extended Korteweg–de Vries soliton (Grimshaw et al. Reference Grimshaw, Pelinovsky, Talipova and Kurkina2010; Kamchatnov et al. Reference Kamchatnov, Kuo, Lin, Horng, Gou, Clift, El and Grimshaw2012),
with

and so the amplitude of this wave packet is $A/B = U_+$![]() .
.
In summary, by considering higher-order terms in the amplitude model we find that these terms are the source of chirping behaviour in both monochromatic wave trains and within wave packets. In the case of the latter, however, we can observe that there is no net shift in the frequency due to the symmetry of the packet. Chirping due to WMC elements would appear to arise, therefore, upon packet interaction as this leads to asymmetry within the wave envelope and thus generates a net frequency shift. This is now explored using numerical means, where we will generate multiple packets, observe their interactions and extract their frequency spectrum to deduce the overall chirp produced by their interplay.
5. Numerical simulation of interacting whistler mode elements
It is clear from the available spacecraft mission data that whistler and chorus wave packets are rarely isolated and propagate in groups of multiple packets. As a result, these packets interact and cause changes to their frequency and amplitude that the above insight of a solitary packet cannot provide. To investigate these interactions, we resort solving (4.1) using a time stepping procedure. For computational ease and to better identify the effects of system parameters on the sweep rate, we rescale (4.1), highlighting two cases dependant on the sign of $\omega _0''$![]() . We employ the scalings
. We employ the scalings

to transform (4.1) into
This reduces the problem to a single tuneable parameter, which we can see from the non-dimensionalisations earlier that
thus reducing the tuneable parameters to just $\varepsilon, W, \varOmega$![]() (or equivalently, $B_0$
(or equivalently, $B_0$![]() ) and $\alpha$
) and $\alpha$![]() which are determined by the plasma environment. For the majority of our simulations we will be using parameter choices representative of those found at $L$
which are determined by the plasma environment. For the majority of our simulations we will be using parameter choices representative of those found at $L$![]() -shell $L\sim 6$
-shell $L\sim 6$![]() . This corresponds to
. This corresponds to
In addition to this, we focus on wave frequencies lying in the lower frequency band range of $0.1 \varOmega$![]() –$0.5\varOmega$
–$0.5\varOmega$![]() .
.
We advance (5.2) in time using an exponential time differencing method with fourth-order Runge–Kutta time stepping (ETDRK4) (Cox & Matthews Reference Cox and Matthews2002; Kassam & Trefethen Reference Kassam and Trefethen2005), using periodic boundary conditions to take advantage of the speed and spectral accuracy of Fourier-based schemes. To initialise a multielement solution and remain close to the analytic solution found, we initialise the simulations with the wave packet

which has amplitude ${1}/({A_0-1})$![]() , width $\varLambda$
, width $\varLambda$![]() and sideband wavenumber $p$
and sideband wavenumber $p$![]() . The width of these has to be suitably large (of the order $10$
. The width of these has to be suitably large (of the order $10$![]() ) in order to generate multiple packets, with smaller $\varLambda$
) in order to generate multiple packets, with smaller $\varLambda$![]() recovering a single wave packet with small amplitude wave radiation and larger widths generating many packets that partially fission before interaction. In our simulations, we allow this initial profile to evolve and we then observe the dynamics of this fissioned structure in time to determine how the emergent wave packets interact with each other and the resulting Fourier spectrum.
recovering a single wave packet with small amplitude wave radiation and larger widths generating many packets that partially fission before interaction. In our simulations, we allow this initial profile to evolve and we then observe the dynamics of this fissioned structure in time to determine how the emergent wave packets interact with each other and the resulting Fourier spectrum.
The result of simulating (5.2) yields wave packets that generate frequency sweeps, with examples appearing in figure 2. These emerge after the initial packet begins to split and interact with the new subelements, and develop further as the packets separate. This separation drives an envelope asymmetry, which from our observations in (4.14) would appear to be the source for the frequency sweeps that emerge numerically. The sweep rate decreases over each simulation, as the subelements grow farther apart, further reinforcing that it is the packet interactions that are the source of rising tones. We find over the course of our numerical investigations that higher magnitude of the ratio in (5.3) enhance the onset of frequency sweeping, which further points to the role that the modified term in the NLS plays in generating frequency shifts in the WMC waves.

Figure 2. Examples of the power spectrum $|B_W|^2/\delta \omega$![]() generated by the parameter choices $(\varepsilon,n_e,\alpha,\varOmega ) = (4\times 10^{-5},1\times 10^7,7.2,2.49\times 10^4)$
generated by the parameter choices $(\varepsilon,n_e,\alpha,\varOmega ) = (4\times 10^{-5},1\times 10^7,7.2,2.49\times 10^4)$![]() and (a) $W=0.2, k_BT =8.02$
and (a) $W=0.2, k_BT =8.02$![]() KeV, (b) $W= 0.35, k_BT =7.37$
KeV, (b) $W= 0.35, k_BT =7.37$![]() KeV.
KeV.
It is worth commenting on the contrast between the simulations here and the more conventional studies using particle-in-cell simulations. These have demonstrated chorus wave frequency chirping in a one-dimensional uniform field, but using reflective boundary conditions for particles and open boundary conditions for electromagnetic waves (Wu et al. Reference Wu, Tao, Zonca, Chen and Wang2020). In that work, the open boundary conditions for the waves facilitate the chirping behaviour in the sense that they allow electromagnetic perturbations to leave the domain and so not to return and interfere with the spatially localised wave–particle interaction that is creating the chirp. The mathematical analysis that is presented in this work is based on the assumption of an infinite uniform plasma in a uniform background magnetic field, and we employ periodic boundary conditions for all quantities in our numerical experiments. However, our experiments still permit the chirping mechanism to be fully local/isolated in the same way as the work by Wu et al. (Reference Wu, Tao, Zonca, Chen and Wang2020), since the spatial dimensions of the domain $[0\le x < L]$![]() are sufficiently large that the relevant phase and group velocities do not traverse a full box-length $L$
are sufficiently large that the relevant phase and group velocities do not traverse a full box-length $L$![]() over the time scale of chirping events and indeed the whole numerical experiment. This is to say that $v_{g}\ll LT^{-1} , L \omega ^{-1}\,\textrm {d}\omega /\textrm{d}t$
over the time scale of chirping events and indeed the whole numerical experiment. This is to say that $v_{g}\ll LT^{-1} , L \omega ^{-1}\,\textrm {d}\omega /\textrm{d}t$![]() . Furthermore, the paper by Wu et al. (Reference Wu, Tao, Zonca, Chen and Wang2020) demonstrates that in their regime, it is the background non-uniformity that establishes a symmetry breaking in order to preferentially permit either rising or falling tones, based on the curvature of the background magnetic field. It is therefore interesting that our results demonstrate a preferential chirping direction (rising tone) in the case of a uniform field. Once again, we state again that our standalone mechanism is of a different origin and nature, and it will be important in future studies to investigate the relationship between this, and others.
. Furthermore, the paper by Wu et al. (Reference Wu, Tao, Zonca, Chen and Wang2020) demonstrates that in their regime, it is the background non-uniformity that establishes a symmetry breaking in order to preferentially permit either rising or falling tones, based on the curvature of the background magnetic field. It is therefore interesting that our results demonstrate a preferential chirping direction (rising tone) in the case of a uniform field. Once again, we state again that our standalone mechanism is of a different origin and nature, and it will be important in future studies to investigate the relationship between this, and others.
The structure of the envelope generated by the interaction of subelements is also noteworthy. In our simulations we find that the packets exhibit an almost time-periodic breathing behaviour, depicted in figure 3(a) akin to the Kuznetsov–Ma soliton found in the NLS (Ma Reference Ma1979; Akhmediev, Eleonskii & Kulagin Reference Akhmediev, Eleonskii and Kulagin1985), albeit with a zero background. The structure of maximum amplification for widths that generate two to three main packets also bears some semblance to higher-order rogue wave solutions (Chabchoub et al. Reference Chabchoub, Hoffmann, Onorato and Akhmediev2012; Slunyaev et al. Reference Slunyaev, Pelinovsky, Sergeeva, Chabchoub, Hoffmann, Onorato and Akhmediev2013), a fact that is not unsurprising given that such solutions are the infinite-period limit of breathers. This seems to suggest, therefore, that isolated rising tone WMC waves may fall into the category of rogue waves themselves, and the repetitive WMC emission events are breather events. This connection between hydrodynamic rogue waves and WMC has not yet been made in the literature and it may be useful to explore this connection further in the future, given also that the occurrence rate of large-amplitude WMC is significant in the magnetosphere.

Figure 3. Snapshots of the time series of (a) the magnetic wave (b) number density and (c) kinetic energy density at several spatial points, demonstrating the breather-like evolution of the wave envelope as the WMC wave travels.
We may also use (3.22) to explore the effect on both the number density and the parallel electron velocity. From the latter, we may also extract the following energy density, a combination of kinetic and thermal energy of the electrons induced by the wave:
which allows us to determine which stage of the WMC evolution energises the electrons. We visualise these quantities in figure 3(c), demonstrating that the maximum amplification of the wave is the stage which imparts the most energy to the particles, increasing the energy by several electronvolts. We may also correlate this moment with the frequency activity of the wave, as we do in figure 4. In it, we can observe that the amplification of the wave develops as one rising tone begins to terminate and another, lower in frequency, rising tone begins to initiates. The kinetic energy density peaks at exactly the point in time where the power of the higher frequency rising tone and the lower frequency rising tone are equal, and beyond this point the lower rising tone takes over as the most powerful part of the signal. This observation would therefore suggest that repetitive rising tone events, that are typical of chorus wave activity (Tsurutani & Smith Reference Tsurutani and Smith1974; Li et al. Reference Li, Thorne, Bortnik, Tao and Angelopoulos2012; Gao et al. Reference Gao, Li, Thorne, Bortnik, Angelopoulos, Lu, Tao and Wang2014), are accelerating electrons most when the tones overlap and there is an exchange in wave power between these elements. It is difficult to conclusively identify this as the amplification mechanism, however, as it could simply be that if the rising tone of higher frequency have been left to climb the amplification may have been much greater. Further study beyond that of this paper will be required to fully explore this interaction and its consequences.

Figure 4. (a) Snapshots of the magnetic field wave versus the power spectra for the time series snapshot for the parameter choice $(\varepsilon,n_e,\alpha,\varOmega, W, k_BT) = (4\times 10^{-5},1\times 10^7,7.2,2.49\times 10^4,0.35, 7.373$![]() KeV). (b) Comparison between the wave envelope (with maxima shifted to the same point in slow time $t_s$
KeV). (b) Comparison between the wave envelope (with maxima shifted to the same point in slow time $t_s$![]() ) over the time frame of one pulsation (the fast time $t_f$
) over the time frame of one pulsation (the fast time $t_f$![]() ) and its short time Fourier transform. The white dashed line denotes the time at which the envelope achieves its maximum.
) and its short time Fourier transform. The white dashed line denotes the time at which the envelope achieves its maximum.
We conclude this section with some final commentary on what aspects of WMC we cannot recreate with our current level of modelling, but could be captured with suitable alterations. Primarily, the modified NLS equation (4.1) appears to be unable to produce a single isolated rising tone event that has been successfully created via other theoretical modelling (e.g. Nunn et al. Reference Nunn, Omura, Matsumoto, Nagano and Yagitani1997; Omura et al. Reference Omura, Katoh and Summers2008; Tao Reference Tao2014). We attribute this to the fact that we have no source term corresponding to a hot electron population which ultimately drives the WMC waves in these existing theories. We anticipate that once such effects are accounted for properly, the simulations here should be able to reproduce these results. Further, another aspect of our simulations we are not able to reproduce is the non-sequential gap between events, as all WMC events in our simulations happen one after another. One can see from the mission data (cf. Agapitov et al. Reference Agapitov, Krasnoselskikh, Zaliznyak, Angelopoulos, Le Contel and Rolland2011; Gao et al. Reference Gao, Chen, Lu, Chen, Chen and Wang2022) that this need not be the case, and there can be considerable separation between WMC occurrences. We hypothesise that once hot electron growth effects are accounted for, these too may be emergent from simulations of our amplitude model.
6. Concluding remarks
This paper has provided an overview of the formation and dynamics of parallel propagating WMC waves with rising tone. We have outlined that the mechanism for packet formation is an instability of modulational type, whose transition is marked by a critical point in the group velocity as well as the sign of $c_g^2-c_s^2$![]() . Further investigations demonstrated that the role of ions within the system is to reduce the latter instability threshold and suggests that their effects, although contributing little elsewhere, are non-negligible and must be accounted for in any analysis of WMC.
. Further investigations demonstrated that the role of ions within the system is to reduce the latter instability threshold and suggests that their effects, although contributing little elsewhere, are non-negligible and must be accounted for in any analysis of WMC.
We here emphasise that the mechanisms proposed in this paper (namely chirping and potential contributions to the power-gap phenomenon as a result of the ponderomotive force and non-zero ion motion) are not proposed to be replacing other proposed mechanisms, such as those that may even include fixed ions in, for example, Katoh & Omura (Reference Katoh and Omura2007) and Tao et al. (Reference Tao, Zonca and Chen2021). Future work should investigate to what extent different viable mechanisms such as these and others interact and compete in different regimes.
Furthermore, we note that the power-gap phenomenon is not always observed in spacecraft measurements, for example, see Teng et al. (Reference Teng, Tao and Li2019). It is interesting to note that the occurrence rate of ‘no-gap’ whistler waves has been observed to peak off the equator ($|\textrm {MLAT}|\approx 8\unicode{x2013} 10^\circ$![]() ), i.e. in regimes where magnetic curvature cannot be ignored. It will be interesting in future work to see if we can obtain similar results. We emphasise once more, the mechanism that we propose is shown to be viable within the context of a uniform plasma with uniform background magnetic field, and it is not yet known how this mechanism will change in different geometry and regimes, and/or compete with other viable mechanisms.
), i.e. in regimes where magnetic curvature cannot be ignored. It will be interesting in future work to see if we can obtain similar results. We emphasise once more, the mechanism that we propose is shown to be viable within the context of a uniform plasma with uniform background magnetic field, and it is not yet known how this mechanism will change in different geometry and regimes, and/or compete with other viable mechanisms.
We have observed here that rising tones emerge from the NLS with higher-order effects, and the degree at which the spectral peak changes can be attributed to either the strength of the background magnetic field and/or the frequency of the original carrier wave. We have also numerically investigated the evolution of multiple WMC wave packets, confirming that the interaction between WMC elements seems to be the mechanism for the emergence of their frequency sweeping. The envelope asymmetry appears to be the reason for this as this interplay overcomes the symmetry of the theoretical solitary WMC element solution which it seemingly does not allow for. This suggested mechanism is supported by the data from the THEMIS and Van Allen missions, where the wave profile for rising tone elements contains both multiple elements and asymmetric wave envelopes.
The assumption of narrow-banded waves implicit in the derivation of the envelope equations captures the phenomenology of WMC. We do, however, note that formally the range of frequencies that the packets can sweep is limited by $\varepsilon$![]() and should not cover a broad range of frequencies simultaneously. This means that the complete picture of a rising tone WMC will involve more complex models which couple multiple frequency bands together and transfer wave energy between one another. This has been seen in other systems, the simplest being coupled NLS models with the limit of such couplings being the Zakharov equation. For parallel propagating WMC, the theoretical analysis should remain tractable due to the lack of second-harmonic terms in the perturbation analysis and yield further insight into the stability and evolution of nonlinear chorus waves.
and should not cover a broad range of frequencies simultaneously. This means that the complete picture of a rising tone WMC will involve more complex models which couple multiple frequency bands together and transfer wave energy between one another. This has been seen in other systems, the simplest being coupled NLS models with the limit of such couplings being the Zakharov equation. For parallel propagating WMC, the theoretical analysis should remain tractable due to the lack of second-harmonic terms in the perturbation analysis and yield further insight into the stability and evolution of nonlinear chorus waves.
An important extension of the approach outlined here is to consider the more general case of WMC propagating obliquely to the magnetic field. This is more reflective of what is observed, where WMC is seen to most commonly propagate at angles of $10^\circ$![]() (close to parallel) or $70^\circ$
(close to parallel) or $70^\circ$![]() to the magnetic field. The work here remains reflective of the former of these cases by virtue of the obliqueness remaining small, but the latter case would require a revised version of the perturbative approach and result in a different modified NLS. The mission data would also suggest that this version of the dynamics would instead lead to wave dynamics which admit falling tone WMC, a feature which may be linked to a negative version of the ratio (5.3). In either case, a quantification of the effect of oblique propagation should be determined and explored in a similar fashion to the field-aligned waves considered in this paper.
to the magnetic field. The work here remains reflective of the former of these cases by virtue of the obliqueness remaining small, but the latter case would require a revised version of the perturbative approach and result in a different modified NLS. The mission data would also suggest that this version of the dynamics would instead lead to wave dynamics which admit falling tone WMC, a feature which may be linked to a negative version of the ratio (5.3). In either case, a quantification of the effect of oblique propagation should be determined and explored in a similar fashion to the field-aligned waves considered in this paper.
Acknowledgements
Editor T. Passot thanks the referees for their advice in evaluating this article.
Funding
D.R. is grateful to the Isaac Newton Institute for Mathematical Sciences, Cambridge, for support and hospitality during the programme Dispersive Hydrodynamics where work on this paper was undertaken. This work was supported by EPSRC grant no. EP/R014604/1. O.A. gratefully acknowledges financial support from the University of Exeter, the University of Birmingham and also from the United Kingdom Research and Innovation (UKRI) Natural Environment Research Council (NERC) Independent Research Fellowship NE/V013963/1 and NE/V013963/2.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Details of the WKB analysis of the electron plasma
First-order terms proportional to $\textrm {e}^{\textrm {i} \theta }$![]() are given by the linear matrix problem
are given by the linear matrix problem

The determinant of this matrix needs to be zero for non-trivial solutions and thus
Useful for later are the following derivative results along the branch of solutions:

For whistler waves, one has that
The left eigenvector of this matrix is also required in order to determine criterion for when
can be solved for ${\boldsymbol A}_1$![]() , namely that the Fredholme alternative is to hold and the right-hand side vanishes when projected in the direction of the left eigenvector. This is given by
, namely that the Fredholme alternative is to hold and the right-hand side vanishes when projected in the direction of the left eigenvector. This is given by

One is then able to show that

The next order of the analysis only requires consideration of zero-harmonic modes, associated with wave–particle interactions. This involves terms which can be written in terms of gradients, and so by considering the expressions under the gradients we have the system

Combining these gives
This constant can be deduced by noticing that the wave-free flow is potential, as there is no indication that such waves have vorticity due to the constant underlying background magnetic field, so that
This would mean that the overall version of this bulk equation would be
At the final order we consider, we must now examine the terms proportional to $\textrm {e}^{\textrm {i} \theta }$![]() , given by
, given by

Now, we project the right-hand side using ${\boldsymbol l}$![]() gives
gives

Now, we could impose that this is zero, but the analysis would be determined to be trivial. Instead, we assume that there is a correction to the frequency, $\delta \omega$![]() , that has amplitude effects within it. Assuming $\omega = \omega _0+\delta \omega$
, that has amplitude effects within it. Assuming $\omega = \omega _0+\delta \omega$![]() , the matrix system (A1) has the amplitude dependent part
, the matrix system (A1) has the amplitude dependent part

which would instead give the (A12) as

Projecting this down to assess whether this is solvable gives
and so
Thus, the two equations that emerge from the WKB theory are