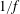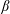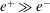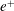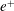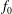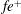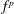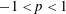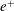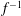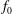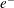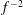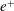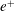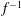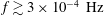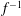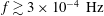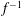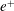1 Introduction
The origin of the solar wind is a long-standing problem (Parker Reference Parker1958) that continues to receive considerable attention. A leading model for the origin of the fast solar wind appeals to Alfvén waves (AWs) that are launched by photospheric motions. As these AWs propagate away from the Sun, they undergo partial reflection due to the radial variation of the Alfvén speed (Heinemann & Olbert Reference Heinemann and Olbert1980). Nonlinear interactions between counter-propagating AWs then cause AW energy to cascade to small scales and dissipate, heating the plasma (Velli, Grappin & Mangeney Reference Velli, Grappin and Mangeney1989; Zhou & Matthaeus Reference Zhou and Matthaeus1989; Cranmer & van Ballegooijen Reference Cranmer and van Ballegooijen2005; Verdini et al. Reference Verdini, Grappin, Pinto and Velli2012; Perez & Chandran Reference Perez and Chandran2013; van Ballegooijen & Asgari-Targhi Reference van Ballegooijen and Asgari-Targhi2017). This heating increases the plasma pressure, which, in conjunction with the wave pressure, accelerates the plasma to high speeds (Suzuki & Inutsuka Reference Suzuki and Inutsuka2005; Cranmer, van Ballegooijen & Edgar Reference Cranmer, van Ballegooijen and Edgar2007; Verdini et al. Reference Verdini, Velli, Matthaeus, Oughton and Dmitruk2010; Chandran et al. Reference Chandran, Dennis, Quataert and Bale2011; van der Holst et al. Reference van der Holst, Sokolov, Meng, Jin, Manchester IV, Tóth and Gombosi2014).
Although non-compressive AWs are the primary mechanism for energizing the solar wind in this model, a number of considerations indicate that compressive fluctuations have a significant impact on the dynamics of turbulence in the corona and solar wind. Observations of the tail of Comet-Lovejoy reveal that the background plasma density
![]() $\unicode[STIX]{x1D70C}_{0}$
at
$\unicode[STIX]{x1D70C}_{0}$
at
![]() $r=1.2R_{\odot }$
(where
$r=1.2R_{\odot }$
(where
![]() $R_{\odot }$
is the radius of the Sun) varies by a factor of
$R_{\odot }$
is the radius of the Sun) varies by a factor of
![]() ${\sim}6$
over distances of a few thousand km measured perpendicular to the background magnetic field
${\sim}6$
over distances of a few thousand km measured perpendicular to the background magnetic field
![]() $\boldsymbol{B}_{0}$
(Raymond et al.
Reference Raymond, McCauley, Cranmer and Downs2014). These density variations (denoted
$\boldsymbol{B}_{0}$
(Raymond et al.
Reference Raymond, McCauley, Cranmer and Downs2014). These density variations (denoted
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70C}$
) lead to phase mixing of AWs, which transports AW energy to smaller scales measured perpendicular to
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70C}$
) lead to phase mixing of AWs, which transports AW energy to smaller scales measured perpendicular to
![]() $\boldsymbol{B}_{0}$
(Heyvaerts & Priest Reference Heyvaerts and Priest1983). Farther from the Sun, where
$\boldsymbol{B}_{0}$
(Heyvaerts & Priest Reference Heyvaerts and Priest1983). Farther from the Sun, where
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D70C}_{0}$
is significantly smaller than
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D70C}_{0}$
is significantly smaller than
![]() $|\unicode[STIX]{x1D6FF}\boldsymbol{B}|/B_{0}$
(Tu & Marsch Reference Tu and Marsch1995; Hollweg, Cranmer & Chandran Reference Hollweg, Cranmer and Chandran2010), AWs still couple to slow magnetosonic waves (‘slow waves’) through the parametric instability, in which outward-propagating AWs decay into outward-propagating slow waves and inward-propagating AWsFootnote
1
(Galeev & Oraevskii Reference Galeev and Oraevskii1963; Sagdeev & Galeev Reference Sagdeev and Galeev1969; Goldstein Reference Goldstein1978; Spangler Reference Spangler1986, Reference Spangler1989, Reference Spangler1990; Hollweg Reference Hollweg1994; Dorfman & Carter Reference Dorfman and Carter2016). This instability and its nonlinear evolution are the focus of the present work.
$|\unicode[STIX]{x1D6FF}\boldsymbol{B}|/B_{0}$
(Tu & Marsch Reference Tu and Marsch1995; Hollweg, Cranmer & Chandran Reference Hollweg, Cranmer and Chandran2010), AWs still couple to slow magnetosonic waves (‘slow waves’) through the parametric instability, in which outward-propagating AWs decay into outward-propagating slow waves and inward-propagating AWsFootnote
1
(Galeev & Oraevskii Reference Galeev and Oraevskii1963; Sagdeev & Galeev Reference Sagdeev and Galeev1969; Goldstein Reference Goldstein1978; Spangler Reference Spangler1986, Reference Spangler1989, Reference Spangler1990; Hollweg Reference Hollweg1994; Dorfman & Carter Reference Dorfman and Carter2016). This instability and its nonlinear evolution are the focus of the present work.
A number of studies have investigated the parametric instability in the solar wind within the framework of magnetohydrodynamics (MHD) (e.g. Malara, Primavera & Veltri Reference Malara, Primavera and Veltri2000; Del Zanna, Velli & Londrillo Reference Del Zanna, Velli and Londrillo2001; Shi et al. Reference Shi, Li, Xiao and Wang2017), while others have gone beyond MHD to account for temperature anisotropy (Tenerani, Velli & Hellinger Reference Tenerani, Velli and Hellinger2017) or kinetic effects such as the Landau damping of slow waves (e.g. Inhester Reference Inhester1990; Vasquez Reference Vasquez1995; Araneda, Marsch & Viñas Reference Araneda, Marsch and Viñas2008; Maneva, Viñas & Ofman Reference Maneva, Viñas and Ofman2013). Cohen & Dewar (Reference Cohen and Dewar1974), for example, derived the growth rate of the parametric instability in the presence of strong slow-wave damping and randomly phased, parallel-propagating AWs. Terasawa et al. (Reference Terasawa, Hoshino, Sakai and Hada1986) carried out one-dimensional (1-D) hybrid simulations and found that Landau damping reduces the growth rate of the parametric instability and that the parametric instability leads to an inverse cascade of AWs to smaller frequencies.
In this paper, weak-turbulence theory is used to investigate the nonlinear evolution of the parametric instability assuming a randomly phased collection of AWs at wavelengths much greater than the proton inertial length
![]() $d_{\text{i}}$
in a low-
$d_{\text{i}}$
in a low-
![]() $\unicode[STIX]{x1D6FD}$
plasma, where
$\unicode[STIX]{x1D6FD}$
plasma, where
![]() $\unicode[STIX]{x1D6FD}$
is the ratio of plasma pressure to magnetic pressure. The fluctuating fields are taken to depend on all three spatial coordinates, but the wave kinetic equations are integrated over the perpendicular (to
$\unicode[STIX]{x1D6FD}$
is the ratio of plasma pressure to magnetic pressure. The fluctuating fields are taken to depend on all three spatial coordinates, but the wave kinetic equations are integrated over the perpendicular (to
![]() $\boldsymbol{B}_{0}$
) wave-vector components, yielding equations for the 1-D power spectra that depend only on the parallel wavenumber and time. The starting point of the analysis is the theory of weak compressible MHD turbulence. Collisionless damping of slow waves is incorporated in a very approximate manner analogous to the approach of Cohen & Dewar (Reference Cohen and Dewar1974), by dropping terms containing the slow-wave energy density in the wave kinetic equations that describe the evolution of the AW power spectra.
$\boldsymbol{B}_{0}$
) wave-vector components, yielding equations for the 1-D power spectra that depend only on the parallel wavenumber and time. The starting point of the analysis is the theory of weak compressible MHD turbulence. Collisionless damping of slow waves is incorporated in a very approximate manner analogous to the approach of Cohen & Dewar (Reference Cohen and Dewar1974), by dropping terms containing the slow-wave energy density in the wave kinetic equations that describe the evolution of the AW power spectra.
The remainder of the paper is organized as follows. Section 2 reviews results from the theory of weak compressible MHD turbulence, and § 3 uses the weak-turbulence wave kinetic equations to recover the results of Cohen & Dewar (Reference Cohen and Dewar1974) in the linear regime. Section 4 shows how the wave kinetic equations imply that AW quanta undergo an inverse cascade towards smaller parallel wavenumbers, and § 5 presents several exact solutions to the wave kinetic equations. The main results of the paper appear in § 6, which uses a numerical solution and an approximate analytic solution to the wave kinetic equations to investigate the parametric decay of an initial population of randomly phased AWs propagating in the same direction with negligible initial power in counter-propagating AWs. The numerical results are compared with observations from the Helios spacecraft at a heliocentric distance of 0.3 astronomical units (AU). Section 7 critically revisits the main assumptions of the analysis and the relevance of the analysis to the solar wind. Section 8 summarizes the key findings of the paper, including predictions that will be tested by NASA’s Parker Solar Probe.
2 The wave kinetic equations for Alfvén waves undergoing parametric decay
In weak-turbulence theory, the quantity
![]() $\unicode[STIX]{x1D714}_{\text{nl}}/\unicode[STIX]{x1D714}_{\text{linear}}$
is treated as a small parameter, where
$\unicode[STIX]{x1D714}_{\text{nl}}/\unicode[STIX]{x1D714}_{\text{linear}}$
is treated as a small parameter, where
![]() $\unicode[STIX]{x1D714}_{\text{nl}}$
is the inverse of the time scale on which nonlinear interactions modify the fluctuations, and
$\unicode[STIX]{x1D714}_{\text{nl}}$
is the inverse of the time scale on which nonlinear interactions modify the fluctuations, and
![]() $\unicode[STIX]{x1D714}_{\text{linear}}$
is the linear wave frequency. Because
$\unicode[STIX]{x1D714}_{\text{linear}}$
is the linear wave frequency. Because
the fluctuations can be viewed as waves to a good approximation. The governing equations lead to a hierarchy of equations for the moments of various fluctuating quantities, in which the time derivatives of the second moments (or second-order correlation functions) depend upon the third moments, and the time derivatives of the third moments depend upon the fourth moments, and so on. This system of equations is closed via the random-phase approximation, which allows the fourth-order correlation functions to be expressed as products of second-order correlation functions (see, e.g. Galtier et al. Reference Galtier, Nazarenko, Newell and Pouquet2000).
The strongest nonlinear interactions in weak MHD turbulence are resonant three-wave interactions. These interactions occur when the frequency and wavenumber of the beat wave produced by two waves is identical to the frequency and wavenumber of some third wave, which enables the beat wave to drive the third wave coherently in time. If the three waves have wavenumbers
![]() $\boldsymbol{p}$
,
$\boldsymbol{p}$
,
![]() $\boldsymbol{q}$
, and
$\boldsymbol{q}$
, and
![]() $\boldsymbol{k}$
and frequencies
$\boldsymbol{k}$
and frequencies
![]() $\unicode[STIX]{x1D714}_{p}$
,
$\unicode[STIX]{x1D714}_{p}$
,
![]() $\unicode[STIX]{x1D714}_{q}$
, and
$\unicode[STIX]{x1D714}_{q}$
, and
![]() $\unicode[STIX]{x1D714}_{k}$
, respectively, then a three-wave resonance requires that
$\unicode[STIX]{x1D714}_{k}$
, respectively, then a three-wave resonance requires that
and
An alternative interpretation of (2.2) and (2.3) arises from viewing the wave fields as a collection of wave quanta at different wavenumbers and frequencies, restricting the frequencies to positive values, and assigning a wave quantum at wavenumber
![]() $\boldsymbol{k}$
and frequency
$\boldsymbol{k}$
and frequency
![]() $\unicode[STIX]{x1D714}_{k}$
the momentum
$\unicode[STIX]{x1D714}_{k}$
the momentum
![]() $\hbar \boldsymbol{k}$
and energy
$\hbar \boldsymbol{k}$
and energy
![]() $\hbar \unicode[STIX]{x1D714}_{k}$
. Equations (2.2) and (2.3) then correspond to the momentum-conservation and energy-conservation relations that arise when either one wave quantum decays into two new wave quanta or two wave quanta merge to produce a new wave quantum.
$\hbar \unicode[STIX]{x1D714}_{k}$
. Equations (2.2) and (2.3) then correspond to the momentum-conservation and energy-conservation relations that arise when either one wave quantum decays into two new wave quanta or two wave quanta merge to produce a new wave quantum.
In the parametric instability in a low-
![]() $\unicode[STIX]{x1D6FD}$
plasma, a parent AW (or AW quantum) at wavenumber
$\unicode[STIX]{x1D6FD}$
plasma, a parent AW (or AW quantum) at wavenumber
![]() $\boldsymbol{k}$
decays into a slow wave at wavenumber
$\boldsymbol{k}$
decays into a slow wave at wavenumber
![]() $\boldsymbol{p}$
propagating in the same direction and an AW at wavenumber
$\boldsymbol{p}$
propagating in the same direction and an AW at wavenumber
![]() $\boldsymbol{q}$
propagating in the opposite direction. Regardless of the direction of the wave vector, the group velocity of an AW is either parallel or anti-parallel to the background magnetic field
$\boldsymbol{q}$
propagating in the opposite direction. Regardless of the direction of the wave vector, the group velocity of an AW is either parallel or anti-parallel to the background magnetic field
and the same is true for slow waves when
which is henceforth assumed. At low
![]() $\unicode[STIX]{x1D6FD}$
slow waves travel along field lines at the sound speed
$\unicode[STIX]{x1D6FD}$
slow waves travel along field lines at the sound speed
![]() $c_{\text{s}}$
, which is approximately
$c_{\text{s}}$
, which is approximately
![]() $\unicode[STIX]{x1D6FD}^{1/2}$
times the Alfvén speed
$\unicode[STIX]{x1D6FD}^{1/2}$
times the Alfvén speed
![]() $v_{\text{A}}$
. Thus, regardless of the perpendicular components of
$v_{\text{A}}$
. Thus, regardless of the perpendicular components of
![]() $\boldsymbol{k}$
,
$\boldsymbol{k}$
,
![]() $\boldsymbol{p}$
, and
$\boldsymbol{p}$
, and
![]() $\boldsymbol{q}$
, the frequency-matching condition (2.3) for the parametric instability is
$\boldsymbol{q}$
, the frequency-matching condition (2.3) for the parametric instability is
Combining the
![]() $z$
component of (2.2) with (2.6) and taking
$z$
component of (2.2) with (2.6) and taking
![]() $c_{\text{s}}\ll v_{\text{A}}$
yields
$c_{\text{s}}\ll v_{\text{A}}$
yields
and
Equation (2.8) implies that the frequency
![]() $|q_{z}v_{\text{A}}|$
of the daughter AW is slightly smaller than the frequency
$|q_{z}v_{\text{A}}|$
of the daughter AW is slightly smaller than the frequency
![]() $|k_{z}v_{\text{A}}|$
of the parent AW (Sagdeev & Galeev Reference Sagdeev and Galeev1969). Thus, the energy of the daughter AW is slightly smaller than the energy of the parent AW. This reduction in AW energy is offset by an increase in slow-wave energy.
$|k_{z}v_{\text{A}}|$
of the parent AW (Sagdeev & Galeev Reference Sagdeev and Galeev1969). Thus, the energy of the daughter AW is slightly smaller than the energy of the parent AW. This reduction in AW energy is offset by an increase in slow-wave energy.
Chandran (Reference Chandran2008) derived the wave kinetic equations for weakly turbulent AWs, slow waves, and fast magnetosonic waves (‘fast waves’) in the low-
![]() $\unicode[STIX]{x1D6FD}$
limit. The resulting equations were expanded in powers of
$\unicode[STIX]{x1D6FD}$
limit. The resulting equations were expanded in powers of
![]() $\unicode[STIX]{x1D6FD}$
, and only the first two orders in the expansion (proportional to
$\unicode[STIX]{x1D6FD}$
, and only the first two orders in the expansion (proportional to
![]() $\unicode[STIX]{x1D6FD}^{-1}$
and
$\unicode[STIX]{x1D6FD}^{-1}$
and
![]() $\unicode[STIX]{x1D6FD}^{0}$
, respectively) were retained. Slow waves are strongly damped in collisionless low-
$\unicode[STIX]{x1D6FD}^{0}$
, respectively) were retained. Slow waves are strongly damped in collisionless low-
![]() $\unicode[STIX]{x1D6FD}$
plasmas (Barnes Reference Barnes1966). Chandran (Reference Chandran2008) neglected collisionless damping during the derivation of the wave kinetic equations, but incorporated it afterward in an ad hoc manner by assuming that the slow-wave power spectrum
$\unicode[STIX]{x1D6FD}$
plasmas (Barnes Reference Barnes1966). Chandran (Reference Chandran2008) neglected collisionless damping during the derivation of the wave kinetic equations, but incorporated it afterward in an ad hoc manner by assuming that the slow-wave power spectrum
![]() $S_{k}^{\pm }$
was small and discarding terms
$S_{k}^{\pm }$
was small and discarding terms
![]() $\propto S_{k}^{\pm }$
unless they were also proportional to
$\propto S_{k}^{\pm }$
unless they were also proportional to
![]() $\unicode[STIX]{x1D6FD}^{-1}$
.Footnote
2
(The
$\unicode[STIX]{x1D6FD}^{-1}$
.Footnote
2
(The
![]() $\pm$
sign in
$\pm$
sign in
![]() $S_{k}^{\pm }$
indicates slow waves propagating parallel (
$S_{k}^{\pm }$
indicates slow waves propagating parallel (
![]() $+$
) or anti-parallel (
$+$
) or anti-parallel (
![]() $-$
) to
$-$
) to
![]() $\boldsymbol{B}_{0}$
.)
$\boldsymbol{B}_{0}$
.)
In the present paper, the wave kinetic equations derived by Chandran (Reference Chandran2008) are used to investigate the nonlinear evolution of the parametric instability. It is assumed that slow-wave damping is sufficiently strong that all terms
![]() $\propto S_{k}^{\pm }$
, even those
$\propto S_{k}^{\pm }$
, even those
![]() $\propto \unicode[STIX]{x1D6FD}^{-1}$
, can be safely discarded. All other types of nonlinear interactions are neglected, including resonant interactions between three AWs, phase mixing and resonant interactions involving fast waves. Given these approximations, equation (8) of Chandran (Reference Chandran2008) becomes
$\propto \unicode[STIX]{x1D6FD}^{-1}$
, can be safely discarded. All other types of nonlinear interactions are neglected, including resonant interactions between three AWs, phase mixing and resonant interactions involving fast waves. Given these approximations, equation (8) of Chandran (Reference Chandran2008) becomes
where
![]() $A_{k}^{+}$
(
$A_{k}^{+}$
(
![]() $A_{k}^{-}$
) is the 3-D wavenumber spectrum of AWs propagating parallel (anti-parallel) to
$A_{k}^{-}$
) is the 3-D wavenumber spectrum of AWs propagating parallel (anti-parallel) to
![]() $\boldsymbol{B}_{0}$
,
$\boldsymbol{B}_{0}$
,
![]() $\unicode[STIX]{x1D6FF}(x)$
is the Dirac delta function, and the integral over each Cartesian component of
$\unicode[STIX]{x1D6FF}(x)$
is the Dirac delta function, and the integral over each Cartesian component of
![]() $\boldsymbol{p}$
and
$\boldsymbol{p}$
and
![]() $\boldsymbol{q}$
extends from
$\boldsymbol{q}$
extends from
![]() $-\infty$
to
$-\infty$
to
![]() $+\infty$
. The 3-D AW power spectra depend upon all three wave-vector components and time. The
$+\infty$
. The 3-D AW power spectra depend upon all three wave-vector components and time. The
![]() $\unicode[STIX]{x1D6FF}(\boldsymbol{k}-\boldsymbol{p}-\boldsymbol{q})$
term enforces the wavenumber-resonance condition (2.2), and the
$\unicode[STIX]{x1D6FF}(\boldsymbol{k}-\boldsymbol{p}-\boldsymbol{q})$
term enforces the wavenumber-resonance condition (2.2), and the
![]() $\unicode[STIX]{x1D6FF}(q_{z}+k_{z})$
term enforces the frequency-resonance condition (2.8) to leading order in
$\unicode[STIX]{x1D6FF}(q_{z}+k_{z})$
term enforces the frequency-resonance condition (2.8) to leading order in
![]() $\unicode[STIX]{x1D6FD}$
. The integral over the components of
$\unicode[STIX]{x1D6FD}$
. The integral over the components of
![]() $p$
in (2.9) can be carried out immediately, thereby annihilating the first delta function. Equation (2.9) can be further simplified by introducing the 1-D wavenumber spectra
$p$
in (2.9) can be carried out immediately, thereby annihilating the first delta function. Equation (2.9) can be further simplified by introducing the 1-D wavenumber spectra
and integrating (2.9) over
![]() $k_{x}$
and
$k_{x}$
and
![]() $k_{y}$
, which yields
$k_{y}$
, which yields
Equation (2.11) describes how the 1-D (parallel) power spectra
![]() $E^{\pm }$
evolve and forms the basis for much of the discussion to follow. Given the aforementioned assumptions, the evolution of the 1-D power spectra
$E^{\pm }$
evolve and forms the basis for much of the discussion to follow. Given the aforementioned assumptions, the evolution of the 1-D power spectra
![]() $E^{\pm }$
is not influenced by the way that
$E^{\pm }$
is not influenced by the way that
![]() $A^{\pm }$
depends on
$A^{\pm }$
depends on
![]() $k_{x}$
and
$k_{x}$
and
![]() $k_{y}$
. For future reference, the normalization of the power spectra is such that
$k_{y}$
. For future reference, the normalization of the power spectra is such that
where
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{v}_{\text{AW}}$
and
$\unicode[STIX]{x1D6FF}\boldsymbol{v}_{\text{AW}}$
and
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{B}_{\text{AW}}$
are the velocity and magnetic-field fluctuations associated with AWs, and
$\unicode[STIX]{x1D6FF}\boldsymbol{B}_{\text{AW}}$
are the velocity and magnetic-field fluctuations associated with AWs, and
![]() $\langle \cdots \rangle$
indicates an average over space and time (Chandran Reference Chandran2008).
$\langle \cdots \rangle$
indicates an average over space and time (Chandran Reference Chandran2008).

Figure 1. Physical interpretation of the wave kinetic equation for parametric decay when slow waves are strongly damped (2.11). The mathematical expressions next to the arrows represent the contributions to
![]() $\unicode[STIX]{x2202}E^{+}(k_{z2})/\unicode[STIX]{x2202}t$
from the parametric decay of AWs at
$\unicode[STIX]{x2202}E^{+}(k_{z2})/\unicode[STIX]{x2202}t$
from the parametric decay of AWs at
![]() $k_{z3}$
, which acts to increase
$k_{z3}$
, which acts to increase
![]() $E^{+}(k_{z2})$
, and the parametric decay of AWs at
$E^{+}(k_{z2})$
, and the parametric decay of AWs at
![]() $k_{z2}$
, which acts to decrease
$k_{z2}$
, which acts to decrease
![]() $E^{+}(k_{z2})$
. In these expressions,
$E^{+}(k_{z2})$
. In these expressions,
![]() $E_{2}^{+}=E^{+}(k_{z2})$
,
$E_{2}^{+}=E^{+}(k_{z2})$
,
![]() $E_{1}^{-}=E^{-}(k_{z1})$
, and
$E_{1}^{-}=E^{-}(k_{z1})$
, and
![]() $E_{3}^{-}=E^{-}(k_{z3})$
.
$E_{3}^{-}=E^{-}(k_{z3})$
.
2.1 Physical interpretation of the wave kinetic equation
Figure 1 offers a way of understanding (2.11). The horizontal colour bars in this figure represent the spectra of outward-propagating and inward-propagating AWs, with red representing longer-wavelength waves and violet representing shorter-wavelength waves. AWs propagating in the
![]() $-\boldsymbol{B}_{0}$
direction at
$-\boldsymbol{B}_{0}$
direction at
![]() $|k_{z}|=k_{z3}$
decay into slow waves propagating anti-parallel to
$|k_{z}|=k_{z3}$
decay into slow waves propagating anti-parallel to
![]() $\boldsymbol{B}_{0}$
at
$\boldsymbol{B}_{0}$
at
![]() $|k_{z}|\simeq 2k_{z3}$
and AWs propagating parallel to
$|k_{z}|\simeq 2k_{z3}$
and AWs propagating parallel to
![]() $\boldsymbol{B}_{0}$
at
$\boldsymbol{B}_{0}$
at
![]() $|k_{z}|=k_{z2}$
. AWs propagating parallel to
$|k_{z}|=k_{z2}$
. AWs propagating parallel to
![]() $\boldsymbol{B}_{0}$
at
$\boldsymbol{B}_{0}$
at
![]() $|k_{z}|=k_{z2}$
decay into slow waves propagating parallel to
$|k_{z}|=k_{z2}$
decay into slow waves propagating parallel to
![]() $\boldsymbol{B}_{0}$
at
$\boldsymbol{B}_{0}$
at
![]() $|k_{z}|\simeq 2k_{z2}$
and AWs propagating anti-parallel to
$|k_{z}|\simeq 2k_{z2}$
and AWs propagating anti-parallel to
![]() $\boldsymbol{B}_{0}$
at
$\boldsymbol{B}_{0}$
at
![]() $|k_{z}|=k_{z1}$
. Equation (2.11) is approximately equivalent to the statement that the rate at which
$|k_{z}|=k_{z1}$
. Equation (2.11) is approximately equivalent to the statement that the rate at which
![]() $E_{2}^{+}=E^{+}(k_{z2})$
increases via the decay of AWs at
$E_{2}^{+}=E^{+}(k_{z2})$
increases via the decay of AWs at
![]() $|k_{z}|=k_{z3}$
is
$|k_{z}|=k_{z3}$
is
where
![]() $E_{3}^{-}=E^{-}(k_{z3})$
, while the rate at which
$E_{3}^{-}=E^{-}(k_{z3})$
, while the rate at which
![]() $E_{2}^{+}$
decreases via the decay of AWs at
$E_{2}^{+}$
decreases via the decay of AWs at
![]() $|k_{z}|=k_{z2}$
is
$|k_{z}|=k_{z2}$
is
where
![]() $E_{1}^{-}=E^{-}(k_{z1})$
. The time derivative of
$E_{1}^{-}=E^{-}(k_{z1})$
. The time derivative of
![]() $E_{2}^{+}$
is
$E_{2}^{+}$
is
![]() $R_{3\rightarrow 2}-R_{2\rightarrow 1}$
, or
$R_{3\rightarrow 2}-R_{2\rightarrow 1}$
, or
Equation (2.8) implies that
![]() $k_{z3}-k_{z1}\sim k_{z2}c_{\text{s}}/v_{\text{A}}\sim \unicode[STIX]{x1D6FD}^{1/2}k_{z2}$
. A Taylor expansion of
$k_{z3}-k_{z1}\sim k_{z2}c_{\text{s}}/v_{\text{A}}\sim \unicode[STIX]{x1D6FD}^{1/2}k_{z2}$
. A Taylor expansion of
![]() $k_{z3}E_{3}^{-}$
and
$k_{z3}E_{3}^{-}$
and
![]() $k_{z1}E_{1}^{-}$
about
$k_{z1}E_{1}^{-}$
about
![]() $k_{z2}$
in (2.15) thus allows this equation to be rewritten as
$k_{z2}$
in (2.15) thus allows this equation to be rewritten as
which is the same as (2.11) to within a factor of order unity.
To be clear, no independent derivation is being presented for (2.13) and (2.14). The foregoing discussion merely points out that (2.13) and (2.14) are equivalent (up to a factor of order unity) to (2.11), which is derived on the basis of weak-turbulence theory. It is worth pointing out, however, that several features of (2.13) and (2.14) make sense on a qualitative level. If either
![]() $E^{+}=0$
or
$E^{+}=0$
or
![]() $E^{-}=0$
, then
$E^{-}=0$
, then
![]() $R_{3\rightarrow 2}=R_{2\rightarrow 1}=0$
, because the parametric instability is a stimulated decay, which ceases if initially all the AWs travel in the same direction. For fixed
$R_{3\rightarrow 2}=R_{2\rightarrow 1}=0$
, because the parametric instability is a stimulated decay, which ceases if initially all the AWs travel in the same direction. For fixed
![]() $E^{+}$
and
$E^{+}$
and
![]() $E^{-}$
,
$E^{-}$
,
![]() $R_{3\rightarrow 2}$
and
$R_{3\rightarrow 2}$
and
![]() $R_{2\rightarrow 1}$
vanish as
$R_{2\rightarrow 1}$
vanish as
![]() $v_{\text{A}}\rightarrow \infty$
, since the fractional nonlinearities vanish in this limit. Also,
$v_{\text{A}}\rightarrow \infty$
, since the fractional nonlinearities vanish in this limit. Also,
![]() $R_{3\rightarrow 2}$
and
$R_{3\rightarrow 2}$
and
![]() $R_{2\rightarrow 1}$
are proportional to
$R_{2\rightarrow 1}$
are proportional to
![]() $\unicode[STIX]{x1D6FD}^{-1/2}$
(when
$\unicode[STIX]{x1D6FD}^{-1/2}$
(when
![]() $S_{k}^{\pm }$
is negligibly small, as assumed) because the parametric-decay contribution to
$S_{k}^{\pm }$
is negligibly small, as assumed) because the parametric-decay contribution to
![]() $\unicode[STIX]{x2202}A_{k}^{\pm }/\unicode[STIX]{x2202}t$
is an integral (over
$\unicode[STIX]{x2202}A_{k}^{\pm }/\unicode[STIX]{x2202}t$
is an integral (over
![]() $\boldsymbol{p}$
and
$\boldsymbol{p}$
and
![]() $\boldsymbol{q}$
) of third-order correlation functions such as
$\boldsymbol{q}$
) of third-order correlation functions such as
![]() $\langle \unicode[STIX]{x1D6FF}\boldsymbol{v}_{k}\boldsymbol{\cdot }\unicode[STIX]{x1D6FF}\boldsymbol{B}_{q}\unicode[STIX]{x1D6FF}n_{p}\rangle$
, where
$\langle \unicode[STIX]{x1D6FF}\boldsymbol{v}_{k}\boldsymbol{\cdot }\unicode[STIX]{x1D6FF}\boldsymbol{B}_{q}\unicode[STIX]{x1D6FF}n_{p}\rangle$
, where
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{v}_{k}$
and
$\unicode[STIX]{x1D6FF}\boldsymbol{v}_{k}$
and
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{B}_{q}$
are the velocity and magnetic-field fluctuations associated with AWs at wave vectors
$\unicode[STIX]{x1D6FF}\boldsymbol{B}_{q}$
are the velocity and magnetic-field fluctuations associated with AWs at wave vectors
![]() $\boldsymbol{k}$
and
$\boldsymbol{k}$
and
![]() $\boldsymbol{q}$
, and
$\boldsymbol{q}$
, and
![]() $\unicode[STIX]{x1D6FF}n_{p}$
is the density fluctuation associated with the slow waves at wave vector
$\unicode[STIX]{x1D6FF}n_{p}$
is the density fluctuation associated with the slow waves at wave vector
![]() $\boldsymbol{p}$
that are driven by the beating of the AWs at wave vectors
$\boldsymbol{p}$
that are driven by the beating of the AWs at wave vectors
![]() $\boldsymbol{k}$
and
$\boldsymbol{k}$
and
![]() $\boldsymbol{q}$
. For fixed AW amplitudes and fixed
$\boldsymbol{q}$
. For fixed AW amplitudes and fixed
![]() $B_{0}$
and
$B_{0}$
and
![]() $v_{\text{A}}$
, this driven density fluctuation is proportional to
$v_{\text{A}}$
, this driven density fluctuation is proportional to
![]() $\unicode[STIX]{x1D6FD}^{-1/2}$
, because as
$\unicode[STIX]{x1D6FD}^{-1/2}$
, because as
![]() $\unicode[STIX]{x1D6FD}$
decreases the thermal pressure is less able to resist the compression along
$\unicode[STIX]{x1D6FD}$
decreases the thermal pressure is less able to resist the compression along
![]() $\boldsymbol{B}_{0}$
resulting from the Lorentz force that arises from the beating of the AWs.
$\boldsymbol{B}_{0}$
resulting from the Lorentz force that arises from the beating of the AWs.
3 Linear growth of the parametric instability
In the linear regime of the parametric instability, the spectrum of AWs propagating in one direction, say
![]() $E^{+}$
, is taken to be fixed, and
$E^{+}$
, is taken to be fixed, and
![]() $E^{-}\ll E^{+}$
. Equation (2.11) then implies that
$E^{-}\ll E^{+}$
. Equation (2.11) then implies that
![]() $E^{-}$
increases exponentially in time with growth rate
$E^{-}$
increases exponentially in time with growth rate
Equation (3.1) is equivalent to equation (18) of Cohen & Dewar (Reference Cohen and Dewar1974) given the different normalizations of the AW power spectra in the two equations. For example, equation (2.12) implies that
![]() $\int _{0}^{\infty }E^{+}\,\text{d}k_{z}=(1/2)\int _{-\infty }^{\infty }E^{+}\,\text{d}k_{z}=\langle |\unicode[STIX]{x1D6FF}\boldsymbol{B}|^{2}\rangle /4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}$
when
$\int _{0}^{\infty }E^{+}\,\text{d}k_{z}=(1/2)\int _{-\infty }^{\infty }E^{+}\,\text{d}k_{z}=\langle |\unicode[STIX]{x1D6FF}\boldsymbol{B}|^{2}\rangle /4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}$
when
![]() $E^{-}\ll E^{+}$
, which can be compared with the un-numbered but displayed equation under equation (9) of Cohen & Dewar (Reference Cohen and Dewar1974). As in the present paper, Cohen & Dewar (Reference Cohen and Dewar1974) assumed that slow waves are strongly damped and that the AWs satisfy the random-phase approximation. The present paper builds upon the results of Cohen & Dewar (Reference Cohen and Dewar1974) by investigating the coupled nonlinear evolution of
$E^{-}\ll E^{+}$
, which can be compared with the un-numbered but displayed equation under equation (9) of Cohen & Dewar (Reference Cohen and Dewar1974). As in the present paper, Cohen & Dewar (Reference Cohen and Dewar1974) assumed that slow waves are strongly damped and that the AWs satisfy the random-phase approximation. The present paper builds upon the results of Cohen & Dewar (Reference Cohen and Dewar1974) by investigating the coupled nonlinear evolution of
![]() $E^{+}$
and
$E^{+}$
and
![]() $E^{-}$
. Also, whereas Cohen & Dewar (Reference Cohen and Dewar1974) took the wave vectors to be parallel or anti-parallel to
$E^{-}$
. Also, whereas Cohen & Dewar (Reference Cohen and Dewar1974) took the wave vectors to be parallel or anti-parallel to
![]() $\boldsymbol{B}_{0}$
, the derivation of (2.11) in the present paper allows for obliquely propagating waves.
$\boldsymbol{B}_{0}$
, the derivation of (2.11) in the present paper allows for obliquely propagating waves.
4 Conservation of wave quanta and inverse cascade
To simplify the presentation, it is assumed that
No generality is lost, because
![]() $E^{\pm }$
is an even function of
$E^{\pm }$
is an even function of
![]() $k_{z}$
, and thus it is sufficient to solve for the spectra at positive
$k_{z}$
, and thus it is sufficient to solve for the spectra at positive
![]() $k_{z}$
values. Equation (2.11) can be rewritten as the two equations
$k_{z}$
values. Equation (2.11) can be rewritten as the two equations
and
where
is the number of wave quanta per unit
![]() $k_{z}$
per unit mass and
$k_{z}$
per unit mass and
is the flux of wave quanta in
![]() $k_{z}$
-space. Equation (4.2) implies that the number of wave quanta per unit mass,
$k_{z}$
-space. Equation (4.2) implies that the number of wave quanta per unit mass,
is conserved. The fact that
![]() $\unicode[STIX]{x1D6E4}$
is negative indicates that there is an inverse cascade of wave quanta from large
$\unicode[STIX]{x1D6E4}$
is negative indicates that there is an inverse cascade of wave quanta from large
![]() $k_{z}$
to small
$k_{z}$
to small
![]() $k_{z}$
(cf. Terasawa et al.
Reference Terasawa, Hoshino, Sakai and Hada1986). The wavenumber drift velocity of the wave quanta,
$k_{z}$
(cf. Terasawa et al.
Reference Terasawa, Hoshino, Sakai and Hada1986). The wavenumber drift velocity of the wave quanta,
is determined primarily by the smaller of
![]() $E^{+}$
and
$E^{+}$
and
![]() $E^{-}$
.
$E^{-}$
.
5 Exact solutions to the wave kinetic equations
In this section, several exact solutions to (2.11) are presented under the assumption that
![]() $k_{z}>0$
. The spectra at negative
$k_{z}>0$
. The spectra at negative
![]() $k_{z}$
follow from the relation
$k_{z}$
follow from the relation
![]() $E^{\pm }(-k_{z},t)=E^{\pm }(k_{z},t)$
.
$E^{\pm }(-k_{z},t)=E^{\pm }(k_{z},t)$
.
5.1 Decaying, balanced turbulence
One family of exact solutions to (2.11) follows from setting
in (2.11), where
is the Heaviside function. When (5.1) is substituted into (2.11), each side of (2.11) becomes the sum of terms proportional to
![]() $\unicode[STIX]{x1D6FF}(k_{z}-b)$
and terms that contain no delta function. By separately equating the two groups of terms, one can show that (5.1) is a solution to (2.11) if
$\unicode[STIX]{x1D6FF}(k_{z}-b)$
and terms that contain no delta function. By separately equating the two groups of terms, one can show that (5.1) is a solution to (2.11) if
and
Equation (5.4) makes use of the relation
![]() $[H(x)]^{2}=H(x)$
and its derivative,
$[H(x)]^{2}=H(x)$
and its derivative,
![]() $2H(x)\unicode[STIX]{x1D6FF}(x)=\unicode[STIX]{x1D6FF}(x)$
. In appendix A it is shown that (5.4) can be recovered by adding a small amount of nonlinear diffusion to (2.11) and replacing the discontinuous jump in the spectrum at
$2H(x)\unicode[STIX]{x1D6FF}(x)=\unicode[STIX]{x1D6FF}(x)$
. In appendix A it is shown that (5.4) can be recovered by adding a small amount of nonlinear diffusion to (2.11) and replacing the discontinuous jump in the spectrum at
![]() $k_{z}=b(t)$
with a boundary layer. Equation (5.4) implies that, for solutions of the form given in (5.1), the mean-square amplitudes of forward- and backward-propagating AWs must be equal just above the break wavenumber
$k_{z}=b(t)$
with a boundary layer. Equation (5.4) implies that, for solutions of the form given in (5.1), the mean-square amplitudes of forward- and backward-propagating AWs must be equal just above the break wavenumber
![]() $b$
. An exact solution to (5.3) and (5.4) corresponding to decaying turbulence is
$b$
. An exact solution to (5.3) and (5.4) corresponding to decaying turbulence is
and
where
![]() $a_{0}$
and
$a_{0}$
and
![]() $b_{0}$
are the values of
$b_{0}$
are the values of
![]() $a$
and
$a$
and
![]() $b$
at
$b$
at
![]() $t=0$
.
$t=0$
.
This solution can be further truncated at large
![]() $k_{z}$
by setting
$k_{z}$
by setting
with
where
![]() $q_{0}$
is the value of
$q_{0}$
is the value of
![]() $q$
at
$q$
at
![]() $t=0$
, which is taken to exceed
$t=0$
, which is taken to exceed
![]() $b_{0}$
. Equations (5.5) through (5.9) can be recovered numerically by solving (2.11) for freely decaying AWs. Whether the spectra satisfy (5.1) and (5.5) through (5.7) or, alternatively, equations (5.6) through (5.9), the number of wave quanta
$b_{0}$
. Equations (5.5) through (5.9) can be recovered numerically by solving (2.11) for freely decaying AWs. Whether the spectra satisfy (5.1) and (5.5) through (5.7) or, alternatively, equations (5.6) through (5.9), the number of wave quanta
![]() $N_{\text{tot}}$
defined in (4.6) is finite and independent of time.
$N_{\text{tot}}$
defined in (4.6) is finite and independent of time.
5.2 Forced, balanced turbulence
An exact solution to (5.3) and (5.4) corresponding to forced turbulence is
and
where
![]() $c$
is a constant and
$c$
is a constant and
![]() $b_{0}$
is the value of
$b_{0}$
is the value of
![]() $b$
at
$b$
at
![]() $t=0$
. In this solution, the number of wave quanta
$t=0$
. In this solution, the number of wave quanta
![]() $N_{\text{tot}}$
is not constant, because there is a non-zero influx of wave quanta from infinity. A version of this solution can be realized in a numerical solution of (2.11) by holding
$N_{\text{tot}}$
is not constant, because there is a non-zero influx of wave quanta from infinity. A version of this solution can be realized in a numerical solution of (2.11) by holding
![]() $E^{\pm }$
fixed at some wavenumber
$E^{\pm }$
fixed at some wavenumber
![]() $k_{\text{f}}$
, which mimics the effects of energy input from external forcing. In this case, the numerical solution at
$k_{\text{f}}$
, which mimics the effects of energy input from external forcing. In this case, the numerical solution at
![]() $k_{z}<k_{\text{f}}$
is described by (5.1), (5.10) and (5.11), with
$k_{z}<k_{\text{f}}$
is described by (5.1), (5.10) and (5.11), with
![]() $b(t)<k_{\text{f}}$
.
$b(t)<k_{\text{f}}$
.
The solution in (5.10) and (5.11) can be truncated at large
![]() $k_{z}$
in a manner analogous to (5.8), but with
$k_{z}$
in a manner analogous to (5.8), but with
![]() $q=[(\unicode[STIX]{x03C0}ct/2v_{\text{A}})+(1/q_{0})]^{-1}$
, where
$q=[(\unicode[STIX]{x03C0}ct/2v_{\text{A}})+(1/q_{0})]^{-1}$
, where
![]() $q_{0}$
is the value of
$q_{0}$
is the value of
![]() $q$
at
$q$
at
![]() $t=0$
. In this solution,
$t=0$
. In this solution,
![]() $N_{\text{tot}}$
is independent of time. Numerical solutions of (2.11) show, however, that this solution is unstable. If the spectra initially satisfy
$N_{\text{tot}}$
is independent of time. Numerical solutions of (2.11) show, however, that this solution is unstable. If the spectra initially satisfy
![]() $E^{\pm }=(c/k_{z})H(k_{z}-b)H(q-k_{z})$
, then they evolve towards the solution described by (5.5) through (5.9).
$E^{\pm }=(c/k_{z})H(k_{z}-b)H(q-k_{z})$
, then they evolve towards the solution described by (5.5) through (5.9).
5.3 Exact solutions extending over all
 $k_{z}$
$k_{z}$
In addition to the truncated solutions described in §§ 5.1 and 5.2, equation (2.11) possesses several exact solutions that extend over all
![]() $k_{z}$
. These solutions are unphysical, because they correspond to infinite AW energy and neglect dissipation (which becomes important at sufficiently large
$k_{z}$
. These solutions are unphysical, because they correspond to infinite AW energy and neglect dissipation (which becomes important at sufficiently large
![]() $k_{z}$
) and finite system size (which becomes important at sufficiently small
$k_{z}$
) and finite system size (which becomes important at sufficiently small
![]() $k_{z}$
). However, they illustrate several features of the nonlinear evolution of the parametric instability, which are summarized at the end of this section.
$k_{z}$
). However, they illustrate several features of the nonlinear evolution of the parametric instability, which are summarized at the end of this section.
The simplest solution to (2.11) spanning all
![]() $k_{z}$
is
$k_{z}$
is
where
![]() $c^{\pm }$
is a constant. It follows from (4.5) that (5.12) corresponds to a constant flux of AW quanta to smaller
$c^{\pm }$
is a constant. It follows from (4.5) that (5.12) corresponds to a constant flux of AW quanta to smaller
![]() $k_{z}$
. In contrast to the truncated
$k_{z}$
. In contrast to the truncated
![]() $E^{\pm }\propto k_{z}^{-1}$
forced-turbulence solution in § 5.2,
$E^{\pm }\propto k_{z}^{-1}$
forced-turbulence solution in § 5.2,
![]() $E^{+}$
and
$E^{+}$
and
![]() $E^{-}$
need not be equal in (5.12).
$E^{-}$
need not be equal in (5.12).
A second, non-truncated, exact solution to (2.11) is given by
and
where
![]() $a_{0}^{+}$
and
$a_{0}^{+}$
and
![]() $a_{0}^{-}$
are the initial values of
$a_{0}^{-}$
are the initial values of
![]() $a^{+}$
and
$a^{+}$
and
![]() $a^{-}$
. In this solution,
$a^{-}$
. In this solution,
If
![]() $a_{0}^{+}>a_{0}^{-}$
, then
$a_{0}^{+}>a_{0}^{-}$
, then
![]() $E^{-}$
decays faster than
$E^{-}$
decays faster than
![]() $E^{+}$
, and, after a long time has passed,
$E^{+}$
, and, after a long time has passed,
![]() $E^{-}$
decays to zero while
$E^{-}$
decays to zero while
![]() $a^{+}$
decays to the value
$a^{+}$
decays to the value
![]() $a_{0}^{+}-a_{0}^{-}$
. Conversely, if
$a_{0}^{+}-a_{0}^{-}$
. Conversely, if
![]() $a_{0}^{-}>a_{0}^{+}$
, then
$a_{0}^{-}>a_{0}^{+}$
, then
![]() $E^{+}$
decays faster than
$E^{+}$
decays faster than
![]() $E^{-}$
, and the turbulence decays to a state in which
$E^{-}$
, and the turbulence decays to a state in which
![]() $E^{+}=0$
. In the limit that
$E^{+}=0$
. In the limit that
![]() $a_{0}^{+}\rightarrow a_{0}^{-}$
,
$a_{0}^{+}\rightarrow a_{0}^{-}$
,
where
![]() $a_{0}=a_{0}^{+}=a_{0}^{-}$
. Equations (5.13) and (5.16) are a non-truncated version of the decaying-turbulence solution presented in § 5.1.
$a_{0}=a_{0}^{+}=a_{0}^{-}$
. Equations (5.13) and (5.16) are a non-truncated version of the decaying-turbulence solution presented in § 5.1.
Equations (5.12) and (5.13) can be combined into a more general class of solution,
where
![]() $d^{+}$
and
$d^{+}$
and
![]() $d^{-}$
are constants and
$d^{-}$
are constants and
![]() $a^{\pm }(t)$
is given by (5.14). Another type of solution combining
$a^{\pm }(t)$
is given by (5.14). Another type of solution combining
![]() $k_{z}^{-1}$
and
$k_{z}^{-1}$
and
![]() $k_{z}^{-2}$
scalings is
$k_{z}^{-2}$
scalings is
where
![]() $c_{0}$
,
$c_{0}$
,
![]() $c_{1}$
, and
$c_{1}$
, and
![]() $c_{2}$
are constants.
$c_{2}$
are constants.
The exact solutions presented in this section illustrate three properties of the nonlinear evolution of the parametric instability at low
![]() $\unicode[STIX]{x1D6FD}$
when slow waves are strongly damped. First, when
$\unicode[STIX]{x1D6FD}$
when slow waves are strongly damped. First, when
![]() $E^{\pm }\propto k_{z}^{-1}$
,
$E^{\pm }\propto k_{z}^{-1}$
,
![]() $\unicode[STIX]{x2202}E^{\mp }/\unicode[STIX]{x2202}t$
vanishes. Second, if
$\unicode[STIX]{x2202}E^{\mp }/\unicode[STIX]{x2202}t$
vanishes. Second, if
![]() $E^{\pm }\propto k_{z}^{-2}$
, then
$E^{\pm }\propto k_{z}^{-2}$
, then
![]() $(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}t)\ln E^{\mp }$
is negative and independent of
$(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}t)\ln E^{\mp }$
is negative and independent of
![]() $k_{z}$
, and
$k_{z}$
, and
![]() $E^{\mp }(k_{z},t)$
can be written as the product of a function of
$E^{\mp }(k_{z},t)$
can be written as the product of a function of
![]() $k_{z}$
and a (decreasing) function of time. (More general principles describing the evolution of
$k_{z}$
and a (decreasing) function of time. (More general principles describing the evolution of
![]() $E^{\pm }$
are summarized in figure 3 and (6.11).) Third, the parametric instability does not necessarily saturate with
$E^{\pm }$
are summarized in figure 3 and (6.11).) Third, the parametric instability does not necessarily saturate with
![]() $E^{+}=E^{-}$
. For example, in (5.13) and (5.14), when
$E^{+}=E^{-}$
. For example, in (5.13) and (5.14), when
![]() $a_{0}^{+}\neq a_{0}^{-}$
, the AWs decay to a maximally aligned state reminiscent of the final state of decaying cross-helical incompressible MHD turbulence (Dobrowolny, Mangeney & Veltri Reference Dobrowolny, Mangeney and Veltri1980).
$a_{0}^{+}\neq a_{0}^{-}$
, the AWs decay to a maximally aligned state reminiscent of the final state of decaying cross-helical incompressible MHD turbulence (Dobrowolny, Mangeney & Veltri Reference Dobrowolny, Mangeney and Veltri1980).
6 Nonlinear evolution of the parametric instability when most of the AWS initially propagate in the same direction
This section describes a numerical solution to (2.11) in which, initially,
As in § 5,
![]() $k_{z}$
is taken to be positive, and the spectra at negative
$k_{z}$
is taken to be positive, and the spectra at negative
![]() $k_{z}$
can be inferred from the fact that
$k_{z}$
can be inferred from the fact that
![]() $E^{\pm }(-k_{z})=E^{\pm }(k_{z})$
. The spectra are advanced forward in time using a second-order Runge–Kutta algorithm on a logarithmic wavenumber grid consisting of 2000 grid points. To prevent the growth of numerical instabilities, a nonlinear diffusion term
$E^{\pm }(-k_{z})=E^{\pm }(k_{z})$
. The spectra are advanced forward in time using a second-order Runge–Kutta algorithm on a logarithmic wavenumber grid consisting of 2000 grid points. To prevent the growth of numerical instabilities, a nonlinear diffusion term
is added to the right-hand side of (2.11), where
![]() $\unicode[STIX]{x1D708}$
is a constant. The value of
$\unicode[STIX]{x1D708}$
is a constant. The value of
![]() $\unicode[STIX]{x1D708}$
is chosen as small as possible subject to the constraint that the diffusion term suppress instabilities at the grid scale.
$\unicode[STIX]{x1D708}$
is chosen as small as possible subject to the constraint that the diffusion term suppress instabilities at the grid scale.
To represent the solution in a way that can be readily compared with spacecraft measurements of solar-wind turbulence, the wavenumber spectra are converted into frequency spectra,
where
![]() $U$
is the solar-wind velocity, and
$U$
is the solar-wind velocity, and
is the frequency in the spacecraft frame that, according to Taylor’s (Reference Taylor1938) hypothesis, corresponds to wavenumber
![]() $k_{z}$
when the background magnetic field is aligned with the nearly radial solar-wind velocity. The Alfvén speed is taken to be the approximate average of the observed values of
$k_{z}$
when the background magnetic field is aligned with the nearly radial solar-wind velocity. The Alfvén speed is taken to be the approximate average of the observed values of
![]() $v_{\text{A}}$
in three fast-solar-wind streams at
$v_{\text{A}}$
in three fast-solar-wind streams at
![]() $r=0.3~\text{AU}$
(see table 1 of Marsch et al. (Reference Marsch, Rosenbauer, Schwenn, Muehlhaeuser and Neubauer1982) and table 1a of Marsch & Tu (Reference Marsch and Tu1990)),
$r=0.3~\text{AU}$
(see table 1 of Marsch et al. (Reference Marsch, Rosenbauer, Schwenn, Muehlhaeuser and Neubauer1982) and table 1a of Marsch & Tu (Reference Marsch and Tu1990)),
In order to compare directly with figure 2–2(c) of Tu & Marsch (Reference Tu and Marsch1995), the solar-wind velocity is taken to be
The power spectra are initialized to the values
and
where
![]() $\unicode[STIX]{x1D70E}^{+}$
,
$\unicode[STIX]{x1D70E}^{+}$
,
![]() $\unicode[STIX]{x1D70E}^{-}$
and
$\unicode[STIX]{x1D70E}^{-}$
and
![]() $f_{0}$
are constants. The values of
$f_{0}$
are constants. The values of
![]() $f_{0}$
and the corresponding wavenumber
$f_{0}$
and the corresponding wavenumber
![]() $k_{z0}$
are chosen so that
$k_{z0}$
are chosen so that
consistent with the arguments of van Ballegooijen & Asgari-Targhi (Reference van Ballegooijen and Asgari-Targhi2016) about the dominant frequency of AW launching by the Sun. The minimum and maximum wavenumbers of the numerical domain are chosen so that
![]() $k_{z\max }=10^{3}k_{z0}=10^{7}k_{z\min }$
. The motivation for the scaling
$k_{z\max }=10^{3}k_{z0}=10^{7}k_{z\min }$
. The motivation for the scaling
![]() $e^{+}(f,t=0)\propto f^{-0.5}$
at small
$e^{+}(f,t=0)\propto f^{-0.5}$
at small
![]() $f$
is the similar scaling observed by Tu & Marsch (Reference Tu and Marsch1995) in the aforementioned fast-solar-wind stream at
$f$
is the similar scaling observed by Tu & Marsch (Reference Tu and Marsch1995) in the aforementioned fast-solar-wind stream at
![]() $10^{-5}~\text{Hz}<f<10^{-4}~\text{Hz}$
. The numerical results shown below suggest that the parametric instability has little effect on
$10^{-5}~\text{Hz}<f<10^{-4}~\text{Hz}$
. The numerical results shown below suggest that the parametric instability has little effect on
![]() $e^{+}$
at these frequencies at
$e^{+}$
at these frequencies at
![]() $r=0.3~\text{AU}$
. The observed
$r=0.3~\text{AU}$
. The observed
![]() $f^{-0.5}$
scaling in this frequency range is thus presumably inherited directly from the spectrum of AWs launched by the Sun. Like the scaling
$f^{-0.5}$
scaling in this frequency range is thus presumably inherited directly from the spectrum of AWs launched by the Sun. Like the scaling
![]() $e^{+}\propto f^{-0.5}$
, the value of
$e^{+}\propto f^{-0.5}$
, the value of
![]() $\unicode[STIX]{x1D70E}^{+}$
is chosen to match the observed spectrum of outward-propagating AWs at 0.3 AU at small
$\unicode[STIX]{x1D70E}^{+}$
is chosen to match the observed spectrum of outward-propagating AWs at 0.3 AU at small
![]() $f$
. The reason for the
$f$
. The reason for the
![]() $f^{-2}$
scaling in
$f^{-2}$
scaling in
![]() $e^{+}$
at large
$e^{+}$
at large
![]() $f$
is that a (parallel)
$f$
is that a (parallel)
![]() $k_{z}^{-2}$
spectrum is observed in the solar wind (Horbury, Forman & Oughton Reference Horbury, Forman and Oughton2008; Podesta Reference Podesta2009; Forman, Wicks & Horbury Reference Forman, Wicks and Horbury2011) and predicted by the theory of critically balanced MHD turbulence (see, e.g. Goldreich & Sridhar Reference Goldreich and Sridhar1995; Mallet, Schekochihin & Chandran Reference Mallet, Schekochihin and Chandran2015). The value of
$k_{z}^{-2}$
spectrum is observed in the solar wind (Horbury, Forman & Oughton Reference Horbury, Forman and Oughton2008; Podesta Reference Podesta2009; Forman, Wicks & Horbury Reference Forman, Wicks and Horbury2011) and predicted by the theory of critically balanced MHD turbulence (see, e.g. Goldreich & Sridhar Reference Goldreich and Sridhar1995; Mallet, Schekochihin & Chandran Reference Mallet, Schekochihin and Chandran2015). The value of
![]() $\unicode[STIX]{x1D70E}^{-}$
is set equal to a minuscule value (
$\unicode[STIX]{x1D70E}^{-}$
is set equal to a minuscule value (
![]() $10^{-12}\unicode[STIX]{x1D70E}^{+}$
), so that the only source of dynamically important, inward-propagating AWs is the parametric decay of outward-propagating AWs.
$10^{-12}\unicode[STIX]{x1D70E}^{+}$
), so that the only source of dynamically important, inward-propagating AWs is the parametric decay of outward-propagating AWs.
Figure 2 summarizes the results of the calculation. Between
![]() $t=0$
and
$t=0$
and
![]() $t=4~\text{h}$
,
$t=4~\text{h}$
,
![]() $e^{+}$
changes little while
$e^{+}$
changes little while
![]() $e^{-}$
grows rapidly between roughly 2 and 5 mHz, where the growth rate
$e^{-}$
grows rapidly between roughly 2 and 5 mHz, where the growth rate
![]() $\unicode[STIX]{x1D6FE}^{-}$
given in (3.1) peaks. Between
$\unicode[STIX]{x1D6FE}^{-}$
given in (3.1) peaks. Between
![]() $t=4$
and
$t=4$
and
![]() $t=8~\text{h}$
,
$t=8~\text{h}$
,
![]() $e^{+}$
develops a broad
$e^{+}$
develops a broad
![]() ${\sim}1/f$
scaling between
${\sim}1/f$
scaling between
![]() $f=3\times 10^{-4}$
and
$f=3\times 10^{-4}$
and
![]() $f=3\times 10^{-2}~\text{Hz}$
, which shuts off the growth of
$f=3\times 10^{-2}~\text{Hz}$
, which shuts off the growth of
![]() $e^{-}$
at these frequencies. At the same time,
$e^{-}$
at these frequencies. At the same time,
![]() $e^{-}$
acquires an
$e^{-}$
acquires an
![]() ${\sim}f^{-2}$
scaling over much of this same frequency range. Between
${\sim}f^{-2}$
scaling over much of this same frequency range. Between
![]() $t=8$
and
$t=8$
and
![]() $t=16~\text{h}$
, the low-frequency limit of the
$t=16~\text{h}$
, the low-frequency limit of the
![]() $1/f$
range of
$1/f$
range of
![]() $e^{+}$
decreases to
$e^{+}$
decreases to
![]() ${\sim}10^{-4}~\text{Hz}$
, and the high-frequency limit of the
${\sim}10^{-4}~\text{Hz}$
, and the high-frequency limit of the
![]() $1/f$
range of
$1/f$
range of
![]() $e^{+}$
increases to
$e^{+}$
increases to
![]() ${\sim}0.1~\text{Hz}$
.
${\sim}0.1~\text{Hz}$
.

Figure 2. Solid lines show the AW power spectra in a numerical solution of (2.11) with plasma parameters and turbulence parameters chosen to model conditions in the fast solar wind at a heliocentric distance of 0.3 AU. The wavenumber spectra
![]() $E^{\pm }(k_{z})$
appearing in (2.11) have been converted, using (6.3) and (6.4), into the frequency spectra
$E^{\pm }(k_{z})$
appearing in (2.11) have been converted, using (6.3) and (6.4), into the frequency spectra
![]() $e^{\pm }(f)$
. The dotted lines in the upper left corners of each plot show the evolutionary tracks of the values of
$e^{\pm }(f)$
. The dotted lines in the upper left corners of each plot show the evolutionary tracks of the values of
![]() $e^{+}$
and
$e^{+}$
and
![]() $e^{-}$
at the low-frequency end of the frequency range in which
$e^{-}$
at the low-frequency end of the frequency range in which
![]() $e^{+}\propto f^{-1}$
in the approximate analytic solution to (2.11) presented in appendix B.
$e^{+}\propto f^{-1}$
in the approximate analytic solution to (2.11) presented in appendix B.

Figure 3. In this figure, it is assumed that the frequency spectra are initially power laws of the form
![]() $e^{\pm }\propto f^{\unicode[STIX]{x1D6FC}^{\pm }}$
, and that
$e^{\pm }\propto f^{\unicode[STIX]{x1D6FC}^{\pm }}$
, and that
![]() $\unicode[STIX]{x1D6FC}^{+}$
and
$\unicode[STIX]{x1D6FC}^{+}$
and
![]() $\unicode[STIX]{x1D6FC}^{-}$
are both negative. According to (6.11), parametric decay alters both the amplitude and slope of
$\unicode[STIX]{x1D6FC}^{-}$
are both negative. According to (6.11), parametric decay alters both the amplitude and slope of
![]() $e^{\pm }$
in the manner shown. For example, if
$e^{\pm }$
in the manner shown. For example, if
![]() $e^{-}\propto f^{-1.5}$
, then
$e^{-}\propto f^{-1.5}$
, then
![]() $E^{+}\propto k_{z}^{-1.5}$
, and (6.11) implies that
$E^{+}\propto k_{z}^{-1.5}$
, and (6.11) implies that
![]() $E^{+}$
decreases at a rate that increases with
$E^{+}$
decreases at a rate that increases with
![]() $k_{z}$
. This in turn implies that
$k_{z}$
. This in turn implies that
![]() $e^{+}$
decreases at a rate that increases with
$e^{+}$
decreases at a rate that increases with
![]() $f$
, so that
$f$
, so that
![]() $e^{+}$
steepens.
$e^{+}$
steepens.

Figure 4. (a,b) Reproductions of the
![]() $t=4$
and
$t=4$
and
![]() $t=8~\text{h}$
panels of figure 2 but with the axis ranges used in figure 2–2(c) of Tu & Marsch (Reference Tu and Marsch1995). (c) From a later time (
$t=8~\text{h}$
panels of figure 2 but with the axis ranges used in figure 2–2(c) of Tu & Marsch (Reference Tu and Marsch1995). (c) From a later time (
![]() $t=32~\text{h}$
) in the same numerical solution.
$t=32~\text{h}$
) in the same numerical solution.
The dotted lines in the upper left corner of each panel in figure 2 show the tracks followed by the values of
![]() $e^{+}$
and
$e^{+}$
and
![]() $e^{-}$
at the low-frequency end of the frequency range in which
$e^{-}$
at the low-frequency end of the frequency range in which
![]() $e^{+}\propto f^{-1}$
in the approximate analytic solution to (2.11) that is described in appendix B. In this solution,
$e^{+}\propto f^{-1}$
in the approximate analytic solution to (2.11) that is described in appendix B. In this solution,
![]() $E^{+}$
and
$E^{+}$
and
![]() $E^{-}$
are expanded in negative powers of
$E^{-}$
are expanded in negative powers of
![]() $k_{z}$
at wavenumbers exceeding a time-dependent break wavenumber
$k_{z}$
at wavenumbers exceeding a time-dependent break wavenumber
![]() $b(t)$
. Below this wavenumber,
$b(t)$
. Below this wavenumber,
![]() $E^{-}=0$
and
$E^{-}=0$
and
![]() $E^{+}=\unicode[STIX]{x1D702}k_{z}^{p}$
, where
$E^{+}=\unicode[STIX]{x1D702}k_{z}^{p}$
, where
![]() $\unicode[STIX]{x1D702}$
and
$\unicode[STIX]{x1D702}$
and
![]() $p$
are constants, and
$p$
are constants, and
![]() $-1<p<1$
. At
$-1<p<1$
. At
![]() $k_{z}>b$
, the dominant term in the expansion of
$k_{z}>b$
, the dominant term in the expansion of
![]() $E^{+}$
(
$E^{+}$
(
![]() $E^{-}$
) scales like
$E^{-}$
) scales like
![]() $k_{z}^{-1}$
(
$k_{z}^{-1}$
(
![]() $k_{z}^{-2}$
), and the ratios of
$k_{z}^{-2}$
), and the ratios of
![]() $E^{+}(b_{+})$
to
$E^{+}(b_{+})$
to
![]() $\unicode[STIX]{x1D702}b_{+}^{p}$
and
$\unicode[STIX]{x1D702}b_{+}^{p}$
and
![]() $E^{+}(b_{+})$
to
$E^{+}(b_{+})$
to
![]() $E^{-}(b_{+})$
are fixed functions of
$E^{-}(b_{+})$
are fixed functions of
![]() $p$
, where
$p$
, where
![]() $b_{+}$
is a wavenumber infinitesimally larger than
$b_{+}$
is a wavenumber infinitesimally larger than
![]() $b$
. For
$b$
. For
![]() $p=-0.5$
,
$p=-0.5$
,
![]() $E^{+}(b_{+})/\unicode[STIX]{x1D702}b_{+}^{p}=5/3$
and
$E^{+}(b_{+})/\unicode[STIX]{x1D702}b_{+}^{p}=5/3$
and
![]() $E^{+}(b_{+})/E^{-}(b_{+})=10$
, in approximate agreement with the numerical results (see also figure 4
c).
$E^{+}(b_{+})/E^{-}(b_{+})=10$
, in approximate agreement with the numerical results (see also figure 4
c).
6.1 Heuristic explanation of the
 $e^{+}\propto f^{-1}$
and
$e^{+}\propto f^{-1}$
and
 $e^{-}\propto f^{-2}$
scalings
$e^{-}\propto f^{-2}$
scalings
In order to understand the time evolution illustrated in figure 2, it is instructive to first consider the case in which
within some interval
![]() $(k_{z1},k_{z2})$
, where
$(k_{z1},k_{z2})$
, where
![]() $c^{\pm }$
and
$c^{\pm }$
and
![]() $\unicode[STIX]{x1D6FC}^{\pm }$
are constants. Equation (2.11) implies that, within this interval,
$\unicode[STIX]{x1D6FC}^{\pm }$
are constants. Equation (2.11) implies that, within this interval,
If
![]() $\unicode[STIX]{x1D6FC}^{\mp }>-1$
, then
$\unicode[STIX]{x1D6FC}^{\mp }>-1$
, then
![]() $\ln E^{\pm }$
grows at a rate that increases with
$\ln E^{\pm }$
grows at a rate that increases with
![]() $k_{z}$
, causing
$k_{z}$
, causing
![]() $E^{\pm }$
to increase and ‘harden’, in the sense that the best-fit value of
$E^{\pm }$
to increase and ‘harden’, in the sense that the best-fit value of
![]() $\unicode[STIX]{x1D6FC}^{\pm }$
within the interval
$\unicode[STIX]{x1D6FC}^{\pm }$
within the interval
![]() $(k_{z1},k_{z2})$
increases. If
$(k_{z1},k_{z2})$
increases. If
![]() $\unicode[STIX]{x1D6FC}^{\mp }=-1$
, then
$\unicode[STIX]{x1D6FC}^{\mp }=-1$
, then
![]() $E^{\pm }$
does not change. If
$E^{\pm }$
does not change. If
![]() $-2<\unicode[STIX]{x1D6FC}^{\mp }<-1$
, then
$-2<\unicode[STIX]{x1D6FC}^{\mp }<-1$
, then
![]() $\ln E^{\pm }$
decreases at a rate that increases with
$\ln E^{\pm }$
decreases at a rate that increases with
![]() $k_{z}$
, which causes the best-fit value of
$k_{z}$
, which causes the best-fit value of
![]() $\unicode[STIX]{x1D6FC}^{\pm }$
within the interval
$\unicode[STIX]{x1D6FC}^{\pm }$
within the interval
![]() $(k_{z1},k_{z2})$
to decrease. If
$(k_{z1},k_{z2})$
to decrease. If
![]() $\unicode[STIX]{x1D6FC}^{\mp }=-2$
, then
$\unicode[STIX]{x1D6FC}^{\mp }=-2$
, then
![]() $\ln E^{\pm }$
decreases at the same rate at all
$\ln E^{\pm }$
decreases at the same rate at all
![]() $k_{z}$
, and
$k_{z}$
, and
![]() $\unicode[STIX]{x1D6FC}^{\pm }$
remains unchanged. Finally, if
$\unicode[STIX]{x1D6FC}^{\pm }$
remains unchanged. Finally, if
![]() $\unicode[STIX]{x1D6FC}^{\mp }<2$
, then
$\unicode[STIX]{x1D6FC}^{\mp }<2$
, then
![]() $E^{\pm }$
decreases at a rate that decreases with
$E^{\pm }$
decreases at a rate that decreases with
![]() $k_{z}$
, which causes the best-fit value of
$k_{z}$
, which causes the best-fit value of
![]() $\unicode[STIX]{x1D6FC}^{\pm }$
in the interval
$\unicode[STIX]{x1D6FC}^{\pm }$
in the interval
![]() $(k_{z1},k_{z2})$
to increase. These rules are summarized in figure 3 and apply to
$(k_{z1},k_{z2})$
to increase. These rules are summarized in figure 3 and apply to
![]() $e^{\pm }\propto f^{\unicode[STIX]{x1D6FC}^{\pm }}$
as well as
$e^{\pm }\propto f^{\unicode[STIX]{x1D6FC}^{\pm }}$
as well as
![]() $E^{\pm }\propto k_{z}^{\unicode[STIX]{x1D6FC}^{\pm }}$
.
$E^{\pm }\propto k_{z}^{\unicode[STIX]{x1D6FC}^{\pm }}$
.
Returning to figure 2, in the early stages of the numerical calculation,
![]() $e^{-}$
grows most rapidly at those frequencies at which
$e^{-}$
grows most rapidly at those frequencies at which
![]() $\unicode[STIX]{x1D6FE}^{-}$
in (3.1) is largest – namely, the high-
$\unicode[STIX]{x1D6FE}^{-}$
in (3.1) is largest – namely, the high-
![]() $f$
end of the
$f$
end of the
![]() $f^{-0.5}$
range of
$f^{-0.5}$
range of
![]() $e^{+}$
. By the time
$e^{+}$
. By the time
![]() $e^{-}$
reaches a sufficient amplitude that
$e^{-}$
reaches a sufficient amplitude that
![]() $e^{+}$
and
$e^{+}$
and
![]() $e^{-}$
evolve on the same time scale,
$e^{-}$
evolve on the same time scale,
![]() $e^{-}$
develops a peaked frequency profile extending from some frequency
$e^{-}$
develops a peaked frequency profile extending from some frequency
![]() $f=f_{\text{low}}$
to some larger frequency
$f=f_{\text{low}}$
to some larger frequency
![]() $f=f_{\text{high}}$
, as illustrated in figure 2(b). Near
$f=f_{\text{high}}$
, as illustrated in figure 2(b). Near
![]() $f_{\text{low}}$
,
$f_{\text{low}}$
,
![]() $\text{d}e^{-}/\text{d}f>0$
(i.e.
$\text{d}e^{-}/\text{d}f>0$
(i.e.
![]() $\unicode[STIX]{x1D6FC}^{-}>0$
), which causes
$\unicode[STIX]{x1D6FC}^{-}>0$
), which causes
![]() $e^{+}$
to grow.Footnote
3
Near
$e^{+}$
to grow.Footnote
3
Near
![]() $f_{\text{high}}$
,
$f_{\text{high}}$
,
![]() $\unicode[STIX]{x1D6FC}^{-}<-1$
, which causes
$\unicode[STIX]{x1D6FC}^{-}<-1$
, which causes
![]() $e^{+}$
to decrease. Thus,
$e^{+}$
to decrease. Thus,
![]() $e^{+}$
steepens across the interval
$e^{+}$
steepens across the interval
![]() $(f_{\text{low}},f_{\text{high}})$
until it attains a
$(f_{\text{low}},f_{\text{high}})$
until it attains a
![]() $1/f$
scaling, at which point
$1/f$
scaling, at which point
![]() $e^{-}$
stops growing between
$e^{-}$
stops growing between
![]() $f_{\text{low}}$
and
$f_{\text{low}}$
and
![]() $f_{\text{high}}$
. However, at frequencies just below
$f_{\text{high}}$
. However, at frequencies just below
![]() $f_{\text{low}}$
,
$f_{\text{low}}$
,
![]() $e^{+}$
and
$e^{+}$
and
![]() $e^{-}$
both continue to grow, causing
$e^{-}$
both continue to grow, causing
![]() $f_{\text{low}}$
to decrease. At the same time,
$f_{\text{low}}$
to decrease. At the same time,
![]() $e^{+}$
continues to decrease at larger
$e^{+}$
continues to decrease at larger
![]() $f$
where
$f$
where
![]() $\unicode[STIX]{x1D6FC}^{-}<-1$
. Together, the growth of
$\unicode[STIX]{x1D6FC}^{-}<-1$
. Together, the growth of
![]() $e^{+}$
just below
$e^{+}$
just below
![]() $f_{\text{low}}$
and the damping of
$f_{\text{low}}$
and the damping of
![]() $e^{+}$
at larger
$e^{+}$
at larger
![]() $f$
cause the
$f$
cause the
![]() $f^{-1}$
range of
$f^{-1}$
range of
![]() $e^{+}$
to broaden in both directions, i.e. towards both smaller and larger frequencies.
$e^{+}$
to broaden in both directions, i.e. towards both smaller and larger frequencies.
The unique scaling of
![]() $e^{-}$
consistent with an
$e^{-}$
consistent with an
![]() $e^{+}$
spectrum
$e^{+}$
spectrum
![]() $\propto f^{-1}$
that is a decreasing function of time is
$\propto f^{-1}$
that is a decreasing function of time is
![]() $e^{-}\propto f^{-2}$
. Moreover, the scalings
$e^{-}\propto f^{-2}$
. Moreover, the scalings
![]() $e^{+}\sim f^{-1}$
and
$e^{+}\sim f^{-1}$
and
![]() $e^{-}\sim f^{-2}$
are, in a sense, stable, as can be inferred from figure 3. For example, if
$e^{-}\sim f^{-2}$
are, in a sense, stable, as can be inferred from figure 3. For example, if
![]() $\unicode[STIX]{x1D6FC}^{-}$
increases from
$\unicode[STIX]{x1D6FC}^{-}$
increases from
![]() $-2$
to a slightly larger value, then
$-2$
to a slightly larger value, then
![]() $e^{+}$
decreases at a rate that increases with
$e^{+}$
decreases at a rate that increases with
![]() $f$
, causing
$f$
, causing
![]() $\unicode[STIX]{x1D6FC}^{+}$
to decrease to a value slightly below
$\unicode[STIX]{x1D6FC}^{+}$
to decrease to a value slightly below
![]() $-1$
. This causes
$-1$
. This causes
![]() $e^{-}$
to decrease at a rate that increases with
$e^{-}$
to decrease at a rate that increases with
![]() $f$
, thereby causing
$f$
, thereby causing
![]() $\unicode[STIX]{x1D6FC}^{-}$
to decrease back towards
$\unicode[STIX]{x1D6FC}^{-}$
to decrease back towards
![]() $-2$
. A similar ‘spectral restoring force’ arises for any other small perturbation to the values
$-2$
. A similar ‘spectral restoring force’ arises for any other small perturbation to the values
![]() $\unicode[STIX]{x1D6FC}^{+}=-1$
and
$\unicode[STIX]{x1D6FC}^{+}=-1$
and
![]() $\unicode[STIX]{x1D6FC}^{-}=-2$
.
$\unicode[STIX]{x1D6FC}^{-}=-2$
.
It is worth emphasizing, in this context, that the analytic solution presented in appendix B is approximate rather than exact. As the spectral break frequency decreases past some fixed frequency
![]() $f_{3}$
, the values of
$f_{3}$
, the values of
![]() $e^{+}$
and
$e^{+}$
and
![]() $e^{-}$
at
$e^{-}$
at
![]() $f_{3}$
suddenly jump, but they do not jump to the precise values needed to extend the
$f_{3}$
suddenly jump, but they do not jump to the precise values needed to extend the
![]() $e^{+}\sim f^{-1}$
and
$e^{+}\sim f^{-1}$
and
![]() $e^{-}\sim f^{-2}$
scalings to smaller
$e^{-}\sim f^{-2}$
scalings to smaller
![]() $f$
. Instead, the spectra need further ‘correcting’ after the break frequency has swept past in order to maintain the scalings
$f$
. Instead, the spectra need further ‘correcting’ after the break frequency has swept past in order to maintain the scalings
![]() $e^{+}\sim f^{-1}$
and
$e^{+}\sim f^{-1}$
and
![]() $e^{-}\sim f^{-2}$
in an approximate way. Also, the decrease in
$e^{-}\sim f^{-2}$
in an approximate way. Also, the decrease in
![]() $e^{-}$
that occurs after
$e^{-}$
that occurs after
![]() $t=4~\text{h}$
is a consequence of the sub-dominant
$t=4~\text{h}$
is a consequence of the sub-dominant
![]() $f^{-2}$
component of
$f^{-2}$
component of
![]() $e^{+}$
. This component of
$e^{+}$
. This component of
![]() $e^{+}$
becomes increasingly prominent near the break frequency as time progresses, leading to the pronounced curvature in the plot of
$e^{+}$
becomes increasingly prominent near the break frequency as time progresses, leading to the pronounced curvature in the plot of
![]() $e^{+}$
near
$e^{+}$
near
![]() $f=10^{-4}~\text{Hz}$
in figure 4(c).
$f=10^{-4}~\text{Hz}$
in figure 4(c).
6.2 Comparison with Helios measurements
In the (average) plasma rest frame, the equations of incompressible MHD can be written in the form
where
![]() $\boldsymbol{z}^{\pm }=\unicode[STIX]{x1D6FF}\boldsymbol{v}\mp \unicode[STIX]{x1D6FF}\boldsymbol{B}/\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}}$
are the Elsasser variables,
$\boldsymbol{z}^{\pm }=\unicode[STIX]{x1D6FF}\boldsymbol{v}\mp \unicode[STIX]{x1D6FF}\boldsymbol{B}/\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}}$
are the Elsasser variables,
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{v}$
and
$\unicode[STIX]{x1D6FF}\boldsymbol{v}$
and
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{B}$
are the velocity and magnetic-field fluctuations,
$\unicode[STIX]{x1D6FF}\boldsymbol{B}$
are the velocity and magnetic-field fluctuations,
![]() $\unicode[STIX]{x1D70C}$
is the mass density,
$\unicode[STIX]{x1D70C}$
is the mass density,
![]() $\boldsymbol{v}_{\text{A}}=\boldsymbol{B}_{0}/\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}}$
is the Alfvén velocity and
$\boldsymbol{v}_{\text{A}}=\boldsymbol{B}_{0}/\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}}$
is the Alfvén velocity and
![]() $\unicode[STIX]{x1D6F1}$
is the total pressure divided by
$\unicode[STIX]{x1D6F1}$
is the total pressure divided by
![]() $\unicode[STIX]{x1D70C}$
(Elsasser Reference Elsasser1950). Although the solar wind is compressible, equation (6.12) provides a reasonable approximation for the non-compressive, AW-like component of solar-wind turbulence. As (6.12) shows, the advection velocity of a
$\unicode[STIX]{x1D70C}$
(Elsasser Reference Elsasser1950). Although the solar wind is compressible, equation (6.12) provides a reasonable approximation for the non-compressive, AW-like component of solar-wind turbulence. As (6.12) shows, the advection velocity of a
![]() $\boldsymbol{z}^{\pm }$
fluctuation is
$\boldsymbol{z}^{\pm }$
fluctuation is
![]() $\boldsymbol{z}^{\mp }\pm \boldsymbol{v}_{\text{A}}$
. This implies, as shown by Maron & Goldreich (Reference Maron and Goldreich2001), that
$\boldsymbol{z}^{\mp }\pm \boldsymbol{v}_{\text{A}}$
. This implies, as shown by Maron & Goldreich (Reference Maron and Goldreich2001), that
![]() $\boldsymbol{z}^{\pm }$
fluctuations propagate along magnetic field lines perturbed by
$\boldsymbol{z}^{\pm }$
fluctuations propagate along magnetic field lines perturbed by
![]() $\boldsymbol{z}^{\mp }$
. As a consequence, in the solar wind, when the root-mean-square (rms) magnetic-field fluctuation
$\boldsymbol{z}^{\mp }$
. As a consequence, in the solar wind, when the root-mean-square (rms) magnetic-field fluctuation
![]() $\unicode[STIX]{x1D6FF}B_{\text{in}}$
associated with inward-propagating AWs (
$\unicode[STIX]{x1D6FF}B_{\text{in}}$
associated with inward-propagating AWs (
![]() $\boldsymbol{z}^{-}$
) is much smaller than the background magnetic field
$\boldsymbol{z}^{-}$
) is much smaller than the background magnetic field
![]() $B_{0}$
, the outward-propagating AWs (
$B_{0}$
, the outward-propagating AWs (
![]() $\boldsymbol{z}^{+}$
) propagate to a good approximation along the direction of
$\boldsymbol{z}^{+}$
) propagate to a good approximation along the direction of
![]() $\boldsymbol{B}_{0}$
. This is true even if the rms magnetic-field fluctuation
$\boldsymbol{B}_{0}$
. This is true even if the rms magnetic-field fluctuation
![]() $\unicode[STIX]{x1D6FF}B_{\text{out}}$
associated with
$\unicode[STIX]{x1D6FF}B_{\text{out}}$
associated with
![]() $\boldsymbol{z}^{+}$
is comparable to
$\boldsymbol{z}^{+}$
is comparable to
![]() $B_{0}$
. In the fast solar wind at
$B_{0}$
. In the fast solar wind at
![]() $r<0.3~\text{AU}$
, the (fractional) cross-helicity is high (i.e.
$r<0.3~\text{AU}$
, the (fractional) cross-helicity is high (i.e.
![]() $E^{+}\gg E^{-}$
), and
$E^{+}\gg E^{-}$
), and
![]() $\unicode[STIX]{x1D6FF}B_{\text{in}}$
is indeed small compared to
$\unicode[STIX]{x1D6FF}B_{\text{in}}$
is indeed small compared to
![]() $B_{0}$
(Bavassano, Pietropaolo & Bruno Reference Bavassano, Pietropaolo and Bruno2000; Cranmer & van Ballegooijen Reference Cranmer and van Ballegooijen2005). Moreover, the background magnetic field at
$B_{0}$
(Bavassano, Pietropaolo & Bruno Reference Bavassano, Pietropaolo and Bruno2000; Cranmer & van Ballegooijen Reference Cranmer and van Ballegooijen2005). Moreover, the background magnetic field at
![]() $r=0.3~\text{AU}$
is nearly in the radial direction, because the Parker-spiral magnetic field begins to deviate appreciably from the radial direction only at larger
$r=0.3~\text{AU}$
is nearly in the radial direction, because the Parker-spiral magnetic field begins to deviate appreciably from the radial direction only at larger
![]() $r$
in the fast wind (Verscharen et al.
Reference Verscharen, Chandran, Bourouaine and Hollweg2015). Hence, in high-cross-helicity fast-wind streams at
$r$
in the fast wind (Verscharen et al.
Reference Verscharen, Chandran, Bourouaine and Hollweg2015). Hence, in high-cross-helicity fast-wind streams at
![]() $r=0.3~\text{AU}$
, the function
$r=0.3~\text{AU}$
, the function
![]() $e^{+}$
defined by (6.3) and (6.4) corresponds to a good approximation to the frequency spectrum of outward-propagating AWs observed by a spacecraft in the solar wind. It is not clear, however, how well
$e^{+}$
defined by (6.3) and (6.4) corresponds to a good approximation to the frequency spectrum of outward-propagating AWs observed by a spacecraft in the solar wind. It is not clear, however, how well
![]() $e^{-}$
corresponds to the observed spectrum of inward-propagating AWs, because the inward-propagating AWs follow field lines perturbed by the outward-propagating AWs, which can be inclined relative to the radial direction by a substantial angle.
$e^{-}$
corresponds to the observed spectrum of inward-propagating AWs, because the inward-propagating AWs follow field lines perturbed by the outward-propagating AWs, which can be inclined relative to the radial direction by a substantial angle.
Figure 4 reproduces the
![]() $t=4~\text{h}$
and
$t=4~\text{h}$
and
![]() $t=8~\text{h}$
panels of figure 2, but with the same axis ranges as those in figure 2–2(c) of Tu & Marsch (Reference Tu and Marsch1995) to facilitate comparison. Figure 4 also includes a third panel that shows the spectra at
$t=8~\text{h}$
panels of figure 2, but with the same axis ranges as those in figure 2–2(c) of Tu & Marsch (Reference Tu and Marsch1995) to facilitate comparison. Figure 4 also includes a third panel that shows the spectra at
![]() $t=32~\text{h}$
. The
$t=32~\text{h}$
. The
![]() $e^{+}$
spectrum in the
$e^{+}$
spectrum in the
![]() $t=8~\text{h}$
panel of figure 2 shares a number of properties with the
$t=8~\text{h}$
panel of figure 2 shares a number of properties with the
![]() $e^{+}$
spectrum in figure 2–2(c) of Tu & Marsch (Reference Tu and Marsch1995), in addition to the
$e^{+}$
spectrum in figure 2–2(c) of Tu & Marsch (Reference Tu and Marsch1995), in addition to the
![]() $f^{-0.5}$
scaling at small
$f^{-0.5}$
scaling at small
![]() $f$
that was built in to the numerical calculation as an initial condition. In particular,
$f$
that was built in to the numerical calculation as an initial condition. In particular,
![]() $e^{+}\gg e^{-}$
at all frequencies,
$e^{+}\gg e^{-}$
at all frequencies,
![]() $e^{+}\sim f^{-1}$
at
$e^{+}\sim f^{-1}$
at
![]() $f\gtrsim 3\times 10^{-4}~\text{Hz}$
, and there is a bump in the
$f\gtrsim 3\times 10^{-4}~\text{Hz}$
, and there is a bump in the
![]() $e^{+}$
spectrum at the transition between the
$e^{+}$
spectrum at the transition between the
![]() $f^{-0.5}$
and
$f^{-0.5}$
and
![]() $f^{-1}$
scaling ranges of
$f^{-1}$
scaling ranges of
![]() $e^{+}$
.
$e^{+}$
.
Although this comparison is suggestive, it is not entirely clear how to map time in the numerical calculation to heliocentric distance in the solar wind, because the plasma parameters in the numerical calculation are independent of position and time, whereas they depend strongly upon heliocentric distance in the solar wind. For example, the turbulence is weaker (in the sense of smaller
![]() $\unicode[STIX]{x1D6FF}v_{0}/v_{\text{A}}$
) the closer one gets to the Sun. (See also the discussion following (7.10).) Also, the choice of initial conditions in the numerical calculation artificially prolongs the linear stage of evolution, since in the solar wind there are sources of inward-propagating waves other than parametric instability, such as non-WKB reflection (Heinemann & Olbert Reference Heinemann and Olbert1980; Velli Reference Velli1993). Nevertheless, as a baseline for comparison, the travel time of an outward-propagating AW from the photosphere to
$\unicode[STIX]{x1D6FF}v_{0}/v_{\text{A}}$
) the closer one gets to the Sun. (See also the discussion following (7.10).) Also, the choice of initial conditions in the numerical calculation artificially prolongs the linear stage of evolution, since in the solar wind there are sources of inward-propagating waves other than parametric instability, such as non-WKB reflection (Heinemann & Olbert Reference Heinemann and Olbert1980; Velli Reference Velli1993). Nevertheless, as a baseline for comparison, the travel time of an outward-propagating AW from the photosphere to
![]() $0.3~\text{AU}$
in the fast-solar-wind model developed by Chandran & Hollweg (Reference Chandran and Hollweg2009) is approximately 12 h.
$0.3~\text{AU}$
in the fast-solar-wind model developed by Chandran & Hollweg (Reference Chandran and Hollweg2009) is approximately 12 h.
7 Discussion of approximations and relevance to the solar wind
This section critically assesses the assumptions underlying the results in §§ 2 through 6 and the degree to which these assumptions apply to the fast solar wind between
![]() $r=10R_{\odot }$
(the approximate perihelion of the Parker Solar Probe) and
$r=10R_{\odot }$
(the approximate perihelion of the Parker Solar Probe) and
![]() $r=0.3~\text{AU}$
.
$r=0.3~\text{AU}$
.
7.1 The weak-turbulence approximation
A central assumption of the analysis is the weak-turbulence criterion in (2.1). Since
![]() $E^{+}$
and
$E^{+}$
and
![]() $E^{-}$
differ in the solar wind, equation (2.1) is really two conditions,
$E^{-}$
differ in the solar wind, equation (2.1) is really two conditions,
where
![]() $\unicode[STIX]{x1D714}_{\text{nl}}^{+}$
(
$\unicode[STIX]{x1D714}_{\text{nl}}^{+}$
(
![]() $\unicode[STIX]{x1D714}_{\text{nl}}^{-}$
) is the inverse of the time scale on which nonlinear interactions modify outward-propagating (inward-propagating) AWs. The contribution to
$\unicode[STIX]{x1D714}_{\text{nl}}^{-}$
) is the inverse of the time scale on which nonlinear interactions modify outward-propagating (inward-propagating) AWs. The contribution to
![]() $\unicode[STIX]{x1D714}_{\text{nl}}^{\pm }$
from the parametric instability is
$\unicode[STIX]{x1D714}_{\text{nl}}^{\pm }$
from the parametric instability is
The contribution to
![]() $\unicode[STIX]{x1D714}_{\text{nl}}^{\pm }$
from one other type of nonlinear interaction is estimated in § 7.3. The estimate of
$\unicode[STIX]{x1D714}_{\text{nl}}^{\pm }$
from one other type of nonlinear interaction is estimated in § 7.3. The estimate of
![]() $\unicode[STIX]{x2202}E^{\pm }/\unicode[STIX]{x2202}t$
in (7.2) follows from (2.11) and setting
$\unicode[STIX]{x2202}E^{\pm }/\unicode[STIX]{x2202}t$
in (7.2) follows from (2.11) and setting
![]() $E^{\mp }\sim |k_{z}|^{\unicode[STIX]{x1D6FC}^{\mp }}$
with
$E^{\mp }\sim |k_{z}|^{\unicode[STIX]{x1D6FC}^{\mp }}$
with
![]() $\unicode[STIX]{x1D6FC}^{\mp }$
not very close to
$\unicode[STIX]{x1D6FC}^{\mp }$
not very close to
![]() $-1$
. An approximate upper limit on
$-1$
. An approximate upper limit on
![]() $\unicode[STIX]{x1D714}_{\text{nl},\text{PI}}^{\pm }$
results from replacing
$\unicode[STIX]{x1D714}_{\text{nl},\text{PI}}^{\pm }$
results from replacing
![]() $k_{z}E^{\mp }$
in (7.2) with
$k_{z}E^{\mp }$
in (7.2) with
![]() $(\unicode[STIX]{x1D6FF}v^{\mp })^{2}$
, where
$(\unicode[STIX]{x1D6FF}v^{\mp })^{2}$
, where
![]() $(\unicode[STIX]{x1D6FF}v^{+})^{2}$
is the mean-square velocity fluctuation associated with outward-propagating AWs, and
$(\unicode[STIX]{x1D6FF}v^{+})^{2}$
is the mean-square velocity fluctuation associated with outward-propagating AWs, and
![]() $(\unicode[STIX]{x1D6FF}v^{-})^{2}$
is the mean-square velocity fluctuation associated with inward-propagating AWs. This leads to an approximate upper limit on
$(\unicode[STIX]{x1D6FF}v^{-})^{2}$
is the mean-square velocity fluctuation associated with inward-propagating AWs. This leads to an approximate upper limit on
![]() $\unicode[STIX]{x1D714}_{\text{nl},\text{PI}}^{\pm }$
because
$\unicode[STIX]{x1D714}_{\text{nl},\text{PI}}^{\pm }$
because
![]() $(\unicode[STIX]{x1D6FF}v^{\pm })^{2}$
includes contributions from all wavenumbers and is much larger than the value of
$(\unicode[STIX]{x1D6FF}v^{\pm })^{2}$
includes contributions from all wavenumbers and is much larger than the value of
![]() $k_{z}E^{\pm }$
at some
$k_{z}E^{\pm }$
at some
![]() $k_{z}$
. Equation (7.1), with
$k_{z}$
. Equation (7.1), with
![]() $\unicode[STIX]{x1D714}_{\text{nl}}\sim \unicode[STIX]{x1D714}_{\text{nl},\text{PI}}$
, is thus satisfied provided
$\unicode[STIX]{x1D714}_{\text{nl}}\sim \unicode[STIX]{x1D714}_{\text{nl},\text{PI}}$
, is thus satisfied provided
Bavassano et al. (Reference Bavassano, Pietropaolo and Bruno2000) analysed Helios measurements of fluctuations in the fast solar wind at
![]() $r=0.4~\text{AU}$
and found that
$r=0.4~\text{AU}$
and found that
![]() $(\unicode[STIX]{x1D6FF}v^{-})^{2}\ll (\unicode[STIX]{x1D6FF}v^{+})^{2}\simeq (60~\text{km}~\text{s}^{-1})^{2}$
. As mentioned above, the typical value of
$(\unicode[STIX]{x1D6FF}v^{-})^{2}\ll (\unicode[STIX]{x1D6FF}v^{+})^{2}\simeq (60~\text{km}~\text{s}^{-1})^{2}$
. As mentioned above, the typical value of
![]() $v_{\text{A}}$
in the fast solar wind at
$v_{\text{A}}$
in the fast solar wind at
![]() $r=0.3~\text{AU}$
is
$r=0.3~\text{AU}$
is
![]() ${\sim}150~\text{km}~\text{s}^{-1}$
(Marsch et al.
Reference Marsch, Rosenbauer, Schwenn, Muehlhaeuser and Neubauer1982; Marsch & Tu Reference Marsch and Tu1990). Near
${\sim}150~\text{km}~\text{s}^{-1}$
(Marsch et al.
Reference Marsch, Rosenbauer, Schwenn, Muehlhaeuser and Neubauer1982; Marsch & Tu Reference Marsch and Tu1990). Near
![]() $r=0.3~\text{AU}$
,
$r=0.3~\text{AU}$
,
![]() $B_{0}\sim 1/r^{2}$
,
$B_{0}\sim 1/r^{2}$
,
![]() $\unicode[STIX]{x1D70C}\sim 1/r^{2}$
and
$\unicode[STIX]{x1D70C}\sim 1/r^{2}$
and
![]() $v_{\text{A}}\sim 1/r$
, and so the typical value of
$v_{\text{A}}\sim 1/r$
, and so the typical value of
![]() $v_{\text{A}}$
in fast-solar-wind streams at
$v_{\text{A}}$
in fast-solar-wind streams at
![]() $r=0.4~\text{AU}$
is
$r=0.4~\text{AU}$
is
![]() ${\sim}112.5~\text{km}~\text{s}^{-1}$
. These measurements indicate that
${\sim}112.5~\text{km}~\text{s}^{-1}$
. These measurements indicate that
in the fast solar wind at
![]() $r=0.4~\text{AU}$
. Since
$r=0.4~\text{AU}$
. Since
![]() $\unicode[STIX]{x1D6FF}v^{\pm }/v_{\text{A}}$
decreases as
$\unicode[STIX]{x1D6FF}v^{\pm }/v_{\text{A}}$
decreases as
![]() $r$
decreases below
$r$
decreases below
![]() $0.4~\text{AU}$
(Cranmer & van Ballegooijen Reference Cranmer and van Ballegooijen2005; Chandran & Hollweg Reference Chandran and Hollweg2009), the condition
$0.4~\text{AU}$
(Cranmer & van Ballegooijen Reference Cranmer and van Ballegooijen2005; Chandran & Hollweg Reference Chandran and Hollweg2009), the condition
![]() $\unicode[STIX]{x1D714}_{\text{nl},\text{PI}}^{+}\ll |k_{z}|v_{\text{A}}$
is well satisfied at
$\unicode[STIX]{x1D714}_{\text{nl},\text{PI}}^{+}\ll |k_{z}|v_{\text{A}}$
is well satisfied at
![]() $r<0.4~\text{AU}$
, and the condition
$r<0.4~\text{AU}$
, and the condition
![]() $\unicode[STIX]{x1D714}_{\text{nl},\text{PI}}^{-}\ll |k_{z}|v_{\text{A}}$
is at least marginally satisfied at
$\unicode[STIX]{x1D714}_{\text{nl},\text{PI}}^{-}\ll |k_{z}|v_{\text{A}}$
is at least marginally satisfied at
![]() $r<0.4~\text{AU}$
.
$r<0.4~\text{AU}$
.
It is worth noting that weak-turbulence theory fails when applied to resonant interactions between three AWs, because such interactions occur only when one of the AWs has zero frequency, violating the weak-turbulence ordering (Schekochihin, Nazarenko & Yousef Reference Schekochihin, Nazarenko and Yousef2012; Meyrand, Kiyani & Galtier Reference Meyrand, Kiyani and Galtier2015). In contrast, the AW/slow-wave interactions in parametric decay do not involve a zero-frequency mode. Weak-turbulence theory is thus in principle a better approximation for the nonlinear evolution of the parametric instability than for incompressible MHD turbulence.
7.2 The low-
 $\unicode[STIX]{x1D6FD}$
assumption
$\unicode[STIX]{x1D6FD}$
assumption
The assumption that
![]() $\unicode[STIX]{x1D6FD}\ll 1$
is not satisfied at
$\unicode[STIX]{x1D6FD}\ll 1$
is not satisfied at
![]() $r\gtrsim 0.3~\text{AU}\simeq 65R_{\odot }$
, where
$r\gtrsim 0.3~\text{AU}\simeq 65R_{\odot }$
, where
![]() $\unicode[STIX]{x1D6FD}$
is typically
$\unicode[STIX]{x1D6FD}$
is typically
![]() ${\sim}1$
, but is reasonable at
${\sim}1$
, but is reasonable at
![]() $r\lesssim 20R_{\odot }$
(Chandran et al.
Reference Chandran, Dennis, Quataert and Bale2011). It is possible that the
$r\lesssim 20R_{\odot }$
(Chandran et al.
Reference Chandran, Dennis, Quataert and Bale2011). It is possible that the
![]() $\unicode[STIX]{x1D6FD}\ll 1$
theory presented here applies at least at a qualitative level provided
$\unicode[STIX]{x1D6FD}\ll 1$
theory presented here applies at least at a qualitative level provided
![]() $\unicode[STIX]{x1D6FD}$
is simply
$\unicode[STIX]{x1D6FD}$
is simply
![]() ${\lesssim}1$
, and indeed this possibility motivates the comparison of the present model with Helios observations. However, further work is needed to investigate how the results of this paper are modified as
${\lesssim}1$
, and indeed this possibility motivates the comparison of the present model with Helios observations. However, further work is needed to investigate how the results of this paper are modified as
![]() $\unicode[STIX]{x1D6FD}$
increases to values
$\unicode[STIX]{x1D6FD}$
increases to values
![]() ${\sim}1$
.
${\sim}1$
.
7.3 Neglect of other types of nonlinear interactions
Another approximation in §§ 2 through 6 is the neglect of all nonlinear interactions besides parametric decay. One of the neglected interactions is the shearing of inward-propagating AWs by outward-propagating AWs, which makes a contribution to
![]() $\unicode[STIX]{x1D714}_{\text{nl}}^{-}$
that depends on the perpendicular length scale of the AWs. At the perpendicular outer scale
$\unicode[STIX]{x1D714}_{\text{nl}}^{-}$
that depends on the perpendicular length scale of the AWs. At the perpendicular outer scale
![]() $L_{\bot }$
(the overall correlation length of the AWs measured perpendicular to
$L_{\bot }$
(the overall correlation length of the AWs measured perpendicular to
![]() $\boldsymbol{B}_{0}$
), the contribution to
$\boldsymbol{B}_{0}$
), the contribution to
![]() $\unicode[STIX]{x1D714}_{\text{nl}}^{-}$
from shearing is approximately
$\unicode[STIX]{x1D714}_{\text{nl}}^{-}$
from shearing is approximately
where
is the critical-balance parameter (Goldreich & Sridhar Reference Goldreich and Sridhar1995; Ng & Bhattacharjee Reference Ng and Bhattacharjee1996; Lithwick, Goldreich & Sridhar Reference Lithwick, Goldreich and Sridhar2007). Equation (7.5) does not apply when
![]() $\unicode[STIX]{x1D712}$
is much larger than 1, but direct numerical simulations suggest that
$\unicode[STIX]{x1D712}$
is much larger than 1, but direct numerical simulations suggest that
![]() $\unicode[STIX]{x1D712}\lesssim 1$
at
$\unicode[STIX]{x1D712}\lesssim 1$
at
![]() $r\gtrsim 10R_{\odot }$
for the bulk of the AW energy (J. Perez, private communication). Thus, at
$r\gtrsim 10R_{\odot }$
for the bulk of the AW energy (J. Perez, private communication). Thus, at
![]() $r\gtrsim 10R_{\odot }$
,
$r\gtrsim 10R_{\odot }$
,
As AWs propagate away from the Sun, they follow magnetic field lines, which leads to the approximate scaling
![]() $L_{\bot }\propto B_{0}^{-1/2}$
. In the WKB limit, the AW frequency in the Sun’s frame
$L_{\bot }\propto B_{0}^{-1/2}$
. In the WKB limit, the AW frequency in the Sun’s frame
![]() $k_{z}(U+v_{\text{A}})$
is independent of
$k_{z}(U+v_{\text{A}})$
is independent of
![]() $r$
. The scaling
$r$
. The scaling
![]() $k_{z}\sim 1/(U+v_{\text{A}})$
thus serves as a rough approximation for outward-propagating AWs in the turbulent solar wind. At the coronal base (just above the transition region), where
$k_{z}\sim 1/(U+v_{\text{A}})$
thus serves as a rough approximation for outward-propagating AWs in the turbulent solar wind. At the coronal base (just above the transition region), where
![]() $k_{z}$
and
$k_{z}$
and
![]() $L_{\bot }$
have the values
$L_{\bot }$
have the values
![]() $k_{z\text{b}}$
and
$k_{z\text{b}}$
and
![]() $L_{\bot \text{b}}$
, the value of
$L_{\bot \text{b}}$
, the value of
![]() $k_{z\text{b}}L_{\bot \text{b}}$
for the energetically dominant AWs launched by the Sun can be estimated (in essence from the critical-balance condition) as
$k_{z\text{b}}L_{\bot \text{b}}$
for the energetically dominant AWs launched by the Sun can be estimated (in essence from the critical-balance condition) as
![]() $\unicode[STIX]{x1D6FF}v_{\text{b}}^{+}/v_{\text{Ab}}$
, where
$\unicode[STIX]{x1D6FF}v_{\text{b}}^{+}/v_{\text{Ab}}$
, where
![]() $\unicode[STIX]{x1D6FF}v_{\text{b}}^{+}$
and
$\unicode[STIX]{x1D6FF}v_{\text{b}}^{+}$
and
![]() $v_{\text{Ab}}$
are the values of
$v_{\text{Ab}}$
are the values of
![]() $\unicode[STIX]{x1D6FF}v^{+}$
and
$\unicode[STIX]{x1D6FF}v^{+}$
and
![]() $v_{\text{A}}$
at the coronal base (Goldreich & Sridhar Reference Goldreich and Sridhar1995; van Ballegooijen & Asgari-Targhi Reference van Ballegooijen and Asgari-Targhi2016). Together, these scalings lead to the estimate
$v_{\text{A}}$
at the coronal base (Goldreich & Sridhar Reference Goldreich and Sridhar1995; van Ballegooijen & Asgari-Targhi Reference van Ballegooijen and Asgari-Targhi2016). Together, these scalings lead to the estimate
where
![]() $B_{0\text{b}}$
and
$B_{0\text{b}}$
and
![]() $U_{\text{b}}$
are the values of the background magnetic field and solar-wind outflow velocity at the coronal base. Between
$U_{\text{b}}$
are the values of the background magnetic field and solar-wind outflow velocity at the coronal base. Between
![]() $r=10R_{\odot }$
and
$r=10R_{\odot }$
and
![]() $r=60R_{\odot }$
,
$r=60R_{\odot }$
,
![]() $B_{0\text{b}}/B_{0}\simeq f_{\max }(r/R_{\odot })^{2}$
, where
$B_{0\text{b}}/B_{0}\simeq f_{\max }(r/R_{\odot })^{2}$
, where
![]() $f_{\max }$
is the super-radial expansion factor (Kopp & Holzer Reference Kopp and Holzer1976). In the fast solar wind within this range of radii,
$f_{\max }$
is the super-radial expansion factor (Kopp & Holzer Reference Kopp and Holzer1976). In the fast solar wind within this range of radii,
![]() $U+v_{\text{A}}\simeq 700{-}800~\text{km}~\text{s}^{-1}$
, which is comparable to
$U+v_{\text{A}}\simeq 700{-}800~\text{km}~\text{s}^{-1}$
, which is comparable to
![]() $U_{\text{b}}+v_{\text{Ab}}\simeq v_{\text{Ab}}\simeq 10^{3}~\text{km}~\text{s}^{-1}$
. Equation (7.8) is thus approximately equivalent to
$U_{\text{b}}+v_{\text{Ab}}\simeq v_{\text{Ab}}\simeq 10^{3}~\text{km}~\text{s}^{-1}$
. Equation (7.8) is thus approximately equivalent to
for the energetically dominant fluctuations launched by the Sun. If we set
![]() $f_{\max }=9$
,
$f_{\max }=9$
,
![]() $\unicode[STIX]{x1D6FF}v_{\text{b}}=30~\text{km}~\text{s}^{-1}$
, and
$\unicode[STIX]{x1D6FF}v_{\text{b}}=30~\text{km}~\text{s}^{-1}$
, and
![]() $v_{\text{Ab}}=900~\text{km}~\text{s}^{-1}$
, then (7.9) becomes
$v_{\text{Ab}}=900~\text{km}~\text{s}^{-1}$
, then (7.9) becomes
for the energetically dominant AWs launched by the Sun. Equations (7.7) and (7.10) suggest that it is reasonable to neglect the shearing of inward-propagating AWs by outward-propagating AWs at
![]() $r\gtrsim 10R_{\odot }$
. On the other hand, at smaller radii, shearing could suppress the growth of inward-propagating AWs that would otherwise result from the parametric instability. Also, the requirement that
$r\gtrsim 10R_{\odot }$
. On the other hand, at smaller radii, shearing could suppress the growth of inward-propagating AWs that would otherwise result from the parametric instability. Also, the requirement that
![]() $k_{z}L_{\bot }>1$
in order for
$k_{z}L_{\bot }>1$
in order for
![]() $\unicode[STIX]{x1D714}_{\text{nl},\text{PI}}^{-}$
to exceed
$\unicode[STIX]{x1D714}_{\text{nl},\text{PI}}^{-}$
to exceed
![]() $\unicode[STIX]{x1D714}_{\text{nl},\bot }^{-}$
could prevent the
$\unicode[STIX]{x1D714}_{\text{nl},\bot }^{-}$
could prevent the
![]() $f^{-1}$
range from spreading to frequencies below some minimum (
$f^{-1}$
range from spreading to frequencies below some minimum (
![]() $r$
-dependent) value.
$r$
-dependent) value.
The other nonlinearities in the weak-turbulence wave kinetic equations that are neglected in this paper include interactions involving fast magnetosonic waves, the turbulent mixing of slow waves by AWs, phase mixing of AWs by slow waves and the shearing of outward-propagating AWs by inward-propagating AWs (Chandran Reference Chandran2008). In situ measurements indicate that fast waves account for only a small fraction of the energy in compressive fluctuations at 1 AU (Yao et al.
Reference Yao, He, Marsch, Tu, Pedersen, Rème and Trotignon2011; Howes et al.
Reference Howes, Bale, Klein, Chen, Salem and TenBarge2012; Klein et al.
Reference Klein, Howes, TenBarge, Bale, Chen and Salem2012). Also, fast waves propagating away from the Sun undergo almost complete reflection before they can escape into the corona (Hollweg Reference Hollweg1978). These findings suggest that nonlinear interactions involving fast waves have little effect upon the conclusions of this paper. The turbulent mixing of slow waves by AWs acts as an additional slow-wave damping mechanism and is thus unlikely to change the conclusions of this paper, which already assume strong slow-wave damping. Phase mixing of AWs by slow waves transports AW energy to larger
![]() $k_{\bot }$
at a rate that increases with
$k_{\bot }$
at a rate that increases with
![]() $|k_{z}|$
(Chandran Reference Chandran2008). Although the fractional density fluctuations between
$|k_{z}|$
(Chandran Reference Chandran2008). Although the fractional density fluctuations between
![]() $r=10R_{\odot }$
and
$r=10R_{\odot }$
and
![]() $r=0.3~\text{AU}$
are fairly small (see, e.g. Tu & Marsch Reference Tu and Marsch1995; Hollweg et al.
Reference Hollweg, Cranmer and Chandran2010), phase mixing could affect the parallel AW power spectra, and further work is needed to investigate this possibility. The shearing of outward-propagating AWs by inward-propagating AWs is enhanced by non-WKB reflection, which makes this shearing more coherent in time (Velli et al.
Reference Velli, Grappin and Mangeney1989). The resulting nonlinear time scale for outward-propagating AWs is approximately
$r=0.3~\text{AU}$
are fairly small (see, e.g. Tu & Marsch Reference Tu and Marsch1995; Hollweg et al.
Reference Hollweg, Cranmer and Chandran2010), phase mixing could affect the parallel AW power spectra, and further work is needed to investigate this possibility. The shearing of outward-propagating AWs by inward-propagating AWs is enhanced by non-WKB reflection, which makes this shearing more coherent in time (Velli et al.
Reference Velli, Grappin and Mangeney1989). The resulting nonlinear time scale for outward-propagating AWs is approximately
![]() $r/(U+v_{\text{A}})$
(Chandran & Hollweg Reference Chandran and Hollweg2009), where
$r/(U+v_{\text{A}})$
(Chandran & Hollweg Reference Chandran and Hollweg2009), where
![]() $U$
is the solar-wind outflow velocity. This time scale is comparable to the AW propagation time from the Sun to heliocentric distance
$U$
is the solar-wind outflow velocity. This time scale is comparable to the AW propagation time from the Sun to heliocentric distance
![]() $r$
, and hence to the parametric-decay time scale at the small-
$r$
, and hence to the parametric-decay time scale at the small-
![]() $f$
end of the
$f$
end of the
![]() $1/f$
range of
$1/f$
range of
![]() $e^{+}$
. How this shearing modifies
$e^{+}$
. How this shearing modifies
![]() $E^{+}(k_{z})$
, however, is not clear. For example, shearing by inward-propagating AWs may transport outward-propagating-AW energy to larger
$E^{+}(k_{z})$
, however, is not clear. For example, shearing by inward-propagating AWs may transport outward-propagating-AW energy to larger
![]() $k_{\bot }=\sqrt{k_{x}^{2}+k_{y}^{2}}$
at a rate that is independent of
$k_{\bot }=\sqrt{k_{x}^{2}+k_{y}^{2}}$
at a rate that is independent of
![]() $|k_{z}|$
, in which case this shearing would reduce
$|k_{z}|$
, in which case this shearing would reduce
![]() $E^{+}(k_{z})$
by approximately the same factor at all
$E^{+}(k_{z})$
by approximately the same factor at all
![]() $k_{z}$
, leaving the functional form of
$k_{z}$
, leaving the functional form of
![]() $E^{+}(k_{z})$
unchanged.
$E^{+}(k_{z})$
unchanged.
7.4 Neglect of spatial inhomogeneity
In this paper, it is assumed that the background plasma is uniform and stationary. In the solar wind, however, as an AW propagates from the low corona to 0.3 AU, the properties of the ambient plasma seen by the AW change dramatically, with
![]() $\unicode[STIX]{x1D6FD}$
increasing from
$\unicode[STIX]{x1D6FD}$
increasing from
![]() ${\sim}10^{-2}$
to
${\sim}10^{-2}$
to
![]() ${\sim}1$
and
${\sim}1$
and
![]() $\unicode[STIX]{x1D6FF}v_{\text{rms}}/v_{\text{A}}$
increasing from
$\unicode[STIX]{x1D6FF}v_{\text{rms}}/v_{\text{A}}$
increasing from
![]() ${\sim}0.02$
to
${\sim}0.02$
to
![]() ${\sim}0.5$
(Bavassano et al.
Reference Bavassano, Pietropaolo and Bruno2000; Cranmer & van Ballegooijen Reference Cranmer and van Ballegooijen2005; Chandran et al.
Reference Chandran, Dennis, Quataert and Bale2011). Further work is needed to determine how this spatial inhomogeneity affects the nonlinear evolution of the parametric instability.
${\sim}0.5$
(Bavassano et al.
Reference Bavassano, Pietropaolo and Bruno2000; Cranmer & van Ballegooijen Reference Cranmer and van Ballegooijen2005; Chandran et al.
Reference Chandran, Dennis, Quataert and Bale2011). Further work is needed to determine how this spatial inhomogeneity affects the nonlinear evolution of the parametric instability.
7.5 Approximate treatment of slow-wave damping
A key assumption in §§ 2 through 6 is that slow waves are strongly damped, and this damping is implemented by neglecting terms in the wave kinetic equations that are proportional to the slow-wave power spectrum
![]() $S_{k}^{\pm }$
. There are two sources of error in this approach. First, damping could modify the polarization properties of slow waves, thereby altering the wave kinetic equations. Second, even if
$S_{k}^{\pm }$
. There are two sources of error in this approach. First, damping could modify the polarization properties of slow waves, thereby altering the wave kinetic equations. Second, even if
![]() $S_{k}^{\pm }$
is much smaller than the AW power spectrum
$S_{k}^{\pm }$
is much smaller than the AW power spectrum
![]() $A_{k}^{\pm }$
, the neglected parametric-decay terms in the wave kinetic equations for AWs that are proportional to
$A_{k}^{\pm }$
, the neglected parametric-decay terms in the wave kinetic equations for AWs that are proportional to
![]() $S_{k}^{\pm }$
could still be important, because they contain a factor of
$S_{k}^{\pm }$
could still be important, because they contain a factor of
![]() $\unicode[STIX]{x1D6FD}^{-1}$
, which is absent in the terms that are retained. This factor arises from the fact that the fractional density fluctuation of a slow wave is
$\unicode[STIX]{x1D6FD}^{-1}$
, which is absent in the terms that are retained. This factor arises from the fact that the fractional density fluctuation of a slow wave is
![]() ${\sim}\unicode[STIX]{x1D6FD}^{-1/2}$
times larger than the fractional magnetic-field fluctuation of an AW with equal energy. These neglected terms act to equalize the 3-D AW power spectra
${\sim}\unicode[STIX]{x1D6FD}^{-1/2}$
times larger than the fractional magnetic-field fluctuation of an AW with equal energy. These neglected terms act to equalize the 3-D AW power spectra
![]() $A^{+}$
and
$A^{+}$
and
![]() $A^{-}$
, and hence to equalize
$A^{-}$
, and hence to equalize
![]() $E^{+}$
and
$E^{+}$
and
![]() $E^{-}$
. If these neglected terms were in fact important, they could invalidate the solutions presented in § 6, in which
$E^{-}$
. If these neglected terms were in fact important, they could invalidate the solutions presented in § 6, in which
![]() $E^{+}\gg E^{-}$
. However, in situ observations indicate that
$E^{+}\gg E^{-}$
. However, in situ observations indicate that
![]() $E^{+}\gg E^{-}$
in the fast solar wind at
$E^{+}\gg E^{-}$
in the fast solar wind at
![]() $r=0.3~\text{AU}$
(Marsch & Tu Reference Marsch and Tu1990; Tu & Marsch Reference Tu and Marsch1995), which suggests that the neglect of these terms is reasonable. Further work is needed to investigate these issues more carefully.
$r=0.3~\text{AU}$
(Marsch & Tu Reference Marsch and Tu1990; Tu & Marsch Reference Tu and Marsch1995), which suggests that the neglect of these terms is reasonable. Further work is needed to investigate these issues more carefully.
8 Conclusion
In this paper, weak-turbulence theory is used to investigate the nonlinear evolution of the parametric instability in low-
![]() $\unicode[STIX]{x1D6FD}$
plasmas. The analysis starts from the wave kinetic equations describing the interactions between AWs and slow waves in weak compressible MHD turbulence. To account for the strong damping of slow waves in collisionless plasmas, terms containing the slow-wave energy density are dropped. The equations allow for all wave-vector directions, but are integrated over the wave-vector components perpendicular to the background magnetic field
$\unicode[STIX]{x1D6FD}$
plasmas. The analysis starts from the wave kinetic equations describing the interactions between AWs and slow waves in weak compressible MHD turbulence. To account for the strong damping of slow waves in collisionless plasmas, terms containing the slow-wave energy density are dropped. The equations allow for all wave-vector directions, but are integrated over the wave-vector components perpendicular to the background magnetic field
![]() $\boldsymbol{B}_{0}$
(
$\boldsymbol{B}_{0}$
(
![]() $k_{x}$
and
$k_{x}$
and
![]() $k_{y}$
), which leads to equations for the 1-D power spectra
$k_{y}$
), which leads to equations for the 1-D power spectra
![]() $E^{+}$
and
$E^{+}$
and
![]() $E^{-}$
that depend only on the parallel wavenumber
$E^{-}$
that depend only on the parallel wavenumber
![]() $k_{z}$
and time. During parametric decay in a low-
$k_{z}$
and time. During parametric decay in a low-
![]() $\unicode[STIX]{x1D6FD}$
plasma, an AW decays into a slow-wave propagating in the same direction and a counter-propagating AW with a frequency slightly smaller than the frequency of the initial AW. The total number of AW quanta is conserved, and the reduction in AW frequencies leads to an inverse cascade of AW quanta towards smaller
$\unicode[STIX]{x1D6FD}$
plasma, an AW decays into a slow-wave propagating in the same direction and a counter-propagating AW with a frequency slightly smaller than the frequency of the initial AW. The total number of AW quanta is conserved, and the reduction in AW frequencies leads to an inverse cascade of AW quanta towards smaller
![]() $\unicode[STIX]{x1D714}$
and
$\unicode[STIX]{x1D714}$
and
![]() $k_{z}$
. The energy of each AW quantum is
$k_{z}$
. The energy of each AW quantum is
![]() $\hbar \unicode[STIX]{x1D714}$
, and the decrease in
$\hbar \unicode[STIX]{x1D714}$
, and the decrease in
![]() $\unicode[STIX]{x1D714}$
during each decay corresponds to a decrease in the AW energy, which is compensated for by an increase in the slow-wave energy. The subsequent damping and dissipation of slow-wave energy results in plasma heating.
$\unicode[STIX]{x1D714}$
during each decay corresponds to a decrease in the AW energy, which is compensated for by an increase in the slow-wave energy. The subsequent damping and dissipation of slow-wave energy results in plasma heating.
The main results of this paper concern the parametric decay of a population of AWs propagating in one direction, say parallel to
![]() $\boldsymbol{B}_{0}$
, when the counter-propagating AWs start out with much smaller amplitudes. If the initial frequency spectrum
$\boldsymbol{B}_{0}$
, when the counter-propagating AWs start out with much smaller amplitudes. If the initial frequency spectrum
![]() $e^{+}$
of the parallel-propagating AWs has a peak frequency
$e^{+}$
of the parallel-propagating AWs has a peak frequency
![]() $f_{0}$
(at which
$f_{0}$
(at which
![]() $fe^{+}$
is maximized) and an ‘infrared’ scaling
$fe^{+}$
is maximized) and an ‘infrared’ scaling
![]() $f^{p}$
at smaller
$f^{p}$
at smaller
![]() $f$
with
$f$
with
![]() $-1<p<1$
, then
$-1<p<1$
, then
![]() $e^{+}$
acquires a
$e^{+}$
acquires a
![]() $1/f$
scaling throughout a range of frequencies that spreads out in both directions from
$1/f$
scaling throughout a range of frequencies that spreads out in both directions from
![]() $f_{0}$
. At the same time, the anti-parallel-propagating AWs acquire a
$f_{0}$
. At the same time, the anti-parallel-propagating AWs acquire a
![]() $1/f^{2}$
spectrum within this same frequency range. If the plasma parameters and infrared
$1/f^{2}$
spectrum within this same frequency range. If the plasma parameters and infrared
![]() $e^{+}$
spectrum are chosen to match conditions in the fast solar wind at a heliocentric distance of 0.3 AU, and the AWs are allowed to evolve for a period of time that is approximately two thirds of the AW travel time from the Sun to 0.3 AU, the resulting form of
$e^{+}$
spectrum are chosen to match conditions in the fast solar wind at a heliocentric distance of 0.3 AU, and the AWs are allowed to evolve for a period of time that is approximately two thirds of the AW travel time from the Sun to 0.3 AU, the resulting form of
![]() $e^{+}$
is similar to the form observed by the Helios spacecraft in the fast solar wind at 0.3 AU. Because the background plasma parameters are time independent in the analysis of this paper but time dependent in the plasma rest frame in the solar wind, it is not clear how to map the time variable in the present analysis to heliocentric distance. Nevertheless, the similarity between the spectra found in this paper and the spectra observed by Helios suggests that parametric decay plays an important role in shaping the AW spectra observed in the fast solar wind at 0.3 AU, at least for wave periods
$e^{+}$
is similar to the form observed by the Helios spacecraft in the fast solar wind at 0.3 AU. Because the background plasma parameters are time independent in the analysis of this paper but time dependent in the plasma rest frame in the solar wind, it is not clear how to map the time variable in the present analysis to heliocentric distance. Nevertheless, the similarity between the spectra found in this paper and the spectra observed by Helios suggests that parametric decay plays an important role in shaping the AW spectra observed in the fast solar wind at 0.3 AU, at least for wave periods
![]() ${\lesssim}1~\text{h}$
.
${\lesssim}1~\text{h}$
.
The frequency
![]() $f^{\ast }$
that dominates the AW energy is the maximum of
$f^{\ast }$
that dominates the AW energy is the maximum of
![]() $(fe^{+}+fe^{-})$
. At the beginning of the numerical calculation presented in § 6,
$(fe^{+}+fe^{-})$
. At the beginning of the numerical calculation presented in § 6,
![]() $f^{\ast }$
is approximately
$f^{\ast }$
is approximately
![]() $f_{0}=0.01~\text{Hz}$
. At
$f_{0}=0.01~\text{Hz}$
. At
![]() $t=8~\text{h}$
in this numerical calculation,
$t=8~\text{h}$
in this numerical calculation,
![]() $f^{\ast }$
is the smallest frequency at which
$f^{\ast }$
is the smallest frequency at which
![]() $e^{+}\sim f^{-1}$
and
$e^{+}\sim f^{-1}$
and
![]() $e^{-}\sim f^{-2}$
, which is
$e^{-}\sim f^{-2}$
, which is
![]() ${\sim}3\times 10^{-4}~\text{Hz}$
. This decrease in
${\sim}3\times 10^{-4}~\text{Hz}$
. This decrease in
![]() $f^{\ast }$
is a consequence of the aforementioned inverse cascade, which transports AW quanta from the initial peak frequency to smaller frequencies. Inverse cascade offers a way to reconcile the observed dominance of AWs at hour-long time scales at 0.3 AU with arguments that the Sun launches most of its AW power at significantly shorter wave periods (Cranmer & van Ballegooijen Reference Cranmer and van Ballegooijen2005; van Ballegooijen & Asgari-Targhi Reference van Ballegooijen and Asgari-Targhi2016).
$f^{\ast }$
is a consequence of the aforementioned inverse cascade, which transports AW quanta from the initial peak frequency to smaller frequencies. Inverse cascade offers a way to reconcile the observed dominance of AWs at hour-long time scales at 0.3 AU with arguments that the Sun launches most of its AW power at significantly shorter wave periods (Cranmer & van Ballegooijen Reference Cranmer and van Ballegooijen2005; van Ballegooijen & Asgari-Targhi Reference van Ballegooijen and Asgari-Targhi2016).
Further work is needed to relax some of the simplifying assumptions in this paper, including the low-
![]() $\unicode[STIX]{x1D6FD}$
approximation, the assumption of spatial homogeneity, the simplistic treatment of slow-wave damping, and the neglect of nonlinear interactions other than parametric decay. Further work is also needed to evaluate the relative contributions of parametric decay and other mechanisms to the generation of
$\unicode[STIX]{x1D6FD}$
approximation, the assumption of spatial homogeneity, the simplistic treatment of slow-wave damping, and the neglect of nonlinear interactions other than parametric decay. Further work is also needed to evaluate the relative contributions of parametric decay and other mechanisms to the generation of
![]() $1/f$
spectra in the solar wind. For example, Matthaeus & Goldstein (Reference Matthaeus and Goldstein1986) argued that the
$1/f$
spectra in the solar wind. For example, Matthaeus & Goldstein (Reference Matthaeus and Goldstein1986) argued that the
![]() $f^{-1}$
spectrum seen at
$f^{-1}$
spectrum seen at
![]() $r=1~\text{AU}$
at
$r=1~\text{AU}$
at
![]() $3\times 10^{-6}<f<8\times 10^{-5}~\text{Hz}$
is a consequence of forcing at the solar surface, and Velli et al. (Reference Velli, Grappin and Mangeney1989) argued that the shearing of outward-propagating AWs by the inward-propagating AWs produced by non-WKB reflection causes the outward-propagating AWs to acquire an
$3\times 10^{-6}<f<8\times 10^{-5}~\text{Hz}$
is a consequence of forcing at the solar surface, and Velli et al. (Reference Velli, Grappin and Mangeney1989) argued that the shearing of outward-propagating AWs by the inward-propagating AWs produced by non-WKB reflection causes the outward-propagating AWs to acquire an
![]() $f^{-1}$
spectrum.
$f^{-1}$
spectrum.
NASA’s Parker Solar Probe (PSP) has a planned launch date in the summer of 2018 and will reach heliocentric distances less than
![]() $10R_{\odot }$
. The FIELDS (Bale et al.
Reference Bale, Goetz, Harvey, Turin, Bonnell, Dudok de Wit, Ergun, MacDowall, Pulupa and Andre2016) and SWEAP (Kasper et al.
Reference Kasper, Abiad, Austin, Balat-Pichelin, Bale, Belcher, Berg, Bergner, Berthomier and Bookbinder2015) instrument suites on PSP will provide the first ever in situ measurements of the magnetic-field, electric-field, velocity and density fluctuations in the solar wind at
$10R_{\odot }$
. The FIELDS (Bale et al.
Reference Bale, Goetz, Harvey, Turin, Bonnell, Dudok de Wit, Ergun, MacDowall, Pulupa and Andre2016) and SWEAP (Kasper et al.
Reference Kasper, Abiad, Austin, Balat-Pichelin, Bale, Belcher, Berg, Bergner, Berthomier and Bookbinder2015) instrument suites on PSP will provide the first ever in situ measurements of the magnetic-field, electric-field, velocity and density fluctuations in the solar wind at
![]() $r<0.29~\text{AU}$
. Although the issues mentioned in the preceding paragraph are sources of uncertainty, the results of this paper lead to the following predictions that will be tested by PSP. First, the
$r<0.29~\text{AU}$
. Although the issues mentioned in the preceding paragraph are sources of uncertainty, the results of this paper lead to the following predictions that will be tested by PSP. First, the
![]() $1/f$
range of
$1/f$
range of
![]() $e^{+}$
in fast-solar-wind streams at
$e^{+}$
in fast-solar-wind streams at
![]() $r<0.3~\text{AU}$
and
$r<0.3~\text{AU}$
and
![]() $f\gtrsim 3\times 10^{-4}~\text{Hz}$
is produced in situ by parametric decay. As a consequence, the
$f\gtrsim 3\times 10^{-4}~\text{Hz}$
is produced in situ by parametric decay. As a consequence, the
![]() $1/f$
range of
$1/f$
range of
![]() $e^{+}$
in fast-solar-wind streams will be much more narrow at small
$e^{+}$
in fast-solar-wind streams will be much more narrow at small
![]() $r$
than at
$r$
than at
![]() $r=0.3~\text{AU}$
. As AWs propagate away from the Sun, the frequency range
$r=0.3~\text{AU}$
. As AWs propagate away from the Sun, the frequency range
![]() $(f_{\min },f_{\max })$
in which
$(f_{\min },f_{\max })$
in which
![]() $e^{+}\sim 1/f$
spreads out in both directions from the near-Sun peak frequency (the maximum of
$e^{+}\sim 1/f$
spreads out in both directions from the near-Sun peak frequency (the maximum of
![]() $fe^{+}$
). Thus,
$fe^{+}$
). Thus,
![]() $f_{\min }$
will be larger closer to the Sun, and
$f_{\min }$
will be larger closer to the Sun, and
![]() $f_{\max }$
will be smaller. Finally, during epochs in which the local magnetic field is aligned with the relative velocity between the plasma and the spacecraft (see the discussion in § 6.2), the spectrum of
$f_{\max }$
will be smaller. Finally, during epochs in which the local magnetic field is aligned with the relative velocity between the plasma and the spacecraft (see the discussion in § 6.2), the spectrum of
![]() $e^{-}$
will scale like
$e^{-}$
will scale like
![]() $1/f^{2}$
in the frequency interval
$1/f^{2}$
in the frequency interval
![]() $(f_{\min },f_{\max })$
.
$(f_{\min },f_{\max })$
.
Acknowledgements
I thank P. Isenberg for discussions about the work of Cohen & Dewar (Reference Cohen and Dewar1974) and the three anonymous reviewers for helpful comments that led to improvements in the manuscript. This work was supported in part by NASA grants NNX15AI80, NNX16AG81G, and NNX17AI18G, NASA grant NNN06AA01C to the Parker Solar Probe FIELDS Experiment and NSF grant PHY-1500041.
Appendix A. Boundary layers in the Alfvén-wave power spectra
In this appendix, a small nonlinear diffusion term is added to the wave kinetic equation, so that (2.11) becomes
where
![]() $\unicode[STIX]{x1D708}$
is a constant that is taken to be very small,
$\unicode[STIX]{x1D708}$
is a constant that is taken to be very small,
and
![]() $\unicode[STIX]{x1D6E5}$
is a wavenumber increment that is
$\unicode[STIX]{x1D6E5}$
is a wavenumber increment that is
![]() $\ll |k_{z}|$
but which remains finite as
$\ll |k_{z}|$
but which remains finite as
![]() $\unicode[STIX]{x1D708}\rightarrow 0$
. A solution to (A 1) is sought in which
$\unicode[STIX]{x1D708}\rightarrow 0$
. A solution to (A 1) is sought in which
![]() $E^{\pm }$
has a boundary layer at some wavenumber
$E^{\pm }$
has a boundary layer at some wavenumber
![]() $k_{z}=b(t)$
. For simplicity, the analysis is restricted to
$k_{z}=b(t)$
. For simplicity, the analysis is restricted to
![]() $k_{z}>0$
. The spectra at negative
$k_{z}>0$
. The spectra at negative
![]() $k_{z}$
values then follow from the fact that
$k_{z}$
values then follow from the fact that
![]() $E^{+}$
and
$E^{+}$
and
![]() $E^{-}$
are even functions of
$E^{-}$
are even functions of
![]() $k_{z}$
.
$k_{z}$
.
It is useful to work with the dimensionless variables defined through the equations
where
![]() $k_{z0}$
is some characteristic wavenumber and
$k_{z0}$
is some characteristic wavenumber and
![]() $(\unicode[STIX]{x1D6FF}v_{0})^{2}$
is the characteristic mean-square AW velocity fluctuation. The analysis is restricted to the case in which
$(\unicode[STIX]{x1D6FF}v_{0})^{2}$
is the characteristic mean-square AW velocity fluctuation. The analysis is restricted to the case in which
Equation (A 1) then takes the form
where
![]() $\overline{H}=\overline{\tilde{E}^{+}}$
and
$\overline{H}=\overline{\tilde{E}^{+}}$
and
Upon setting
![]() $H=H(x,\unicode[STIX]{x1D70F})$
in (A 5), where
$H=H(x,\unicode[STIX]{x1D70F})$
in (A 5), where
and discarding terms
![]() $\ll \unicode[STIX]{x1D716}^{-1}$
, one obtains
$\ll \unicode[STIX]{x1D716}^{-1}$
, one obtains
where
![]() $\overline{H}$
is independent of
$\overline{H}$
is independent of
![]() $x$
.
$x$
.
As in (5.1) and (5.8), it is assumed that
![]() $H=0$
on the small-
$H=0$
on the small-
![]() $k_{z}$
side of the boundary layer at
$k_{z}$
side of the boundary layer at
![]() $s=\tilde{b}$
. The value of
$s=\tilde{b}$
. The value of
![]() $H$
at dimensionless wavenumbers slightly larger than
$H$
at dimensionless wavenumbers slightly larger than
![]() $\tilde{b}$
is denoted
$\tilde{b}$
is denoted
![]() $H_{{>}}$
. The solution to (A 8) must thus satisfy the boundary conditions
$H_{{>}}$
. The solution to (A 8) must thus satisfy the boundary conditions
with
![]() $\overline{H}=H_{{>}}/2$
. Upon substituting
$\overline{H}=H_{{>}}/2$
. Upon substituting
into (A 8), one finds that
By separately equating the
![]() $\operatorname{sech}^{2}(x/a)$
terms and the
$\operatorname{sech}^{2}(x/a)$
terms and the
![]() $\tanh (x/a)\operatorname{sech}^{2}(x/a)$
terms, one obtains
$\tanh (x/a)\operatorname{sech}^{2}(x/a)$
terms, one obtains
and
Thus, the desired solution to (A 8) is (A 10) with
![]() $a$
and
$a$
and
![]() $\tilde{b}$
given by (A 12) and (A 13). Equation (A 12) can be rewritten in terms of the original variables as
$\tilde{b}$
given by (A 12) and (A 13). Equation (A 12) can be rewritten in terms of the original variables as
where
![]() $E_{{>}}=H_{{>}}(\unicode[STIX]{x1D6FF}v_{0})^{2}/k_{z0}$
, which is equivalent to (5.4).
$E_{{>}}=H_{{>}}(\unicode[STIX]{x1D6FF}v_{0})^{2}/k_{z0}$
, which is equivalent to (5.4).
Appendix B. Approximate analytic solution for decaying, cross-helical Alfvén waves in the nonlinear regime
In this appendix, a solution to (2.11) is sought in which
and
where
![]() $H(x)$
is the Heaviside function,
$H(x)$
is the Heaviside function,
![]() $a_{n}$
,
$a_{n}$
,
![]() $b$
and
$b$
and
![]() $c_{n}$
are functions of time, and
$c_{n}$
are functions of time, and
![]() $\unicode[STIX]{x1D702}$
and
$\unicode[STIX]{x1D702}$
and
![]() $p$
are constants, with
$p$
are constants, with
Substituting (B 1) and (B 2) into (2.11) and making use of (B 3) leads to the following approximate solutions for
![]() $b$
,
$b$
,
![]() $c_{1}$
and
$c_{1}$
and
![]() $a_{2}$
:
$a_{2}$
:
where
![]() $\unicode[STIX]{x1D6EC}$
is a constant of integration,
$\unicode[STIX]{x1D6EC}$
is a constant of integration,
and
Equations (B 5) through (B 7) imply that the break wavenumber
![]() $b(t)$
decreases in time, and that the ratios
$b(t)$
decreases in time, and that the ratios
![]() $E^{+}(b_{+})/\unicode[STIX]{x1D702}b_{+}^{p}$
and
$E^{+}(b_{+})/\unicode[STIX]{x1D702}b_{+}^{p}$
and
![]() $E^{+}(b_{+})/E^{-}(b_{+})$
remain constant, where
$E^{+}(b_{+})/E^{-}(b_{+})$
remain constant, where
![]() $b_{+}$
is a wavenumber infinitesimally larger than
$b_{+}$
is a wavenumber infinitesimally larger than
![]() $b$
. For example, if the infrared spectral index
$b$
. For example, if the infrared spectral index
![]() $p$
is
$p$
is
![]() $-1/2$
, then
$-1/2$
, then
and
Equations (B 8) and (B 9) are shown as dotted lines in figures 2 and 4.