2. Basic definitions

The underlying assumption is that far enough from the shock transition, in the upstream and downstream regions, the magnetic fields and plasmas are uniform and the distributions are gyrotropic but not necessarily isotropic. The analysis will be done in HT frame where the motional electric field is absent in both uniform regions. If a shock is stationary and planar, there exists an electrostatic field $E_x(x)$ inside the transition region, so that the cross-shock potential is

(2.1)\begin{equation} \phi_{HT}(x)={-}\int_0^x E_x(x')\,{{\rm d}x}' \end{equation}

where $x$ is the coordinate along the shock normal and $E_x=0$ for $x<0$. Other coordinates are chosen so that $B_y=0$ in both uniform regions. Hereinafter, the subscripts $u$ and $d$ denote upstream and downstream, respectively. The uniform magnetic field and velocity vectors are

(2.2)\begin{gather} \boldsymbol{B}=B\cos\theta\hat{x} +B\sin\theta\hat{z} \end{gather}

(2.3)\begin{gather}\boldsymbol{V}=V|\cos\theta|\hat{x} +V\sin\theta\ {\rm sign}(\cos\theta)\hat{z} \end{gather}

Here ${\rm sign}(x)=1$ for $x>0$ and ${\rm sign}(x)=-1$ for $x<0$, whereas $\hat {x}$ and $\hat {z}$ are unit vectors in $x$ and $z$ directions, respectively. The sign of the plasma velocity is chosen so that the positive direction of $x$ is from upstream to downstream. We also refer to the normal incidence frame (NIF), in which the upstream plasma velocity is along the shock normal. For brevity of expressions, in what follows, we restrict ourselves with non-relativistic velocities, including the relative velocity of the frames $\boldsymbol {V}_{NIF\rightarrow HT}=(0,0,V_u\tan \theta _u)$, so that for each particle $\boldsymbol {v}_{HT}=\boldsymbol {v}_{NIF}+\boldsymbol {V}_{NIF\rightarrow HT}$:

(2.4a–c)\begin{gather} v_x^{(HT)}=v_x^{(NIF)},\quad v_y^{(HT)}=v_y^{(NIF)},\quad v_z^{(HT)}=v_z^{(NIF)}+V_u\tan\theta_u \end{gather}

(2.5)\begin{gather}v_\parallel^{(HT)}=v_x^{(HT)}\cos\theta + v_z^{(HT)}\sin\theta = v_x^{(NIF)}\cos\theta + v_z^{(NIF)}\sin\theta +V_u\tan\theta_u\sin\theta \end{gather}

and $v_\perp ^2=v^2-v_\parallel ^2$. However, some relations will be given in a fully relativistic form for future use. In the chosen non-relativistic limit, the magnetic fields are the same in both frames, whereas the electric fields are related by the expression: $\boldsymbol {E}_{NIF}=\boldsymbol {E}_{HT}+\boldsymbol {V}_{NIF\rightarrow HT}\times \boldsymbol {B}/c$. The last expression means that there exists the motional electric field $E_{y,NIF}=V_uB_u\sin \theta _u/c$ and that the cross-shock electrostatic fields and potentials are different in both frames (Formisano Reference Formisano1982; Goodrich & Scudder Reference Goodrich and Scudder1984; Schwartz et al. Reference Schwartz, Thomsen, Bame and Stansberry1988; Gedalin & Balikhin Reference Gedalin and Balikhin2004; Baring & Summerlin Reference Baring and Summerlin2007; Dimmock et al. Reference Dimmock, Balikhin, Krasnoselskikh, Walker, Bale and Hobara2012; Cohen et al. Reference Cohen, Schwartz, Goodrich, Ahmadi, Ergun, Fuselier, Desai, Christian, McComas and Zank2019).

Figure 1 schematically shows the magnetic field profile and the upstream and downstream regions. The full distribution function $f_u(\,\boldsymbol {p})$ is assumed independent of time and coordinates in the upstream region. Upon crossing the shock, at $x=D$, the distribution function is profoundly gyrophase dependent. Further gyrotropization occurs due to the kinematic collisionless relaxation, without energy change of the ions (Balikhin et al. Reference Balikhin, Zhang, Gedalin, Ganushkina and Pope2008; Gedalin Reference Gedalin2015; Gedalin et al. Reference Gedalin, Friedman and Balikhin2015b; Gedalin, Friedman & Balikhin Reference Gedalin, Friedman and Balikhin2015c; Gedalin Reference Gedalin2019a,Reference Gedalinb). Therefore, the full downstream distribution function $f_d(\,\boldsymbol {p},x)$ depends on the coordinate along the shock normal until it become gyrotropic. Following our analysis in the HT frame, we wish to replace $f(\,\boldsymbol {p},x)$ with the reduced gyrotropic distribution function $f(p,\mu )$, where $p=mv$ is the total momentum and $\mu =p_\parallel /p$. In this approach, all information about the gyrophase is lost. Moments are calculated by integration over the volume ${\rm d}\varOmega =2{\rm \pi} p^2 \,{\rm d} p \,{\rm d}\mu$ in the momentum space:

(2.6)\begin{gather} n=\int f(p,\mu)\,{\rm d}\varOmega \end{gather}

(2.7)\begin{gather}nV_\parallel{=}\int v\mu f(p,\mu)\,{\rm d}\varOmega \end{gather}

(2.8)\begin{gather}P_{{\parallel}{\parallel}}=\int pv\mu^2 f(p,\mu)\,{\rm d}\varOmega \end{gather}

(2.9)\begin{gather}P_{{\perp}{\perp}}=\int pv(1-\mu^2) f(p,\mu)\,{\rm d}\varOmega \end{gather}

(2.10)\begin{gather}P_{{\perp}{\parallel}}=\int pv\mu\sqrt{1-\mu^2} f(p,\mu)\,{\rm d}\varOmega \end{gather}

Here $n$ is the number density, $V_\parallel$ is the plasma velocity along the magnetic field and $P_{\parallel \parallel }, P_{\perp \perp }, P_{\perp \parallel }$ are the components of the total pressure tensor. The speed $v=p/m\gamma$, where $\gamma =\sqrt {p^2/m^2c^2+1}$. The multiplier $2{\rm \pi}$ in ${\rm d}\varOmega$ arises from integration over $\phi$.

Figure 1. The magnetic field profile (schematically). The magnetic field increase occurs between $x=0$ and $x=D$. The region $x<0$ is the upstream region, the region $x>D$ is the downstream region.

3. Scattering probabilities

The probabilistic approach deals with the uniform asymptotic upstream and downstream regions where the gyrophase information is already lost and ion distributions are gyrotropic. The probabilities will be defined in the HT frame. Let a particle enter the shock with the momentum $p_i$ and pitch-angle cosine $\mu _i$ and leave it with $p_f$ and $\mu _f$. The initial and final points are in the regions where the distributions are already gyrotropic. Note that the entry and exit points may be on either side, i.e. the following scenarios are possible: (a) an ion comes from upstream and proceeds to downstream (transmission), (b) an ion comes from upstream and returns to upstream (backstreaming) and (c) and ion comes from downstream and proceeds to upstream (leakage). The option where an ion comes from downstream and returns to downstream does not exist for fast mode shocks which are considered here (Toptyghin Reference Toptyghin1980). As the initial $p_i,\mu _i$ do not unambiguously determine the final $p_f,\mu _f$, we define the probability $W(\mu _i,\mu _f;p_i,p_f)$ of scattering from the initial state to the final state as follows:

(3.1)\begin{equation} f_f(p_f,\mu_f)=\int W(\mu_i,\mu_f;p_i,p_f) f_i(p_i,\mu_i)\,{\rm d}\varOmega_i\end{equation}

This definition is valid separately for all three types of scattering: transmission, backstreaming and leakage. Given the initial distribution $f_i(p_i,\mu _i)$ the contribution to the moments of the final distribution will take the form

(3.2)\begin{gather} P_{f\parallel{\parallel}}=\int p_fv_f\mu_f^2 W(\mu_i,\mu_f;p_i,p_f) f_i(p_i,\mu_i)\,{\rm d}\varOmega_i\,{\rm d}\varOmega_f \end{gather}

(3.3)\begin{gather}P_{f\perp{\perp}}=\int p_fv_f(1-\mu_f^2) W(\mu_i,\mu_f;p_i,p_f) f_i(p_i,\mu_i)\,{\rm d}\varOmega_i\,{\rm d}\varOmega_f \end{gather}

(3.4)\begin{gather}P_{f\perp{\parallel}}=\int p_fv_f\mu_f\sqrt{1-\mu_f^2} W(\mu_i,\mu_f;p_i,p_f) f_i(p_i,\mu_i)\,{\rm d}\varOmega_i \,{\rm d}\varOmega_f \end{gather}

If the HT frame is well-defined, the energy is conserved, $\gamma _f-\gamma _i=\text {const}$, and $p_f=p_f(p_i)$ is a single-valued function, so that the probability can be represented as follows:

(3.5)\begin{equation} W(\mu_i,\mu_f;p_i,p_f)=w(\mu_i,\mu_f;p_i)\delta(p_f-p_f(p_i))\end{equation}

Using the newly defined $w(\mu _i,\mu _f;p_i)$ the relation between the initial and the final distributions takes the form

(3.6)\begin{gather} f_f(p_f(p_i),\mu_f)=C(p_i)\int w(\mu_i,\mu_f;p_i) f_i(p_i,\mu_i)\,{\rm d}\mu_i \end{gather}

(3.7)\begin{gather}C(p_i)=2{\rm \pi} p_i^2\left|\frac{{\rm d} p_f}{{\rm d} p_i}\right|^{{-}1}=2{\rm \pi} m\gamma_i p_iv_f \end{gather}

where we have used the relations

(3.8)\begin{equation} \frac{p_f}{p_i}\frac{{\rm d} p_f}{{\rm d} p_i}=\frac{\gamma_f}{\gamma_i} \frac{{\rm d}\gamma_f}{{\rm d}\gamma_i} \quad \Rightarrow \quad \left|\frac{{\rm d} p_f}{{\rm d} p_i}\right|^{{-}1}=\left|\frac{v_f}{v_i}\right| \end{equation}

In the non-relativistic regime the coefficient $C$ reduces to $C=2{\rm \pi} m^2v_iv_f$.

4. Scattering probabilities for transmitted ions in the narrow shock approximation

The main objective of the present paper is to illustrate our reformulation of the problem of the determination of the ion distribution in the simplest case where an analytical treatment is possible. We assume that the shock is planar, stationary and narrow, see figure 1. We will be treating only transmitted ions which enter the shock from upstream at $x=0$ and leave it at $x=D$ to proceed further downstream. As the downstream region is uniform, the momentum, magnitude and pitch angle of an ion does not change any longer for $x>D$. Let $f(p_d,\mu _d,\varphi _d)$ be the gyrophase-dependent distribution at $x=D$. From the Vlasov equation

(4.1)\begin{equation} f_d(\mu_d,\varphi_d; v_u)=f_u(\tilde{\mu}_u(\mu_d,\varphi_d); v_d) \end{equation}

where it is taken into account that the upstream distribution function is gyrotropic, $f_u=f_u(\mu _u;v_u)$, and $\mu _u=\tilde {\mu }_u(\mu _d,\varphi _d;v_u)$ is the function expressing the initial $\mu _u$ in terms of the final $\mu _d$ and $\varphi _d$. The upstream and downstream speeds are related by the energy conservation $mv_d^2/2=mv_u^2/2-q\phi _{HT}$. Dependence on the speed will be omitted for brevity in all calculations and restored in the end, if needed. The downstream gyrotropic distribution is obtained by the gyrophase averaging

(4.2)\begin{equation} f_d(\mu_d)=\frac{1}{2{\rm \pi}}\int_0^{2{\rm \pi}} {\rm d}\varphi_d\, f_d(\mu_d,\varphi_d) = \frac{1}{2{\rm \pi}}\int_0^{2{\rm \pi}}{\rm d}\varphi_d\, f_u(\tilde{\mu}_u(\mu_d,\varphi_d)) \end{equation}

In order to find the probability we use (3.6) with $f_i(p_i,\mu )=\delta (\mu -\mu _i)$ which gives

(4.3)\begin{gather} Cw(\mu_i,\mu_f;p_i)=f_f(p_f(p_i),\mu_f) \end{gather}

(4.4)\begin{gather}Cw(\mu_u,\mu_d)=\frac{1}{2{\rm \pi}}\int_0^{2{\rm \pi}}{\rm d}\varphi_d\, \delta(\mu_u-\tilde{\mu}_u(\mu_d,\varphi_d))=\frac{1}{2{\rm \pi}}\sum_s \left|\frac{\partial\widetilde{\mu_u}}{\partial\varphi_d}\right|_{s}^{{-}1} \end{gather}

where the summation is over all solutions of the equation

(4.5)\begin{equation} \mu_u=\tilde{\mu}_u(\mu_d,\varphi_d) \end{equation}

for which the ion enters from the upstream region, $v_{u,x}>0, v_{d,x}>0$. The coefficient $C$ from (3.7) depends only on $v_u$. Thus, the problem is reduced to finding $\tilde {\mu }_u(\mu _d,\varphi _d)$. The equations of motion for an ion inside the shock transition are

(4.6)\begin{gather} \frac{{\rm d} v_x}{{\rm d} t}=\frac{q}{mc}\left(cE_x+v_yB_z-v_zB_y\right) \end{gather}

(4.7)\begin{gather}\frac{{\rm d} v_y}{{\rm d} t}=\frac{q}{mc}\left(v_zB_x-v_xB_z\right) \end{gather}

(4.8)\begin{gather}\frac{{\rm d} v_z}{{\rm d} t}=\frac{q}{mc}\left(v_xB_y-v_yB_x\right) \end{gather}

In what follows we shall assume that all ions cross the shock without stopping inside, so that $v_x>0$ in the region $0< x< D$. This assumption is justified when $v_T/V_u$ is not large and the cross-shock potential is not exceptionally high or low (Schwartz et al. Reference Schwartz, Thomsen, Bame and Stansberry1988; Dimmock et al. Reference Dimmock, Balikhin, Krasnoselskikh, Walker, Bale and Hobara2012). Ions which are reflected require special treatment. Here we restrict ourselves with the directly transmitted ions for approximate analytical treatment. Then ${\rm d}/{\rm d} t=v_x({\rm d}/{{\rm d}x})$ and one has

(4.9)\begin{gather} \varDelta \left(\frac{v_x^2}{2}\right)={-}\frac{q}{m} \phi_{HT}+ \frac{q}{mc}\int_0^D \left(v_yB_z-v_zB_y\right){{\rm d}x} \end{gather}

(4.10)\begin{gather}{\rm \Delta} v_y=\frac{q}{mc}\int_0^D \left(\frac{v_zB_x}{v_x}-B_z\right){{\rm d}x} \end{gather}

(4.11)\begin{gather}{\rm \Delta} v_z=\frac{q}{mc}\int_0^D \left(B_y-\frac{v_yB_x}{v_x}\right) \end{gather}

The energy conservation gives

(4.12)\begin{equation} \varDelta \left(\frac{mv^2}{2}\right)={-}q\phi_{HT} \end{equation}

Note that (Goodrich & Scudder Reference Goodrich and Scudder1984)

(4.13)\begin{equation} \frac{V_u\tan\theta_u}{c}\int_0^D B_y\,{\rm d} x=\phi_{NIF}-\phi_{HT} \end{equation}

In the narrow shock approximation, $D\rightarrow 0$, one has

(4.14)\begin{gather} {\rm \Delta} v_y=v_{d,y}-v_{u,y}= 0 \end{gather}

(4.15)\begin{gather}{\rm \Delta} v_z=v_{d,z}-v_{u,z}=\frac{q(\phi_{NIF}-\phi_{HT})}{mV_u\tan\theta_u} \end{gather}

In what follows it will be convenient to use the normalized variables $\boldsymbol {v}/V_u$, $\boldsymbol {B}/B_u$, and $s=2q\phi /mV_u^2$. Thus,

(4.16)\begin{gather} v_{u,y}=v_{d,y} \end{gather}

(4.17a,b)\begin{gather}v_{u,z}=v_{d,z}-\bar{s}, \quad \bar{s}=\frac{s_{NIF}-s_{HT}}{2\tan\theta_u} \end{gather}

The remaining component of the velocity is obtained from energy conservation:

(4.18)\begin{gather} v_u^2=v_d^2+s_{HT} \end{gather}

(4.19)\begin{gather}v_{u,x}=\sqrt{v_{d,x}^2+v_{d,z}^2+s_{HT}-\left(v_{d,z}-\bar{s}\right)^2} \end{gather}

(4.20)\begin{gather}=\sqrt{v_{d,x}^2+2v_{d,z}\bar{s}+s_{HT}-\bar{s}^2} \end{gather}

Note that a shock is essentially a discontinuity in this approximation. The corrections depending on the shock width are given in Gedalin (Reference Gedalin1997). In terms of the pitch-angle cosine one has

(4.21)\begin{gather} v_{d,x}=v_d\left(\mu_d\cos\theta_d+\sqrt{1-\mu_d^2} \cos\varphi_d\sin\theta_d\right) \end{gather}

(4.22)\begin{gather}v_{d,y}=v_{d}\sqrt{1-\mu_d^2} \sin\varphi_d \end{gather}

(4.23)\begin{gather}v_{d,z}= v_{d}\left(\mu_d\sin\theta_d-\sqrt{1-\mu_d^2} \cos\varphi_d\cos\theta_d\right) \end{gather}

where $\varphi _d$ is the gyrophase of the ion at the exit point. The upstream pitch angle cosine is then

(4.24)\begin{equation} \mu_u=\frac{v_{u,x}\cos\theta_u+v_{u,z}\sin\theta_u}{\sqrt{v_d^2+s_{HT}}} \end{equation}

(4.25)\begin{align} v_{u,x} & = \left[v_d^2\left(\mu_d\cos\theta_d+\sqrt{1-\mu_d^2} \cos\varphi_d\sin\theta_d\right)^2 \right. \nonumber\\ & \quad \left.\vphantom{\left(\mu_d\cos\theta_d+\sqrt{1-\mu_d^2}\cos\varphi_d\sin\theta_d\right)^2} + 2 v_{d}\left(\mu_d\sin\theta_d-\sqrt{1-\mu_d^2} \cos\varphi_d\cos\theta_d\right)\bar{s}+s_{HT}-\bar{s}^2\right]^{1/2} \end{align}

(4.26)\begin{gather} v_{u,z}=v_{d}\left(\mu_d\sin\theta_d-\sqrt{1-\mu_d^2} \cos\varphi_d\cos\theta_d\right)-\bar{s} \end{gather}

(4.27)\begin{gather}\frac{\cos\theta_u}{\cos\theta_d} =\frac{B_d}{B_u}\equiv R \end{gather}

These expressions determine $\mu _u$ as a function of $v_d,\mu _d,\varphi _d$.

5. Effect of the magnetic field rotation

The dependence $\mu _u=\tilde {\mu }_u(\mu _d,\varphi _d)$ results from the global change of the magnetic field and the cross-shock potential. It is instructive to show separately the effect of the rotation of the magnetic field vector at the shock crossing, when $s_{NIF}=s_{HT}=0$. In this case $v_{u,x}=v_{d,x}$, $v_{u,z}=v_{d,z}$ and

(5.1)\begin{gather} \mu_u=\left(\mu_d\cos\theta_d+\sqrt{1-\mu_d^2} \cos\varphi_d\sin\theta_d\right)\cos\theta_u \end{gather}

(5.2)\begin{gather}+\left(\mu_d\sin\theta_d-\sqrt{1-\mu_d^2} \cos\varphi_d\cos\theta_d\right)\sin\theta_u \end{gather}

(5.3)\begin{gather}=\mu_d\cos\varDelta + \sqrt{1-\mu_d^2} \sin\varDelta \cos\varphi_d \end{gather}

(5.4)\begin{gather}\varDelta =\theta_d-\theta_u \end{gather}

Now

(5.5)\begin{equation} f_d(\mu_d)=\frac{1}{2{\rm \pi}}\int_0^{2{\rm \pi}} {\rm d}\varphi_d\, f_u\left(\mu_d\cos\varDelta + \sqrt{1-\mu_d^2} \sin\varDelta \cos\varphi_d\right) \end{equation}

and for $f_u=\delta (\mu _d\cos \varDelta + \sqrt {1-\mu _d^2} \sin \varDelta \cos \varphi _d-\mu _u)$ one has

(5.6)\begin{equation} f_d(\mu_d)=\frac{1}{\rm \pi} \frac{1}{|\sqrt{1-\mu_d^2} \sin\varDelta \sin\varphi_d|} \end{equation}

where

(5.7)\begin{equation} \cos\varphi_d=\frac{\mu_u-\mu_d\cos\varDelta}{\sqrt{1-\mu_d^2} \sin\varDelta} \end{equation}

The factor $1/2$ disappears because there are two solutions $\sin \varphi _d=\pm \sqrt {1-\cos ^2\varphi _d}$ with the same absolute value. After some algebra, we find that the rotation of the magnetic field results in the scattering at the shock front described by the probability

(5.8)\begin{equation} Cw(\mu_u,\mu_d) =\frac{1}{{\rm \pi} \left[(1-\mu_u^2)(1-\mu_d^2) -(\mu_u\mu_d-\cos\varDelta)^2\right]^{1/2}}\end{equation}

provided

(5.9)\begin{gather} (1-\mu_u^2)(1-\mu_d^2) -(\mu_u\mu_d-\cos\varDelta)^2>0 \end{gather}

(5.10)\begin{gather}\mu_u\sin\theta_d-\mu_d\sin\theta_u>0 \end{gather}

The first requirement is the condition of existence of $\phi _d$ for given $\mu _u,\mu _d$. The second requirement means that the ion moves toward the downstream region from the ramp and not in the opposite direction. It is obvious also that $\mu _u>0$, $\mu _d>0$. In this case $C=2{\rm \pi} m^2 v_u^2$.

6. Effect of the cross-shock potential

Analytical expressions can also be written in the narrow shock approximation for nonzero $s$. However, they become too lengthy and difficult for qualitative understanding of the behaviour of the probabilities. Instead, we present several plots of $Cw(\mu _i,\mu _d)$. In the case $s_{HT}=s_{NIF}=0$ the probability (5.8) does not depend on the speed (apart of the multiplier $C$). For nonzero $s$ this is not so. For visualization we chose $v_u=1/\cos \theta _u$ which is the flow speed in HT frame. If the upstream distribution were cold, all ions would have this upstream speed and $\mu _u=1$. If the upstream thermal speed $v_T\ll 1$, the pitch-angle cosines remain in the vicinity of $\mu =1$, so that in the plots we restrict ourselves with the range $0.9\leq \mu _u\leq 1$, $0.9\leq \mu _d\leq 1$. Figure 2 shows the probability $Cw(\mu _i,\mu _d)$, on a logarithmic scale, for $\theta =70^\circ$ and two values of the magnetic compression, $R=1.5$ and $R=2.5$, both for zero $s$ and nonzero $s$. The thin black lines in each plot correspond to the approximation of the magnetic moment conservation $(1-\mu _d^2)=R(1-\mu _u^2)$. It is seen that the magnetic moment is not conserved. The downstream $\mu _d$ is no longer a single-valued function of $\mu _u$. The main effect is that a sudden change of the magnetic field direction immediately causes substantial gyration of an ion around the downstream magnetic field vector. The cross-shock potential reduces the ion energy and, therefore, moderates the gyration.

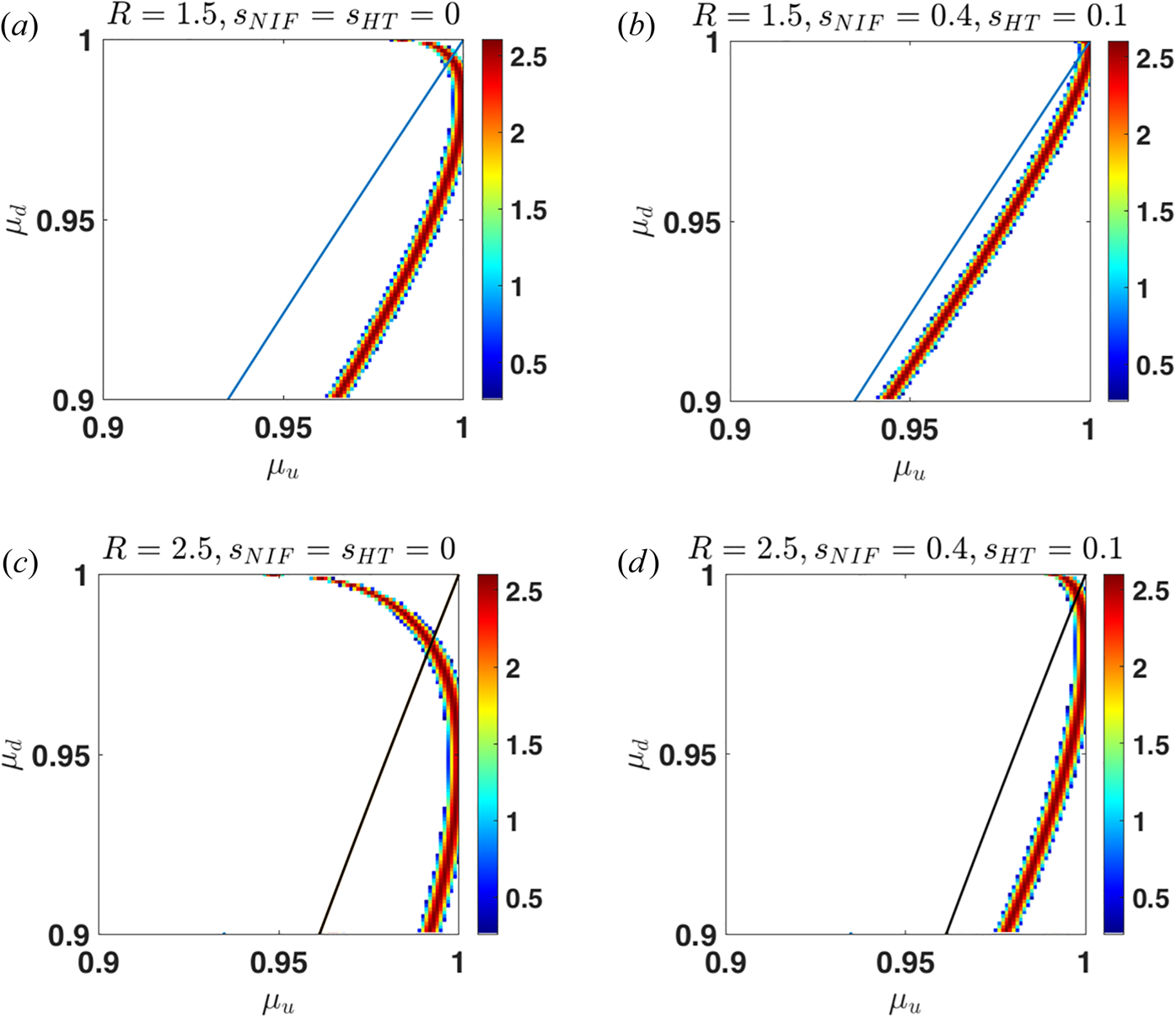
Figure 2. Filled contour plots for the probability $Cw(\mu _i,\mu _d)$ for $\theta =70^\circ$ and four cases. For the top row $R=1.5$, for the bottom row $R=2.5$. For the left column $s_{HT}=s_{NIF}=0$, for the right column $s_{HT}=0,1, s_{NIF}=0.4$. The thin black line shows the widely used assumption of the magnetic moment conservation.