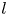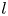1. Introduction
It is well known that the transverse dynamics of a non-neutral, single-species plasma stored in a Penning–Malmberg trap (PMT) can be taken as a perfect analogous system to a two-dimensional (2-D) inviscid and incompressible fluid (Levy Reference Levy1965; Briggs, Daugherty & Levy Reference Briggs, Daugherty and Levy1970). In a PMT (Malmberg & de Grassie Reference Malmberg and de Grassie1975), a cylindrical, axisymmetric device where particles are subjected to axial electrostatic trapping (thanks to a series of hollow electrodes) and transverse magnetic confinement (thanks to a highly homogeneous axial magnetic field), there is a correspondence between the plasma and fluid velocity fields as well as between the line-integrated plasma density and the fluid vorticity. A trapped plasma column is therefore equivalent to a 2-D fluid vortex. In this respect, PMT-confined magnetized plasmas offer desirable properties, such as negligible 3-D effects, the absence of friction at the boundary, the ability to fine tune the experimental system parameters and accurate diagnostics. The resulting continued interest in the study of fluid systems through non-neutral magnetized plasmas has yielded a wealth of results concerning the stability properties of vorticity patterns, the formation and interaction of vorticity structures (vortex crystals) and the turbulent features of the evolution of such systems (Driscoll & Fine Reference Driscoll and Fine1990; Fine et al. Reference Fine, Cass, Flynn and Driscoll1995; Durkin & Fajans Reference Durkin and Fajans2000; Kawai et al. Reference Kawai, Kiwamoto, Soga and Aoki2007; Lepreti et al. Reference Lepreti, Romé, Maero, Paroli, Pozzoli and Carbone2013; Romé, Chen & Maero Reference Romé, Chen and Maero2017).
We direct our attention in particular to the instance of non-axisymmetric isolated vortices. Recently, Hurst and coauthors have extensively studied the evolution of a deformed vortex embedded in a static or slowly evolving strain field, which in the plasma analogy is the electric field obtained by imposing suitable potentials on the azimuthally sectored cylindrical wall of the trapping volume (Hurst et al. Reference Hurst, Danielson, Dubin and Surko2016, Reference Hurst, Danielson, Dubin and Surko2020, Reference Hurst, Danielson, Dubin and Surko2021). Rotating deformed vortices, on the contrary, can arise as a consequence of Kelvin–Helmholtz (KH) perturbations, i.e. of an azimuthal velocity shear in the vortex rotation state. Extending Kirchhoff's finding about the stability of a rotating vortex of elliptical shape, i.e. with a deformation of order $l=2$![]() , Deem and Zabusky's theoretical work showed the possibility of stability for any nonlinear $l$
, Deem and Zabusky's theoretical work showed the possibility of stability for any nonlinear $l$![]() -fold symmetric patch of uniform vorticity, or V-state (Deem & Zabusky Reference Deem and Zabusky1978), with l a non-negative integer number. The most straightforward way to excite an $l$
-fold symmetric patch of uniform vorticity, or V-state (Deem & Zabusky Reference Deem and Zabusky1978), with l a non-negative integer number. The most straightforward way to excite an $l$![]() th-order KH perturbation up to the nonlinear regime in a trapped plasma column is through the application of a potential oscillating at a frequency matching that of the rotation of the perturbation wave. The potential must be applied on the sectored boundary with a multipolarity corresponding to the deformation order. In principle, given $N$
th-order KH perturbation up to the nonlinear regime in a trapped plasma column is through the application of a potential oscillating at a frequency matching that of the rotation of the perturbation wave. The potential must be applied on the sectored boundary with a multipolarity corresponding to the deformation order. In principle, given $N$![]() sectors evenly occupying the whole $2{\rm \pi}$
sectors evenly occupying the whole $2{\rm \pi}$![]() angle of the electrode's azimuthal extent (a configuration very often found in experimental setups, with $N = 4, 6, 8$
angle of the electrode's azimuthal extent (a configuration very often found in experimental setups, with $N = 4, 6, 8$![]() ) the highest attainable multipole potential is of order $N$
) the highest attainable multipole potential is of order $N$![]() , yielding a KH wavemode of order $l=N/2$
, yielding a KH wavemode of order $l=N/2$![]() . This represents a hardware limitation in the access to high-order V-states. Different sectoring choices may modify, but not remove completely, this limit.
. This represents a hardware limitation in the access to high-order V-states. Different sectoring choices may modify, but not remove completely, this limit.
Members of this research group have shown in the past that a rotating electric field arrangement could excite non-trivial wavemodes, and in particular an $l=3$![]() KH wave was induced by a dipole field rotating with opposite orientation with respect to the vortex rotation (Bettega et al. Reference Bettega, Paroli, Pozzoli and Romé2009). Here, we generalize that early work, laying out of for the first time a full linear theory for the mode excitation and then detailing a perfected routine leading to the first ever experimental achievement of V-states up to order $l=7$
KH wave was induced by a dipole field rotating with opposite orientation with respect to the vortex rotation (Bettega et al. Reference Bettega, Paroli, Pozzoli and Romé2009). Here, we generalize that early work, laying out of for the first time a full linear theory for the mode excitation and then detailing a perfected routine leading to the first ever experimental achievement of V-states up to order $l=7$![]() , where some previous experimental and analysis limitations are also overcome and further insight is gained into the features of the wave growth.
, where some previous experimental and analysis limitations are also overcome and further insight is gained into the features of the wave growth.
Previous theoretical and simulation works have investigated the growth of the vortex deformation and indicated the possible influence of parameters of interest such as the V-state amplitude or radial vorticity profile on the evolution and stability of the deformed vortices (Dritschel Reference Dritschel1998; Friedland & Shagalov Reference Friedland and Shagalov2000), in this respect considering a generalization of the concept of V-state to a non-uniform vorticity patch. The ability to precisely excite KH waves of generic order and high amplitude, reaching the nonlinear regime, may offer unprecedented opportunities for experimental studies on the free and forced dynamics of V-states under well-controlled conditions. This work is therefore meant to lay the ground for investigations in this direction, which we shall address in forthcoming articles.
Another current topical interest that motivates studies of this kind is related to the use of PMTs as the tool of choice for low-energy antimatter investigations (see for instance Danielson et al. Reference Danielson, Dubin, Greaves and Surko2015; Fajans & Surko Reference Fajans and Surko2020 and references therein). Within this context, the ability to excite, as well as the need to avoid, perturbations in the trapped samples have direct implications for plasma diagnostic techniques and stable confinement, respectively. Very close examples of plasma manipulation are the so-called rotating-wall compression, where the rotating electric field is used to squeeze the transverse cross-section of the trapped sample, and the autoresonant control of the bulk rotation of an off-axis vortex (Huang & Driscoll Reference Huang and Driscoll1994; Fajans, Gilson & Friedland Reference Fajans, Gilson and Friedland1999; Singer et al. Reference Singer, König, Stoneking, Steinbrunner, Danielson, Schweikhard and Sunn Pedersen2021; Hunter Reference Hunter, Amsler, Breuker, Bumbar, Chesnevskaya, Costantini, Ferragut, Giammarchi, Gligorova and Gosta2023).
The article is organized as follows. Section 2 lays out the linear perturbation theory for a 2-D vortex subjected to a rotating strain, showing the presence of a resonant, single KH mode interaction with the drive upon suitable conditions. Section 3 revises the essential features of the apparatus and the experimental routine devised to prepare the initial, axisymmetric vortex state. Section 4 presents the systematic experimental results for the selective mode growth in the linear and nonlinear regime up to saturation and collapse. Section 5 finally summarizes and discusses our findings with an eye to further investigations about the forced and free dynamics of non-axisymmetric vortices.
2. Linear theory
We describe the interaction between the plasma column and the electric perturbation at the trap wall within the framework of the 2-D electrostatic, cold fluid drift model, whose details are found in Davidson (Reference Davidson1990). In brief, in an electrostatic approximation the electric field is related to the electric potential as $\boldsymbol {E}( \boldsymbol {r},t ) = -\boldsymbol {\nabla } \phi ( \boldsymbol {r},t)$![]() ; after averaging over the fast axial bounce and cyclotron rotation and neglecting inertial effects, the velocity of the plasma (fluid) element in the transverse plane is reduced to $\boldsymbol {v}( \boldsymbol {r},t) = -\boldsymbol {\nabla } \phi ( \boldsymbol {r},t)/B \times \hat {e}_z$
; after averaging over the fast axial bounce and cyclotron rotation and neglecting inertial effects, the velocity of the plasma (fluid) element in the transverse plane is reduced to $\boldsymbol {v}( \boldsymbol {r},t) = -\boldsymbol {\nabla } \phi ( \boldsymbol {r},t)/B \times \hat {e}_z$![]() , where B is the intensity of the magnetic field, directed along the longitudinal axis $\hat{e}_z$
, where B is the intensity of the magnetic field, directed along the longitudinal axis $\hat{e}_z$![]() . These relations are coupled to the 2-D continuity equation $\partial _t n( \boldsymbol {r},t)+\boldsymbol {v}( \boldsymbol {r},t)\boldsymbol {\cdot }\boldsymbol {\nabla }( n( \boldsymbol {r},t) )=0$
. These relations are coupled to the 2-D continuity equation $\partial _t n( \boldsymbol {r},t)+\boldsymbol {v}( \boldsymbol {r},t)\boldsymbol {\cdot }\boldsymbol {\nabla }( n( \boldsymbol {r},t) )=0$![]() and to the Poisson equation $\nabla ^2\phi ( \boldsymbol {r},t) = en( \boldsymbol {r},t)/\varepsilon _0$
and to the Poisson equation $\nabla ^2\phi ( \boldsymbol {r},t) = en( \boldsymbol {r},t)/\varepsilon _0$![]() , for a distribution of electrons of charge $-e$
, for a distribution of electrons of charge $-e$![]() and density $n( \boldsymbol {r},t)$
and density $n( \boldsymbol {r},t)$![]() with the boundary conditions at the trap wall $r = R_w$
with the boundary conditions at the trap wall $r = R_w$![]() , and $\varepsilon_0$
, and $\varepsilon_0$![]() the vacuum permittivity. By the aforementioned analogy, the plasma properties $\{ en/\varepsilon _0B, \boldsymbol {v}, \phi /B\}$
the vacuum permittivity. By the aforementioned analogy, the plasma properties $\{ en/\varepsilon _0B, \boldsymbol {v}, \phi /B\}$![]() result isomorphic to the fluid ones $\{ \zeta, \boldsymbol {v}, \psi \}$
result isomorphic to the fluid ones $\{ \zeta, \boldsymbol {v}, \psi \}$![]() , where $\zeta = ( \boldsymbol {\nabla } \times \boldsymbol {v})_z$
, where $\zeta = ( \boldsymbol {\nabla } \times \boldsymbol {v})_z$![]() is the fluid vorticity and $\psi$
is the fluid vorticity and $\psi$![]() is the streamfunction defined by the relation $\boldsymbol {v} = -\boldsymbol {\nabla }\psi \times \hat {e}_z$
is the streamfunction defined by the relation $\boldsymbol {v} = -\boldsymbol {\nabla }\psi \times \hat {e}_z$![]() .
.
A linear treatment considers small perturbations of the axisymmetric equilibrium density $n^0( r)$![]() and electric potential $\phi ^0( r)$
and electric potential $\phi ^0( r)$![]() , expressed as a series of azimuthally travelling waves (KH modes, also called diocotron modes in the non-neutral plasma nomenclature)
, expressed as a series of azimuthally travelling waves (KH modes, also called diocotron modes in the non-neutral plasma nomenclature)


with $\omega$![]() the complex oscillation frequency. Plugging these into the continuity and Poisson equations we get the eigenvalue equation for the generic $l$
the complex oscillation frequency. Plugging these into the continuity and Poisson equations we get the eigenvalue equation for the generic $l$![]() th perturbation mode. For a uniform equilibrium density $\tilde {n}$
th perturbation mode. For a uniform equilibrium density $\tilde {n}$![]() and radius $R_p$
and radius $R_p$![]() , i.e. $n^0( r) = \tilde {n}H(R_p - r)$
, i.e. $n^0( r) = \tilde {n}H(R_p - r)$![]() (with $H$
(with $H$![]() the Heaviside step function), in the absence of potential perturbations at the wall, the solution of the eigenvalue equation yields the linear eigenfrequency $\varOmega _l$
the Heaviside step function), in the absence of potential perturbations at the wall, the solution of the eigenvalue equation yields the linear eigenfrequency $\varOmega _l$![]() for each diocotron mode $l$
for each diocotron mode $l$![]()

with $\omega _D = \tilde {n}e/2\varepsilon _0B$![]() the fundamental diocotron frequency, that is also the rigid rotation frequency $\omega _r$
the fundamental diocotron frequency, that is also the rigid rotation frequency $\omega _r$![]() of the unperturbed circular vortex.
of the unperturbed circular vortex.
For our specific problem with its own boundary condition (b.c.), i.e. an electric potential perturbation at the wall $R_w$![]() , the general solution scheme proceeds as follows:
, the general solution scheme proceeds as follows:
(i) The b.c. is recast as a Fourier series $\delta \phi ( R_w,\vartheta,t) = \sum _{l=-\infty }^{+\infty }c_l( t)\exp ( {\rm i}l\vartheta )$
 .
.(ii) The b.c. thus obtained is Laplace transformed in the time variable to get $\delta \phi ( R_w,\vartheta,s) = \sum _{l=-\infty }^{+\infty }c_l( s)\exp ( {\rm i}l\vartheta )$
 .
.(iii) The eigenvalue problem is solved in the Laplace-transformed domain to obtain the perturbed potential at the plasma surface $\delta \phi ( R_p,\vartheta,s)$
 .
.(iv) By Laplace inverse transforming the solution we finally get $\delta \phi ( R_p,\vartheta,t)$
 . Depending on the form of the b.c., this expression will manifest an eventual resonance condition yielding a secular growth of a specific mode.
. Depending on the form of the b.c., this expression will manifest an eventual resonance condition yielding a secular growth of a specific mode.
The general solution of the problem is in the form

whose coefficients are found using the b.c. as well as potential finiteness at $r=0$![]() , radial electric field discontinuity at $r=R_p$
, radial electric field discontinuity at $r=R_p$![]() and potential continuity at $r=R_p$
and potential continuity at $r=R_p$![]() . In the Laplace-transformed domain they read
. In the Laplace-transformed domain they read

As an explicit example, let us use a dipole rotating-field b.c. for $N=4$![]() sectors
sectors

with
This condition corresponds indeed to four potentials $V_m$![]() oscillating with amplitude $V_{dr}$
oscillating with amplitude $V_{dr}$![]() and a $\sigma m {\rm \pi}/2$
and a $\sigma m {\rm \pi}/2$![]() phase shift between adjacent sectors; in particular, with $\sigma = -1$
phase shift between adjacent sectors; in particular, with $\sigma = -1$![]() the potential is a corotating dipole, i.e. a dipole field rotating with the same orientation as $\omega _r$
the potential is a corotating dipole, i.e. a dipole field rotating with the same orientation as $\omega _r$![]() , while $\sigma = +1$
, while $\sigma = +1$![]() is a counterrotating dipole. For $\sigma = \pm 2$
is a counterrotating dipole. For $\sigma = \pm 2$![]() we would have a purely oscillating (non-rotating) quadrupole. Let us consider $\sigma = \pm 1$
we would have a purely oscillating (non-rotating) quadrupole. Let us consider $\sigma = \pm 1$![]() . Rewriting the b.c. as a Fourier series, only some terms of the series appear, and specifically only odd ones
. Rewriting the b.c. as a Fourier series, only some terms of the series appear, and specifically only odd ones
and with $V_m$![]() forms of (2.7) for $m = 0,1$
forms of (2.7) for $m = 0,1$![]() we get two different cases for $\sigma = \pm 1$
we get two different cases for $\sigma = \pm 1$![]()

and

To observe the evolution of the perturbation on the vortex edge, we Laplace transform the coefficients

and

Using these expressions in (2.5) we can evaluate the potential (2.4) and in particular the perturbation value at the plasma edge. For the case $\sigma =+1$![]() , via Laplace inverse transform we get $\delta \phi (R_p,\vartheta,t)$
, via Laplace inverse transform we get $\delta \phi (R_p,\vartheta,t)$![]() to be
to be

where we can see that, while the coefficients $l = 4k+1$![]() have no poles, the $l = 4k+3$
have no poles, the $l = 4k+3$![]() ones yield a resonance at $\omega _{dr} = \varOmega _l$
ones yield a resonance at $\omega _{dr} = \varOmega _l$![]() . In this case the potential perturbation can be recast as
. In this case the potential perturbation can be recast as

where a secular growth appears for a specific mode with $l = 4k+3$![]() , where $k$
, where $k$![]() is automatically selected as the drive frequency matches one of the $l = 4k+3$
is automatically selected as the drive frequency matches one of the $l = 4k+3$![]() -type modes. If we chose $\sigma = -1$
-type modes. If we chose $\sigma = -1$![]() the roles would be flipped in (2.13) and the resonant growth would occur for $l = 4k+1$
the roles would be flipped in (2.13) and the resonant growth would occur for $l = 4k+1$![]() wavenumbers while the $l = 4k+3$
wavenumbers while the $l = 4k+3$![]() ones would be stable. Similarly, the choice $\sigma = \pm 2$
ones would be stable. Similarly, the choice $\sigma = \pm 2$![]() would yield coefficients with $l = 4k+2$
would yield coefficients with $l = 4k+2$![]() terms only, leading to resonant secular growth of modes with such $l$
terms only, leading to resonant secular growth of modes with such $l$![]() values.
values.
Again, it would just be a matter of lengthy but similar algebra to evaluate the case of the b.c. applied to $N=8$![]() sectors. In this case the b.c. reads
sectors. In this case the b.c. reads

with
where $\sigma$![]() can take a larger number of values, corresponding to dipole ($\sigma = \pm 1$
can take a larger number of values, corresponding to dipole ($\sigma = \pm 1$![]() ), quadrupole ($\sigma = \pm 2$
), quadrupole ($\sigma = \pm 2$![]() ) and sextupole ($\sigma = \pm 3$
) and sextupole ($\sigma = \pm 3$![]() ) rotating fields or an oscillating octupole field ($\sigma = \pm 4$
) rotating fields or an oscillating octupole field ($\sigma = \pm 4$![]() ). The respective driven modes are listed in table 1.
). The respective driven modes are listed in table 1.
Table 1. Summary of KH modes that can be excited with a rotating electric field. Given a number $N$![]() of sectors with a corresponding sector angular span ${\rm \pi} /2$
of sectors with a corresponding sector angular span ${\rm \pi} /2$![]() (for $N=4$
(for $N=4$![]() ) or ${\rm \pi} /4$
) or ${\rm \pi} /4$![]() (for $N=8$
(for $N=8$![]() ), the suitable multipolarity and rotation orientation of the field is determined by the phase shift between adjacent sectors $\Delta \varphi$
), the suitable multipolarity and rotation orientation of the field is determined by the phase shift between adjacent sectors $\Delta \varphi$![]() . First column indicates the modes $l$
. First column indicates the modes $l$![]() excited with a 4-fold split electrode, second and third rows with an 8-fold split electrode. The integer $k = 0,1,2,\ldots$
excited with a 4-fold split electrode, second and third rows with an 8-fold split electrode. The integer $k = 0,1,2,\ldots$![]() finally determines the unique excited mode and is automatically chosen by setting the resonant mode frequency.
finally determines the unique excited mode and is automatically chosen by setting the resonant mode frequency.

We detailed the cases $N=4,8$![]() as they are the most common choices in experimental set-ups, yet from this analysis we can easily extrapolate to a general case. For any even number of sectors $N$
as they are the most common choices in experimental set-ups, yet from this analysis we can easily extrapolate to a general case. For any even number of sectors $N$![]() , it is possible to generate co- and counterrotating fields of multipolar order $\leq N-2$
, it is possible to generate co- and counterrotating fields of multipolar order $\leq N-2$![]() (i.e. $|\sigma | \leq N/2-1$
(i.e. $|\sigma | \leq N/2-1$![]() ) and an oscillating $N$
) and an oscillating $N$![]() -polar field ($|\sigma | = N/2$
-polar field ($|\sigma | = N/2$![]() ), which enables the excitation of all modes with the exception of wavenumbers that are integer multiples of $N$
), which enables the excitation of all modes with the exception of wavenumbers that are integer multiples of $N$![]() . Odd sectoring $N$
. Odd sectoring $N$![]() makes it possible to generate only rotating fields of multipolar order $\leq N-1$
makes it possible to generate only rotating fields of multipolar order $\leq N-1$![]() ; again, all modes can be excited except the integer multiples of $N$
; again, all modes can be excited except the integer multiples of $N$![]() .
.
3. Apparatus, preparation routine and diagnostics
All experiments were performed in the ELTRAP (ELectron TRAP) device, a PMT whose electrode stack is sketched (not to scale) in figure 1. The electrodes are hollow cylindrical shells with an inner diameter of $90$![]() mm made out of oxygen-free high-conductivity copper. The ‘C’ electrodes are $90$
mm made out of oxygen-free high-conductivity copper. The ‘C’ electrodes are $90$![]() mm long, ‘S’ ones are $150$
mm long, ‘S’ ones are $150$![]() mm long. Any pair of non-adjacent electrodes can be biased to a negative potential – typically $-100$
mm long. Any pair of non-adjacent electrodes can be biased to a negative potential – typically $-100$![]() to $-200$
to $-200$![]() V – to create an axial electrostatic well with a maximum trapping length ${\sim }1$
V – to create an axial electrostatic well with a maximum trapping length ${\sim }1$![]() m. Electrodes S2, S4 and S8 are azimuthally split into 2, 4 and 8 patches, respectively, which can be used either to impart electric field perturbations or to detect transverse collective modes of the confined particle sample (see figure 2). As one of the confinement voltages is reduced to zero, the plasma can be destructively detected as it flows out of the trap and hits either a charge collector plate (on the left) or a P43 phosphor screen (on the right) set to a positive potential high enough to produce phosphorescence by electron impact (in these experiments, $7$
m. Electrodes S2, S4 and S8 are azimuthally split into 2, 4 and 8 patches, respectively, which can be used either to impart electric field perturbations or to detect transverse collective modes of the confined particle sample (see figure 2). As one of the confinement voltages is reduced to zero, the plasma can be destructively detected as it flows out of the trap and hits either a charge collector plate (on the left) or a P43 phosphor screen (on the right) set to a positive potential high enough to produce phosphorescence by electron impact (in these experiments, $7$![]() kV) and thus producing an image of the axially integrated density distribution. The image is captured by a charge-coupled device (CCD) camera with a maximum resolution of $1344\times 1024$
kV) and thus producing an image of the axially integrated density distribution. The image is captured by a charge-coupled device (CCD) camera with a maximum resolution of $1344\times 1024$![]() pixels. The electrode stack is installed within a vacuum vessel; the pressure in these experiments was typically in the mid $10^{-9}$
pixels. The electrode stack is installed within a vacuum vessel; the pressure in these experiments was typically in the mid $10^{-9}$![]() mbar, corresponding to electron–neutral collision times of the order of some tens to $100$
mbar, corresponding to electron–neutral collision times of the order of some tens to $100$![]() ms. The whole apparatus is surrounded by a solenoid providing a uniform magnetic field of intensity $B\leq 0.2$
ms. The whole apparatus is surrounded by a solenoid providing a uniform magnetic field of intensity $B\leq 0.2$![]() T directed along the trap axis.
T directed along the trap axis.

Figure 1. Sketch of the ELTRAP electrode stack. Hollow cylinders C0 to SH are aligned to form a cylindrical trapping volume with the longitudinal axis set along the direction of a uniform magnetic field $B$![]() . Diagnostic tools are placed at the ends of the stack: on the left, a collector plate connected to a digital oscilloscope, on the right, a phosphor screen biased to a potential $V_{ph} \geq 4$
. Diagnostic tools are placed at the ends of the stack: on the left, a collector plate connected to a digital oscilloscope, on the right, a phosphor screen biased to a potential $V_{ph} \geq 4$![]() kV yielding images at plasma ejection that can be captured by a CCD camera. Azimuthally split electrodes S2, S4 and S8 can be used for electric excitations or non-destructive, induced-current diagnostics.
kV yielding images at plasma ejection that can be captured by a CCD camera. Azimuthally split electrodes S2, S4 and S8 can be used for electric excitations or non-destructive, induced-current diagnostics.

Figure 2. Sketch and naming convention of sectored electrodes. Here, the S2, S4 and S8 electrodes are azimuthally segmented and labelled as depicted, looking from the phosphor screen into the trap.
The electron plasma is produced in situ by means of a ‘sourceless’ technique, namely a very low-power radio-frequency (RF) discharge initiated by a stochastic heating of free electrons in the neutral background. If a RF potential of amplitude 1–10 V and frequency 1–20 MHz is applied to any electrode within the trapping region, a free electron bouncing across the trap length can stochastically increase its energy to some ten electronvolts by interacting with the RF field, thus reaching energies above the first ionization threshold for light gases (the residual atmospheric gas in the vacuum chamber; no additional gas injection is performed). Over times of the order of some seconds, i.e. over many collision times, an electron plasma accumulates in the trapping region, and can reach a steady-state configuration with a production–loss balance. Further details about the RF breeding of the electron plasma can be found in Paroli et al. (Reference Paroli, De Luca, Maero, Pozzoli and Romé2010), Maero et al. (Reference Maero, Chen, Pozzoli and Romé2015) and Maero (Reference Maero2017).
The electron plasma column may often lie off axis and thus entertain a bulk rotation ($l=1$![]() diocotron mode). After the ionizing RF drive is turned off, the plasma is brought to the trap axis by an active feedback damping (Fine Reference Fine1988) of the offset using two opposite sectors of the S4 electrode: the amplified, filtered and phase-tuned induced-current signal picked up by a sector is sent to the opposite one and the retarding electric field slows down the rotation, thus reducing its amplitude (which is proportional to the mode frequency). Feedback damping is also required as some of the positive ions generated in the plasma-breeding stage, although not efficiently trapped, have a finite residence time in the trapping region and a destructive ion-induced instability of the $l=1$
diocotron mode). After the ionizing RF drive is turned off, the plasma is brought to the trap axis by an active feedback damping (Fine Reference Fine1988) of the offset using two opposite sectors of the S4 electrode: the amplified, filtered and phase-tuned induced-current signal picked up by a sector is sent to the opposite one and the retarding electric field slows down the rotation, thus reducing its amplitude (which is proportional to the mode frequency). Feedback damping is also required as some of the positive ions generated in the plasma-breeding stage, although not efficiently trapped, have a finite residence time in the trapping region and a destructive ion-induced instability of the $l=1$![]() mode (Fajans Reference Fajans1993; Kabantsev & Driscoll Reference Kabantsev and Driscoll2007; Maero Reference Maero2017) would occur otherwise. A few seconds of feedback damping are enough to let the residual ions leave while the ionization drops as the electrons cool down. The result is a centred electron plasma column (fluid vortex) with a monotonically decreasing radial profile. Depending on the control parameters, we achieve a range of radial density profiles, and albeit there is no perfectly flat radial profile, the decrease is acceptably smooth and monotonic, so that such vortices are stable against diocotron instabilities; furthermore, they have a well-defined edge with a sharp fall-off region, which is another characteristic featured in the theoretical model. Vortices of this kind will be the initial state for the diocotron mode excitation.
mode (Fajans Reference Fajans1993; Kabantsev & Driscoll Reference Kabantsev and Driscoll2007; Maero Reference Maero2017) would occur otherwise. A few seconds of feedback damping are enough to let the residual ions leave while the ionization drops as the electrons cool down. The result is a centred electron plasma column (fluid vortex) with a monotonically decreasing radial profile. Depending on the control parameters, we achieve a range of radial density profiles, and albeit there is no perfectly flat radial profile, the decrease is acceptably smooth and monotonic, so that such vortices are stable against diocotron instabilities; furthermore, they have a well-defined edge with a sharp fall-off region, which is another characteristic featured in the theoretical model. Vortices of this kind will be the initial state for the diocotron mode excitation.
All the experiments reported here were performed with the following set of parameters: magnetic field intensity $0.13$![]() T; confinement potential $-160$
T; confinement potential $-160$![]() V on C1 and C7; RF plasma-breeding drive in the range 5–8 V, 3–10 MHz on C2; rotating-field drive on S8; diocotron mode pickups on S2T ($l=3$
V on C1 and C7; RF plasma-breeding drive in the range 5–8 V, 3–10 MHz on C2; rotating-field drive on S8; diocotron mode pickups on S2T ($l=3$![]() mode detection) and S4L+S4R (quadrupolar configuration for $l=2$
mode detection) and S4L+S4R (quadrupolar configuration for $l=2$![]() mode). Figure 3 shows the two classes of initial states, achieved with slightly different parameters in a sequence of separate measurement sessions that were necessary to the systematic investigation presented in the next section (we shall refer to them as profiles A and B, respectively). Each radial density profile (black line) is obtained as a $\theta$
mode). Figure 3 shows the two classes of initial states, achieved with slightly different parameters in a sequence of separate measurement sessions that were necessary to the systematic investigation presented in the next section (we shall refer to them as profiles A and B, respectively). Each radial density profile (black line) is obtained as a $\theta$![]() -average of the CCD image, denoised and remapped onto a polar grid and then averaged over several shots ($25$
-average of the CCD image, denoised and remapped onto a polar grid and then averaged over several shots ($25$![]() on the left, $10$
on the left, $10$![]() on the right). The shot-to-shot repeatability is very good: as repeatability indices, both total charge and dispersion of the plasma radius exhibit fluctuations of $1\,\%-2\,\%$
on the right). The shot-to-shot repeatability is very good: as repeatability indices, both total charge and dispersion of the plasma radius exhibit fluctuations of $1\,\%-2\,\%$![]() . The initial axisymmetric vortex states displayed radii $R_p\simeq 0.5-0.55 R_w$
. The initial axisymmetric vortex states displayed radii $R_p\simeq 0.5-0.55 R_w$![]() and core densities of low- to mid $10^{12}$
and core densities of low- to mid $10^{12}$![]() m$^{-3}$
m$^{-3}$![]() , yielding rotation frequencies (also shown in figure 3, blue lines) of some ten kHz; as a consequence, the experiments can be considered collision free as at least thousands of rotation periods are guaranteed before collisional diffusion can be observed.
, yielding rotation frequencies (also shown in figure 3, blue lines) of some ten kHz; as a consequence, the experiments can be considered collision free as at least thousands of rotation periods are guaranteed before collisional diffusion can be observed.

Figure 3. Typical density and rotation profiles of the initial axisymmetric vortex. (a) Profile type A. (b) Profile type B. Black line: radial density profile. Blue line: rotation frequency calculated from the density profile.
4. Selective mode excitation
After the plasma column is prepared in the initial state as described in § 3, the rotating-field drive is applied for a set time on the patches of electrode S8, after which the plasma is released onto the phosphor screen by grounding electrode C7. The phosphor screen image will be the primary source of information on the vortex deformation in this work; the data analysis routine implemented to extract the azimuthal mode decomposition from the image proceeds as follows. We can define the total $l$![]() th mode coefficient or amplitude $A_l$
th mode coefficient or amplitude $A_l$![]() as
as
hence, the image is denoised and remapped onto a polar grid; the density profile $n(r,\vartheta )$![]() is decomposed into a Fourier series to obtain the azimuthal perturbation coefficients for each (discrete) radial position $\delta n^{l}(r)$
is decomposed into a Fourier series to obtain the azimuthal perturbation coefficients for each (discrete) radial position $\delta n^{l}(r)$![]() ; each coefficient is integrated (summed) over the trap cross-section as in (4.1). The mode amplitudes of the unperturbed initial density profile, stemming from small residual asymmetries, are subtracted; they will anyway be one to two orders of magnitude smaller than the resonant deformation values. In the following, the total mode amplitude $A_l$
; each coefficient is integrated (summed) over the trap cross-section as in (4.1). The mode amplitudes of the unperturbed initial density profile, stemming from small residual asymmetries, are subtracted; they will anyway be one to two orders of magnitude smaller than the resonant deformation values. In the following, the total mode amplitude $A_l$![]() is always shown as normalized to the amplitude $A_0$
is always shown as normalized to the amplitude $A_0$![]() , i.e. the total fluid circulation or plasma line density. We remark that this procedure is in general more accurate than others such as the analysis of the contour deformation, used for instance in Bettega et al. (Reference Bettega, Paroli, Pozzoli and Romé2009), as it yields an integral information that includes the density perturbation over the whole cross-section of the 2-D domain. This is crucial, especially when the vorticity profile does not exhibit a steep fall off: in such a case, the identification of the vortex edge can be difficult and arbitrary and the density perturbation can extend over a significant thickness of the vortex outermost region.
, i.e. the total fluid circulation or plasma line density. We remark that this procedure is in general more accurate than others such as the analysis of the contour deformation, used for instance in Bettega et al. (Reference Bettega, Paroli, Pozzoli and Romé2009), as it yields an integral information that includes the density perturbation over the whole cross-section of the 2-D domain. This is crucial, especially when the vorticity profile does not exhibit a steep fall off: in such a case, the identification of the vortex edge can be difficult and arbitrary and the density perturbation can extend over a significant thickness of the vortex outermost region.
4.1. Mode excitation features: $l=3$ mode analysis
mode analysis
In this and the next subsection we consider the excitation of the $l=3$![]() mode as a paradigmatic example to analyse the main features of the phenomenon under study. The following § 4.3 will extend the discussion to the whole range of modes we observed. In the vicinity of the resonance, the selected mode grows to its maximum amplitude within some hundred microseconds, corresponding to some tens of mode periods. The approximate frequency location of the resonance can be found from the calculation of the rotation frequency in the vortex core (see figure 3) and the equation for the linear mode frequency. The dependence of the maximum amplitude reached by the excited mode on the drive amplitude is shown in figure 4(a). Here, the $l=3$
mode as a paradigmatic example to analyse the main features of the phenomenon under study. The following § 4.3 will extend the discussion to the whole range of modes we observed. In the vicinity of the resonance, the selected mode grows to its maximum amplitude within some hundred microseconds, corresponding to some tens of mode periods. The approximate frequency location of the resonance can be found from the calculation of the rotation frequency in the vortex core (see figure 3) and the equation for the linear mode frequency. The dependence of the maximum amplitude reached by the excited mode on the drive amplitude is shown in figure 4(a). Here, the $l=3$![]() mode is induced in a vortex with the profile type A by means of a counterrotating dipole drive (see table 1, left column) in an $N=4$
mode is induced in a vortex with the profile type A by means of a counterrotating dipole drive (see table 1, left column) in an $N=4$![]() electrode configuration. This drive configuration is obtained by grouping the S8 sectors into four pairs of adjacent patches. The excitation is applied for a time period of $300\,\mathrm {\mu }\mathrm {s}$
electrode configuration. This drive configuration is obtained by grouping the S8 sectors into four pairs of adjacent patches. The excitation is applied for a time period of $300\,\mathrm {\mu }\mathrm {s}$![]() , at a rotation frequency of $132$
, at a rotation frequency of $132$![]() kHz, which is found experimentally to be the approximate resonance frequency value. The diagram shows a linear dependence of the mode amplitude $A_3/A_0$
kHz, which is found experimentally to be the approximate resonance frequency value. The diagram shows a linear dependence of the mode amplitude $A_3/A_0$![]() vs drive amplitude up to a saturation region above $1.5$
vs drive amplitude up to a saturation region above $1.5$![]() V. Further increase of either the amplitude or the time duration of the excitation does not result in a further growth of the mode, but induces filamentation from the nonlinear structures, i.e. the vertices of the deformed vortex, as seen in figure 4(b): here, the contour plot of the transverse density distribution image is shown for a vortex perturbed with a $1.7$
V. Further increase of either the amplitude or the time duration of the excitation does not result in a further growth of the mode, but induces filamentation from the nonlinear structures, i.e. the vertices of the deformed vortex, as seen in figure 4(b): here, the contour plot of the transverse density distribution image is shown for a vortex perturbed with a $1.7$![]() V drive; the nascent filamentation has created lobes (‘cat's eye’ structures) starting from the tips of the triangle. Once the mode reaches saturation, damping through filamentation progresses and the excited mode will eventually collapse catastrophically, initiating a cascade to lower modes towards the final axisymmetric state. As stated in the introduction, the analysis of the decay stage is among our future goals and will not be discussed here; for the reader's convenience, we just mention that a variety of diocotron mode decay mechanisms has already been observed in the past (Driscoll & Fine Reference Driscoll and Fine1990; Mitchell & Driscoll Reference Mitchell and Driscoll1994; Kabantsev et al. Reference Kabantsev, Chim, O'Neil and Driscoll2014). Notice also that mode saturation is reached already within a small-perturbation regime, as the plasma electrostatic potential at the edge of the core ($r\simeq R_w/2$
V drive; the nascent filamentation has created lobes (‘cat's eye’ structures) starting from the tips of the triangle. Once the mode reaches saturation, damping through filamentation progresses and the excited mode will eventually collapse catastrophically, initiating a cascade to lower modes towards the final axisymmetric state. As stated in the introduction, the analysis of the decay stage is among our future goals and will not be discussed here; for the reader's convenience, we just mention that a variety of diocotron mode decay mechanisms has already been observed in the past (Driscoll & Fine Reference Driscoll and Fine1990; Mitchell & Driscoll Reference Mitchell and Driscoll1994; Kabantsev et al. Reference Kabantsev, Chim, O'Neil and Driscoll2014). Notice also that mode saturation is reached already within a small-perturbation regime, as the plasma electrostatic potential at the edge of the core ($r\simeq R_w/2$![]() ) is around $20$
) is around $20$![]() V, where a $1.5$
V, where a $1.5$![]() V dipole drive at the trap wall drops to half its value, so that the perturbation-to-plasma potential ratio is less than $5\times 10^{-2}$
V dipole drive at the trap wall drops to half its value, so that the perturbation-to-plasma potential ratio is less than $5\times 10^{-2}$![]() .
.

Figure 4. Growth of the excited mode vs drive amplitude. (a) The normalized amplitude of mode $l=3$![]() is shown for a $300\,\mathrm {\mu }\mathrm {s}$
is shown for a $300\,\mathrm {\mu }\mathrm {s}$![]() counterrotating dipole excitation of profile A at a frequency of $132$
counterrotating dipole excitation of profile A at a frequency of $132$![]() kHz. On the right, a contour plot of the axially integrated transverse density distribution for a $1.7$
kHz. On the right, a contour plot of the axially integrated transverse density distribution for a $1.7$![]() V drive shows the beginning of mode damping in the form of filamentation creating cat's eye structures. The square box has the size of the trap inner diameter.
V drive shows the beginning of mode damping in the form of filamentation creating cat's eye structures. The square box has the size of the trap inner diameter.
We can draw complementary information from the electrostatic signals induced by the transverse collective motions on proper electrode sectors. With this non-destructive and non-perturbative diagnostics, the long-term vortex evolution can be tracked by maintaining the rotating drive well beyond the selected mode saturation. Currently, our electronics, combined with the weak signals induced by high-order diocotron modes, limits our detection to modes up to $l=3$![]() . As mentioned in § 3, a ${\rm \pi}$
. As mentioned in § 3, a ${\rm \pi}$![]() -span S2 sector (dipole configuration) can pick up modes $l=1,3$
-span S2 sector (dipole configuration) can pick up modes $l=1,3$![]() and two opposite ${\rm \pi} /2$
and two opposite ${\rm \pi} /2$![]() S4 sectors (quadrupole configuration) can detect mode $l=2$
S4 sectors (quadrupole configuration) can detect mode $l=2$![]() . We recorded a $25$
. We recorded a $25$![]() ms $l=3$
ms $l=3$![]() excitation of a vortex very similar to profile B, albeit with a $20\,\%$
excitation of a vortex very similar to profile B, albeit with a $20\,\%$![]() lower density level; the resonance at $1$
lower density level; the resonance at $1$![]() V drive amplitude was found at $54$
V drive amplitude was found at $54$![]() kHz. The dipole and quadrupole time signals (red and blue lines, respectively) are shown in the two upper left panels of figure 5; on the right, the frequency regions of interest of their spectrograms are shown, from which the mode contributions can be extracted so that the mode power can be plotted in the bottom panel. First, the signals prove that the vortex deformation seen by means of the optical diagnostics is indeed a KH rotating perturbation and not a static structure. Second, they confirm the growth and damping dynamics described before: mode $3$
kHz. The dipole and quadrupole time signals (red and blue lines, respectively) are shown in the two upper left panels of figure 5; on the right, the frequency regions of interest of their spectrograms are shown, from which the mode contributions can be extracted so that the mode power can be plotted in the bottom panel. First, the signals prove that the vortex deformation seen by means of the optical diagnostics is indeed a KH rotating perturbation and not a static structure. Second, they confirm the growth and damping dynamics described before: mode $3$![]() reaches saturation within approximately $2$
reaches saturation within approximately $2$![]() ms and collapses, hence the fast insurgence of a mode 2 that is then also damped away within $15$
ms and collapses, hence the fast insurgence of a mode 2 that is then also damped away within $15$![]() ms. Despite the resolution limitations of the spectrograms imposed by the fast dynamics, it can be seen that the damping of both modes is accompanied by a rising mode frequency, a sign of the nonlinear regime. The constant-frequency line in the dipole signal (also resulting in the higher plateau of the mode power line, bottom panel) is the track of the set frequency drive active along the whole vortex evolution.
ms. Despite the resolution limitations of the spectrograms imposed by the fast dynamics, it can be seen that the damping of both modes is accompanied by a rising mode frequency, a sign of the nonlinear regime. The constant-frequency line in the dipole signal (also resulting in the higher plateau of the mode power line, bottom panel) is the track of the set frequency drive active along the whole vortex evolution.

Figure 5. Electrostatic signals detected during the vortex excitation. (a,c) Signals detected by ${\rm \pi}$![]() - and quadrupole ${\rm \pi} /2$
- and quadrupole ${\rm \pi} /2$![]() angular span pickups. (b,d) Insets of the corresponding spectrograms, showing the presence of an $l=3$
angular span pickups. (b,d) Insets of the corresponding spectrograms, showing the presence of an $l=3$![]() wave decaying into an $l=2$
wave decaying into an $l=2$![]() wave. (e) Mode power extracted from the spectrogram, showing the cascade from the parent mode $3$
wave. (e) Mode power extracted from the spectrogram, showing the cascade from the parent mode $3$![]() to the daughter mode $2$
to the daughter mode $2$![]() .
.
4.2. Resonance curve analysis
We also systematically studied the behaviour of the resonance curve against the drive amplitude. We take again as an example the $l=3$![]() mode, induced this time by the application of a $400\,\mathrm {\mu }\mathrm {s}$
mode, induced this time by the application of a $400\,\mathrm {\mu }\mathrm {s}$![]() corotating sextupole drive (see table 1, middle column) in an $N=8$
corotating sextupole drive (see table 1, middle column) in an $N=8$![]() sector configuration on a vortex with profile B. A resonance curve is obtained by repeating the vortex preparation, mode excitation and image acquisition cycle for a set of excitation frequencies around the resonance; iterating the resonance scan for different drive amplitudes we obtained the mode amplitude patterns shown in figure 6(a). Each data point in the diagram is the average over $5$
sector configuration on a vortex with profile B. A resonance curve is obtained by repeating the vortex preparation, mode excitation and image acquisition cycle for a set of excitation frequencies around the resonance; iterating the resonance scan for different drive amplitudes we obtained the mode amplitude patterns shown in figure 6(a). Each data point in the diagram is the average over $5$![]() values, with a maximum relative error $\delta A_3/A_3$
values, with a maximum relative error $\delta A_3/A_3$![]() below $10^{-1}$
below $10^{-1}$![]() ; the error bars are not displayed for image clarity. Here, as the forcing amplitude increases, the deformation grows into the nonlinear regime, highlighted not only by the increase in the peak value of the normalized mode amplitude $A_3/A_0$
; the error bars are not displayed for image clarity. Here, as the forcing amplitude increases, the deformation grows into the nonlinear regime, highlighted not only by the increase in the peak value of the normalized mode amplitude $A_3/A_0$![]() , but also by the peak shift and the broadening of the resonance curve. The frequency downshift of the resonance peak for increasing drive (and consequently, mode) amplitude is visible in figure 6(b), despite the fact that our sampling resolution limits the accuracy of data points to an uncertainty of ${\pm }0.5$
, but also by the peak shift and the broadening of the resonance curve. The frequency downshift of the resonance peak for increasing drive (and consequently, mode) amplitude is visible in figure 6(b), despite the fact that our sampling resolution limits the accuracy of data points to an uncertainty of ${\pm }0.5$![]() kHz, and it is an apparent sign that, above a drive amplitude of $500$
kHz, and it is an apparent sign that, above a drive amplitude of $500$![]() mV, the oscillator is already in the nonlinear territory, where the constant mode frequency expression obtained for the linear regime no longer holds. Another nonlinearity flag is the significant progressive broadening of the resonance curve, measured by the full width at half-maximum normalized to the peak frequency and reported in figure 6(c).
mV, the oscillator is already in the nonlinear territory, where the constant mode frequency expression obtained for the linear regime no longer holds. Another nonlinearity flag is the significant progressive broadening of the resonance curve, measured by the full width at half-maximum normalized to the peak frequency and reported in figure 6(c).

Figure 6. Resonance curve behaviour vs drive amplitude for an $l=3$![]() mode (profile B). (a) Resonance curves for the normalized mode amplitude $A_3/A_0$
mode (profile B). (a) Resonance curves for the normalized mode amplitude $A_3/A_0$![]() at different drive amplitudes. (b) Frequency position of the resonance peak vs drive amplitude. The uncertainty is dominated by the $1$
at different drive amplitudes. (b) Frequency position of the resonance peak vs drive amplitude. The uncertainty is dominated by the $1$![]() kHz resolution of the resonance curve sampling. (c) Full width at half-maximum $\delta \omega$
kHz resolution of the resonance curve sampling. (c) Full width at half-maximum $\delta \omega$![]() , normalized to the peak frequency, vs the drive amplitude. The uncertainty is once again dominated by the sampling resolution and does not exceed $\pm 1.5\times 10^{-2}$
, normalized to the peak frequency, vs the drive amplitude. The uncertainty is once again dominated by the sampling resolution and does not exceed $\pm 1.5\times 10^{-2}$![]() .
.
4.3. Excitation of modes $3$ to $7$
to $7$
The features discussed for the excitation of mode $l=3$![]() in §§ 4.1 and 4.2 are common to higher-order modes. We successfully excited all modes up to $l=7$
in §§ 4.1 and 4.2 are common to higher-order modes. We successfully excited all modes up to $l=7$![]() , using in some cases more than one field configuration. As a summary, let us view figure 7, where resonance curves are reported for all these modes. The curves were obtained for a vortex with profile B; all modes were excited with an $N=8$
, using in some cases more than one field configuration. As a summary, let us view figure 7, where resonance curves are reported for all these modes. The curves were obtained for a vortex with profile B; all modes were excited with an $N=8$![]() electrode sector configuration and the proper multipolar field (see table 1, middle and right column) at an amplitude of $1.5$
electrode sector configuration and the proper multipolar field (see table 1, middle and right column) at an amplitude of $1.5$![]() V for consistency, and adjusting the drive duration in order to reach saturation at resonance ($400\,\mathrm {\mu }\mathrm {s}$
V for consistency, and adjusting the drive duration in order to reach saturation at resonance ($400\,\mathrm {\mu }\mathrm {s}$![]() for modes $3$
for modes $3$![]() to $5$
to $5$![]() , $1$
, $1$![]() ms for modes $6$
ms for modes $6$![]() and $7$
and $7$![]() ). Each data point is the average over $5$
). Each data point is the average over $5$![]() shots; the uncertainties are not reported in the diagram as the absolute error is of the order of $10^{-4}-10^{-3}$
shots; the uncertainties are not reported in the diagram as the absolute error is of the order of $10^{-4}-10^{-3}$![]() . All resonances are well defined; all curves display a contrast (peak-to-tail ratio) $\geq 20$
. All resonances are well defined; all curves display a contrast (peak-to-tail ratio) $\geq 20$![]() and the peak frequencies are evenly spaced, with $\nu _{l+1}-\nu _{l} = 32-33$
and the peak frequencies are evenly spaced, with $\nu _{l+1}-\nu _{l} = 32-33$![]() kHz. The phosphor screen images at the resonance peaks, displayed in figure 8, show that all modes have reached nonlinear saturation, indicated by the lobe structures generated by filamentation around the deformed vortex core, visible to the naked eye. The understandably very weak mode $7$
kHz. The phosphor screen images at the resonance peaks, displayed in figure 8, show that all modes have reached nonlinear saturation, indicated by the lobe structures generated by filamentation around the deformed vortex core, visible to the naked eye. The understandably very weak mode $7$![]() makes an exception to these general considerations and it is hardly recognized by visual inspection, yet an identifiable resonance emerges from the image analysis.
makes an exception to these general considerations and it is hardly recognized by visual inspection, yet an identifiable resonance emerges from the image analysis.

Figure 7. Resonant curves for different mode excitations (profile B). All modes were induced by suitable rotating drives in an $N=8$![]() sector configuration (see table 1) at $1.5$
sector configuration (see table 1) at $1.5$![]() V amplitude.
V amplitude.

Figure 8. Vortex deformations at respective resonant frequencies. Axially integrated transverse density distributions are shown for mode excitations from $l=3$![]() to $7$
to $7$![]() , at the mode resonant frequencies $67$
, at the mode resonant frequencies $67$![]() , $100$
, $100$![]() , $133$
, $133$![]() , $165$
, $165$![]() and $193$
and $193$![]() kHz, respectively, according to the resonance curves displayed in figure 7. The square boxes have the size of the trap inner diameter.
kHz, respectively, according to the resonance curves displayed in figure 7. The square boxes have the size of the trap inner diameter.
A proof of the perfect selectivity of this mode driving scheme is given by examining all the $A_l$![]() coefficients. Figure 9 reports coefficients $2$
coefficients. Figure 9 reports coefficients $2$![]() to $10$
to $10$![]() for each excitation geometry, at the respective resonances (e.g. corresponding to the density maps in figure 8). The dominant mode (data point circled in black) is always the one that was intentionally driven, while all other coefficients are at least one order of magnitude lower. There are some exceptions, e.g. $A_6$
for each excitation geometry, at the respective resonances (e.g. corresponding to the density maps in figure 8). The dominant mode (data point circled in black) is always the one that was intentionally driven, while all other coefficients are at least one order of magnitude lower. There are some exceptions, e.g. $A_6$![]() and $A_9$
and $A_9$![]() in the $l=3$
in the $l=3$![]() excitation, or $A_8$
excitation, or $A_8$![]() in the $l=4$
in the $l=4$![]() excitation: these are not higher wavemodes but harmonics of the $l=3,4$
excitation: these are not higher wavemodes but harmonics of the $l=3,4$![]() dominant modes. We can conclude that spurious deformation components are minimized by this method, while the dominant mode is maximized (saturated).
dominant modes. We can conclude that spurious deformation components are minimized by this method, while the dominant mode is maximized (saturated).

Figure 9. Deformation mode coefficients for excitation of modes $l=3$![]() to $7$
to $7$![]() . Each colour represents the deformation amplitudes $A_2$
. Each colour represents the deformation amplitudes $A_2$![]() to $A_{10}$
to $A_{10}$![]() for the excitation of a single mode at the respective resonant frequency, corresponding to the peaks in figure 7. The intended and dominant coefficient is circled in black. Dashed lines are drawn only as a guide for the reader.
for the excitation of a single mode at the respective resonant frequency, corresponding to the peaks in figure 7. The intended and dominant coefficient is circled in black. Dashed lines are drawn only as a guide for the reader.
5. Conclusions and outlook
In this work we have experimentally demonstrated that rotating electric fields can be used to efficiently excite KH waves of generic order, far beyond commonly studied low-order modes, and we have detailed the nonlinear growth of modes up to saturation. High-order modes have of course been excited to some extent in the past using more basic electrode patch choices, which exploited the presence of multipolar terms in the potential generated, e.g. by a single sector of angular span ${\rm \pi} /2$![]() or ${\rm \pi}$
or ${\rm \pi}$![]() (for instance, in the latter case odd multipole terms will be present). Nonetheless the theory presented here shows how a very well-defined dominant mode is resonantly selected upon a suitable choice of the drive field. Once again we would like to remark that, while the theory is based upon a linear perturbation approach and applies to a uniform density (vorticity) clump, the experimental realization reaches far beyond these limits, and shows that all modes can be driven to high amplitude. To the best of our knowledge, for the first time the $N/2$
(for instance, in the latter case odd multipole terms will be present). Nonetheless the theory presented here shows how a very well-defined dominant mode is resonantly selected upon a suitable choice of the drive field. Once again we would like to remark that, while the theory is based upon a linear perturbation approach and applies to a uniform density (vorticity) clump, the experimental realization reaches far beyond these limits, and shows that all modes can be driven to high amplitude. To the best of our knowledge, for the first time the $N/2$![]() limit (with $N$
limit (with $N$![]() the number of azimuthal electrode sectors) is consistently overcome and all KH perturbations are made to reach the full nonlinear regime, i.e. the condition of generalized V-states, also regardless of the vorticity profile. In this sense, this technique is ‘optimal’ as it allows the user to selectively drive the desired mode without spurious deformation components and control its final amplitude up to the point where instabilities cause the collapse and cascade of modes towards axisymmetry.
the number of azimuthal electrode sectors) is consistently overcome and all KH perturbations are made to reach the full nonlinear regime, i.e. the condition of generalized V-states, also regardless of the vorticity profile. In this sense, this technique is ‘optimal’ as it allows the user to selectively drive the desired mode without spurious deformation components and control its final amplitude up to the point where instabilities cause the collapse and cascade of modes towards axisymmetry.
This technique is promising in view of further studies on the dynamics of V-states, the scope being the observation of their behaviour both in free-evolution conditions and under continuous excitation. To better control the growth and final deformation, we are also considering autoresonant forcing, i.e. a swept-frequency excitation that may result in a locking between the KH wave and the drive. We remark that, while some theoretical works have addressed autoresonant excitation of KH modes/V-states, the phenomenon is extensively documented in experiments only for the $l=1$![]() mode, which is used to control the positioning of plasma samples in the confinement volume (Fajans et al. Reference Fajans, Gilson and Friedland1999; Singer et al. Reference Singer, König, Stoneking, Steinbrunner, Danielson, Schweikhard and Sunn Pedersen2021), with a single reference existing for the $l=2$
mode, which is used to control the positioning of plasma samples in the confinement volume (Fajans et al. Reference Fajans, Gilson and Friedland1999; Singer et al. Reference Singer, König, Stoneking, Steinbrunner, Danielson, Schweikhard and Sunn Pedersen2021), with a single reference existing for the $l=2$![]() mode (Gomberoff et al. Reference Gomberoff, Higaki, Kaga, Ito and Okamoto2016). Our investigations will be assisted and augmented by simulations with a particle-in-cell code (Maero et al. Reference Maero, Romé, Lepreti and Cavenago2014), which we have adapted to implement the suitable rotating-wall boundary conditions.
mode (Gomberoff et al. Reference Gomberoff, Higaki, Kaga, Ito and Okamoto2016). Our investigations will be assisted and augmented by simulations with a particle-in-cell code (Maero et al. Reference Maero, Romé, Lepreti and Cavenago2014), which we have adapted to implement the suitable rotating-wall boundary conditions.
Acknowledgements
Editor F. Califano thanks the referees for their advice in evaluating this article.
Funding
This work was performed with the partial support of INFN-CSN5.
Declaration of interests
The authors report no conflict of interest.