Hostname: page-component-7dd5485656-dk7s8 Total loading time: 0 Render date: 2025-10-31T22:08:52.232Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent fluxes of entropy and internal energy in temperature stratified flows

Part of: Macroscopic Randomness

Published online by Cambridge University Press:  03 August 2015

I. Rogachevskii  and
N. Kleeorin
I. Rogachevskii*
Affiliation:
Department of Mechanical Engineering, Ben-Gurion University of the Negev, P.O. Box 653, 84105 Beer-Sheva, Israel Nordita, KTH Royal Institute of Technology and Stockholm University, Roslagstullsbacken 23, 10691 Stockholm, Sweden
N. Kleeorin
Affiliation:
Department of Mechanical Engineering, Ben-Gurion University of the Negev, P.O. Box 653, 84105 Beer-Sheva, Israel Nordita, KTH Royal Institute of Technology and Stockholm University, Roslagstullsbacken 23, 10691 Stockholm, Sweden
*
†Email address for correspondence: gary@bgu.ac.il
Get access Rights & Permissions [Opens in a new window]

Abstract

We derive equations for the mean entropy and the mean internal energy in low-Mach-number temperature stratified turbulence (i.e. for turbulent convection or stably stratified turbulence), and show that turbulent flux of entropy is given by 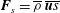$\boldsymbol{F}_{s}=\overline{{\it\rho}}\,\overline{\boldsymbol{u}s}$ , where 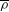$\overline{{\it\rho}}$ is the mean fluid density, $s$ is fluctuation of entropy and overbars denote averaging over an ensemble of turbulent velocity fields, $\boldsymbol{u}$ . We demonstrate that the turbulent flux of entropy is different from the turbulent convective flux, 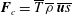$\boldsymbol{F}_{c}=\overline{T}\,\overline{{\it\rho}}\,\overline{\boldsymbol{u}s}$ , of the fluid internal energy, where 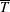$\overline{T}$ is the mean fluid temperature. This turbulent convective flux is well-known in the astrophysical and geophysical literature, and it cannot be used as a turbulent flux in the equation for the mean entropy. This result is exact for low-Mach-number temperature stratified turbulence and is independent of the model used. We also derive equations for the velocity–entropy correlation, 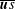$\overline{\boldsymbol{u}s}$ , in the limits of small and large Péclet numbers, using the quasi-linear approach and the spectral ${\it\tau}$ approximation, respectively. This study is important in view of different applications to astrophysical and geophysical temperature stratified turbulence.

Information

Type
Research Article
Information
Journal of Plasma Physics , Volume 81 , Issue 5 , October 2015 , 395810504
Copyright
© Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Batchelor, G. K. 1971 The Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
Batchelor, G. K., Howells, I. D. & Townsend, A. A. 1959 Small-scale variation of convected quantities like temperature in turbulent fluid. Part 2. The case of large conductivity. J. Fluid Mech. 5, 134–139.CrossRefGoogle Scholar
Braginsky, S. I. & Roberts, P. H. 1995 Equations governing convection in earth’s core and the geodynamo. Geophys. Astrophys. Fluid Dyn. 79, 1–97.CrossRefGoogle Scholar
Brandenburg, A. & Subramanian, K. 2005 Astrophysical magnetic fields and nonlinear dynamo theory. Phys. Rep. 417, 1–209.CrossRefGoogle Scholar
Brun, A. S., Miesch, M. S. & Toomre, J. 2004 Global-scale turbulent convection and magnetic dynamo action in the solar envelope. Astrophys. J. 614, 1073–1098.CrossRefGoogle Scholar
Canuto, V. M. 2009 Turbulence in astrophysical and geophysical flows. In Interdisciplinary Aspects of Turbulence (ed. Hillebrandt, W. & Kupka, F.), Lecture Notes in Physics, vol. 756, p. 107. Springer.CrossRefGoogle Scholar
Chassaing, P., Antonia, R. A., Anselmet, F., Joly, L. & Sarkar, S. 2002 Variable Density Fluid Turbulence. 380 pp. Kluwer.CrossRefGoogle Scholar
Clarke, C. & Carswell, B. 2007 Principles of Astrophysical Fluid Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Elperin, T., Kleeorin, N. & Rogachevskii, I. 1995 Dynamics of the passive scalar in compressible turbulent flow: large-scale patterns and small-scale fluctuations. Phys. Rev. E 52, 2617–2634.CrossRefGoogle ScholarPubMed
Elperin, T., Kleeorin, N. & Rogachevskii, I. 1996 Isotropic and anisotropic spectra of passive scalar fluctuations in turbulent fluid flow. Phys. Rev. E 53, 3431–3441.CrossRefGoogle ScholarPubMed
Glatzmaier, G. A. & Roberts, P. H. 1996a An anelastic evolutionary geodynamo simulation driven by compositional and thermal convection. Physica D 97, 81–94.CrossRefGoogle Scholar
Glatzmaier, G. A. & Roberts, P. H. 1996b Rotation and magnetism of Earth’s inner core. Science 274, 1887–1891.CrossRefGoogle ScholarPubMed
Jones, C. A. & Kuzanyan, K. M. 2009 Compressible convection in the deep atmospheres of giant planets. Icarus 204, 227–238.CrossRefGoogle Scholar
Jones, C. A., Kuzanyan, K. M. & Mitchell, R. H. 2009 Linear theory of compressible convection in rapidly rotating spherical shells, using the anelastic approximation. J. Fluid Mech. 634, 291–319.CrossRefGoogle Scholar
Käpylä, P. J., Mantere, M. J. & Brandenburg, A. 2012 Cyclic magnetic activity due to turbulent convection in spherical wedge geometry. Astrophys. J. Lett. 755, L22.CrossRefGoogle Scholar
Kitchatinov, L. L. & Mazur, M. V. 2000 Stability and equilibrium of emerged magnetic flux. Solar Phys. 191, 325–340.CrossRefGoogle Scholar
Kraichnan, R. H. 1968 Small-scale structure of a scalar field convected by turbulence. Phys. Fluids 11, 945–953.CrossRefGoogle Scholar
Krause, F. & Raedler, K. H. 1980 Mean-Field Magnetohydrodynamics and Dynamo Theory. Pergamon.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1959 Fluid Mechanics. Pergamon.Google Scholar
McComb, W. D. 1990 The Physics of Fluid Turbulence. Clarendon.CrossRefGoogle Scholar
Miesch, M. S., Brun, A. S., De Rosa, M. L. & Toomre, J. 2008 Structure and evolution of giant cells in global models of solar convection. Astrophys. J. 673, 557–575.CrossRefGoogle Scholar
Moffatt, H. K. 1978 Magnetic Field Generation in Electrically Conducting Fluids. Cambridge University Press.Google Scholar
Monin, A. S. & Yaglom, A. M. 1975 Statistical Fluid Mechanics: Mechanics of Turbulence, vol. 2, revised and enlarged edition. MIT Press.Google Scholar
Orszag, S. A. 1970 Analytical theories of turbulence. J. Fluid Mech. 41, 363–386.CrossRefGoogle Scholar
Peebles, P. J. E. 1980 The Large-Scale Structure of the Universe. Princeton University Press.Google Scholar
Pouquet, A., Frisch, U. & Leorat, J. 1976 Strong MHD helical turbulence and the nonlinear dynamo effect. J. Fluid Mech. 77, 321–354.CrossRefGoogle Scholar
Roberts, P. H. & Soward, A. M. 1975 A unified approach to mean field electrodynamics. Astron. Nachr. 296, 49–64.CrossRefGoogle Scholar
Rogachevskii, I. & Kleeorin, N. 2007 Magnetic fluctuations and formation of large-scale inhomogeneous magnetic structures in a turbulent convection. Phys. Rev. E 76 (5), 056307.CrossRefGoogle Scholar
Rogachevskii, I., Kleeorin, N., Käpylä, P. J. & Brandenburg, A. 2011 Pumping velocity in homogeneous helical turbulence with shear. Phys. Rev. E 84 (5), 056314.CrossRefGoogle ScholarPubMed
Ruzmaikin, A. A., Sokolov, D. D. & Shukurov, A. M. 1988 Magnetic Fields of Galaxies. Kluwer Academic.CrossRefGoogle Scholar
Shakura, N. I., Sunyaev, R. A. & Zilitinkevich, S. S. 1978 On the turbulent energy transport in accretion discs. Astron. Astrophys. 62, 179–187.Google Scholar
Zeldovich, I. B., Ruzmaikin, A. A. & Sokolov, D. D. 1983 Magnetic Fields in Astrophysics. Gordon and Breach Science.Google Scholar
Zeldovich, Y. B., Ruzmaikin, A. A. & Sokoloff, D. D. 1990 The Almighty Chance. World Scientific.CrossRefGoogle Scholar
Zilitinkevich, S. S. 1991 Turbulent Penetrative Convection. Avebury Technical.Google Scholar
Zilitinkevich, S. S., Elperin, T., Kleeorin, N., Rogachevskii, I. & Esau, I. 2013 A hierarchy of energy- and flux-budget (EFB) turbulence closure models for stably-stratified geophysical flows. Boundary-Layer Meteorol. 146, 341–373.CrossRefGoogle Scholar
Zilitinkevich, S. S., Elperin, T., Kleeorin, N., Rogachevskii, I., Esau, I., Mauritsen, T. & Miles, M. W. 2008 Turbulence energetics in stably stratified geophysical flows: strong and weak mixing regimes. Q. J. R. Meteorol. Soc. 134, 793–799.CrossRefGoogle Scholar