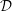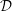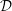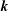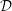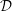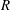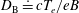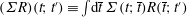1. Introduction
The first steps toward theories of plasma turbulence occurred in the early 1960s with the development of quasi-linear theory (Drummond & Pines Reference Drummond and Pines1962; Vedenov, Velikhov & Sagdeev Reference Vedenov, Velikhov and Sagdeev1962). It was, of course, appreciated that the quasi-linear approximation had a restricted domain of applicability. For calculation of the lowest-order nonlinear corrections, it was natural to use regular perturbation theory, such as in the work of Kadomtsev & Petviashvili (Reference Kadomtsev and Petviashvili1963); however, the way forward to an analytical description of strong turbulence was not very clear. It was therefore a significant event when Kadomtsev (1920–1998Footnote 1 ) published his review/monograph on plasma turbulence (in Russian, as an article in vol. 4 of Problems in Plasma Theory (1964); in English translation, as a book entitled Plasma Turbulence (1965)Footnote 2 ), which addressed not only quasi-linear and weak-turbulence theory but also sophisticated results about strong turbulence. Because of the diversity and unfamiliarity of many of the ideas, it was a challenge to understand. A reviewer wrote (Drummond Reference Drummond1966):
It is not an easy book to read. The method of presentation is in most cases extremely brief and often it is not clear how the conclusions follow from the discussion. [It] is such that it is also difficult to distinguish between those results which are speculative and those which have been more rigorously derived. . . .
The third chapter, which is the most speculative, contains a description of what is apparently recent work in the theory of strong turbulence. Although some ideas are presented clearly, it is next to impossible to follow in detail and the conclusions reached are evidently of a speculative character.
Nevertheless, Kadomtsev’s insights were seminal and the reviewer ultimately concluded that ‘it should be required reading for any serious student in this field’ – and so it served. It was a bible for multiple generations of plasma theorists. And although some of the conclusions may have appeared at the time to be speculative, in fact Kadomtsev’s discussion contained, among many other notable ideas, a deep and entirely correct insight about a deficiency of the leading theory of strong turbulence, the direct-interaction approximation (DIA) of Kraichnan (Reference Kraichnan1959). It is ironic that Kadomtsev’s contribution is better known in fields other than plasma physics (Monin & Yaglom Reference Monin and Yaglom1971, vol. 2, p. 307). I shall explain the issue in § 5.1.
Shortly after the 1965 western publication of Kadomtsev’s book, Dupree (Reference Dupree1966) published the paper ‘A perturbation theory for strong plasma turbulence’. Subsequently the formalism, including further significant advances by Dupree (Reference Dupree1967) and Weinstock (Reference Weinstock1968, Reference Weinstock1969, Reference Weinstock1970), came to be known as resonance-broadening theory (RBT); that work was also extremely influential.Footnote 3
It is now a half-century since those watershed events. Over that time the theory of turbulence in both fluids and plasmas has developed substantially, and a beginning researcher interested in turbulence will find that much conceptual background is assumed. Fluid turbulence theory has been addressed in multiple books (Leslie Reference Leslie1973; McComb Reference McComb1990, Reference McComb2014; Frisch Reference Frisch1995; Lesieur Reference Lesieur1997) and articles (Eyink & Sreenivasan Reference Eyink and Sreenivasan2006; Falkovich Reference Falkovich, Shats and Punzmann2006; Boffetta & Ecke Reference Boffetta and Ecke2012). The plasma literature is sparser, although a review by Yoshizawa et al. (Reference Yoshizawa, Itoh, Itoh and Yokoi2001) ranges broadly over many conceptual and practical topics for both fluids and plasmas, a comprehensive review of analytical statistical turbulence theory with a focus on plasma issues is available (Krommes Reference Krommes2002), and the book by Diamond, Itoh & Itoh (Reference Diamond, Itoh and Itoh2010) provides an introductory survey of various approaches to plasma turbulence.Footnote 4 But absorbing all of this material is a formidable undertaking. The purpose of this article is to provide some help by introducing, in a tutorialFootnote 5 way, a few highlights of the statistical description of turbulence, using Kadomtsev’s review and the resonance-broadening theory as springboards. Whereas all of the discussion should be of interest to plasma theorists, some other parts apply equally to fluids and to plasmas, thus serving to unify those specialties.
1.1. The role of analytical theory
This article addresses analytical turbulence theory. It is a reasonable question to ask: Why should one care? The experimental situation has improved dramatically since the 1960s at both laboratory and (pre-)reactor scales, and we now have refined diagnostics and data-analysis capabilities that provide direct windows into nature. Certainly the biggest advance over the last half-century has been the explosive rise in computing power,Footnote 6 which has enabled entirely new methods of scientific discovery.Footnote 7 A companion tool has been the nonlinear gyrokinetic formalism (c. 1982), which has become indispensable for both analytical insights into, and the numerical simulation of, turbulence in magnetized plasmas. We have learned much more about plasma turbulence from both experiments and simulations than we have from sophisticated theory. Nevertheless, there are good arguments in favour of analytical approaches, as I discuss in the next several paragraphs.
It is worth emphasizing that before one attempts to build a technically sophisticated
formalism, one should understand the dimensional and scaling consequences of the
governing partial differential equations (PDEs), which are assumed to be given.
Consider, for example, random motion in one spatial dimension and suppose that, in a
statistical sense, the dynamics are entirely specified in terms of just two
dimensional parameters,
![]() ${\it\sigma}$
and
${\it\sigma}$
and
![]() ${\it\tau}$
, having the dimensions of space and time, respectively. I shall
indicate random variables by a tilde. It follows that the mean-square displacement
must obey
${\it\tau}$
, having the dimensions of space and time, respectively. I shall
indicate random variables by a tilde. It follows that the mean-square displacement
must obey
 $\langle \,\widetilde{x}^{\,2}\rangle =\,f(t;{\it\sigma},{\it\tau})$
, where
$\langle \,\widetilde{x}^{\,2}\rangle =\,f(t;{\it\sigma},{\it\tau})$
, where
![]() $f$
is an unknown function.Footnote
8
By dimensional and scaling analysis (Barenblatt Reference Barenblatt1996; Krommes Reference Krommes2002,
appendix B), it follows that
$f$
is an unknown function.Footnote
8
By dimensional and scaling analysis (Barenblatt Reference Barenblatt1996; Krommes Reference Krommes2002,
appendix B), it follows that
![]() $f$
must have the form
$f$
must have the form
 $f(t;{\it\sigma},{\it\tau})={\it\sigma}^{2}g(t/{\it\tau})$
, where
$f(t;{\it\sigma},{\it\tau})={\it\sigma}^{2}g(t/{\it\tau})$
, where
![]() $g$
is a dimensionless function of a dimensionless argument. Although
$g$
is a dimensionless function of a dimensionless argument. Although
![]() $g$
can be measured in experiments or simulations, much deeper
understanding follows from theories that predict the form of
$g$
can be measured in experiments or simulations, much deeper
understanding follows from theories that predict the form of
![]() $g$
, such as models of continuous-time random walks (Klafter,
Shlesinger & Zumofen Reference Klafter, Shlesinger and Zumofen1996; Metzler &
Klafter Reference Metzler and Klafter2000). One of many possibilities is
$g$
, such as models of continuous-time random walks (Klafter,
Shlesinger & Zumofen Reference Klafter, Shlesinger and Zumofen1996; Metzler &
Klafter Reference Metzler and Klafter2000). One of many possibilities is
 $g(\overline{t})=A\overline{t}^{{\it\alpha}}$
, where the dimensionless constants
$g(\overline{t})=A\overline{t}^{{\it\alpha}}$
, where the dimensionless constants
![]() $A$
and
$A$
and
![]() ${\it\alpha}$
are not determined by scaling analysis. The value
${\it\alpha}$
are not determined by scaling analysis. The value
![]() ${\it\alpha}=1$
corresponds to the classical random walk, but subdiffusive or
superdiffusive values of
${\it\alpha}=1$
corresponds to the classical random walk, but subdiffusive or
superdiffusive values of
![]() ${\it\alpha}$
are also possible in some interesting physical situations.
${\it\alpha}$
are also possible in some interesting physical situations.
By generalizing from such examples, one can argue (Connor & Taylor Reference Connor and Taylor1977; Connor Reference Connor1988) that when faced with a new problem in statistical theory one should always first extract the maximum amount of information accessible from scaling analysis of the governing equations. In some cases, that fully determines the form of the answer except for a numerical constant. More generally, it couches the answer in terms of various dimensionless functions. It is the role of experimental observation, numerical simulation, and analytical theory to determine the forms of those functions and to identify the physics that underlies them.
The basic challenge for any of those approaches, especially for theory, is that the dynamical equations are nonlinear. Nonlinearity leads to rich and interesting behaviour, including turbulent transport, fluctuation spectra with suggestive shapes, and probability density functions (PDFs) that are frequently non-Gaussian. Analytical turbulence theory provides methods to explain and predict that behaviour both qualitatively and quantitatively. Qualitatively, it has proven fruitful to discuss turbulence in the same language of random walks and (generalized) Langevin equations that has long enriched our understanding of classical Brownian motion. Quantitatively, statistical theory provides formulas for turbulence-induced transport fluxes in terms of weighted sums over fluctuation spectra, and it also leads to approximate equations for those spectra; the predictions can be directly compared with experimental measurements or computer simulations. More sophisticated techniques (not discussed in this article) can predict entire PDFs. Analytical methods have also been useful in addressing the generation mechanisms of zonal flows, which are important in regulating the levels of turbulence and transport. In some cases, one can analytically predict the threshold for the onset of zonal flows and the characteristic scale of those flows, among other things. Furthermore, from analytical statistical descriptions one can gain unique insights into the mechanisms by which those flows are self-sustained.
The restricted goal of this article is to introduce some of the conceptual issues and technical challenges relating to the analytical, especially statistical, description of turbulence; that provides a language for discussion and a framework for thinking and modelling,Footnote 9 and it can lead to quantitative predictions. It is remarkable how much the pioneers understood of this subject 50 years ago, and that deserves to be celebrated; it is also instructive to see how far we have (or have not) come.
1.2. The plan of the article
Broadly speaking, one can say that the two key concepts in statistical turbulence
theory (introduced in § 2) are
nonlinearity-induced incoherent noise and coherent damping, which are generalizations
of analogous effects in the simple Langevin description of classical Brownian motion.
Both of those are already present in systems involving passive advection, as I shall
illustrate with an exactly solvable model in § 2.3. Self-consistency adds additional complications, including the concept
of a dielectric function
![]() ${\mathcal{D}}(\boldsymbol{k},{\it\omega})$
. The dielectric function is a fundamental object in plasma physics.
In its lowest-order (linearized-Vlasov) approximation, it is treated exhaustively in
many textbooks. Yet not one of those discusses how to systematically treat dielectric
shielding when the system is turbulent, which is the case almost universally
encountered in practice. Then
${\mathcal{D}}(\boldsymbol{k},{\it\omega})$
. The dielectric function is a fundamental object in plasma physics.
In its lowest-order (linearized-Vlasov) approximation, it is treated exhaustively in
many textbooks. Yet not one of those discusses how to systematically treat dielectric
shielding when the system is turbulent, which is the case almost universally
encountered in practice. Then
![]() ${\mathcal{D}}$
becomes a functional of the turbulence level, so it is sometimes
referred to as the ‘nonlinear dielectric function’. Failure by some to appreciate
that nonlinear corrections to
${\mathcal{D}}$
becomes a functional of the turbulence level, so it is sometimes
referred to as the ‘nonlinear dielectric function’. Failure by some to appreciate
that nonlinear corrections to
![]() ${\mathcal{D}}$
are essential in steady-state turbulence has led to confusion.
${\mathcal{D}}$
are essential in steady-state turbulence has led to confusion.
It is a common belief that the existence of a nontrivial
![]() ${\mathcal{D}}$
importantly distinguishes the electromagnetic, polarizable plasma
from the neutral fluid. Plasma physicists proudly lay claim to
${\mathcal{D}}$
importantly distinguishes the electromagnetic, polarizable plasma
from the neutral fluid. Plasma physicists proudly lay claim to
![]() ${\mathcal{D}}$
as a special feature of their field, with its potpourri of linear
waves. In fact, however, even the incompressible Navier–Stokes turbulent fluid
possesses a well-defined
${\mathcal{D}}$
as a special feature of their field, with its potpourri of linear
waves. In fact, however, even the incompressible Navier–Stokes turbulent fluid
possesses a well-defined
![]() ${\mathcal{D}}$
, as I shall show. The consequences of this result are unclear
because
${\mathcal{D}}$
, as I shall show. The consequences of this result are unclear
because
![]() ${\mathcal{D}}$
is subsumed by the infinitesimal response function
${\mathcal{D}}$
is subsumed by the infinitesimal response function
![]() $R$
with which statistical turbulence theory is usually formulated.
However, it does imply that turbulent plasmas are not conceptually as special as one
might have thought, and it lends itself to a unified discussion of the spectral
balances in both plasmas and fluids.
$R$
with which statistical turbulence theory is usually formulated.
However, it does imply that turbulent plasmas are not conceptually as special as one
might have thought, and it lends itself to a unified discussion of the spectral
balances in both plasmas and fluids.
I shall discuss in § 3 the definition and
meaning of the nonlinear dielectric function of a turbulent plasma, then note that
![]() ${\mathcal{D}}$
cannot be practically evaluated without a statistical approximation
or ‘closure’. I shall sketch some of Dupree’s early work on the subject. However, the
limitations of his approach can only be appreciated in the context of a more complete
formalism. The general theory is formulated in terms of a response function
${\mathcal{D}}$
cannot be practically evaluated without a statistical approximation
or ‘closure’. I shall sketch some of Dupree’s early work on the subject. However, the
limitations of his approach can only be appreciated in the context of a more complete
formalism. The general theory is formulated in terms of a response function
![]() $R$
that subsumes
$R$
that subsumes
![]() ${\mathcal{D}}$
, so it is never necessary to evaluate
${\mathcal{D}}$
, so it is never necessary to evaluate
![]() ${\mathcal{D}}$
independently. Nevertheless, introducing
${\mathcal{D}}$
independently. Nevertheless, introducing
![]() ${\mathcal{D}}$
aids in heuristic understanding. Although fluid-turbulence
theorists focus on
${\mathcal{D}}$
aids in heuristic understanding. Although fluid-turbulence
theorists focus on
![]() $R$
whereas many plasma physicists (still strongly influenced by
Dupree’s work) are inclined to think in terms of
$R$
whereas many plasma physicists (still strongly influenced by
Dupree’s work) are inclined to think in terms of
![]() ${\mathcal{D}}$
, in fact
${\mathcal{D}}$
, in fact
![]() $R$
and
$R$
and
![]() ${\mathcal{D}}$
are intimately related, as I shall explain.
${\mathcal{D}}$
are intimately related, as I shall explain.
An important self-consistent closure is the DIA. It provides coupled equations that
balance the excitation due to nonlinearly produced incoherent noise with classical
dissipation and nonlinear coherent damping, including a proper shielding of the noise
by dielectric polarization. In § 4 I shall
present a new approach to the DIA that exploits the Furutsu–Novikov theorem
(appendix B). I shall also describe an
algorithm that defines the direct-interaction approximation to
![]() ${\mathcal{D}}$
for arbitrary quadratically nonlinear systems. With the DIA in
hand, I shall briefly explain in § 5 its
difficulty with random Galilean invariance, understood independently by Kadomtsev and
by Kraichnan. I shall also emphasize the important role of nonlinear noise in the
spectral balance for saturated turbulence, and I shall discuss the famous
mixing-length formula for the saturation level of drift waves, illustrating with the
aid of an exactly solvable model that includes nonlinear noise. Kadomtsev well
appreciated the content of the DIA, but it is instructive to take a fresh look with
the hindsight of 50 years of experience.
${\mathcal{D}}$
for arbitrary quadratically nonlinear systems. With the DIA in
hand, I shall briefly explain in § 5 its
difficulty with random Galilean invariance, understood independently by Kadomtsev and
by Kraichnan. I shall also emphasize the important role of nonlinear noise in the
spectral balance for saturated turbulence, and I shall discuss the famous
mixing-length formula for the saturation level of drift waves, illustrating with the
aid of an exactly solvable model that includes nonlinear noise. Kadomtsev well
appreciated the content of the DIA, but it is instructive to take a fresh look with
the hindsight of 50 years of experience.
A different perspective on the role of infinitesimal response arises when one
considers the instability of homogeneous turbulence to the generation of mean fields.
I shall discuss that in § 6.2, where I
describe how
![]() $R$
figures in contemporary research on the generation of zonal flows.
That leads to a brief discussion of the so-called second-order cumulant expansion
(CE2) and the closely related stochastic structural stability theory (S3T) that are
currently popular for studies of the interactions between turbulent eddies and mean
(e.g., zonal) fields. Understanding those processes involves the concept of Reynolds
stress, which I shall describe.
$R$
figures in contemporary research on the generation of zonal flows.
That leads to a brief discussion of the so-called second-order cumulant expansion
(CE2) and the closely related stochastic structural stability theory (S3T) that are
currently popular for studies of the interactions between turbulent eddies and mean
(e.g., zonal) fields. Understanding those processes involves the concept of Reynolds
stress, which I shall describe.
Virtually all of the ideas and concepts discussed in the mid-1960s have been much further developed over the last half-century, and new ones have been introduced. I emphasize that this article is not a comprehensive review of that huge body of work; it is an introductory tutorial. However, in § 7 I shall mention selected highlights and provide some entry points to the literature.
I shall enumerate some open problems in § 8, which concludes the body of the article. Three appendices are also included: drift-wave terminology is defined in appendix A, a simple proof of Novikov’s theorem is given in appendix B, and a list of notation is provided in appendix C.
Much of practical plasma physics involves the use of basic tools such as dimensional analysis, simple model building at the cartoon level, and back-of-the-envelope estimates of scaling laws, saturation levels, and transport coefficients. In the face of a rich phenomenology, such elementary approaches are essential, and they can carry one a long way. Some of the simplest arguments found in Kadomtsev’s review, such as saturation at the mixing-length level, continue to influence one’s thinking about plasma turbulence. Nevertheless, in the last half-century the field has advanced significantly beyond mere hand waving. It is important to appreciate what has already been learned, not only to avoid reinventing the wheel but also to acquire the tools and perspective to build on existing methodology in ways that are presently unforeseen.
This article is intended to be accessible to advanced graduate students. No sophisticated mathematics is used.Footnote 10 The ideas, however, are profound. Even if one reproduces every step of the mathematics, it is unlikely that the full implications of the necessarily brief discussion will be appreciated on a first reading. A half-century of ideas (a full century, if one includes research on neutral-fluid turbulenceFootnote 11 ) cannot be absorbed in one sitting. But I hope that this article will provide historical perspective and an entrée to the intriguing edifice that is modern turbulence theory.
2. Statistical descriptions of turbulence; the statistical closure problem
The basic goals of a statistical theory of turbulence are (i) to predict experimentally measurable quantities such as the mean field (e.g., profiles of density, temperature, and flow), two-point fluctuation spectra, or transport coefficients, and (ii) to understand the physical processes that underlie the observations. These require one to consider the famous statistical closure problem, which arises because the PDEs of interest are nonlinear.
2.1. The statistical closure problem
The fundamental PDE of many-body plasma physics is the Klimontovich equation
(Klimontovich Reference Klimontovich and ter Harr1967), written here for zero
magnetic field
![]() $\boldsymbol{B}$
:
$\boldsymbol{B}$
:
 $$\begin{eqnarray}\partial _{t}\widetilde{N}_{s}(\boldsymbol{x},\boldsymbol{v},t)+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\widetilde{N}+\widetilde{\boldsymbol{E}}\boldsymbol{\cdot }\boldsymbol{\partial }\widetilde{N}=0,\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t}\widetilde{N}_{s}(\boldsymbol{x},\boldsymbol{v},t)+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\widetilde{N}+\widetilde{\boldsymbol{E}}\boldsymbol{\cdot }\boldsymbol{\partial }\widetilde{N}=0,\end{eqnarray}$$
where
 $$\begin{eqnarray}\widetilde{N}_{s}(\boldsymbol{x},\boldsymbol{v},t)\doteq \frac{1}{\overline{n}_{s}}\mathop{\sum }_{i\in s}{\it\delta}(\boldsymbol{x}-\widetilde{\boldsymbol{x}}_{i}(t)){\it\delta}(\boldsymbol{v}-\widetilde{\boldsymbol{v}}_{i}(t))\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{N}_{s}(\boldsymbol{x},\boldsymbol{v},t)\doteq \frac{1}{\overline{n}_{s}}\mathop{\sum }_{i\in s}{\it\delta}(\boldsymbol{x}-\widetilde{\boldsymbol{x}}_{i}(t)){\it\delta}(\boldsymbol{v}-\widetilde{\boldsymbol{v}}_{i}(t))\end{eqnarray}$$
is the phase-space microdensity of species
![]() $s$
,
$s$
,
![]() $\doteq$
denotes a definition,
$\doteq$
denotes a definition,
![]() $\overline{n}$
is the mean density,
$\overline{n}$
is the mean density,
 $\boldsymbol{\partial }\doteq (q/m)\,\partial /\partial \boldsymbol{v}$
,
$\boldsymbol{\partial }\doteq (q/m)\,\partial /\partial \boldsymbol{v}$
,
![]() $q$
and
$q$
and
![]() $m$
are charge and mass, and
$m$
are charge and mass, and
![]() $\widetilde{\boldsymbol{E}}$
is the microscopic electric field. In electrostatics, to which this
article is restricted for simplicity, it is sufficient to write
$\widetilde{\boldsymbol{E}}$
is the microscopic electric field. In electrostatics, to which this
article is restricted for simplicity, it is sufficient to write
 $\widetilde{\boldsymbol{E}}=-\boldsymbol{{\rm\nabla}}\widetilde{{\it\phi}}$
and to determine
$\widetilde{\boldsymbol{E}}=-\boldsymbol{{\rm\nabla}}\widetilde{{\it\phi}}$
and to determine
![]() $\widetilde{\boldsymbol{E}}$
or
$\widetilde{\boldsymbol{E}}$
or
![]() $\widetilde{{\it\phi}}$
from Poisson’s equation,
$\widetilde{{\it\phi}}$
from Poisson’s equation,
 $$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\widetilde{\boldsymbol{E}}=-{\rm\nabla}^{2}\widetilde{{\it\phi}}=4{\rm\pi}\widetilde{{\it\rho}}=4{\rm\pi}\mathop{\sum }_{\overline{s}}(\overline{n}q)_{\overline{s}}\int \!\text{d}\overline{\boldsymbol{v}}\;\widetilde{N}_{\overline{s}}(\boldsymbol{x},\overline{\boldsymbol{v}},t).\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\widetilde{\boldsymbol{E}}=-{\rm\nabla}^{2}\widetilde{{\it\phi}}=4{\rm\pi}\widetilde{{\it\rho}}=4{\rm\pi}\mathop{\sum }_{\overline{s}}(\overline{n}q)_{\overline{s}}\int \!\text{d}\overline{\boldsymbol{v}}\;\widetilde{N}_{\overline{s}}(\boldsymbol{x},\overline{\boldsymbol{v}},t).\end{eqnarray}$$
The functions
![]() $\widetilde{\boldsymbol{x}}(t)$
and
$\widetilde{\boldsymbol{x}}(t)$
and
![]() $\widetilde{\boldsymbol{v}}(t)$
are the random particle trajectories that evolve from certain
initial conditions. The quantities
$\widetilde{\boldsymbol{v}}(t)$
are the random particle trajectories that evolve from certain
initial conditions. The quantities
![]() $\widetilde{\boldsymbol{x}}$
and
$\widetilde{\boldsymbol{x}}$
and
![]() $\widetilde{\boldsymbol{v}}$
, and hence
$\widetilde{\boldsymbol{v}}$
, and hence
![]() $\widetilde{N}$
and
$\widetilde{N}$
and
![]() $\widetilde{\boldsymbol{E}}$
, are random because it is assumed that at some initial time the
phase-space locations of the particles are sampled from some ensemble, i.e.,
$\widetilde{\boldsymbol{E}}$
, are random because it is assumed that at some initial time the
phase-space locations of the particles are sampled from some ensemble, i.e.,
![]() $\widetilde{N}$
describes the phase-space dynamics of one particular realization of
that ensemble. An observable quantity is the ensemble or statistical
average, denoted by
$\widetilde{N}$
describes the phase-space dynamics of one particular realization of
that ensemble. An observable quantity is the ensemble or statistical
average, denoted by
![]() $\langle \cdots \rangle$
, of a random variable. For example, the so-called one-particle
distribution function isFootnote
12
$\langle \cdots \rangle$
, of a random variable. For example, the so-called one-particle
distribution function isFootnote
12
 $f_{s}(\boldsymbol{x},\boldsymbol{v},t)\doteq \langle \widetilde{N}_{s}(\boldsymbol{x},\boldsymbol{v},t)\rangle$
. One is also interested in higher-order statistics of the
fluctuation
$f_{s}(\boldsymbol{x},\boldsymbol{v},t)\doteq \langle \widetilde{N}_{s}(\boldsymbol{x},\boldsymbol{v},t)\rangle$
. One is also interested in higher-order statistics of the
fluctuation
 ${\it\delta}N\doteq \widetilde{N}-\langle \widetilde{N}\rangle$
, such as
${\it\delta}N\doteq \widetilde{N}-\langle \widetilde{N}\rangle$
, such as
 $\langle {\it\delta}N(t){\it\delta}N(t^{\prime })\rangle$
. In classical, near-equilibrium plasmas, that two-point correlation
function is used to derive the Balescu–Lenard collision operator (usually
approximated in practice by the Landau operatorFootnote
13
) that describes the effects of particle discreteness in the limit of weak
coupling (
$\langle {\it\delta}N(t){\it\delta}N(t^{\prime })\rangle$
. In classical, near-equilibrium plasmas, that two-point correlation
function is used to derive the Balescu–Lenard collision operator (usually
approximated in practice by the Landau operatorFootnote
13
) that describes the effects of particle discreteness in the limit of weak
coupling (
 ${\it\epsilon}_{\text{p}}\doteq 1/(n{\it\lambda}_{\text{D}}^{3})\ll 1$
, where
${\it\epsilon}_{\text{p}}\doteq 1/(n{\it\lambda}_{\text{D}}^{3})\ll 1$
, where
![]() ${\it\lambda}_{\text{D}}$
is the Debye lengthFootnote
14
). But even in the continuum limit
${\it\lambda}_{\text{D}}$
is the Debye lengthFootnote
14
). But even in the continuum limit
![]() ${\it\epsilon}_{\text{p}}\rightarrow 0$
, turbulent fluctuations of the phase-space fluid can occur
(Davidson Reference Davidson1972). The goal is to determine
their effects on observable spectra and turbulent transport.Footnote
15
${\it\epsilon}_{\text{p}}\rightarrow 0$
, turbulent fluctuations of the phase-space fluid can occur
(Davidson Reference Davidson1972). The goal is to determine
their effects on observable spectra and turbulent transport.Footnote
15
For neutral fluids, the paradigmatic PDE is the Navier–Stokes equation constrained by incompressibility:
 $$\begin{eqnarray}\displaystyle & \partial _{t}\widetilde{\boldsymbol{u}}(\boldsymbol{x},t)+\widetilde{\boldsymbol{u}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\widetilde{\boldsymbol{u}}=-{\it\rho}_{\text{m}}^{-1}\boldsymbol{{\rm\nabla}}\widetilde{P}+{\it\mu}{\rm\nabla}^{2}\widetilde{\boldsymbol{u}}+\,\widetilde{\boldsymbol{f}}\vphantom{f}^{\text{ext}}(\boldsymbol{x},t), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \partial _{t}\widetilde{\boldsymbol{u}}(\boldsymbol{x},t)+\widetilde{\boldsymbol{u}}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\widetilde{\boldsymbol{u}}=-{\it\rho}_{\text{m}}^{-1}\boldsymbol{{\rm\nabla}}\widetilde{P}+{\it\mu}{\rm\nabla}^{2}\widetilde{\boldsymbol{u}}+\,\widetilde{\boldsymbol{f}}\vphantom{f}^{\text{ext}}(\boldsymbol{x},t), & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\widetilde{\boldsymbol{u}}=0. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\widetilde{\boldsymbol{u}}=0. & \displaystyle\end{eqnarray}$$
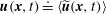 $\boldsymbol{u}(\boldsymbol{x},t)\doteq \langle \widetilde{\boldsymbol{u}}(\boldsymbol{x},t)\rangle$
and in higher-order statistics such as the two-point correlation
function
$\boldsymbol{u}(\boldsymbol{x},t)\doteq \langle \widetilde{\boldsymbol{u}}(\boldsymbol{x},t)\rangle$
and in higher-order statistics such as the two-point correlation
function
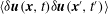 $\langle {\it\delta}\boldsymbol{u}(\boldsymbol{x},t){\it\delta}\boldsymbol{u}(\boldsymbol{x}^{\prime },t^{\prime })\rangle$
, the Fourier transform of which with respect to difference
variables is the energy spectrum in wavenumber and frequency. The mean flow
$\langle {\it\delta}\boldsymbol{u}(\boldsymbol{x},t){\it\delta}\boldsymbol{u}(\boldsymbol{x}^{\prime },t^{\prime })\rangle$
, the Fourier transform of which with respect to difference
variables is the energy spectrum in wavenumber and frequency. The mean flow
 $f_{s}(\boldsymbol{x},\boldsymbol{v},t)$
in the sense that both are the ensemble averages of random
variables. (Unlike
$f_{s}(\boldsymbol{x},\boldsymbol{v},t)$
in the sense that both are the ensemble averages of random
variables. (Unlike
Operationally, ensemble averaging is well defined. One is given some probability density function(al) of initial conditions and/or random forcing, and averages are taken with that PDF. A question is whether the result of the averaging has something useful to say about the observable macroscopic world. In particular, whereas Newton’s laws of motion are time-reversible, ensemble averaging (often together with certain asymptotic limiting procedures) typically introduces irreversibility (one manifestation of which one sees in the laboratory as turbulent transport). The use of ensembles and the origins of irreversibility are subtle topics.Footnote 17 A readable article on the subject as applied to many-body theory is by Lebowitz (Reference Lebowitz1993), who says (the italics are his):
We neither have nor do we need ensembles when we carry out observations.. . . What we do need and can expect to have is typical behavior. Ensembles are merely mathematical tools, useful for computing typical behavior as long as the dispersion in the quantities of interest is sufficiently small.
There is no such typicality with respect to ensembles describing the time evolution of a system with only a few degrees of freedom. This is an essential difference (unfortunately frequently overlooked or misunderstood) between the irreversible and the chaotic behavior of Hamiltonian systems. The latter, which can be observed already in systems consisting of only a few particles, will not have a unidirectional time behavior in any particular realization. Thus if we had only a few hard spheres in a box, we would get plenty of chaotic dynamics and very good ergodic behavior, but we could not tell the time order of any sequence of snapshots.
Having thus warned the reader, I shall continue with the use of ensemble averages, which are technically convenient. In practice they can often be equated to some sort of time average, providing a link between the processing of simulation data and the analytical theory.
Both of equations (2.1) and (2.4) are quadratically nonlinear, so they are special cases of the generic quadratic PDE
 $$\begin{eqnarray}\partial _{t_{1}}\widetilde{{\it\psi}}(1)=U_{2}(1,2)\widetilde{{\it\psi}}(2)+\frac{1}{2}U_{3}(1,2,3)\widetilde{{\it\psi}}(2)\widetilde{{\it\psi}}(3)+\widetilde{f}^{\text{ext}}(1),\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t_{1}}\widetilde{{\it\psi}}(1)=U_{2}(1,2)\widetilde{{\it\psi}}(2)+\frac{1}{2}U_{3}(1,2,3)\widetilde{{\it\psi}}(2)\widetilde{{\it\psi}}(3)+\widetilde{f}^{\text{ext}}(1),\end{eqnarray}$$
where 1 stands for the complete set of independent variables,Footnote
18
the coupling coefficients
![]() $U_{i}$
are specified (e.g., see (3.10a
) and (3.10b
)),
$U_{i}$
are specified (e.g., see (3.10a
) and (3.10b
)),
![]() $U_{3}$
can be assumed to be symmetric in its last two arguments, an
integration–summation convention over repeated arguments is assumed, and
$U_{3}$
can be assumed to be symmetric in its last two arguments, an
integration–summation convention over repeated arguments is assumed, and
![]() $\widetilde{f}^{\text{ext}}$
is external random forcing. It is conventional to choose
$\widetilde{f}^{\text{ext}}$
is external random forcing. It is conventional to choose
![]() $\widetilde{f}^{\text{ext}}$
to be Gaussian for simplicity, so it is completely specified by its
mean
$\widetilde{f}^{\text{ext}}$
to be Gaussian for simplicity, so it is completely specified by its
mean
![]() $\langle \,\widetilde{f}^{\text{ext}}\rangle$
and covariance
$\langle \,\widetilde{f}^{\text{ext}}\rangle$
and covariance
 $F^{\text{ext}}(1,1^{\prime })\doteq \langle {\it\delta}f^{\text{ext}}(1){\it\delta}f^{\text{ext}}(1^{\prime })\rangle$
. There are two basic approaches to determining the statistics of
$F^{\text{ext}}(1,1^{\prime })\doteq \langle {\it\delta}f^{\text{ext}}(1){\it\delta}f^{\text{ext}}(1^{\prime })\rangle$
. There are two basic approaches to determining the statistics of
![]() $\widetilde{{\it\psi}}$
: either formulate approximate coupled equations for a few low-order
cumulants, or ambitiously try to find an equation for the entire PDFFootnote
19
of
$\widetilde{{\it\psi}}$
: either formulate approximate coupled equations for a few low-order
cumulants, or ambitiously try to find an equation for the entire PDFFootnote
19
of
![]() $\widetilde{{\it\psi}}$
. The cumulant approach is easier and traditional, and it is the one
I shall describe here. An article that summarizes aspects of both approaches is by
Kraichnan (Reference Kraichnan and Sirovich1991).
$\widetilde{{\it\psi}}$
. The cumulant approach is easier and traditional, and it is the one
I shall describe here. An article that summarizes aspects of both approaches is by
Kraichnan (Reference Kraichnan and Sirovich1991).
The simplest statistical quantity is the mean field, which exactly obeys
 $$\begin{eqnarray}\displaystyle \partial _{t_{1}}\langle {\it\psi}\rangle (1) & = & \displaystyle U_{2}(1,2)\langle {\it\psi}\rangle (2)+\frac{1}{2}U_{3}(1,2,3)\langle {\it\psi}\rangle (2)\langle {\it\psi}\rangle (3)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2}U_{3}(1,2,3)C(2,3)+\langle \,f^{\text{ext}}\rangle (1).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \partial _{t_{1}}\langle {\it\psi}\rangle (1) & = & \displaystyle U_{2}(1,2)\langle {\it\psi}\rangle (2)+\frac{1}{2}U_{3}(1,2,3)\langle {\it\psi}\rangle (2)\langle {\it\psi}\rangle (3)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2}U_{3}(1,2,3)C(2,3)+\langle \,f^{\text{ext}}\rangle (1).\end{eqnarray}$$
This already exhibits a closure problem: the mean field is determined
by the covariance
 $C(2,3)\doteq \langle {\it\delta}{\it\psi}(2){\it\delta}{\it\psi}(3)\rangle$
, which is unknown. To obtain an equation for
$C(2,3)\doteq \langle {\it\delta}{\it\psi}(2){\it\delta}{\it\psi}(3)\rangle$
, which is unknown. To obtain an equation for
![]() $C$
, subtract (2.6)
from (2.5) to find that the
fluctuations obey
$C$
, subtract (2.6)
from (2.5) to find that the
fluctuations obey
 $$\begin{eqnarray}\displaystyle \partial _{t_{1}}{\it\delta}{\it\psi}(1) & = & \displaystyle U_{2}(1,2){\it\delta}{\it\psi}(2)+U_{3}(1,2,3)\langle {\it\psi}\rangle (2){\it\delta}{\it\psi}(3)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2}U_{3}(1,2,3)[{\it\delta}{\it\psi}(2){\it\delta}{\it\psi}(3)-C(2,3)]+{\it\delta}f^{\text{ext}}(1).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \partial _{t_{1}}{\it\delta}{\it\psi}(1) & = & \displaystyle U_{2}(1,2){\it\delta}{\it\psi}(2)+U_{3}(1,2,3)\langle {\it\psi}\rangle (2){\it\delta}{\it\psi}(3)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2}U_{3}(1,2,3)[{\it\delta}{\it\psi}(2){\it\delta}{\it\psi}(3)-C(2,3)]+{\it\delta}f^{\text{ext}}(1).\end{eqnarray}$$
Upon multiplying (2.7) by
![]() ${\it\delta}{\it\psi}(1^{\prime })$
and averaging, one finds that
${\it\delta}{\it\psi}(1^{\prime })$
and averaging, one finds that
![]() $C(1,1^{\prime })$
obeysFootnote
20
$C(1,1^{\prime })$
obeysFootnote
20
 $$\begin{eqnarray}\displaystyle \partial _{t_{1}}C(1,1^{\prime }) & = & \displaystyle U_{2}(1,2)C(2,1^{\prime })+U_{3}(1,2,3)\langle {\it\psi}\rangle (2)C(3,1^{\prime })\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2}U_{3}(1,2,3)T(2,3,1^{\prime })+\langle {\it\delta}f^{\text{ext}}(1){\it\delta}{\it\psi}(1^{\prime })\rangle ,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \partial _{t_{1}}C(1,1^{\prime }) & = & \displaystyle U_{2}(1,2)C(2,1^{\prime })+U_{3}(1,2,3)\langle {\it\psi}\rangle (2)C(3,1^{\prime })\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2}U_{3}(1,2,3)T(2,3,1^{\prime })+\langle {\it\delta}f^{\text{ext}}(1){\it\delta}{\it\psi}(1^{\prime })\rangle ,\end{eqnarray}$$
where the three-point correlation function is
 $$\begin{eqnarray}T(2,3,1^{\prime })\doteq \langle {\it\delta}{\it\psi}(2){\it\delta}{\it\psi}(3){\it\delta}{\it\psi}(1^{\prime })\rangle .\end{eqnarray}$$
$$\begin{eqnarray}T(2,3,1^{\prime })\doteq \langle {\it\delta}{\it\psi}(2){\it\delta}{\it\psi}(3){\it\delta}{\it\psi}(1^{\prime })\rangle .\end{eqnarray}$$
Quantities such as
![]() $\langle {\it\psi}\rangle$
,
$\langle {\it\psi}\rangle$
,
![]() $C$
, or
$C$
, or
![]() $T$
are cumulants, a central concept.Footnote
21
An important property is that multipoint cumulants of statistically
independent quantities vanish. We see that
$T$
are cumulants, a central concept.Footnote
21
An important property is that multipoint cumulants of statistically
independent quantities vanish. We see that
![]() $n$
-point cumulants are driven by
$n$
-point cumulants are driven by
![]() $(n+1)$
-point cumulants; the cumulant hierarchy is unclosed. This is the
classical statistical closure problem (Kraichnan Reference Kraichnan1962; Leslie Reference Leslie1973; Orszag Reference Orszag, Balian and Peube1977; McComb Reference McComb1990, Reference McComb2014; Krommes Reference Krommes2002, and references therein). To close the
system at the covariance level, one must express the triplet correlation function
$(n+1)$
-point cumulants; the cumulant hierarchy is unclosed. This is the
classical statistical closure problem (Kraichnan Reference Kraichnan1962; Leslie Reference Leslie1973; Orszag Reference Orszag, Balian and Peube1977; McComb Reference McComb1990, Reference McComb2014; Krommes Reference Krommes2002, and references therein). To close the
system at the covariance level, one must express the triplet correlation function
![]() $T$
and the cross-correlation of
$T$
and the cross-correlation of
![]() ${\it\delta}f^{\text{ext}}$
and
${\it\delta}f^{\text{ext}}$
and
![]() ${\it\delta}{\it\psi}$
in terms of one-point (the mean field) and two-point quantities
(such as
${\it\delta}{\it\psi}$
in terms of one-point (the mean field) and two-point quantities
(such as
![]() $C$
; a two-point response function
$C$
; a two-point response function
![]() $R$
will also be important).
$R$
will also be important).
Statistical closure would not be a problem if the PDF of
![]() $\widetilde{{\it\psi}}$
were Gaussian. General PDFs can usually be represented in terms of
an infinite set of cumulants;Footnote
22
Gaussians are special because they possess just two cumulants – namely, the
mean and the variance. A theorem states that the sum of two Gaussian variables is
again Gaussian, so if the dynamics were linear (i.e.,
$\widetilde{{\it\psi}}$
were Gaussian. General PDFs can usually be represented in terms of
an infinite set of cumulants;Footnote
22
Gaussians are special because they possess just two cumulants – namely, the
mean and the variance. A theorem states that the sum of two Gaussian variables is
again Gaussian, so if the dynamics were linear (i.e.,
![]() $U_{3}=0$
),
$U_{3}=0$
),
![]() $\widetilde{{\it\psi}}$
would be Gaussian if it evolved from Gaussian initial conditions
under Gaussian forcing. Unfortunately, nonlinearity confounds this result. The
product of two Gaussian variables is not Gaussian, so even if the initial conditions
were Gaussian, non-Gaussian statistics would develop after just one time step.Footnote
23
Once non-Gaussianity arises, it is compounded during each subsequent time
interval. After long times a statistically steady PDF can develop, but it will be
non-Gaussian in a self-consistent way that is difficult to determine
analytically.Footnote
24
The inevitable development of non-Gaussian statistics in nonlinear PDEs is
the essence of the closure problem.
$\widetilde{{\it\psi}}$
would be Gaussian if it evolved from Gaussian initial conditions
under Gaussian forcing. Unfortunately, nonlinearity confounds this result. The
product of two Gaussian variables is not Gaussian, so even if the initial conditions
were Gaussian, non-Gaussian statistics would develop after just one time step.Footnote
23
Once non-Gaussianity arises, it is compounded during each subsequent time
interval. After long times a statistically steady PDF can develop, but it will be
non-Gaussian in a self-consistent way that is difficult to determine
analytically.Footnote
24
The inevitable development of non-Gaussian statistics in nonlinear PDEs is
the essence of the closure problem.
Over roughly the last century, enormous efforts have been expended toward obtaining satisfactory statistical closures. A famous example is the DIA; it will be discussed in § 4. Some simpler approximations have enjoyed good successes for the description of the interactions of mean fields with turbulence; see § 6.3.
2.2. Interlude: Langevin equations
Although statistical closures for realistic nonlinear PDEs such as the Klimontovich equation are difficult and nontrivial, a good deal of the physics embodied in such equations can be understood with simple intuition. A good example is the use of Langevin equations (Lemons & Gythiel Reference Lemons and Gythiel1997; Gardiner Reference Gardiner2004) to describe the statistical properties of classical Brownian motion. I shall include a few words of introduction here so that later I can interpret certain exact and closure results in terms of generalized Langevin descriptions.
2.2.1. Classical Brownian motion
In physics, classical Brownian motion refers to the random motion of a heavy
‘test’ particle (mass
![]() $M$
) moving in a thermal bath (temperature
$M$
) moving in a thermal bath (temperature
![]() $T$
) of light particles. The original model was motivated by
observationsFootnote
25
(Brown Reference Brown1828) of the jittery motion
of particles ejected by pollen grains suspended in water; in plasmas, the
description applies equally well to an ion moving in a sea of electrons. In the
simplest Langevin model, Newton’s second law of motion for the velocity of an
unmagnetized test particle is written approximately (in one dimension for
simplicity) asFootnote
26
$T$
) of light particles. The original model was motivated by
observationsFootnote
25
(Brown Reference Brown1828) of the jittery motion
of particles ejected by pollen grains suspended in water; in plasmas, the
description applies equally well to an ion moving in a sea of electrons. In the
simplest Langevin model, Newton’s second law of motion for the velocity of an
unmagnetized test particle is written approximately (in one dimension for
simplicity) asFootnote
26
 $$\begin{eqnarray}\dot{\widetilde{v}}+{\it\nu}\widetilde{v}=\widetilde{a}(t).\end{eqnarray}$$
$$\begin{eqnarray}\dot{\widetilde{v}}+{\it\nu}\widetilde{v}=\widetilde{a}(t).\end{eqnarray}$$
Here the time axis has been assumed to be coarse-grained into
intervals that are much larger than the time for a single interaction between the
test particle and a bath particle. Then the effects of the microscopic
interactions have been replaced by a coarse-grained force divided into two
physically distinct parts:
![]() $\widetilde{a}$
is a centred Gaussian random variable that describes the random
or incoherent kicks due to the light particles, and
$\widetilde{a}$
is a centred Gaussian random variable that describes the random
or incoherent kicks due to the light particles, and
![]() $-{\it\nu}\widetilde{v}$
describes the coherent drag experienced by the test particle as
it pushes through the sea. Of course, that drag arises microscopically from
discrete interactions with the bath particles, so both
$-{\it\nu}\widetilde{v}$
describes the coherent drag experienced by the test particle as
it pushes through the sea. Of course, that drag arises microscopically from
discrete interactions with the bath particles, so both
![]() ${\it\nu}$
and the statistics of
${\it\nu}$
and the statistics of
![]() $\widetilde{a}$
can ultimately be determined in terms of microscopic statistical
dynamics. Because of the coarse-graining, it is conventional to take the
fluctuation
$\widetilde{a}$
can ultimately be determined in terms of microscopic statistical
dynamics. Because of the coarse-graining, it is conventional to take the
fluctuation
![]() ${\it\delta}a$
to be delta-correlated:
${\it\delta}a$
to be delta-correlated:
 $$\begin{eqnarray}\langle {\it\delta}a(t){\it\delta}a(t^{\prime })\rangle =2D_{v}{\it\delta}(t-t^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}\langle {\it\delta}a(t){\it\delta}a(t^{\prime })\rangle =2D_{v}{\it\delta}(t-t^{\prime }).\end{eqnarray}$$
For short times (
![]() ${\it\nu}t\ll 1$
), one finds from (2.10) that
${\it\nu}t\ll 1$
), one finds from (2.10) that
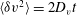 $\langle {\it\delta}v^{2}\rangle =2D_{v}t$
, so
$\langle {\it\delta}v^{2}\rangle =2D_{v}t$
, so
![]() $D_{v}$
is the diffusion coefficient for a simple random walk (Rudnick
& Gaspari Reference Rudnick and Gaspari2004) in velocity space. At
long times one finds (Wang & Uhlenbeck Reference Wang and Uhlenbeck1945)
$D_{v}$
is the diffusion coefficient for a simple random walk (Rudnick
& Gaspari Reference Rudnick and Gaspari2004) in velocity space. At
long times one finds (Wang & Uhlenbeck Reference Wang and Uhlenbeck1945)
 $$\begin{eqnarray}\lim _{t\rightarrow \infty }\langle {\it\delta}v^{2}\rangle \equiv \lim _{t\rightarrow \infty }C(t,t)=D_{v}/{\it\nu},\end{eqnarray}$$
$$\begin{eqnarray}\lim _{t\rightarrow \infty }\langle {\it\delta}v^{2}\rangle \equiv \lim _{t\rightarrow \infty }C(t,t)=D_{v}/{\it\nu},\end{eqnarray}$$
which describes the fluctuation level arising from a steady-state balance between forcing and dissipation; in that same limit, one finds the two-time correlation function to be
 $$\begin{eqnarray}C(t,t^{\prime })\doteq \langle {\it\delta}v(t){\it\delta}v(t^{\prime })\rangle =(D_{v}/{\it\nu})\text{e}^{-{\it\nu}|t-t^{\prime }|}.\end{eqnarray}$$
$$\begin{eqnarray}C(t,t^{\prime })\doteq \langle {\it\delta}v(t){\it\delta}v(t^{\prime })\rangle =(D_{v}/{\it\nu})\text{e}^{-{\it\nu}|t-t^{\prime }|}.\end{eqnarray}$$
This depends on only the time difference
 ${\it\tau}\doteq t-t^{\prime }$
, so one can Fourier-transformFootnote
27
with respect to
${\it\tau}\doteq t-t^{\prime }$
, so one can Fourier-transformFootnote
27
with respect to
![]() ${\it\tau}$
:
${\it\tau}$
:
 $$\begin{eqnarray}\widehat{C}({\it\omega})=2(D_{v}/{\it\nu})\,\text{Re}\,\widehat{g}({\it\omega}),\end{eqnarray}$$
$$\begin{eqnarray}\widehat{C}({\it\omega})=2(D_{v}/{\it\nu})\,\text{Re}\,\widehat{g}({\it\omega}),\end{eqnarray}$$
where
 $g({\it\tau})\doteq H({\it\tau})\text{e}^{-{\it\nu}{\it\tau}}$
is Green’s functionFootnote
28
for the left-hand side of (2.10). Equations (2.13) and (2.14) are
called fluctuation–dissipation relations, where relation (as
opposed to theorem) implies that one has not yet asserted a
connection between forcing and dissipation. If one does so by invoking microscopic
statistical equilibration according to
$g({\it\tau})\doteq H({\it\tau})\text{e}^{-{\it\nu}{\it\tau}}$
is Green’s functionFootnote
28
for the left-hand side of (2.10). Equations (2.13) and (2.14) are
called fluctuation–dissipation relations, where relation (as
opposed to theorem) implies that one has not yet asserted a
connection between forcing and dissipation. If one does so by invoking microscopic
statistical equilibration according to
 $M\langle {\it\delta}v^{2}\rangle /2=T/2$
, one is led to the Einstein (Reference Einstein1905) relation
$M\langle {\it\delta}v^{2}\rangle /2=T/2$
, one is led to the Einstein (Reference Einstein1905) relation
 $D_{v}/{\it\nu}=T/M\equiv V_{\text{t}}^{2}$
. Then
$D_{v}/{\it\nu}=T/M\equiv V_{\text{t}}^{2}$
. Then
 $C({\it\tau})=V_{\text{t}}^{2}\exp (-{\it\nu}|{\it\tau}|)$
, or
$C({\it\tau})=V_{\text{t}}^{2}\exp (-{\it\nu}|{\it\tau}|)$
, or
 $$\begin{eqnarray}\widehat{C}({\it\omega})=2V_{\text{t}}^{2}\,\text{Re}\,\widehat{g}({\it\omega}).\end{eqnarray}$$
$$\begin{eqnarray}\widehat{C}({\it\omega})=2V_{\text{t}}^{2}\,\text{Re}\,\widehat{g}({\it\omega}).\end{eqnarray}$$
This is the simplest example of a fluctuation–dissipation theorem (Kubo Reference Kubo1966; Martin Reference Martin, deWitt and Balian1968; Zwanzig Reference Zwanzig2001). Such theorems are derived most fundamentally by studying the linear response of a Hamiltonian system perturbed from a Gibbsian thermal equilibrium.
This superficial treatment of Langevin equations merely scratches the surface. For example, because the statistics of all dependent variables of a Gaussianly forced linear Langevin system are jointly Gaussian, a variety of exact results (including the complete form of the PDF) can be obtained; see the articles by Fox & Uhlenbeck (Reference Fox and Uhlenbeck1970) and Fox (Reference Fox1978). A wealth of information about linear and nonlinear Langevin equations is contained in the book by Zwanzig (Reference Zwanzig2001). Some aspects of stochastic differential equations are reviewed by van Kampen (Reference van Kampen1976).
The fact that the statistics of the Brownian particle follow from a Langevin
amplitude equation (an equation for a random variable, not a mean quantity) has
profound implications. It guarantees that the statistics calculated from the model
must obey all of the realizability inequalities (Kraichnan Reference Kraichnan and Helleman1980; van Kampen Reference van Kampen1981) that stem from the requirement that the PDF be non-negative. The
simplest realizability inequality is
 $\langle \widetilde{v}^{2}\rangle \geqslant \langle \widetilde{v}\rangle ^{2}$
, i.e.,
$\langle \widetilde{v}^{2}\rangle \geqslant \langle \widetilde{v}\rangle ^{2}$
, i.e.,
 $C\equiv C(t,t)\doteq \langle {\it\delta}v^{2}\rangle \geqslant 0$
. In the latter form, this is obvious if one has an explicit
solution for the real quantity
$C\equiv C(t,t)\doteq \langle {\it\delta}v^{2}\rangle \geqslant 0$
. In the latter form, this is obvious if one has an explicit
solution for the real quantity
![]() ${\it\delta}v(t)$
, as in the linear Langevin model (2.10). But in closure theory one usually formulates
approximate evolution equations for cumulants like
${\it\delta}v(t)$
, as in the linear Langevin model (2.10). But in closure theory one usually formulates
approximate evolution equations for cumulants like
![]() $C$
rather than for random variables:
$C$
rather than for random variables:
 $\partial _{t}C=f(C)$
, where
$\partial _{t}C=f(C)$
, where
![]() $f$
can be a complicated nonlinear function. In general, there is no
guarantee that solutions of such nonlinear equations preserve the non-negativity
of
$f$
can be a complicated nonlinear function. In general, there is no
guarantee that solutions of such nonlinear equations preserve the non-negativity
of
![]() $C$
for all time. If they do not, catastrophes such as finite-time
blowup can ensue (Ogura Reference Ogura1962a
,Reference Ogura
b
, Reference Ogura1963; Bowman, Krommes &
Ottaviani Reference Bowman, Krommes and Ottaviani1993). However,
positive-semidefiniteness is guaranteed if it is known that the
$C$
for all time. If they do not, catastrophes such as finite-time
blowup can ensue (Ogura Reference Ogura1962a
,Reference Ogura
b
, Reference Ogura1963; Bowman, Krommes &
Ottaviani Reference Bowman, Krommes and Ottaviani1993). However,
positive-semidefiniteness is guaranteed if it is known that the
![]() $\partial _{t}C$
equation follows rigorously from an underlying amplitude
equation for a random variable. That is the case, for example, for the DIA; see
(4.29) and the discussion
nearby.
$\partial _{t}C$
equation follows rigorously from an underlying amplitude
equation for a random variable. That is the case, for example, for the DIA; see
(4.29) and the discussion
nearby.
2.2.2. The Taylor formula for a diffusion coefficient
Note that (2.11) can be inverted:
 $$\begin{eqnarray}D_{v}=\int _{0}^{\infty }\!\text{d}{\it\tau}\,\langle {\it\delta}a({\it\tau}){\it\delta}a(0)\rangle .\end{eqnarray}$$
$$\begin{eqnarray}D_{v}=\int _{0}^{\infty }\!\text{d}{\it\tau}\,\langle {\it\delta}a({\it\tau}){\it\delta}a(0)\rangle .\end{eqnarray}$$
This is the simplest example of the Taylor formula (Taylor Reference Taylor1921) for the diffusion coefficient
![]() $D_{z}$
of a test particle or fluid element evolving in variable
$D_{z}$
of a test particle or fluid element evolving in variable
![]() $z$
according to
$z$
according to
![]() $\dot{\widetilde{z}}=\widetilde{V}$
:
$\dot{\widetilde{z}}=\widetilde{V}$
:
 $$\begin{eqnarray}D_{z}=\int _{0}^{\infty }\!\text{d}{\it\tau}\,C_{VV}({\it\tau}),\end{eqnarray}$$
$$\begin{eqnarray}D_{z}=\int _{0}^{\infty }\!\text{d}{\it\tau}\,C_{VV}({\it\tau}),\end{eqnarray}$$
where
 $$\begin{eqnarray}C_{VV}({\it\tau})\doteq \langle {\it\delta}V({\it\tau}){\it\delta}V(0)\rangle\end{eqnarray}$$
$$\begin{eqnarray}C_{VV}({\it\tau})\doteq \langle {\it\delta}V({\it\tau}){\it\delta}V(0)\rangle\end{eqnarray}$$
is called the Lagrangian correlation function. Here
 $\widetilde{V}({\it\tau})\equiv \widetilde{V}(\widetilde{\boldsymbol{x}}({\it\tau}),\widetilde{\boldsymbol{v}}({\it\tau}),{\it\tau})$
; i.e., it is measured along the random phase-space trajectory
$\widetilde{V}({\it\tau})\equiv \widetilde{V}(\widetilde{\boldsymbol{x}}({\it\tau}),\widetilde{\boldsymbol{v}}({\it\tau}),{\it\tau})$
; i.e., it is measured along the random phase-space trajectory
 $\{\widetilde{\boldsymbol{x}}({\it\tau}),\widetilde{\boldsymbol{v}}({\it\tau})\}$
. Whether diffusion happens in position space (
$\{\widetilde{\boldsymbol{x}}({\it\tau}),\widetilde{\boldsymbol{v}}({\it\tau})\}$
. Whether diffusion happens in position space (
![]() $z=x$
) or velocity space (
$z=x$
) or velocity space (
![]() $z=v$
) depends on which variable suffers random kicks. In the case of
an unmagnetized Brownian particle, the generalized ‘velocity’ of the general
theory is actually acceleration; diffusion occurs in velocity space (for times
much shorter than a collision time).Footnote
29
For a magnetized test particle moving across a magnetic field,
$z=v$
) depends on which variable suffers random kicks. In the case of
an unmagnetized Brownian particle, the generalized ‘velocity’ of the general
theory is actually acceleration; diffusion occurs in velocity space (for times
much shorter than a collision time).Footnote
29
For a magnetized test particle moving across a magnetic field,
![]() $\widetilde{V}$
would be the
$\widetilde{V}$
would be the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
velocity and diffusion would occur in
$\boldsymbol{E}\times \boldsymbol{B}$
velocity and diffusion would occur in
![]() $\boldsymbol{x}$
space.
$\boldsymbol{x}$
space.
If one defines a Lagrangian correlation time by
 $$\begin{eqnarray}{\it\tau}_{\text{ac}}^{(\text{L})}\doteq [C_{VV}(0)]^{-1}\int _{0}^{\infty }\!\text{d}{\it\tau}\,C_{VV}({\it\tau}),\end{eqnarray}$$
$$\begin{eqnarray}{\it\tau}_{\text{ac}}^{(\text{L})}\doteq [C_{VV}(0)]^{-1}\int _{0}^{\infty }\!\text{d}{\it\tau}\,C_{VV}({\it\tau}),\end{eqnarray}$$
then one can write formula (2.17) as
 $$\begin{eqnarray}D_{z}=\overline{V}^{2}{\it\tau}_{\text{ac}}^{(\text{L})},\end{eqnarray}$$
$$\begin{eqnarray}D_{z}=\overline{V}^{2}{\it\tau}_{\text{ac}}^{(\text{L})},\end{eqnarray}$$
where
 $\overline{V}\doteq [C_{VV}(0)]^{1/2}$
is the root-mean-square level of the generalized velocity
fluctuations. This formula is exact; the problem lies in determining
$\overline{V}\doteq [C_{VV}(0)]^{1/2}$
is the root-mean-square level of the generalized velocity
fluctuations. This formula is exact; the problem lies in determining
![]() $\overline{V}$
and
$\overline{V}$
and
![]() ${\it\tau}_{\text{ac}}^{(\text{L})}$
. In general, relating Lagrangian correlation functions to more
easily observable or calculable Eulerian ones is a difficult task that again
requires one to face up to a closure problem. One does not see that difficulty in
the linear Langevin model because the Langevin equation is coarse-grained in time
and
${\it\tau}_{\text{ac}}^{(\text{L})}$
. In general, relating Lagrangian correlation functions to more
easily observable or calculable Eulerian ones is a difficult task that again
requires one to face up to a closure problem. One does not see that difficulty in
the linear Langevin model because the Langevin equation is coarse-grained in time
and
![]() $D_{v}$
is simply prescribed. More realistically, one must ‘open up’ the
physics of the short time scale on which the random kicks occur and perform a
nontrivial calculation of the Lagrangian correlation function; formula (2.17) then connects the short-time
physics to the more macroscopic time scale on which diffusion is observed. This is
what is done in the derivation of the Balescu–Lenard collision operator, and there
are analogues of that procedure for turbulence.Footnote
30
$D_{v}$
is simply prescribed. More realistically, one must ‘open up’ the
physics of the short time scale on which the random kicks occur and perform a
nontrivial calculation of the Lagrangian correlation function; formula (2.17) then connects the short-time
physics to the more macroscopic time scale on which diffusion is observed. This is
what is done in the derivation of the Balescu–Lenard collision operator, and there
are analogues of that procedure for turbulence.Footnote
30
2.3. An exactly solvable model of passive advection
There are actually two levels of difficulty in cumulant-based statistical closure.
Problems arise even for passive advection. (In plasmas, that is frequently called
stochastic acceleration (Orszag Reference Orszag and Fox1969),
implying no back-reaction of the particles on the electric field.) Self-consistency
(in plasmas, determining the field from the particles rather than prescribing the
field externally) adds more complications (polarization effects) and leads to the
concept of a dielectric function
![]() ${\mathcal{D}}$
.
${\mathcal{D}}$
.
2.3.1. The stochastic oscillator
Before turning to self-consistency, let us see how things work in a simple,
exactly solvable passive model. The discussion introduces various important
concepts and issues relating to random nonlinear systems, and I shall build on it
in the next section, where I discuss the additional effects relating to
self-consistency. Although there are important differences between passive and
self-consistent problems, many points can be illustrated with passive models
because, although they are dynamically linear, they are stochastically nonlinear –
for example, (2.21) involves the
product of the random variables
![]() $\widetilde{\boldsymbol{V}}$
and
$\widetilde{\boldsymbol{V}}$
and
![]() $\widetilde{{\it\psi}}$
– and thus possess the closure problem (Kraichnan Reference Kraichnan1961). Thus consider the passive-advection
equation
$\widetilde{{\it\psi}}$
– and thus possess the closure problem (Kraichnan Reference Kraichnan1961). Thus consider the passive-advection
equation
 $$\begin{eqnarray}\partial _{t}\widetilde{{\it\psi}}(\boldsymbol{x},t)+{\it\nu}\widetilde{{\it\psi}}+\widetilde{\boldsymbol{V}}(t)\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\widetilde{{\it\psi}}=\,\widetilde{f}^{\text{ext}}(\boldsymbol{x},t),\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t}\widetilde{{\it\psi}}(\boldsymbol{x},t)+{\it\nu}\widetilde{{\it\psi}}+\widetilde{\boldsymbol{V}}(t)\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\widetilde{{\it\psi}}=\,\widetilde{f}^{\text{ext}}(\boldsymbol{x},t),\end{eqnarray}$$
where
![]() ${\it\nu}$
is a positive constant,
${\it\nu}$
is a positive constant,
![]() $\widetilde{\boldsymbol{V}}$
is a centred Gaussian random velocity with a specified two-time
correlation function, and
$\widetilde{\boldsymbol{V}}$
is a centred Gaussian random velocity with a specified two-time
correlation function, and
![]() $\widetilde{f}^{\text{ext}}$
is a Gaussian random forcing that is homogeneous in space,
stationary in time, and uncorrelated with
$\widetilde{f}^{\text{ext}}$
is a Gaussian random forcing that is homogeneous in space,
stationary in time, and uncorrelated with
![]() $\widetilde{\boldsymbol{V}}$
. For simplicity, I assume that
$\widetilde{\boldsymbol{V}}$
. For simplicity, I assume that
![]() $\widetilde{f}^{\text{ext}}$
is white noise, so its covariance
$\widetilde{f}^{\text{ext}}$
is white noise, so its covariance
![]() $F^{\text{ext}}$
has the form
$F^{\text{ext}}$
has the form
 $$\begin{eqnarray}\displaystyle F^{\text{ext}}({\bf\rho},{\it\tau}) & \doteq & \displaystyle \langle {\it\delta}f^{\text{ext}}(\boldsymbol{x}+{\bf\rho},t+{\it\tau}){\it\delta}f^{\text{ext}}(\boldsymbol{x},t)\rangle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F^{\text{ext}}({\bf\rho},{\it\tau}) & \doteq & \displaystyle \langle {\it\delta}f^{\text{ext}}(\boldsymbol{x}+{\bf\rho},t+{\it\tau}){\it\delta}f^{\text{ext}}(\boldsymbol{x},t)\rangle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & = & \displaystyle 2{\it\varepsilon}({\bf\rho}){\it\delta}({\it\tau}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle 2{\it\varepsilon}({\bf\rho}){\it\delta}({\it\tau}),\end{eqnarray}$$
 $$\begin{eqnarray}\partial _{t}\widetilde{{\it\psi}}(\boldsymbol{k},t)+{\it\nu}\widetilde{{\it\psi}}(\boldsymbol{k},t)+\text{i}\widetilde{{\it\omega}}(\boldsymbol{k},t)\widetilde{{\it\psi}}(\boldsymbol{k},t)=\widetilde{f}^{\text{ext}}(\boldsymbol{k},t),\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t}\widetilde{{\it\psi}}(\boldsymbol{k},t)+{\it\nu}\widetilde{{\it\psi}}(\boldsymbol{k},t)+\text{i}\widetilde{{\it\omega}}(\boldsymbol{k},t)\widetilde{{\it\psi}}(\boldsymbol{k},t)=\widetilde{f}^{\text{ext}}(\boldsymbol{k},t),\end{eqnarray}$$
with
 $\widetilde{{\it\omega}}(\boldsymbol{k},t)\doteq \boldsymbol{k}\boldsymbol{\cdot }\widetilde{\boldsymbol{V}}(t)$
and
$\widetilde{{\it\omega}}(\boldsymbol{k},t)\doteq \boldsymbol{k}\boldsymbol{\cdot }\widetilde{\boldsymbol{V}}(t)$
and
 $\widehat{F}^{\text{ext}}(\boldsymbol{k},{\it\tau})=2\widehat{{\it\varepsilon}}(\boldsymbol{k}){\it\delta}({\it\tau})$
. Because the
$\widehat{F}^{\text{ext}}(\boldsymbol{k},{\it\tau})=2\widehat{{\it\varepsilon}}(\boldsymbol{k}){\it\delta}({\it\tau})$
. Because the
![]() $\boldsymbol{k}$
’s are uncoupled, one can drop the
$\boldsymbol{k}$
’s are uncoupled, one can drop the
![]() $\boldsymbol{k}$
’s and consider the stochastic oscillator (Kubo Reference Kubo, Brittin and Dunham1959; Kraichnan Reference Kraichnan1961)
$\boldsymbol{k}$
’s and consider the stochastic oscillator (Kubo Reference Kubo, Brittin and Dunham1959; Kraichnan Reference Kraichnan1961)
 $$\begin{eqnarray}\partial _{t}\widetilde{{\it\psi}}(t)+{\it\nu}\widetilde{{\it\psi}}+\text{i}\widetilde{{\it\omega}}(t)\widetilde{{\it\psi}}=\,\widetilde{f}^{\text{ext}}(t),\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t}\widetilde{{\it\psi}}(t)+{\it\nu}\widetilde{{\it\psi}}+\text{i}\widetilde{{\it\omega}}(t)\widetilde{{\it\psi}}=\,\widetilde{f}^{\text{ext}}(t),\end{eqnarray}$$
where the meanFootnote
31
![]() $\overline{{\it\omega}}$
and the covariance
$\overline{{\it\omega}}$
and the covariance
![]() $W({\it\tau})$
of
$W({\it\tau})$
of
![]() $\widetilde{{\it\omega}}$
are prescribed. The normalized area under
$\widetilde{{\it\omega}}$
are prescribed. The normalized area under
![]() $W({\it\tau})$
defines an advection-related autocorrelation time according to
$W({\it\tau})$
defines an advection-related autocorrelation time according to
 $$\begin{eqnarray}{\it\tau}_{\text{ac}}^{(W)}\doteq [W(0)]^{-1}\int _{0}^{\infty }\!\text{d}{\it\tau}\,W({\it\tau}).\end{eqnarray}$$
$$\begin{eqnarray}{\it\tau}_{\text{ac}}^{(W)}\doteq [W(0)]^{-1}\int _{0}^{\infty }\!\text{d}{\it\tau}\,W({\it\tau}).\end{eqnarray}$$
I shall consider two limitsFootnote
32
– one in which
![]() $\widetilde{\boldsymbol{V}}$
is delta-correlated, so
$\widetilde{\boldsymbol{V}}$
is delta-correlated, so
 $\langle {\it\delta}\widetilde{\boldsymbol{V}}({\it\tau}){\it\delta}\widetilde{\boldsymbol{V}}(0)\rangle =2D{\it\delta}({\it\tau})\unicode[STIX]{x1D644}$
; and one in which it is time-independent (but still random) with
variance
$\langle {\it\delta}\widetilde{\boldsymbol{V}}({\it\tau}){\it\delta}\widetilde{\boldsymbol{V}}(0)\rangle =2D{\it\delta}({\it\tau})\unicode[STIX]{x1D644}$
; and one in which it is time-independent (but still random) with
variance
![]() ${\it\beta}^{2}$
:
${\it\beta}^{2}$
:
 $$\begin{eqnarray}W({\it\tau})\doteq \langle {\it\delta}\widetilde{{\it\omega}}({\it\tau}){\it\delta}\widetilde{{\it\omega}}(0)\rangle =\left\{\begin{array}{@{}ll@{}}2k^{2}D{\it\delta}({\it\tau})\quad & \text{if}~{\it\tau}_{\text{ac}}^{(W)}\rightarrow 0,\\ {\it\beta}^{2}\quad & \text{if}~{\it\tau}_{\text{ac}}^{(W)}\rightarrow \infty .\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}W({\it\tau})\doteq \langle {\it\delta}\widetilde{{\it\omega}}({\it\tau}){\it\delta}\widetilde{{\it\omega}}(0)\rangle =\left\{\begin{array}{@{}ll@{}}2k^{2}D{\it\delta}({\it\tau})\quad & \text{if}~{\it\tau}_{\text{ac}}^{(W)}\rightarrow 0,\\ {\it\beta}^{2}\quad & \text{if}~{\it\tau}_{\text{ac}}^{(W)}\rightarrow \infty .\end{array}\right.\end{eqnarray}$$
2.3.2. Exact solution of the stochastic oscillator
Being dynamically linear, the stochastic oscillator can be solved exactly. By
doing so, I shall be able to introduce the concepts of a random Green’s function
or propagatorFootnote
33
![]() $\widetilde{g}(t;t^{\prime })$
as well as the mean ‘propagator’Footnote
34
$\widetilde{g}(t;t^{\prime })$
as well as the mean ‘propagator’Footnote
34
![]() $g\doteq \langle \widetilde{g}\rangle$
, and we shall be able to see how
$g\doteq \langle \widetilde{g}\rangle$
, and we shall be able to see how
![]() $g({\it\tau})$
relates the correlation function
$g({\it\tau})$
relates the correlation function
 $C(t,t^{\prime })\doteq \langle {\it\delta}{\it\psi}(t){\it\delta}{\it\psi}^{\ast }(t^{\prime })\rangle$
to the external forcing. Green’s function for (2.24) obeys
$C(t,t^{\prime })\doteq \langle {\it\delta}{\it\psi}(t){\it\delta}{\it\psi}^{\ast }(t^{\prime })\rangle$
to the external forcing. Green’s function for (2.24) obeys
 $$\begin{eqnarray}[\partial _{t}+{\it\nu}+\text{i}\widetilde{{\it\omega}}(t)]\widetilde{g}(t;t^{\prime })={\it\delta}(t-t^{\prime })\end{eqnarray}$$
$$\begin{eqnarray}[\partial _{t}+{\it\nu}+\text{i}\widetilde{{\it\omega}}(t)]\widetilde{g}(t;t^{\prime })={\it\delta}(t-t^{\prime })\end{eqnarray}$$
with the boundary condition
 $\widetilde{g}(-\infty ;t^{\prime })=0$
. Upon ignoring an initial condition at
$\widetilde{g}(-\infty ;t^{\prime })=0$
. Upon ignoring an initial condition at
![]() $t=-\infty$
, one finds that the exact driven solution of (2.24) is
$t=-\infty$
, one finds that the exact driven solution of (2.24) is
 $$\begin{eqnarray}\widetilde{{\it\psi}}(t)=\int _{-\infty }^{t}\!\text{d}\overline{t}\,\widetilde{g}(t;\overline{t})\,\widetilde{f}^{\text{ext}}(\overline{t}).\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{{\it\psi}}(t)=\int _{-\infty }^{t}\!\text{d}\overline{t}\,\widetilde{g}(t;\overline{t})\,\widetilde{f}^{\text{ext}}(\overline{t}).\end{eqnarray}$$
(The upper limit can be replaced by
![]() $\infty$
because
$\infty$
because
 $\widetilde{g}(t;\overline{t})\propto H(t-\overline{t})$
.) The mean field follows as
$\widetilde{g}(t;\overline{t})\propto H(t-\overline{t})$
.) The mean field follows as
 $$\begin{eqnarray}\langle {\it\psi}\rangle (t)=\int _{-\infty }^{t}\!\text{d}\overline{t}\,g(t;\overline{t})\langle \,\widetilde{f}^{\text{ext}}\rangle (\overline{t}),\end{eqnarray}$$
$$\begin{eqnarray}\langle {\it\psi}\rangle (t)=\int _{-\infty }^{t}\!\text{d}\overline{t}\,g(t;\overline{t})\langle \,\widetilde{f}^{\text{ext}}\rangle (\overline{t}),\end{eqnarray}$$
where again
![]() $g\doteq \langle \widetilde{g}\rangle$
. (Here I used the fact that
$g\doteq \langle \widetilde{g}\rangle$
. (Here I used the fact that
![]() $\widetilde{f}^{\text{ext}}$
and
$\widetilde{f}^{\text{ext}}$
and
![]() $\widetilde{{\it\omega}}$
are uncorrelated, which for Gaussian variables implies
statistical independence, in order to factor the average.)
$\widetilde{{\it\omega}}$
are uncorrelated, which for Gaussian variables implies
statistical independence, in order to factor the average.)
It is straightforward to find that
 $$\begin{eqnarray}\widetilde{g}(t;t^{\prime })=H(t-t^{\prime })\exp \left(-{\it\nu}(t-t^{\prime })-\text{i}\int _{t^{\prime }}^{t}\!\text{d}\overline{t}\,\widetilde{{\it\omega}}(\overline{t})\right).\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{g}(t;t^{\prime })=H(t-t^{\prime })\exp \left(-{\it\nu}(t-t^{\prime })-\text{i}\int _{t^{\prime }}^{t}\!\text{d}\overline{t}\,\widetilde{{\it\omega}}(\overline{t})\right).\end{eqnarray}$$
Because
![]() $\widetilde{{\it\omega}}$
is Gaussian, the cumulant expansion of the average of (2.30) truncates at second order:
$\widetilde{{\it\omega}}$
is Gaussian, the cumulant expansion of the average of (2.30) truncates at second order:
 $$\begin{eqnarray}\displaystyle g({\it\tau}) & = & \displaystyle H({\it\tau})\text{e}^{-\text{i}\overline{{\it\omega}}{\it\tau}-{\it\nu}{\it\tau}}\exp \left(-\frac{1}{2}\int _{0}^{{\it\tau}}\!\text{d}\overline{t}\int _{0}^{{\it\tau}}\!\text{d}\overline{t}^{\prime }W(\overline{t}-\overline{t}^{\prime })\right)\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g({\it\tau}) & = & \displaystyle H({\it\tau})\text{e}^{-\text{i}\overline{{\it\omega}}{\it\tau}-{\it\nu}{\it\tau}}\exp \left(-\frac{1}{2}\int _{0}^{{\it\tau}}\!\text{d}\overline{t}\int _{0}^{{\it\tau}}\!\text{d}\overline{t}^{\prime }W(\overline{t}-\overline{t}^{\prime })\right)\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & = & \displaystyle H({\it\tau})\text{e}^{-\text{i}\overline{{\it\omega}}{\it\tau}-{\it\nu}{\it\tau}}\left\{\begin{array}{@{}ll@{}}\text{e}^{-k^{2}D{\it\tau}}\quad & \text{if}~{\it\tau}_{\text{ac}}^{(W)}\rightarrow 0,\\ \text{e}^{-{\it\beta}^{2}{\it\tau}^{2}/2}\quad & \text{if}~{\it\tau}_{\text{ac}}^{(W)}\rightarrow \infty .\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle H({\it\tau})\text{e}^{-\text{i}\overline{{\it\omega}}{\it\tau}-{\it\nu}{\it\tau}}\left\{\begin{array}{@{}ll@{}}\text{e}^{-k^{2}D{\it\tau}}\quad & \text{if}~{\it\tau}_{\text{ac}}^{(W)}\rightarrow 0,\\ \text{e}^{-{\it\beta}^{2}{\it\tau}^{2}/2}\quad & \text{if}~{\it\tau}_{\text{ac}}^{(W)}\rightarrow \infty .\end{array}\right.\end{eqnarray}$$
Another perspective is obtained by looking in frequency space. The Fourier transform of (2.31b ) is
 $$\begin{eqnarray}\widehat{g}({\it\omega})=\left\{\begin{array}{@{}ll@{}}\displaystyle \frac{1}{-\text{i}[{\it\omega}-\overline{{\it\omega}}+\text{i}({\it\nu}+k^{2}D)]}\quad & \text{if}~{\it\tau}_{\text{ac}}^{(W)}\rightarrow 0,\\ \displaystyle \sqrt{\frac{{\rm\pi}}{2}}\frac{1}{{\it\beta}}w[({\it\omega}-\overline{{\it\omega}}+\text{i}{\it\nu})/(\sqrt{2}{\it\beta})]\quad & \text{if}~{\it\tau}_{\text{ac}}^{(W)}\rightarrow \infty ,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\widehat{g}({\it\omega})=\left\{\begin{array}{@{}ll@{}}\displaystyle \frac{1}{-\text{i}[{\it\omega}-\overline{{\it\omega}}+\text{i}({\it\nu}+k^{2}D)]}\quad & \text{if}~{\it\tau}_{\text{ac}}^{(W)}\rightarrow 0,\\ \displaystyle \sqrt{\frac{{\rm\pi}}{2}}\frac{1}{{\it\beta}}w[({\it\omega}-\overline{{\it\omega}}+\text{i}{\it\nu})/(\sqrt{2}{\it\beta})]\quad & \text{if}~{\it\tau}_{\text{ac}}^{(W)}\rightarrow \infty ,\end{array}\right.\end{eqnarray}$$
whereFootnote 36
 $$\begin{eqnarray}w(z)\doteq \text{e}^{-z^{2}}\text{erfc}(-\text{i}z)=\text{e}^{-z^{2}}\left(1+\frac{2\text{i}}{\sqrt{{\rm\pi}}}\int _{0}^{z}\!\text{d}t\,\text{e}^{t^{2}}\right).\end{eqnarray}$$
$$\begin{eqnarray}w(z)\doteq \text{e}^{-z^{2}}\text{erfc}(-\text{i}z)=\text{e}^{-z^{2}}\left(1+\frac{2\text{i}}{\sqrt{{\rm\pi}}}\int _{0}^{z}\!\text{d}t\,\text{e}^{t^{2}}\right).\end{eqnarray}$$
The small-
![]() ${\it\tau}_{\text{ac}}^{(W)}$
result demonstrates that the effect of the random Doppler shifts
is to enhance the dissipative broadening of the Lorentzian-shaped resonance:
${\it\tau}_{\text{ac}}^{(W)}$
result demonstrates that the effect of the random Doppler shifts
is to enhance the dissipative broadening of the Lorentzian-shaped resonance:
 $$\begin{eqnarray}\text{Re}\,\widehat{g}({\it\omega})=\frac{{\it\nu}+k^{2}D}{({\it\omega}-\overline{{\it\omega}})^{2}+({\it\nu}+k^{2}D)^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}\text{Re}\,\widehat{g}({\it\omega})=\frac{{\it\nu}+k^{2}D}{({\it\omega}-\overline{{\it\omega}})^{2}+({\it\nu}+k^{2}D)^{2}}.\end{eqnarray}$$
Whereas for
![]() ${\it\nu}\rightarrow 0$
and
${\it\nu}\rightarrow 0$
and
![]() $D\rightarrow 0$
one would have
$D\rightarrow 0$
one would have
 $\text{Re}\,\widehat{g}({\it\omega})\approx {\rm\pi}{\it\delta}({\it\omega}-\overline{{\it\omega}})$
, the random Doppler shifts provide additional line broadening,
distributing power to all frequencies
$\text{Re}\,\widehat{g}({\it\omega})\approx {\rm\pi}{\it\delta}({\it\omega}-\overline{{\it\omega}})$
, the random Doppler shifts provide additional line broadening,
distributing power to all frequencies
 $0\leqslant |{\it\omega}-\overline{{\it\omega}}|\lesssim {\it\nu}+k^{2}D$
. In Vlasov theory, this amounts to a broadening of the Landau
wave–particle resonance, which is the effect discussed in the original paper of
Dupree (Reference Dupree1966). This justifies the
nomenclature ‘resonance-broadening theory’ for Dupree’s early line of attack
(which with regard to the nonlinearity was a theory of passive advection, though
that was not clarified by DupreeFootnote
37
). For infinite
$0\leqslant |{\it\omega}-\overline{{\it\omega}}|\lesssim {\it\nu}+k^{2}D$
. In Vlasov theory, this amounts to a broadening of the Landau
wave–particle resonance, which is the effect discussed in the original paper of
Dupree (Reference Dupree1966). This justifies the
nomenclature ‘resonance-broadening theory’ for Dupree’s early line of attack
(which with regard to the nonlinearity was a theory of passive advection, though
that was not clarified by DupreeFootnote
37
). For infinite
![]() ${\it\tau}_{\text{ac}}$
the resonance is not Lorentzian, but it maintains the same
general features. The function
${\it\tau}_{\text{ac}}$
the resonance is not Lorentzian, but it maintains the same
general features. The function
![]() $w(z)$
is graphed in figure 1.
Also plotted there is the equivalent single-pole approximation or Lorentzian shape
for which the functions agree at
$w(z)$
is graphed in figure 1.
Also plotted there is the equivalent single-pole approximation or Lorentzian shape
for which the functions agree at
![]() $z=0$
. An interpretation of this choice is given in footnote 40 on
page 19.
$z=0$
. An interpretation of this choice is given in footnote 40 on
page 19.

Figure 1. The function
![]() $w(z)$
(2.33)
and the equivalent single-pole approximation.
$w(z)$
(2.33)
and the equivalent single-pole approximation.
Now let us turn to the fluctuation spectrum; for simplicity, I now consider
 $\langle \,f^{\text{ext}}\rangle =0$
. From (2.28),
the two-time correlation function then follows as
$\langle \,f^{\text{ext}}\rangle =0$
. From (2.28),
the two-time correlation function then follows as
 $$\begin{eqnarray}\displaystyle C(t,t^{\prime }) & = & \displaystyle \int _{-\infty }^{t}\!\text{d}\overline{t}\int _{-\infty }^{t^{\prime }}\!\text{d}\overline{t}^{\prime }\,\langle \widetilde{g}(t;\overline{t})F^{\text{ext}}(\overline{t};\overline{t}^{\prime })\widetilde{g}^{\ast }(t^{\prime };\overline{t}^{\prime })\rangle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle C(t,t^{\prime }) & = & \displaystyle \int _{-\infty }^{t}\!\text{d}\overline{t}\int _{-\infty }^{t^{\prime }}\!\text{d}\overline{t}^{\prime }\,\langle \widetilde{g}(t;\overline{t})F^{\text{ext}}(\overline{t};\overline{t}^{\prime })\widetilde{g}^{\ast }(t^{\prime };\overline{t}^{\prime })\rangle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & = & \displaystyle 2{\it\varepsilon}\int _{-\infty }^{\text{min}(t,t^{\prime })}\!\text{d}\overline{t}\,\langle \widetilde{g}(t;\overline{t})\widetilde{g}^{\ast }(t^{\prime };\overline{t})\rangle .\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle 2{\it\varepsilon}\int _{-\infty }^{\text{min}(t,t^{\prime })}\!\text{d}\overline{t}\,\langle \widetilde{g}(t;\overline{t})\widetilde{g}^{\ast }(t^{\prime };\overline{t})\rangle .\end{eqnarray}$$
Upon recalling (2.30), one can easily work out (2.35b ):Footnote 38
 $$\begin{eqnarray}\displaystyle & \displaystyle C({\it\tau})=\left(\frac{{\it\varepsilon}}{{\it\nu}}\right)\text{e}^{-\text{i}\overline{{\it\omega}}{\it\tau}-{\it\nu}|{\it\tau}|}\left\{\begin{array}{@{}ll@{}}\text{e}^{-k^{2}D|{\it\tau}|}\quad & \text{if}~{\it\tau}_{\text{ac}}^{(W)}\rightarrow 0,\\ \text{e}^{-{\it\beta}^{2}{\it\tau}^{2}/2}\quad & \text{if}~{\it\tau}_{\text{ac}}^{(W)}\rightarrow \infty ,\end{array}\right. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle C({\it\tau})=\left(\frac{{\it\varepsilon}}{{\it\nu}}\right)\text{e}^{-\text{i}\overline{{\it\omega}}{\it\tau}-{\it\nu}|{\it\tau}|}\left\{\begin{array}{@{}ll@{}}\text{e}^{-k^{2}D|{\it\tau}|}\quad & \text{if}~{\it\tau}_{\text{ac}}^{(W)}\rightarrow 0,\\ \text{e}^{-{\it\beta}^{2}{\it\tau}^{2}/2}\quad & \text{if}~{\it\tau}_{\text{ac}}^{(W)}\rightarrow \infty ,\end{array}\right. & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \widehat{C}({\it\omega})=2\left(\frac{{\it\varepsilon}}{{\it\nu}}\right)\,\text{Re}\,\widehat{g}({\it\omega})\quad (\text{for arbitrary }{\it\tau}_{\text{ac}}^{(W)}) & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \widehat{C}({\it\omega})=2\left(\frac{{\it\varepsilon}}{{\it\nu}}\right)\,\text{Re}\,\widehat{g}({\it\omega})\quad (\text{for arbitrary }{\it\tau}_{\text{ac}}^{(W)}) & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}C(0)=\int _{-\infty }^{\infty }\!\frac{\text{d}{\it\omega}}{2{\rm\pi}}\,\widehat{C}({\it\omega})=\frac{{\it\varepsilon}}{{\it\nu}},\end{eqnarray}$$
$$\begin{eqnarray}C(0)=\int _{-\infty }^{\infty }\!\frac{\text{d}{\it\omega}}{2{\rm\pi}}\,\widehat{C}({\it\omega})=\frac{{\it\varepsilon}}{{\it\nu}},\end{eqnarray}$$
which has the same form as (2.12).
2.3.3. Autocorrelation time
By contemplating the inverse Fourier transform of (2.36b
), one learns that the detailed time dependence of the correlation function
depends on all of the Fourier components of
![]() $\widehat{g}({\it\omega})$
. As a special case, one can define an autocorrelation time
asFootnote
40
$\widehat{g}({\it\omega})$
. As a special case, one can define an autocorrelation time
asFootnote
40
 $$\begin{eqnarray}{\it\tau}_{\text{ac}}=[C(0)]^{-1}\int _{0}^{\infty }\!\text{d}{\it\tau}\,C({\it\tau})=\frac{1}{2}[C(0)]^{-1}\int _{-\infty }^{\infty }\!\text{d}{\it\tau}\,C({\it\tau})=\frac{1}{2}[C(0)]^{-1}\widehat{C}(0)=\text{Re}\,\widehat{g}(0).\end{eqnarray}$$
$$\begin{eqnarray}{\it\tau}_{\text{ac}}=[C(0)]^{-1}\int _{0}^{\infty }\!\text{d}{\it\tau}\,C({\it\tau})=\frac{1}{2}[C(0)]^{-1}\int _{-\infty }^{\infty }\!\text{d}{\it\tau}\,C({\it\tau})=\frac{1}{2}[C(0)]^{-1}\widehat{C}(0)=\text{Re}\,\widehat{g}(0).\end{eqnarray}$$
In general, this is built from the four frequencies or rates
![]() $\overline{{\it\omega}}$
,
$\overline{{\it\omega}}$
,
![]() ${\it\nu}$
,
${\it\nu}$
,
![]() ${\it\beta}$
, and
${\it\beta}$
, and
![]() $({\it\tau}_{\text{ac}}^{(W)})^{-1}$
. These four dimensional quantities determine three dimensionless
parameters. I have already introduced the Kubo number
$({\it\tau}_{\text{ac}}^{(W)})^{-1}$
. These four dimensional quantities determine three dimensionless
parameters. I have already introduced the Kubo number
 ${\mathcal{K}}\doteq {\it\beta}{\it\tau}_{\text{ac}}^{(W)}$
; a second important parameter is
${\mathcal{K}}\doteq {\it\beta}{\it\tau}_{\text{ac}}^{(W)}$
; a second important parameter is
 ${\mathcal{R}}\doteq {\it\beta}/{\it\nu}$
, which plays the role of a Reynolds number.Footnote
41
The third dimensionless ratio is
${\mathcal{R}}\doteq {\it\beta}/{\it\nu}$
, which plays the role of a Reynolds number.Footnote
41
The third dimensionless ratio is
![]() ${\it\nu}/\overline{{\it\omega}}$
. Various regimes of the
${\it\nu}/\overline{{\it\omega}}$
. Various regimes of the
![]() ${\mathcal{K}}{-}{\mathcal{R}}$
space for
${\mathcal{K}}{-}{\mathcal{R}}$
space for
![]() $\overline{{\it\omega}}=0$
were discussed by Krommes & Smith (Reference Krommes and Smith1987).
$\overline{{\it\omega}}=0$
were discussed by Krommes & Smith (Reference Krommes and Smith1987).
To further understand the significance of
![]() ${\it\tau}_{\text{ac}}$
or
${\it\tau}_{\text{ac}}$
or
![]() $\widehat{g}(0)$
, let us write in general
$\widehat{g}(0)$
, let us write in general
 $$\begin{eqnarray}\widehat{g}({\it\omega})=\frac{1}{-\text{i}[{\it\omega}-\overline{{\it\omega}}+\text{i}({\it\nu}+\widehat{{\it\Sigma}}_{{\it\omega}})]}\end{eqnarray}$$
$$\begin{eqnarray}\widehat{g}({\it\omega})=\frac{1}{-\text{i}[{\it\omega}-\overline{{\it\omega}}+\text{i}({\it\nu}+\widehat{{\it\Sigma}}_{{\it\omega}})]}\end{eqnarray}$$
for some
![]() $\widehat{{\it\Sigma}}_{{\it\omega}}$
(sometimes called the mass operatorFootnote
42
because of deep connections to quantum field theory (Martin, Siggia &
Rose Reference Martin, Siggia and Rose1973; Krommes Reference Krommes2002)). It is technically convenient to introduce
$\widehat{{\it\Sigma}}_{{\it\omega}}$
(sometimes called the mass operatorFootnote
42
because of deep connections to quantum field theory (Martin, Siggia &
Rose Reference Martin, Siggia and Rose1973; Krommes Reference Krommes2002)). It is technically convenient to introduce
![]() ${\it\Sigma}$
because
${\it\Sigma}$
because
![]() $g$
has a resonance form that is difficult to handle in approximate
theories; approximating the inverse of the propagator (i.e., changing the focus to
$g$
has a resonance form that is difficult to handle in approximate
theories; approximating the inverse of the propagator (i.e., changing the focus to
![]() ${\it\Sigma}$
) is much easier to do. Upon writing
${\it\Sigma}$
) is much easier to do. Upon writing
 $\widehat{{\it\Sigma}}=\widehat{{\it\Sigma}}^{\text{r}}+\text{i}\widehat{{\it\Sigma}}^{\text{i}}$
, then defining
$\widehat{{\it\Sigma}}=\widehat{{\it\Sigma}}^{\text{r}}+\text{i}\widehat{{\it\Sigma}}^{\text{i}}$
, then defining
 $\widehat{{\it\varpi}}_{{\it\omega}}\doteq \overline{{\it\omega}}+\widehat{{\it\Sigma}}_{{\it\omega}}^{\text{i}}$
and
$\widehat{{\it\varpi}}_{{\it\omega}}\doteq \overline{{\it\omega}}+\widehat{{\it\Sigma}}_{{\it\omega}}^{\text{i}}$
and
 $\widehat{{\it\eta}}_{{\it\omega}}\doteq {\it\nu}+\widehat{{\it\Sigma}}_{{\it\omega}}^{\text{r}}$
, one finds
$\widehat{{\it\eta}}_{{\it\omega}}\doteq {\it\nu}+\widehat{{\it\Sigma}}_{{\it\omega}}^{\text{r}}$
, one finds
 $$\begin{eqnarray}\text{Re}\,\widehat{g}({\it\omega})=\frac{\widehat{{\it\eta}}_{{\it\omega}}}{({\it\omega}-\widehat{{\it\varpi}}_{{\it\omega}})^{2}+\widehat{{\it\eta}}_{{\it\omega}}^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}\text{Re}\,\widehat{g}({\it\omega})=\frac{\widehat{{\it\eta}}_{{\it\omega}}}{({\it\omega}-\widehat{{\it\varpi}}_{{\it\omega}})^{2}+\widehat{{\it\eta}}_{{\it\omega}}^{2}}.\end{eqnarray}$$
We see that
![]() $\widehat{{\it\Sigma}}^{\text{r}}$
introduces additional resonance broadening,Footnote
43
whereas
$\widehat{{\it\Sigma}}^{\text{r}}$
introduces additional resonance broadening,Footnote
43
whereas
![]() $\widehat{{\it\Sigma}}^{\text{i}}$
provides a nonlinear frequency shift. If one defines
$\widehat{{\it\Sigma}}^{\text{i}}$
provides a nonlinear frequency shift. If one defines
![]() ${\it\varpi}\doteq \widehat{{\it\varpi}}_{0}$
and
${\it\varpi}\doteq \widehat{{\it\varpi}}_{0}$
and
![]() ${\it\eta}\doteq \widehat{{\it\eta}}_{0}$
, then one has
${\it\eta}\doteq \widehat{{\it\eta}}_{0}$
, then one has
 $$\begin{eqnarray}{\it\tau}_{\text{ac}}=\text{Re}\,\widehat{g}(0)=\frac{{\it\eta}}{{\it\varpi}^{2}+{\it\eta}^{2}}\approx \left\{\begin{array}{@{}ll@{}}({\it\eta}/{\it\varpi}){\it\varpi}^{-1}\quad & \text{if}~{\it\eta}/{\it\varpi}\ll 1,\\ {\it\eta}^{-1}\quad & \text{if}~{\it\eta}/{\it\varpi}\gg 1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\it\tau}_{\text{ac}}=\text{Re}\,\widehat{g}(0)=\frac{{\it\eta}}{{\it\varpi}^{2}+{\it\eta}^{2}}\approx \left\{\begin{array}{@{}ll@{}}({\it\eta}/{\it\varpi}){\it\varpi}^{-1}\quad & \text{if}~{\it\eta}/{\it\varpi}\ll 1,\\ {\it\eta}^{-1}\quad & \text{if}~{\it\eta}/{\it\varpi}\gg 1.\end{array}\right.\end{eqnarray}$$
Thus the size of
![]() ${\it\tau}_{\text{ac}}$
depends on whether the broadening is weak or strong. For weak
broadening, one has a weakly damped oscillator. For that limit, one has
${\it\tau}_{\text{ac}}$
depends on whether the broadening is weak or strong. For weak
broadening, one has a weakly damped oscillator. For that limit, one has
 ${\it\tau}_{\text{ac}}\approx ({\it\eta}/{\it\varpi}){\it\varpi}^{-1}\ll {\it\varpi}^{-1}$
. It may at first seem counterintuitive that
${\it\tau}_{\text{ac}}\approx ({\it\eta}/{\it\varpi}){\it\varpi}^{-1}\ll {\it\varpi}^{-1}$
. It may at first seem counterintuitive that
![]() ${\it\tau}_{\text{ac}}$
is smaller than the oscillator period, but that is easily
explained with the aid of figure 2; only a
small amount of decorrelation or dissipation occurs per cycle.
${\it\tau}_{\text{ac}}$
is smaller than the oscillator period, but that is easily
explained with the aid of figure 2; only a
small amount of decorrelation or dissipation occurs per cycle.

Figure 2. Example of a correlation function for weak broadening:
 $C({\it\tau})=\text{Re}\,\exp (-\text{i}{\it\varpi}{\it\tau}-{\it\eta}|{\it\tau}|)$
. The autocorrelation time is the area under the curve.
For a weakly damped oscillator, the positive and negative areas almost
cancel over one cycle. Reprinted from figure 13 of Krommes (Reference Krommes2002), copyright 2002, with
permission from Elsevier.
$C({\it\tau})=\text{Re}\,\exp (-\text{i}{\it\varpi}{\it\tau}-{\it\eta}|{\it\tau}|)$
. The autocorrelation time is the area under the curve.
For a weakly damped oscillator, the positive and negative areas almost
cancel over one cycle. Reprinted from figure 13 of Krommes (Reference Krommes2002), copyright 2002, with
permission from Elsevier.
Equation (2.41) makes sense only
if
![]() ${\it\eta}\geqslant 0$
. I shall demonstrate that at the end of the next section.
${\it\eta}\geqslant 0$
. I shall demonstrate that at the end of the next section.
2.3.4. Internal or incoherent noise
Note that (2.40) can be written as
 $$\begin{eqnarray}\text{Re}\,\widehat{g}({\it\omega})=|\widehat{g}({\it\omega})|^{2}({\it\nu}+\widehat{{\it\Sigma}}_{{\it\omega}}^{\text{r}}).\end{eqnarray}$$
$$\begin{eqnarray}\text{Re}\,\widehat{g}({\it\omega})=|\widehat{g}({\it\omega})|^{2}({\it\nu}+\widehat{{\it\Sigma}}_{{\it\omega}}^{\text{r}}).\end{eqnarray}$$
Substitution of (2.42) into (2.36b ) gives
 $$\begin{eqnarray}\widehat{C}({\it\omega})=\widehat{g}({\it\omega})\widehat{F}({\it\omega})\widehat{g}^{\ast }({\it\omega}),\end{eqnarray}$$
$$\begin{eqnarray}\widehat{C}({\it\omega})=\widehat{g}({\it\omega})\widehat{F}({\it\omega})\widehat{g}^{\ast }({\it\omega}),\end{eqnarray}$$
where
 $$\begin{eqnarray}\widehat{F}({\it\omega})\doteq 2{\it\varepsilon}[(\widehat{{\it\Sigma}}_{{\it\omega}}^{\text{r}}/{\it\nu})+1].\end{eqnarray}$$
$$\begin{eqnarray}\widehat{F}({\it\omega})\doteq 2{\it\varepsilon}[(\widehat{{\it\Sigma}}_{{\it\omega}}^{\text{r}}/{\it\nu})+1].\end{eqnarray}$$
Equation (2.43)
should be compared with (2.35a
), which involves
![]() $\widetilde{g}$
rather than
$\widetilde{g}$
rather than
![]() $g$
. In (2.44),
the 1 arises from the external forcing. For the purpose of calculating
second-order statistics, the interpretation of (2.43) and (2.44) is that instead of propagating
$g$
. In (2.44),
the 1 arises from the external forcing. For the purpose of calculating
second-order statistics, the interpretation of (2.43) and (2.44) is that instead of propagating
![]() ${\it\delta}f^{\text{ext}}$
with the random propagator
${\it\delta}f^{\text{ext}}$
with the random propagator
![]() $\widetilde{g}$
(2.28), then
averaging at the end, one is entitled to propagate noise with the
mean propagator
$\widetilde{g}$
(2.28), then
averaging at the end, one is entitled to propagate noise with the
mean propagator
![]() $g$
provided that one enhances the external noise with a certain
effective internal noise (called incoherent noise by Dupree
(Reference Dupree1972)). Thus one can write
$g$
provided that one enhances the external noise with a certain
effective internal noise (called incoherent noise by Dupree
(Reference Dupree1972)). Thus one can write
 $$\begin{eqnarray}\widehat{F}({\it\omega})=\widehat{F}^{\text{int}}({\it\omega})+\widehat{F}^{\text{ext}}({\it\omega}),\end{eqnarray}$$
$$\begin{eqnarray}\widehat{F}({\it\omega})=\widehat{F}^{\text{int}}({\it\omega})+\widehat{F}^{\text{ext}}({\it\omega}),\end{eqnarray}$$
where (for white-noise external forcing)
 $$\begin{eqnarray}\widehat{F}^{\text{int}}({\it\omega})=2{\it\varepsilon}(\widehat{{\it\Sigma}}_{{\it\omega}}^{\text{r}}/{\it\nu}),\quad \widehat{F}^{\text{ext}}({\it\omega})=2{\it\varepsilon}.\end{eqnarray}$$
$$\begin{eqnarray}\widehat{F}^{\text{int}}({\it\omega})=2{\it\varepsilon}(\widehat{{\it\Sigma}}_{{\it\omega}}^{\text{r}}/{\it\nu}),\quad \widehat{F}^{\text{ext}}({\it\omega})=2{\it\varepsilon}.\end{eqnarray}$$
The concept of internal noise is central to modern theories of statistical dynamics.
It is a consequence of Parseval’s theorem that
![]() $\widehat{C}({\it\omega})$
is real and non-negative. From (2.43),
$\widehat{C}({\it\omega})$
is real and non-negative. From (2.43),
![]() $\widehat{F}({\it\omega})$
inherits the same properties. From (2.44), this implies that
$\widehat{F}({\it\omega})$
inherits the same properties. From (2.44), this implies that
![]() $\widehat{{\it\eta}}_{{\it\omega}}\geqslant 0$
, which is an important constraint on the turbulent
broadening.
$\widehat{{\it\eta}}_{{\it\omega}}\geqslant 0$
, which is an important constraint on the turbulent
broadening.
2.3.5. Generalized Langevin equation
The representation (2.39) together with (2.45) and (2.46) lead one to the generalized Langevin equationFootnote 44
 $$\begin{eqnarray}(\partial _{t}+\text{i}\overline{{\it\omega}}+{\it\nu})\widetilde{{\it\psi}}(t)+\int _{-\infty }^{t}\!\text{d}\overline{t}\,{\it\Sigma}(t;\overline{t})\widetilde{{\it\psi}}(\overline{t})=\,\widetilde{f}^{\text{int}}(t)+\,\widetilde{f}^{\text{ext}}(t)\doteq \,\widetilde{f}^{\text{tot}}(t).\end{eqnarray}$$
$$\begin{eqnarray}(\partial _{t}+\text{i}\overline{{\it\omega}}+{\it\nu})\widetilde{{\it\psi}}(t)+\int _{-\infty }^{t}\!\text{d}\overline{t}\,{\it\Sigma}(t;\overline{t})\widetilde{{\it\psi}}(\overline{t})=\,\widetilde{f}^{\text{int}}(t)+\,\widetilde{f}^{\text{ext}}(t)\doteq \,\widetilde{f}^{\text{tot}}(t).\end{eqnarray}$$
Here
![]() ${\it\Sigma}({\it\tau})$
is the inverse Fourier transform of
${\it\Sigma}({\it\tau})$
is the inverse Fourier transform of
![]() $\widehat{{\it\Sigma}}({\it\omega})$
, and
$\widehat{{\it\Sigma}}({\it\omega})$
, and
![]() $\widetilde{f}^{\text{int}}$
is an auxiliary random variable (assumed to be statistically
independent of
$\widetilde{f}^{\text{int}}$
is an auxiliary random variable (assumed to be statistically
independent of
![]() $\widetilde{f}^{\text{ext}}$
) whose covariance is
$\widetilde{f}^{\text{ext}}$
) whose covariance is
 $$\begin{eqnarray}F^{\text{int}}({\it\tau})=2{\it\varepsilon}{\it\Sigma}^{\prime }({\it\tau})/{\it\nu},\end{eqnarray}$$
$$\begin{eqnarray}F^{\text{int}}({\it\tau})=2{\it\varepsilon}{\it\Sigma}^{\prime }({\it\tau})/{\it\nu},\end{eqnarray}$$
where
![]() ${\it\Sigma}^{\prime }({\it\tau})$
is the inverse Fourier transform of
${\it\Sigma}^{\prime }({\it\tau})$
is the inverse Fourier transform of
![]() $\widehat{{\it\Sigma}}_{{\it\omega}}^{\text{r}}$
. Generalized means that the equation is
nonlocal in time due to the time-history integral. Such generalized Langevin
representations arise frequently in modern turbulence theory.
$\widehat{{\it\Sigma}}_{{\it\omega}}^{\text{r}}$
. Generalized means that the equation is
nonlocal in time due to the time-history integral. Such generalized Langevin
representations arise frequently in modern turbulence theory.
The solution of (2.47) is
 $$\begin{eqnarray}\widetilde{{\it\psi}}(t)=\int _{-\infty }^{t}\!\text{d}\overline{t}\,g(t;\overline{t})\,\widetilde{f}^{\text{tot}}(\overline{t}),\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{{\it\psi}}(t)=\int _{-\infty }^{t}\!\text{d}\overline{t}\,g(t;\overline{t})\,\widetilde{f}^{\text{tot}}(\overline{t}),\end{eqnarray}$$
which should be compared with (2.28). It must be emphasized that (2.49) is not an exact solution for a
single realization since all realizations are coupled through
![]() ${\it\Sigma}$
, which determines both
${\it\Sigma}$
, which determines both
![]() $g$
and the covarianceFootnote
45
of
$g$
and the covarianceFootnote
45
of
![]() $\widetilde{f}^{\text{int}}$
. However, it is equivalent to that solution at the level of
second-order statistics. This remark holds as well for the original Langevin
equation (2.10).
$\widetilde{f}^{\text{int}}$
. However, it is equivalent to that solution at the level of
second-order statistics. This remark holds as well for the original Langevin
equation (2.10).
2.4. Statistical closure and the stochastic oscillator
It is instructive to try to recover the essence of these exact results from
statistical closure approximations because exact solutions are not available for
realistic, nonlinear PDEs. This topic has been treated extensively in the literature.
An important early paper (the first part of which is quite pedagogical) is by
Kraichnan (Reference Kraichnan1961), who considered aspects of
the infinite-
![]() ${\it\tau}_{\text{ac}}$
problem; further discussion and references are given by Krommes
(Reference Krommes, Galeev and Sudan1984) and, more thoroughly, by Krommes
(Reference Krommes2002). Here I shall just give a brief
introduction.
${\it\tau}_{\text{ac}}$
problem; further discussion and references are given by Krommes
(Reference Krommes, Galeev and Sudan1984) and, more thoroughly, by Krommes
(Reference Krommes2002). Here I shall just give a brief
introduction.
Consider the restricted problem of finding an approximation to the mean response
function
![]() $g({\it\tau})$
for (2.24). The
random response function
$g({\it\tau})$
for (2.24). The
random response function
![]() $\widetilde{g}(t;t^{\prime })$
obeys (2.27).
Instead of writing a formally exact solution (which would not be useful if the
primitive amplitude equation were really a PDE), let us write the evolution equation
for
$\widetilde{g}(t;t^{\prime })$
obeys (2.27).
Instead of writing a formally exact solution (which would not be useful if the
primitive amplitude equation were really a PDE), let us write the evolution equation
for
![]() $g$
by averaging (2.27). One gets
$g$
by averaging (2.27). One gets
 $$\begin{eqnarray}\partial _{t}g(t;t^{\prime })+(\text{i}\overline{{\it\omega}}+{\it\nu})g+\langle \text{i}{\it\delta}\widetilde{{\it\omega}}(t){\it\delta}\widetilde{g}(t;t^{\prime })\rangle ={\it\delta}(t-t^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t}g(t;t^{\prime })+(\text{i}\overline{{\it\omega}}+{\it\nu})g+\langle \text{i}{\it\delta}\widetilde{{\it\omega}}(t){\it\delta}\widetilde{g}(t;t^{\prime })\rangle ={\it\delta}(t-t^{\prime }).\end{eqnarray}$$
To be consistent with (2.47), I shall write this as
 $$\begin{eqnarray}\partial _{t}g(t;t^{\prime })+(\text{i}\overline{{\it\omega}}+{\it\nu})g+\int _{t^{\prime }}^{t}\!\text{d}\overline{t}\,{\it\Sigma}(t;\overline{t})g(\overline{t};t^{\prime })={\it\delta}(t-t^{\prime })\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t}g(t;t^{\prime })+(\text{i}\overline{{\it\omega}}+{\it\nu})g+\int _{t^{\prime }}^{t}\!\text{d}\overline{t}\,{\it\Sigma}(t;\overline{t})g(\overline{t};t^{\prime })={\it\delta}(t-t^{\prime })\end{eqnarray}$$
or
 $$\begin{eqnarray}\partial _{t}g({\it\tau})+(\text{i}\overline{{\it\omega}}+{\it\nu})g+\int _{0}^{{\it\tau}}\!\text{d}\overline{{\it\tau}}\,{\it\Sigma}(\overline{{\it\tau}})g({\it\tau}-\overline{{\it\tau}})={\it\delta}({\it\tau}).\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t}g({\it\tau})+(\text{i}\overline{{\it\omega}}+{\it\nu})g+\int _{0}^{{\it\tau}}\!\text{d}\overline{{\it\tau}}\,{\it\Sigma}(\overline{{\it\tau}})g({\it\tau}-\overline{{\it\tau}})={\it\delta}({\it\tau}).\end{eqnarray}$$
Either of these forms is called a Dyson equationFootnote 46 after the famous unification by Dyson (Reference Dyson1949) of various approaches to quantum electrodynamics.
The goal is to find an approximate formula for
![]() ${\it\Sigma}$
. One has exactly
${\it\Sigma}$
. One has exactly
 $$\begin{eqnarray}\partial _{t}{\it\delta}g(t;t^{\prime })+(\text{i}\overline{{\it\omega}}+{\it\nu}){\it\delta}g+\text{i}{\it\delta}{\it\omega}(t)g(t;t^{\prime })+\text{i}[{\it\delta}{\it\omega}(t){\it\delta}g(t;t^{\prime })-\langle {\it\delta}{\it\omega}\,{\it\delta}g\rangle ]=0.\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t}{\it\delta}g(t;t^{\prime })+(\text{i}\overline{{\it\omega}}+{\it\nu}){\it\delta}g+\text{i}{\it\delta}{\it\omega}(t)g(t;t^{\prime })+\text{i}[{\it\delta}{\it\omega}(t){\it\delta}g(t;t^{\prime })-\langle {\it\delta}{\it\omega}\,{\it\delta}g\rangle ]=0.\end{eqnarray}$$
To proceed, one must assess the importance of the (stochastically)
nonlinear term
![]() ${\it\delta}{\it\omega}\,{\it\delta}g$
, and that depends on the values of the dimensionless parameters.
For present purposes, if either
${\it\delta}{\it\omega}\,{\it\delta}g$
, and that depends on the values of the dimensionless parameters.
For present purposes, if either
![]() ${\mathcal{K}}$
or
${\mathcal{K}}$
or
![]() ${\mathcal{R}}$
is small, it is appropriate to drop the nonlinear term, in which
case the solution of (2.53) is
${\mathcal{R}}$
is small, it is appropriate to drop the nonlinear term, in which
case the solution of (2.53) is
 $$\begin{eqnarray}{\it\delta}g(t;t^{\prime })=-\int _{t^{\prime }}^{t}\!\text{d}\overline{t}\,g_{0}(t;\overline{t})\text{i}{\it\delta}{\it\omega}(\overline{t})g(\overline{t};t^{\prime }),\end{eqnarray}$$
$$\begin{eqnarray}{\it\delta}g(t;t^{\prime })=-\int _{t^{\prime }}^{t}\!\text{d}\overline{t}\,g_{0}(t;\overline{t})\text{i}{\it\delta}{\it\omega}(\overline{t})g(\overline{t};t^{\prime }),\end{eqnarray}$$
where
 $g_{0}({\it\tau})\doteq H({\it\tau})\exp (-\text{i}\overline{{\it\omega}}{\it\tau}-{\it\nu}{\it\tau})$
is the lowest-order Green’s function. Thus
$g_{0}({\it\tau})\doteq H({\it\tau})\exp (-\text{i}\overline{{\it\omega}}{\it\tau}-{\it\nu}{\it\tau})$
is the lowest-order Green’s function. Thus
 $$\begin{eqnarray}\langle \text{i}{\it\delta}{\it\omega}(t){\it\delta}g(t;t^{\prime })\rangle =\int _{t^{\prime }}^{t}\!\text{d}\overline{t}\,{\it\Sigma}(t;\overline{t})g(\overline{t};t^{\prime })=\int _{0}^{{\it\tau}}\!\text{d}\overline{{\it\tau}}\,{\it\Sigma}(\overline{{\it\tau}})g({\it\tau}-\overline{{\it\tau}}),\end{eqnarray}$$
$$\begin{eqnarray}\langle \text{i}{\it\delta}{\it\omega}(t){\it\delta}g(t;t^{\prime })\rangle =\int _{t^{\prime }}^{t}\!\text{d}\overline{t}\,{\it\Sigma}(t;\overline{t})g(\overline{t};t^{\prime })=\int _{0}^{{\it\tau}}\!\text{d}\overline{{\it\tau}}\,{\it\Sigma}(\overline{{\it\tau}})g({\it\tau}-\overline{{\it\tau}}),\end{eqnarray}$$
where
 $$\begin{eqnarray}{\it\Sigma}({\it\tau})\approx {\it\Sigma}_{0}({\it\tau})\doteq g_{0}({\it\tau})W({\it\tau}).\end{eqnarray}$$
$$\begin{eqnarray}{\it\Sigma}({\it\tau})\approx {\it\Sigma}_{0}({\it\tau})\doteq g_{0}({\it\tau})W({\it\tau}).\end{eqnarray}$$
This has the form of (2.52) with a particular approximation for
![]() ${\it\Sigma}$
. Since in the present case
${\it\Sigma}$
. Since in the present case
![]() ${\it\Sigma}$
has been constructed with the unperturbed propagator
${\it\Sigma}$
has been constructed with the unperturbed propagator
![]() $g_{0}$
but describes the nonlinearity, one may call this the quasi-linear
approximation.Footnote
47
$g_{0}$
but describes the nonlinearity, one may call this the quasi-linear
approximation.Footnote
47
(As a consistency check, for
![]() ${\mathcal{K}}\rightarrow 0$
one has
${\mathcal{K}}\rightarrow 0$
one has
 ${\it\Sigma}({\it\tau})\rightarrow g_{0}({\it\tau})2k^{2}D{\it\delta}({\it\tau})=k^{2}D{\it\delta}({\it\tau})$
, in agreement with (2.32).)
${\it\Sigma}({\it\tau})\rightarrow g_{0}({\it\tau})2k^{2}D{\it\delta}({\it\tau})=k^{2}D{\it\delta}({\it\tau})$
, in agreement with (2.32).)
For the quasi-linear approximation to be valid, the nonlinear term in the equation
for the fluctuations must be smaller than the linear term. For simplicity, assume
that
![]() $\overline{{\it\omega}}=0$
. Then the ratio of nonlinear to linear rates is
$\overline{{\it\omega}}=0$
. Then the ratio of nonlinear to linear rates is
 ${\it\beta}^{2}{\it\tau}_{\text{ac}}^{({\it\Sigma}_{0})}/{\it\nu}$
, which becomes large as
${\it\beta}^{2}{\it\tau}_{\text{ac}}^{({\it\Sigma}_{0})}/{\it\nu}$
, which becomes large as
 ${\it\nu}\rightarrow 0~({\mathcal{R}}\rightarrow \infty )$
. In this situation, quasi-linear theory is unjustifiable and
advanced techniques must be used to effect a proper closure. As discussed by
Kraichnan (Reference Kraichnan1961), a plausible approximation
is the DIA. For the oscillator model, that amounts to replacing the
${\it\nu}\rightarrow 0~({\mathcal{R}}\rightarrow \infty )$
. In this situation, quasi-linear theory is unjustifiable and
advanced techniques must be used to effect a proper closure. As discussed by
Kraichnan (Reference Kraichnan1961), a plausible approximation
is the DIA. For the oscillator model, that amounts to replacing the
![]() $g_{0}$
in (2.56) by the
as-yet-unknown
$g_{0}$
in (2.56) by the
as-yet-unknown
![]() $g$
:
$g$
:
 ${\it\Sigma}({\it\tau})\approx g({\it\tau})W({\it\tau})$
. The exact Dyson equation (2.52) is then used to solve for
${\it\Sigma}({\it\tau})\approx g({\it\tau})W({\it\tau})$
. The exact Dyson equation (2.52) is then used to solve for
![]() $g$
self-consistently.Footnote
48
For
$g$
self-consistently.Footnote
48
For
![]() ${\mathcal{K}}\rightarrow \infty$
one has
${\mathcal{K}}\rightarrow \infty$
one has
 ${\it\eta}={\it\beta}^{2}{\it\tau}_{\text{ac}}$
, and the balance
${\it\eta}={\it\beta}^{2}{\it\tau}_{\text{ac}}$
, and the balance
![]() $\partial _{{\it\tau}}\sim {\it\eta}$
self-consistently determines
$\partial _{{\it\tau}}\sim {\it\eta}$
self-consistently determines
![]() ${\it\tau}_{\text{ac}}$
to be
${\it\tau}_{\text{ac}}$
to be
![]() $O({\it\beta}^{-1})$
. This is consistent with the exact solution; see (2.36a
). Note that in this strong-turbulence limit the Markovian approximation
breaks down because
$O({\it\beta}^{-1})$
. This is consistent with the exact solution; see (2.36a
). Note that in this strong-turbulence limit the Markovian approximation
breaks down because
![]() ${\it\Sigma}({\it\tau})$
and
${\it\Sigma}({\it\tau})$
and
![]() $g({\it\tau})$
vary on the same time scale; the physics is intrinsically nonlocal
in time. I shall give a derivation of the DIA in § 4.1.
$g({\it\tau})$
vary on the same time scale; the physics is intrinsically nonlocal
in time. I shall give a derivation of the DIA in § 4.1.
2.5. Renormalization
The replacement of
![]() $g_{0}$
by
$g_{0}$
by
![]() $g$
is an example of renormalization. A thorough discussion of the
technical meaning of renormalization and of all of its ramifications is unfortunately
beyond the scope of this article. Heuristically, it implies the broadening of
resonance functions due to random nonlinear effects; in perturbation theory, that
broadening is represented as a sum of certain terms through all orders of the
nonlinear coupling. In general, the broadening must be determined self-consistently.
An elucidating collection of articles with historical perspectives was edited by
Brown (Reference Brown1993), a beginner’s guide to
methodology is by McComb (Reference McComb2004), and an
advanced book is by Zinn-Justin (Reference Zinn-Justin1996). Some
of the connections to quantum field theory are reviewed by Krommes (Reference Krommes2002). Renormalization has a deep connection to
so-called anomalous scaling, frequently discussed in the theory of phase transitions
(Goldenfeld Reference Goldenfeld1992). A brief discussion of
anomalous scaling that uses the stochastic oscillator as an example is given in
§ 6.1.2 of Krommes (Reference Krommes2002). The basic point is
that the naive quasi-linear result for
$g$
is an example of renormalization. A thorough discussion of the
technical meaning of renormalization and of all of its ramifications is unfortunately
beyond the scope of this article. Heuristically, it implies the broadening of
resonance functions due to random nonlinear effects; in perturbation theory, that
broadening is represented as a sum of certain terms through all orders of the
nonlinear coupling. In general, the broadening must be determined self-consistently.
An elucidating collection of articles with historical perspectives was edited by
Brown (Reference Brown1993), a beginner’s guide to
methodology is by McComb (Reference McComb2004), and an
advanced book is by Zinn-Justin (Reference Zinn-Justin1996). Some
of the connections to quantum field theory are reviewed by Krommes (Reference Krommes2002). Renormalization has a deep connection to
so-called anomalous scaling, frequently discussed in the theory of phase transitions
(Goldenfeld Reference Goldenfeld1992). A brief discussion of
anomalous scaling that uses the stochastic oscillator as an example is given in
§ 6.1.2 of Krommes (Reference Krommes2002). The basic point is
that the naive quasi-linear result for
![]() ${\it\Sigma}$
scales with
${\it\Sigma}$
scales with
![]() ${\it\beta}^{2}$
, but a self-consistent calculation of the nonlinear damping rate
for large
${\it\beta}^{2}$
, but a self-consistent calculation of the nonlinear damping rate
for large
![]() ${\mathcal{K}}$
and
${\mathcal{K}}$
and
![]() ${\mathcal{R}}$
leads to a scaling with
${\mathcal{R}}$
leads to a scaling with
![]() ${\it\beta}^{1}$
; here the power 1 is called an anomalous exponent. Introductory
pedagogical discussion of renormalization and anomalous scaling can also be found in
the article by Krommes (Reference Krommes2009), which provides
some useful background for the present tutorial.
${\it\beta}^{1}$
; here the power 1 is called an anomalous exponent. Introductory
pedagogical discussion of renormalization and anomalous scaling can also be found in
the article by Krommes (Reference Krommes2009), which provides
some useful background for the present tutorial.
3. Self-consistency, polarization, and dielectric shielding
Passive systems are (relatively) simple because the advecting velocity is not modified by the system response. When instead that velocity is self-consistently determined, additional effects come into play. In particular, once a fluctuation arises, it can polarize the medium (that back-reaction being a manifestation of self-consistency); the resulting polarization field shields the fluctuation and modifies its effect. This is dielectric response.
3.1. Prelude: dielectric polarization in electromagnetism
Ultimately I shall consider turbulent systems that are not necessarily electromagnetic in nature, such as the Navier–Stokes fluid. However, it is useful to begin on familiar footing by discussing electromagnetic systems, fully ionized plasmas being a prominent example.
3.1.1. Introductory concepts from electromagnetism
In electromagnetism, the dielectric function
![]() ${\mathcal{D}}$
is introduced as a way of describing the macroscopic
polarizability properties of a microscopically random medium. Specifically, in
elementary discussions the total charge density
${\mathcal{D}}$
is introduced as a way of describing the macroscopic
polarizability properties of a microscopically random medium. Specifically, in
elementary discussions the total charge density
![]() ${\it\rho}^{\text{tot}}$
is divided into free charge and bound charge, and Maxwell’s
equation
${\it\rho}^{\text{tot}}$
is divided into free charge and bound charge, and Maxwell’s
equation
 $$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{E}=4{\rm\pi}{\it\rho}^{\text{tot}}=4{\rm\pi}({\it\rho}^{\text{free}}+{\it\rho}^{\text{bound}})\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{E}=4{\rm\pi}{\it\rho}^{\text{tot}}=4{\rm\pi}({\it\rho}^{\text{free}}+{\it\rho}^{\text{bound}})\end{eqnarray}$$
is rewritten as
 $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{D}=4{\rm\pi}{\it\rho}^{\text{free}}$
, where the electrical displacement is
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{D}=4{\rm\pi}{\it\rho}^{\text{free}}$
, where the electrical displacement is
 $\boldsymbol{D}\doteq \boldsymbol{E}+4{\rm\pi}\boldsymbol{P}$
and the polarization vector
$\boldsymbol{D}\doteq \boldsymbol{E}+4{\rm\pi}\boldsymbol{P}$
and the polarization vector
![]() $\boldsymbol{P}$
obeys
$\boldsymbol{P}$
obeys
 $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{P}=-{\it\rho}^{\text{bound}}$
. If
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{P}=-{\it\rho}^{\text{bound}}$
. If
![]() $\boldsymbol{P}$
is assumed to be linear in the macroscopic field
$\boldsymbol{P}$
is assumed to be linear in the macroscopic field
![]() $\boldsymbol{E}$
, then one can introduce a susceptibility tensor
$\boldsymbol{E}$
, then one can introduce a susceptibility tensor
![]() $\unicode[STIX]{x1D653}$
by
$\unicode[STIX]{x1D653}$
by
 $\boldsymbol{P}=(4{\rm\pi})^{-1}\unicode[STIX]{x1D653}\boldsymbol{\cdot }\boldsymbol{E}$
and one has
$\boldsymbol{P}=(4{\rm\pi})^{-1}\unicode[STIX]{x1D653}\boldsymbol{\cdot }\boldsymbol{E}$
and one has
 $\boldsymbol{D}=\unicode[STIX]{x1D63F}\boldsymbol{\cdot }\boldsymbol{E}$
with
$\boldsymbol{D}=\unicode[STIX]{x1D63F}\boldsymbol{\cdot }\boldsymbol{E}$
with
 $\unicode[STIX]{x1D63F}\doteq \unicode[STIX]{x1D644}+\unicode[STIX]{x1D653}$
being the dielectric tensor. A standard generalization is to
introduce the wavenumber- and frequency-dependent dielectric tensor
$\unicode[STIX]{x1D63F}\doteq \unicode[STIX]{x1D644}+\unicode[STIX]{x1D653}$
being the dielectric tensor. A standard generalization is to
introduce the wavenumber- and frequency-dependent dielectric tensor
![]() $\unicode[STIX]{x1D63F}(\boldsymbol{k},{\it\omega})$
, appropriate for a medium that is on the average invariant under
translations in space (statistically homogeneous) and time (statistically
stationary). For a homogeneous, isotropic, and stationary plasma in the
electrostatic approximation
$\unicode[STIX]{x1D63F}(\boldsymbol{k},{\it\omega})$
, appropriate for a medium that is on the average invariant under
translations in space (statistically homogeneous) and time (statistically
stationary). For a homogeneous, isotropic, and stationary plasma in the
electrostatic approximation
 $\boldsymbol{E}=-\boldsymbol{{\rm\nabla}}{\it\phi}$
, it is sufficient to work with the longitudinal dielectric
scalar
$\boldsymbol{E}=-\boldsymbol{{\rm\nabla}}{\it\phi}$
, it is sufficient to work with the longitudinal dielectric
scalar
 ${\mathcal{D}}(\boldsymbol{k},{\it\omega})\doteq \widehat{\boldsymbol{k}}\boldsymbol{\cdot }\unicode[STIX]{x1D63F}(\boldsymbol{k},{\it\omega})\boldsymbol{\cdot }\widehat{\boldsymbol{k}}$
, so
${\mathcal{D}}(\boldsymbol{k},{\it\omega})\doteq \widehat{\boldsymbol{k}}\boldsymbol{\cdot }\unicode[STIX]{x1D63F}(\boldsymbol{k},{\it\omega})\boldsymbol{\cdot }\widehat{\boldsymbol{k}}$
, so
 $\boldsymbol{D}(\boldsymbol{k},{\it\omega})={\mathcal{D}}(\boldsymbol{k},{\it\omega})\boldsymbol{E}(\boldsymbol{k},{\it\omega})$
. For simplicity, I shall consider only the longitudinal
dielectric function in this article.
$\boldsymbol{D}(\boldsymbol{k},{\it\omega})={\mathcal{D}}(\boldsymbol{k},{\it\omega})\boldsymbol{E}(\boldsymbol{k},{\it\omega})$
. For simplicity, I shall consider only the longitudinal
dielectric function in this article.
The quantity
 ${\mathcal{D}}^{-1}(\boldsymbol{k},{\it\omega})$
describes the first-order response to the addition of free
charge or external potential; it is a so-called linear response function. If a
turbulent plasma is perturbed by a potential of the form
${\mathcal{D}}^{-1}(\boldsymbol{k},{\it\omega})$
describes the first-order response to the addition of free
charge or external potential; it is a so-called linear response function. If a
turbulent plasma is perturbed by a potential of the form
 ${\it\phi}^{\text{ext}}(t)={\it\Delta}\text{e}^{{\it\epsilon}t}H(-t)$
(i.e., by adiabatically raising
${\it\phi}^{\text{ext}}(t)={\it\Delta}\text{e}^{{\it\epsilon}t}H(-t)$
(i.e., by adiabatically raising
![]() ${\it\phi}^{\text{ext}}$
from 0 at
${\it\phi}^{\text{ext}}$
from 0 at
![]() $t=-\infty$
to a value
$t=-\infty$
to a value
![]() ${\it\Delta}$
at
${\it\Delta}$
at
![]() $t=0_{-}$
), it can be shown (Martin Reference Martin, deWitt and Balian1968) that the Fourier transform of the subsequent one-sided response
of the internal or induced potential,
$t=0_{-}$
), it can be shown (Martin Reference Martin, deWitt and Balian1968) that the Fourier transform of the subsequent one-sided response
of the internal or induced potential,
 ${\it\phi}_{+}^{\text{int}}(t)\doteq H(t){\it\phi}^{\text{int}}(t)$
, is
${\it\phi}_{+}^{\text{int}}(t)\doteq H(t){\it\phi}^{\text{int}}(t)$
, is
 $$\begin{eqnarray}\widehat{{\it\phi}}_{+}^{\text{int}}(\boldsymbol{k},{\it\omega})=\frac{{\it\Delta}}{\text{i}{\it\omega}{\mathcal{D}}(\boldsymbol{k},{\it\omega})}\left(\frac{{\it\chi}(\boldsymbol{k},{\it\omega})}{{\it\chi}(\boldsymbol{k},0)}-1\right).\end{eqnarray}$$
$$\begin{eqnarray}\widehat{{\it\phi}}_{+}^{\text{int}}(\boldsymbol{k},{\it\omega})=\frac{{\it\Delta}}{\text{i}{\it\omega}{\mathcal{D}}(\boldsymbol{k},{\it\omega})}\left(\frac{{\it\chi}(\boldsymbol{k},{\it\omega})}{{\it\chi}(\boldsymbol{k},0)}-1\right).\end{eqnarray}$$
Note that this expression has no pole at
![]() ${\it\omega}=0$
. If
${\it\omega}=0$
. If
![]() ${\mathcal{D}}$
were to vanish at a real frequency
${\mathcal{D}}$
were to vanish at a real frequency
![]() ${\it\omega}={\it\Omega}_{\boldsymbol{k}}$
, the system would oscillate even in the absence of external
forcing; this is called a normal mode. That does not usually happen for real
${\it\omega}={\it\Omega}_{\boldsymbol{k}}$
, the system would oscillate even in the absence of external
forcing; this is called a normal mode. That does not usually happen for real
![]() ${\it\omega}$
; however, the analytical continuation of
${\it\omega}$
; however, the analytical continuation of
![]() ${\mathcal{D}}(\boldsymbol{k},{\it\omega})$
into the complex
${\mathcal{D}}(\boldsymbol{k},{\it\omega})$
into the complex
![]() ${\it\omega}$
plane can possess a complex zero
${\it\omega}$
plane can possess a complex zero
 ${\it\omega}_{\boldsymbol{k}}={\it\Omega}_{\boldsymbol{k}}+\text{i}{\it\gamma}_{\boldsymbol{k}}$
. One continues to speak of a normal mode provided that
${\it\omega}_{\boldsymbol{k}}={\it\Omega}_{\boldsymbol{k}}+\text{i}{\it\gamma}_{\boldsymbol{k}}$
. One continues to speak of a normal mode provided that
 $|{\it\gamma}_{\boldsymbol{k}}/{\it\Omega}_{\boldsymbol{k}}|\ll 1$
(i.e., that the oscillation is underdamped). For the sign of
$|{\it\gamma}_{\boldsymbol{k}}/{\it\Omega}_{\boldsymbol{k}}|\ll 1$
(i.e., that the oscillation is underdamped). For the sign of
![]() ${\it\gamma}_{\boldsymbol{k}}$
, see the discussion at the end of this section.
${\it\gamma}_{\boldsymbol{k}}$
, see the discussion at the end of this section.
It is important to understand that all of
![]() $\boldsymbol{E}$
,
$\boldsymbol{E}$
,
![]() $\boldsymbol{D}$
,
$\boldsymbol{D}$
,
![]() $\boldsymbol{P}$
, and
$\boldsymbol{P}$
, and
![]() ${\it\rho}$
are statistical averages over the random microscopic
configuration; for example,
${\it\rho}$
are statistical averages over the random microscopic
configuration; for example,
![]() ${\it\rho}\doteq \langle \widetilde{{\it\rho}}\rangle$
, where
${\it\rho}\doteq \langle \widetilde{{\it\rho}}\rangle$
, where
 $\widetilde{{\it\rho}}(\boldsymbol{x},t)\doteq \sum _{\overline{s}}(\overline{n}q)_{\overline{s}}\int \!\text{d}\overline{\boldsymbol{v}}\,\widetilde{N}_{\overline{s}}(\boldsymbol{x},\overline{\boldsymbol{v}},t)$
is the microscopic charge density. Thus
$\widetilde{{\it\rho}}(\boldsymbol{x},t)\doteq \sum _{\overline{s}}(\overline{n}q)_{\overline{s}}\int \!\text{d}\overline{\boldsymbol{v}}\,\widetilde{N}_{\overline{s}}(\boldsymbol{x},\overline{\boldsymbol{v}},t)$
is the microscopic charge density. Thus
![]() ${\mathcal{D}}$
describes the mean response of a random system of charged
particles to infinitesimal perturbations. But although
${\mathcal{D}}$
describes the mean response of a random system of charged
particles to infinitesimal perturbations. But although
![]() ${\mathcal{D}}^{-1}$
is a linear response functionFootnote
49
(see figure 3), the nature of that
response inherits properties of the fluctuations in the unperturbed system;
${\mathcal{D}}^{-1}$
is a linear response functionFootnote
49
(see figure 3), the nature of that
response inherits properties of the fluctuations in the unperturbed system;
![]() ${\mathcal{D}}$
is a nonlinearFootnote
50
functional of those fluctuations through all orders. In thermal
equilibrium one has the famous fluctuation–dissipation theorem,Footnote
51
which relates the two-time correlation function
${\mathcal{D}}$
is a nonlinearFootnote
50
functional of those fluctuations through all orders. In thermal
equilibrium one has the famous fluctuation–dissipation theorem,Footnote
51
which relates the two-time correlation function
![]() $C$
to
$C$
to
![]() ${\mathcal{D}}^{-1}$
. For non-equilibrium turbulence, we shall see that generalized
fluctuation–dissipation relations can be written. Indeed, a spontaneous
fluctuation in the random medium effectively behaves as another internal source of
free charge that is then shielded by the dielectric properties of the medium, so
we shall find that
${\mathcal{D}}^{-1}$
. For non-equilibrium turbulence, we shall see that generalized
fluctuation–dissipation relations can be written. Indeed, a spontaneous
fluctuation in the random medium effectively behaves as another internal source of
free charge that is then shielded by the dielectric properties of the medium, so
we shall find that
![]() ${\mathcal{D}}$
figures importantly in the spectral balance equation that
describes the non-Gaussian final state achieved by the turbulent system.
${\mathcal{D}}$
figures importantly in the spectral balance equation that
describes the non-Gaussian final state achieved by the turbulent system.

Figure 3. Illustration of the linear response of a turbulent system. The top sketch
shows that the internal potential measured in the steady state is a
random function of time
![]() $\widetilde{{\it\phi}}^{\text{int}}(t)$
. In the middle sketch, the system is perturbed by an
external potential
$\widetilde{{\it\phi}}^{\text{int}}(t)$
. In the middle sketch, the system is perturbed by an
external potential
![]() ${\it\phi}^{\text{ext}}$
of size
${\it\phi}^{\text{ext}}$
of size
![]() ${\it\Delta}$
. Because of nonlinearity, the measured output (red
dotted curve) is a random signal containing terms of all orders in
${\it\Delta}$
. Because of nonlinearity, the measured output (red
dotted curve) is a random signal containing terms of all orders in
![]() ${\it\Delta}$
:
${\it\Delta}$
:
 $\widetilde{{\it\phi}}^{\text{int}}=\widetilde{{\it\phi}}+\sum _{n=1}^{\infty }O({\it\Delta}^{n})$
. The bottom plot shows the first-order part of the
perturbed output after ensemble averaging. If the turbulence level is
$\widetilde{{\it\phi}}^{\text{int}}=\widetilde{{\it\phi}}+\sum _{n=1}^{\infty }O({\it\Delta}^{n})$
. The bottom plot shows the first-order part of the
perturbed output after ensemble averaging. If the turbulence level is
![]() $C$
, nonlinear scrambling should make the mean perturbation
decay faster for larger
$C$
, nonlinear scrambling should make the mean perturbation
decay faster for larger
![]() $C$
, for example, like
$C$
, for example, like
 $\exp (-Ct)$
. Thus the mean linear response will depend on the
fluctuation level of the background turbulence through all orders in
$\exp (-Ct)$
. Thus the mean linear response will depend on the
fluctuation level of the background turbulence through all orders in
![]() $C$
. The inverse of the dielectric function,
$C$
. The inverse of the dielectric function,
![]() ${\mathcal{D}}^{-1}$
, is a first-order response function. Terms of
${\mathcal{D}}^{-1}$
, is a first-order response function. Terms of
![]() $O({\it\Delta}^{n})$
for
$O({\it\Delta}^{n})$
for
![]() $n>1$
define higher-order response functions, which are not
discussed in this article.
$n>1$
define higher-order response functions, which are not
discussed in this article.
When
![]() ${\mathcal{D}}$
is calculated in the linear approximation, one can often find
unstable eigenvalues with linear growth rate
${\mathcal{D}}$
is calculated in the linear approximation, one can often find
unstable eigenvalues with linear growth rate
![]() ${\it\gamma}_{\boldsymbol{k}}^{\text{lin}}>0$
. But in a turbulent steady state, which is assumed to be stable
against small perturbations, (3.2) guarantees that any complex zeros of
${\it\gamma}_{\boldsymbol{k}}^{\text{lin}}>0$
. But in a turbulent steady state, which is assumed to be stable
against small perturbations, (3.2) guarantees that any complex zeros of
![]() ${\mathcal{D}}(\boldsymbol{k},{\it\omega})$
lie in the lower (stable) half of the
${\mathcal{D}}(\boldsymbol{k},{\it\omega})$
lie in the lower (stable) half of the
![]() ${\it\omega}$
plane; i.e., the true ‘growth’ rate satisfies
${\it\omega}$
plane; i.e., the true ‘growth’ rate satisfies
![]() ${\it\gamma}_{\boldsymbol{k}}<0$
. Thus in steady-state (‘saturated’) turbulence, linear growth
must be overcompensated by nonlinear damping effects. Further discussion of this
point can be found in Krommes (Reference Krommes2007).
${\it\gamma}_{\boldsymbol{k}}<0$
. Thus in steady-state (‘saturated’) turbulence, linear growth
must be overcompensated by nonlinear damping effects. Further discussion of this
point can be found in Krommes (Reference Krommes2007).
3.1.2. Digression: gyrokinetics and dielectric response
Before delving into the difficult subject of dielectric response in the presence of nonlinearity and turbulence, I shall illustrate some basic concepts about polarization with the aid of the linear approximation to the gyrokinetic dielectric function.Footnote 52
Low-frequency gyrokinetics is an analytical reduction of the description of
magnetized plasma in which the rapid gyrospiralling of a particle around a
magnetic field line is eliminated in favour of particle drifts and effective
(gyroaveraged) potentials. It is appropriate for the treatment of fluctuations
whose frequencies are much smaller than the ion gyrofrequency:
 ${\it\omega}/{\it\omega}_{\text{c}i}\ll 1$
. A revolution in analytical formalism occurred with the
development of nonlinear gyrokinetics by Frieman & Chen (Reference Frieman and Chen1982), Lee (Reference Lee1983),
Dubin et al. (Reference Dubin, Krommes, Oberman and Lee1983), and
many subsequent researchers. Krommes (Reference Krommes2012b
) provides an introductory review and also cites previous reviews (e.g.,
Garbet et al.
Reference Garbet, Idomura, Villard and Watanabe2010) and fundamental papers, including
ones on linear gyrokinetics (e.g., Catto Reference Catto1978b
). The gyrokinetic formalism is now the major tool for both analytical
descriptions and numerical simulations of low-frequency fluctuations in turbulent
magnetized plasmas. The theory of gyrokinetic transport equations is discussed in
a comprehensive review of multiscale gyrokinetics by Abel et al.
(Reference Abel, Plunk, Wang, Barnes, Cowley, Dorland and Schekochihin2013).
${\it\omega}/{\it\omega}_{\text{c}i}\ll 1$
. A revolution in analytical formalism occurred with the
development of nonlinear gyrokinetics by Frieman & Chen (Reference Frieman and Chen1982), Lee (Reference Lee1983),
Dubin et al. (Reference Dubin, Krommes, Oberman and Lee1983), and
many subsequent researchers. Krommes (Reference Krommes2012b
) provides an introductory review and also cites previous reviews (e.g.,
Garbet et al.
Reference Garbet, Idomura, Villard and Watanabe2010) and fundamental papers, including
ones on linear gyrokinetics (e.g., Catto Reference Catto1978b
). The gyrokinetic formalism is now the major tool for both analytical
descriptions and numerical simulations of low-frequency fluctuations in turbulent
magnetized plasmas. The theory of gyrokinetic transport equations is discussed in
a comprehensive review of multiscale gyrokinetics by Abel et al.
(Reference Abel, Plunk, Wang, Barnes, Cowley, Dorland and Schekochihin2013).
The works of Lee (Reference Lee1983) and Dubin
et al. (Reference Dubin, Krommes, Oberman and Lee1983) showed
that gyrocentres can be treated in the same sense as the free charge introduced in
the theory of dielectric media (§ 3.1.1).
Gyrocentres can be said to move in an effective gyrokinetic vacuum (Krommes Reference Krommes1993, Reference Krommes2012b
) endowed with a large dielectric permittivityFootnote
53
![]() ${\mathcal{D}}_{\bot }$
that takes account of the polarization drift that particles
undergo when exposed to a slowly varying potential. Thus gyrocentres do
not move with the polarization drift; instead, polarization is
taken into account in the gyrokinetic Poisson equation. This interpretation is
satisfyingly intuitive, and it is given a rigorous justification by modern
mathematical methods (Brizard & Hahm Reference Brizard and Hahm2007).
${\mathcal{D}}_{\bot }$
that takes account of the polarization drift that particles
undergo when exposed to a slowly varying potential. Thus gyrocentres do
not move with the polarization drift; instead, polarization is
taken into account in the gyrokinetic Poisson equation. This interpretation is
satisfyingly intuitive, and it is given a rigorous justification by modern
mathematical methods (Brizard & Hahm Reference Brizard and Hahm2007).
Let us illustrate the procedure for obtaining a dielectric function by deriving
the simplest (linear) gyrokinetic
![]() ${\mathcal{D}}$
, then using that to recover the drift-wave dispersion relation.
(The symbols used in this discussion are defined in appendix A.) For uniform magnetic field, uniform background density,
and cold ions, the gyrokinetic equationreduces (Dubin et al.
Reference Dubin, Krommes, Oberman and Lee1983) to
${\mathcal{D}}$
, then using that to recover the drift-wave dispersion relation.
(The symbols used in this discussion are defined in appendix A.) For uniform magnetic field, uniform background density,
and cold ions, the gyrokinetic equationreduces (Dubin et al.
Reference Dubin, Krommes, Oberman and Lee1983) to
 $$\begin{eqnarray}\partial _{t}F+v_{\Vert }\boldsymbol{{\rm\nabla}}_{\Vert }F+\boldsymbol{V}_{E}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}F+E_{\Vert }\partial _{\Vert }F=0\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t}F+v_{\Vert }\boldsymbol{{\rm\nabla}}_{\Vert }F+\boldsymbol{V}_{E}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}F+E_{\Vert }\partial _{\Vert }F=0\end{eqnarray}$$
(describing the facts that gyrocentres are electrically
accelerated along the field lines and move across the field with the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
drift), and the gyrokinetic Poisson equation (in the
approximation of quasi-neutrality) becomes
$\boldsymbol{E}\times \boldsymbol{B}$
drift), and the gyrokinetic Poisson equation (in the
approximation of quasi-neutrality) becomes
 $$\begin{eqnarray}-\!{\mathcal{D}}_{\bot }{\rm\nabla}_{\bot }^{2}{\it\phi}=4{\rm\pi}{\it\rho}^{\text{G}}\quad \text{or}\quad -\!{\it\rho}_{\text{s}}^{2}{\rm\nabla}_{\bot }^{2}{\it\varphi}=n_{i}^{\text{G}}/\overline{n}_{i}-n_{e}^{\text{G}}/\overline{n}_{e},\end{eqnarray}$$
$$\begin{eqnarray}-\!{\mathcal{D}}_{\bot }{\rm\nabla}_{\bot }^{2}{\it\phi}=4{\rm\pi}{\it\rho}^{\text{G}}\quad \text{or}\quad -\!{\it\rho}_{\text{s}}^{2}{\rm\nabla}_{\bot }^{2}{\it\varphi}=n_{i}^{\text{G}}/\overline{n}_{i}-n_{e}^{\text{G}}/\overline{n}_{e},\end{eqnarray}$$
where
 ${\mathcal{D}}_{\bot }\doteq {\it\rho}_{\text{s}}^{2}/{\it\lambda}_{\text{D}e}^{2}$
and
${\mathcal{D}}_{\bot }\doteq {\it\rho}_{\text{s}}^{2}/{\it\lambda}_{\text{D}e}^{2}$
and
 $n_{s}^{\text{G}}\doteq \overline{n}_{s}\int \!\text{d}\boldsymbol{v}\,F_{s}$
. The right-hand side of this equation describes
gyrocentre (free) charge; the left-hand side is the negative of the polarization
charge
$n_{s}^{\text{G}}\doteq \overline{n}_{s}\int \!\text{d}\boldsymbol{v}\,F_{s}$
. The right-hand side of this equation describes
gyrocentre (free) charge; the left-hand side is the negative of the polarization
charge
![]() ${\it\rho}^{\text{pol}}$
, which plays the role of bound charge in the general theory.
This can be seen by considering the linearized continuity equation
${\it\rho}^{\text{pol}}$
, which plays the role of bound charge in the general theory.
This can be seen by considering the linearized continuity equation
 $\partial _{t}{\it\delta}n_{i}^{\text{pol}}+\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }({\it\delta}\boldsymbol{V}^{\text{pol}}n_{i})=0$
, where
$\partial _{t}{\it\delta}n_{i}^{\text{pol}}+\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }({\it\delta}\boldsymbol{V}^{\text{pol}}n_{i})=0$
, where
 $\boldsymbol{V}^{\text{pol}}\doteq {\it\omega}_{\text{c}i}^{-1}\partial _{t}(c\boldsymbol{E}_{\bot }/B)$
is the ion polarization drift. Upon integrating with respect to
time, one is led to the expressionFootnote
54
$\boldsymbol{V}^{\text{pol}}\doteq {\it\omega}_{\text{c}i}^{-1}\partial _{t}(c\boldsymbol{E}_{\bot }/B)$
is the ion polarization drift. Upon integrating with respect to
time, one is led to the expressionFootnote
54
 ${\it\delta}n_{i}^{\text{pol}}/n_{i}={\it\rho}_{\text{s}}^{2}{\rm\nabla}_{\bot }^{2}{\it\varphi}$
.
${\it\delta}n_{i}^{\text{pol}}/n_{i}={\it\rho}_{\text{s}}^{2}{\rm\nabla}_{\bot }^{2}{\it\varphi}$
.
Thus the coupled gyrokinetic–Poisson equations build in the particle polarization
that arises from slowly varying fields in the magnetized plasma. This new
dynamical system possesses interesting properties. It contains some, though not
all, of the normal modes of the full Vlasov–Poisson system. To learn about the
gyrokinetic normal modes, one can straightforwardly linearize (3.3) around a Maxwellian, add an
external potential
![]() ${\it\varphi}^{\text{ext}}$
(that must be done in both of the
${\it\varphi}^{\text{ext}}$
(that must be done in both of the
![]() $\boldsymbol{V}_{E}$
and
$\boldsymbol{V}_{E}$
and
![]() $E_{\Vert }$
terms), and find that the total potential (the induced or
polarization part proportional to
$E_{\Vert }$
terms), and find that the total potential (the induced or
polarization part proportional to
![]() ${\it\delta}F$
, plus
${\it\delta}F$
, plus
![]() ${\it\varphi}^{\text{ext}}$
) obeys
${\it\varphi}^{\text{ext}}$
) obeys
 $\widehat{{\it\varphi}}^{\text{tot}}(\boldsymbol{k},{\it\omega})=({\mathcal{D}}_{\text{G}}^{(0)})^{-1}(\boldsymbol{k},{\it\omega})\widehat{{\it\varphi}}^{\text{ext}}(\boldsymbol{k},{\it\omega})$
, where
$\widehat{{\it\varphi}}^{\text{tot}}(\boldsymbol{k},{\it\omega})=({\mathcal{D}}_{\text{G}}^{(0)})^{-1}(\boldsymbol{k},{\it\omega})\widehat{{\it\varphi}}^{\text{ext}}(\boldsymbol{k},{\it\omega})$
, where
 $$\begin{eqnarray}{\mathcal{D}}_{\text{G}}^{(0)}(\boldsymbol{k},{\it\omega})\doteq 1+\frac{1}{{\mathcal{D}}_{\bot }}\mathop{\sum }_{\overline{s}}\frac{k_{\text{D}\overline{s}}^{2}}{k_{\bot }^{2}}\int \!\text{d}\overline{\boldsymbol{v}}\,\left(\frac{{\it\omega}_{\ast \overline{s}}-k_{\Vert }\overline{v}_{\Vert }}{{\it\omega}-k_{\Vert }\overline{v}_{\Vert }+\text{i}{\it\epsilon}}\right)F_{\text{M}\overline{s}}(\overline{\boldsymbol{v}}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{D}}_{\text{G}}^{(0)}(\boldsymbol{k},{\it\omega})\doteq 1+\frac{1}{{\mathcal{D}}_{\bot }}\mathop{\sum }_{\overline{s}}\frac{k_{\text{D}\overline{s}}^{2}}{k_{\bot }^{2}}\int \!\text{d}\overline{\boldsymbol{v}}\,\left(\frac{{\it\omega}_{\ast \overline{s}}-k_{\Vert }\overline{v}_{\Vert }}{{\it\omega}-k_{\Vert }\overline{v}_{\Vert }+\text{i}{\it\epsilon}}\right)F_{\text{M}\overline{s}}(\overline{\boldsymbol{v}}).\end{eqnarray}$$
The
![]() $(0)$
superscript indicates that nonlinear corrections have been
ignored. This form closely parallels the one that follows from unmagnetized
linearized Vlasov theory, the crucial difference being the appearance of the large
$(0)$
superscript indicates that nonlinear corrections have been
ignored. This form closely parallels the one that follows from unmagnetized
linearized Vlasov theory, the crucial difference being the appearance of the large
![]() ${\mathcal{D}}_{\bot }$
– that being a consequence of ion polarization and a fundamental
property of the gyrokinetic vacuum. In the limit
${\mathcal{D}}_{\bot }$
– that being a consequence of ion polarization and a fundamental
property of the gyrokinetic vacuum. In the limit
 $k_{\Vert }v_{\text{t}i}\ll {\it\omega},\hspace{2.22198pt}{{\it\omega}_{\ast }}_{s}\ll k_{\Vert }v_{\text{t}e}$
,
$k_{\Vert }v_{\text{t}i}\ll {\it\omega},\hspace{2.22198pt}{{\it\omega}_{\ast }}_{s}\ll k_{\Vert }v_{\text{t}e}$
,
![]() ${\mathcal{D}}_{\text{G}}^{(0)}$
reduces to
${\mathcal{D}}_{\text{G}}^{(0)}$
reduces to
 $$\begin{eqnarray}\displaystyle {\mathcal{D}}_{\text{G}}^{(0)}(\boldsymbol{k},{\it\omega}) & {\approx} & \displaystyle 1+\frac{1}{{\mathcal{D}}_{\bot }}\left[\left(\frac{k_{\text{D}e}^{2}}{k_{\bot }^{2}}\right)+\left(\frac{k_{\text{D}i}^{2}}{k_{\bot }^{2}}\right)\left(\frac{{{\it\omega}_{\ast }}_{\text{i}}}{{\it\omega}}\right)\right]\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{D}}_{\text{G}}^{(0)}(\boldsymbol{k},{\it\omega}) & {\approx} & \displaystyle 1+\frac{1}{{\mathcal{D}}_{\bot }}\left[\left(\frac{k_{\text{D}e}^{2}}{k_{\bot }^{2}}\right)+\left(\frac{k_{\text{D}i}^{2}}{k_{\bot }^{2}}\right)\left(\frac{{{\it\omega}_{\ast }}_{\text{i}}}{{\it\omega}}\right)\right]\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & = & \displaystyle 1+\frac{1}{k_{\bot }^{2}{\it\rho}_{\text{s}}^{2}}-\frac{1}{k_{\bot }^{2}{\it\rho}_{\text{s}}^{2}}\left(\frac{{{\it\omega}_{\ast }}_{\text{e}}}{{\it\omega}}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle 1+\frac{1}{k_{\bot }^{2}{\it\rho}_{\text{s}}^{2}}-\frac{1}{k_{\bot }^{2}{\it\rho}_{\text{s}}^{2}}\left(\frac{{{\it\omega}_{\ast }}_{\text{e}}}{{\it\omega}}\right).\end{eqnarray}$$
 $$\begin{eqnarray}{\it\omega}_{\boldsymbol{k}}={\it\Omega}_{\boldsymbol{k}}\doteq \frac{{\it\omega}_{\ast \boldsymbol{k}}}{1+k_{\bot }^{2}{\it\rho}_{\text{s}}^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\omega}_{\boldsymbol{k}}={\it\Omega}_{\boldsymbol{k}}\doteq \frac{{\it\omega}_{\ast \boldsymbol{k}}}{1+k_{\bot }^{2}{\it\rho}_{\text{s}}^{2}}.\end{eqnarray}$$
The dispersive term in the denominator arises from ion polarization; it persists in the limit of cold ions, so it is not fundamentally due to a finite (nonzero) Larmor radius. The nonlinear description of this wave will be discussed in § 5.2.
More refined treatments predict the existence of various drift instabilities
driven by gradients in the background density or temperature profiles. Thus
fluctuations will grow and ultimately saturate due to nonlinear effects; in
general, steady-state turbulence results. That turbulence can respond
self-consistently to perturbations, so it behaves like a polarizable medium and
possesses a nonlinear dielectric response function
![]() ${\mathcal{D}}_{\text{G}}$
that generalizes
${\mathcal{D}}_{\text{G}}$
that generalizes
![]() ${\mathcal{D}}_{\text{G}}^{(0)}$
to the nonlinear regime. The spectral balance describes the
fluctuations that arise from a renormalized gyrocentre that moves in the turbulent
background and is shielded by nonlinear dielectric response. The nonlinear
dielectric response function
${\mathcal{D}}_{\text{G}}^{(0)}$
to the nonlinear regime. The spectral balance describes the
fluctuations that arise from a renormalized gyrocentre that moves in the turbulent
background and is shielded by nonlinear dielectric response. The nonlinear
dielectric response function
![]() ${\mathcal{D}}_{\text{G}}$
is the permittivity of the turbulent background state in the
same sense that
${\mathcal{D}}_{\text{G}}$
is the permittivity of the turbulent background state in the
same sense that
![]() ${\mathcal{D}}_{\bot }$
is the permittivity of the gyrokinetic vacuum. As a
generalization of the previous algorithm for the calculation of
${\mathcal{D}}_{\bot }$
is the permittivity of the gyrokinetic vacuum. As a
generalization of the previous algorithm for the calculation of
![]() ${\mathcal{D}}_{\text{G}}^{(0)}$
,
${\mathcal{D}}_{\text{G}}^{(0)}$
,
![]() ${\mathcal{D}}_{\text{G}}$
will be calculated from the relation between total averaged
potential and external potential. Indeed, the procedure is not restricted to
gyrokinetics. We shall see that turbulent systems quite generally possess a
dielectric function
${\mathcal{D}}_{\text{G}}$
will be calculated from the relation between total averaged
potential and external potential. Indeed, the procedure is not restricted to
gyrokinetics. We shall see that turbulent systems quite generally possess a
dielectric function
![]() ${\mathcal{D}}$
that describes turbulent polarization effects analogous to the
particle polarization discussed above. This is true even for non-electromagnetic
systems such as the Navier–Stokes fluid.
${\mathcal{D}}$
that describes turbulent polarization effects analogous to the
particle polarization discussed above. This is true even for non-electromagnetic
systems such as the Navier–Stokes fluid.
3.2. Self-consistency and the dielectric function of a turbulent plasma
I shall show in § 4.2 how dielectric response
can be defined for an arbitrary quadratically nonlinear PDE (2.5). However, for initial discussion it
is best to be more concrete, so I shall first discuss the Klimontovich equation
(2.1) as a particular, very
important example. Here
![]() $\widetilde{\boldsymbol{E}}$
is linearly related to
$\widetilde{\boldsymbol{E}}$
is linearly related to
![]() $\widetilde{N}$
through Poisson’s equation, so one has
$\widetilde{N}$
through Poisson’s equation, so one has
 $\widetilde{\boldsymbol{E}}=\pmb{\mathbb{E}}\widetilde{N}$
for a particular linear (vector) operator
$\widetilde{\boldsymbol{E}}=\pmb{\mathbb{E}}\widetilde{N}$
for a particular linear (vector) operator
![]() $\pmb{\mathbb{E}}$
. In general, it is necessary to introduce a dielectric tensor that
describes the response to external currents. However, it is simplest for pedagogical
purposes to consider the electrostatic limit
$\pmb{\mathbb{E}}$
. In general, it is necessary to introduce a dielectric tensor that
describes the response to external currents. However, it is simplest for pedagogical
purposes to consider the electrostatic limit
 $\boldsymbol{E}=-\boldsymbol{{\rm\nabla}}{\it\phi}$
, in which case one can work with a dielectric scalar that describes
the response to external charge or electrostatic potential. In electrostatics, the
Green’s function solution of Poisson’s equation leads toFootnote
55
$\boldsymbol{E}=-\boldsymbol{{\rm\nabla}}{\it\phi}$
, in which case one can work with a dielectric scalar that describes
the response to external charge or electrostatic potential. In electrostatics, the
Green’s function solution of Poisson’s equation leads toFootnote
55
 $$\begin{eqnarray}\pmb{\mathbb{E}}(1,\overline{1})\doteq -\boldsymbol{{\rm\nabla}}_{1}|\boldsymbol{x}_{1}-\boldsymbol{x}_{\overline{1}}|^{-1}4{\rm\pi}(\overline{n}q)_{s_{\overline{1}}}{\it\delta}(t_{1}-t_{\overline{1}}).\end{eqnarray}$$
$$\begin{eqnarray}\pmb{\mathbb{E}}(1,\overline{1})\doteq -\boldsymbol{{\rm\nabla}}_{1}|\boldsymbol{x}_{1}-\boldsymbol{x}_{\overline{1}}|^{-1}4{\rm\pi}(\overline{n}q)_{s_{\overline{1}}}{\it\delta}(t_{1}-t_{\overline{1}}).\end{eqnarray}$$
Thus the Klimontovich equation can be written as
 $$\begin{eqnarray}\partial _{t}\widetilde{N}_{s}(\boldsymbol{x},\boldsymbol{v},t)+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\widetilde{N}+(\pmb{\mathbb{E}}\widetilde{N})\boldsymbol{\cdot }\boldsymbol{\partial }\widetilde{N}=0.\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t}\widetilde{N}_{s}(\boldsymbol{x},\boldsymbol{v},t)+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\widetilde{N}+(\pmb{\mathbb{E}}\widetilde{N})\boldsymbol{\cdot }\boldsymbol{\partial }\widetilde{N}=0.\end{eqnarray}$$
This is a self-consistent (
![]() $\widetilde{\boldsymbol{E}}$
is determined by
$\widetilde{\boldsymbol{E}}$
is determined by
![]() $\widetilde{N}$
, not specified externally), multiplicatively stochastic PDE. It has
the form of (2.5) with coupling
coefficients
$\widetilde{N}$
, not specified externally), multiplicatively stochastic PDE. It has
the form of (2.5) with coupling
coefficients
 $$\begin{eqnarray}\displaystyle & U_{2}(1,2)\doteq -\boldsymbol{v}_{1}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{1}{\it\delta}(1-2), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & U_{2}(1,2)\doteq -\boldsymbol{v}_{1}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}_{1}{\it\delta}(1-2), & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & U_{3}(1,2,3)\doteq -\pmb{\mathbb{E}}(1,2)\boldsymbol{\cdot }\boldsymbol{\partial }_{1}{\it\delta}(1-3)+(2\leftrightarrow 3). & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & U_{3}(1,2,3)\doteq -\pmb{\mathbb{E}}(1,2)\boldsymbol{\cdot }\boldsymbol{\partial }_{1}{\it\delta}(1-3)+(2\leftrightarrow 3). & \displaystyle\end{eqnarray}$$
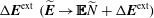 ${\rm\Delta}\boldsymbol{E}^{\text{ext}}~(\widetilde{\boldsymbol{E}}\rightarrow \pmb{\mathbb{E}}\widetilde{N}+{\rm\Delta}\boldsymbol{E}^{\text{ext}})$
and consider the equation for first-order response
${\rm\Delta}\boldsymbol{E}^{\text{ext}}~(\widetilde{\boldsymbol{E}}\rightarrow \pmb{\mathbb{E}}\widetilde{N}+{\rm\Delta}\boldsymbol{E}^{\text{ext}})$
and consider the equation for first-order response
 $$\begin{eqnarray}\partial _{t}{\rm\Delta}\widetilde{N}+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\rm\Delta}\widetilde{N}+\widetilde{\boldsymbol{E}}\boldsymbol{\cdot }\boldsymbol{\partial }{\rm\Delta}\widetilde{N}+\underline{(\pmb{\mathbb{E}}{\rm\Delta}\widetilde{N})}\boldsymbol{\cdot }\boldsymbol{\partial }\widetilde{N}=-\boldsymbol{\partial }\widetilde{N}\boldsymbol{\cdot }{\rm\Delta}\boldsymbol{E}^{\text{ext}}.\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t}{\rm\Delta}\widetilde{N}+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\rm\Delta}\widetilde{N}+\widetilde{\boldsymbol{E}}\boldsymbol{\cdot }\boldsymbol{\partial }{\rm\Delta}\widetilde{N}+\underline{(\pmb{\mathbb{E}}{\rm\Delta}\widetilde{N})}\boldsymbol{\cdot }\boldsymbol{\partial }\widetilde{N}=-\boldsymbol{\partial }\widetilde{N}\boldsymbol{\cdot }{\rm\Delta}\boldsymbol{E}^{\text{ext}}.\end{eqnarray}$$
The underlining here and subsequently identifies the self-consistent
response term that would be absent for passive advection. Note that, although
![]() ${\rm\Delta}\boldsymbol{E}^{\text{ext}}$
is not random,
${\rm\Delta}\boldsymbol{E}^{\text{ext}}$
is not random,
![]() ${\rm\Delta}\widetilde{N}$
is random because it evolves in the random background of
${\rm\Delta}\widetilde{N}$
is random because it evolves in the random background of
![]() $\widetilde{N}$
. That is, there are random coefficients
$\widetilde{N}$
. That is, there are random coefficients
![]() $\widetilde{\boldsymbol{E}}$
and
$\widetilde{\boldsymbol{E}}$
and
![]() $\widetilde{N}$
on the left-hand side of (3.11), and
$\widetilde{N}$
on the left-hand side of (3.11), and
![]() ${\rm\Delta}\boldsymbol{E}^{\text{ext}}$
couples to the random
${\rm\Delta}\boldsymbol{E}^{\text{ext}}$
couples to the random
![]() $\widetilde{N}$
on the right-hand side. Ultimately we must calculate the mean
response
$\widetilde{N}$
on the right-hand side. Ultimately we must calculate the mean
response
![]() $\langle {\rm\Delta}\widetilde{N}\rangle$
, which will involve us with a closure problem.
$\langle {\rm\Delta}\widetilde{N}\rangle$
, which will involve us with a closure problem.
The left-hand side of (3.11) is just
the linearization of the Klimontovich equation (2.1). It can be solved by introducing a random infinitesimal
response function
![]() $\widetilde{R}$
, which is just Green’s functionFootnote
56
for the left-hand side of (3.11). It obeys
$\widetilde{R}$
, which is just Green’s functionFootnote
56
for the left-hand side of (3.11). It obeys
 $$\begin{eqnarray}(\partial _{t}+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}+\widetilde{\boldsymbol{E}}\boldsymbol{\cdot }\boldsymbol{\partial }+\boldsymbol{\partial }\widetilde{N}\boldsymbol{\cdot }\underline{\pmb{\mathbb{E}}})\widetilde{R}_{ss^{\prime }}(\boldsymbol{x},\boldsymbol{v},t;\boldsymbol{x}^{\prime },\boldsymbol{v}^{\prime },t^{\prime })={\it\delta}_{ss^{\prime }}{\it\delta}(\boldsymbol{x}-\boldsymbol{x}^{\prime }){\it\delta}(\boldsymbol{v}-\boldsymbol{v}^{\prime }){\it\delta}(t-t^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}(\partial _{t}+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}+\widetilde{\boldsymbol{E}}\boldsymbol{\cdot }\boldsymbol{\partial }+\boldsymbol{\partial }\widetilde{N}\boldsymbol{\cdot }\underline{\pmb{\mathbb{E}}})\widetilde{R}_{ss^{\prime }}(\boldsymbol{x},\boldsymbol{v},t;\boldsymbol{x}^{\prime },\boldsymbol{v}^{\prime },t^{\prime })={\it\delta}_{ss^{\prime }}{\it\delta}(\boldsymbol{x}-\boldsymbol{x}^{\prime }){\it\delta}(\boldsymbol{v}-\boldsymbol{v}^{\prime }){\it\delta}(t-t^{\prime }).\end{eqnarray}$$
Thus, upon omitting all variables except the time for brevity, one finds
 $$\begin{eqnarray}{\rm\Delta}\widetilde{N}(t)=-\int _{-\infty }^{t}\!\text{d}\overline{t}\;\widetilde{R}(t;\overline{t})\boldsymbol{\partial }\widetilde{N}(\overline{t})\boldsymbol{\cdot }{\rm\Delta}\boldsymbol{E}^{\text{ext}}(\overline{t}).\end{eqnarray}$$
$$\begin{eqnarray}{\rm\Delta}\widetilde{N}(t)=-\int _{-\infty }^{t}\!\text{d}\overline{t}\;\widetilde{R}(t;\overline{t})\boldsymbol{\partial }\widetilde{N}(\overline{t})\boldsymbol{\cdot }{\rm\Delta}\boldsymbol{E}^{\text{ext}}(\overline{t}).\end{eqnarray}$$
This result is analogous to (2.28); the right-hand side of (3.11) can be recognized as a particular kind of forcing.
However, there are two crucial differences. First, the forcing is not purely external
because it involves the background quantity
![]() $\widetilde{N}$
; consequently, it is correlated to
$\widetilde{N}$
; consequently, it is correlated to
![]() $\widetilde{R}$
and the neat factorizations involved in (2.29) and (2.35a
) no longer hold. Second,
$\widetilde{R}$
and the neat factorizations involved in (2.29) and (2.35a
) no longer hold. Second,
![]() $\widetilde{R}$
is distinct from
$\widetilde{R}$
is distinct from
![]() $\widetilde{g}$
because of the presence of the
$\widetilde{g}$
because of the presence of the
![]() $\pmb{\mathbb{E}}$
term on the left-hand side of (3.12). That describes the self-consistent response to a small
perturbation; it is absent in a passive problem.
$\pmb{\mathbb{E}}$
term on the left-hand side of (3.12). That describes the self-consistent response to a small
perturbation; it is absent in a passive problem.
Given
![]() $\widetilde{R}$
, one can calculate the mean internally produced field by averaging
(3.13) and evaluating
$\widetilde{R}$
, one can calculate the mean internally produced field by averaging
(3.13) and evaluating
![]() $\pmb{\mathbb{E}}\langle {\rm\Delta}\widetilde{N}\rangle$
. One can then add
$\pmb{\mathbb{E}}\langle {\rm\Delta}\widetilde{N}\rangle$
. One can then add
![]() ${\rm\Delta}\boldsymbol{E}^{\text{ext}}$
to obtain the total mean field in the medium. Finally,
${\rm\Delta}\boldsymbol{E}^{\text{ext}}$
to obtain the total mean field in the medium. Finally,
![]() ${\mathcal{D}}$
is defined from the relation
${\mathcal{D}}$
is defined from the relation
 $$\begin{eqnarray}{\rm\Delta}\boldsymbol{E}^{\text{tot}}={\mathcal{D}}^{-1}{\rm\Delta}\boldsymbol{E}^{\text{ext}};\end{eqnarray}$$
$$\begin{eqnarray}{\rm\Delta}\boldsymbol{E}^{\text{tot}}={\mathcal{D}}^{-1}{\rm\Delta}\boldsymbol{E}^{\text{ext}};\end{eqnarray}$$
one findsFootnote 57
 $$\begin{eqnarray}{\mathcal{D}}^{-1}=1-\pmb{\mathbb{E}}\boldsymbol{\cdot }\langle \widetilde{R}\,\boldsymbol{\partial }\widetilde{N}\rangle .\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{D}}^{-1}=1-\pmb{\mathbb{E}}\boldsymbol{\cdot }\langle \widetilde{R}\,\boldsymbol{\partial }\widetilde{N}\rangle .\end{eqnarray}$$
(This symbolic notation is a bit tricky because
![]() ${\mathcal{D}}$
is a function of only spatial coordinates whereas
${\mathcal{D}}$
is a function of only spatial coordinates whereas
![]() $\pmb{\mathbb{E}}$
and
$\pmb{\mathbb{E}}$
and
![]() $\widetilde{R}$
operate in phase space.Footnote
58
) This is as far as one can go without facing up to statistical closure, i.e.,
an approximate calculation of
$\widetilde{R}$
operate in phase space.Footnote
58
) This is as far as one can go without facing up to statistical closure, i.e.,
an approximate calculation of
![]() $\langle \widetilde{R}\,\widetilde{N}\rangle$
.
$\langle \widetilde{R}\,\widetilde{N}\rangle$
.
One way of proceeding, ultimately not fruitful, is to first express
![]() $\widetilde{R}$
in terms of
$\widetilde{R}$
in terms of
![]() $\widetilde{g}$
, then attempt to average. The Klimontovich
$\widetilde{g}$
, then attempt to average. The Klimontovich
![]() $\widetilde{R}$
obeys (3.12) with
the last term on the left-hand side omitted. Thus (3.12) can be written schematically as
$\widetilde{R}$
obeys (3.12) with
the last term on the left-hand side omitted. Thus (3.12) can be written schematically as
 $$\begin{eqnarray}\widetilde{g}^{-1}\widetilde{R}+\boldsymbol{\partial }\widetilde{N}\boldsymbol{\cdot }\underline{\pmb{\mathbb{E}}\widetilde{R}}=1.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{g}^{-1}\widetilde{R}+\boldsymbol{\partial }\widetilde{N}\boldsymbol{\cdot }\underline{\pmb{\mathbb{E}}\widetilde{R}}=1.\end{eqnarray}$$
Given
![]() $\pmb{\mathbb{E}}\widetilde{R}$
, the formal solution of (3.16) is
$\pmb{\mathbb{E}}\widetilde{R}$
, the formal solution of (3.16) is
 $$\begin{eqnarray}\widetilde{R}=\widetilde{g}-\widetilde{g}\,\boldsymbol{\partial }\widetilde{N}\boldsymbol{\cdot }\underline{\pmb{\mathbb{E}}\widetilde{R}}.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{R}=\widetilde{g}-\widetilde{g}\,\boldsymbol{\partial }\widetilde{N}\boldsymbol{\cdot }\underline{\pmb{\mathbb{E}}\widetilde{R}}.\end{eqnarray}$$
An equation for
![]() $\pmb{\mathbb{E}}\widetilde{R}$
follows by applying
$\pmb{\mathbb{E}}\widetilde{R}$
follows by applying
![]() $\pmb{\mathbb{E}}$
to both sides of (3.17), then bringing the
$\pmb{\mathbb{E}}$
to both sides of (3.17), then bringing the
![]() $\pmb{\mathbb{E}}\widetilde{R}$
term on the right-hand side to the left:
$\pmb{\mathbb{E}}\widetilde{R}$
term on the right-hand side to the left:
 $$\begin{eqnarray}(\unicode[STIX]{x1D644}+\pmb{\mathbb{E}}\widetilde{g}\boldsymbol{\partial }\widetilde{N})\boldsymbol{\cdot }\pmb{\mathbb{E}}\widetilde{R}=\pmb{\mathbb{E}}\widetilde{g}.\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D644}+\pmb{\mathbb{E}}\widetilde{g}\boldsymbol{\partial }\widetilde{N})\boldsymbol{\cdot }\pmb{\mathbb{E}}\widetilde{R}=\pmb{\mathbb{E}}\widetilde{g}.\end{eqnarray}$$
In the electrostatic approximation, this can be solved to find
 $$\begin{eqnarray}\pmb{\mathbb{E}}\widetilde{R}=\widetilde{{\mathcal{D}}}^{-1}\pmb{\mathbb{E}}\widetilde{g},\end{eqnarray}$$
$$\begin{eqnarray}\pmb{\mathbb{E}}\widetilde{R}=\widetilde{{\mathcal{D}}}^{-1}\pmb{\mathbb{E}}\widetilde{g},\end{eqnarray}$$
where
 $$\begin{eqnarray}\widetilde{{\mathcal{D}}}\doteq 1+\underline{\pmb{\mathbb{E}}\boldsymbol{\cdot }\widetilde{g}\,\boldsymbol{\partial }\widetilde{N}}.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{{\mathcal{D}}}\doteq 1+\underline{\pmb{\mathbb{E}}\boldsymbol{\cdot }\widetilde{g}\,\boldsymbol{\partial }\widetilde{N}}.\end{eqnarray}$$
Thus
 $$\begin{eqnarray}\widetilde{R}=\widetilde{g}-\widetilde{g}\,\boldsymbol{\partial }\widetilde{N}\boldsymbol{\cdot }\underline{\widetilde{{\mathcal{D}}}^{-1}\pmb{\mathbb{E}}\widetilde{g}}.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{R}=\widetilde{g}-\widetilde{g}\,\boldsymbol{\partial }\widetilde{N}\boldsymbol{\cdot }\underline{\widetilde{{\mathcal{D}}}^{-1}\pmb{\mathbb{E}}\widetilde{g}}.\end{eqnarray}$$
The quantity
![]() $\widetilde{{\mathcal{D}}}$
is a kind of ‘random dielectric function’ (although that concept is
not defined), and the form (3.21)
emphasizes, through its second term, that self-consistency is crucial. However, how
to calculate the correlation between
$\widetilde{{\mathcal{D}}}$
is a kind of ‘random dielectric function’ (although that concept is
not defined), and the form (3.21)
emphasizes, through its second term, that self-consistency is crucial. However, how
to calculate the correlation between
![]() $\widetilde{R}$
and
$\widetilde{R}$
and
![]() $\widetilde{N}$
that is required for formula (3.15) is not apparent because of the wildly nonlinear way in
which random variables are mixed throughout the last term of (3.21). Thus a different approach must
be taken, as I now describe.
$\widetilde{N}$
that is required for formula (3.15) is not apparent because of the wildly nonlinear way in
which random variables are mixed throughout the last term of (3.21). Thus a different approach must
be taken, as I now describe.
Instead of following the route of first solving for
![]() ${\rm\Delta}\widetilde{N}$
, then averaging, in traditional closures one averages (3.11) directly. Upon recalling that
${\rm\Delta}\widetilde{N}$
, then averaging, in traditional closures one averages (3.11) directly. Upon recalling that
![]() $f=\langle \widetilde{N}\rangle$
, one finds
$f=\langle \widetilde{N}\rangle$
, one finds
 $$\begin{eqnarray}\partial _{t}{\rm\Delta}f+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\rm\Delta}f+\boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{\partial }{\rm\Delta}f+\underline{\underline{{\rm\Delta}\langle {\it\delta}\boldsymbol{E}\,{\it\delta}N\rangle }}=-\boldsymbol{\partial }f\boldsymbol{\cdot }{\rm\Delta}\boldsymbol{E}^{\text{ext}}.\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t}{\rm\Delta}f+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\rm\Delta}f+\boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{\partial }{\rm\Delta}f+\underline{\underline{{\rm\Delta}\langle {\it\delta}\boldsymbol{E}\,{\it\delta}N\rangle }}=-\boldsymbol{\partial }f\boldsymbol{\cdot }{\rm\Delta}\boldsymbol{E}^{\text{ext}}.\end{eqnarray}$$
The last term on the left-hand side must be evaluated by statistical
closure. (A doubly underlined term indicates that at least part of the term contains
self-consistent response that would be absent for passive advection.) The problem is
essentially the same one that arises in closing the equation for
![]() $R$
itself. The most general way of proceeding is to use the method of
sources introduced in the classical context by Martin et al. (Reference Martin, Siggia and Rose1973, henceforth MSR), motivated by prior
developments in quantum field theory. I shall not give a full description of the MSR
formalism here; see Krommes (Reference Krommes2002) for
extensive discussion. Briefly, the procedure is to enquire about the response to an
external, nonrandom source. By looking at infinitesimal variations of that source,
one can obtain functional relations between the various statistical observables that
can be usefully closed. For example, add an external sourceFootnote
59
$R$
itself. The most general way of proceeding is to use the method of
sources introduced in the classical context by Martin et al. (Reference Martin, Siggia and Rose1973, henceforth MSR), motivated by prior
developments in quantum field theory. I shall not give a full description of the MSR
formalism here; see Krommes (Reference Krommes2002) for
extensive discussion. Briefly, the procedure is to enquire about the response to an
external, nonrandom source. By looking at infinitesimal variations of that source,
one can obtain functional relations between the various statistical observables that
can be usefully closed. For example, add an external sourceFootnote
59
![]() $\widehat{{\it\eta}}$
to the right-hand side of the Klimontovich equation (3.9). The random response function
$\widehat{{\it\eta}}$
to the right-hand side of the Klimontovich equation (3.9). The random response function
![]() $\widetilde{R}$
is defined by the functional derivative (Beran Reference Beran1968)
$\widetilde{R}$
is defined by the functional derivative (Beran Reference Beran1968)
 $$\begin{eqnarray}\widetilde{R}(t;t^{\prime })=\left.\frac{{\it\delta}\textstyle \widetilde{N}(t)}{{\it\delta}\widehat{{\it\eta}}(t^{\prime })}\right|_{\widehat{{\it\eta}}=0},\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{R}(t;t^{\prime })=\left.\frac{{\it\delta}\textstyle \widetilde{N}(t)}{{\it\delta}\widehat{{\it\eta}}(t^{\prime })}\right|_{\widehat{{\it\eta}}=0},\end{eqnarray}$$
and the mean response is
 $$\begin{eqnarray}R(t;t^{\prime })=\langle \widetilde{R}(t;t^{\prime })\rangle =\left.\frac{{\it\delta}f(t)}{{\it\delta}\widehat{{\it\eta}}(t^{\prime })}\right|_{\widehat{{\it\eta}}=0}.\end{eqnarray}$$
$$\begin{eqnarray}R(t;t^{\prime })=\langle \widetilde{R}(t;t^{\prime })\rangle =\left.\frac{{\it\delta}f(t)}{{\it\delta}\widehat{{\it\eta}}(t^{\prime })}\right|_{\widehat{{\it\eta}}=0}.\end{eqnarray}$$
Thus one can obtain an equation for
![]() $R$
by functionally differentiating the mean equation,
$R$
by functionally differentiating the mean equation,
 $$\begin{eqnarray}\partial _{t}\,f+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}f+\boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{\partial }f+\boldsymbol{\partial }\boldsymbol{\cdot }\langle {\it\delta}\boldsymbol{E}\,{\it\delta}N\rangle =\widehat{{\it\eta}}(t),\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t}\,f+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}f+\boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{\partial }f+\boldsymbol{\partial }\boldsymbol{\cdot }\langle {\it\delta}\boldsymbol{E}\,{\it\delta}N\rangle =\widehat{{\it\eta}}(t),\end{eqnarray}$$
to find
 $$\begin{eqnarray}\partial _{t}R(t;t^{\prime })+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}R+\boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{\partial }R+\boldsymbol{\partial }f\boldsymbol{\cdot }\underline{\pmb{\mathbb{E}}R}+\underline{\underline{\left.\frac{{\it\delta}[\boldsymbol{\partial }\boldsymbol{\cdot }\langle {\it\delta}\boldsymbol{E}\,{\it\delta}N\rangle (t)]}{{\it\delta}\widehat{{\it\eta}}(t^{\prime })}\right|_{\widehat{{\it\eta}}=0}}}={\it\delta}(t-t^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t}R(t;t^{\prime })+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}R+\boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{\partial }R+\boldsymbol{\partial }f\boldsymbol{\cdot }\underline{\pmb{\mathbb{E}}R}+\underline{\underline{\left.\frac{{\it\delta}[\boldsymbol{\partial }\boldsymbol{\cdot }\langle {\it\delta}\boldsymbol{E}\,{\it\delta}N\rangle (t)]}{{\it\delta}\widehat{{\it\eta}}(t^{\prime })}\right|_{\widehat{{\it\eta}}=0}}}={\it\delta}(t-t^{\prime }).\end{eqnarray}$$
The key to usefully reducing the last term on the left-hand side is
to recognize that, as
![]() $\widehat{{\it\eta}}$
changes,
$\widehat{{\it\eta}}$
changes,
![]() $f[\widehat{{\it\eta}}]$
changes in concert. One can therefore use a functional chain rule:
$f[\widehat{{\it\eta}}]$
changes in concert. One can therefore use a functional chain rule:
 $$\begin{eqnarray}\frac{{\it\delta}}{{\it\delta}\widehat{{\it\eta}}(t^{\prime })}=\int \!\text{d}\overline{t}\,\frac{{\it\delta}f(\overline{t})}{{\it\delta}\widehat{{\it\eta}}(t^{\prime })}\frac{{\it\delta}}{{\it\delta}f(\overline{t})}=\int \!\text{d}\overline{t}\,R(\overline{t};t^{\prime })\frac{{\it\delta}}{{\it\delta}f(\overline{t})},\end{eqnarray}$$
$$\begin{eqnarray}\frac{{\it\delta}}{{\it\delta}\widehat{{\it\eta}}(t^{\prime })}=\int \!\text{d}\overline{t}\,\frac{{\it\delta}f(\overline{t})}{{\it\delta}\widehat{{\it\eta}}(t^{\prime })}\frac{{\it\delta}}{{\it\delta}f(\overline{t})}=\int \!\text{d}\overline{t}\,R(\overline{t};t^{\prime })\frac{{\it\delta}}{{\it\delta}f(\overline{t})},\end{eqnarray}$$
where (3.24) was
used in the last step. This formally closes the equation for
![]() $R$
in the form of a Dyson equation (Dyson Reference Dyson1949; Krommes Reference Krommes2002, Reference Krommes2009):
$R$
in the form of a Dyson equation (Dyson Reference Dyson1949; Krommes Reference Krommes2002, Reference Krommes2009):
 $$\begin{eqnarray}(\partial _{t}+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}+\boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{\partial }R+\boldsymbol{\partial }f\boldsymbol{\cdot }\underline{\pmb{\mathbb{E}}R}+\underline{\underline{{\it\Sigma}}})R(t;t^{\prime })={\it\delta}(t-t^{\prime }),\end{eqnarray}$$
$$\begin{eqnarray}(\partial _{t}+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}+\boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{\partial }R+\boldsymbol{\partial }f\boldsymbol{\cdot }\underline{\pmb{\mathbb{E}}R}+\underline{\underline{{\it\Sigma}}})R(t;t^{\prime })={\it\delta}(t-t^{\prime }),\end{eqnarray}$$
whereFootnote 60
 $$\begin{eqnarray}{\it\Sigma}(t;\overline{t})\doteq \frac{{\it\delta}[\boldsymbol{\partial }\boldsymbol{\cdot }\langle {\it\delta}\boldsymbol{E}\,{\it\delta}N\rangle (t)]}{{\it\delta}f(\overline{t})}\end{eqnarray}$$
$$\begin{eqnarray}{\it\Sigma}(t;\overline{t})\doteq \frac{{\it\delta}[\boldsymbol{\partial }\boldsymbol{\cdot }\langle {\it\delta}\boldsymbol{E}\,{\it\delta}N\rangle (t)]}{{\it\delta}f(\overline{t})}\end{eqnarray}$$
is still unknown at this point. It can be evaluated in various statistical closures such as the DIA; see § 4.
In a seminal paper, DuBois & Espedal (Reference DuBois and Espedal1978) showed that one further manipulation puts the
![]() $R$
equation into a very suggestive form that is an obvious
generalization of linear theory. Note that
$R$
equation into a very suggestive form that is an obvious
generalization of linear theory. Note that
![]() ${\it\Sigma}$
, whatever it is, will contain two kinds of terms: ones that operate
directly on
${\it\Sigma}$
, whatever it is, will contain two kinds of terms: ones that operate
directly on
![]() $R$
, such as
$R$
, such as
![]() $\ldots \boldsymbol{\partial }R$
; and ones that apply the electric-field operator to
$\ldots \boldsymbol{\partial }R$
; and ones that apply the electric-field operator to
 $R~(\ldots \pmb{\mathbb{E}}R)$
. Call those terms
$R~(\ldots \pmb{\mathbb{E}}R)$
. Call those terms
![]() ${\it\Sigma}^{g}R$
and
${\it\Sigma}^{g}R$
and
![]() ${\it\Sigma}^{f}R$
, respectively, and group the
${\it\Sigma}^{f}R$
, respectively, and group the
![]() ${\it\Sigma}^{f}$
terms with the explicit
${\it\Sigma}^{f}$
terms with the explicit
![]() $\boldsymbol{\partial }f\boldsymbol{\cdot }\pmb{\mathbb{E}}R$
term in (3.28),
thereby changing
$\boldsymbol{\partial }f\boldsymbol{\cdot }\pmb{\mathbb{E}}R$
term in (3.28),
thereby changing
![]() $\boldsymbol{\partial }f$
to a fluctuation-dependent quantity
$\boldsymbol{\partial }f$
to a fluctuation-dependent quantity
 $\boldsymbol{\partial }\overline{f}\doteq \boldsymbol{\partial }f+\boldsymbol{\partial }{\it\delta}\overline{f}$
with
$\boldsymbol{\partial }\overline{f}\doteq \boldsymbol{\partial }f+\boldsymbol{\partial }{\it\delta}\overline{f}$
with
 $\boldsymbol{\partial }{\it\delta}\overline{f}\boldsymbol{\cdot }\pmb{\mathbb{E}}\equiv {\it\Sigma}^{f}$
. Equation (3.28)
then becomes
$\boldsymbol{\partial }{\it\delta}\overline{f}\boldsymbol{\cdot }\pmb{\mathbb{E}}\equiv {\it\Sigma}^{f}$
. Equation (3.28)
then becomes
 $$\begin{eqnarray}g^{-1}R+\underline{\boldsymbol{\partial }\overline{f}\boldsymbol{\cdot }\pmb{\mathbb{E}}R}=1,\end{eqnarray}$$
$$\begin{eqnarray}g^{-1}R+\underline{\boldsymbol{\partial }\overline{f}\boldsymbol{\cdot }\pmb{\mathbb{E}}R}=1,\end{eqnarray}$$
where the renormalized particle propagator
![]() $g$
obeys
$g$
obeys
 $$\begin{eqnarray}(\partial _{t}+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}+\boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{\partial }+{\it\Sigma}^{g})g=1.\end{eqnarray}$$
$$\begin{eqnarray}(\partial _{t}+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}+\boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{\partial }+{\it\Sigma}^{g})g=1.\end{eqnarray}$$
Equation (3.30) now has the same form as (3.16), but importantly it contains only statistically averaged quantities. The method of solution is the same, however, so one obtains (cf. (3.20) and (3.21))
 $$\begin{eqnarray}\displaystyle & R=g-g\,\underline{\boldsymbol{\partial }\overline{f}\boldsymbol{\cdot }{\mathcal{D}}^{-1}\pmb{\mathbb{E}}g}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & R=g-g\,\underline{\boldsymbol{\partial }\overline{f}\boldsymbol{\cdot }{\mathcal{D}}^{-1}\pmb{\mathbb{E}}g}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & {\mathcal{D}}\doteq 1+\underline{\pmb{\mathbb{E}}\boldsymbol{\cdot }g\,\boldsymbol{\partial }\overline{f}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & {\mathcal{D}}\doteq 1+\underline{\pmb{\mathbb{E}}\boldsymbol{\cdot }g\,\boldsymbol{\partial }\overline{f}}, & \displaystyle\end{eqnarray}$$
The somewhat mysterious correction
![]() ${\it\delta}\overline{f}$
is necessary for one to recover the proper form of the matrix
elements in a reduction to weak-turbulence theory (Krommes Reference Krommes2002). It is also required for the satisfaction of constraints
such as energy conservation. A special case was considered by Dupree & Tetreault
(Reference Dupree and Tetreault1978) and also discussed by Diamond
et al. (Reference Diamond, Itoh and Itoh2010,
§ 4.4.4).
${\it\delta}\overline{f}$
is necessary for one to recover the proper form of the matrix
elements in a reduction to weak-turbulence theory (Krommes Reference Krommes2002). It is also required for the satisfaction of constraints
such as energy conservation. A special case was considered by Dupree & Tetreault
(Reference Dupree and Tetreault1978) and also discussed by Diamond
et al. (Reference Diamond, Itoh and Itoh2010,
§ 4.4.4).
It follows from (3.32a ) (and was an intermediate step of the solution methodology; cf. (3.19)) that
 $$\begin{eqnarray}\pmb{\mathbb{E}}R={\mathcal{D}}^{-1}\pmb{\mathbb{E}}g.\end{eqnarray}$$
$$\begin{eqnarray}\pmb{\mathbb{E}}R={\mathcal{D}}^{-1}\pmb{\mathbb{E}}g.\end{eqnarray}$$
This crucial result is a statement of dielectric shielding. Its
interpretation is that the field due to a particle streaming through the random
medium (that streaming being appropriately renormalized by the effects contained in
![]() ${\it\Sigma}^{g}$
, such as turbulent diffusion) is shielded by the self-consistent
response of that medium, which behaves on the average as a macroscopic
dielectric.
${\it\Sigma}^{g}$
, such as turbulent diffusion) is shielded by the self-consistent
response of that medium, which behaves on the average as a macroscopic
dielectric.
One can generalize these results to define the dielectric function for an arbitrary turbulent system. I shall show how to do this in § 4.2 after I have given further background on closure by deriving the DIA in § 4.1.
3.3. Spectral balance and dielectric response
In § 2.3 I showed that, for a particular
problem of passive advection, the two-time correlation function
![]() $C({\it\tau})$
or the fluctuation spectrum
$C({\it\tau})$
or the fluctuation spectrum
![]() $\widehat{C}({\it\omega})$
can be written schematically as (cf. (2.43))
$\widehat{C}({\it\omega})$
can be written schematically as (cf. (2.43))
 $$\begin{eqnarray}C=gFg^{\text{T}},\end{eqnarray}$$
$$\begin{eqnarray}C=gFg^{\text{T}},\end{eqnarray}$$
where
![]() $g$
is the mean Green’s function, T denotes transpose [
$g$
is the mean Green’s function, T denotes transpose [
 $g^{\text{T}}(1,2)\doteq g(2,1)$
], and
$g^{\text{T}}(1,2)\doteq g(2,1)$
], and
![]() $F$
is the sum of the internal and external covariances of the
incoherent noise. Although I shall not prove it here, it is plausible that a similar
formula holds for self-consistent systems:
$F$
is the sum of the internal and external covariances of the
incoherent noise. Although I shall not prove it here, it is plausible that a similar
formula holds for self-consistent systems:
 $$\begin{eqnarray}C(1,1^{\prime })=R(1;\overline{1})F(\overline{1},\overline{1}^{\prime })R(1^{\prime };\overline{1}^{\prime })\end{eqnarray}$$
$$\begin{eqnarray}C(1,1^{\prime })=R(1;\overline{1})F(\overline{1},\overline{1}^{\prime })R(1^{\prime };\overline{1}^{\prime })\end{eqnarray}$$
for some noise covariance
 $F=F^{\text{int}}+F^{\text{ext}}$
, where
$F=F^{\text{int}}+F^{\text{ext}}$
, where
![]() $F^{\text{int}}$
is determined by closure. (It is intimately related to
$F^{\text{int}}$
is determined by closure. (It is intimately related to
![]() ${\it\Sigma}$
by a generalization of (2.48).) The form
${\it\Sigma}$
by a generalization of (2.48).) The form
 $R^{-1}C=FR^{\text{T}}$
can also be viewed as a Dyson equation.Footnote
62
This equation follows in general from the MSR formalism.Footnote
63
Closures such as the DIA discussed in § 4 provide specific formulas for
$R^{-1}C=FR^{\text{T}}$
can also be viewed as a Dyson equation.Footnote
62
This equation follows in general from the MSR formalism.Footnote
63
Closures such as the DIA discussed in § 4 provide specific formulas for
![]() ${\it\Sigma}$
and
${\it\Sigma}$
and
![]() $F^{\text{int}}$
. Note that each of the functions in (3.35) depends on all of the independent variables of the
problem. For the immediately following discussion, it is useful to imagine that one
is dealing with a kinetic plasma description, for which the independent variables are
space, velocity, species, and time. Electromagnetic fields are calculated by
performing weighted integrations over velocity and summations over species. By doing
so, we shall see how dielectric response is contained in the balance equation (3.35).
$F^{\text{int}}$
. Note that each of the functions in (3.35) depends on all of the independent variables of the
problem. For the immediately following discussion, it is useful to imagine that one
is dealing with a kinetic plasma description, for which the independent variables are
space, velocity, species, and time. Electromagnetic fields are calculated by
performing weighted integrations over velocity and summations over species. By doing
so, we shall see how dielectric response is contained in the balance equation (3.35).
Because
![]() $R$
comprises two terms according to (3.32a
), there are various pieces to the formula (3.35), but those collapse when one calculates the
electric-field fluctuation spectrum by applying
$R$
comprises two terms according to (3.32a
), there are various pieces to the formula (3.35), but those collapse when one calculates the
electric-field fluctuation spectrum by applying
![]() $\pmb{\mathbb{E}}$
to each of the arguments 1 and
$\pmb{\mathbb{E}}$
to each of the arguments 1 and
![]() $1^{\prime }$
of (3.35) and
using (3.33):
$1^{\prime }$
of (3.35) and
using (3.33):
 $$\begin{eqnarray}\langle {\it\delta}\boldsymbol{E}\,{\it\delta}\boldsymbol{E}\rangle (\boldsymbol{k},{\it\omega})\doteq \frac{[\pmb{\mathbb{E}}(gFg^{\text{T}})\pmb{\mathbb{E}}^{\text{T}}](\boldsymbol{k},{\it\omega})}{|{\mathcal{D}}(\boldsymbol{k},{\it\omega})|^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}\langle {\it\delta}\boldsymbol{E}\,{\it\delta}\boldsymbol{E}\rangle (\boldsymbol{k},{\it\omega})\doteq \frac{[\pmb{\mathbb{E}}(gFg^{\text{T}})\pmb{\mathbb{E}}^{\text{T}}](\boldsymbol{k},{\it\omega})}{|{\mathcal{D}}(\boldsymbol{k},{\it\omega})|^{2}}.\end{eqnarray}$$
Thus the appropriately propagated incoherent noise is shielded by the coherent dielectric polarization. The beauty and elegance of this representation, which is one form of a spectral balance equation, are hopefully apparent. This balance was already known to Kadomtsev & Petviashvili (Reference Kadomtsev and Petviashvili1963) in the context of weak-turbulence theory. Some physical interpretations of the balance equation for steady-state, isotropic, neutral-fluid turbulence were given by Kraichnan (Reference Kraichnan1964a ), although he did not explicitly introduce the concept of a dielectric function.
Equations (3.35) and (3.36) are generalized
fluctuation–dissipation relations. They determine the fluctuation spectrum implicitly
since it occurs in all of
![]() $g$
,
$g$
,
![]() ${\mathcal{D}}$
, and
${\mathcal{D}}$
, and
![]() $F$
(or in
$F$
(or in
![]() $R$
and
$R$
and
![]() $F$
).
$F$
).
The fact that the fluctuation balance can be represented as
 $C=RFR^{\text{T}}$
(3.35) implies
that it is unnecessary to explicitly introduce either the renormalized propagator
$C=RFR^{\text{T}}$
(3.35) implies
that it is unnecessary to explicitly introduce either the renormalized propagator
![]() $g$
or the dielectric function
$g$
or the dielectric function
![]() ${\mathcal{D}}$
; one only requires approximate formulas for
${\mathcal{D}}$
; one only requires approximate formulas for
![]() ${\it\Sigma}$
and
${\it\Sigma}$
and
![]() $F^{\text{int}}$
. Indeed, initial-value solutions of two-time statistical closures
such as the DIA merely advance
$F^{\text{int}}$
. Indeed, initial-value solutions of two-time statistical closures
such as the DIA merely advance
![]() $R(t;t^{\prime })$
and
$R(t;t^{\prime })$
and
![]() $C(t,t^{\prime })$
. The purposes of stressing the decomposition (3.32a
) for
$C(t,t^{\prime })$
. The purposes of stressing the decomposition (3.32a
) for
![]() $R$
and the formula (3.32b
) for
$R$
and the formula (3.32b
) for
![]() ${\mathcal{D}}$
are to provide insight into the physical content of
${\mathcal{D}}$
are to provide insight into the physical content of
![]() $R$
and to show that the effects of turbulence can be incorporated as a
natural generalization of the familiar linear theory. Awareness of the relationships
between
$R$
and to show that the effects of turbulence can be incorporated as a
natural generalization of the familiar linear theory. Awareness of the relationships
between
![]() $R$
,
$R$
,
![]() $g$
, and
$g$
, and
![]() ${\mathcal{D}}$
is useful in understanding the content and limitations of various
approximations, beginning with the approach taken in Dupree’s early work, discussed
in the next section.
${\mathcal{D}}$
is useful in understanding the content and limitations of various
approximations, beginning with the approach taken in Dupree’s early work, discussed
in the next section.
The principal results of this section are summarized in table 1.
Table 1. Key formulas of statistical turbulence theory. For a turbulent plasma,
 $g_{0}^{-1}\doteq \partial _{t}+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}+\boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{\partial }$
. The effective distribution function is
$g_{0}^{-1}\doteq \partial _{t}+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}+\boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{\partial }$
. The effective distribution function is
 $\overline{f}\doteq \,f+{\it\delta}\overline{f}$
. The quantities
$\overline{f}\doteq \,f+{\it\delta}\overline{f}$
. The quantities
![]() ${\it\Sigma}$
(or equivalently
${\it\Sigma}$
(or equivalently
![]() ${\it\Sigma}^{g}$
and
${\it\Sigma}^{g}$
and
![]() $\boldsymbol{\partial }{\it\delta}\overline{f}$
) and
$\boldsymbol{\partial }{\it\delta}\overline{f}$
) and
![]() $F^{\text{int}}$
must be approximated by a statistical closure. The
interpretation of the spectral balance (3.36) is that incoherent electric-field fluctuations
(with covariance
$F^{\text{int}}$
must be approximated by a statistical closure. The
interpretation of the spectral balance (3.36) is that incoherent electric-field fluctuations
(with covariance
![]() $F$
) behave like moving test particles (
$F$
) behave like moving test particles (
![]() $g$
) that are shielded by the dielectric or polarization
properties of the turbulent medium (
$g$
) that are shielded by the dielectric or polarization
properties of the turbulent medium (
![]() ${\mathcal{D}}$
).
${\mathcal{D}}$
).

3.4. The
 $D_{\bot }={\it\gamma}/k_{\bot }^{2}$
formula
$D_{\bot }={\it\gamma}/k_{\bot }^{2}$
formula
In the last section I argued that one representation of the steady-state fluctuation
spectrum,
 ${\mathcal{E}}(\boldsymbol{k},{\it\omega})\doteq \langle {\it\delta}\boldsymbol{E}\boldsymbol{\cdot }{\it\delta}\boldsymbol{E}\rangle (\boldsymbol{k},{\it\omega})$
, is given by
${\mathcal{E}}(\boldsymbol{k},{\it\omega})\doteq \langle {\it\delta}\boldsymbol{E}\boldsymbol{\cdot }{\it\delta}\boldsymbol{E}\rangle (\boldsymbol{k},{\it\omega})$
, is given by
 $$\begin{eqnarray}{\mathcal{E}}(\boldsymbol{k},{\it\omega})=\frac{{\mathcal{N}}(\boldsymbol{k},{\it\omega})}{|{\mathcal{D}}(\boldsymbol{k},{\it\omega})|^{2}},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{E}}(\boldsymbol{k},{\it\omega})=\frac{{\mathcal{N}}(\boldsymbol{k},{\it\omega})}{|{\mathcal{D}}(\boldsymbol{k},{\it\omega})|^{2}},\end{eqnarray}$$
where
![]() ${\mathcal{N}}$
is the trace of the numerator of (3.36). In general, explicitly solving this equation for
${\mathcal{N}}$
is the trace of the numerator of (3.36). In general, explicitly solving this equation for
![]() ${\mathcal{E}}$
is quite complicated because
${\mathcal{E}}$
is quite complicated because
![]() ${\mathcal{E}}$
is buried in both
${\mathcal{E}}$
is buried in both
![]() ${\mathcal{N}}$
and
${\mathcal{N}}$
and
![]() ${\mathcal{D}}$
. A straightforward though nontrivial method of attack would be to
solve the kinetic DIA directly as an initial-value problem; if that were done,
spectral functions would be calculated as subsidiary quantities. However, one can use
(3.37) directly to interpret the
approach taken by Dupree, which was very popular for a time and is still instructive.
Let us enquire about the wavenumber spectrum
${\mathcal{D}}$
. A straightforward though nontrivial method of attack would be to
solve the kinetic DIA directly as an initial-value problem; if that were done,
spectral functions would be calculated as subsidiary quantities. However, one can use
(3.37) directly to interpret the
approach taken by Dupree, which was very popular for a time and is still instructive.
Let us enquire about the wavenumber spectrum
 $$\begin{eqnarray}{\mathcal{E}}(\boldsymbol{k})\doteq \int _{-\infty }^{\infty }\!\frac{\text{d}{\it\omega}}{2{\rm\pi}}\,{\mathcal{E}}(\boldsymbol{k},{\it\omega})=\int _{-\infty }^{\infty }\!\frac{\text{d}{\it\omega}}{2{\rm\pi}}\,\frac{{\mathcal{N}}(\boldsymbol{k},{\it\omega})}{|{\mathcal{D}}(\boldsymbol{k},{\it\omega})|^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{E}}(\boldsymbol{k})\doteq \int _{-\infty }^{\infty }\!\frac{\text{d}{\it\omega}}{2{\rm\pi}}\,{\mathcal{E}}(\boldsymbol{k},{\it\omega})=\int _{-\infty }^{\infty }\!\frac{\text{d}{\it\omega}}{2{\rm\pi}}\,\frac{{\mathcal{N}}(\boldsymbol{k},{\it\omega})}{|{\mathcal{D}}(\boldsymbol{k},{\it\omega})|^{2}}.\end{eqnarray}$$
The
![]() ${\it\omega}$
dependence of both
${\it\omega}$
dependence of both
![]() ${\mathcal{N}}$
and
${\mathcal{N}}$
and
![]() ${\mathcal{D}}$
contribute to this integral, so it cannot be done in general.Footnote
64
But assume that the system supports a weakly damped normal mode, i.e.,
${\mathcal{D}}$
contribute to this integral, so it cannot be done in general.Footnote
64
But assume that the system supports a weakly damped normal mode, i.e.,
 ${\mathcal{D}}(\boldsymbol{k},{\it\omega}_{\boldsymbol{k}})=0$
for complex frequency
${\mathcal{D}}(\boldsymbol{k},{\it\omega}_{\boldsymbol{k}})=0$
for complex frequency
 ${\it\omega}_{\boldsymbol{k}}={\it\Omega}_{\boldsymbol{k}}+\text{i}{\it\gamma}_{\boldsymbol{k}}$
with
${\it\omega}_{\boldsymbol{k}}={\it\Omega}_{\boldsymbol{k}}+\text{i}{\it\gamma}_{\boldsymbol{k}}$
with
 $|{\it\gamma}_{\boldsymbol{k}}/{\it\Omega}_{\boldsymbol{k}}|\ll 1$
. Here
$|{\it\gamma}_{\boldsymbol{k}}/{\it\Omega}_{\boldsymbol{k}}|\ll 1$
. Here
![]() ${\it\gamma}_{\boldsymbol{k}}$
is the total growth rate, including all nonlinear corrections;
crucially, as I remarked previously, it must be negative in order that a steady
state can be achieved. (Therefore nonlinear contributions to
${\it\gamma}_{\boldsymbol{k}}$
is the total growth rate, including all nonlinear corrections;
crucially, as I remarked previously, it must be negative in order that a steady
state can be achieved. (Therefore nonlinear contributions to
![]() ${\it\gamma}_{\boldsymbol{k}}$
are essential in order to overcompensate a positive
${\it\gamma}_{\boldsymbol{k}}$
are essential in order to overcompensate a positive
![]() ${\it\gamma}_{\boldsymbol{k}}^{\text{lin}}$
and balance the positive-definite nonlinear noise.) To enquire
about the contribution of a given normal mode to the spectrum, one can expand
${\it\gamma}_{\boldsymbol{k}}^{\text{lin}}$
and balance the positive-definite nonlinear noise.) To enquire
about the contribution of a given normal mode to the spectrum, one can expand
 $$\begin{eqnarray}\displaystyle {\mathcal{D}}({\it\omega}) & {\approx} & \displaystyle {\mathcal{D}}({\it\omega}_{\boldsymbol{k}})+({\it\omega}-{\it\omega}_{\boldsymbol{k}})\left.\frac{\partial {\mathcal{D}}}{\partial {\it\omega}}\right|_{{\it\omega}_{\boldsymbol{k}}}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{D}}({\it\omega}) & {\approx} & \displaystyle {\mathcal{D}}({\it\omega}_{\boldsymbol{k}})+({\it\omega}-{\it\omega}_{\boldsymbol{k}})\left.\frac{\partial {\mathcal{D}}}{\partial {\it\omega}}\right|_{{\it\omega}_{\boldsymbol{k}}}\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \equiv & \displaystyle ({\it\omega}-{\it\Omega}_{\boldsymbol{k}}-\text{i}{\it\gamma}_{\boldsymbol{k}}){\mathcal{D}}_{\boldsymbol{k}}^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \equiv & \displaystyle ({\it\omega}-{\it\Omega}_{\boldsymbol{k}}-\text{i}{\it\gamma}_{\boldsymbol{k}}){\mathcal{D}}_{\boldsymbol{k}}^{\prime }.\end{eqnarray}$$
 $$\begin{eqnarray}\frac{1}{({\it\omega}-{\it\Omega}_{\boldsymbol{k}})^{2}+{\it\gamma}_{\boldsymbol{k}}^{2}}\approx \frac{1}{|{\it\gamma}_{\boldsymbol{k}}|}{\rm\pi}{\it\delta}({\it\omega}-{\it\Omega}_{\boldsymbol{k}}).\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{({\it\omega}-{\it\Omega}_{\boldsymbol{k}})^{2}+{\it\gamma}_{\boldsymbol{k}}^{2}}\approx \frac{1}{|{\it\gamma}_{\boldsymbol{k}}|}{\rm\pi}{\it\delta}({\it\omega}-{\it\Omega}_{\boldsymbol{k}}).\end{eqnarray}$$
Let us assume that only this mode contributes to the fluctuation
level. (This cannot really be correct since the modes are coupled nonlinearly.) Then
the
![]() ${\it\omega}$
integration can be performed:
${\it\omega}$
integration can be performed:
 $$\begin{eqnarray}-\!2{\it\gamma}_{\boldsymbol{k}}{\mathcal{E}}(\boldsymbol{k})={\mathcal{N}}(\boldsymbol{k},{\it\Omega}_{\boldsymbol{k}})/|{\mathcal{D}}_{\boldsymbol{k}}^{\prime }|^{2},\end{eqnarray}$$
$$\begin{eqnarray}-\!2{\it\gamma}_{\boldsymbol{k}}{\mathcal{E}}(\boldsymbol{k})={\mathcal{N}}(\boldsymbol{k},{\it\Omega}_{\boldsymbol{k}})/|{\mathcal{D}}_{\boldsymbol{k}}^{\prime }|^{2},\end{eqnarray}$$
where I used the fact that
![]() ${\it\gamma}_{\boldsymbol{k}}<0$
. This is still an implicit equation for
${\it\gamma}_{\boldsymbol{k}}<0$
. This is still an implicit equation for
![]() ${\mathcal{E}}(\boldsymbol{k})$
, which enters in both
${\mathcal{E}}(\boldsymbol{k})$
, which enters in both
![]() ${\mathcal{N}}$
and
${\mathcal{N}}$
and
![]() ${\mathcal{D}}^{\prime }$
. However, if the nonlinear noise is neglected altogether (see
further discussion at the end of this section), one is led to the saturation
condition
${\mathcal{D}}^{\prime }$
. However, if the nonlinear noise is neglected altogether (see
further discussion at the end of this section), one is led to the saturation
condition
If one further writes
 $$\begin{eqnarray}{\it\gamma}_{\boldsymbol{k}}={\it\gamma}_{\boldsymbol{k}}^{\text{lin}}-{\it\eta}_{\boldsymbol{ k}},\end{eqnarray}$$
$$\begin{eqnarray}{\it\gamma}_{\boldsymbol{k}}={\it\gamma}_{\boldsymbol{k}}^{\text{lin}}-{\it\eta}_{\boldsymbol{ k}},\end{eqnarray}$$
where
![]() ${\it\eta}_{\boldsymbol{k}}$
describesFootnote
65
the nonlinear effects, then the saturation condition becomes
${\it\eta}_{\boldsymbol{k}}$
describesFootnote
65
the nonlinear effects, then the saturation condition becomes
 $$\begin{eqnarray}{\it\eta}_{\boldsymbol{k}}={\it\gamma}_{\boldsymbol{k}}^{\text{lin}},\end{eqnarray}$$
$$\begin{eqnarray}{\it\eta}_{\boldsymbol{k}}={\it\gamma}_{\boldsymbol{k}}^{\text{lin}},\end{eqnarray}$$
describing a balance between the nonlinear coherent damping and the
linear drive. For the case of magnetized plasma, for which fluid elements move
cross-field with
![]() $\boldsymbol{E}\times \boldsymbol{B}$
drifts, the approximations of Dupree (Reference Dupree1967) and Weinstock (Reference Weinstock1968, Reference Weinstock1969, Reference Weinstock1970) for
$\boldsymbol{E}\times \boldsymbol{B}$
drifts, the approximations of Dupree (Reference Dupree1967) and Weinstock (Reference Weinstock1968, Reference Weinstock1969, Reference Weinstock1970) for
![]() ${\it\eta}_{\boldsymbol{k}}$
amounted to saying
${\it\eta}_{\boldsymbol{k}}$
amounted to saying
 $$\begin{eqnarray}{\it\eta}_{\boldsymbol{k}}\approx k_{\bot }^{2}D_{\bot }\end{eqnarray}$$
$$\begin{eqnarray}{\it\eta}_{\boldsymbol{k}}\approx k_{\bot }^{2}D_{\bot }\end{eqnarray}$$
for some
![]() $D_{\bot }$
that is a measure of cross-field transport. Not accidentally, this
is the same formula for
$D_{\bot }$
that is a measure of cross-field transport. Not accidentally, this
is the same formula for
![]() ${\it\eta}_{\boldsymbol{k}}$
that we found in the small-
${\it\eta}_{\boldsymbol{k}}$
that we found in the small-
![]() ${\it\tau}_{\text{ac}}$
passive oscillator discussed in § 2.3.
${\it\tau}_{\text{ac}}$
passive oscillator discussed in § 2.3.
The virtue of (3.45) is that in
conjunction with (3.44) it seems to
directly determine the diffusion coefficient to be
 $D_{\bot }={\it\gamma}_{\boldsymbol{k}}^{\text{lin}}/k_{\bot }^{2}$
. An immediate objection is that this cannot literally be so because
$D_{\bot }={\it\gamma}_{\boldsymbol{k}}^{\text{lin}}/k_{\bot }^{2}$
. An immediate objection is that this cannot literally be so because
![]() $D_{\bot }$
was assumed to be
$D_{\bot }$
was assumed to be
![]() $\boldsymbol{k}$
-independent but
$\boldsymbol{k}$
-independent but
![]() ${\it\gamma}_{\boldsymbol{k}}^{\text{lin}}$
is not proportional to
${\it\gamma}_{\boldsymbol{k}}^{\text{lin}}$
is not proportional to
![]() $k_{\bot }^{2}$
in general. (Furthermore, not all
$k_{\bot }^{2}$
in general. (Furthermore, not all
![]() ${\it\gamma}_{\boldsymbol{k}}^{\text{lin}}$
need be positive.) The more general (3.44) does not necessarily have this problem because
${\it\gamma}_{\boldsymbol{k}}^{\text{lin}}$
need be positive.) The more general (3.44) does not necessarily have this problem because
![]() ${\it\eta}_{\boldsymbol{k}}$
is a functional of the wavenumber spectrum, which could in
principle adjust so that (3.44)
holds for all
${\it\eta}_{\boldsymbol{k}}$
is a functional of the wavenumber spectrum, which could in
principle adjust so that (3.44)
holds for all
![]() $\boldsymbol{k}$
. However, the diffusive approximation is valid only at small
$\boldsymbol{k}$
. However, the diffusive approximation is valid only at small
![]() $\boldsymbol{k}$
,Footnote
66
so it is pointless to worry about detailed
$\boldsymbol{k}$
,Footnote
66
so it is pointless to worry about detailed
![]() $\boldsymbol{k}$
dependence. The saturation criterion is best evaluated at some
typicalFootnote
67
wavevector
$\boldsymbol{k}$
dependence. The saturation criterion is best evaluated at some
typicalFootnote
67
wavevector
![]() $\overline{\boldsymbol{k}}$
(one must have
$\overline{\boldsymbol{k}}$
(one must have
![]() ${\it\gamma}_{\overline{\boldsymbol{k}}}^{\text{lin}}>0$
); then a gross estimate is
${\it\gamma}_{\overline{\boldsymbol{k}}}^{\text{lin}}>0$
); then a gross estimate is
 $$\begin{eqnarray}D_{\bot }={\it\gamma}_{\overline{\boldsymbol{k}}}^{\text{lin}}/\overline{k}_{\bot }^{2}.\end{eqnarray}$$
$$\begin{eqnarray}D_{\bot }={\it\gamma}_{\overline{\boldsymbol{k}}}^{\text{lin}}/\overline{k}_{\bot }^{2}.\end{eqnarray}$$
This formula, essentially also given by Kadomtsev (p. 107),Footnote 68 is crude but effective. It states that the fluctuation and transport levels scale with a typical linear growth rate, which can be tested. It is often reasonable.
This is not the place for a thorough review of the subsequent developments of RBT,
which addressed various refinements and applications of the basic theme. Regarding
its validity, there are really two issues: How does one adequately approximate the
coherent damping
![]() ${\it\eta}_{\boldsymbol{k}}$
? And how important is the nonlinear noise
${\it\eta}_{\boldsymbol{k}}$
? And how important is the nonlinear noise
![]() ${\mathcal{N}}_{\boldsymbol{k}}$
? Note that there are important situations in which
${\mathcal{N}}_{\boldsymbol{k}}$
? Note that there are important situations in which
![]() ${\mathcal{N}}$
can be neglected. In weak-turbulence theory, where the spectrum
comprises weakly coupled waves, the lowest-order approximation to
${\mathcal{N}}$
can be neglected. In weak-turbulence theory, where the spectrum
comprises weakly coupled waves, the lowest-order approximation to
![]() ${\mathcal{N}}$
vanishes unless the resonance condition
${\mathcal{N}}$
vanishes unless the resonance condition
 ${\it\Omega}_{\boldsymbol{k}}+{\it\Omega}_{\boldsymbol{p}}+{\it\Omega}_{\boldsymbol{q}}=0$
is satisfied for
${\it\Omega}_{\boldsymbol{k}}+{\it\Omega}_{\boldsymbol{p}}+{\it\Omega}_{\boldsymbol{q}}=0$
is satisfied for
 $\boldsymbol{k}+\boldsymbol{p}+\boldsymbol{q}=\mathbf{0}$
. Linear dispersion relations of ‘nondecay’ type (Kadomtsev Reference Kadomtsev1965; Sagdeev & Galeev Reference Sagdeev and Galeev1969) do not (by definition) obey that condition. In that case,
nontrivial steady states require that (3.42) be satisfied (unless higher-order, e.g., four-wave, interactions are
considered). The nonlinear corrections to
$\boldsymbol{k}+\boldsymbol{p}+\boldsymbol{q}=\mathbf{0}$
. Linear dispersion relations of ‘nondecay’ type (Kadomtsev Reference Kadomtsev1965; Sagdeev & Galeev Reference Sagdeev and Galeev1969) do not (by definition) obey that condition. In that case,
nontrivial steady states require that (3.42) be satisfied (unless higher-order, e.g., four-wave, interactions are
considered). The nonlinear corrections to
![]() ${\mathcal{D}}$
in this case describe wave–wave–particle (and higher-order)
interactions and can be systematically calculated by perturbation theory.Footnote
69
Kadomtsev (Reference Kadomtsev1965) and later Sagdeev
& Galeev (Reference Sagdeev and Galeev1969) and Sagdeev (Reference Sagdeev1979) discussed some instances of this
situation; an example of a greatly refined analysis of such effects is the work of
Horton & Choi (Reference Horton and Choi1979).
${\mathcal{D}}$
in this case describe wave–wave–particle (and higher-order)
interactions and can be systematically calculated by perturbation theory.Footnote
69
Kadomtsev (Reference Kadomtsev1965) and later Sagdeev
& Galeev (Reference Sagdeev and Galeev1969) and Sagdeev (Reference Sagdeev1979) discussed some instances of this
situation; an example of a greatly refined analysis of such effects is the work of
Horton & Choi (Reference Horton and Choi1979).
In later research, Dupree attempted to take the nonlinear noise into consideration. A difficulty is that at the kinetic level the incoherent noise is associated with several distinct kinds of physical processes: renormalized free-streaming particles, which enter into discussions by Dupree (Reference Dupree1972) and later authors (DuBois & Espedal Reference DuBois and Espedal1978; Boutros-Ghali & Dupree Reference Boutros-Ghali and Dupree1981) of phase-space granulationsFootnote 70 in plasmas; and fluid mode-coupling effects that are not sensitive to the details of the velocity space. Those effects must not be neglected; failure to recognize this can easily lead to paradoxes or misconceptions (Krommes & Kim Reference Krommes and Kim1988). The mode coupling is exposed more transparently in statistical closures such as the DIA applied directly to fluid models (Weinstock & Williams Reference Weinstock and Williams1971), for which there has been much work (some of which is described below).
4. The direct-interaction approximation
The general equations (3.32b
) for
![]() ${\mathcal{D}}$
, (3.28) for
${\mathcal{D}}$
, (3.28) for
![]() $R$
, and (3.35) for
$R$
, and (3.35) for
![]() $C$
are not useful until the various terms
$C$
are not useful until the various terms
![]() ${\it\Sigma}^{g}$
,
${\it\Sigma}^{g}$
,
 ${\it\delta}\overline{f}~({\it\Sigma}={\it\Sigma}^{g}+\boldsymbol{\partial }{\it\delta}\overline{f}\boldsymbol{\cdot }\pmb{\mathbb{E}})$
, and
${\it\delta}\overline{f}~({\it\Sigma}={\it\Sigma}^{g}+\boldsymbol{\partial }{\it\delta}\overline{f}\boldsymbol{\cdot }\pmb{\mathbb{E}})$
, and
![]() $F^{\text{int}}$
are calculated from statistical closure. That is a vast subject that
cannot be fully treated here. The most famous closure is the DIA of Kraichnan (Reference Kraichnan1959), and the literature is full of many
discussions, developments, and offshoots of that theory. (Some perspectives on
Kraichnan’s seminal contributions are given by Eyink & Frisch (Reference Eyink, Frisch, Davidson, Kaneda, Moffatt and Sreenivasan2011).) However, a tutorial article of this nature would not be
complete without some words about the DIA. Its derivation has been variously discussed
in terms of the perturbative effect of one Fourier amplitude out of many (Kraichnan
Reference Kraichnan1959), random-coupling models (Kraichnan
Reference Kraichnan1961; Orszag & Kraichnan Reference Orszag and Kraichnan1967), renormalized perturbation theory (Kraichnan
Reference Kraichnan1961), Langevin representations (Kraichnan
Reference Kraichnan1970; Leith Reference Leith1971), systems with infinite dimensionality (Mou & Weichman Reference Mou and Weichman1993), and more; discussion and many references can
be found in Krommes (Reference Krommes2002). The book of Leslie
(Reference Leslie1973) explains in great detail Kraichnan’s
work up to that time; McComb (Reference McComb1990) also treats
the DIA extensively.
$F^{\text{int}}$
are calculated from statistical closure. That is a vast subject that
cannot be fully treated here. The most famous closure is the DIA of Kraichnan (Reference Kraichnan1959), and the literature is full of many
discussions, developments, and offshoots of that theory. (Some perspectives on
Kraichnan’s seminal contributions are given by Eyink & Frisch (Reference Eyink, Frisch, Davidson, Kaneda, Moffatt and Sreenivasan2011).) However, a tutorial article of this nature would not be
complete without some words about the DIA. Its derivation has been variously discussed
in terms of the perturbative effect of one Fourier amplitude out of many (Kraichnan
Reference Kraichnan1959), random-coupling models (Kraichnan
Reference Kraichnan1961; Orszag & Kraichnan Reference Orszag and Kraichnan1967), renormalized perturbation theory (Kraichnan
Reference Kraichnan1961), Langevin representations (Kraichnan
Reference Kraichnan1970; Leith Reference Leith1971), systems with infinite dimensionality (Mou & Weichman Reference Mou and Weichman1993), and more; discussion and many references can
be found in Krommes (Reference Krommes2002). The book of Leslie
(Reference Leslie1973) explains in great detail Kraichnan’s
work up to that time; McComb (Reference McComb1990) also treats
the DIA extensively.
Sections 4.1 and 4.2 contain more technical details than does the rest of the article. They can be skipped on a first reading – but do take the time to absorb the basic message stated in the next paragraph.
4.1. Heuristic derivation of the DIA
In the present section, I shall present a route to the DIA that seems to be modestly
new. It is designed to emphasize the principal intuitive points that all beginners
must grasp, which are that the statistics of turbulence are non-Gaussian and the goal
of closure is to calculate those non-Gaussian corrections self-consistently. The
method essentially provides an
![]() $\boldsymbol{x}$
-space version of Kraichnan’s original approach (Kraichnan Reference Kraichnan1959), which was anchored in
$\boldsymbol{x}$
-space version of Kraichnan’s original approach (Kraichnan Reference Kraichnan1959), which was anchored in
![]() $\boldsymbol{k}$
space.
$\boldsymbol{k}$
space.
If one were dealing with Gaussian statistics, the Furutsu–Novikov theorem (Novikov’s
theorem for brevity) would be useful. That theorem (also known as Gaussian
integration by parts) states that for a centred Gaussian random variable
![]() $\widetilde{{\it\psi}}^{\prime }$
(with covariance
$\widetilde{{\it\psi}}^{\prime }$
(with covariance
![]() $C$
) and a functional
$C$
) and a functional
![]() ${\mathcal{F}}$
of that variable, one has
${\mathcal{F}}$
of that variable, one has
 $$\begin{eqnarray}\langle {\mathcal{F}}[\widetilde{{\it\psi}}^{\prime }]\widetilde{{\it\psi}}^{\prime }(1)\rangle =\left\langle \frac{{\it\delta}{\mathcal{F}}[\widetilde{{\it\psi}}^{\prime }]}{{\it\delta}\widetilde{{\it\psi}}^{\prime }(\overline{1})}\right\rangle C(\overline{1},1),\end{eqnarray}$$
$$\begin{eqnarray}\langle {\mathcal{F}}[\widetilde{{\it\psi}}^{\prime }]\widetilde{{\it\psi}}^{\prime }(1)\rangle =\left\langle \frac{{\it\delta}{\mathcal{F}}[\widetilde{{\it\psi}}^{\prime }]}{{\it\delta}\widetilde{{\it\psi}}^{\prime }(\overline{1})}\right\rangle C(\overline{1},1),\end{eqnarray}$$
where
![]() ${\it\delta}/{\it\delta}\widetilde{{\it\psi}}^{\prime }$
denotes functional differentiation and I use
${\it\delta}/{\it\delta}\widetilde{{\it\psi}}^{\prime }$
denotes functional differentiation and I use
![]() $\widetilde{{\it\psi}}^{\prime }$
in this section as an alternative notation for the fluctuation
$\widetilde{{\it\psi}}^{\prime }$
in this section as an alternative notation for the fluctuation
![]() $\widetilde{{\it\psi}}-\langle \widetilde{{\it\psi}}\rangle$
. See appendix B for the
proof. Cook (Reference Cook1978) discussed the use of
Novikov’s theorem to obtain closures for passive advection; the present work focuses
on self-consistent problems. Thus the goal is to approximate the triplet correlation function
$\widetilde{{\it\psi}}-\langle \widetilde{{\it\psi}}\rangle$
. See appendix B for the
proof. Cook (Reference Cook1978) discussed the use of
Novikov’s theorem to obtain closures for passive advection; the present work focuses
on self-consistent problems. Thus the goal is to approximate the triplet correlation function
![]() $T$
introduced in § 2; see (2.8) and (2.9). One can cast
$T$
introduced in § 2; see (2.8) and (2.9). One can cast
![]() $T$
into the form of the left-hand side of Novikov’s theorem:
$T$
into the form of the left-hand side of Novikov’s theorem:
 $$\begin{eqnarray}T(2,3,1^{\prime })=\langle {\mathcal{F}}[\widetilde{{\it\psi}}^{\prime }]\widetilde{{\it\psi}}^{\prime }(1^{\prime })\rangle ,\end{eqnarray}$$
$$\begin{eqnarray}T(2,3,1^{\prime })=\langle {\mathcal{F}}[\widetilde{{\it\psi}}^{\prime }]\widetilde{{\it\psi}}^{\prime }(1^{\prime })\rangle ,\end{eqnarray}$$
where
 ${\mathcal{F}}[\widetilde{{\it\psi}}^{\prime }]=\widetilde{C}(2,3)$
with
${\mathcal{F}}[\widetilde{{\it\psi}}^{\prime }]=\widetilde{C}(2,3)$
with
 $\widetilde{C}(2,3)\doteq \widetilde{{\it\psi}}^{\prime }(2)\widetilde{{\it\psi}}^{\prime }(3)$
. However, one cannot trivially employ Novikov’s theorem to evaluate
$\widetilde{C}(2,3)\doteq \widetilde{{\it\psi}}^{\prime }(2)\widetilde{{\it\psi}}^{\prime }(3)$
. However, one cannot trivially employ Novikov’s theorem to evaluate
![]() $T$
because that theorem applies only to Gaussian statistics and, as I
discussed in § 2.1,
$T$
because that theorem applies only to Gaussian statistics and, as I
discussed in § 2.1,
![]() $\widetilde{{\it\psi}}^{\prime }$
becomes non-Gaussian already after the first time step. If one
attempts to assert that
$\widetilde{{\it\psi}}^{\prime }$
becomes non-Gaussian already after the first time step. If one
attempts to assert that
![]() $\widetilde{{\it\psi}}^{\prime }$
is Gaussian, then one finds the trivial result
$\widetilde{{\it\psi}}^{\prime }$
is Gaussian, then one finds the trivial result
![]() $T=0$
(third- and higher-order cumulants of a Gaussian vanish),
consistent with the direct use of Novikov’s theorem:
$T=0$
(third- and higher-order cumulants of a Gaussian vanish),
consistent with the direct use of Novikov’s theorem:
 $$\begin{eqnarray}\displaystyle \langle {\mathcal{F}}[\widetilde{{\it\psi}}^{\prime }]\widetilde{{\it\psi}}^{\prime }(1^{\prime })\rangle & = & \displaystyle \left<\frac{{\it\delta}[\widetilde{{\it\psi}}^{\prime }(2)\widetilde{{\it\psi}}^{\prime }(3)]}{{\it\delta}\widetilde{{\it\psi}}^{\prime }(\overline{1})}\right>C(\overline{1},1^{\prime })\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle {\mathcal{F}}[\widetilde{{\it\psi}}^{\prime }]\widetilde{{\it\psi}}^{\prime }(1^{\prime })\rangle & = & \displaystyle \left<\frac{{\it\delta}[\widetilde{{\it\psi}}^{\prime }(2)\widetilde{{\it\psi}}^{\prime }(3)]}{{\it\delta}\widetilde{{\it\psi}}^{\prime }(\overline{1})}\right>C(\overline{1},1^{\prime })\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & = & \displaystyle \langle {\it\delta}(2-\overline{1})\widetilde{{\it\psi}}^{\prime }(3)+\widetilde{{\it\psi}}^{\prime }(2){\it\delta}(3-\overline{1})\rangle C(\overline{1},1^{\prime })\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle \langle {\it\delta}(2-\overline{1})\widetilde{{\it\psi}}^{\prime }(3)+\widetilde{{\it\psi}}^{\prime }(2){\it\delta}(3-\overline{1})\rangle C(\overline{1},1^{\prime })\end{eqnarray}$$
 $\langle \widetilde{{\it\psi}}^{\prime }\rangle \equiv 0$
.
$\langle \widetilde{{\it\psi}}^{\prime }\rangle \equiv 0$
.
Non-Gaussian statistics are induced by the last
![]() $U_{3}$
term in (2.7). Let
us write
$U_{3}$
term in (2.7). Let
us write
 $$\begin{eqnarray}\widetilde{{\it\psi}}^{\prime }=\widetilde{{\it\psi}}_{\text{G}}^{\prime }+{\rm\Delta}\widetilde{{\it\psi}}^{\prime },\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{{\it\psi}}^{\prime }=\widetilde{{\it\psi}}_{\text{G}}^{\prime }+{\rm\Delta}\widetilde{{\it\psi}}^{\prime },\end{eqnarray}$$
where
![]() $\widetilde{{\it\psi}}_{\text{G}}^{\prime }$
is a Gaussian fluctuation with covariance
$\widetilde{{\it\psi}}_{\text{G}}^{\prime }$
is a Gaussian fluctuation with covariance
 $\langle \widetilde{{\it\psi}}_{\text{G}}^{\prime }(1)\widetilde{{\it\psi}}_{\text{G}}^{\prime }(1^{\prime })\rangle =C(1,1^{\prime })$
(this will later be determined self-consistently) and
$\langle \widetilde{{\it\psi}}_{\text{G}}^{\prime }(1)\widetilde{{\it\psi}}_{\text{G}}^{\prime }(1^{\prime })\rangle =C(1,1^{\prime })$
(this will later be determined self-consistently) and
![]() ${\rm\Delta}\widetilde{{\it\psi}}^{\prime }$
is a non-Gaussian correction. One therefore has
${\rm\Delta}\widetilde{{\it\psi}}^{\prime }$
is a non-Gaussian correction. One therefore has
 $$\begin{eqnarray}\displaystyle T(2,3,1^{\prime })\! & = & \displaystyle \!\langle \widetilde{{\it\psi}}_{\text{G}}^{\prime }(2)\widetilde{{\it\psi}}_{\text{G}}^{\prime }(3)\widetilde{{\it\psi}}_{\text{G}}^{\prime }(1^{\prime })\rangle +\langle [{\rm\Delta}\widetilde{{\it\psi}}^{\prime }(2)\widetilde{{\it\psi}}_{\text{G}}^{\prime }(3)]\widetilde{{\it\psi}}_{\text{G}}^{\prime }(1^{\prime })\rangle \nonumber\\ \displaystyle & & \displaystyle +\,\langle [{\rm\Delta}\widetilde{{\it\psi}}^{\prime }(3)\widetilde{{\it\psi}}_{\text{G}}^{\prime }(1^{\prime })]\widetilde{{\it\psi}}_{\text{G}}^{\prime }(2)\rangle +\langle [{\rm\Delta}\widetilde{{\it\psi}}^{\prime }(1^{\prime })\widetilde{{\it\psi}}_{\text{G}}^{\prime }(2)]\widetilde{{\it\psi}}_{\text{G}}^{\prime }(3)\rangle +O({\rm\Delta}\widetilde{{\it\psi}}^{\prime 2}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T(2,3,1^{\prime })\! & = & \displaystyle \!\langle \widetilde{{\it\psi}}_{\text{G}}^{\prime }(2)\widetilde{{\it\psi}}_{\text{G}}^{\prime }(3)\widetilde{{\it\psi}}_{\text{G}}^{\prime }(1^{\prime })\rangle +\langle [{\rm\Delta}\widetilde{{\it\psi}}^{\prime }(2)\widetilde{{\it\psi}}_{\text{G}}^{\prime }(3)]\widetilde{{\it\psi}}_{\text{G}}^{\prime }(1^{\prime })\rangle \nonumber\\ \displaystyle & & \displaystyle +\,\langle [{\rm\Delta}\widetilde{{\it\psi}}^{\prime }(3)\widetilde{{\it\psi}}_{\text{G}}^{\prime }(1^{\prime })]\widetilde{{\it\psi}}_{\text{G}}^{\prime }(2)\rangle +\langle [{\rm\Delta}\widetilde{{\it\psi}}^{\prime }(1^{\prime })\widetilde{{\it\psi}}_{\text{G}}^{\prime }(2)]\widetilde{{\it\psi}}_{\text{G}}^{\prime }(3)\rangle +O({\rm\Delta}\widetilde{{\it\psi}}^{\prime 2}).\end{eqnarray}$$
The first term vanishes because it is the third-order cumulant of a
Gaussian process. The remaining three explicit terms have been written in a form
suitable for application of Novikov’s theorem; the terms in square brackets define
![]() ${\mathcal{F}}$
. (I shall actually evaluate the second explicit term as
${\mathcal{F}}$
. (I shall actually evaluate the second explicit term as
 $\langle [{\rm\Delta}\widetilde{{\it\psi}}^{\prime }(3)\widetilde{{\it\psi}}_{\text{G}}^{\prime }(2)]\widetilde{{\it\psi}}_{\text{G}}^{\prime }(1^{\prime })\rangle$
.) The DIA is defined by the neglect of the terms of
$\langle [{\rm\Delta}\widetilde{{\it\psi}}^{\prime }(3)\widetilde{{\it\psi}}_{\text{G}}^{\prime }(2)]\widetilde{{\it\psi}}_{\text{G}}^{\prime }(1^{\prime })\rangle$
.) The DIA is defined by the neglect of the terms of
 $O({\rm\Delta}\widetilde{{\it\psi}}^{\prime 2})$
. (Unfortunately,
$O({\rm\Delta}\widetilde{{\it\psi}}^{\prime 2})$
. (Unfortunately,
![]() ${\rm\Delta}\widetilde{{\it\psi}}^{\prime }$
is not small in general, which leads to subtle deficiencies in the
DIA; see § 5.1 for further discussion.) An
equation for
${\rm\Delta}\widetilde{{\it\psi}}^{\prime }$
is not small in general, which leads to subtle deficiencies in the
DIA; see § 5.1 for further discussion.) An
equation for
![]() ${\rm\Delta}\widetilde{{\it\psi}}^{\prime }$
follows from (2.7);
correct to first order in
${\rm\Delta}\widetilde{{\it\psi}}^{\prime }$
follows from (2.7);
correct to first order in
![]() ${\rm\Delta}\widetilde{{\it\psi}}^{\prime }$
, it is
${\rm\Delta}\widetilde{{\it\psi}}^{\prime }$
, it is
 $$\begin{eqnarray}\displaystyle \partial _{t}{\rm\Delta}\widetilde{{\it\psi}}^{\prime }(1) & = & \displaystyle U_{2}(1,2){\rm\Delta}\widetilde{{\it\psi}}^{\prime }(2)+U_{3}(1,2,3)[\langle {\it\psi}\rangle (2)+\widetilde{{\it\psi}}_{\text{G}}^{\prime }(2)]{\rm\Delta}\widetilde{{\it\psi}}^{\prime }(3)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2}U_{3}(1,2,3)[\widetilde{{\it\psi}}_{\text{G}}^{\prime }(2)\widetilde{{\it\psi}}_{\text{G}}^{\prime }(3)-C(2,3)].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \partial _{t}{\rm\Delta}\widetilde{{\it\psi}}^{\prime }(1) & = & \displaystyle U_{2}(1,2){\rm\Delta}\widetilde{{\it\psi}}^{\prime }(2)+U_{3}(1,2,3)[\langle {\it\psi}\rangle (2)+\widetilde{{\it\psi}}_{\text{G}}^{\prime }(2)]{\rm\Delta}\widetilde{{\it\psi}}^{\prime }(3)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{1}{2}U_{3}(1,2,3)[\widetilde{{\it\psi}}_{\text{G}}^{\prime }(2)\widetilde{{\it\psi}}_{\text{G}}^{\prime }(3)-C(2,3)].\end{eqnarray}$$
This equation can be represented more compactly by introducing the random infinitesimal response function
 $$\begin{eqnarray}\widetilde{R}(1;1^{\prime })\doteq \frac{{\it\delta}\widetilde{{\it\psi}}(1)}{{\it\delta}\widetilde{f}(1^{\prime })},\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{R}(1;1^{\prime })\doteq \frac{{\it\delta}\widetilde{{\it\psi}}(1)}{{\it\delta}\widetilde{f}(1^{\prime })},\end{eqnarray}$$
which according to (2.5) obeys
 $$\begin{eqnarray}\partial _{t_{1}}\widetilde{R}(1;1^{\prime })-U_{2}(1,2)\widetilde{R}(2;1^{\prime })-U_{3}(1,2,3)\widetilde{{\it\psi}}(2)\widetilde{R}(3;1^{\prime })={\it\delta}(1-1^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t_{1}}\widetilde{R}(1;1^{\prime })-U_{2}(1,2)\widetilde{R}(2;1^{\prime })-U_{3}(1,2,3)\widetilde{{\it\psi}}(2)\widetilde{R}(3;1^{\prime })={\it\delta}(1-1^{\prime }).\end{eqnarray}$$
Here
![]() $\widetilde{R}$
is a functional of
$\widetilde{R}$
is a functional of
![]() $\widetilde{{\it\psi}}$
:
$\widetilde{{\it\psi}}$
:
 $\widetilde{R}=\widetilde{R}[\widetilde{{\it\psi}}]$
. The quantity
$\widetilde{R}=\widetilde{R}[\widetilde{{\it\psi}}]$
. The quantity
 $\widetilde{R}[\langle {\it\psi}\rangle +\widetilde{{\it\psi}}_{\text{G}}^{\prime }]\equiv \widetilde{R}_{\text{G}}$
is Green’s function for the terms explicitly involving
$\widetilde{R}[\langle {\it\psi}\rangle +\widetilde{{\it\psi}}_{\text{G}}^{\prime }]\equiv \widetilde{R}_{\text{G}}$
is Green’s function for the terms explicitly involving
![]() ${\rm\Delta}\widetilde{{\it\psi}}^{\prime }$
in (4.6); thus
(4.6) has the formal solution
${\rm\Delta}\widetilde{{\it\psi}}^{\prime }$
in (4.6); thus
(4.6) has the formal solution
 $$\begin{eqnarray}{\rm\Delta}\widetilde{{\it\psi}}^{\prime }(1)=\widetilde{R}_{\text{G}}(1;\overline{4})\frac{1}{2}U_{3}(\overline{4},\overline{2},\overline{3})[\widetilde{{\it\psi}}_{\text{G}}^{\prime }(\overline{2})\widetilde{{\it\psi}}_{\text{G}}^{\prime }(\overline{3})-C(\overline{2},\overline{3})].\end{eqnarray}$$
$$\begin{eqnarray}{\rm\Delta}\widetilde{{\it\psi}}^{\prime }(1)=\widetilde{R}_{\text{G}}(1;\overline{4})\frac{1}{2}U_{3}(\overline{4},\overline{2},\overline{3})[\widetilde{{\it\psi}}_{\text{G}}^{\prime }(\overline{2})\widetilde{{\it\psi}}_{\text{G}}^{\prime }(\overline{3})-C(\overline{2},\overline{3})].\end{eqnarray}$$
This describes how non-Gaussian statistics are generated by the nonlinear coupling of Gaussian fluctuations.
One can now work out all of the
![]() $O({\rm\Delta}\widetilde{{\it\psi}}^{\prime })$
terms in (4.5) by
approximating the consequences of Novikov’s theorem, assuming that all terms are
functionals of
$O({\rm\Delta}\widetilde{{\it\psi}}^{\prime })$
terms in (4.5) by
approximating the consequences of Novikov’s theorem, assuming that all terms are
functionals of
![]() $\widetilde{{\it\psi}}_{\text{G}}^{\prime }$
. One has
$\widetilde{{\it\psi}}_{\text{G}}^{\prime }$
. One has
 $$\begin{eqnarray}\langle [{\rm\Delta}\widetilde{{\it\psi}}^{\prime }(2)\widetilde{{\it\psi}}_{\text{G}}^{\prime }(3)]\widetilde{{\it\psi}}_{\text{G}}^{\prime }(1^{\prime })\rangle =\left<\frac{{\it\delta}[{\rm\Delta}\widetilde{{\it\psi}}^{\prime }(2)\widetilde{{\it\psi}}_{\text{G}}^{\prime }(3)]}{{\it\delta}\widetilde{{\it\psi}}_{\text{G}}^{\prime }(\overline{1})}\right>C(\overline{1},1^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}\langle [{\rm\Delta}\widetilde{{\it\psi}}^{\prime }(2)\widetilde{{\it\psi}}_{\text{G}}^{\prime }(3)]\widetilde{{\it\psi}}_{\text{G}}^{\prime }(1^{\prime })\rangle =\left<\frac{{\it\delta}[{\rm\Delta}\widetilde{{\it\psi}}^{\prime }(2)\widetilde{{\it\psi}}_{\text{G}}^{\prime }(3)]}{{\it\delta}\widetilde{{\it\psi}}_{\text{G}}^{\prime }(\overline{1})}\right>C(\overline{1},1^{\prime }).\end{eqnarray}$$
From (4.9), the functional derivative is approximately
 $$\begin{eqnarray}\displaystyle \frac{{\it\delta}[{\rm\Delta}\widetilde{{\it\psi}}^{\prime }(2)\widetilde{{\it\psi}}_{\text{G}}^{\prime }(3)]}{{\it\delta}\widetilde{{\it\psi}}_{\text{G}}^{\prime }(\overline{1})} & = & \displaystyle \widetilde{R}_{\text{G}}(2;\overline{4})\left\{U_{3}(\overline{4},\overline{2},\overline{1})\widetilde{{\it\psi}}_{\text{G}}^{\prime }(\overline{2})\widetilde{{\it\psi}}_{\text{G}}^{\prime }(3)\phantom{\frac{1}{2}}\right.\nonumber\\ \displaystyle & & \displaystyle +\,\left.\frac{1}{2}U_{3}(\overline{4},\overline{2},\overline{3})[\widetilde{{\it\psi}}_{\text{G}}^{\prime }(\overline{2})\widetilde{{\it\psi}}_{\text{G}}^{\prime }(\overline{3})-C(\overline{2},\overline{3})]{\it\delta}(3-\overline{1})\right\}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{{\it\delta}\widetilde{R}_{\text{G}}(1;\overline{4})}{{\it\delta}\widetilde{{\it\psi}}_{\text{G}}^{\prime }(\overline{1})}\frac{1}{2}U_{3}(\overline{4},\overline{2},\overline{3})[\widetilde{{\it\psi}}_{\text{G}}^{\prime }(\overline{2})\widetilde{{\it\psi}}_{\text{G}}^{\prime }(\overline{3})-C(\overline{2},\overline{3})].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{{\it\delta}[{\rm\Delta}\widetilde{{\it\psi}}^{\prime }(2)\widetilde{{\it\psi}}_{\text{G}}^{\prime }(3)]}{{\it\delta}\widetilde{{\it\psi}}_{\text{G}}^{\prime }(\overline{1})} & = & \displaystyle \widetilde{R}_{\text{G}}(2;\overline{4})\left\{U_{3}(\overline{4},\overline{2},\overline{1})\widetilde{{\it\psi}}_{\text{G}}^{\prime }(\overline{2})\widetilde{{\it\psi}}_{\text{G}}^{\prime }(3)\phantom{\frac{1}{2}}\right.\nonumber\\ \displaystyle & & \displaystyle +\,\left.\frac{1}{2}U_{3}(\overline{4},\overline{2},\overline{3})[\widetilde{{\it\psi}}_{\text{G}}^{\prime }(\overline{2})\widetilde{{\it\psi}}_{\text{G}}^{\prime }(\overline{3})-C(\overline{2},\overline{3})]{\it\delta}(3-\overline{1})\right\}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{{\it\delta}\widetilde{R}_{\text{G}}(1;\overline{4})}{{\it\delta}\widetilde{{\it\psi}}_{\text{G}}^{\prime }(\overline{1})}\frac{1}{2}U_{3}(\overline{4},\overline{2},\overline{3})[\widetilde{{\it\psi}}_{\text{G}}^{\prime }(\overline{2})\widetilde{{\it\psi}}_{\text{G}}^{\prime }(\overline{3})-C(\overline{2},\overline{3})].\end{eqnarray}$$
Upon differentiating the identity
 $$\begin{eqnarray}\widetilde{R}(1;2)\widetilde{R}^{-1}(2;1^{\prime })={\it\delta}(1-1^{\prime }),\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{R}(1;2)\widetilde{R}^{-1}(2;1^{\prime })={\it\delta}(1-1^{\prime }),\end{eqnarray}$$
which leads to
 ${\rm\Delta}\widetilde{R}=-\widetilde{R}{\rm\Delta}(\widetilde{R}^{-1})\widetilde{R}$
, and noting from (4.8) that
${\rm\Delta}\widetilde{R}=-\widetilde{R}{\rm\Delta}(\widetilde{R}^{-1})\widetilde{R}$
, and noting from (4.8) that
 $$\begin{eqnarray}\widetilde{R}^{-1}(1;1^{\prime })=\partial _{t_{1}}{\it\delta}(1-1^{\prime })-U_{2}(1,1^{\prime })-U_{3}(1,2,1^{\prime })\widetilde{{\it\psi}}(2),\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{R}^{-1}(1;1^{\prime })=\partial _{t_{1}}{\it\delta}(1-1^{\prime })-U_{2}(1,1^{\prime })-U_{3}(1,2,1^{\prime })\widetilde{{\it\psi}}(2),\end{eqnarray}$$
one finds
 $$\begin{eqnarray}\displaystyle \frac{{\it\delta}\widetilde{R}_{\text{G}}(1;\overline{4})}{{\it\delta}\widetilde{{\it\psi}}_{\text{G}}^{\prime }(\overline{1})} & = & \displaystyle -\widetilde{R}_{\text{G}}(1;5)\frac{{\it\delta}\widetilde{R}_{\text{G}}^{-1}(5;\overline{5})}{{\it\delta}\widetilde{{\it\psi}}_{\text{G}}^{\prime }(\overline{1})}\widetilde{R}_{\text{G}}(\overline{5};\overline{4})\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{{\it\delta}\widetilde{R}_{\text{G}}(1;\overline{4})}{{\it\delta}\widetilde{{\it\psi}}_{\text{G}}^{\prime }(\overline{1})} & = & \displaystyle -\widetilde{R}_{\text{G}}(1;5)\frac{{\it\delta}\widetilde{R}_{\text{G}}^{-1}(5;\overline{5})}{{\it\delta}\widetilde{{\it\psi}}_{\text{G}}^{\prime }(\overline{1})}\widetilde{R}_{\text{G}}(\overline{5};\overline{4})\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & = & \displaystyle \widetilde{R}_{\text{G}}(1;5)U_{3}(5,\overline{1},\overline{5})\widetilde{R}_{\text{G}}(\overline{5};\overline{4}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle \widetilde{R}_{\text{G}}(1;5)U_{3}(5,\overline{1},\overline{5})\widetilde{R}_{\text{G}}(\overline{5};\overline{4}).\end{eqnarray}$$
For use in (4.10), one must average
(4.11) using the result (4.14b
). Since all quantities have been expressed in terms of
![]() $\widetilde{{\it\psi}}_{\text{G}}^{\prime }$
, which is Gaussian by assumption, the averages can be performed by
using the functional generalization of results like
$\widetilde{{\it\psi}}_{\text{G}}^{\prime }$
, which is Gaussian by assumption, the averages can be performed by
using the functional generalization of results like
 $$\begin{eqnarray}\displaystyle \langle {\mathcal{F}}(\widetilde{{\it\psi}}^{\prime })\widetilde{{\it\psi}}^{\prime }\widetilde{{\it\psi}}^{\prime }\rangle \! & = & \displaystyle \!\langle [{\mathcal{F}}(\widetilde{{\it\psi}}^{\prime })\,\widetilde{{\it\psi}}^{\prime }]\widetilde{{\it\psi}}^{\prime }\rangle =\left<\frac{\text{d}({\mathcal{F}}\,\widetilde{{\it\psi}}^{\prime })}{\text{d}\widetilde{{\it\psi}}^{\prime }}\right>{\it\sigma}^{2}\nonumber\\ \displaystyle \! & = & \displaystyle \!\langle {\mathcal{F}}\rangle {\it\sigma}^{2}+\left<\frac{\text{d}{\mathcal{F}}}{\text{d}\widetilde{{\it\psi}}^{\prime }}\,\widetilde{{\it\psi}}^{\prime }\right>{\it\sigma}^{2}=\langle {\mathcal{F}}\rangle {\it\sigma}^{2}+\left<\frac{\text{d}^{2}{\mathcal{F}}}{\text{d}\widetilde{{\it\psi}}^{\prime 2}}\right>{\it\sigma}^{4}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle {\mathcal{F}}(\widetilde{{\it\psi}}^{\prime })\widetilde{{\it\psi}}^{\prime }\widetilde{{\it\psi}}^{\prime }\rangle \! & = & \displaystyle \!\langle [{\mathcal{F}}(\widetilde{{\it\psi}}^{\prime })\,\widetilde{{\it\psi}}^{\prime }]\widetilde{{\it\psi}}^{\prime }\rangle =\left<\frac{\text{d}({\mathcal{F}}\,\widetilde{{\it\psi}}^{\prime })}{\text{d}\widetilde{{\it\psi}}^{\prime }}\right>{\it\sigma}^{2}\nonumber\\ \displaystyle \! & = & \displaystyle \!\langle {\mathcal{F}}\rangle {\it\sigma}^{2}+\left<\frac{\text{d}{\mathcal{F}}}{\text{d}\widetilde{{\it\psi}}^{\prime }}\,\widetilde{{\it\psi}}^{\prime }\right>{\it\sigma}^{2}=\langle {\mathcal{F}}\rangle {\it\sigma}^{2}+\left<\frac{\text{d}^{2}{\mathcal{F}}}{\text{d}\widetilde{{\it\psi}}^{\prime 2}}\right>{\it\sigma}^{4}.\end{eqnarray}$$
(Here
 ${\it\sigma}^{2}\doteq \langle \widetilde{{\it\psi}}^{\prime }\widetilde{{\it\psi}}^{\prime }\rangle$
; see appendix B.) However,
terms that bring in extra factors of
${\it\sigma}^{2}\doteq \langle \widetilde{{\it\psi}}^{\prime }\widetilde{{\it\psi}}^{\prime }\rangle$
; see appendix B.) However,
terms that bring in extra factors of
![]() $U_{3}$
(any of the terms that arise from differentiating
$U_{3}$
(any of the terms that arise from differentiating
![]() $\widetilde{R}^{-1}$
) should be neglected because the role of
$\widetilde{R}^{-1}$
) should be neglected because the role of
![]() $U_{3}$
is to induce allegedly small non-Gaussian statistics and we have
already (for better or worse) neglected terms of higher than first order in that
correction. This amounts to saying that one should retain only the first term of
(4.15) and should approximate
$U_{3}$
is to induce allegedly small non-Gaussian statistics and we have
already (for better or worse) neglected terms of higher than first order in that
correction. This amounts to saying that one should retain only the first term of
(4.15) and should approximate
 $\widetilde{R}_{\text{G}}\approx \langle \widetilde{R}\rangle \equiv R$
. Only the first line of (4.11) then survives the average, and one finds a contribution to
$\widetilde{R}_{\text{G}}\approx \langle \widetilde{R}\rangle \equiv R$
. Only the first line of (4.11) then survives the average, and one finds a contribution to
![]() $U_{3}T/2$
of the form
$U_{3}T/2$
of the form
 $-{\it\Sigma}(1;\overline{1})C(\overline{1},1^{\prime })/2$
, where
$-{\it\Sigma}(1;\overline{1})C(\overline{1},1^{\prime })/2$
, where
 $$\begin{eqnarray}\displaystyle {\it\Sigma}(1;\overline{1})\doteq -U_{3}(1,2,3)R(2;\overline{2})C(3,\overline{3})U_{3}(\overline{2},\overline{3},\overline{1}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\Sigma}(1;\overline{1})\doteq -U_{3}(1,2,3)R(2;\overline{2})C(3,\overline{3})U_{3}(\overline{2},\overline{3},\overline{1}). & & \displaystyle\end{eqnarray}$$
The second and third terms of
![]() $O({\rm\Delta}\widetilde{{\it\psi}}^{\prime })$
in (4.5) can be
worked out in a similar fashion. By symmetry, the second term is equal to the first.
The third term gives a distinct contribution to the term
$O({\rm\Delta}\widetilde{{\it\psi}}^{\prime })$
in (4.5) can be
worked out in a similar fashion. By symmetry, the second term is equal to the first.
The third term gives a distinct contribution to the term
![]() $U_{3}T/2$
in (2.8) of the
form
$U_{3}T/2$
in (2.8) of the
form
 $F^{\text{int}}(1,\overline{1})R(1^{\prime };\overline{1})$
, where
$F^{\text{int}}(1,\overline{1})R(1^{\prime };\overline{1})$
, where
 $$\begin{eqnarray}\displaystyle F^{\text{int}}(1,\overline{1})\doteq \frac{1}{2}U_{3}(1,2,3)C(2,\overline{2})C(3,\overline{3})U_{3}(\overline{1},\overline{2},\overline{3}). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F^{\text{int}}(1,\overline{1})\doteq \frac{1}{2}U_{3}(1,2,3)C(2,\overline{2})C(3,\overline{3})U_{3}(\overline{1},\overline{2},\overline{3}). & & \displaystyle\end{eqnarray}$$
This function can be interpreted as the covariance of an internal emission or noise term arising from the nonlinearity.
Next, one must evaluate the cross-correlation
 $\langle \,\widetilde{f}^{\text{ext}\prime }(1)\widetilde{{\it\psi}}^{\prime }(1^{\prime })\rangle$
required in (2.8).
This can be done exactly if one assumes that
$\langle \,\widetilde{f}^{\text{ext}\prime }(1)\widetilde{{\it\psi}}^{\prime }(1^{\prime })\rangle$
required in (2.8).
This can be done exactly if one assumes that
![]() $\widetilde{{\it\psi}}$
evolves from Gaussian initial conditions
$\widetilde{{\it\psi}}$
evolves from Gaussian initial conditions
![]() $\widetilde{{\it\psi}}_{0}$
that are uncorrelated with the Gaussian
$\widetilde{{\it\psi}}_{0}$
that are uncorrelated with the Gaussian
![]() $\widetilde{f}^{\text{ext}}$
. From Novikov’s theorem, one has
$\widetilde{f}^{\text{ext}}$
. From Novikov’s theorem, one has
 $$\begin{eqnarray}\displaystyle \langle \,\widetilde{f}^{\text{ext}\prime }(1)\widetilde{{\it\psi}}^{\prime }(1^{\prime })\rangle & = & \displaystyle \langle \widetilde{{\it\psi}}(1^{\prime })\,\widetilde{f}^{\text{ext}\prime }(1)\rangle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle \,\widetilde{f}^{\text{ext}\prime }(1)\widetilde{{\it\psi}}^{\prime }(1^{\prime })\rangle & = & \displaystyle \langle \widetilde{{\it\psi}}(1^{\prime })\,\widetilde{f}^{\text{ext}\prime }(1)\rangle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & = & \displaystyle \left<\frac{{\it\delta}\widetilde{{\it\psi}}(1^{\prime })}{{\it\delta}\widetilde{{\it\psi}}_{0}(\underline{\overline{1}})}\right>\langle \widetilde{{\it\psi}}_{0}^{\prime }(\underline{\overline{1}})\,\widetilde{f}^{\text{ext}\prime }(1)\rangle +\left<\frac{{\it\delta}\widetilde{{\it\psi}}(1^{\prime })}{{\it\delta}\widetilde{f}^{\text{ext}}(\overline{1})}\right>\langle \,\widetilde{f}^{\text{ext}\prime }(\overline{1})\,\widetilde{f}^{\text{ext}\prime }(1)\rangle .\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle \left<\frac{{\it\delta}\widetilde{{\it\psi}}(1^{\prime })}{{\it\delta}\widetilde{{\it\psi}}_{0}(\underline{\overline{1}})}\right>\langle \widetilde{{\it\psi}}_{0}^{\prime }(\underline{\overline{1}})\,\widetilde{f}^{\text{ext}\prime }(1)\rangle +\left<\frac{{\it\delta}\widetilde{{\it\psi}}(1^{\prime })}{{\it\delta}\widetilde{f}^{\text{ext}}(\overline{1})}\right>\langle \,\widetilde{f}^{\text{ext}\prime }(\overline{1})\,\widetilde{f}^{\text{ext}\prime }(1)\rangle .\end{eqnarray}$$
 $\langle \widetilde{{\it\psi}}_{0}\,\widetilde{f}^{\text{ext}\prime }\rangle =0$
, and by definition one has
$\langle \widetilde{{\it\psi}}_{0}\,\widetilde{f}^{\text{ext}\prime }\rangle =0$
, and by definition one has
 $\langle {\it\delta}\widetilde{{\it\psi}}(1^{\prime })/{\it\delta}\widetilde{f}^{\text{ext}}(\overline{1})\rangle =R(1^{\prime };\overline{1})$
. ThusFootnote
71
$\langle {\it\delta}\widetilde{{\it\psi}}(1^{\prime })/{\it\delta}\widetilde{f}^{\text{ext}}(\overline{1})\rangle =R(1^{\prime };\overline{1})$
. ThusFootnote
71
 $$\begin{eqnarray}\langle \,\widetilde{f}^{\text{ext}\prime }(1)\widetilde{{\it\psi}}^{\prime }(1^{\prime })\rangle =R(1^{\prime };\overline{1})F^{\text{ext}}(1,\overline{1}).\end{eqnarray}$$
$$\begin{eqnarray}\langle \,\widetilde{f}^{\text{ext}\prime }(1)\widetilde{{\it\psi}}^{\prime }(1^{\prime })\rangle =R(1^{\prime };\overline{1})F^{\text{ext}}(1,\overline{1}).\end{eqnarray}$$
This leads to the covariance equation
 $$\begin{eqnarray}\displaystyle & & \displaystyle \partial _{t_{1}}C(1,1^{\prime })-U_{2}(1,\overline{1})C(\overline{1},1^{\prime })-U_{3}(1,2,\overline{1})\langle {\it\psi}\rangle (2)C(\overline{1},1^{\prime })+{\it\Sigma}(1;\overline{1})C(\overline{1},1^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad =[F^{\text{int}}(1,\overline{1})+F^{\text{ext}}(1,\overline{1})]R(1^{\prime };\overline{1}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \partial _{t_{1}}C(1,1^{\prime })-U_{2}(1,\overline{1})C(\overline{1},1^{\prime })-U_{3}(1,2,\overline{1})\langle {\it\psi}\rangle (2)C(\overline{1},1^{\prime })+{\it\Sigma}(1;\overline{1})C(\overline{1},1^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad =[F^{\text{int}}(1,\overline{1})+F^{\text{ext}}(1,\overline{1})]R(1^{\prime };\overline{1}).\end{eqnarray}$$
Finally, one can obtain a closed equation for the mean response function
![]() $R$
by noting from (4.8) that
$R$
by noting from (4.8) that
![]() $R$
obeys
$R$
obeys
 $$\begin{eqnarray}\displaystyle & & \displaystyle \partial _{t}R(1;1^{\prime })-U_{2}(1,2)R(2;1^{\prime })-U_{3}(1,2,3)\langle {\it\psi}\rangle (2)R(3;1^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad -\,U_{3}(1,2,3)\langle \widetilde{R}(2;1^{\prime })\widetilde{{\it\psi}}^{\prime }(3)\rangle ={\it\delta}(1-1^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \partial _{t}R(1;1^{\prime })-U_{2}(1,2)R(2;1^{\prime })-U_{3}(1,2,3)\langle {\it\psi}\rangle (2)R(3;1^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad -\,U_{3}(1,2,3)\langle \widetilde{R}(2;1^{\prime })\widetilde{{\it\psi}}^{\prime }(3)\rangle ={\it\delta}(1-1^{\prime }).\end{eqnarray}$$
If one approximates
![]() $\widetilde{{\it\psi}}^{\prime }\approx \widetilde{{\it\psi}}_{\text{G}}^{\prime }$
, the last term can be evaluated by Novikov’s theorem:
$\widetilde{{\it\psi}}^{\prime }\approx \widetilde{{\it\psi}}_{\text{G}}^{\prime }$
, the last term can be evaluated by Novikov’s theorem:
 $$\begin{eqnarray}\displaystyle \langle \widetilde{R}_{\text{G}}(2;1^{\prime })\widetilde{{\it\psi}}_{\text{G}}^{\prime }(3)\rangle & = & \displaystyle \left<\frac{{\it\delta}\widetilde{R}_{\text{G}}(2;1^{\prime })}{{\it\delta}\widetilde{{\it\psi}}_{\text{G}}^{\prime }(\overline{3})}\right>C(\overline{3},3)\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle \widetilde{R}_{\text{G}}(2;1^{\prime })\widetilde{{\it\psi}}_{\text{G}}^{\prime }(3)\rangle & = & \displaystyle \left<\frac{{\it\delta}\widetilde{R}_{\text{G}}(2;1^{\prime })}{{\it\delta}\widetilde{{\it\psi}}_{\text{G}}^{\prime }(\overline{3})}\right>C(\overline{3},3)\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & = & \displaystyle -\left<\widetilde{R}_{\text{G}}(2;\overline{2})\frac{{\it\delta}\widetilde{R}_{\text{G}}^{-1}(\overline{2},\overline{1})}{{\it\delta}\widetilde{{\it\psi}}_{\text{G}}^{\prime }(\overline{3})}\widetilde{R}(\overline{1};1^{\prime })\right>C(\overline{3},3)\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle -\left<\widetilde{R}_{\text{G}}(2;\overline{2})\frac{{\it\delta}\widetilde{R}_{\text{G}}^{-1}(\overline{2},\overline{1})}{{\it\delta}\widetilde{{\it\psi}}_{\text{G}}^{\prime }(\overline{3})}\widetilde{R}(\overline{1};1^{\prime })\right>C(\overline{3},3)\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & {\approx} & \displaystyle R(2;\overline{2})C(\overline{3},3)U_{3}(\overline{2},\overline{3},\overline{1})R(\overline{1};1^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & {\approx} & \displaystyle R(2;\overline{2})C(\overline{3},3)U_{3}(\overline{2},\overline{3},\overline{1})R(\overline{1};1^{\prime }).\end{eqnarray}$$
 ${\it\Sigma}(1;\overline{1})R(\overline{1};1^{\prime })$
; therefore
${\it\Sigma}(1;\overline{1})R(\overline{1};1^{\prime })$
; therefore  $$\begin{eqnarray}\partial _{t_{1}}R(1;1^{\prime })-U_{2}(1,\overline{1})R(\overline{1};1^{\prime })-U_{3}(1,2,\overline{1})\langle {\it\psi}\rangle (2)R(\overline{1};1^{\prime })+{\it\Sigma}(1;\overline{1})R(\overline{1};1^{\prime })={\it\delta}(1-1^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t_{1}}R(1;1^{\prime })-U_{2}(1,\overline{1})R(\overline{1};1^{\prime })-U_{3}(1,2,\overline{1})\langle {\it\psi}\rangle (2)R(\overline{1};1^{\prime })+{\it\Sigma}(1;\overline{1})R(\overline{1};1^{\prime })={\it\delta}(1-1^{\prime }).\end{eqnarray}$$
This result shows that the operator on the left-hand side of (4.20) is just
![]() $R^{-1}$
. Upon formally solving (4.20), one is then led to the symmetrical form
$R^{-1}$
. Upon formally solving (4.20), one is then led to the symmetrical form
 $$\begin{eqnarray}C(1,1^{\prime })=R(1;\overline{1})[F^{\text{int}}(\overline{1},\overline{1}^{\prime })+F^{\text{ext}}(\overline{1},\overline{1}^{\prime })]R(1^{\prime };\overline{1}^{\prime })\end{eqnarray}$$
$$\begin{eqnarray}C(1,1^{\prime })=R(1;\overline{1})[F^{\text{int}}(\overline{1},\overline{1}^{\prime })+F^{\text{ext}}(\overline{1},\overline{1}^{\prime })]R(1^{\prime };\overline{1}^{\prime })\end{eqnarray}$$
or concisely
 $C=RFR^{\text{T}}$
.
$C=RFR^{\text{T}}$
.
This closure, consisting of (2.6) for
the mean field, equations (4.20) or
(4.24) for the covariance, and
(4.23) for the response
function, along with the definitions (4.16) for
![]() ${\it\Sigma}$
and (4.17) for
${\it\Sigma}$
and (4.17) for
![]() $F^{\text{int}}$
, is precisely the DIA. A thorough discussion and alternative
derivation of the DIA for Vlasov turbulence was given by DuBois & Pesme (Reference DuBois and Pesme1985).
$F^{\text{int}}$
, is precisely the DIA. A thorough discussion and alternative
derivation of the DIA for Vlasov turbulence was given by DuBois & Pesme (Reference DuBois and Pesme1985).
For homogeneous turbulence, the DIA equations are often written in
![]() $\boldsymbol{k}$
space. If the quadratic PDE for a fluid description (no velocity
space) is written asFootnote
72
$\boldsymbol{k}$
space. If the quadratic PDE for a fluid description (no velocity
space) is written asFootnote
72
 $$\begin{eqnarray}\partial _{t}\widetilde{{\it\psi}}_{\boldsymbol{k}}=L_{\boldsymbol{k}}\widetilde{{\it\psi}}_{\boldsymbol{k}}+\frac{1}{2}\mathop{\sum }_{\boldsymbol{p},\boldsymbol{q}}{\it\delta}_{\boldsymbol{k}+\boldsymbol{p}+\boldsymbol{q},\mathbf{0}}M_{\boldsymbol{k}\boldsymbol{p}\boldsymbol{q}}\widetilde{{\it\psi}}_{\boldsymbol{p}}^{\ast }\widetilde{{\it\psi}}_{\boldsymbol{ q}}^{\ast }+\,\widetilde{f}_{\boldsymbol{ k}}^{\text{ext}},\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t}\widetilde{{\it\psi}}_{\boldsymbol{k}}=L_{\boldsymbol{k}}\widetilde{{\it\psi}}_{\boldsymbol{k}}+\frac{1}{2}\mathop{\sum }_{\boldsymbol{p},\boldsymbol{q}}{\it\delta}_{\boldsymbol{k}+\boldsymbol{p}+\boldsymbol{q},\mathbf{0}}M_{\boldsymbol{k}\boldsymbol{p}\boldsymbol{q}}\widetilde{{\it\psi}}_{\boldsymbol{p}}^{\ast }\widetilde{{\it\psi}}_{\boldsymbol{ q}}^{\ast }+\,\widetilde{f}_{\boldsymbol{ k}}^{\text{ext}},\end{eqnarray}$$
then in the DIA
 $$\begin{eqnarray}\widehat{{\it\Sigma}}_{\boldsymbol{k}}(t;\overline{t})=-\mathop{\sum }_{\boldsymbol{p},\boldsymbol{q}}{\it\delta}_{\boldsymbol{k}+\boldsymbol{p}+\boldsymbol{q},\mathbf{0}}M_{\boldsymbol{k}\boldsymbol{p}\boldsymbol{q}}M_{\boldsymbol{p}\boldsymbol{q}\boldsymbol{k}}^{\ast }\widehat{R}_{\boldsymbol{ p}}^{\ast }(t;\overline{t})\widehat{C}_{\boldsymbol{ q}}^{\ast }(t;\overline{t})\end{eqnarray}$$
$$\begin{eqnarray}\widehat{{\it\Sigma}}_{\boldsymbol{k}}(t;\overline{t})=-\mathop{\sum }_{\boldsymbol{p},\boldsymbol{q}}{\it\delta}_{\boldsymbol{k}+\boldsymbol{p}+\boldsymbol{q},\mathbf{0}}M_{\boldsymbol{k}\boldsymbol{p}\boldsymbol{q}}M_{\boldsymbol{p}\boldsymbol{q}\boldsymbol{k}}^{\ast }\widehat{R}_{\boldsymbol{ p}}^{\ast }(t;\overline{t})\widehat{C}_{\boldsymbol{ q}}^{\ast }(t;\overline{t})\end{eqnarray}$$
and
 $$\begin{eqnarray}\widehat{F}_{\boldsymbol{k}}^{\text{int}}(t,\overline{t})=\frac{1}{2}\mathop{\sum }_{\boldsymbol{p},\boldsymbol{q}}{\it\delta}_{\boldsymbol{k}+\boldsymbol{p}+\boldsymbol{q},\mathbf{0}}|M_{\boldsymbol{k}\boldsymbol{p}\boldsymbol{q}}|^{2}\widehat{C}_{\boldsymbol{ p}}^{\ast }(t,\overline{t})\widehat{C}_{\boldsymbol{ q}}^{\ast }(t,\overline{t}),\end{eqnarray}$$
$$\begin{eqnarray}\widehat{F}_{\boldsymbol{k}}^{\text{int}}(t,\overline{t})=\frac{1}{2}\mathop{\sum }_{\boldsymbol{p},\boldsymbol{q}}{\it\delta}_{\boldsymbol{k}+\boldsymbol{p}+\boldsymbol{q},\mathbf{0}}|M_{\boldsymbol{k}\boldsymbol{p}\boldsymbol{q}}|^{2}\widehat{C}_{\boldsymbol{ p}}^{\ast }(t,\overline{t})\widehat{C}_{\boldsymbol{ q}}^{\ast }(t,\overline{t}),\end{eqnarray}$$
where
![]() $M\equiv U_{3}$
. If
$M\equiv U_{3}$
. If
![]() ${\it\psi}_{\boldsymbol{k}}$
has been normalized in such a way that
${\it\psi}_{\boldsymbol{k}}$
has been normalized in such a way that
 $M_{\boldsymbol{k}\boldsymbol{p}\boldsymbol{q}}+M_{\boldsymbol{p}\boldsymbol{q}\boldsymbol{k}}+M_{\boldsymbol{q}\boldsymbol{k}\boldsymbol{p}}=0$
, then one can verify that
$M_{\boldsymbol{k}\boldsymbol{p}\boldsymbol{q}}+M_{\boldsymbol{p}\boldsymbol{q}\boldsymbol{k}}+M_{\boldsymbol{q}\boldsymbol{k}\boldsymbol{p}}=0$
, then one can verify that
 $$\begin{eqnarray}\mathop{\sum }_{\boldsymbol{k}}[-\widehat{{\it\Sigma}}_{\boldsymbol{k}}(t;\overline{t})\widehat{C}_{\boldsymbol{k}}^{\ast }(t,\overline{t})+\widehat{F}_{\boldsymbol{ k}}(t;\overline{t})\widehat{R}_{\boldsymbol{k}}^{\ast }(t;\overline{t})]=0.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\boldsymbol{k}}[-\widehat{{\it\Sigma}}_{\boldsymbol{k}}(t;\overline{t})\widehat{C}_{\boldsymbol{k}}^{\ast }(t,\overline{t})+\widehat{F}_{\boldsymbol{ k}}(t;\overline{t})\widehat{R}_{\boldsymbol{k}}^{\ast }(t;\overline{t})]=0.\end{eqnarray}$$
This is a statement of ‘energy’ conservation by the nonlinear terms:
 $\sum _{\boldsymbol{k}}\!\left.C_{\boldsymbol{k}}(t,t)\right|_{\text{n.l.}}=0$
. (The proof can as easily be conducted in
$\sum _{\boldsymbol{k}}\!\left.C_{\boldsymbol{k}}(t,t)\right|_{\text{n.l.}}=0$
. (The proof can as easily be conducted in
![]() $\boldsymbol{x}$
space.) This result is inherited from the primitive amplitude
equation; it is an essential property that any credible closure should satisfy.
$\boldsymbol{x}$
space.) This result is inherited from the primitive amplitude
equation; it is an essential property that any credible closure should satisfy.
The pros and cons of the DIA have been discussed at great length (Krommes Reference Krommes2002, and references therein). Significantly, it is known that the DIA is realizable; it provides the exact description of the second-order statistics for certain stochastic models. Some general discussion and original references are given by Kraichnan (Reference Kraichnan and Sirovich1991). Although the first demonstration of realizability involved a so-called random-coupling model (Kraichnan Reference Kraichnan1961), a more intuitive generalized Langevin representation was later displayed by Kraichnan (Reference Kraichnan1970) and Leith (Reference Leith1971). For homogeneous statistics, that model is
 $$\begin{eqnarray}\partial _{t}\widetilde{{\it\psi}}_{\boldsymbol{k}}(t)-L_{\boldsymbol{k}}\widetilde{{\it\psi}}_{\boldsymbol{k}}+\int _{0}^{t}\!\text{d}\overline{t}\,\widehat{{\it\Sigma}}_{\boldsymbol{ k}}(t;\overline{t})\widetilde{{\it\psi}}_{\boldsymbol{k}}(\overline{t})=\,\widetilde{f}_{\boldsymbol{k}}^{\text{int}}(t)+\,\widetilde{f}_{\boldsymbol{ k}}^{\text{ext}}(t),\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t}\widetilde{{\it\psi}}_{\boldsymbol{k}}(t)-L_{\boldsymbol{k}}\widetilde{{\it\psi}}_{\boldsymbol{k}}+\int _{0}^{t}\!\text{d}\overline{t}\,\widehat{{\it\Sigma}}_{\boldsymbol{ k}}(t;\overline{t})\widetilde{{\it\psi}}_{\boldsymbol{k}}(\overline{t})=\,\widetilde{f}_{\boldsymbol{k}}^{\text{int}}(t)+\,\widetilde{f}_{\boldsymbol{ k}}^{\text{ext}}(t),\end{eqnarray}$$
where
![]() $\widehat{{\it\Sigma}}_{\boldsymbol{k}}$
has the DIA form (4.26),
$\widehat{{\it\Sigma}}_{\boldsymbol{k}}$
has the DIA form (4.26),
 $$\begin{eqnarray}\widetilde{f}_{\boldsymbol{k}}^{\text{int}}(t)\doteq \frac{1}{2}\mathop{\sum }_{\boldsymbol{p},\boldsymbol{q}}{\it\delta}_{\boldsymbol{k}+\boldsymbol{p}+\boldsymbol{q},\mathbf{0}}M_{\boldsymbol{k}\boldsymbol{p}\boldsymbol{q}}\widetilde{{\it\xi}}_{\boldsymbol{p}}^{\ast }(t)\widetilde{{\it\xi}}_{\boldsymbol{ q}}^{\ast }(t),\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{f}_{\boldsymbol{k}}^{\text{int}}(t)\doteq \frac{1}{2}\mathop{\sum }_{\boldsymbol{p},\boldsymbol{q}}{\it\delta}_{\boldsymbol{k}+\boldsymbol{p}+\boldsymbol{q},\mathbf{0}}M_{\boldsymbol{k}\boldsymbol{p}\boldsymbol{q}}\widetilde{{\it\xi}}_{\boldsymbol{p}}^{\ast }(t)\widetilde{{\it\xi}}_{\boldsymbol{ q}}^{\ast }(t),\end{eqnarray}$$
and
![]() $\widetilde{{\it\xi}}_{\boldsymbol{p}}$
is an auxiliary random variable having covariance
$\widetilde{{\it\xi}}_{\boldsymbol{p}}$
is an auxiliary random variable having covariance
![]() $C_{\boldsymbol{p}}$
. It is left as an instructive exercise for the reader to verify
that the equations for the response function and covariance that follow from (4.29) reproduce the DIA.
$C_{\boldsymbol{p}}$
. It is left as an instructive exercise for the reader to verify
that the equations for the response function and covariance that follow from (4.29) reproduce the DIA.
In addition to realizability (which guarantees a positive-semidefinite covariance),
the DIA properly reduces to weak-turbulence theory at the level of wave–wave–particle
or three-wave coupling (but omits some terms associated with higher-order
processesFootnote
73
). Its self-consistent, nonlinearly energy-conserving determination of
![]() $R$
and
$R$
and
![]() $C$
is a definite plus, and it has enjoyed considerable successes
(Kraichnan Reference Kraichnan1964a
; Krommes Reference Krommes2002). However, the
approximation described in the present section, and others like it, merely define
algorithms; for arbitrarily strong turbulence, they cannot be systematically defended
because one does not have a controlled estimate of the size of the non-Gaussian
effects. A well-known qualitative issue related to the lack of random Galilean
invariance is discussed in § 5.1. The DIA
cannot deal properly with mixtures of turbulent motions and coherent structures. And
even for regimes in which the DIA is expected to be good, it is quite complicated.
Alternative, simpler approximations are mentioned later in the article.
$C$
is a definite plus, and it has enjoyed considerable successes
(Kraichnan Reference Kraichnan1964a
; Krommes Reference Krommes2002). However, the
approximation described in the present section, and others like it, merely define
algorithms; for arbitrarily strong turbulence, they cannot be systematically defended
because one does not have a controlled estimate of the size of the non-Gaussian
effects. A well-known qualitative issue related to the lack of random Galilean
invariance is discussed in § 5.1. The DIA
cannot deal properly with mixtures of turbulent motions and coherent structures. And
even for regimes in which the DIA is expected to be good, it is quite complicated.
Alternative, simpler approximations are mentioned later in the article.
4.2. Perturbative algorithm for the dielectric function of a general turbulent medium in the direct-interaction approximation
As I discussed after (3.29), the
essence of the
![]() $R{-}g{-}{\mathcal{D}}$
factorization obtained by DuBois and Espedal was the grouping of
the nonlinear terms in the equation for the response function into two parts. In
their words, they ‘temporarily consider [
$R{-}g{-}{\mathcal{D}}$
factorization obtained by DuBois and Espedal was the grouping of
the nonlinear terms in the equation for the response function into two parts. In
their words, they ‘temporarily consider [
![]() $f$
] and [
$f$
] and [
![]() $\boldsymbol{E}$
] as independent functional variables’ and replace
$\boldsymbol{E}$
] as independent functional variables’ and replace
![]() ${\it\delta}/{\it\delta}f$
in (3.29) by
${\it\delta}/{\it\delta}f$
in (3.29) by
 $$\begin{eqnarray}\left.\frac{{\it\delta}}{{\it\delta}f}\right|_{\boldsymbol{E}}+\frac{{\it\delta}\boldsymbol{E}}{{\it\delta}f}\boldsymbol{\cdot }\left.\frac{{\it\delta}}{{\it\delta}\boldsymbol{E}}\right|_{f}=\left.\frac{{\it\delta}}{{\it\delta}f}\right|_{\boldsymbol{E}}+\left.\frac{{\it\delta}}{{\it\delta}\boldsymbol{E}}\right|_{f}\boldsymbol{\cdot }\pmb{\mathbb{E}}.\end{eqnarray}$$
$$\begin{eqnarray}\left.\frac{{\it\delta}}{{\it\delta}f}\right|_{\boldsymbol{E}}+\frac{{\it\delta}\boldsymbol{E}}{{\it\delta}f}\boldsymbol{\cdot }\left.\frac{{\it\delta}}{{\it\delta}\boldsymbol{E}}\right|_{f}=\left.\frac{{\it\delta}}{{\it\delta}f}\right|_{\boldsymbol{E}}+\left.\frac{{\it\delta}}{{\it\delta}\boldsymbol{E}}\right|_{f}\boldsymbol{\cdot }\pmb{\mathbb{E}}.\end{eqnarray}$$
However, if one tries the same approach for the
Navier–Stokes equation, the nonlinear term of which is essentially (modulo the
constraint of incompressibility)
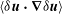 $\langle {\it\delta}\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\delta}\boldsymbol{u}\rangle$
, confusion arises because the two
$\langle {\it\delta}\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\delta}\boldsymbol{u}\rangle$
, confusion arises because the two
![]() $\boldsymbol{u}$
’s are obviously not functionally independent. In fact, the
assumption of functional independence is problematic even for the plasma case because
$\boldsymbol{u}$
’s are obviously not functionally independent. In fact, the
assumption of functional independence is problematic even for the plasma case because
![]() $\boldsymbol{E}$
and
$\boldsymbol{E}$
and
![]() $f$
are related by
$f$
are related by
![]() $\boldsymbol{E}=\pmb{\mathbb{E}}f$
. Operationally, what is really being done is keeping track of which
term is responsible for the advection, then organizing the terms in such a way that
the self-consistent response is split off. This leads one to a formula for the
dielectric of a general (quadratically nonlinear) system. I shall illustrate the
procedure in the DIA.
$\boldsymbol{E}=\pmb{\mathbb{E}}f$
. Operationally, what is really being done is keeping track of which
term is responsible for the advection, then organizing the terms in such a way that
the self-consistent response is split off. This leads one to a formula for the
dielectric of a general (quadratically nonlinear) system. I shall illustrate the
procedure in the DIA.
The approach will be to calculate nonlinear corrections to
![]() $R$
perturbatively, then to heuristically renormalize by replacing
certain zeroth- or second-order quantities by their exact counterparts. This is one
of the standard elementary procedures for obtaining the DIA itself (Kraichnan Reference Kraichnan1977; DuBois & Pesme Reference DuBois and Pesme1985); where the methodology differs is that the symmetrized form
of the mode-coupling coefficient will not be used here. Working with the
unsymmetrized form allows one to distinguish terms associated with advection and with
self-consistent response; this leads to a procedure that generalizes the approach of
DuBois and Espedal.
$R$
perturbatively, then to heuristically renormalize by replacing
certain zeroth- or second-order quantities by their exact counterparts. This is one
of the standard elementary procedures for obtaining the DIA itself (Kraichnan Reference Kraichnan1977; DuBois & Pesme Reference DuBois and Pesme1985); where the methodology differs is that the symmetrized form
of the mode-coupling coefficient will not be used here. Working with the
unsymmetrized form allows one to distinguish terms associated with advection and with
self-consistent response; this leads to a procedure that generalizes the approach of
DuBois and Espedal.
For conciseness, I shall use a subscript notation that looks like a Fourier
representation. In fact, however, the notation works in either
![]() $\boldsymbol{x}$
space or
$\boldsymbol{x}$
space or
![]() $\boldsymbol{k}$
space. A subscript
$\boldsymbol{k}$
space. A subscript
![]() $k$
could be a combination of discrete index (say for a Cartesian
velocity component) and continuous variable (either
$k$
could be a combination of discrete index (say for a Cartesian
velocity component) and continuous variable (either
![]() $\boldsymbol{k}$
or
$\boldsymbol{k}$
or
![]() $\boldsymbol{x}$
, and
$\boldsymbol{x}$
, and
![]() $t$
). Again, sums over repeated indices are assumed. Let the dynamical
equation be written
$t$
). Again, sums over repeated indices are assumed. Let the dynamical
equation be written
 $$\begin{eqnarray}(R_{k}^{(0)})^{-1}\widetilde{{\it\psi}}_{k}-\widehat{M}_{k\,\widehat{p}\,q}\widetilde{{\it\psi}}_{\widehat{p}}\widetilde{{\it\psi}}_{q}=\widehat{{\it\eta}}_{k}.\end{eqnarray}$$
$$\begin{eqnarray}(R_{k}^{(0)})^{-1}\widetilde{{\it\psi}}_{k}-\widehat{M}_{k\,\widehat{p}\,q}\widetilde{{\it\psi}}_{\widehat{p}}\widetilde{{\it\psi}}_{q}=\widehat{{\it\eta}}_{k}.\end{eqnarray}$$
The hatted index identifies the advection term. Here
![]() $\widehat{M}_{}$
is not symmetric in its last two indices. Let me again underline
terms that do not exist for passive advection. Then the random response function
obeys
$\widehat{M}_{}$
is not symmetric in its last two indices. Let me again underline
terms that do not exist for passive advection. Then the random response function
obeys
 $$\begin{eqnarray}(R^{(0)})^{-1}\widetilde{R}_{k\,k^{\prime }}-\widehat{M}_{k\,\widehat{p}\,q}(\widetilde{{\it\psi}}_{\widehat{p}}\widetilde{R}_{q\,k^{\prime }}+\underline{\widetilde{R}_{\widehat{p}\,k^{\prime }}\widetilde{{\it\psi}}_{q}})={\it\delta}_{k\,k^{\prime }}.\end{eqnarray}$$
$$\begin{eqnarray}(R^{(0)})^{-1}\widetilde{R}_{k\,k^{\prime }}-\widehat{M}_{k\,\widehat{p}\,q}(\widetilde{{\it\psi}}_{\widehat{p}}\widetilde{R}_{q\,k^{\prime }}+\underline{\widetilde{R}_{\widehat{p}\,k^{\prime }}\widetilde{{\it\psi}}_{q}})={\it\delta}_{k\,k^{\prime }}.\end{eqnarray}$$
At first order, one has
 $$\begin{eqnarray}\widetilde{R}_{k\,k^{\prime }}^{(1)}=R_{k\,\overline{k}}^{(0)}\widehat{M}_{\overline{k}\,\overline{p}\,\overline{q}}(\widetilde{{\it\psi}}_{\widehat{\overline{p}}}^{(1)}\widetilde{R}_{\overline{q}\,k^{\prime }}^{(0)}+\underline{\widetilde{R}_{\widehat{\overline{p}}\,k^{\prime }}^{(0)}\widetilde{{\it\psi}}_{\overline{q}}^{(1)}}).\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{R}_{k\,k^{\prime }}^{(1)}=R_{k\,\overline{k}}^{(0)}\widehat{M}_{\overline{k}\,\overline{p}\,\overline{q}}(\widetilde{{\it\psi}}_{\widehat{\overline{p}}}^{(1)}\widetilde{R}_{\overline{q}\,k^{\prime }}^{(0)}+\underline{\widetilde{R}_{\widehat{\overline{p}}\,k^{\prime }}^{(0)}\widetilde{{\it\psi}}_{\overline{q}}^{(1)}}).\end{eqnarray}$$
Upon averaging (4.33), one finds that through second order
![]() $R$
obeys
$R$
obeys
 $$\begin{eqnarray}(R^{(0)})^{-1}R_{k\,k^{\prime }}-\widehat{M}_{k\,p\,q}(\langle \widetilde{{\it\psi}}_{\widehat{p}}^{(1)}\widetilde{R}_{q\,k^{\prime }}^{(1)}\rangle +\underline{\langle \widetilde{R}_{\widehat{p}\,k^{\prime }}^{(1)}\widetilde{{\it\psi}}_{q}^{(1)}\rangle })={\it\delta}_{k\,k^{\prime }}.\end{eqnarray}$$
$$\begin{eqnarray}(R^{(0)})^{-1}R_{k\,k^{\prime }}-\widehat{M}_{k\,p\,q}(\langle \widetilde{{\it\psi}}_{\widehat{p}}^{(1)}\widetilde{R}_{q\,k^{\prime }}^{(1)}\rangle +\underline{\langle \widetilde{R}_{\widehat{p}\,k^{\prime }}^{(1)}\widetilde{{\it\psi}}_{q}^{(1)}\rangle })={\it\delta}_{k\,k^{\prime }}.\end{eqnarray}$$
Substitution of (4.34) gives
 $$\begin{eqnarray}\displaystyle & & \displaystyle (R^{(0)})^{-1}R_{k\,k^{\prime }}-\widehat{M}_{k\,\widehat{p}\,q}R_{q\,\overline{k}}^{(0)}\widehat{M}_{\overline{k}\,\widehat{\overline{p}}\,\overline{q}}(C_{\widehat{p}\,\widehat{\overline{p}}}^{(2)}R_{\overline{q}\,k^{\prime }}^{(0)}+\underline{C_{\widehat{p}\,\overline{q}}^{(2)}R_{\widehat{\overline{p}}\,k^{\prime }}^{(0)}})\nonumber\\ \displaystyle & & \displaystyle \quad -\,\widehat{M}_{k\,\widehat{p}\,q}R_{\widehat{p}\,\overline{k}}^{(0)}\widehat{M}_{\overline{k}\,\widehat{\overline{p}}\,\overline{q}}(C_{\widehat{\overline{p}}\,q}^{(2)}R_{\overline{q}\,k^{\prime }}^{(0)}+\underline{R_{\widehat{\overline{p}}\,k^{\prime }}^{(0)}C_{\overline{q}\,q}^{(2)}})={\it\delta}_{k\,k^{\prime }}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (R^{(0)})^{-1}R_{k\,k^{\prime }}-\widehat{M}_{k\,\widehat{p}\,q}R_{q\,\overline{k}}^{(0)}\widehat{M}_{\overline{k}\,\widehat{\overline{p}}\,\overline{q}}(C_{\widehat{p}\,\widehat{\overline{p}}}^{(2)}R_{\overline{q}\,k^{\prime }}^{(0)}+\underline{C_{\widehat{p}\,\overline{q}}^{(2)}R_{\widehat{\overline{p}}\,k^{\prime }}^{(0)}})\nonumber\\ \displaystyle & & \displaystyle \quad -\,\widehat{M}_{k\,\widehat{p}\,q}R_{\widehat{p}\,\overline{k}}^{(0)}\widehat{M}_{\overline{k}\,\widehat{\overline{p}}\,\overline{q}}(C_{\widehat{\overline{p}}\,q}^{(2)}R_{\overline{q}\,k^{\prime }}^{(0)}+\underline{R_{\widehat{\overline{p}}\,k^{\prime }}^{(0)}C_{\overline{q}\,q}^{(2)}})={\it\delta}_{k\,k^{\prime }}.\end{eqnarray}$$
In the last expression, the underlined quantities identify terms in
which a hatted index is associated with
![]() $R$
. Applying a hatted index to
$R$
. Applying a hatted index to
![]() $R$
is the generalization of applying the
$R$
is the generalization of applying the
![]() $\pmb{\mathbb{E}}$
operator in the original manipulations of DuBois and Espedal; i.e.,
it is related to the last term in (4.31). I shall group terms involving a hatted index on
$\pmb{\mathbb{E}}$
operator in the original manipulations of DuBois and Espedal; i.e.,
it is related to the last term in (4.31). I shall group terms involving a hatted index on
![]() $R$
separately, and I shall also interchange indices so that the names
of the indices on each
$R$
separately, and I shall also interchange indices so that the names
of the indices on each
![]() $C$
and
$C$
and
![]() $R$
match. Furthermore, one can heuristically renormalize by dropping
the superscripts on all quantities. Then one obtains
$R$
match. Furthermore, one can heuristically renormalize by dropping
the superscripts on all quantities. Then one obtains
 $$\begin{eqnarray}g_{k\,\overline{k}}^{-1}R_{\overline{k}\,k^{\prime }}+{\it\Sigma}_{k\widehat{\overline{k}}}^{f}R_{\widehat{\overline{k}}\,k^{\prime }}={\it\delta}_{k\,k^{\prime }},\end{eqnarray}$$
$$\begin{eqnarray}g_{k\,\overline{k}}^{-1}R_{\overline{k}\,k^{\prime }}+{\it\Sigma}_{k\widehat{\overline{k}}}^{f}R_{\widehat{\overline{k}}\,k^{\prime }}={\it\delta}_{k\,k^{\prime }},\end{eqnarray}$$
where
 $$\begin{eqnarray}(g_{0}^{-1}+{\it\Sigma}_{k\,\overline{k}}^{g})g_{\overline{k}\,k^{\prime }}={\it\delta}_{k\,k^{\prime }}\end{eqnarray}$$
$$\begin{eqnarray}(g_{0}^{-1}+{\it\Sigma}_{k\,\overline{k}}^{g})g_{\overline{k}\,k^{\prime }}={\it\delta}_{k\,k^{\prime }}\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle {\it\Sigma}_{k\,\overline{k}}^{g} & \doteq & \displaystyle -\widehat{M}_{k\,\widehat{p}\,q}(R_{q\,\overline{q}}C_{\widehat{p}\,\widehat{\overline{p}}}\widehat{M}_{\overline{q}\,\widehat{\overline{p}}\,\overline{k}}+R_{\widehat{p}\overline{p}}C_{\widehat{\overline{q}}q}\widehat{M}_{\overline{p}\,\widehat{\overline{q}}\,\overline{k}})\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\Sigma}_{k\,\overline{k}}^{g} & \doteq & \displaystyle -\widehat{M}_{k\,\widehat{p}\,q}(R_{q\,\overline{q}}C_{\widehat{p}\,\widehat{\overline{p}}}\widehat{M}_{\overline{q}\,\widehat{\overline{p}}\,\overline{k}}+R_{\widehat{p}\overline{p}}C_{\widehat{\overline{q}}q}\widehat{M}_{\overline{p}\,\widehat{\overline{q}}\,\overline{k}})\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & = & \displaystyle -M_{k\,p\,q}R_{p\,\overline{p}}C_{q\,\overline{q}}\widehat{M}_{\overline{p}\,\overline{q}\,\overline{k}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle -M_{k\,p\,q}R_{p\,\overline{p}}C_{q\,\overline{q}}\widehat{M}_{\overline{p}\,\overline{q}\,\overline{k}},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle {\it\Sigma}_{k\,\widehat{\overline{k}}}^{f} & \doteq & \displaystyle -\widehat{M}_{k\,\widehat{p}\,q}(R_{q\,\overline{q}}C_{\widehat{p}\,\overline{p}}\widehat{M}_{\overline{q}\,\widehat{\overline{k}}\,\overline{p}}+R_{\widehat{p}\,\overline{p}}C_{\overline{q}\,q}\widehat{M}_{\overline{p}\,\widehat{\overline{k}}\,\overline{q}})\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\Sigma}_{k\,\widehat{\overline{k}}}^{f} & \doteq & \displaystyle -\widehat{M}_{k\,\widehat{p}\,q}(R_{q\,\overline{q}}C_{\widehat{p}\,\overline{p}}\widehat{M}_{\overline{q}\,\widehat{\overline{k}}\,\overline{p}}+R_{\widehat{p}\,\overline{p}}C_{\overline{q}\,q}\widehat{M}_{\overline{p}\,\widehat{\overline{k}}\,\overline{q}})\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & = & \displaystyle -M_{k\,p\,q}R_{p\,\overline{p}}C_{q\,\overline{q}}\widehat{M}_{\overline{p}\,\widehat{\overline{k}}\,\overline{q}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle -M_{k\,p\,q}R_{p\,\overline{p}}C_{q\,\overline{q}}\widehat{M}_{\overline{p}\,\widehat{\overline{k}}\,\overline{q}}.\end{eqnarray}$$
 $M_{k\,p\,q}\doteq \widehat{M}_{k\,p\,q}+\widehat{M}_{k\,q\,p}$
and redundant hats were dropped in each of the final expressions.)
The quantity
$M_{k\,p\,q}\doteq \widehat{M}_{k\,p\,q}+\widehat{M}_{k\,q\,p}$
and redundant hats were dropped in each of the final expressions.)
The quantity
These general formulas work for both kinetic problems, where the indices are six-dimensional (plus time), and fluid problems, where there is no velocity variable. When the latter case is applied to a scalar field, the operations become purely multiplicative; no summations or integrations occur. Then one can define a dielectric function simply by the ratio of particle to total response:
 $$\begin{eqnarray}{\mathcal{D}}(\boldsymbol{k},{\it\omega})=\frac{g(\boldsymbol{k},{\it\omega})}{R(\boldsymbol{k},{\it\omega})}=\frac{(g_{0}^{-1}+{\it\Sigma})(\boldsymbol{k},{\it\omega})}{(g_{0}^{-1}+{\it\Sigma}^{g})(\boldsymbol{k},{\it\omega})}=1+\frac{{\it\Sigma}^{f}(\boldsymbol{k},{\it\omega})}{(g_{0}^{-1}+{\it\Sigma}^{g})(\boldsymbol{k},{\it\omega})},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{D}}(\boldsymbol{k},{\it\omega})=\frac{g(\boldsymbol{k},{\it\omega})}{R(\boldsymbol{k},{\it\omega})}=\frac{(g_{0}^{-1}+{\it\Sigma})(\boldsymbol{k},{\it\omega})}{(g_{0}^{-1}+{\it\Sigma}^{g})(\boldsymbol{k},{\it\omega})}=1+\frac{{\it\Sigma}^{f}(\boldsymbol{k},{\it\omega})}{(g_{0}^{-1}+{\it\Sigma}^{g})(\boldsymbol{k},{\it\omega})},\end{eqnarray}$$
where
 ${\it\Sigma}\doteq {\it\Sigma}^{g}+{\it\Sigma}^{f}$
and formula (4.41) holds for the case of zero mean field. An important example of this
situation is the guiding-centre plasma model (a system of charged rods moving across
a very large magnetic field with
${\it\Sigma}\doteq {\it\Sigma}^{g}+{\it\Sigma}^{f}$
and formula (4.41) holds for the case of zero mean field. An important example of this
situation is the guiding-centre plasma model (a system of charged rods moving across
a very large magnetic field with
![]() $\boldsymbol{E}\times \boldsymbol{B}$
motion). In a most elegant paper, Taylor (Reference Taylor1974) found the proper form of
$\boldsymbol{E}\times \boldsymbol{B}$
motion). In a most elegant paper, Taylor (Reference Taylor1974) found the proper form of
![]() ${\mathcal{D}}$
for the guiding-centre model (
${\mathcal{D}}$
for the guiding-centre model (
 $g_{0}^{-1}=-\text{i}{\it\omega}$
) in thermal equilibrium. He used a linear response formalism that
applied only to Gibbsian thermal equilibrium; subsequently Krommes & Similon
(Reference Krommes and Similon1980) showed how Taylor’s result follows
from the DIA. The present formalism recovers those results.
$g_{0}^{-1}=-\text{i}{\it\omega}$
) in thermal equilibrium. He used a linear response formalism that
applied only to Gibbsian thermal equilibrium; subsequently Krommes & Similon
(Reference Krommes and Similon1980) showed how Taylor’s result follows
from the DIA. The present formalism recovers those results.
It should be noted that self-consistency is not only responsible for dielectric
shielding, it also affects the form of the renormalized particle propagator
![]() $g$
. Whereas passive advection leads to a generalized diffusion
operator for
$g$
. Whereas passive advection leads to a generalized diffusion
operator for
![]() ${\it\Sigma}^{g}$
, polarization modifies that operator, producing among other things
a smaller effective diffusion coefficient. This was discussed by Krommes and Similon
for the guiding-centre model; the general polarization effect is described by the
second term in (4.39a
). (The first term in that equation would be the sole one arising in passive
advection because it involves a
${\it\Sigma}^{g}$
, polarization modifies that operator, producing among other things
a smaller effective diffusion coefficient. This was discussed by Krommes and Similon
for the guiding-centre model; the general polarization effect is described by the
second term in (4.39a
). (The first term in that equation would be the sole one arising in passive
advection because it involves a
![]() $C$
with two hatted indices, i.e., the covariance of the advecting
velocity.)
$C$
with two hatted indices, i.e., the covariance of the advecting
velocity.)
The method of construction guarantees that the formulas (3.32b
) and (3.33) for the
dielectric function and shielded response function hold provided that one can
identify in
![]() $\widehat{M}_{}$
the analogue of the
$\widehat{M}_{}$
the analogue of the
![]() $\pmb{\mathbb{E}}$
and
$\pmb{\mathbb{E}}$
and
![]() $\boldsymbol{\partial }$
operators; cf. (3.10b
). This appears to be most useful for cases with a two-level description – for
example, involving a velocity space that, with the
$\boldsymbol{\partial }$
operators; cf. (3.10b
). This appears to be most useful for cases with a two-level description – for
example, involving a velocity space that, with the
![]() $\widehat{p}$
index in (4.32),
must be integrated over, as in Klimontovich theory. For the plasma case, the results
are recorded in table 2. For fluid cases
without a phase-space variable (such as the guiding-centre plasma or the
Navier–Stokes equation),
$\widehat{p}$
index in (4.32),
must be integrated over, as in Klimontovich theory. For the plasma case, the results
are recorded in table 2. For fluid cases
without a phase-space variable (such as the guiding-centre plasma or the
Navier–Stokes equation),
![]() ${\mathcal{D}}$
can still be defined although the implications of this are not
fully understood. It is noteworthy that dielectric response is mentioned nowhere in
the most recent book on homogeneous turbulence (McComb Reference McComb2014). Indeed, it is unnecessary to explicitly introduce
${\mathcal{D}}$
can still be defined although the implications of this are not
fully understood. It is noteworthy that dielectric response is mentioned nowhere in
the most recent book on homogeneous turbulence (McComb Reference McComb2014). Indeed, it is unnecessary to explicitly introduce
![]() ${\mathcal{D}}$
since the response function
${\mathcal{D}}$
since the response function
![]() $R$
carries the relevant information. Nevertheless, it is clear that
nonlinear dielectric response operates in Navier–Stokes turbulence. It is not
excluded that new perspectives on certain nonlinear processes in fluid turbulence may
be obtained by expressing them in terms of the nonlinear
$R$
carries the relevant information. Nevertheless, it is clear that
nonlinear dielectric response operates in Navier–Stokes turbulence. It is not
excluded that new perspectives on certain nonlinear processes in fluid turbulence may
be obtained by expressing them in terms of the nonlinear
![]() ${\mathcal{D}}$
.
${\mathcal{D}}$
.
Table 2. Statistical closure in the DIA. See table 1 for the general form of the Dyson equations. The symmetrized
mode-coupling coefficient is
 $U_{3}(1,2,3)=\widehat{U}_{3}(1,2,3)+\widehat{U}_{3}(1,3,2)$
, where advection is associated with the second argument of
$U_{3}(1,2,3)=\widehat{U}_{3}(1,2,3)+\widehat{U}_{3}(1,3,2)$
, where advection is associated with the second argument of
![]() $\widehat{U}_{3}$
.
$\widehat{U}_{3}$
.

The key DIA formulas obtained in this section are summarized in table 2.
5. Some key points about statistical closures, especially for plasma physicists
We have now gained some intuition about the DIA, and we have seen how to obtain the
dielectric function for turbulence in the DIA. I shall say nothing explicit about
practical calculations involving
![]() ${\mathcal{D}}_{\text{DIA}}$
. But the discussion in §§ 3,
4.1, and 4.2 shows that
${\mathcal{D}}_{\text{DIA}}$
. But the discussion in §§ 3,
4.1, and 4.2 shows that
![]() ${\mathcal{D}}_{\text{DIA}}$
is included in the full DIA formalism. Any calculation that obtains
statistics in the DIA (or in any similar closure) is ipso facto
calculating the turbulent dielectric function along the way.
${\mathcal{D}}_{\text{DIA}}$
is included in the full DIA formalism. Any calculation that obtains
statistics in the DIA (or in any similar closure) is ipso facto
calculating the turbulent dielectric function along the way.
5.1. Kadomtsev and the DIA
The most general mathematical formulation of the last statement was presumably not known to Kadomtsev, although it is probable that he appreciated it at least intuitively. What is clear is that Kadomtsev understood an important deficiency of the DIA,Footnote 74 which I shall now describe.
It was already known to Kraichnan in 1959 that the DIA did not predict the famous
![]() $k^{-5/3}$
inertial-range spectrum of Navier–Stokes turbulence that follows
from the
$k^{-5/3}$
inertial-range spectrum of Navier–Stokes turbulence that follows
from the
![]() $\boldsymbol{x}$
-space self-similarity considerations of Kolmogorov (Reference Kolmogorov1941). (For some careful discussion, see Frisch
(Reference Frisch1995).) Instead, the DIA predicts
$\boldsymbol{x}$
-space self-similarity considerations of Kolmogorov (Reference Kolmogorov1941). (For some careful discussion, see Frisch
(Reference Frisch1995).) Instead, the DIA predicts
![]() $k^{-3/2}$
, and for a time Kraichnan entertained the possibility that
Kolmogorov was incorrect. However, the tidal-basin measurements of Grant, Stewart
& Moilliet (Reference Grant, Stewart and Moilliet1962) confirmed Kolmogorov’s
prediction, so Kraichnan was led to reconsider the structure of the DIA. In 1964 he
explained (Kraichnan Reference Kraichnan1964c
) that the difficulty is that the DIA is not invariant to random Galilean
transformations. Ordinary Galilean invariance implies that, under the addition of an
infinite-wavelength flow, short-scale eddies should be carried along unchanged. In
fact, the DIA is Galilean invariant in that respect (McComb Reference McComb2014). But if one considers an ensemble of such flows with
random direction and strength, phase-mixing effects arise as a consequence of
ensemble averaging. Those are captured correctly by the two-time
$k^{-3/2}$
, and for a time Kraichnan entertained the possibility that
Kolmogorov was incorrect. However, the tidal-basin measurements of Grant, Stewart
& Moilliet (Reference Grant, Stewart and Moilliet1962) confirmed Kolmogorov’s
prediction, so Kraichnan was led to reconsider the structure of the DIA. In 1964 he
explained (Kraichnan Reference Kraichnan1964c
) that the difficulty is that the DIA is not invariant to random Galilean
transformations. Ordinary Galilean invariance implies that, under the addition of an
infinite-wavelength flow, short-scale eddies should be carried along unchanged. In
fact, the DIA is Galilean invariant in that respect (McComb Reference McComb2014). But if one considers an ensemble of such flows with
random direction and strength, phase-mixing effects arise as a consequence of
ensemble averaging. Those are captured correctly by the two-time
![]() $R$
, as in the stochastic-oscillator model. However, because of the
intimate way in which the DIA couples
$R$
, as in the stochastic-oscillator model. However, because of the
intimate way in which the DIA couples
![]() $R(t;t^{\prime })$
and
$R(t;t^{\prime })$
and
![]() $C(t,t^{\prime })$
to
$C(t,t^{\prime })$
to
![]() $C(t,t)$
(discussed in mathematical detail by Kraichnan (Reference Kraichnan1964c
); see also footnote 33 on page 16), that phase mixing introduces spurious
distortion into the small-scale eddies (see figure 4), which shows up as an incorrect inertial-range spectrum.
$C(t,t)$
(discussed in mathematical detail by Kraichnan (Reference Kraichnan1964c
); see also footnote 33 on page 16), that phase mixing introduces spurious
distortion into the small-scale eddies (see figure 4), which shows up as an incorrect inertial-range spectrum.

Figure 4. Illustration of difficulties with random Galilean invariance. In the top panel, an infinite-wavelength flow (no shear) translates an eddy unchanged. In the bottom panel, the average over an ensemble of such flows produces in the DIA a spurious distortion of a typical eddy, violating random Galilean invariance.
Also in 1964, Kadomtsev’s review appeared in Russian. It contains, after some discussion about the differences between resonant and adiabatic wave interactions and the role of wavepackets, the following observation (p. 55):
[The weak coupling approximation, a.k.a. DIA] over-estimates the part played by the large-scale fluctuations, which is in fact no more than the convection of higher modes which are deformed adiabatically in the process.
Kadomtsev’s discussion was not as crisply technical as Kraichnan’s, but certainly he understood the intuitive essence of the issue. Because of the publication dates, writing styles, and lack of cross-references, it seems clear that the analyses were independent.
The issue of random Galilean invariance has received much attention and fostered many attempts at a cure. In general, it has been understood that the problem cannot be cured within a systematically renormalized Eulerian formulation (which includes the MSR formalism). A heuristic Eulerian approximation that does respect random Galilean invariance is the eddy-damped quasi-normal Markovian closure (Orszag Reference Orszag1970), and various more or less successful Lagrangian schemes have also been discussed (Kraichnan Reference Kraichnan1965; McComb Reference McComb2014). But it should be emphasized that in many problems of practical interest the issue is only of secondary importance. In particular, turbulent transport is usually dominated by the long-wavelength, energy-containing fluctuations, in which case it is insensitive to the precise form of the inertial range. Although there are situations (for example, the intermittent mixing of contaminants) in which one cares about detailed inertial-range structure, they are well beyond the scope of this article; see Falkovich, Gawȩdzki & Vergassola (Reference Falkovich, Gawȩdzki and Vergassola2001). Fusion plasma physicists should not be overly concerned with inertial-range spectra, although the shapes of those spectra sometimes figure in discussions of closures for large-eddy simulations (see footnote 9 on page 6).
5.2. Drift-wave saturation and the mixing-length formula
The DIA for Vlasov turbulence was first discussed by Orszag & Kraichnan (Reference Orszag and Kraichnan1967); further contributions were made by DuBois & Espedal (Reference DuBois and Espedal1978), Krommes (Reference Krommes1978), and DuBois & Pesme (Reference DuBois and Pesme1985). However, kinetic DIA calculations proved mostly too hard to perform at the time. Plasma physicists slowly latched on to the use of the DIA for fluid models (Krommes Reference Krommes1982; Waltz Reference Waltz1983; Sudan & Pfirsch Reference Sudan and Pfirsch1985), though even there it is rather complicated for anisotropic turbulence. That difficulty fostered the development of DIA-based Markovian closures for plasma turbulence (Waltz Reference Waltz1983; Bowman Reference Bowman1992; Bowman et al. Reference Bowman, Krommes and Ottaviani1993; Bowman & Krommes Reference Bowman and Krommes1997), and those can be used to quantify some important heuristic drift-wave scalings discussed by Kadomtsev. Here I shall give a brief introduction. Definitions of the symbols used in the following discussion are given in appendix A.
5.2.1. The Hasegawa–Mima equation
More than ten years after Kadomtsev’s monograph, Hasegawa & Mima (Reference Hasegawa and Mima1978) proposed a nonlinear PDE, now known as the Hasegawa–Mima equation (HME), that serves as a very useful paradigm for understanding the basic physics of drift-wave turbulence. The equation isFootnote 75
 $$\begin{eqnarray}(\underbrace{1}_{(\text{i})}-\underbrace{{\it\rho}_{\text{s}}^{2}{\rm\nabla}_{\bot }^{2}}_{(\text{ii})})\partial _{t}{\it\varphi}+\underbrace{V_{\ast }\partial _{\text{y}}{\it\varphi}}_{(\text{iii})}+\underbrace{\boldsymbol{V}_{E}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}(-{\it\rho}_{\text{s}}^{2}{\rm\nabla}_{\bot }^{2}{\it\varphi})}_{(\text{iv})}=0;\end{eqnarray}$$
$$\begin{eqnarray}(\underbrace{1}_{(\text{i})}-\underbrace{{\it\rho}_{\text{s}}^{2}{\rm\nabla}_{\bot }^{2}}_{(\text{ii})})\partial _{t}{\it\varphi}+\underbrace{V_{\ast }\partial _{\text{y}}{\it\varphi}}_{(\text{iii})}+\underbrace{\boldsymbol{V}_{E}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}(-{\it\rho}_{\text{s}}^{2}{\rm\nabla}_{\bot }^{2}{\it\varphi})}_{(\text{iv})}=0;\end{eqnarray}$$
it has been studied extensively. Indeed, the HME has the same form
as the equation of Charney & Stern (Reference Charney and Stern1962) for Rossby-wave turbulence with finite deformation radiusFootnote
76
![]() $L_{\text{d}}$
. (In the HME,
$L_{\text{d}}$
. (In the HME,
![]() ${\it\rho}_{\text{s}}$
plays the role of
${\it\rho}_{\text{s}}$
plays the role of
![]() $L_{\text{d}}$
.) For infinite
$L_{\text{d}}$
.) For infinite
![]() $L_{\text{d}}$
, the equation reduces to the barotropic vorticity equation that
is a subject of intense interest in geophysics and related areas; see various
articles in Galperin & Read (Reference Galperin and Read2015).
$L_{\text{d}}$
, the equation reduces to the barotropic vorticity equation that
is a subject of intense interest in geophysics and related areas; see various
articles in Galperin & Read (Reference Galperin and Read2015).
In plasma physics, the interpretations of the various terms of the HME are as
follows: (i) adiabatic response of electrons, streaming along magnetic field
lines, to the slowly changing electrostatic potential of the drift wave; (ii) wave
dispersion due to ion polarization drift; (iii)
![]() $\boldsymbol{E}\times \boldsymbol{B}$
advection of the background density profile; and (iv)
$\boldsymbol{E}\times \boldsymbol{B}$
advection of the background density profile; and (iv)
![]() $\boldsymbol{E}\times \boldsymbol{B}$
advection of vorticity (frequently called the polarization-drift
nonlinearity). The linear dispersion relation of the HME reproduces (3.7).
$\boldsymbol{E}\times \boldsymbol{B}$
advection of vorticity (frequently called the polarization-drift
nonlinearity). The linear dispersion relation of the HME reproduces (3.7).
The drift-wave dispersion relation (3.7) contains no linear growth or damping. That is consistent with the
fact that the basic HME is time-reversible. That property stems from the
approximate derivation of the HME from kinetic theory, in which the wave–particle
resonance is neglected in the determination of the electron response. That effect
can be restored by hand by calculating the effects of the resonance directly from
linear kinetic theory (see formula (3.5)) and expressing the result for the electron response as
 ${\it\delta}n_{e}/n_{e}=(1-\text{i}{\it\delta}){\it\varphi}$
, where
${\it\delta}n_{e}/n_{e}=(1-\text{i}{\it\delta}){\it\varphi}$
, where
![]() ${\it\delta}$
is a wavenumber-dependent operator. This changes
${\it\delta}$
is a wavenumber-dependent operator. This changes
 $1-{\it\rho}_{\text{s}}^{2}{\rm\nabla}_{\bot }^{2}$
to
$1-{\it\rho}_{\text{s}}^{2}{\rm\nabla}_{\bot }^{2}$
to
 $1-{\it\rho}_{\text{s}}^{2}{\rm\nabla}_{\bot }^{2}-\text{i}{\it\delta}$
and leads to the modified linear dispersion relation
$1-{\it\rho}_{\text{s}}^{2}{\rm\nabla}_{\bot }^{2}-\text{i}{\it\delta}$
and leads to the modified linear dispersion relation
 ${\it\omega}_{\boldsymbol{k}}={\it\omega}_{\ast \boldsymbol{k}}/(1+k_{\bot }^{2}{\it\rho}_{\text{s}}^{2}-\text{i}{\it\delta}_{\boldsymbol{k}})-{\it\nu}_{i\boldsymbol{k}}$
, where an ion damping
${\it\omega}_{\boldsymbol{k}}={\it\omega}_{\ast \boldsymbol{k}}/(1+k_{\bot }^{2}{\it\rho}_{\text{s}}^{2}-\text{i}{\it\delta}_{\boldsymbol{k}})-{\it\nu}_{i\boldsymbol{k}}$
, where an ion damping
![]() ${\it\nu}_{i}$
was also added. (Thus
${\it\nu}_{i}$
was also added. (Thus
![]() ${\it\delta}_{\boldsymbol{k}}$
is proportional to the ratio of the electron growth rate and the
mode frequency.) When the
${\it\delta}_{\boldsymbol{k}}$
is proportional to the ratio of the electron growth rate and the
mode frequency.) When the
![]() $\text{i}{\it\delta}$
is included in both the linear and nonlinear terms, the result
is called the Terry–Horton equation after the original research of Terry &
Horton (Reference Terry and Horton1982). For tutorial purposes, I
shall instead assume that
$\text{i}{\it\delta}$
is included in both the linear and nonlinear terms, the result
is called the Terry–Horton equation after the original research of Terry &
Horton (Reference Terry and Horton1982). For tutorial purposes, I
shall instead assume that
![]() $\text{i}{\it\delta}$
is neglected in the nonlinear term and thus just introduces a
linear growth rate, leading one to another example of a quadratically nonlinear
PDE, called the
$\text{i}{\it\delta}$
is neglected in the nonlinear term and thus just introduces a
linear growth rate, leading one to another example of a quadratically nonlinear
PDE, called the
![]() $\text{i}{\it\delta}$
model (Waltz Reference Waltz1983), that
takes the form (4.25) with
$\text{i}{\it\delta}$
model (Waltz Reference Waltz1983), that
takes the form (4.25) with
 $L_{\boldsymbol{k}}=-\text{i}{\it\omega}_{\boldsymbol{k}}$
and
$L_{\boldsymbol{k}}=-\text{i}{\it\omega}_{\boldsymbol{k}}$
and
 $$\begin{eqnarray}M_{\boldsymbol{k}\boldsymbol{p}\boldsymbol{q}}=\left(\frac{c_{\text{s}}}{{\it\rho}_{\text{s}}}\right)\frac{\widehat{\boldsymbol{b}}\boldsymbol{\cdot }(\boldsymbol{p}\times \boldsymbol{q})(q^{2}-p^{2})}{1+k^{2}}\end{eqnarray}$$
$$\begin{eqnarray}M_{\boldsymbol{k}\boldsymbol{p}\boldsymbol{q}}=\left(\frac{c_{\text{s}}}{{\it\rho}_{\text{s}}}\right)\frac{\widehat{\boldsymbol{b}}\boldsymbol{\cdot }(\boldsymbol{p}\times \boldsymbol{q})(q^{2}-p^{2})}{1+k^{2}}\end{eqnarray}$$
(upon dropping the
![]() $\bot$
and normalizing lengths to
$\bot$
and normalizing lengths to
![]() ${\it\rho}_{\text{s}}$
). Although the details of these various nonlinear equations
definitely matter, the basic point is that irreversible effects can lead to
instability and forced, dissipative turbulence. This was already well known to
Kadomtsev.
${\it\rho}_{\text{s}}$
). Although the details of these various nonlinear equations
definitely matter, the basic point is that irreversible effects can lead to
instability and forced, dissipative turbulence. This was already well known to
Kadomtsev.
5.2.2. Drift-wave saturation at the mixing-length level
Kadomtsev did not have the HME available to him, but he did understand the basic
physics of the drift wave, which involves radial cross-field advection of a parcel
of background ion density profile by the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
velocity according to
$\boldsymbol{E}\times \boldsymbol{B}$
velocity according to
 $$\begin{eqnarray}\partial _{t}{\it\delta}n_{i}=-{\it\delta}\boldsymbol{V}_{E}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}n_{i}.\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t}{\it\delta}n_{i}=-{\it\delta}\boldsymbol{V}_{E}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}n_{i}.\end{eqnarray}$$
Let
![]() ${\rm\Delta}t$
be a characteristic mode period. Then the ion density
fluctuation generated under coherent advection in a time
${\rm\Delta}t$
be a characteristic mode period. Then the ion density
fluctuation generated under coherent advection in a time
![]() ${\rm\Delta}t$
is
${\rm\Delta}t$
is
 $$\begin{eqnarray}\frac{{\it\delta}n_{i}}{n_{i}}\sim \frac{{\rm\Delta}\ell }{L_{n}},\end{eqnarray}$$
$$\begin{eqnarray}\frac{{\it\delta}n_{i}}{n_{i}}\sim \frac{{\rm\Delta}\ell }{L_{n}},\end{eqnarray}$$
where
![]() ${\rm\Delta}\ell$
is the distance
${\rm\Delta}\ell$
is the distance
![]() ${\it\delta}V_{E,x}{\rm\Delta}t$
moved by the fluid element and
${\it\delta}V_{E,x}{\rm\Delta}t$
moved by the fluid element and
 $L_{n}^{-1}\doteq -\partial _{\text{x}}\ln n_{i}$
. By quasi-neutrality, the electron density fluctuation must
equal this. Since the electrons are free to stream along the field lines,Footnote
77
they rapidly adjust to the ambient potential according to
$L_{n}^{-1}\doteq -\partial _{\text{x}}\ln n_{i}$
. By quasi-neutrality, the electron density fluctuation must
equal this. Since the electrons are free to stream along the field lines,Footnote
77
they rapidly adjust to the ambient potential according to
 ${\it\delta}n_{e}/n_{e}=e{\it\delta}{\it\phi}/T_{e}$
. If one balances this with the right-hand side of (5.4) and uses
${\it\delta}n_{e}/n_{e}=e{\it\delta}{\it\phi}/T_{e}$
. If one balances this with the right-hand side of (5.4) and uses
 ${\it\delta}V_{E,x}=-(c/B)k_{y}{\it\delta}{\it\phi}$
, one is readily led to the linear mode frequency
${\it\delta}V_{E,x}=-(c/B)k_{y}{\it\delta}{\it\phi}$
, one is readily led to the linear mode frequency
![]() ${\it\Omega}={\it\omega}_{\ast }$
. A more refined argument (Stoltzfus-Dueck, Scott & Krommes
Reference Stoltzfus-Dueck, Scott and Krommes2013) can take account of the
dispersive polarization-drift correction as well and can also explain how
dissipation leads to instability. As the modes grow, the density fluctuations
continue to obey (5.4), while
${\it\Omega}={\it\omega}_{\ast }$
. A more refined argument (Stoltzfus-Dueck, Scott & Krommes
Reference Stoltzfus-Dueck, Scott and Krommes2013) can take account of the
dispersive polarization-drift correction as well and can also explain how
dissipation leads to instability. As the modes grow, the density fluctuations
continue to obey (5.4), while
![]() ${\rm\Delta}\ell$
increases with
${\rm\Delta}\ell$
increases with
![]() ${\it\delta}V_{\text{E}}$
. However,
${\it\delta}V_{\text{E}}$
. However,
![]() ${\rm\Delta}\ell$
cannot increase indefinitely. When the turbulence saturates, it
will possess a characteristic correlation length
${\rm\Delta}\ell$
cannot increase indefinitely. When the turbulence saturates, it
will possess a characteristic correlation length
![]() $L_{\text{ac}}$
. The coherence of the advection postulated above will be
destroyed on that length scale; thus at saturation
$L_{\text{ac}}$
. The coherence of the advection postulated above will be
destroyed on that length scale; thus at saturation
 ${\rm\Delta}\ell \sim L_{\text{ac}}$
. Since one has
${\rm\Delta}\ell \sim L_{\text{ac}}$
. Since one has
 $L_{\text{ac}}\sim \overline{k}_{\bot }^{-1}$
, where
$L_{\text{ac}}\sim \overline{k}_{\bot }^{-1}$
, where
![]() $\overline{k}_{\bot }$
is a characteristic wavenumber,Footnote
78
one can rewrite the steady-state balance as
$\overline{k}_{\bot }$
is a characteristic wavenumber,Footnote
78
one can rewrite the steady-state balance as
 $\overline{k}_{\bot }{\it\delta}n\sim n/L_{n}$
, which means that at saturation the gradient of the typical
density fluctuation becomes of the order of the background profile gradient. This
criterion was asserted (with less discussion) by Kadomtsev (pp. 106–107),Footnote
79
and it is often quoted. Note that the argument does not by itself determine
$\overline{k}_{\bot }{\it\delta}n\sim n/L_{n}$
, which means that at saturation the gradient of the typical
density fluctuation becomes of the order of the background profile gradient. This
criterion was asserted (with less discussion) by Kadomtsev (pp. 106–107),Footnote
79
and it is often quoted. Note that the argument does not by itself determine
![]() $L_{\text{ac}}$
. But dimensional analysis of the HME with periodic boundary
conditions shows that the sole perpendicular scale in the problem is the sound
radius
$L_{\text{ac}}$
. But dimensional analysis of the HME with periodic boundary
conditions shows that the sole perpendicular scale in the problem is the sound
radius
![]() ${\it\rho}_{\text{s}}$
, so
${\it\rho}_{\text{s}}$
, so
![]() $L_{\text{ac}}$
must scale with
$L_{\text{ac}}$
must scale with
![]() ${\it\rho}_{\text{s}}$
. This leads to the saturation level
${\it\rho}_{\text{s}}$
. This leads to the saturation level
 ${\it\delta}n/n\sim {\it\rho}_{\text{s}}/L_{n}$
, which corresponds to fluctuating velocities of the order of the
diamagnetic speed
${\it\delta}n/n\sim {\it\rho}_{\text{s}}/L_{n}$
, which corresponds to fluctuating velocities of the order of the
diamagnetic speed
![]() $V_{\ast }$
.
$V_{\ast }$
.
An alternative term for correlation length in this context is mixing length, after the famous work of Prandtl (Reference Prandtl1925) on turbulent jets, and the drift-wave saturation level estimatedFootnote 80 above has come to be called the mixing-length level. Various authors such as Connor & Pogutse (Reference Connor and Pogutse2001) cite Kadomtsev (Reference Kadomtsev1965) in this context. In fact, however, Kadomtsev does not actually use the phrase ‘mixing length’ in his § IV.4 where he discusses turbulent diffusion due to drift waves, though he introduces the concept earlier in his review in connection with Reynolds stress, a topic that I shall discuss in more detail in § 6.1.
Originally Kadomtsev (Reference Kadomtsev1962) believed that
the cross-field diffusion coefficient due to saturated drift waves should be the
one that Bohm (Reference Bohm, Guthrie and Wakerling1949) obtained
experimentally and that is usually quoted as
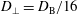 $D_{\bot }=D_{\text{B}}/16$
, where
$D_{\bot }=D_{\text{B}}/16$
, where
 $D_{\text{B}}\doteq cT_{e}/eB={\it\rho}_{\text{s}}c_{\text{s}}$
. Taylor (Reference Taylor1961) employed
Langevin equations to argue that the diffusion of a test ion can never exceed the
Bohm levelFootnote
81
(with some uncertainty in the numerical coefficient). In his book,
Kadomtsev referred to Bohm diffusion but presciently observed (p. 4),
$D_{\text{B}}\doteq cT_{e}/eB={\it\rho}_{\text{s}}c_{\text{s}}$
. Taylor (Reference Taylor1961) employed
Langevin equations to argue that the diffusion of a test ion can never exceed the
Bohm levelFootnote
81
(with some uncertainty in the numerical coefficient). In his book,
Kadomtsev referred to Bohm diffusion but presciently observed (p. 4),
It has now become evident, however, that the coefficient of turbulent diffusion cannot be obtained without a detailed investigation of the instability of an inhomogeneous plasma and in particular of its drift instability.
Indeed, the above arguments based on the HME imply that a local gyrokinetic description must lead to gyro-Bohm diffusion:
 $$\begin{eqnarray}D_{\bot }\sim \left(\frac{{\it\rho}_{\text{s}}}{L_{n}}\right)D_{\text{B}}\equiv D_{\text{gB}},\end{eqnarray}$$
$$\begin{eqnarray}D_{\bot }\sim \left(\frac{{\it\rho}_{\text{s}}}{L_{n}}\right)D_{\text{B}}\equiv D_{\text{gB}},\end{eqnarray}$$
which is much smaller than the Bohm value and has a more
favourable scaling with magnetic field. This scaling follows from the basic
dimensional analysis of drift-wave physics given above and in appendix A. It can also be recovered from the general
estimate
 $D_{\bot }\sim {\it\gamma}^{\text{lin}}/k_{\bot }^{2}$
, obtained by both Kadomtsev (chapter IV.4) and Dupree (Reference Dupree1967), if the linear growth rate is taken to
scale with the drift-wave frequency
$D_{\bot }\sim {\it\gamma}^{\text{lin}}/k_{\bot }^{2}$
, obtained by both Kadomtsev (chapter IV.4) and Dupree (Reference Dupree1967), if the linear growth rate is taken to
scale with the drift-wave frequency
![]() ${\it\omega}_{\ast }$
and fluctuation wavelengths are taken to scale with
${\it\omega}_{\ast }$
and fluctuation wavelengths are taken to scale with
 ${\it\rho}_{\text{s}}~(k_{\bot }{\it\rho}_{\text{s}}=O(1))$
:
${\it\rho}_{\text{s}}~(k_{\bot }{\it\rho}_{\text{s}}=O(1))$
:
 ${\it\omega}_{\ast }/k_{\bot }^{2}=(k_{y}{\it\rho}_{\text{s}}c_{\text{s}}/L_{n})/k_{\bot }^{2}=(k_{y}{\it\rho}_{\text{s}})({\it\rho}_{\text{s}}^{2}c_{\text{s}}/L_{n})/(k_{\bot }{\it\rho}_{\text{s}})^{2}\sim ({\it\rho}_{\text{s}}/L_{n})D_{\text{B}}$
. It took a surprisingly long time for this fact to be fully
appreciated, especially in the face of experimental results that often showed Bohm
scaling (Perkins et al.
Reference Perkins, Barnes, Johnson, Scott, Zarnstorff, Bell, Bell, Bush, Grek, Hill, Mansfield, Park, Ramsey, Schivell, Stratton and Synakowski1993). However, with the advent of modern
supercomputers, it was ultimately possible to give numerical demonstrations (Lin
et al.
Reference Lin, Ethier, Hahm and Tang2002, Reference Lin, Ethier, Hahm and Tang2012) that turbulent gyrokinetic plasmas transition from Bohm to
gyro-Bohm diffusion as
${\it\omega}_{\ast }/k_{\bot }^{2}=(k_{y}{\it\rho}_{\text{s}}c_{\text{s}}/L_{n})/k_{\bot }^{2}=(k_{y}{\it\rho}_{\text{s}})({\it\rho}_{\text{s}}^{2}c_{\text{s}}/L_{n})/(k_{\bot }{\it\rho}_{\text{s}})^{2}\sim ({\it\rho}_{\text{s}}/L_{n})D_{\text{B}}$
. It took a surprisingly long time for this fact to be fully
appreciated, especially in the face of experimental results that often showed Bohm
scaling (Perkins et al.
Reference Perkins, Barnes, Johnson, Scott, Zarnstorff, Bell, Bell, Bush, Grek, Hill, Mansfield, Park, Ramsey, Schivell, Stratton and Synakowski1993). However, with the advent of modern
supercomputers, it was ultimately possible to give numerical demonstrations (Lin
et al.
Reference Lin, Ethier, Hahm and Tang2002, Reference Lin, Ethier, Hahm and Tang2012) that turbulent gyrokinetic plasmas transition from Bohm to
gyro-Bohm diffusion as
 ${\it\rho}_{\ast }\doteq {\it\rho}_{i}/a$
is reduced. Here
${\it\rho}_{\ast }\doteq {\it\rho}_{i}/a$
is reduced. Here
![]() $a$
is the minor radius of a tokamak.
$a$
is the minor radius of a tokamak.
5.2.3. Mixing-length saturation and statistical closure
Given that all of these results are essentially dimensional in nature, one can
pose the following question. What does statistical closure have to add? One
obvious answer is that it can make quantitative predictions; for example,
dimensional analysis cannot pin down the numerical value of a diffusion
coefficient. Closure also shows in detail how the nonlinear mode coupling works.
That is of both conceptual and practical interest since predictions for the
wavenumber spectrum can be compared with numerical simulations or, in principal,
with experiments. Early important work along these lines was by Sudan &
Pfirsch (Reference Sudan and Pfirsch1985), who discussed the
relationship between the mixing-length concept and DIA-type theories. However,
since those authors did not consider drift waves, let us contemplate the
statistical analysis of an
![]() $\text{i}{\it\delta}$
generalization of the HME.
$\text{i}{\it\delta}$
generalization of the HME.
Detailed solutions of statistical closures such as the DIA must be done
numerically (LoDestro et al.
Reference LoDestro, Cohen, Cohen, Dimits, Matsuda, Nevins, Newcomb, Williams, Koniges, Dannevik, Crotinger, Sydora, Dawson, Ma, Decyk, Lee, Hahm, Naitou and Kamimura1991); that is entirely nontrivial in
general because of both mode coupling and especially time-history
integrations.Footnote
82
Therefore let us consider a Markovian approximation, which eliminates the
time-history integrals at the price of a less faithful representation of the
two-time correlations. A Markovianized version of the DIA provides an evolution
equation for the equal-time covarianceFootnote
83
![]() $C_{\boldsymbol{k}}(t)$
that takes the form (Kraichnan Reference Kraichnan1971; Bowman Reference Bowman1992; Bowman
et al.
Reference Bowman, Krommes and Ottaviani1993; Bowman & Krommes Reference Bowman and Krommes1997)
$C_{\boldsymbol{k}}(t)$
that takes the form (Kraichnan Reference Kraichnan1971; Bowman Reference Bowman1992; Bowman
et al.
Reference Bowman, Krommes and Ottaviani1993; Bowman & Krommes Reference Bowman and Krommes1997)
 $$\begin{eqnarray}\partial _{t}C_{\boldsymbol{k}}-2{\it\gamma}_{\boldsymbol{k}}^{\text{lin}}C_{\boldsymbol{ k}}+2\,\text{Re}\,{\it\eta}_{\boldsymbol{k}}C_{\boldsymbol{k}}=2F_{\boldsymbol{k}},\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t}C_{\boldsymbol{k}}-2{\it\gamma}_{\boldsymbol{k}}^{\text{lin}}C_{\boldsymbol{ k}}+2\,\text{Re}\,{\it\eta}_{\boldsymbol{k}}C_{\boldsymbol{k}}=2F_{\boldsymbol{k}},\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle & \displaystyle {\it\eta}_{\boldsymbol{k}}\doteq -\mathop{\sum }_{\boldsymbol{p},\boldsymbol{q}}{\it\delta}_{\boldsymbol{k}+\boldsymbol{p}+\boldsymbol{q},\mathbf{0}}M_{\boldsymbol{k}\boldsymbol{p}\boldsymbol{q}}M_{\boldsymbol{p}\boldsymbol{q}\boldsymbol{k}}^{\ast }{\it\theta}_{\boldsymbol{k}\boldsymbol{p}\boldsymbol{q}}^{\ast }C_{\boldsymbol{q}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\eta}_{\boldsymbol{k}}\doteq -\mathop{\sum }_{\boldsymbol{p},\boldsymbol{q}}{\it\delta}_{\boldsymbol{k}+\boldsymbol{p}+\boldsymbol{q},\mathbf{0}}M_{\boldsymbol{k}\boldsymbol{p}\boldsymbol{q}}M_{\boldsymbol{p}\boldsymbol{q}\boldsymbol{k}}^{\ast }{\it\theta}_{\boldsymbol{k}\boldsymbol{p}\boldsymbol{q}}^{\ast }C_{\boldsymbol{q}}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle F_{\boldsymbol{k}}^{\text{int}}\doteq \frac{1}{2}\mathop{\sum }_{\boldsymbol{p},\boldsymbol{q}}{\it\delta}_{\boldsymbol{k}+\boldsymbol{p}+\boldsymbol{q},\mathbf{0}}|M_{\boldsymbol{k}\boldsymbol{p}\boldsymbol{q}}|^{2}\,\text{Re}\,{\it\theta}_{\boldsymbol{k}\boldsymbol{p}\boldsymbol{q}}C_{\boldsymbol{p}}C_{\boldsymbol{q}}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle F_{\boldsymbol{k}}^{\text{int}}\doteq \frac{1}{2}\mathop{\sum }_{\boldsymbol{p},\boldsymbol{q}}{\it\delta}_{\boldsymbol{k}+\boldsymbol{p}+\boldsymbol{q},\mathbf{0}}|M_{\boldsymbol{k}\boldsymbol{p}\boldsymbol{q}}|^{2}\,\text{Re}\,{\it\theta}_{\boldsymbol{k}\boldsymbol{p}\boldsymbol{q}}C_{\boldsymbol{p}}C_{\boldsymbol{q}}. & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\frac{\text{Re}\,{\it\eta}_{\boldsymbol{k}}}{{\it\gamma}_{\boldsymbol{k}}^{\text{lin}}}=1-\frac{{\it\gamma}_{\boldsymbol{k}}^{\text{lin}}}{{\rm\Delta}{\it\gamma}}\quad \text{and}\quad \frac{F_{\boldsymbol{k}}^{\text{int}}/C_{\boldsymbol{k}}}{{\it\gamma}_{\boldsymbol{k}}^{\text{lin}}}=-\frac{{\it\gamma}_{\boldsymbol{k}}^{\text{lin}}}{{\rm\Delta}{\it\gamma}},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{Re}\,{\it\eta}_{\boldsymbol{k}}}{{\it\gamma}_{\boldsymbol{k}}^{\text{lin}}}=1-\frac{{\it\gamma}_{\boldsymbol{k}}^{\text{lin}}}{{\rm\Delta}{\it\gamma}}\quad \text{and}\quad \frac{F_{\boldsymbol{k}}^{\text{int}}/C_{\boldsymbol{k}}}{{\it\gamma}_{\boldsymbol{k}}^{\text{lin}}}=-\frac{{\it\gamma}_{\boldsymbol{k}}^{\text{lin}}}{{\rm\Delta}{\it\gamma}},\end{eqnarray}$$
as well as the total saturation level,
 $$\begin{eqnarray}{\mathcal{E}}=\left(\frac{{\rm\Delta}({\it\gamma}^{2})}{({\rm\Delta}{\it\gamma})^{2}}\right)\left(\frac{({\rm\Delta}{\it\Omega})^{2}+({\rm\Delta}{\it\gamma})^{2}}{({\rm\Delta}{\it\gamma})^{2}}\right)\left(\frac{{\it\Gamma}^{2}}{M^{2}}\right),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{E}}=\left(\frac{{\rm\Delta}({\it\gamma}^{2})}{({\rm\Delta}{\it\gamma})^{2}}\right)\left(\frac{({\rm\Delta}{\it\Omega})^{2}+({\rm\Delta}{\it\gamma})^{2}}{({\rm\Delta}{\it\gamma})^{2}}\right)\left(\frac{{\it\Gamma}^{2}}{M^{2}}\right),\end{eqnarray}$$
where
 ${\mathcal{E}}\doteq \sum _{\boldsymbol{k}}{\it\sigma}_{\boldsymbol{k}}C_{\boldsymbol{k}}$
is an energy-like quantity. The weight factors
${\mathcal{E}}\doteq \sum _{\boldsymbol{k}}{\it\sigma}_{\boldsymbol{k}}C_{\boldsymbol{k}}$
is an energy-like quantity. The weight factors
![]() ${\it\sigma}_{\boldsymbol{k}}$
are assumed to be positive-definite and to obey
${\it\sigma}_{\boldsymbol{k}}$
are assumed to be positive-definite and to obey
 $\sum _{\boldsymbol{k}}{\it\sigma}_{\boldsymbol{k}}M_{\boldsymbol{k}}=0~(M_{\boldsymbol{K}}\equiv M_{\boldsymbol{K}\boldsymbol{P}\boldsymbol{Q}})$
. The characteristic mode-coupling coefficient
$\sum _{\boldsymbol{k}}{\it\sigma}_{\boldsymbol{k}}M_{\boldsymbol{k}}=0~(M_{\boldsymbol{K}}\equiv M_{\boldsymbol{K}\boldsymbol{P}\boldsymbol{Q}})$
. The characteristic mode-coupling coefficient
![]() $M$
and growth rate
$M$
and growth rate
![]() ${\it\Gamma}$
are defined by
${\it\Gamma}$
are defined by
 $$\begin{eqnarray}\frac{1}{M^{2}}\doteq {\rm\Delta}\left(\frac{1}{M_{\boldsymbol{P}}M_{\boldsymbol{Q}}}\right),\quad {\it\Gamma}^{2}\doteq M^{2}{\rm\Delta}\left[{\it\sigma}_{\boldsymbol{K}}\left(\frac{{\it\gamma}_{\boldsymbol{P}}^{\text{lin}}{\it\gamma}_{\boldsymbol{Q}}^{\text{lin}}}{M_{\boldsymbol{P}}M_{\boldsymbol{Q}}}\right)\right].\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{M^{2}}\doteq {\rm\Delta}\left(\frac{1}{M_{\boldsymbol{P}}M_{\boldsymbol{Q}}}\right),\quad {\it\Gamma}^{2}\doteq M^{2}{\rm\Delta}\left[{\it\sigma}_{\boldsymbol{K}}\left(\frac{{\it\gamma}_{\boldsymbol{P}}^{\text{lin}}{\it\gamma}_{\boldsymbol{Q}}^{\text{lin}}}{M_{\boldsymbol{P}}M_{\boldsymbol{Q}}}\right)\right].\end{eqnarray}$$
In these expressions the
![]() ${\rm\Delta}$
operator sums over all wavenumbers (e.g.,
${\rm\Delta}$
operator sums over all wavenumbers (e.g.,
 ${\rm\Delta}{\it\gamma}\equiv {\it\gamma}_{\boldsymbol{K}}^{\text{lin}}+{\it\gamma}_{\boldsymbol{P}}^{\text{lin}}+{\it\gamma}_{\boldsymbol{Q}}^{\text{lin}}$
). It can be shown that steady state requires
${\rm\Delta}{\it\gamma}\equiv {\it\gamma}_{\boldsymbol{K}}^{\text{lin}}+{\it\gamma}_{\boldsymbol{P}}^{\text{lin}}+{\it\gamma}_{\boldsymbol{Q}}^{\text{lin}}$
). It can be shown that steady state requires
![]() ${\rm\Delta}{\it\gamma}<0$
. First focus on (5.8). Basic RBT would correspond to
${\rm\Delta}{\it\gamma}<0$
. First focus on (5.8). Basic RBT would correspond to
 $\text{Re}\,{\it\eta}_{\boldsymbol{k}}/{\it\gamma}_{\boldsymbol{k}}^{\text{lin}}=1$
and
$\text{Re}\,{\it\eta}_{\boldsymbol{k}}/{\it\gamma}_{\boldsymbol{k}}^{\text{lin}}=1$
and
 $F_{\boldsymbol{k}}^{\text{int}}/C_{\boldsymbol{k}}=0$
; the actual solution is clearly different, involving
nonvanishing nonlinear noise. (This is not surprising since both
$F_{\boldsymbol{k}}^{\text{int}}/C_{\boldsymbol{k}}=0$
; the actual solution is clearly different, involving
nonvanishing nonlinear noise. (This is not surprising since both
![]() $F_{\boldsymbol{k}}^{\text{int}}$
and
$F_{\boldsymbol{k}}^{\text{int}}$
and
![]() ${\it\eta}_{\boldsymbol{k}}$
are measures of the same basic triadic mode coupling.
Furthermore, as I noted in § 4, nonvanishing
noise is required in order that energy is conserved by the nonlinear terms.)
Indeed, the fraction
${\it\eta}_{\boldsymbol{k}}$
are measures of the same basic triadic mode coupling.
Furthermore, as I noted in § 4, nonvanishing
noise is required in order that energy is conserved by the nonlinear terms.)
Indeed, the fraction
![]() $|{\it\gamma}_{\boldsymbol{k}}/{\rm\Delta}{\it\gamma}|$
can be larger, possibly much larger, than unity because at least one
$|{\it\gamma}_{\boldsymbol{k}}/{\rm\Delta}{\it\gamma}|$
can be larger, possibly much larger, than unity because at least one
![]() ${\it\gamma}_{\boldsymbol{k}}^{\text{lin}}$
must be negative, which reduces
${\it\gamma}_{\boldsymbol{k}}^{\text{lin}}$
must be negative, which reduces
![]() ${\rm\Delta}{\it\gamma}$
. (This property was noted in the related numerical work by Hu,
Krommes & Bowman (Reference Hu, Krommes and Bowman1995, Reference Hu, Krommes and Bowman1997) on the system of Hasegawa &
Wakatani (Reference Hasegawa and Wakatani1983); it was responsible for
large differences in the measured flux from the quasi-linear prediction.)
Nevertheless, the total saturation level is in accord with expectations. For the
typical caseFootnote
85
in which
${\rm\Delta}{\it\gamma}$
. (This property was noted in the related numerical work by Hu,
Krommes & Bowman (Reference Hu, Krommes and Bowman1995, Reference Hu, Krommes and Bowman1997) on the system of Hasegawa &
Wakatani (Reference Hasegawa and Wakatani1983); it was responsible for
large differences in the measured flux from the quasi-linear prediction.)
Nevertheless, the total saturation level is in accord with expectations. For the
typical caseFootnote
85
in which
 $|{\rm\Delta}{\it\gamma}/{\rm\Delta}{\it\Omega}|\ll 1$
, formula (5.9)
becomes
$|{\rm\Delta}{\it\gamma}/{\rm\Delta}{\it\Omega}|\ll 1$
, formula (5.9)
becomes
 $$\begin{eqnarray}{\mathcal{E}}\sim {\mathcal{E}}^{\text{ml}}\doteq ({\rm\Delta}{\it\Omega})^{2}/M^{2}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{E}}\sim {\mathcal{E}}^{\text{ml}}\doteq ({\rm\Delta}{\it\Omega})^{2}/M^{2}.\end{eqnarray}$$
This is indeed the mixing-length level, as can be seen by taking
 ${\rm\Delta}{\it\Omega}\sim {\it\omega}_{\ast }\sim c_{\text{s}}/L_{n}$
and
${\rm\Delta}{\it\Omega}\sim {\it\omega}_{\ast }\sim c_{\text{s}}/L_{n}$
and
 $M\sim c_{\text{s}}/{\it\rho}_{\text{s}}$
(see (5.2));
then
$M\sim c_{\text{s}}/{\it\rho}_{\text{s}}$
(see (5.2));
then
 $$\begin{eqnarray}{\mathcal{E}}\doteq \left\langle \left(\frac{e{\it\delta}{\it\phi}}{T_{e}}\right)^{2}\right\rangle \sim \left(\frac{{\it\rho}_{\text{s}}}{L_{n}}\right)^{2}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{E}}\doteq \left\langle \left(\frac{e{\it\delta}{\it\phi}}{T_{e}}\right)^{2}\right\rangle \sim \left(\frac{{\it\rho}_{\text{s}}}{L_{n}}\right)^{2}.\end{eqnarray}$$
Obviously the details of the wavenumber spectrum are complicated, but they are also predicted by the closure.
This simple example shows how closure can predict the intricacies of the nonlinear mode coupling and the steady-state balance between linear and nonlinear effects (in a way that is compatible with the constraints arising from scaling analysis). Details of the analysis of Markovian closures with many coupled modes can be found in the papers by Bowman et al. (Reference Bowman, Krommes and Ottaviani1993) and Bowman & Krommes (Reference Bowman and Krommes1997) for general three-wave coupling and the Hasegawa–Mima equation, and by Hu et al. (Reference Hu, Krommes and Bowman1995, Reference Hu, Krommes and Bowman1997) for the Hasegawa–Wakatani equations. A message is that technically one has come a long way from the early qualitative considerations. However, Kadomtsev’s insights are seen to be upheld;Footnote 86 they capture the essence of the basic drift-wave paradigm.Footnote 87
5.3. The impact of zonal flows on the Hasegawa–Mima equation
Zonal potentials are ones with
 $k_{y}=k_{\text{z}}=0$
(in slab geometry) or with no variation within a flux surface (in
toroidal geometry). The resulting
$k_{y}=k_{\text{z}}=0$
(in slab geometry) or with no variation within a flux surface (in
toroidal geometry). The resulting
![]() $\boldsymbol{E}\times \boldsymbol{B}$
drifts (mostly poloidal) are called zonal flows; they are important
in multiple contexts.Footnote
88
In fusion plasmas, for example, they play an important role in the regulation
of the levels of drift-wave turbulence and transport, either by shearing of turbulent
eddies (Diamond et al.
Reference Diamond, Itoh, Itoh and Hahm2005) or by catalysing the coupling of
unstable fluctuations to stable normal modes (Hatch et al.
Reference Hatch, Terry, Jenko, Merz, Pueschel, Nevins and Wang2011b
).
$\boldsymbol{E}\times \boldsymbol{B}$
drifts (mostly poloidal) are called zonal flows; they are important
in multiple contexts.Footnote
88
In fusion plasmas, for example, they play an important role in the regulation
of the levels of drift-wave turbulence and transport, either by shearing of turbulent
eddies (Diamond et al.
Reference Diamond, Itoh, Itoh and Hahm2005) or by catalysing the coupling of
unstable fluctuations to stable normal modes (Hatch et al.
Reference Hatch, Terry, Jenko, Merz, Pueschel, Nevins and Wang2011b
).
Zonal flows are strongly non-adiabatic: because they have
![]() $k_{\Vert }=0$
, the adiabatic ordering
$k_{\Vert }=0$
, the adiabatic ordering
 ${\it\omega}/k_{\Vert }v_{\text{t}e}\ll 1$
is violated. Dorland & Hammett (Reference Dorland and Hammett1993) emphasized that Poisson’s equation must be modified as a
consequence, giving rise to an enhanced response for the zonal modes. In the simplest
model, the electron response is taken to vanish altogether for zonal modes. This can
be implemented by writing
${\it\omega}/k_{\Vert }v_{\text{t}e}\ll 1$
is violated. Dorland & Hammett (Reference Dorland and Hammett1993) emphasized that Poisson’s equation must be modified as a
consequence, giving rise to an enhanced response for the zonal modes. In the simplest
model, the electron response is taken to vanish altogether for zonal modes. This can
be implemented by writing
 ${\it\delta}n_{e,\boldsymbol{k}}/n_{e}={\it\alpha}_{\boldsymbol{k}}{\it\delta}{\it\varphi}_{\boldsymbol{k}}$
, where
${\it\delta}n_{e,\boldsymbol{k}}/n_{e}={\it\alpha}_{\boldsymbol{k}}{\it\delta}{\it\varphi}_{\boldsymbol{k}}$
, where
![]() ${\it\alpha}_{\boldsymbol{k}}$
vanishes for zonal modes and is equal to 1 otherwise. A consequence
is that the derivation of the Hasegawa–Mima equation must be reconsidered; one finds
instead the modified Hasegawa–Mima equation
${\it\alpha}_{\boldsymbol{k}}$
vanishes for zonal modes and is equal to 1 otherwise. A consequence
is that the derivation of the Hasegawa–Mima equation must be reconsidered; one finds
instead the modified Hasegawa–Mima equation
 $$\begin{eqnarray}({\it\alpha}-{\it\rho}_{\text{s}}^{2}{\rm\nabla}_{\bot }^{2})\partial _{t}{\it\varphi}+{\it\alpha}V_{\ast }\partial _{\text{y}}{\it\varphi}+\boldsymbol{V}_{E}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}({\it\alpha}-{\it\rho}_{\text{s}}^{2}{\rm\nabla}_{\bot }^{2}{\it\varphi})=0.\end{eqnarray}$$
$$\begin{eqnarray}({\it\alpha}-{\it\rho}_{\text{s}}^{2}{\rm\nabla}_{\bot }^{2})\partial _{t}{\it\varphi}+{\it\alpha}V_{\ast }\partial _{\text{y}}{\it\varphi}+\boldsymbol{V}_{E}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}({\it\alpha}-{\it\rho}_{\text{s}}^{2}{\rm\nabla}_{\bot }^{2}{\it\varphi})=0.\end{eqnarray}$$
This equation has been used in various studies related to the physics of zonal flows (Krommes & Kim Reference Krommes and Kim2000; Parker & Krommes Reference Parker and Krommes2013); it is further discussed in § 6.2.
5.4. Further developments in closure theory
For other facets of closure theory, I point the reader to the discussion and references in Krommes (Reference Krommes2002) and McComb (Reference McComb2014). The latter focuses on homogeneous turbulence. In the next section, I shall describe some aspects of the theory of inhomogeneous turbulence.
6. Recent results on inhomogeneous turbulence
The easiest applications of closure approximations are to spatially homogeneous situations. However, while it is often possible to impose a homogeneous statistical ensemble, that may not reflect the physical reality. Kraichnan (Reference Kraichnan1964b ) pointed out that, when inhomogeneous turbulence is of concern, the choice of ensemble is crucial. For example, it seems counterproductive to describe the visibly banded Jovian atmosphere (see footnote 88) by a homogeneous ensemble. In the present section, I shall discuss some basic results relating to inhomogeneous ensembles. They include fundamental ideas about Reynolds stress (§ 6.1), the symmetry-breaking bifurcation to inhomogeneous turbulence (§ 6.2), and some closures particularly suitable for states of inhomogeneous turbulence with significant mean fields (§ 6.3).
6.1. Reynolds stress
Kadomtsev (p. 59) wrote,
We have shown . . . that the transition to strong turbulence leads to integral equations in the [DIA], in which the resonant and adiabatic interaction must be separated. At present we have no rigorous method of performing this separation and of reducing the integral equations, and the description given by this theory is inevitably only approximate. We have as yet no indication of the accuracy of this approximation.
However, in describing strong turbulence in a plasma we can use an analogy with ordinary turbulence. Here the principal results have been obtained from a purely phenomenological approach. It is natural, therefore, to use this approach in plasma turbulence theory.
In the last paragraph, Kadomtsev was referring to the modelling of the so-called
Reynolds stress by means of ‘the mixing-length concept introduced by Prandtl (Reference Prandtl1925)’. In its original interpretation, Reynolds stress
![]() ${\bf\tau}$
described the contribution of fluctuations in the fluid velocity to
the mean Navier–Stokes momentum equation:
${\bf\tau}$
described the contribution of fluctuations in the fluid velocity to
the mean Navier–Stokes momentum equation:
 $$\begin{eqnarray}\partial _{t}\boldsymbol{u}+\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}=-{\it\rho}_{\text{m}}^{-1}\boldsymbol{{\rm\nabla}}P-{\it\rho}_{\text{m}}^{-1}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\tau}+{\it\mu}{\rm\nabla}^{2}\boldsymbol{u},\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t}\boldsymbol{u}+\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}=-{\it\rho}_{\text{m}}^{-1}\boldsymbol{{\rm\nabla}}P-{\it\rho}_{\text{m}}^{-1}\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\tau}+{\it\mu}{\rm\nabla}^{2}\boldsymbol{u},\end{eqnarray}$$
whereFootnote
89
 ${\bf\tau}\doteq {\it\rho}_{\text{m}}\langle {\it\delta}\boldsymbol{u}\,{\it\delta}\boldsymbol{u}\rangle$
. Prandtl’s estimate for the size of a fluctuating velocity
component in a free jet was
${\bf\tau}\doteq {\it\rho}_{\text{m}}\langle {\it\delta}\boldsymbol{u}\,{\it\delta}\boldsymbol{u}\rangle$
. Prandtl’s estimate for the size of a fluctuating velocity
component in a free jet was
 ${\it\delta}u\approx \ell |\partial \langle u\rangle /\partial y|$
, where
${\it\delta}u\approx \ell |\partial \langle u\rangle /\partial y|$
, where
![]() $u$
is the longitudinal velocity,
$u$
is the longitudinal velocity,
![]() $y$
is the transverse coordinate, and
$y$
is the transverse coordinate, and
![]() $\ell$
is the transverse mixing length. Kadomtsev (p. 59) reviewed a
solution by Tollmien of the steady-state system of momentum and continuity equations
that results when one takes
$\ell$
is the transverse mixing length. Kadomtsev (p. 59) reviewed a
solution by Tollmien of the steady-state system of momentum and continuity equations
that results when one takes
![]() $\ell =cx$
, where
$\ell =cx$
, where
![]() $c$
is a fitting constant; agreement with experiment is excellent when
$c$
is a fitting constant; agreement with experiment is excellent when
![]() $c$
is chosen appropriately.
$c$
is chosen appropriately.
Note that it is only the divergence of the stress tensor that contributes to the mean
momentum equation. For homogeneous turbulence, that divergence vanishes, so
inhomogeneity is essential.Footnote
90
As an example, let us discuss the off-diagonal Reynolds stress due to
![]() $\boldsymbol{E}\times \boldsymbol{B}$
flows in a two-dimensional model with constant magnetic field. One
has
$\boldsymbol{E}\times \boldsymbol{B}$
flows in a two-dimensional model with constant magnetic field. One
has
 ${\it\tau}_{xy}\propto \langle {\it\delta}V_{E,x}{\it\delta}V_{E,y}\rangle$
with
${\it\tau}_{xy}\propto \langle {\it\delta}V_{E,x}{\it\delta}V_{E,y}\rangle$
with
 $\boldsymbol{V}_{E}\propto \,\widehat{\boldsymbol{b}}\times \boldsymbol{{\rm\nabla}}\widetilde{{\it\phi}}$
and
$\boldsymbol{V}_{E}\propto \,\widehat{\boldsymbol{b}}\times \boldsymbol{{\rm\nabla}}\widetilde{{\it\phi}}$
and
![]() $\widetilde{{\it\phi}}$
being the random electrostatic potential. Contours of constant
$\widetilde{{\it\phi}}$
being the random electrostatic potential. Contours of constant
![]() $\widetilde{{\it\phi}}$
are the streamlines of the velocity. Consider an elliptical ‘eddy’,
of major axis
$\widetilde{{\it\phi}}$
are the streamlines of the velocity. Consider an elliptical ‘eddy’,
of major axis
![]() $a$
and minor axis
$a$
and minor axis
![]() $b$
, inclined at random angle
$b$
, inclined at random angle
![]() $\widetilde{{\it\theta}}$
from the
$\widetilde{{\it\theta}}$
from the
![]() $x$
direction:
$x$
direction:
 $$\begin{eqnarray}\widetilde{{\it\phi}}(x,y)=\frac{(\,\widetilde{c}x-\widetilde{s}y)^{2}}{a^{2}}+\frac{(\,\widetilde{s}x+\widetilde{c}y)^{2}}{b^{2}},\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{{\it\phi}}(x,y)=\frac{(\,\widetilde{c}x-\widetilde{s}y)^{2}}{a^{2}}+\frac{(\,\widetilde{s}x+\widetilde{c}y)^{2}}{b^{2}},\end{eqnarray}$$
where
 $\widetilde{c}\equiv \cos \widetilde{{\it\theta}}$
and
$\widetilde{c}\equiv \cos \widetilde{{\it\theta}}$
and
 $\widetilde{s}\equiv \sin \widetilde{{\it\theta}}$
. It is straightforward to calculate
$\widetilde{s}\equiv \sin \widetilde{{\it\theta}}$
. It is straightforward to calculate
 $\widetilde{V}_{E,x}\propto -\partial _{\text{y}}\widetilde{{\it\phi}}$
,
$\widetilde{V}_{E,x}\propto -\partial _{\text{y}}\widetilde{{\it\phi}}$
,
 $\widetilde{V}_{E,y}\propto \partial _{\text{x}}\widetilde{{\it\phi}}$
, and the product
$\widetilde{V}_{E,y}\propto \partial _{\text{x}}\widetilde{{\it\phi}}$
, and the product
 $\widetilde{{\it\tau}}_{xy}\doteq {\it\delta}\widetilde{V}_{E,x}{\it\delta}\widetilde{V}_{E,y}$
. I assume that
$\widetilde{{\it\tau}}_{xy}\doteq {\it\delta}\widetilde{V}_{E,x}{\it\delta}\widetilde{V}_{E,y}$
. I assume that
![]() $y$
is a direction of symmetry.Footnote
91
The purely
$y$
is a direction of symmetry.Footnote
91
The purely
![]() $x$
-dependent part of the result (which after averaging gives the
contribution to
$x$
-dependent part of the result (which after averaging gives the
contribution to
![]() $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\tau}$
) is
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }{\bf\tau}$
) is
 $$\begin{eqnarray}\widetilde{{\it\tau}}_{xy}\propto ~\widetilde{c}\,\widetilde{s}\left(\frac{\widetilde{c}^{2}}{a^{2}}+\frac{\widetilde{s}^{2}}{b^{2}}\right)\left(\frac{1}{a^{2}}-\frac{1}{b^{2}}\right)x^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{{\it\tau}}_{xy}\propto ~\widetilde{c}\,\widetilde{s}\left(\frac{\widetilde{c}^{2}}{a^{2}}+\frac{\widetilde{s}^{2}}{b^{2}}\right)\left(\frac{1}{a^{2}}-\frac{1}{b^{2}}\right)x^{2}.\end{eqnarray}$$
For the case of circular eddies (
 $a^{2}=b^{2}=r^{2}$
), this vanishes.Footnote
92
Even for elliptical eddies,
$a^{2}=b^{2}=r^{2}$
), this vanishes.Footnote
92
Even for elliptical eddies,
 ${\it\tau}_{xy}\doteq \langle \widetilde{{\it\tau}}_{xy}\rangle$
vanishes by symmetry when it is averaged over a symmetrical
distribution in
${\it\tau}_{xy}\doteq \langle \widetilde{{\it\tau}}_{xy}\rangle$
vanishes by symmetry when it is averaged over a symmetrical
distribution in
![]() ${\it\theta}$
. But if
${\it\theta}$
. But if
![]() $\widetilde{{\it\theta}}$
is distributed according to the PDF
$\widetilde{{\it\theta}}$
is distributed according to the PDF
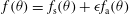 $f({\it\theta})=\,f_{\text{s}}({\it\theta})+{\it\epsilon}f_{\text{a}}({\it\theta})$
, where s and a denote symmetric and antisymmetric parts, then the
antisymmetric part contributes and one finds
$f({\it\theta})=\,f_{\text{s}}({\it\theta})+{\it\epsilon}f_{\text{a}}({\it\theta})$
, where s and a denote symmetric and antisymmetric parts, then the
antisymmetric part contributes and one finds
 ${\it\tau}_{xy}\propto {\it\epsilon}{\it\Delta}x^{2}$
, where
${\it\tau}_{xy}\propto {\it\epsilon}{\it\Delta}x^{2}$
, where
 ${\it\Delta}\doteq b^{-2}-a^{-2}$
. This example shows the importance of asymmetry in producing
nonvanishing Reynolds stress, and it suggests that toroidal devices with up–down
asymmetry may, in the presence of microturbulence, have larger Reynolds stresses.
Those may be important in limiting the size of the turbulence and in the generation
of intrinsic rotation.Footnote
93
${\it\Delta}\doteq b^{-2}-a^{-2}$
. This example shows the importance of asymmetry in producing
nonvanishing Reynolds stress, and it suggests that toroidal devices with up–down
asymmetry may, in the presence of microturbulence, have larger Reynolds stresses.
Those may be important in limiting the size of the turbulence and in the generation
of intrinsic rotation.Footnote
93
It is well known that the deformation tensor
![]() $\boldsymbol{{\rm\nabla}}\boldsymbol{u}$
of a general flow field
$\boldsymbol{{\rm\nabla}}\boldsymbol{u}$
of a general flow field
![]() $\boldsymbol{u}(\boldsymbol{x})$
can be decomposed into a symmetric part (the rate-of-strain tensor
$\boldsymbol{u}(\boldsymbol{x})$
can be decomposed into a symmetric part (the rate-of-strain tensor
![]() $\unicode[STIX]{x1D64E}$
, associated with both stretching at constant volume and possibly
compression) and an antisymmetric part (associated with vorticity and leading to
rigid-body rotation). Therefore tilted elliptical eddies, hence Reynolds stress, can
arise by subjecting a circular eddy to an inhomogeneous velocity field. One source of
inhomogeneity is the generation of zonal flows due to the (divergence of the)
Reynolds stress. As an example, consider a slab zonal flow with constant shear:Footnote
94
$\unicode[STIX]{x1D64E}$
, associated with both stretching at constant volume and possibly
compression) and an antisymmetric part (associated with vorticity and leading to
rigid-body rotation). Therefore tilted elliptical eddies, hence Reynolds stress, can
arise by subjecting a circular eddy to an inhomogeneous velocity field. One source of
inhomogeneity is the generation of zonal flows due to the (divergence of the)
Reynolds stress. As an example, consider a slab zonal flow with constant shear:Footnote
94
 $\boldsymbol{u}={\it\Omega}_{0}x\widehat{\boldsymbol{y}}$
, with
$\boldsymbol{u}={\it\Omega}_{0}x\widehat{\boldsymbol{y}}$
, with
 $\boldsymbol{{\rm\nabla}}\times \boldsymbol{u}={\it\Omega}_{0}\widehat{\boldsymbol{z}}$
and
$\boldsymbol{{\rm\nabla}}\times \boldsymbol{u}={\it\Omega}_{0}\widehat{\boldsymbol{z}}$
and
 $\unicode[STIX]{x1D64E}={\it\Omega}_{0}(\widehat{\boldsymbol{x}}\,\widehat{\boldsymbol{y}}+\widehat{\boldsymbol{y}}\,\widehat{\boldsymbol{x}})/2$
(the principal axes of which are
$\unicode[STIX]{x1D64E}={\it\Omega}_{0}(\widehat{\boldsymbol{x}}\,\widehat{\boldsymbol{y}}+\widehat{\boldsymbol{y}}\,\widehat{\boldsymbol{x}})/2$
(the principal axes of which are
 $(1,\hspace{2.22198pt}\pm 1)^{\text{T}}/\sqrt{2}$
). Tilt arises from the vorticity, and ellipticity (at constant
area) arises from the straining. Thus one has a classic problem of the chicken and
the egg. Inhomogeneous Reynolds stress drives zonal flows, and such stress can arise
from the modulation of homogeneous turbulence by zonal flows; a feedback loop is
indicated. But given homogeneous turbulence, there is no divergence of the Reynolds
stress, hence no zonal-flow generation (see footnote 90), hence no inhomogeneity,
hence no effect due to Reynolds stress. However, such homogeneous turbulence can be
unstable to the generation of inhomogeneous flows, as I shall describe in the next
section. Thus inhomogeneous states can result in which zonal flows and
microturbulence are coupled self-consistently.
$(1,\hspace{2.22198pt}\pm 1)^{\text{T}}/\sqrt{2}$
). Tilt arises from the vorticity, and ellipticity (at constant
area) arises from the straining. Thus one has a classic problem of the chicken and
the egg. Inhomogeneous Reynolds stress drives zonal flows, and such stress can arise
from the modulation of homogeneous turbulence by zonal flows; a feedback loop is
indicated. But given homogeneous turbulence, there is no divergence of the Reynolds
stress, hence no zonal-flow generation (see footnote 90), hence no inhomogeneity,
hence no effect due to Reynolds stress. However, such homogeneous turbulence can be
unstable to the generation of inhomogeneous flows, as I shall describe in the next
section. Thus inhomogeneous states can result in which zonal flows and
microturbulence are coupled self-consistently.
6.2. Infinitesimal response, symmetry breaking, and zonostrophic instability
A basic question is this: Under what circumstances is a state of steady homogeneous
turbulence unstable to the symmetry-breaking generation of inhomogeneity? This can be
addressed by linearizing around the homogeneous state (allowing for inhomogeneous
perturbations) and enquiring about the onset of a zero eigenvalue that solves a
certain dispersion relation. I shall show, expanding on the original beautiful paper
of Carnevale & Martin (Reference Carnevale and Martin1982), that that
dispersion relation is intimately related to a certain approximation to the inverse
of the infinitesimal response function
![]() $R$
for the homogeneous turbulent state. In the theory of zonal-flow
generation, the instability of homogeneous turbulence is called the zonostrophic
instability (Srinivasan & Young Reference Srinivasan and Young2012).
$R$
for the homogeneous turbulent state. In the theory of zonal-flow
generation, the instability of homogeneous turbulence is called the zonostrophic
instability (Srinivasan & Young Reference Srinivasan and Young2012).
Mention of a zero eigenvalue in the context of homogeneous turbulence might be
confusing. Recall that in earlier sections we saw how the nonlinear dielectric
function participates in the spectral balance of the turbulence by shielding
nonlinear noise, which I argued is important and cannot generally be neglected. Also
recall that in steady state the zeros of
![]() ${\mathcal{D}}(\boldsymbol{k},{\it\omega})$
or
${\mathcal{D}}(\boldsymbol{k},{\it\omega})$
or
 $R^{-1}(\boldsymbol{k},{\it\omega})$
are in the lower half of the
$R^{-1}(\boldsymbol{k},{\it\omega})$
are in the lower half of the
![]() ${\it\omega}$
plane, not on the real line. Now the dielectric function (or
inverse response function) referred to here relates internal incoherent noise to the
covariance of the fluctuations (for homogeneous turbulence, there is no mean flow).
But if one admits the possibility of inhomogeneity, there will arise an effective
dielectric tensor that operates on an extended vector containing not only
fluctuations but also mean fields. At the symmetry-breaking bifurcation of
homogeneous turbulence to the generation of mean fields, that tensor will develop a
zero eigenvalue.
${\it\omega}$
plane, not on the real line. Now the dielectric function (or
inverse response function) referred to here relates internal incoherent noise to the
covariance of the fluctuations (for homogeneous turbulence, there is no mean flow).
But if one admits the possibility of inhomogeneity, there will arise an effective
dielectric tensor that operates on an extended vector containing not only
fluctuations but also mean fields. At the symmetry-breaking bifurcation of
homogeneous turbulence to the generation of mean fields, that tensor will develop a
zero eigenvalue.
If one writes
![]() $Z\equiv \langle {\it\psi}\rangle$
, (2.6) for zero
forcing becomes
$Z\equiv \langle {\it\psi}\rangle$
, (2.6) for zero
forcing becomes
 $$\begin{eqnarray}\partial _{t_{1}}Z(1)=U_{2}(1,2)Z(2)+\frac{1}{2}U_{3}(1,2,3)Z(2)Z(3)+\frac{1}{2}U_{3}(1,2,3)C(2,3).\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t_{1}}Z(1)=U_{2}(1,2)Z(2)+\frac{1}{2}U_{3}(1,2,3)Z(2)Z(3)+\frac{1}{2}U_{3}(1,2,3)C(2,3).\end{eqnarray}$$
The linearization of this equation is
 $$\begin{eqnarray}\partial _{t_{1}}{\rm\Delta}Z(1)=U_{2}(1,2){\rm\Delta}Z(2)+U_{3}(1,2,3)\underline{Z(2)}{\rm\Delta}Z(3)+\frac{1}{2}U_{3}(1,2,3){\rm\Delta}C(2,3).\end{eqnarray}$$
$$\begin{eqnarray}\partial _{t_{1}}{\rm\Delta}Z(1)=U_{2}(1,2){\rm\Delta}Z(2)+U_{3}(1,2,3)\underline{Z(2)}{\rm\Delta}Z(3)+\frac{1}{2}U_{3}(1,2,3){\rm\Delta}C(2,3).\end{eqnarray}$$
In particular, I shall linearize around a homogeneous state for which
it is assumed that
![]() $Z=0$
; the terms that vanish with this assumption are underlined. The
(generally inhomogeneous) fluctuation spectrum is assumed to obey the Dyson equation
$Z=0$
; the terms that vanish with this assumption are underlined. The
(generally inhomogeneous) fluctuation spectrum is assumed to obey the Dyson equation
 $$\begin{eqnarray}\displaystyle \partial _{t_{1}}C(1,1^{\prime }) & = & \displaystyle U_{2}(1,2)C(2,1^{\prime })+U_{3}(1,2,3)Z(2)C(3,1^{\prime })\nonumber\\ \displaystyle & & \displaystyle -\,{\it\Sigma}(1,\overline{1})C(\overline{1},1^{\prime })+F(1,\overline{1})R(1^{\prime };\overline{1}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \partial _{t_{1}}C(1,1^{\prime }) & = & \displaystyle U_{2}(1,2)C(2,1^{\prime })+U_{3}(1,2,3)Z(2)C(3,1^{\prime })\nonumber\\ \displaystyle & & \displaystyle -\,{\it\Sigma}(1,\overline{1})C(\overline{1},1^{\prime })+F(1,\overline{1})R(1^{\prime };\overline{1}).\end{eqnarray}$$
Linear perturbations to the spectrum obey
 $$\begin{eqnarray}\displaystyle \partial _{t_{1}}{\rm\Delta}C(1,1^{\prime }) & = & \displaystyle U_{2}(1,2){\rm\Delta}C(2,1^{\prime })+U_{3}(1,2,3)[{\rm\Delta}Z(2)C(3,1^{\prime })+\underline{Z(2)}{\rm\Delta}C(3,1^{\prime })]\nonumber\\ \displaystyle & & \displaystyle -\,\underline{\underline{{\it\Sigma}(1,\overline{1}){\rm\Delta}C(\overline{1},1^{\prime })}}-\underline{\underline{{\rm\Delta}{\it\Sigma}(1;\overline{1})C(\overline{1},1^{\prime })}}+F(1,\overline{1}){\rm\Delta}R(1^{\prime };\overline{1})\nonumber\\ \displaystyle & & \displaystyle +\,\underline{\underline{{\rm\Delta}F(1,\overline{1})R(1^{\prime };\overline{1})}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \partial _{t_{1}}{\rm\Delta}C(1,1^{\prime }) & = & \displaystyle U_{2}(1,2){\rm\Delta}C(2,1^{\prime })+U_{3}(1,2,3)[{\rm\Delta}Z(2)C(3,1^{\prime })+\underline{Z(2)}{\rm\Delta}C(3,1^{\prime })]\nonumber\\ \displaystyle & & \displaystyle -\,\underline{\underline{{\it\Sigma}(1,\overline{1}){\rm\Delta}C(\overline{1},1^{\prime })}}-\underline{\underline{{\rm\Delta}{\it\Sigma}(1;\overline{1})C(\overline{1},1^{\prime })}}+F(1,\overline{1}){\rm\Delta}R(1^{\prime };\overline{1})\nonumber\\ \displaystyle & & \displaystyle +\,\underline{\underline{{\rm\Delta}F(1,\overline{1})R(1^{\prime };\overline{1})}}.\end{eqnarray}$$
Doubly underlined terms are
 $O(C\,{\rm\Delta}C)$
; they describe fluctuation–fluctuation interactions. Let us neglect
those and focus on the coupling between the mean fields and the turbulence. Because
$O(C\,{\rm\Delta}C)$
; they describe fluctuation–fluctuation interactions. Let us neglect
those and focus on the coupling between the mean fields and the turbulence. Because
 ${\rm\Delta}R=-R{\rm\Delta}(R^{-1})R$
and
${\rm\Delta}R=-R{\rm\Delta}(R^{-1})R$
and
 $$\begin{eqnarray}R^{-1}(1;\overline{1})=\partial _{t_{1}}{\it\delta}(1-\overline{1})-U_{2}(1,\overline{1})-U_{3}(1,2,\overline{1})Z(2)+{\it\Sigma}(1,\overline{1}),\end{eqnarray}$$
$$\begin{eqnarray}R^{-1}(1;\overline{1})=\partial _{t_{1}}{\it\delta}(1-\overline{1})-U_{2}(1,\overline{1})-U_{3}(1,2,\overline{1})Z(2)+{\it\Sigma}(1,\overline{1}),\end{eqnarray}$$
one has
 $$\begin{eqnarray}{\rm\Delta}(R^{-1})(1;\overline{1})=-U_{3}(1,2,\overline{1}){\rm\Delta}Z(2)+\underline{\underline{{\rm\Delta}{\it\Sigma}(1;\overline{1})}}.\end{eqnarray}$$
$$\begin{eqnarray}{\rm\Delta}(R^{-1})(1;\overline{1})=-U_{3}(1,2,\overline{1}){\rm\Delta}Z(2)+\underline{\underline{{\rm\Delta}{\it\Sigma}(1;\overline{1})}}.\end{eqnarray}$$
The doubly underlined term contains pieces of order
![]() $C\,{\rm\Delta}R$
and
$C\,{\rm\Delta}R$
and
![]() $R\,{\rm\Delta}C$
; those can be ignored because when multiplied by
$R\,{\rm\Delta}C$
; those can be ignored because when multiplied by
![]() $F$
, as required for (6.7), they contribute effects of order
$F$
, as required for (6.7), they contribute effects of order
![]() $C^{2}$
or
$C^{2}$
or
![]() $C\,{\rm\Delta}C$
. The solution to (6.7) is then, after some permutation of indices,
$C\,{\rm\Delta}C$
. The solution to (6.7) is then, after some permutation of indices,
 $$\begin{eqnarray}{\rm\Delta}C(2,3)\approx R_{0}(2;\overline{2})U_{3}(\overline{2},\overline{3},\overline{1})C(\overline{3},3){\rm\Delta}Z(\overline{1})+(2\leftrightarrow 3).\end{eqnarray}$$
$$\begin{eqnarray}{\rm\Delta}C(2,3)\approx R_{0}(2;\overline{2})U_{3}(\overline{2},\overline{3},\overline{1})C(\overline{3},3){\rm\Delta}Z(\overline{1})+(2\leftrightarrow 3).\end{eqnarray}$$
(The last term, which ensures symmetry, comes from the first term on
the right-hand side in (6.9) after
using steady-state balance to replace the
![]() $F$
in
$F$
in
![]() $F{\rm\Delta}R$
with
$F{\rm\Delta}R$
with
 $R^{-1}C(R^{-1})^{\text{T}}$
.) When this solution is inserted into (6.5), one finds
$R^{-1}C(R^{-1})^{\text{T}}$
.) When this solution is inserted into (6.5), one finds
 $$\begin{eqnarray}[\partial _{t_{1}}{\it\delta}(1-\overline{1})-U_{2}(1,\overline{1})+{\it\Sigma}_{0}(1;\overline{1})]{\rm\Delta}Z(\overline{1})=0,\end{eqnarray}$$
$$\begin{eqnarray}[\partial _{t_{1}}{\it\delta}(1-\overline{1})-U_{2}(1,\overline{1})+{\it\Sigma}_{0}(1;\overline{1})]{\rm\Delta}Z(\overline{1})=0,\end{eqnarray}$$
where
 $$\begin{eqnarray}{\it\Sigma}_{0}(1;\overline{1})\doteq -U_{3}(1,2,3)R_{0}(2;\overline{2})C(3,\overline{3})U_{3}(\overline{2},\overline{3},\overline{1}).\end{eqnarray}$$
$$\begin{eqnarray}{\it\Sigma}_{0}(1;\overline{1})\doteq -U_{3}(1,2,3)R_{0}(2;\overline{2})C(3,\overline{3})U_{3}(\overline{2},\overline{3},\overline{1}).\end{eqnarray}$$
A consistent (fluctuation–dissipation) approximation (Carnevale &
Martin Reference Carnevale and Martin1982) is to replace the two-time
dependence of
![]() $C(3,\overline{3})$
with that of
$C(3,\overline{3})$
with that of
![]() $R_{0}(3;\overline{3})$
. Because the coefficients of
$R_{0}(3;\overline{3})$
. Because the coefficients of
![]() ${\rm\Delta}Z$
are all calculated in the homogeneous state, one can
Fourier-transform as usual. If one follows the common convention of using
${\rm\Delta}Z$
are all calculated in the homogeneous state, one can
Fourier-transform as usual. If one follows the common convention of using
![]() $\boldsymbol{q}$
to refer to the wavevector of the mean field, one then arrives at
the dispersion relation
$\boldsymbol{q}$
to refer to the wavevector of the mean field, one then arrives at
the dispersion relation
 $$\begin{eqnarray}R_{1}^{-1}(\boldsymbol{q},{\it\omega})=0,\end{eqnarray}$$
$$\begin{eqnarray}R_{1}^{-1}(\boldsymbol{q},{\it\omega})=0,\end{eqnarray}$$
where
![]() $R_{1}$
is the first renormalized approximation to
$R_{1}$
is the first renormalized approximation to
![]() $R$
. (In (6.8), replace
$R$
. (In (6.8), replace
![]() ${\it\Sigma}$
by
${\it\Sigma}$
by
![]() ${\it\Sigma}_{0}$
and
${\it\Sigma}_{0}$
and
![]() $R$
by
$R$
by
![]() $R_{1}$
.) The solution determines the eigenvalue
$R_{1}$
.) The solution determines the eigenvalue
![]() ${\it\omega}$
as a functional of the level
${\it\omega}$
as a functional of the level
![]() $C$
of the homogeneous turbulence (as well as
$C$
of the homogeneous turbulence (as well as
![]() $\boldsymbol{q}$
and the various parameters):
$\boldsymbol{q}$
and the various parameters):
 ${\it\omega}={\it\omega}_{\boldsymbol{q}}[C]$
. Setting
${\it\omega}={\it\omega}_{\boldsymbol{q}}[C]$
. Setting
 ${\it\omega}_{\boldsymbol{q}}[C]=0$
determines the neutral curve
${\it\omega}_{\boldsymbol{q}}[C]=0$
determines the neutral curve
 $C=C(\boldsymbol{q})$
; larger values of
$C=C(\boldsymbol{q})$
; larger values of
![]() $C$
are unstable to the generation of inhomogeneous mean fields (see
figure 5). This process is analogous to the
general phenomenon of pattern formation, as discussed by Parker & Krommes (Reference Parker and Krommes2013).Footnote
95
In the context of the barotropic vorticity equation, the zonostrophic
dispersion relation was analysed in detail in a beautiful paper by Srinivasan &
Young (Reference Srinivasan and Young2012). Further results have been
reported by Parker & Krommes (Reference Parker and Krommes2014, Reference Parker, Krommes, Galperin and Read2015).
$C$
are unstable to the generation of inhomogeneous mean fields (see
figure 5). This process is analogous to the
general phenomenon of pattern formation, as discussed by Parker & Krommes (Reference Parker and Krommes2013).Footnote
95
In the context of the barotropic vorticity equation, the zonostrophic
dispersion relation was analysed in detail in a beautiful paper by Srinivasan &
Young (Reference Srinivasan and Young2012). Further results have been
reported by Parker & Krommes (Reference Parker and Krommes2014, Reference Parker, Krommes, Galperin and Read2015).

Figure 5. Cartoon of a neutral curve
 $C=C(q)$
for zonostrophic instability. Below the neutral curve, the
homogeneous turbulent state is stable. Above it, the homogeneous turbulence
is unstable to the generation of inhomogeneous mean fields. Instability
first sets in at a critical wavenumber
$C=C(q)$
for zonostrophic instability. Below the neutral curve, the
homogeneous turbulent state is stable. Above it, the homogeneous turbulence
is unstable to the generation of inhomogeneous mean fields. Instability
first sets in at a critical wavenumber
![]() $q_{c}$
. For given
$q_{c}$
. For given
![]() $C$
in the unstable region, zonal-flow equilibria with a
continuum of
$C$
in the unstable region, zonal-flow equilibria with a
continuum of
![]() $q$
values are allowed. Further analysis must be done to
examine the stability of those solutions (Parker & Krommes Reference Parker and Krommes2014).
$q$
values are allowed. Further analysis must be done to
examine the stability of those solutions (Parker & Krommes Reference Parker and Krommes2014).
This zonostrophic instability is a generalization of the often-discussed modulational
instability (Dewar & Abdullatif Reference Dewar, Abdullatif, Denier and Frederiksen2006;
Connaughton et al.
Reference Connaughton, Nadiga, Nazarenko and Quinn2010), in which one considers the instability
of a fixed ‘pump’ wave at wavevector
![]() $\boldsymbol{K}$
to the generation of fluctuations at wavevector
$\boldsymbol{K}$
to the generation of fluctuations at wavevector
![]() $\boldsymbol{Q}$
with sidebands at
$\boldsymbol{Q}$
with sidebands at
 $\boldsymbol{P}_{\pm }=-\boldsymbol{K}\pm \boldsymbol{Q}$
(see figure 6). The
relationship between the zonostrophic and modulational instabilities was first
demonstrated by Carnevale & Martin (Reference Carnevale and Martin1982),
though their result was not widely appreciated. It has recently been discussed in
more detail by Parker & Krommes (Reference Parker, Krommes, Galperin and Read2015),
whose work was further generalized by Bakas, Constantinou & Ioannou (Reference Bakas, Constantinou and Ioannou2015, appendix C).
$\boldsymbol{P}_{\pm }=-\boldsymbol{K}\pm \boldsymbol{Q}$
(see figure 6). The
relationship between the zonostrophic and modulational instabilities was first
demonstrated by Carnevale & Martin (Reference Carnevale and Martin1982),
though their result was not widely appreciated. It has recently been discussed in
more detail by Parker & Krommes (Reference Parker, Krommes, Galperin and Read2015),
whose work was further generalized by Bakas, Constantinou & Ioannou (Reference Bakas, Constantinou and Ioannou2015, appendix C).

Figure 6. Wavevectors for the modulational instability of a fixed pump wave
![]() $\boldsymbol{K}$
to fluctuations at
$\boldsymbol{K}$
to fluctuations at
![]() $\boldsymbol{Q}$
; the sidebands are
$\boldsymbol{Q}$
; the sidebands are
 $\boldsymbol{P}_{\pm }\doteq -(\boldsymbol{K}\pm \boldsymbol{Q})$
. The mode coupling obeys
$\boldsymbol{P}_{\pm }\doteq -(\boldsymbol{K}\pm \boldsymbol{Q})$
. The mode coupling obeys
 $\boldsymbol{K}+\boldsymbol{P}_{\pm }\pm \boldsymbol{Q}=\mathbf{0}$
. This process can be extracted from the general dispersion
relation for zonostrophic instability by inserting the background spectrum
$\boldsymbol{K}+\boldsymbol{P}_{\pm }\pm \boldsymbol{Q}=\mathbf{0}$
. This process can be extracted from the general dispersion
relation for zonostrophic instability by inserting the background spectrum
 $C_{\boldsymbol{k}}\propto {\it\delta}(\boldsymbol{k}-\boldsymbol{K})+{\it\delta}(\boldsymbol{k}+\boldsymbol{K})$
.
$C_{\boldsymbol{k}}\propto {\it\delta}(\boldsymbol{k}-\boldsymbol{K})+{\it\delta}(\boldsymbol{k}+\boldsymbol{K})$
.
6.3. The CE2 and S3T closures
The dispersion relation (6.13) also follows from a superficially distinct closure theory, the so-called CE2 (second-order cumulant) closure (see Tobias, Dagon & Marston Reference Tobias, Dagon and Marston2011, Srinivasan & Young Reference Srinivasan and Young2012, and references therein). In this approximation, the small-scale turbulence is represented by merely an external white-noise forcing; otherwise, ‘eddy–eddy interactions’ are neglected and the retained interactions are between only the mean fields and the turbulence. It is left to the reader to learn more about this closure (see the discussion below as well as various articles in Galperin & Read (Reference Galperin and Read2015)) and to ponder why the dispersion relations should be equivalent.
In the general notation of (2.6)–(2.8), the CE2
closure omits the terms of
![]() $O({\it\delta}{\it\psi}^{2})$
in (2.7) or the
third-order cumulant
$O({\it\delta}{\it\psi}^{2})$
in (2.7) or the
third-order cumulant
![]() $T$
in (2.8) (those
terms describe the eddy–eddy interactions) while keeping (2.6) for the mean field intact. With
white-noise forcing, (2.8) closes in
terms of
$T$
in (2.8) (those
terms describe the eddy–eddy interactions) while keeping (2.6) for the mean field intact. With
white-noise forcing, (2.8) closes in
terms of
![]() $\langle {\it\psi}\rangle (t)$
,
$\langle {\it\psi}\rangle (t)$
,
![]() $C(t,t)$
, and the known strength of the forcing; the truncated form of
(2.7) ensures that this
approximation is realizable. Tobias et al. (Reference Tobias, Dagon and Marston2011), Tobias & Marston (Reference Tobias and Marston2013), and Marston, Qi & Tobias (Reference Marston, Qi, Tobias, Galperin and Read2015) have referred to the numerical solutions of such truncated cumulant
systems as ‘direct statistical simulations’.
$C(t,t)$
, and the known strength of the forcing; the truncated form of
(2.7) ensures that this
approximation is realizable. Tobias et al. (Reference Tobias, Dagon and Marston2011), Tobias & Marston (Reference Tobias and Marston2013), and Marston, Qi & Tobias (Reference Marston, Qi, Tobias, Galperin and Read2015) have referred to the numerical solutions of such truncated cumulant
systems as ‘direct statistical simulations’.
Realizability is an important property of CE2. While one can define higher-order
approximations CE
![]() $n$
for
$n$
for
![]() $n>2$
, none of those are realizable.Footnote
96
Marston (Reference Marston2012) and Marston
et al. (Reference Marston, Qi, Tobias, Galperin and Read2015) have
explored several phenomenologically modified versions of CE3 that appear to
pragmatically restore realizability. The presence of eddy–eddy interactions in those
closures leads to results that are superior to those from CE2 in some situations.
However, a more systematic approach is desirable.
$n>2$
, none of those are realizable.Footnote
96
Marston (Reference Marston2012) and Marston
et al. (Reference Marston, Qi, Tobias, Galperin and Read2015) have
explored several phenomenologically modified versions of CE3 that appear to
pragmatically restore realizability. The presence of eddy–eddy interactions in those
closures leads to results that are superior to those from CE2 in some situations.
However, a more systematic approach is desirable.
Studies of CE
![]() $n$
closures (by that name) were preceded by the research of Farrell
and coworkers on the so-called stochastic structural stability theory (SSST or S3T),
the fundamental paper being that of Farrell & Ioannou (Reference Farrell and Ioannou2003); see also Farrell & Ioannou (Reference Farrell, Ioannou, Galperin and Read2015) for an overview. One version of the theory is
mathematically identical to CE2, a philosophical difference being the interpretation
of the random forcing. In strict CE2, the forcing is viewed as being entirely
extrinsic – for example, due to modes that are otherwise unaccounted for. In S3T, the
forcing is frequently said to represent the effects of the eddy–eddy interactions as
well as any extrinsic noise. That would be in accord with a Langevin representation
of the turbulence provided that an energy-conserving coherent damping due to the
eddy–eddy terms was also included. Sometimes that has been done, as in the work of
DelSole (Reference DelSole2001) and Farrell & Ioannou
(Reference Farrell and Ioannou2009b
); other times it has been omitted, as in the application by Farrell &
Ioannou (Reference Farrell and Ioannou2009a
) of S3T to the Hasegawa–Wakatani system. Omission of that damping fosters
uncertainty about some of the details reported in the latter work (without, however,
vitiating the principal message).
$n$
closures (by that name) were preceded by the research of Farrell
and coworkers on the so-called stochastic structural stability theory (SSST or S3T),
the fundamental paper being that of Farrell & Ioannou (Reference Farrell and Ioannou2003); see also Farrell & Ioannou (Reference Farrell, Ioannou, Galperin and Read2015) for an overview. One version of the theory is
mathematically identical to CE2, a philosophical difference being the interpretation
of the random forcing. In strict CE2, the forcing is viewed as being entirely
extrinsic – for example, due to modes that are otherwise unaccounted for. In S3T, the
forcing is frequently said to represent the effects of the eddy–eddy interactions as
well as any extrinsic noise. That would be in accord with a Langevin representation
of the turbulence provided that an energy-conserving coherent damping due to the
eddy–eddy terms was also included. Sometimes that has been done, as in the work of
DelSole (Reference DelSole2001) and Farrell & Ioannou
(Reference Farrell and Ioannou2009b
); other times it has been omitted, as in the application by Farrell &
Ioannou (Reference Farrell and Ioannou2009a
) of S3T to the Hasegawa–Wakatani system. Omission of that damping fosters
uncertainty about some of the details reported in the latter work (without, however,
vitiating the principal message).
Farrell & Ioannou (Reference Farrell, Ioannou, Galperin and Read2015) have reviewed some calculations using S3T and have also embedded that approximation into a more general framework that they call statistical state dynamics. The basic philosophy is that working with an ensemble (even one that is characterized by only the first few cumulants) provides information about cooperative and self-consistent behaviour that is superior to that gained from studies of individual realizations. A technical justification for a simple stochastic parametrization of the eddy–eddy interactions involves the non-normalityFootnote 97 of the linear operator in the presence of mean fields; consult Farrell & Ioannou (Reference Farrell, Ioannou, Galperin and Read2015, and references therein) for further discussion of the implications of non-normality.
In the original applications of these types of closures, coupled equations for mean fields and eddy covariance were obtained by applying a zonal average to the original PDE. However, Bakas et al. (Reference Bakas, Constantinou and Ioannou2015) have generalized the procedure to show that one can consider the onset of both zonal and nonzonal perturbations; many detailed results about barotropic beta-plane turbulence are contained in that beautiful paper, which has implications for drift-wave physics as well.
There are many opportunities for further research. For example, some current work focuses on applying CE2-type ideas to the study of dynamo action in accretion disks (Squire & Bhattacharjee Reference Squire and Bhattacharjee2015). Also, the kinds of inhomogeneous states described in this section, which involve steady or quasi-steady zonal jets, do not appear to be relevant for microturbulence in tokamaks; see footnote 90 on page 52 as well as challenge 6 in § 8.
7. Highlights of some research threads
Now that the reader has gained an overview of the subject from a modern perspective, I wish to provide additional representative references that chronicle the progression of some lines of plasma turbulence research that emanate from the mid-1960s, as well as to mention some ideas and techniques that arose only later. It is fascinating to watch the emergence and development of ideas in the course of a half-century of research. Unfortunately, I cannot give a complete review of the subject, which is vast. Any one of the subsections below merits a full-length review in its own right, and I have omitted some important areas altogether; here I merely want to whet the reader’s interest and provide some entry points to the literature. I restrict my attention to basic conceptual topics. The consequences of turbulence for plasma confinement are beyond the scope of this article, although they are obviously of paramount importance.Footnote 98
7.1. Some ideas discussed by Kadomtsev
7.1.1. Bifurcations
Early in his book, Kadomtsev introduced (p. 5) the topic of bifurcations, either ‘soft’ (supercritical) or ‘hard’ (subcritical). Hinton & Horton (Reference Hinton and Horton1971) did a nice bifurcation calculation of a collisional drift-wave instability. Much more recently, Kolesnikov & Krommes (Reference Kolesnikov and Krommes2005a ,Reference Kolesnikov and Krommes b ) attempted to consider the transition to ion-temperature-gradient-driven turbulence in the present of zonal flows, motivated by the numerically observed phenomenon of the Dimits shiftFootnote 99 (Dimits et al. Reference Dimits, Bateman, Beer, Cohen, Dorland, Hammett, Kim, Kinsey, Kotschenreuther, Kritz, Lao, Mandrekas, Nevins, Parker, Redd, Shumaker, Sydora and Weiland2000). Although they used modern techniques such as the centre-manifold theorem (Guckenheimer & Holmes Reference Guckenheimer and Holmes1983; Kuznetsov Reference Kuznetsov1998), the results were ultimately unsatisfactory; considerable further work is indicated.
Also in the context of bifurcations, Kadomtsev (p. 6) referred to Landau’s scenario for the transition to turbulence. A revolution occurred when Ruelle & Takens (Reference Ruelle and Takens1971) argued for a qualitatively different scenario involving strange attractors, which had been discovered without fanfare years earlier by Lorenz (Reference Lorenz1963). Some good discussion of issues and phenomenology related to modern nonlinear dynamics is given by Holmes, Lumley & Berkooz (Reference Holmes, Lumley and Berkooz1996).
Subcritical bifurcation provides a route to subcritical or submarginal turbulence, a difficult topic about which I have said little. The phenomenon was subsequently observed in a variety of computer simulations, representative examples of which include the works of Scott (Reference Scott1992) and Drake, Zeiler & Biskamp (Reference Drake, Zeiler and Biskamp1995).Footnote 100 Itoh et al. (Reference Itoh, Itoh, Yagi and Fukuyama1996) and Itoh, Itoh & Fukuyama (Reference Itoh, Itoh and Fukuyama1999) discussed the topic in terms of nonlinear dispersion relations that follow from crude statistical closures. There is much more work to do; see challenge 4 in § 8.
7.1.2. Quasi-linear theory
Kadomtsev (§ I.3) reviewed the basic ingredients of the plasma quasi-linear theory, which had appeared just a few years earlier (Drummond & Pines Reference Drummond and Pines1962; Vedenov et al. Reference Vedenov, Velikhov and Sagdeev1962). About five years later, the monograph of Sagdeev & Galeev (Reference Sagdeev and Galeev1969), based on lectures from a few years earlier, treated the subject in somewhat more detail. They displayed an appreciation of the importance of stochastic phase-space trajectories, and they cited Dupree (Reference Dupree1966) for the most rigorous justification of the diffusion operator.Footnote 101 However, none of those authors discussed what is now called the Chirikov criterion (island overlap) for the onset of stochasticity;Footnote 102 Chirikov’s thesis only appeared a few years later (Chirikov Reference Chirikov1969). That was the tip of the iceberg associated with the emerging awareness by the plasma community of Hamiltonian chaos and nonlinear dynamics, which gained force during the 1970s. Modern understanding is described in the books by Lichtenberg & Lieberman (Reference Lichtenberg and Lieberman1992) and (more briefly but very elegantly) by Diacu & Holmes (Reference Diacu and Holmes1996).
7.1.3. Wave kinetics
Kadomtsev discussed wave–wave coupling in his book (chapter I.3). That theme was also taken up by Sagdeev & Galeev (Reference Sagdeev and Galeev1969); a modern book is by Nazarenko (Reference Nazarenko2011). Recent advances in the theory of plasma waves are described by Dodin (Reference Dodin2014a ,Reference Dodin b ).
7.1.4. Noise due to particle discreteness, and the transition to unstable, nonlinearly saturated turbulence in plasmas
By the early 1960s, one had a clear picture of the consequences of particle discreteness for a weakly coupled stable plasma in the form of the Balescu–Lenard and Landau collision operators. The theory was briefly described by Kadomtsev (§ II.2(b)) and treated in more detail by Montgomery & Tidman (Reference Montgomery and Tidman1964).
To discuss the qualitative transition from stable to unstable plasma, Kadomtsev considered (p. 46) the equation
 $$\begin{eqnarray}\frac{\text{d}I}{\text{d}t}=2{\it\gamma}I+q-{\it\alpha}I^{2},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}I}{\text{d}t}=2{\it\gamma}I+q-{\it\alpha}I^{2},\end{eqnarray}$$
where
![]() $I$
denotes spectral intensity,
$I$
denotes spectral intensity,
![]() ${\it\gamma}$
is a typical linear growth rate,
${\it\gamma}$
is a typical linear growth rate,
![]() $q$
is a source of fluctuations due to moving discrete particles,
and
$q$
is a source of fluctuations due to moving discrete particles,
and
![]() ${\it\alpha}$
is a mode-coupling coefficient. For stable plasma, he described
the discreteness-induced noise level as a balance between emission and
absorption:Footnote
103
${\it\alpha}$
is a mode-coupling coefficient. For stable plasma, he described
the discreteness-induced noise level as a balance between emission and
absorption:Footnote
103
 $I=q/(2|{\it\gamma}|)$
. As the modal growth rate transitions through zero to positive
values, nonlinear mode-coupling effects enter and the steady state is given by
$I=q/(2|{\it\gamma}|)$
. As the modal growth rate transitions through zero to positive
values, nonlinear mode-coupling effects enter and the steady state is given by
 $I=2{\it\gamma}/{\it\alpha}$
; see Kadomtsev’s figure 11. Detailed treatment of this
transition is difficult even in weak-turbulence theory (Rogister & Oberman
Reference Rogister and Oberman1968, Reference Rogister and Oberman1969). In principle, it can be described by the general equations of
Rose (Reference Rose1979).
$I=2{\it\gamma}/{\it\alpha}$
; see Kadomtsev’s figure 11. Detailed treatment of this
transition is difficult even in weak-turbulence theory (Rogister & Oberman
Reference Rogister and Oberman1968, Reference Rogister and Oberman1969). In principle, it can be described by the general equations of
Rose (Reference Rose1979).
Discreteness-related noise is also important in particle-in-cell (PIC) simulations of plasmas. For unmagnetized plasmas, the relevant kinetic theory is described by Birdsall & Langdon (Reference Birdsall and Langdon1985, chapter 12). The theory of noise in gyrokinetic plasma is especially interesting because the gyrokinetic noise level is substantially lower than that of the true many-body plasma. Theoretical analysis of gyrokinetic noise in both electrostatic (Krommes, Lee & Oberman Reference Krommes, Lee and Oberman1986) and electromagnetic (Krommes Reference Krommes1993) regimes were followed by detailed calculations of the noise level in gyrokinetic PIC simulations (Nevins et al. Reference Nevins, Hammett, Dimits, Dorland and Shumaker2005); the latter work inspired a vigorous and useful debate about signal-to-noise ratios and resolution requirements in the simulations. The theory was reviewed by Krommes (Reference Krommes2007).
7.2. Some ideas discussed by Dupree and Weinstock
7.2.1. Energy conservation
Dupree’s original RBT did not conserve energy; as I noted in footnote 37 on page 17, it was appropriate for passive, not self-consistent, problems. This and other difficulties were discussed by Orszag & Kraichnan (Reference Orszag and Kraichnan1967), whose paper on variants of the DIA for kinetic plasma turbulence was full of important insights. Unfortunately, that paper appears to have been mostly ignored for about a decade until the rise of interest in the mid-1970s in systematically renormalized closures by DuBois and coworkers, Krommes and others. Dupree & Tetreault (Reference Dupree and Tetreault1978) also discussed the problem with energy conservation in a restricted context.
7.2.2. Phase-space granulation
Subsequently, Dupree focused his research on considerations of small-scale granulations and the related topics of ‘clumps’, ‘holes’, and coherent structures (areas not discussed by Kadomtsev). Boutros-Ghali & Dupree (Reference Boutros-Ghali and Dupree1981) gave a thorough discussion of the consequences of the one- and two-time equations for the two-point correlation function, with reference to coherent and incoherent response. They challenged some of the conclusions reached by DuBois & Espedal (Reference DuBois and Espedal1978) relating to phase-space granulation and clumps. However, in the opinion of the present author, DuBois and Espedal were correct.Footnote 104 For fluctuations in phase space, the role of coherent structures remains of interest today (Diamond et al. Reference Diamond, Itoh and Itoh2010; Lesur & Diamond Reference Lesur and Diamond2013). The application of clump-related ideas to fluid problems is rather subtle, as explained by Krommes (Reference Krommes1997). His discussion was in part motivated by the celebrated Kraichnan model (Kraichnan Reference Kraichnan1994) of passive advection involving a random coefficient delta-correlated in time but with specified wavenumber spectrum. That model proved to be enormously useful and ultimately led to the discoveries about anomalous scaling reviewed by Falkovich et al. (Reference Falkovich, Gawȩdzki and Vergassola2001) – truly one of the major triumphs of the modern statistical theory of turbulent fluids. To be clear, these latter results were not motivated by Dupree’s early work; they are just beautiful physics, and they set a very high standard for the theoretical analysis of turbulent systems.
7.2.3. Averaging and projection operators
The papers of Weinstock (Reference Weinstock1969, Reference Weinstock1970) introduced the concept of an averaging
operator, with which he showed how to interpret and generalize the analyses of
Dupree (Reference Dupree1966, Reference Dupree1967). (The systematic use of cumulants (Weinstock Reference Weinstock1968) was also important in the discussion.)
An averaging operator is a special case of a linear projection operator
![]() $\text{P}$
, which obeys
$\text{P}$
, which obeys
![]() $\text{P}^{2}=\text{P}$
. Define also the orthogonal projector
$\text{P}^{2}=\text{P}$
. Define also the orthogonal projector
 $\text{Q}\doteq 1-\text{P}$
. Then a dynamical equation for a field
$\text{Q}\doteq 1-\text{P}$
. Then a dynamical equation for a field
![]() ${\it\psi}$
can be projected onto a ‘relevant’ subspace with
${\it\psi}$
can be projected onto a ‘relevant’ subspace with
![]() $\text{P}$
, and onto everything else (the orthogonal subspace) with
$\text{P}$
, and onto everything else (the orthogonal subspace) with
![]() $\text{Q}$
. Elimination of the irrelevant dynamics
$\text{Q}$
. Elimination of the irrelevant dynamics
![]() $\text{Q}{\it\psi}$
then leads to a formally closed equation for the
$\text{Q}{\it\psi}$
then leads to a formally closed equation for the
![]() $\text{P}$
projection. Such methodology was used in a famous paper by Mori
(Reference Mori1965), who showed how to use
projection operators to derive generalized Langevin equations, and it figures
importantly in modern derivations of linear and nonlinear theories of transport in
many-body systems (Zwanzig Reference Zwanzig2001).
$\text{P}$
projection. Such methodology was used in a famous paper by Mori
(Reference Mori1965), who showed how to use
projection operators to derive generalized Langevin equations, and it figures
importantly in modern derivations of linear and nonlinear theories of transport in
many-body systems (Zwanzig Reference Zwanzig2001).
The elimination of
![]() $\text{Q}{\it\psi}$
formally solves the closure problem! Of course, the devil is in
the detail. Exactly how to best define relevant is unclear. And
even given such a definition, for nonlinear systems the elimination of the
irrelevant dynamics is nontrivial; ultimately, the various approximate techniques
for carrying that out amount to a restatement of the kinds of approaches employed
in traditional closure theory (with all of their difficulties). Nevertheless,
Weinstock’s averaging-operator approach elucidated the mechanics of Dupree’s
formalism and clarified the structure of plasma turbulence theory.
Projection-operator methods should be in the toolbox of a well-rounded turbulence
theorist, although they are definitely not a panacea and should be used only with
the greatest of care.
$\text{Q}{\it\psi}$
formally solves the closure problem! Of course, the devil is in
the detail. Exactly how to best define relevant is unclear. And
even given such a definition, for nonlinear systems the elimination of the
irrelevant dynamics is nontrivial; ultimately, the various approximate techniques
for carrying that out amount to a restatement of the kinds of approaches employed
in traditional closure theory (with all of their difficulties). Nevertheless,
Weinstock’s averaging-operator approach elucidated the mechanics of Dupree’s
formalism and clarified the structure of plasma turbulence theory.
Projection-operator methods should be in the toolbox of a well-rounded turbulence
theorist, although they are definitely not a panacea and should be used only with
the greatest of care.
7.3. Some miscellaneous topics related to analytical methods
The following subsections mention representative topics that have emerged subsequent to the early works by Kadomtsev, Dupree, and Weinstock.
7.3.1. Entropy, dissipation and phase-space cascades
It is implicit in the spectral balance equations that a forced steady state cannot
be achieved in the absence of dissipation; see, for example, the presence of
![]() ${\it\nu}^{-1}$
in (2.36b
). A basic paper on the general relationship between dissipation, entropy,
and spectral cascades is by Krommes & Hu (Reference Krommes and Hu1994).Footnote
105
That work focused on fluid models. However, modern astrophysical and
space-physics applications, enlightened by high-quality telescope and satellite
data, have led to considerable interest in cascades of free energy in phase space.
Some beautiful and detailed calculations were done by Schekochihin
et al. (Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Plunk, Quataert and Tatsuno2008, Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009).
${\it\nu}^{-1}$
in (2.36b
). A basic paper on the general relationship between dissipation, entropy,
and spectral cascades is by Krommes & Hu (Reference Krommes and Hu1994).Footnote
105
That work focused on fluid models. However, modern astrophysical and
space-physics applications, enlightened by high-quality telescope and satellite
data, have led to considerable interest in cascades of free energy in phase space.
Some beautiful and detailed calculations were done by Schekochihin
et al. (Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Plunk, Quataert and Tatsuno2008, Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009).
7.3.2. Optimal variables
The statistical closures described in this article are generally applied directly to a given PDE and are couched in terms of the original independent variables of that equation. It is not clear that this procedure is optimal from the point of view of capturing interesting physics. For example, the most elegant formulation of quasi-linear theory is in terms of oscillation-centre variables (Dewar Reference Dewar1973) that remove the nonresonant particle oscillations in the wavefields. Dewar (Reference Dewar1976, Reference Dewar1985) invested considerable effort in trying to generalize such techniques to turbulent situations. Although that work was not entirely successful, it was well motivated and highly original; some perspectives and discussion are given by Krommes (Reference Krommes2012a ). Further results in this area would be very welcome.
7.3.3. Fractional diffusion
While many aspects of turbulence phenomenology can be satisfactorily described in terms of classical Brownian motion, Langevin equations, and Fokker–Planck equations, others cannot. For example, if the conditions of the standard central limit theorem (which assumes finite variance) are violated, then generalized random walks (Lévy processes) become possible. Those can be described by generalized Fokker–Planck equations that involve fractional derivatives. Good introductions are given by Klafter et al. (Reference Klafter, Shlesinger and Zumofen1996), Balescu (Reference Balescu1997), Metzler & Klafter (Reference Metzler and Klafter2000), and Zaslavsky (Reference Zaslavsky2002). An example of work along these lines in the plasma context is by del Castillo-Negrete, Carreras & Lynch (Reference del Castillo-Negrete, Carreras and Lynch2004).
7.3.4. Variational methods
At the heart of the MSR formalism is a cumulant generating functional. Normally, that is used to obtain formally closed Dyson equations that are then approximated. An alternative approach is to approximate the generating functional directly. One example of a serious attempt in that direction is by Spineanu & Vlad (Reference Spineanu and Vlad2005).
7.3.5. Saddle-point methods
Although I have said little in this introductory article about methods aimed at entire PDFs, I do not mean to imply that they are not useful or unimportant. They are well suited to situations involving large intermittency, which manifests as non-Gaussian tails on PDFs. One technique for addressing that problem is the (saddle-point) method of instantons (Zinn-Justin Reference Zinn-Justin1996); for some plasma-related work, see, for example, Kim et al. (Reference Kim, Diamond, Malkov, Hahm, Itoh, Itoh, Champeaux, Gruzinov, Gurcan, Holland, Rosenbluth and Smolyakov2003) or Anderson & Xanthopoulos (Reference Anderson and Xanthopoulos2010).
7.3.6. Magnetohydrodynamic turbulence
A major area of current interest is the description and role of electromagnetic effects in turbulence. Those are relevant to microturbulence in modern, high-pressure toroidal devices, and basic electromagnetic corrections to drift-wave theory were already discussed by Kadomtsev (p. 82). However, he specifically omitted discussion of ‘problems of astrophysical application’ (p. 4). Recently the theory of macroscopic magnetohydrodynamic (MHD) turbulence, especially in astrophysics, has developed rapidly; some reviews are by Sridhar (Reference Sridhar2010) and Tobias et al. (Reference Tobias, Cattaneo, Boldyrev, Davidson, Kaneda and Sreenivasan2013).
7.3.7. Critical balance
MHD turbulence is anisotropic in the presence of a background magnetic field; gyrokinetic turbulence is also intrinsically anisotropic. While the statistical closures I have discussed in this article, such as the DIA, are generally valid for anisotropic turbulence, the lack of complete symmetry makes the extraction of practical information and understanding from them entirely nontrivial. A crucial part of the modern insights about anisotropic turbulence, both for MHD (Goldreich & Sridhar Reference Goldreich and Sridhar1995) and more generally (Nazarenko & Schekochihin Reference Nazarenko and Schekochihin2011), is the conjecture of critical balance. The concept is defined slightly differently depending on the author; in essence, the turbulence is supposed to adjust so that the correlation times associated with parallel and perpendicular effects are comparable. The idea has had a huge impact on one’s understanding of both MHD and microturbulence in realistic, magnetized situations. For further references to the extensive MHD literature, see the above-mentioned reviews. In research on magnetic fusion, the conjecture is supported by both simulations (Barnes, Parra & Schekochihin Reference Barnes, Parra and Schekochihin2011) and experiments (Grim et al. Reference Grim, Schekochihin, Field, Abel, Barnes, Colyer, Cowley, Parra, Dunai and Zoletnik2013). From the point of view of analytical methods, on which the present § 7.3 focuses, the justification of critical balance has been argued by detailed analyses of the nonlinear mode coupling (see especially the MHD references) as well as with the aid of stochastic-oscillator models (Lithwick & Goldreich Reference Lithwick and Goldreich2003).
8. Summary; outstanding issues
The new material presented in this article includes (i) arguments based on Novikov’s
theorem that provide a heuristic,
![]() $\boldsymbol{x}$
-space derivation of the DIA (§ 4.1), and (ii) an algorithmic approach to the determination of the dielectric
response function
$\boldsymbol{x}$
-space derivation of the DIA (§ 4.1), and (ii) an algorithmic approach to the determination of the dielectric
response function
![]() ${\mathcal{D}}$
in the DIA to a general quadratically nonlinear PDE (§ 4.2).
${\mathcal{D}}$
in the DIA to a general quadratically nonlinear PDE (§ 4.2).
The general goal of the tutorial was to describe some of the highlights of the
statistical theory of turbulence, motivations being the seminal insights of Kadomtsev on
strong turbulence and the pioneering attempts by Dupree and Weinstock to obtain and deal
with the consequences of a nonlinear
![]() ${\mathcal{D}}$
. I mentioned nonlinear incoherent noise and coherent damping (both
present in passive problems) as well as self-consistent dielectric polarization.
Dielectric response is subsumed by the infinitesimal response function
${\mathcal{D}}$
. I mentioned nonlinear incoherent noise and coherent damping (both
present in passive problems) as well as self-consistent dielectric polarization.
Dielectric response is subsumed by the infinitesimal response function
![]() $R$
, which participates along with the covariance
$R$
, which participates along with the covariance
![]() $C$
in the steady-state spectral balance for a self-consistent turbulent
system. An approximation to
$C$
in the steady-state spectral balance for a self-consistent turbulent
system. An approximation to
![]() $R$
also determines the dispersion relation for the bifurcation of
homogeneous turbulence into inhomogeneous turbulence with nonvanishing mean fields; that
is of great interest for the problem of zonal-flow generation. The CE2 and S3T closures
(more generally, studies of statistical state dynamics) have had important successes in
elucidating some physics of the interactions of zonal flows with turbulence.
$R$
also determines the dispersion relation for the bifurcation of
homogeneous turbulence into inhomogeneous turbulence with nonvanishing mean fields; that
is of great interest for the problem of zonal-flow generation. The CE2 and S3T closures
(more generally, studies of statistical state dynamics) have had important successes in
elucidating some physics of the interactions of zonal flows with turbulence.
Specific facts about
![]() ${\mathcal{D}}$
are as follows. (i)
${\mathcal{D}}$
are as follows. (i)
![]() ${\mathcal{D}}^{-1}$
is related to the first-order mean response to perturbations of
self-consistent turbulence. (ii)
${\mathcal{D}}^{-1}$
is related to the first-order mean response to perturbations of
self-consistent turbulence. (ii)
![]() ${\mathcal{D}}$
is a nonlinear functional of the fluctuation spectrum through all
orders. (iii) Nonlinear corrections to
${\mathcal{D}}$
is a nonlinear functional of the fluctuation spectrum through all
orders. (iii) Nonlinear corrections to
![]() ${\mathcal{D}}$
are essential because they guarantee that the total growth rate
(linear plus nonlinear) is negative in a steady state, as it must be to balance the
positive-definite nonlinear noise that arises from mode coupling. (iv) In a kinetic
description,
${\mathcal{D}}$
are essential because they guarantee that the total growth rate
(linear plus nonlinear) is negative in a steady state, as it must be to balance the
positive-definite nonlinear noise that arises from mode coupling. (iv) In a kinetic
description,
![]() ${\mathcal{D}}$
includes the wave–wave–particle interactions of weak-turbulence theory
as well as part of the
${\mathcal{D}}$
includes the wave–wave–particle interactions of weak-turbulence theory
as well as part of the
![]() $n$
-wave coupling processes. (v) A
$n$
-wave coupling processes. (v) A
![]() ${\mathcal{D}}$
can be defined not only for plasmas but for turbulent fluids and
additional nonlinear systems as well. (vi)
${\mathcal{D}}$
can be defined not only for plasmas but for turbulent fluids and
additional nonlinear systems as well. (vi)
![]() ${\mathcal{D}}$
is subsumed by the infinitesimal response function
${\mathcal{D}}$
is subsumed by the infinitesimal response function
![]() $R$
.
$R$
.
Specific facts about nonlinear noise are as follows: (i) Internal nonlinear noise is
present in the statistical description of all nonlinear systems. (ii) Nonlinear noise is
necessary in order to guarantee, along with coherent damping, the conservation of robust
nonlinear invariants. (iii) Nonlinear noise includes part of the
![]() $n$
-wave coupling processes of weak-turbulence theory. (iv) Furthermore,
it is required in order to ensure the proper small-distance behaviour of relative
diffusion coefficients.
$n$
-wave coupling processes of weak-turbulence theory. (iv) Furthermore,
it is required in order to ensure the proper small-distance behaviour of relative
diffusion coefficients.
Some outstanding challenges related to fundamental statistical descriptions include the following:
-
(1) There is a difficult literature on the kinetic plasma DIA (DuBois & Pesme Reference DuBois and Pesme1985) that has more or less ground to a halt in the absence of numerical solutions. It would be interesting to revisit that, given advances in modern computing; further insights about the interpretation of quasi-linear theory (Laval & Pesme Reference Laval and Pesme1984) and the importance of mode coupling would be forthcoming.
-
(2) Although it is clear how to define the operator
 ${\it\Sigma}^{f}\doteq \boldsymbol{\partial }{\it\delta}\overline{f}\boldsymbol{\cdot }\pmb{\mathbb{E}}$
that defines the nonlinear corrections to the background
distribution function in the renormalized dielectric, the physical
interpretation of those terms is still largely absent for kinetic problems
(mostly for lack of trying, although see DuBois & Pesme (Reference DuBois and Pesme1985)). A hint comes from the work of
Krommes (Reference Krommes2009), where it was shown how
the notions of oscillation-centre variables and ponderomotive force are buried
in the renormalizations. An outstanding question is whether such analysis can
be extended to
${\it\Sigma}^{f}\doteq \boldsymbol{\partial }{\it\delta}\overline{f}\boldsymbol{\cdot }\pmb{\mathbb{E}}$
that defines the nonlinear corrections to the background
distribution function in the renormalized dielectric, the physical
interpretation of those terms is still largely absent for kinetic problems
(mostly for lack of trying, although see DuBois & Pesme (Reference DuBois and Pesme1985)). A hint comes from the work of
Krommes (Reference Krommes2009), where it was shown how
the notions of oscillation-centre variables and ponderomotive force are buried
in the renormalizations. An outstanding question is whether such analysis can
be extended to
 ${\it\delta}\overline{f}$
. Results here would bear on the question of optimal variables
and might suggest more physically useful approximations.
${\it\delta}\overline{f}$
. Results here would bear on the question of optimal variables
and might suggest more physically useful approximations. -
(3) Second-order closures such as the DIA or its Markovian relatives are limited in their ability to deal with the consequences of coherent structures and intermittency (Chen et al. Reference Chen, Herring, Kerr and Kraichnan1989; Krommes Reference Krommes1996), for which it is better to focus on entire PDFs. Kraichnan has proposed an ingenious mapping closure for PDFs (Kraichnan Reference Kraichnan and Sirovich1991; Das & Kaw Reference Das and Kaw1995), but many questions remain open. For example, it would be of great interest to develop a workable mapping closure for the Hasegawa–Wakatani system. (There are difficulties associated with the treatment of the perpendicular Laplacian.)
-
(4) The statistical theory of subcritical turbulence should be much further developed. One needs to meld insights and techniques from nonlinear dynamics (Waleffe Reference Waleffe1995, Reference Waleffe1997) with systematic statistical closure. Because non-normality is required for this phenomenon, some of the knowledge that has been gained from research on CE2/S3T closures might be useful.
-
(5) The theory of the instability of homogeneous turbulence (§ 6.2) is in its infancy. Definite calculations have been done in the CE2 approximation; however, that neglects eddy–eddy interactions. The forced, dissipative CE2 solution for the homogeneous turbulence regime is physically simplistic; one should study perturbations of more realistic homogeneous steady states. One should also study the consequences of dispersion relations that go beyond (6.13). Such analysis should ultimately be conducted with models that include some toroidal effects.
-
(6) Some solutions of the CE2/S3T closure reach a time-independent steady state (a stable fixed point), which seems to provide a reasonable explanation of the basically time-independent zonal jets observed on the large planets. But in other regimes, solutions can be quasi-periodic or even stochastic (Farrell & Ioannou Reference Farrell and Ioannou2009a , Reference Farrell, Ioannou, Galperin and Read2015). Stochastic solutions would appear to be relevant to the kinds of microturbulence observed in magnetic confinement devices, but additional work needs to be done in order to understand the meaning of such solutions, their relation to homogeneous ensembles, and their implications for the physics of zonal flows in tokamaks.
-
(7) Further research should be done to incorporate the salient effects of eddy–eddy interactions into generalizations of the CE2 closure. First steps have been taken by Marston et al. (Reference Marston, Qi, Tobias, Galperin and Read2015), but they raise a variety of questions that remain unanswered. It is tantalizing to contemplate workable hybrid numerical-plus-closure schemes, long a holy grail, that are built on CE
 $n$
. Those too should be formulated in toroidal geometry.
$n$
. Those too should be formulated in toroidal geometry.
In this tutorial I have covered considerable ground, from the simplest scaling estimates of transport coefficients to advanced, renormalized statistical closures. All of this is part of the subject, and a theorist wishing to work in the field should be aware of all of its facets. But it is worth enquiring again whether advanced formalism is really necessary. A stark comparison is between the physics of magnetically confined fusion plasmas and of the Lamb shift in quantum electrodynamics. Precise calculations of that shift are in agreement with measurements to a remarkable precision of perhaps 10 kHz out of a gigahertz. That is a triumph that will never be matched in fusion research, where complicated geometries, rich mixtures of physical processes, and hostile environments for diagnostics lead to substantial uncertainties in both theoretical descriptions and experimental measurements. But appreciating the structure of the formalism is still important. For example, an understanding of the form and content of the DIA gives some perspective to the CE2/S3T closures, which in turn have been useful in interpreting direct numerical simulations and experimental observations of zonal flows in the natural world. Nevertheless, if the current state of statistical plasma turbulence theory does not satisfy your needs, I encourage you to work at improving it. You will enjoy the ride.
In conclusion, I have given a taste of the complications that arise when a statistical description of a nonlinear PDE is attempted. Kadomtsev closed his review article by saying (p. 139),
One must hope that it will be possible in the course of the next few years of hectic development of the theory, in conjunction with detailed and accurate experiments, to set up a complete picture of the turbulence of plasmas.
Unfortunately, fifty years and billions of hours of supercomputer processor time later, we are still not there – but we are definitely closer. Perhaps this tutorial will provide a useful launch point for further study of the rich and challenging theory of turbulence in both plasmas and fluids.
Acknowledgements
I am grateful to J. Burby, D. Ruiz, and Y. Shi for their candid criticisms of an early draft of the manuscript, which led to wholesale revisions. Congratulations to E. Shi for successfully playing the editing game. I gladly incorporated excellent suggestions from A. Bhattacharjee, I. Dodin, and G. Hammett. The final form of the manuscript benefited substantially from expert advice of an anonymous referee. This work was supported by the US Department of Energy Contract DE-AC02-09CH11466.
Appendix A. Common quantities in drift-wave theory
A basic reference quantity in drift-wave theory is the sound speed
 $c_{\text{s}}\doteq (ZT_{e}/m_{i})^{1/2}$
, where
$c_{\text{s}}\doteq (ZT_{e}/m_{i})^{1/2}$
, where
![]() $Z$
is the atomic number. From that and the ion gyrofrequency
$Z$
is the atomic number. From that and the ion gyrofrequency
 ${\it\omega}_{\text{c}i}\doteq (qB/mc)_{i}$
, one can form the sound radius
${\it\omega}_{\text{c}i}\doteq (qB/mc)_{i}$
, one can form the sound radius
 ${\it\rho}_{\text{s}}\doteq c_{\text{s}}/{\it\omega}_{\text{c}i}$
. This is the characteristic fluctuation scale that appears in the
Hasegawa–Mima equation (5.1).
${\it\rho}_{\text{s}}\doteq c_{\text{s}}/{\it\omega}_{\text{c}i}$
. This is the characteristic fluctuation scale that appears in the
Hasegawa–Mima equation (5.1).
Because the electron response to nonzonal perturbations is adiabatic (in the sense of
slow variations),
 ${\it\delta}n_{e}/n_{e}\approx e{\it\delta}{\it\phi}/T_{e}$
, it is useful to introduce the normalized potential
${\it\delta}n_{e}/n_{e}\approx e{\it\delta}{\it\phi}/T_{e}$
, it is useful to introduce the normalized potential
 ${\it\varphi}\doteq e{\it\phi}/T_{e}$
. Then the
${\it\varphi}\doteq e{\it\phi}/T_{e}$
. Then the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
velocity is
$\boldsymbol{E}\times \boldsymbol{B}$
velocity is
 $\boldsymbol{V}_{E}\doteq (c/B)\widehat{\boldsymbol{b}}\times \boldsymbol{{\rm\nabla}}{\it\phi}=D_{\text{B}}\widehat{\boldsymbol{b}}\times \boldsymbol{{\rm\nabla}}{\it\varphi}$
, where the Bohm diffusion coefficient (sans factor
of
$\boldsymbol{V}_{E}\doteq (c/B)\widehat{\boldsymbol{b}}\times \boldsymbol{{\rm\nabla}}{\it\phi}=D_{\text{B}}\widehat{\boldsymbol{b}}\times \boldsymbol{{\rm\nabla}}{\it\varphi}$
, where the Bohm diffusion coefficient (sans factor
of
![]() $1/16$
) is
$1/16$
) is
 $D_{\text{B}}\doteq cT_{e}/eB={\it\rho}_{\text{s}}c_{\text{s}}$
. The
$D_{\text{B}}\doteq cT_{e}/eB={\it\rho}_{\text{s}}c_{\text{s}}$
. The
![]() $\boldsymbol{E}\times \boldsymbol{B}$
advection of a background ion density profile, described by
$\boldsymbol{E}\times \boldsymbol{B}$
advection of a background ion density profile, described by
 $\boldsymbol{V}_{E}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\langle n_{i}\rangle$
, thus becomes
$\boldsymbol{V}_{E}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\langle n_{i}\rangle$
, thus becomes
 $\langle n_{i}\rangle V_{\ast }\partial _{\text{y}}{\it\varphi}$
, where
$\langle n_{i}\rangle V_{\ast }\partial _{\text{y}}{\it\varphi}$
, where
 $V_{\ast }\doteq ({\it\rho}_{\text{s}}/L_{n})c_{\text{s}}=cT_{e}/(eBL_{n})$
and it is assumed that
$V_{\ast }\doteq ({\it\rho}_{\text{s}}/L_{n})c_{\text{s}}=cT_{e}/(eBL_{n})$
and it is assumed that
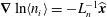 $\boldsymbol{{\rm\nabla}}\ln \langle n_{i}\rangle =-L_{n}^{-1}\widehat{\boldsymbol{x}}$
. (If one defines
$\boldsymbol{{\rm\nabla}}\ln \langle n_{i}\rangle =-L_{n}^{-1}\widehat{\boldsymbol{x}}$
. (If one defines
 $V_{\ast s}\doteq -cT_{s}/(q_{s}BL_{n})$
, then
$V_{\ast s}\doteq -cT_{s}/(q_{s}BL_{n})$
, then
![]() $V_{\ast }\equiv V_{\ast e}$
.) Although
$V_{\ast }\equiv V_{\ast e}$
.) Although
![]() $V_{\ast }$
is numerically equal to the diamagnetic flow speed of the electron
fluid for constant
$V_{\ast }$
is numerically equal to the diamagnetic flow speed of the electron
fluid for constant
![]() $T_{e}$
, the physics of the basic drift wave has nothing to do with
electron diamagnetic flow; as discussed in § 5.2.2, the appearance of
$T_{e}$
, the physics of the basic drift wave has nothing to do with
electron diamagnetic flow; as discussed in § 5.2.2, the appearance of
![]() $V_{\ast }$
describes the generation of ion density fluctuations by
$V_{\ast }$
describes the generation of ion density fluctuations by
![]() $\boldsymbol{E}\times \boldsymbol{B}$
advection of the background ion density profile. The Fourier
transform of
$\boldsymbol{E}\times \boldsymbol{B}$
advection of the background ion density profile. The Fourier
transform of
![]() $V_{\ast }\partial _{\text{y}}{\it\varphi}$
is
$V_{\ast }\partial _{\text{y}}{\it\varphi}$
is
![]() $\text{i}{\it\omega}_{\ast }{\it\varphi}_{\boldsymbol{k}}$
, where
$\text{i}{\it\omega}_{\ast }{\it\varphi}_{\boldsymbol{k}}$
, where
 ${\it\omega}_{\ast }\doteq k_{y}V_{\ast }$
is known as the diamagnetic frequency. One has
${\it\omega}_{\ast }\doteq k_{y}V_{\ast }$
is known as the diamagnetic frequency. One has
 ${\it\omega}_{\ast }=k_{y}{\it\rho}_{\text{s}}c_{\text{s}}/L_{n}=O(c_{\text{s}}/L_{n})$
for fluctuations with
${\it\omega}_{\ast }=k_{y}{\it\rho}_{\text{s}}c_{\text{s}}/L_{n}=O(c_{\text{s}}/L_{n})$
for fluctuations with
 $k_{\bot }{\it\rho}_{\text{s}}=O(1)$
. This identifies
$k_{\bot }{\it\rho}_{\text{s}}=O(1)$
. This identifies
![]() $L_{n}/c_{\text{s}}$
(basically the time for a sound wave to cross the system) as a
characteristic time for drift-wave dynamics.
$L_{n}/c_{\text{s}}$
(basically the time for a sound wave to cross the system) as a
characteristic time for drift-wave dynamics.
Dimensional analysis of the HME shows that the scaling of the basic turbulent
diffusion coefficient
![]() $D_{\bot }$
is not with
$D_{\bot }$
is not with
![]() $D_{\text{B}}$
but rather with the gyro-Bohm diffusion coefficient
$D_{\text{B}}$
but rather with the gyro-Bohm diffusion coefficient
 $D_{\text{gB}}\doteq ({\it\rho}_{\text{s}}/L_{n})D_{\text{B}}$
. This is much smaller than
$D_{\text{gB}}\doteq ({\it\rho}_{\text{s}}/L_{n})D_{\text{B}}$
. This is much smaller than
![]() $D_{\text{B}}$
and has the more favourable scaling
$D_{\text{B}}$
and has the more favourable scaling
![]() $B^{-2}$
instead of Bohm’s
$B^{-2}$
instead of Bohm’s
![]() $B^{-1}$
. (In fact,
$B^{-1}$
. (In fact,
![]() $D_{\bot }$
vanishes altogether in the strict, time-reversible HME. However,
the basic gyro-Bohm scaling is reinstated when growth and damping are introduced, as
discussed in footnote 86 on page 50.)
$D_{\bot }$
vanishes altogether in the strict, time-reversible HME. However,
the basic gyro-Bohm scaling is reinstated when growth and damping are introduced, as
discussed in footnote 86 on page 50.)
Appendix B. The Furutsu–Novikov theorem
For completeness, I give here a brief derivation of Novikov’s theorem. This is
equivalent to the original procedure of Novikov (Reference Novikov1964), but is algebraically more concise. Let
![]() $\widetilde{{\it\phi}}$
be a centred Gaussian random variable with variance
$\widetilde{{\it\phi}}$
be a centred Gaussian random variable with variance
![]() ${\it\sigma}^{2}$
, and let
${\it\sigma}^{2}$
, and let
![]() ${\mathcal{F}}(\widetilde{{\it\phi}})$
be an arbitrary differentiable function of
${\mathcal{F}}(\widetilde{{\it\phi}})$
be an arbitrary differentiable function of
![]() $\widetilde{{\it\phi}}$
. Then consider the average
$\widetilde{{\it\phi}}$
. Then consider the average
 $$\begin{eqnarray}\langle {\mathcal{F}}(\widetilde{{\it\phi}})\widetilde{{\it\phi}}\rangle \equiv \int _{-\infty }^{\infty }\!\text{d}{\it\phi}\,{\mathcal{F}}({\it\phi}){\it\phi}\frac{\text{e}^{-{\it\phi}^{2}/2{\it\sigma}^{2}}}{(2{\rm\pi}{\it\sigma}^{2})^{1/2}}.\end{eqnarray}$$
$$\begin{eqnarray}\langle {\mathcal{F}}(\widetilde{{\it\phi}})\widetilde{{\it\phi}}\rangle \equiv \int _{-\infty }^{\infty }\!\text{d}{\it\phi}\,{\mathcal{F}}({\it\phi}){\it\phi}\frac{\text{e}^{-{\it\phi}^{2}/2{\it\sigma}^{2}}}{(2{\rm\pi}{\it\sigma}^{2})^{1/2}}.\end{eqnarray}$$
Upon using a generating-function approach, one has
 $$\begin{eqnarray}\langle {\mathcal{F}}(\widetilde{{\it\phi}})\widetilde{{\it\phi}}\rangle =\frac{\partial }{\partial {\it\eta}}\left.\langle {\mathcal{F}}(\widetilde{{\it\phi}})\text{e}^{\widetilde{{\it\phi}}{\it\eta}}\rangle \right|_{{\it\eta}=0}.\end{eqnarray}$$
$$\begin{eqnarray}\langle {\mathcal{F}}(\widetilde{{\it\phi}})\widetilde{{\it\phi}}\rangle =\frac{\partial }{\partial {\it\eta}}\left.\langle {\mathcal{F}}(\widetilde{{\it\phi}})\text{e}^{\widetilde{{\it\phi}}{\it\eta}}\rangle \right|_{{\it\eta}=0}.\end{eqnarray}$$
Upon completing the square, one is led to
 $$\begin{eqnarray}\displaystyle \langle {\mathcal{F}}(\widetilde{{\it\phi}})\text{e}^{\widetilde{{\it\phi}}{\it\eta}}\rangle & = & \displaystyle \int _{-\infty }^{\infty }\!\text{d}{\it\phi}\,{\mathcal{F}}({\it\phi})\frac{\text{e}^{-({\it\phi}-{\it\sigma}^{2}{\it\eta})^{2}/2{\it\sigma}^{2}}}{(2{\rm\pi}{\it\sigma}^{2})^{1/2}}\text{e}^{{\it\sigma}^{2}{\it\eta}^{2}/2}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle {\mathcal{F}}(\widetilde{{\it\phi}})\text{e}^{\widetilde{{\it\phi}}{\it\eta}}\rangle & = & \displaystyle \int _{-\infty }^{\infty }\!\text{d}{\it\phi}\,{\mathcal{F}}({\it\phi})\frac{\text{e}^{-({\it\phi}-{\it\sigma}^{2}{\it\eta})^{2}/2{\it\sigma}^{2}}}{(2{\rm\pi}{\it\sigma}^{2})^{1/2}}\text{e}^{{\it\sigma}^{2}{\it\eta}^{2}/2}\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & = & \displaystyle \langle {\mathcal{F}}(\widetilde{{\it\phi}}+{\it\sigma}^{2}{\it\eta})\rangle \text{e}^{{\it\sigma}^{2}{\it\eta}^{2}/2}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle \langle {\mathcal{F}}(\widetilde{{\it\phi}}+{\it\sigma}^{2}{\it\eta})\rangle \text{e}^{{\it\sigma}^{2}{\it\eta}^{2}/2}\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & = & \displaystyle \langle {\mathcal{F}}(\widetilde{{\it\phi}})\rangle +\left<\frac{\text{d}{\mathcal{F}}(\widetilde{{\it\phi}})}{\text{d}\widetilde{{\it\phi}}}\right>{\it\sigma}^{2}{\it\eta}+O({\it\eta}^{2}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle \langle {\mathcal{F}}(\widetilde{{\it\phi}})\rangle +\left<\frac{\text{d}{\mathcal{F}}(\widetilde{{\it\phi}})}{\text{d}\widetilde{{\it\phi}}}\right>{\it\sigma}^{2}{\it\eta}+O({\it\eta}^{2}).\end{eqnarray}$$
 $$\begin{eqnarray}\langle {\mathcal{F}}(\widetilde{{\it\phi}})\widetilde{{\it\phi}}\rangle =\left<\frac{\text{d}{\mathcal{F}}(\widetilde{{\it\phi}})}{\text{d}\widetilde{{\it\phi}}}\right>{\it\sigma}^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\langle {\mathcal{F}}(\widetilde{{\it\phi}})\widetilde{{\it\phi}}\rangle =\left<\frac{\text{d}{\mathcal{F}}(\widetilde{{\it\phi}})}{\text{d}\widetilde{{\it\phi}}}\right>{\it\sigma}^{2}.\end{eqnarray}$$
The essence of this procedure is the introduction of
![]() ${\it\eta}$
to create an ensemble with nonzero mean, followed by enquiry about
the differential behaviour of statistics in the modified ensemble. Nontrivial
generalizations of this procedure are used in modern field-theoretic methods such as
the MSR formalism (Martin et al.
Reference Martin, Siggia and Rose1973).
${\it\eta}$
to create an ensemble with nonzero mean, followed by enquiry about
the differential behaviour of statistics in the modified ensemble. Nontrivial
generalizations of this procedure are used in modern field-theoretic methods such as
the MSR formalism (Martin et al.
Reference Martin, Siggia and Rose1973).
The theorem can be generalized to a finite collection of multivariate centred
Gaussian variables
![]() $\widetilde{{\it\phi}}_{i}$
:
$\widetilde{{\it\phi}}_{i}$
:
 $$\begin{eqnarray}\langle {\mathcal{F}}(\widetilde{{\bf\phi}})\widetilde{{\it\phi}}_{i}\rangle =\mathop{\sum }_{j}\left<\frac{\partial {\mathcal{F}}}{\partial \widetilde{{\it\phi}}_{j}}\right>\unicode[STIX]{x1D60A}_{ji},\end{eqnarray}$$
$$\begin{eqnarray}\langle {\mathcal{F}}(\widetilde{{\bf\phi}})\widetilde{{\it\phi}}_{i}\rangle =\mathop{\sum }_{j}\left<\frac{\partial {\mathcal{F}}}{\partial \widetilde{{\it\phi}}_{j}}\right>\unicode[STIX]{x1D60A}_{ji},\end{eqnarray}$$
where
 $\unicode[STIX]{x1D60A}_{ij}\doteq \langle {\it\delta}{\it\phi}_{i}{\it\delta}{\it\phi}_{j}\rangle$
is the covariance matrix. Finally, a further generalization to a
Gaussian random field
$\unicode[STIX]{x1D60A}_{ij}\doteq \langle {\it\delta}{\it\phi}_{i}{\it\delta}{\it\phi}_{j}\rangle$
is the covariance matrix. Finally, a further generalization to a
Gaussian random field
 $\widetilde{{\it\phi}}(\boldsymbol{x},t)\equiv \widetilde{{\it\phi}}(x)$
, where
$\widetilde{{\it\phi}}(\boldsymbol{x},t)\equiv \widetilde{{\it\phi}}(x)$
, where
 $\{\boldsymbol{x},t\}\equiv x$
are nonrandom observer coordinates in spacetime, leads to
$\{\boldsymbol{x},t\}\equiv x$
are nonrandom observer coordinates in spacetime, leads to
 $$\begin{eqnarray}\langle {\mathcal{F}}[\widetilde{{\it\phi}}]\widetilde{{\it\phi}}(x)\rangle =\int _{-\infty }^{\infty }\!\text{d}\overline{x}\,\left<\frac{{\it\delta}{\mathcal{F}}}{{\it\delta}\widetilde{{\it\phi}}(\overline{x})}\right>C(\overline{x},x),\end{eqnarray}$$
$$\begin{eqnarray}\langle {\mathcal{F}}[\widetilde{{\it\phi}}]\widetilde{{\it\phi}}(x)\rangle =\int _{-\infty }^{\infty }\!\text{d}\overline{x}\,\left<\frac{{\it\delta}{\mathcal{F}}}{{\it\delta}\widetilde{{\it\phi}}(\overline{x})}\right>C(\overline{x},x),\end{eqnarray}$$
where square brackets denote functional dependence,
![]() ${\it\delta}{\mathcal{F}}/{\it\delta}\widetilde{{\it\phi}}$
denotes the functional derivative (which satisfies
${\it\delta}{\mathcal{F}}/{\it\delta}\widetilde{{\it\phi}}$
denotes the functional derivative (which satisfies
 ${\it\delta}{\it\phi}(x)/{\it\delta}{\it\phi}(x^{\prime })={\it\delta}(x-x^{\prime })$
), and
${\it\delta}{\it\phi}(x)/{\it\delta}{\it\phi}(x^{\prime })={\it\delta}(x-x^{\prime })$
), and
 $C(x,x^{\prime })\doteq \langle {\it\delta}{\it\psi}(x){\it\delta}{\it\psi}(x^{\prime })\rangle$
.
$C(x,x^{\prime })\doteq \langle {\it\delta}{\it\psi}(x){\it\delta}{\it\psi}(x^{\prime })\rangle$
.
If
![]() $\widetilde{{\it\phi}}$
has nonzero mean, it is easy to show that the previous results
generalize straightforwardly to include the term
$\widetilde{{\it\phi}}$
has nonzero mean, it is easy to show that the previous results
generalize straightforwardly to include the term
 $\langle {\mathcal{F}}[\widetilde{{\it\phi}}]\rangle \langle \widetilde{{\it\phi}}\rangle$
.
$\langle {\mathcal{F}}[\widetilde{{\it\phi}}]\rangle \langle \widetilde{{\it\phi}}\rangle$
.
Appendix C. Notation
-
Symbols
-
 $a$
$a$
-
acceleration
-
 ${\it\alpha}$
${\it\alpha}$
-
switch that vanishes for zonal modes and equals one otherwise
-
 $\boldsymbol{B}$
$\boldsymbol{B}$
-
magnetic field
-
 $\widehat{\boldsymbol{b}}$
$\widehat{\boldsymbol{b}}$
-
unit vector in direction of
 $\boldsymbol{B}$
$\boldsymbol{B}$
-
 ${\it\beta}$
${\it\beta}$
-
standard deviation of random coefficient at infinite
 ${\mathcal{K}}$
${\mathcal{K}}$
-
 $C(1,2)$
$C(1,2)$
-
two-point correlation function
-
 $c$
$c$
-
speed of light (occasionally, a constant)
-
 $c_{\text{s}}$
$c_{\text{s}}$
-
sound speed:
 $c_{\text{s}}\doteq (ZT_{e}/m_{i})^{1/2}$
$c_{\text{s}}\doteq (ZT_{e}/m_{i})^{1/2}$
-
 ${\it\chi}$
${\it\chi}$
-
propagator
-
 $\unicode[STIX]{x1D63F}$
$\unicode[STIX]{x1D63F}$
-
dielectric tensor
-
 $\boldsymbol{D}$
$\boldsymbol{D}$
-
electric displacement:
 $\boldsymbol{D}=\boldsymbol{E}+4{\rm\pi}\boldsymbol{P}$
$\boldsymbol{D}=\boldsymbol{E}+4{\rm\pi}\boldsymbol{P}$
-
 $D$
$D$
-
diffusion coefficient
-
 $D_{v}$
$D_{v}$
-
velocity-space diffusion coefficient
-
 $D_{\text{B}}$
$D_{\text{B}}$
-
Bohm diffusion coefficient:
 $D_{\text{B}}\doteq cT_{e}/eB$
$D_{\text{B}}\doteq cT_{e}/eB$
-
 $D_{\text{gB}}$
$D_{\text{gB}}$
-
gyro-Bohm diffusion coefficient:
 $D_{\text{gB}}\doteq ({\it\rho}_{\text{s}}/L_{n})D_{\text{B}}$
$D_{\text{gB}}\doteq ({\it\rho}_{\text{s}}/L_{n})D_{\text{B}}$
-
 $d$
$d$
-
dimensionality of space
-
 ${\it\Delta}$
${\it\Delta}$
-
infinitesimal perturbation
-
 ${\rm\Delta}t$
${\rm\Delta}t$
-
characteristic time interval or mode period
-
 ${\it\delta}$
${\it\delta}$
-
 $\text{non-adiabatic response}\times \text{i}$
$\text{non-adiabatic response}\times \text{i}$
-
 ${\it\delta}\overline{f}$
${\it\delta}\overline{f}$
-
nonlinear correction to distribution function
-
 ${\it\delta}k$
${\it\delta}k$
-
mode spacing:
 ${\it\delta}k\doteq 2{\rm\pi}/L$
${\it\delta}k\doteq 2{\rm\pi}/L$
-
 ${\mathcal{D}}$
${\mathcal{D}}$
-
dielectric function
-
 ${\mathcal{D}}_{\bot }$
${\mathcal{D}}_{\bot }$
-
permittivity of gyrokinetic vacuum:
 ${\mathcal{D}}_{\bot }\doteq {\it\rho}_{\text{s}}^{2}/{\it\lambda}_{\text{D}e}^{2}$
${\mathcal{D}}_{\bot }\doteq {\it\rho}_{\text{s}}^{2}/{\it\lambda}_{\text{D}e}^{2}$
-
 $\boldsymbol{\partial }$
$\boldsymbol{\partial }$
-
 $(q/m)\partial /\partial \boldsymbol{v}$
$(q/m)\partial /\partial \boldsymbol{v}$
-
 $\boldsymbol{E}$
$\boldsymbol{E}$
-
electric field
-
 $\pmb{\mathbb{E}}$
$\pmb{\mathbb{E}}$
-
electric-field operator:
 $\boldsymbol{E}=\pmb{\mathbb{E}}f$
$\boldsymbol{E}=\pmb{\mathbb{E}}f$
-
 ${\mathcal{E}}$
${\mathcal{E}}$
-
fluctuation spectrum of electric field
-
 $e$
$e$
-
magnitude of electron charge
-
 ${\it\epsilon}$
${\it\epsilon}$
-
positive infinitesimal
-
 ${\it\epsilon}_{\text{p}}$
${\it\epsilon}_{\text{p}}$
-
plasma parameter:
 ${\it\epsilon}_{\text{p}}\doteq 1/(n{\it\lambda}_{\text{D}}^{3})$
${\it\epsilon}_{\text{p}}\doteq 1/(n{\it\lambda}_{\text{D}}^{3})$
-
 ${\it\varepsilon}$
${\it\varepsilon}$
-
rate of energy input
-
 ${\it\eta}$
${\it\eta}$
-
nonlinear coherent damping
-
 $\widehat{{\it\eta}}$
$\widehat{{\it\eta}}$
-
additive source in mean equation
-
 $F$
$F$
-
covariance of random forcing or incoherent noise;
-
gyrocentre distribution function
-
 $f$
$f$
-
one-particle distribution function
-
 $\overline{f}$
$\overline{f}$
-
effective distribution in renormalized theory (not a PDF)
-
 $\widetilde{f}$
$\widetilde{f}$
-
random forcing (covariance
 $F$
)
$F$
) -
 $g$
$g$
-
particle Green’s function
-
 ${\it\Gamma}$
${\it\Gamma}$
-
flux (e.g., of particles)
-
 ${\it\gamma}$
${\it\gamma}$
-
growth rate
-
 $H$
$H$
-
Heaviside unit step function
-
 ${\mathcal{K}}$
${\mathcal{K}}$
-
Kubo number
-
 $\boldsymbol{k}$
$\boldsymbol{k}$
-
Fourier wavevector conjugate to position
 $\boldsymbol{x}$
$\boldsymbol{x}$
-
 $\overline{k}$
$\overline{k}$
-
characteristic wavenumber
-
 $k_{\text{D}}$
$k_{\text{D}}$
-
Debye wavenumber:
 $k_{\text{D}}^{2}\doteq \sum _{s}k_{\text{D}s}^{2}$
, where
$k_{\text{D}}^{2}\doteq \sum _{s}k_{\text{D}s}^{2}$
, where
 $k_{\text{D}s}\doteq [4{\rm\pi}(nq^{2}/T)_{s}]^{1/2}$
$k_{\text{D}s}\doteq [4{\rm\pi}(nq^{2}/T)_{s}]^{1/2}$
-
 ${\it\kappa}$
${\it\kappa}$
-
 $L_{n}^{-1}$
$L_{n}^{-1}$
-
 $L$
$L$
-
box size
-
 $L_{\boldsymbol{k}}$
$L_{\boldsymbol{k}}$
-
linear operator
-
 $L_{n}$
$L_{n}$
-
density gradient scale length
-
 $L_{\text{ac}}$
$L_{\text{ac}}$
-
autocorrelation length
-
 $\ell$
$\ell$
-
mixing length
-
 ${\it\lambda}_{\text{D}}$
${\it\lambda}_{\text{D}}$
-
Debye length:
 ${\it\lambda}_{\text{D}}\doteq k_{\text{D}}^{-1}$
${\it\lambda}_{\text{D}}\doteq k_{\text{D}}^{-1}$
-
 $M$
$M$
-
mode-coupling coefficient
-
 $m$
$m$
-
mass
-
 ${\it\mu}$
${\it\mu}$
-
kinematic viscosity
-
 $\widetilde{N}$
$\widetilde{N}$
-
Klimontovich microdensity
-
 ${\mathcal{N}}$
${\mathcal{N}}$
-
numerator of spectral balance relation; nonlinear noise
-
 $n$
$n$
-
density
-
 $\overline{n}$
$\overline{n}$
-
mean density
-
 ${\it\nu}$
${\it\nu}$
-
drag or damping coefficient
-
 ${\it\Omega}_{\boldsymbol{k}}$
${\it\Omega}_{\boldsymbol{k}}$
-
real part of mode frequency
-
 ${\it\omega}$
${\it\omega}$
-
Fourier variable conjugate to time
 $t$
$t$
-
 ${\it\omega}_{\text{c}}$
${\it\omega}_{\text{c}}$
-
gyrofrequency:
 ${\it\omega}_{\text{c}s}\doteq q_{s}B/m_{s}c$
${\it\omega}_{\text{c}s}\doteq q_{s}B/m_{s}c$
-
 ${\it\omega}_{\ast }$
${\it\omega}_{\ast }$
-
diamagnetic frequency:
 ${\it\omega}_{\ast }\doteq k_{y}V_{\ast }$
${\it\omega}_{\ast }\doteq k_{y}V_{\ast }$
-
 ${\it\omega}_{\boldsymbol{k}}$
${\it\omega}_{\boldsymbol{k}}$
-
complex mode frequency:
 ${\it\omega}_{\boldsymbol{k}}\doteq {\it\Omega}_{\boldsymbol{k}}+\text{i}{\it\gamma}_{\boldsymbol{k}}$
${\it\omega}_{\boldsymbol{k}}\doteq {\it\Omega}_{\boldsymbol{k}}+\text{i}{\it\gamma}_{\boldsymbol{k}}$
-
 $\boldsymbol{P}$
$\boldsymbol{P}$
-
polarization vector
-
 $P$
$P$
-
pressure
- P
-
projection operator
-
 $\boldsymbol{p}$
$\boldsymbol{p}$
-
wavevector
-
 ${\it\phi}$
${\it\phi}$
-
electrostatic potential
-
 ${\it\varphi}$
${\it\varphi}$
-
normalized potential:
 ${\it\varphi}\doteq e{\it\phi}/T_{e}$
${\it\varphi}\doteq e{\it\phi}/T_{e}$
- Q
-
orthogonal projection operator:
 $\text{Q}\doteq 1-\text{P}$
$\text{Q}\doteq 1-\text{P}$
-
 $\boldsymbol{q}$
$\boldsymbol{q}$
-
wavevector (often used for zonal modes)
-
 $q$
$q$
-
particle charge (
 $q_{e}=-e$
)
$q_{e}=-e$
) -
 $R$
$R$
-
mean infinitesimal response function
-
 ${\mathcal{R}}$
${\mathcal{R}}$
-
Reynolds number
-
 ${\it\rho}$
${\it\rho}$
-
charge density; gyroradius:
 ${\it\rho}\doteq v_{\bot }/{\it\omega}_{\text{c}}$
${\it\rho}\doteq v_{\bot }/{\it\omega}_{\text{c}}$
-
 ${\it\rho}_{\text{m}}$
${\it\rho}_{\text{m}}$
-
mass density:
 ${\it\rho}_{\text{m}}\doteq nm$
${\it\rho}_{\text{m}}\doteq nm$
-
 ${\it\rho}_{\text{s}}$
${\it\rho}_{\text{s}}$
-
sound radius:
 ${\it\rho}_{\text{s}}\doteq c_{\text{s}}/{\it\omega}_{\text{c}i}$
${\it\rho}_{\text{s}}\doteq c_{\text{s}}/{\it\omega}_{\text{c}i}$
-
 $\unicode[STIX]{x1D64E}$
$\unicode[STIX]{x1D64E}$
-
rate-of-strain tensor
-
 $s$
$s$
-
species index
-
 ${\it\Sigma}$
${\it\Sigma}$
-
mass operator (coherent turbulent collision operator)
-
 ${\it\sigma}$
${\it\sigma}$
-
weight factor relating energy to covariance
-
 $T$
$T$
-
temperature
-
 $T(1,2,3)$
$T(1,2,3)$
-
three-point correlation function
-
 $t$
$t$
-
time
-
 ${\bf\tau}$
${\bf\tau}$
-
Reynolds stress
-
 ${\it\tau}_{\text{ac}}$
${\it\tau}_{\text{ac}}$
-
autocorrelation time
-
 ${\it\theta}$
${\it\theta}$
-
triad interaction time
-
 $U_{n}$
$U_{n}$
-
 $n$
th-order coupling coefficient
$n$
th-order coupling coefficient -
 $\boldsymbol{u}$
$\boldsymbol{u}$
-
fluid velocity
-
 $\boldsymbol{V}_{E}$
$\boldsymbol{V}_{E}$
-
 $\boldsymbol{E}\times \boldsymbol{B}$
velocity:
$\boldsymbol{E}\times \boldsymbol{B}$
velocity:
 $\boldsymbol{V}_{E}\doteq (c/B)\boldsymbol{E}\times \widehat{\boldsymbol{b}}$
$\boldsymbol{V}_{E}\doteq (c/B)\boldsymbol{E}\times \widehat{\boldsymbol{b}}$
-
 $V$
$V$
-
volume of entire system
-
 $\overline{V}$
$\overline{V}$
-
characteristic velocity
-
 $V_{\ast }$
$V_{\ast }$
-
diamagnetic speed
-
 $\boldsymbol{v}$
$\boldsymbol{v}$
-
particle velocity
-
 $v_{\text{t}}$
$v_{\text{t}}$
-
thermal velocity:
 $v_{\text{t}}\doteq (T/m)^{1/2}$
$v_{\text{t}}\doteq (T/m)^{1/2}$
-
 $W$
$W$
-
covariance of random coefficient
-
 $w(z)$
$w(z)$
-
 $Z(z)/(\text{i}\sqrt{{\rm\pi}})$
$Z(z)/(\text{i}\sqrt{{\rm\pi}})$
-
 $\unicode[STIX]{x1D653}$
$\unicode[STIX]{x1D653}$
-
susceptibility tensor
-
 ${\it\xi}$
${\it\xi}$
-
auxiliary random variable in Langevin representation
-
 $Z$
$Z$
-
atomic number
-
 $Z(z)$
$Z(z)$
-
plasma dispersion function
-
 $Z(1)$
$Z(1)$
-
mean field
-
Miscellaneous notation
-
 $\widetilde{A}$
$\widetilde{A}$
-
random variable
-
 $\widetilde{A}^{\prime }$
$\widetilde{A}^{\prime }$
-
fluctuation:
 $\widetilde{A}^{\prime }\doteq \widetilde{A}-\langle \widetilde{A}\rangle$
. See also
$\widetilde{A}^{\prime }\doteq \widetilde{A}-\langle \widetilde{A}\rangle$
. See also
 ${\it\delta}A$
${\it\delta}A$
-
 $\widehat{A}(\boldsymbol{k},{\it\omega})$
$\widehat{A}(\boldsymbol{k},{\it\omega})$
-
Fourier transform of
 $A(\boldsymbol{x},t)$
$A(\boldsymbol{x},t)$
-
 $A^{\ast }$
$A^{\ast }$
-
complex conjugate of
 $A$
$A$
-
 $A_{+}(t)$
$A_{+}(t)$
-
 $H(t)A(t)$
$H(t)A(t)$
-
 $A_{\Vert }$
$A_{\Vert }$
-
 $\boldsymbol{A}\boldsymbol{\cdot }\widehat{\boldsymbol{b}}$
$\boldsymbol{A}\boldsymbol{\cdot }\widehat{\boldsymbol{b}}$
-
 $\boldsymbol{A}_{\bot }$
$\boldsymbol{A}_{\bot }$
-
 $\boldsymbol{A}-A_{\Vert }\widehat{\boldsymbol{b}}=\widehat{\boldsymbol{b}}\times (\boldsymbol{A}\times \widehat{\boldsymbol{b}})$
$\boldsymbol{A}-A_{\Vert }\widehat{\boldsymbol{b}}=\widehat{\boldsymbol{b}}\times (\boldsymbol{A}\times \widehat{\boldsymbol{b}})$
-
 $A[{\it\psi}]$
$A[{\it\psi}]$
-
 $A$
is a functional of
$A$
is a functional of
 ${\it\psi}$
${\it\psi}$
-
 $\unicode[STIX]{x1D63C}^{\text{T}}$
$\unicode[STIX]{x1D63C}^{\text{T}}$
-
transpose of
 $\unicode[STIX]{x1D63C}$
$\unicode[STIX]{x1D63C}$
-
 ${\it\delta}A$
${\it\delta}A$
-
fluctuation:
 ${\it\delta}A\doteq \widetilde{A}-\langle \widetilde{A}\rangle$
. See also
${\it\delta}A\doteq \widetilde{A}-\langle \widetilde{A}\rangle$
. See also
 $A^{\prime }$
$A^{\prime }$
-
 ${\it\delta}({\it\tau})$
${\it\delta}({\it\tau})$
-
Dirac delta function
-
 ${\it\delta}_{i,j}$
${\it\delta}_{i,j}$
-
Kronecker delta function
-
 ${\it\delta}/{\it\delta}{\it\eta}$
${\it\delta}/{\it\delta}{\it\eta}$
-
functional derivative
-
 ${\it\psi}(1)$
${\it\psi}(1)$
-
 ${\it\psi}_{s_{1}}(\boldsymbol{x}_{1},\boldsymbol{v}_{1},t_{1})$
${\it\psi}_{s_{1}}(\boldsymbol{x}_{1},\boldsymbol{v}_{1},t_{1})$
-
 $\doteq$
$\doteq$
-
definition
-
 $\langle \ldots \rangle$
$\langle \ldots \rangle$
-
ensemble average
-
Abbreviations and acronyms
- CE
 $n$
$n$
-
 $n$
th-order cumulant expansion
$n$
th-order cumulant expansion - DIA
-
direct-interaction approximation
- ext
-
external
- int
-
internal
- lin
-
linear
- pol
-
polarization
- PDE
-
partial differential equation
-
probability density function
- PIC
-
particle-in-cell
- RBT
-
resonance-broadening theory
- S3T
-
stochastic structural stability theory (also SSST)
- tot
-
total