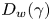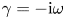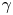1. Introduction
Tokamak plasma discharges with non-circular cross-section are common features in modern-day magnetic fusion experiments. An important advantage of such configurations is higher instability thresholds, in terms of toroidal plasma current and beta ($=$![]() kinetic/magnetic pressure) values, against ideal-magnetohydrodynamic (MHD) modes. Furthermore, plasma shaping is associated with magnetic divertors, which ameliorate the problem of plasma–wall interaction and allow access to high confinement regimes (so-called H-modes, Wagner et al. Reference Wagner, Becker, Behringer, Campbell, Eberhagen, Engelhardt, Fussmann, Gehre, Gernhardt and Gierke1982). On the other hand, elongated plasmas are prone to an instability, initiated by an axisymmetric perturbation with toroidal mode number $n=0$
kinetic/magnetic pressure) values, against ideal-magnetohydrodynamic (MHD) modes. Furthermore, plasma shaping is associated with magnetic divertors, which ameliorate the problem of plasma–wall interaction and allow access to high confinement regimes (so-called H-modes, Wagner et al. Reference Wagner, Becker, Behringer, Campbell, Eberhagen, Engelhardt, Fussmann, Gehre, Gernhardt and Gierke1982). On the other hand, elongated plasmas are prone to an instability, initiated by an axisymmetric perturbation with toroidal mode number $n=0$![]() , leading to vertical displacement events (VDEs) (Strait et al. Reference Strait, Lao, Luxon and Reis1991; Granetz et al. Reference Granetz, Hutchinson, Sorci, Irby, LaBombard and Gwinn1996; Albanese, Mattei & Villone Reference Albanese, Mattei and Villone2004; Riccardo & JET EFDA Contributors Reference Riccardo2009), where the entire plasma shifts vertically until it touches the vacuum chamber. Uncontrolled VDEs must be avoided, as they lead to plasma current disruptions, which are dangerous in that they can severely damage the first wall of the vacuum chamber and the mechanical structure of the tokamak device. For this reason, a vast amount of literature has been dedicated to the theoretical study of vertical plasma displacements, starting from the pioneering work by Laval, Pellat & Soule (Reference Laval, Pellat and Soule1974), and continuing throughout the years (Okabayashi & Sheffield Reference Okabayashi and Sheffield1974; Haas Reference Haas1975; Rebhan Reference Rebhan1975; Perrone & Wesson Reference Perrone and Wesson1981; Lazarus, Lister & Neilson Reference Lazarus, Lister and Neilson1990; Fitzpatrick Reference Fitzpatrick2009; Zakharov, Galkin & Gerasimov Reference Zakharov, Galkin and Gerasimov2012; Portone Reference Portone2017; Clauser, Jardin & Ferraro Reference Clauser, Jardin and Ferraro2019; Krebs et al. Reference Krebs, Artola, Sovinec, Jardin, Bunkers, Hoelzl and Ferraro2020 provide a non-exhaustive sample), up until very recently, where the impact of magnetic divertor X-points on $n=0$
, leading to vertical displacement events (VDEs) (Strait et al. Reference Strait, Lao, Luxon and Reis1991; Granetz et al. Reference Granetz, Hutchinson, Sorci, Irby, LaBombard and Gwinn1996; Albanese, Mattei & Villone Reference Albanese, Mattei and Villone2004; Riccardo & JET EFDA Contributors Reference Riccardo2009), where the entire plasma shifts vertically until it touches the vacuum chamber. Uncontrolled VDEs must be avoided, as they lead to plasma current disruptions, which are dangerous in that they can severely damage the first wall of the vacuum chamber and the mechanical structure of the tokamak device. For this reason, a vast amount of literature has been dedicated to the theoretical study of vertical plasma displacements, starting from the pioneering work by Laval, Pellat & Soule (Reference Laval, Pellat and Soule1974), and continuing throughout the years (Okabayashi & Sheffield Reference Okabayashi and Sheffield1974; Haas Reference Haas1975; Rebhan Reference Rebhan1975; Perrone & Wesson Reference Perrone and Wesson1981; Lazarus, Lister & Neilson Reference Lazarus, Lister and Neilson1990; Fitzpatrick Reference Fitzpatrick2009; Zakharov, Galkin & Gerasimov Reference Zakharov, Galkin and Gerasimov2012; Portone Reference Portone2017; Clauser, Jardin & Ferraro Reference Clauser, Jardin and Ferraro2019; Krebs et al. Reference Krebs, Artola, Sovinec, Jardin, Bunkers, Hoelzl and Ferraro2020 provide a non-exhaustive sample), up until very recently, where the impact of magnetic divertor X-points on $n=0$![]() modes was analysed within the framework of the ideal-MHD model (Yolbarsop, Porcelli & Fitzpatrick Reference Yolbarsop, Porcelli and Fitzpatrick2021; Yolbarsop et al. Reference Yolbarsop, Porcelli, Liu and Fitzpatrick2022).
modes was analysed within the framework of the ideal-MHD model (Yolbarsop, Porcelli & Fitzpatrick Reference Yolbarsop, Porcelli and Fitzpatrick2021; Yolbarsop et al. Reference Yolbarsop, Porcelli, Liu and Fitzpatrick2022).
The focus of this article is, however, somewhat different. We derive analytically the dispersion relation for vertical displacement normal modes, and focus our attention on the oscillatory solutions, with a discrete frequency of oscillation in the poloidal Alfvén frequency range. These discrete modes, which we will refer to as ‘vertical displacement oscillatory modes’ (VDOM), are different from the well-known global Alfvén eigenmodes (Villard & Vaclavik Reference Villard and Vaclavik1997) with toroidal mode number $n=0$![]() , as discussed more at length in the Conclusion section. The VDOM are weakly damped by wall resistivity. The existence of these lightly damped solutions was noted before, see, e.g. Olofsson (Reference Olofsson2022) and Pfefferlé & Bhattacharjee (Reference Pfefferlé and Bhattacharjee2018); however, in those references, the emphasis was on the growth and control of the usual, non-rotating vertical resistive wall mode, while the importance of the oscillatory solutions was played down. In fact, in our view, the VDOM solutions of the relevant dispersion relation are very interesting, as their oscillatory character opens the possibility that they are driven unstable by the resonant interaction with energetic particles, see also Barberis, Porcelli & Yolbarsop (Reference Barberis, Porcelli and Yolbarsop2022). Observations of saturated $n=0$
, as discussed more at length in the Conclusion section. The VDOM are weakly damped by wall resistivity. The existence of these lightly damped solutions was noted before, see, e.g. Olofsson (Reference Olofsson2022) and Pfefferlé & Bhattacharjee (Reference Pfefferlé and Bhattacharjee2018); however, in those references, the emphasis was on the growth and control of the usual, non-rotating vertical resistive wall mode, while the importance of the oscillatory solutions was played down. In fact, in our view, the VDOM solutions of the relevant dispersion relation are very interesting, as their oscillatory character opens the possibility that they are driven unstable by the resonant interaction with energetic particles, see also Barberis, Porcelli & Yolbarsop (Reference Barberis, Porcelli and Yolbarsop2022). Observations of saturated $n=0$![]() oscillations were reported in recent JET experiments where energetic fast ion populations were produced by intense auxiliary plasma heating (Oliver et al. Reference Oliver, Sharapov, Breizman and Zheng2017; Kiptily et al. Reference Kiptily, Fitzgerald, Kazakov, Ongena, Nocente, Sharapov, Dreval, Štancar, Craciunescu and Garcia2021).
oscillations were reported in recent JET experiments where energetic fast ion populations were produced by intense auxiliary plasma heating (Oliver et al. Reference Oliver, Sharapov, Breizman and Zheng2017; Kiptily et al. Reference Kiptily, Fitzgerald, Kazakov, Ongena, Nocente, Sharapov, Dreval, Štancar, Craciunescu and Garcia2021).
Thus, this article contains two main results. The first result is a fully analytic derivation, based on the reduced MHD model, of the cubic dispersion relation for $n=0$![]() vertical modes with elliptical-angle mode number $m=1$
vertical modes with elliptical-angle mode number $m=1$![]() , valid for arbitrary values of the ellipticity parameter $e_0$
, valid for arbitrary values of the ellipticity parameter $e_0$![]() (defined in (2.2) below), in the presence of a resistive wall. As far as we are aware, our analytic derivation is new and adds valuable insight into the frequency and spatial structure of the relevant $n=0$
(defined in (2.2) below), in the presence of a resistive wall. As far as we are aware, our analytic derivation is new and adds valuable insight into the frequency and spatial structure of the relevant $n=0$![]() modes. Analytic progress was possible thanks to the choice of a much idealized equilibrium, but we do hope that our analytic theory will motivate numerical work using more realistic tokamak geometries. The second result is a detailed discussion of the $n=0$
modes. Analytic progress was possible thanks to the choice of a much idealized equilibrium, but we do hope that our analytic theory will motivate numerical work using more realistic tokamak geometries. The second result is a detailed discussion of the $n=0$![]() VDOM.
VDOM.
Our analysis adopts the same equilibrium configuration as Laval et al. (Reference Laval, Pellat and Soule1974), where the plasma boundary and the nearby wall of the containment vacuum chamber are assumed to be confocal ellipses. Based on the ideal-MHD energy principle, it was concluded in Laval et al. (Reference Laval, Pellat and Soule1974) that a perfectly conducting, ideal wall is capable of passively stabilizing vertical plasma displacements. Adding to the work of Laval et al. (Reference Laval, Pellat and Soule1974) and of subsequent publications, our article presents the analytic derivation of the mode structure and cubic dispersion relation for vertical modes with toroidal mode number $n=0$![]() and elliptical-angle mode number $m=1$
and elliptical-angle mode number $m=1$![]() . This dispersion relation is valid for arbitrary values of the ellipticity parameter; it includes the effects of a resistive wall through a single, frequency-dependent parameter, $D_w(\gamma )$
. This dispersion relation is valid for arbitrary values of the ellipticity parameter; it includes the effects of a resistive wall through a single, frequency-dependent parameter, $D_w(\gamma )$![]() , defined in (4.29) below. An in-depth discussion of the three relevant roots of the dispersion relation is presented. Under relevant experimental conditions, two of the three roots have a frequency of oscillation just below the poloidal Alfvén frequency and are weakly damped by wall resistivity. The third root, instead, is purely growing on the wall resistivity time scale; this third root is the usual, non-rotating vertical resistive-wall mode, which can be suppressed by active feedback stabilization (Lazarus et al. Reference Lazarus, Lister and Neilson1990; Lister et al. Reference Lister, Lazarus, Kellman, Moret, Ferron, Helton, Lao, Leuer, Strait and Taylor1990; Albanese et al. Reference Albanese, Mattei and Villone2004; Portone Reference Portone2017).
, defined in (4.29) below. An in-depth discussion of the three relevant roots of the dispersion relation is presented. Under relevant experimental conditions, two of the three roots have a frequency of oscillation just below the poloidal Alfvén frequency and are weakly damped by wall resistivity. The third root, instead, is purely growing on the wall resistivity time scale; this third root is the usual, non-rotating vertical resistive-wall mode, which can be suppressed by active feedback stabilization (Lazarus et al. Reference Lazarus, Lister and Neilson1990; Lister et al. Reference Lister, Lazarus, Kellman, Moret, Ferron, Helton, Lao, Leuer, Strait and Taylor1990; Albanese et al. Reference Albanese, Mattei and Villone2004; Portone Reference Portone2017).
This article is organized as follows. The cubic dispersion relation for $n=0$![]() modes is first derived heuristically in § 2. In § 3, the normal-mode spatial structure is resolved based on the reduced ideal-MHD model. The most original results are presented in § 4; in this section, first, a general dispersion relation is obtained with the use of quadratic forms; then, relevant solutions of the dispersion relation are obtained for three scenarios of interest: the no-wall case, the ideal wall limit and the case of a resistive wall. Conclusions are presented in § 5.
modes is first derived heuristically in § 2. In § 3, the normal-mode spatial structure is resolved based on the reduced ideal-MHD model. The most original results are presented in § 4; in this section, first, a general dispersion relation is obtained with the use of quadratic forms; then, relevant solutions of the dispersion relation are obtained for three scenarios of interest: the no-wall case, the ideal wall limit and the case of a resistive wall. Conclusions are presented in § 5.
2. Heuristic model
Insight into the mechanism and time scales of the vertical instability can be gained with the help of a simple heuristic model, involving currents flowing in three parallel rectilinear wires. This toy model is well known, and a simple derivation of the relevant dispersion relation for the case of an ideal wall can be found, e.g. in Yolbarsop et al. (Reference Yolbarsop, Porcelli and Fitzpatrick2021, Reference Yolbarsop, Porcelli, Liu and Fitzpatrick2022) and Pfefferlé & Bhattacharjee (Reference Pfefferlé and Bhattacharjee2018). This calculation is repeated here for the reader's convenience, together with its extension to the case of a resistive wall.
With reference to figure 1, let $y$![]() be the vertical direction. The currents flow along the $z$
be the vertical direction. The currents flow along the $z$![]() direction, which mimics the toroidal direction of a tokamak plasma. The two ‘external’ currents, $I_{{\rm Ext}}$
direction, which mimics the toroidal direction of a tokamak plasma. The two ‘external’ currents, $I_{{\rm Ext}}$![]() , are equal and positive and are fixed at $y = \pm l$
, are equal and positive and are fixed at $y = \pm l$![]() , while the ‘plasma’ current, $I_p$
, while the ‘plasma’ current, $I_p$![]() , can drift along the vertical direction. A vacuum surrounds the three wires. Clearly, $y=0$
, can drift along the vertical direction. A vacuum surrounds the three wires. Clearly, $y=0$![]() is an unstable equilibrium point for the plasma wire. Also shown in figure 1 are magnetic X-points located at $y=\pm l_y < l$
is an unstable equilibrium point for the plasma wire. Also shown in figure 1 are magnetic X-points located at $y=\pm l_y < l$![]() .
.

Figure 1. Schematic diagram of the heuristic model for the vertical instability.
The equation of motion for the plasma wire is
with $\mu _m$![]() the linear mass density, $c$
the linear mass density, $c$![]() the speed of light and an over-dot denotes time derivative (c.g.s. units have been adopted). Neglecting self- and mutual induction currents, $I_P$
the speed of light and an over-dot denotes time derivative (c.g.s. units have been adopted). Neglecting self- and mutual induction currents, $I_P$![]() and $I_{ {\rm Ext} }$
and $I_{ {\rm Ext} }$![]() remain constant as the plasma wire is displaced. For small $y\ll l$
remain constant as the plasma wire is displaced. For small $y\ll l$![]() , the solution of (2.1) is $y =y_0\,{\rm e}^{\gamma _H\,t}$
, the solution of (2.1) is $y =y_0\,{\rm e}^{\gamma _H\,t}$![]() , where $y_0$
, where $y_0$![]() is an initial displacement, and ${ \gamma }_{ H } = ( 1/l ) ( 4I_P I_{ {\rm Ext} } / \mu _m c^{2} )^{ 1/2 }$
is an initial displacement, and ${ \gamma }_{ H } = ( 1/l ) ( 4I_P I_{ {\rm Ext} } / \mu _m c^{2} )^{ 1/2 }$![]() .
.
If, instead of a plasma wire, we consider a vertically elongated plasma with uniform current density up to an elliptical magnetic surface with minor semi-axis $a$![]() and major semi-axis $b$
and major semi-axis $b$![]() , then, according to the analysis of Porcelli & Yolbarsop (Reference Porcelli and Yolbarsop2019), a relationship is found involving the currents $I_P$
, then, according to the analysis of Porcelli & Yolbarsop (Reference Porcelli and Yolbarsop2019), a relationship is found involving the currents $I_P$![]() and $I_{{\rm Ext}}$
and $I_{{\rm Ext}}$![]() and the distance $l$
and the distance $l$![]() : ${ I }_{ {\rm Ext} }/{ I }_{ P } = [(b-a)/(b+a)] [l^{2}/(a^{2} + b^{2})]$
: ${ I }_{ {\rm Ext} }/{ I }_{ P } = [(b-a)/(b+a)] [l^{2}/(a^{2} + b^{2})]$![]() . With this expression, ${ \gamma }_{ H }$
. With this expression, ${ \gamma }_{ H }$![]() turns out to depend only on the plasma current $I_P$
turns out to depend only on the plasma current $I_P$![]() and on the semi-axes $a$
and on the semi-axes $a$![]() and $b$
and $b$![]() , but not on $I_{ {\rm Ext} }$
, but not on $I_{ {\rm Ext} }$![]() and $l$
and $l$![]() . Also, $\mu _m$
. Also, $\mu _m$![]() can be replaced by $\mu _m \rightarrow {\rm \pi}\, a\,b\,{ \varrho }_{ m }$
can be replaced by $\mu _m \rightarrow {\rm \pi}\, a\,b\,{ \varrho }_{ m }$![]() , where ${ \varrho }_{ m }$
, where ${ \varrho }_{ m }$![]() is the volume mass density. After straightforward algebra, and taking the limit of small ellipticity, $e_0 \ll 1$
is the volume mass density. After straightforward algebra, and taking the limit of small ellipticity, $e_0 \ll 1$![]() , where
, where
the growth rate can be written as
where ${\tau _A}^{-1 } = {{ B_P }^{\prime }} / { ( 4{\rm \pi} \,{ \varrho }_{ m } ) }^{ 1/2 }$![]() is the inverse Alfvén time, and ${ B_P }^{'}$
is the inverse Alfvén time, and ${ B_P }^{'}$![]() is the radial derivative of the poloidal magnetic field on the magnetic axis. Note that, for a circular plasma cross-section, $e_0 = 0$
is the radial derivative of the poloidal magnetic field on the magnetic axis. Note that, for a circular plasma cross-section, $e_0 = 0$![]() and the growth rate $\gamma _H$
and the growth rate $\gamma _H$![]() vanish. Considering typical values of present-day tokamak experiments, $\gamma _H^{-1}$
vanish. Considering typical values of present-day tokamak experiments, $\gamma _H^{-1}$![]() is indeed a swift growth time of the order of a few microseconds.
is indeed a swift growth time of the order of a few microseconds.
A perfectly conducting wall close to the plasma can provide passive feedback stabilization of the vertical instability. The stabilization mechanism is explained as follows. When the plasma is displaced from its equilibrium position, image currents are induced at the wall. The sign of these currents is such that the corresponding net force opposes the motion of the plasma wire. In the heuristic model, we can model this effect by assuming two currents of opposite sign, $\pm \delta I$![]() , proportional to the displacement of the plasma column, and localized at $y=\pm l$
, proportional to the displacement of the plasma column, and localized at $y=\pm l$![]() . Then,
. Then,
where $L$![]() is an effective inductance and $D$
is an effective inductance and $D$![]() is a dimensionless proportionality constant, which, in the case of a tokamak plasma, can be determined in terms of the wall geometry (see § 4 here below). After straightforward algebra, and taking the limit $y\ll l$
is a dimensionless proportionality constant, which, in the case of a tokamak plasma, can be determined in terms of the wall geometry (see § 4 here below). After straightforward algebra, and taking the limit $y\ll l$![]() , the equation of motion modified by the feedback currents becomes
, the equation of motion modified by the feedback currents becomes
Thus, the vertical instability is suppressed when $D > 1$![]() , which, in the actual tokamak case, translates into a criterion related to the proximity of the wall to the plasma column. As we shall see in § 4, for the special case where the plasma boundary and the wall are modelled by confocal ellipses, the marginal stability criterion corresponds to the magnetic X-points lying on the wall, while feedback stabilization, $D>1$
, which, in the actual tokamak case, translates into a criterion related to the proximity of the wall to the plasma column. As we shall see in § 4, for the special case where the plasma boundary and the wall are modelled by confocal ellipses, the marginal stability criterion corresponds to the magnetic X-points lying on the wall, while feedback stabilization, $D>1$![]() , requires the X-points to lie beyond the wall. In the latter case, (2.5) implies that the plasma oscillates vertically with frequency
, requires the X-points to lie beyond the wall. In the latter case, (2.5) implies that the plasma oscillates vertically with frequency
These two solutions with frequency $\omega = \pm \omega _H$![]() are a first indication of what we dub the VDOM.
are a first indication of what we dub the VDOM.
For the more realistic case of a resistive wall, (2.4) is modified into
After straightforward algebra, and again in the limit $y \ll l$![]() , we find
, we find
Eliminating $\dot {\delta I}$![]() , we obtain the third-order differential equation for $y$
, we obtain the third-order differential equation for $y$![]()
where $\tau _R = L/R$![]() is the resistive-wall penetration time.
is the resistive-wall penetration time.
We restrict the discussion that follows to the limit $D>1$![]() . Thus, searching for solutions of the type $y(t)\sim y_0{\rm e}^{\gamma t}$
. Thus, searching for solutions of the type $y(t)\sim y_0{\rm e}^{\gamma t}$![]() , a cubic dispersion relation for complex $\gamma$
, a cubic dispersion relation for complex $\gamma$![]() is obtained
is obtained
where $\omega _H$![]() is defined in (2.6). In the limit of small wall resistivity, $\omega _H\tau _R \gg 1$
is defined in (2.6). In the limit of small wall resistivity, $\omega _H\tau _R \gg 1$![]() , the two VDOM oscillatory roots of the ideal wall case turn out to be damped; setting $\gamma = -{\rm i}\omega$
, the two VDOM oscillatory roots of the ideal wall case turn out to be damped; setting $\gamma = -{\rm i}\omega$![]() , the two damped modes have a complex frequency
, the two damped modes have a complex frequency
On the other hand, the third root corresponds to a purely growing resistive instability with a growth rate
For this non-rotating, unstable mode, the inverse growth rate scales with $\tau _R$![]() , which, for typical tokamak parameters, gives rise to a characteristic growth time of the order of a few milliseconds. It is then possible to counter the growth of the resistive-wall vertical instability by means of active feedback control associated with currents flowing outside the tokamak vacuum chamber (Lazarus et al. Reference Lazarus, Lister and Neilson1990; Lister et al. Reference Lister, Lazarus, Kellman, Moret, Ferron, Helton, Lao, Leuer, Strait and Taylor1990; Albanese et al. Reference Albanese, Mattei and Villone2004; Portone Reference Portone2017). We point out that, as long as the VDOM are damped, and as long as their oscillation frequency is well separated from the bandwidth of the vertical stabilization closed loop, they are not expected to have an impact on the active feedback stabilization system applied to the non-rotating, vertical resistive-wall mode.
, which, for typical tokamak parameters, gives rise to a characteristic growth time of the order of a few milliseconds. It is then possible to counter the growth of the resistive-wall vertical instability by means of active feedback control associated with currents flowing outside the tokamak vacuum chamber (Lazarus et al. Reference Lazarus, Lister and Neilson1990; Lister et al. Reference Lister, Lazarus, Kellman, Moret, Ferron, Helton, Lao, Leuer, Strait and Taylor1990; Albanese et al. Reference Albanese, Mattei and Villone2004; Portone Reference Portone2017). We point out that, as long as the VDOM are damped, and as long as their oscillation frequency is well separated from the bandwidth of the vertical stabilization closed loop, they are not expected to have an impact on the active feedback stabilization system applied to the non-rotating, vertical resistive-wall mode.
In § 4, a more general dispersion relation, valid for arbitrary values of $e_0$![]() , is obtained based on a complete solution of the ideal-MHD normal-mode problem applied to $n=0$
, is obtained based on a complete solution of the ideal-MHD normal-mode problem applied to $n=0$![]() perturbations. In the limit of small ellipticity, the general dispersion relation reduces to the cubic equation (2.10), confirming in this way the validity of the heuristic model.
perturbations. In the limit of small ellipticity, the general dispersion relation reduces to the cubic equation (2.10), confirming in this way the validity of the heuristic model.
3. Vertical rigid-shift mode structure
The analysis of this section follows that already published by us in Porcelli et al. (Reference Porcelli, Yolbarsop, Barberis and Fitzpatrick2021) and Yolbarsop et al. (Reference Yolbarsop, Porcelli and Fitzpatrick2021, Reference Yolbarsop, Porcelli, Liu and Fitzpatrick2022), which we briefly summarize here for the reader's convenience. An adequate model for the normal-mode analysis of the vertical instability is the well-known reduced ideal-MHD model (Strauss Reference Strauss1976). For axisymmetric modes, toroidal effects do not play an important role and, therefore, the straight-tokamak approximation is adopted. The magnetic field is ${\boldsymbol {B} }={\boldsymbol {e} }_{ z }\times \boldsymbol {\nabla } \psi +{ B }_{ z }\,{\boldsymbol {e} }_{ z }$![]() , where ${\boldsymbol {e}}_{ z }$
, where ${\boldsymbol {e}}_{ z }$![]() is the unit vector along the ignorable $z$
is the unit vector along the ignorable $z$![]() -direction, which mimics the toroidal coordinate, and $B_z$
-direction, which mimics the toroidal coordinate, and $B_z$![]() is constant. The plasma flow is $\boldsymbol {v} = {\boldsymbol {e }}_{z} \times \boldsymbol {\nabla } \varphi +v_{ z }\,{\boldsymbol {e} }_{ z }$
is constant. The plasma flow is $\boldsymbol {v} = {\boldsymbol {e }}_{z} \times \boldsymbol {\nabla } \varphi +v_{ z }\,{\boldsymbol {e} }_{ z }$![]() . In the standard low-$\beta$
. In the standard low-$\beta$![]() limit for a tokamak plasma, the fields $B_z$
limit for a tokamak plasma, the fields $B_z$![]() and $v_z$
and $v_z$![]() decouple from the fields $\psi$
decouple from the fields $\psi$![]() and $\varphi$
and $\varphi$![]() . Therefore, the magnetic flux function, $\psi$
. Therefore, the magnetic flux function, $\psi$![]() , and the streamfunction, $\varphi$
, and the streamfunction, $\varphi$![]() , obey the model equations (Strauss Reference Strauss1976)
, obey the model equations (Strauss Reference Strauss1976)
In these equations, all quantities are dimensionless, brackets are defined as $[ \chi,\eta ] ={\boldsymbol {e} }_{ z }\,\boldsymbol {\cdot }\,\boldsymbol {\nabla } \chi \times \boldsymbol {\nabla } \eta$![]() , $J={\nabla }^{2}\psi$
, $J={\nabla }^{2}\psi$![]() is the normalized current density and $U={ \nabla }^{2}\varphi$
is the normalized current density and $U={ \nabla }^{2}\varphi$![]() is the normalized flow vorticity. Space and time are normalized as $\hat {r } =r /{ r }_{ 0 }$
is the normalized flow vorticity. Space and time are normalized as $\hat {r } =r /{ r }_{ 0 }$![]() , where ${ r }_{ 0 }=a\,b/[ ( { a }^{ 2 }+{ b }^{ 2 } ) /2 ]^{ 1/ 2 }$
, where ${ r }_{ 0 }=a\,b/[ ( { a }^{ 2 }+{ b }^{ 2 } ) /2 ]^{ 1/ 2 }$![]() is a convenient equilibrium scale length, and $\hat {t} = t / { \tau }_{ A }$
is a convenient equilibrium scale length, and $\hat {t} = t / { \tau }_{ A }$![]() , where ${ \tau }_{A}$
, where ${ \tau }_{A}$![]() is the poloidal Alfvén time defined below (2.3). The dimensionless fields are normalized as $\hat { \psi } =\psi /( { { B }_{ p } }^{\prime } { r }_{ 0 }^{ 2 } )$
is the poloidal Alfvén time defined below (2.3). The dimensionless fields are normalized as $\hat { \psi } =\psi /( { { B }_{ p } }^{\prime } { r }_{ 0 }^{ 2 } )$![]() , $\hat {\varphi } = ( \tau _A/{ r_{ 0 }}^{2}) \varphi$
, $\hat {\varphi } = ( \tau _A/{ r_{ 0 }}^{2}) \varphi$![]() ; the plasma density is normalized to its on-axis value, $\hat {\varrho } =\varrho _m /{ \varrho }_{ m0 }$
; the plasma density is normalized to its on-axis value, $\hat {\varrho } =\varrho _m /{ \varrho }_{ m0 }$![]() , and the current density is $\hat {J } = (4{\rm \pi} /c{ { B }_{ p } }^{\prime }){ J }_{ z }$
, and the current density is $\hat {J } = (4{\rm \pi} /c{ { B }_{ p } }^{\prime }){ J }_{ z }$![]() . In order to simplify the notation, over-hats are actually dropped in (3.1) and (3.2), and in the following.
. In order to simplify the notation, over-hats are actually dropped in (3.1) and (3.2), and in the following.
At equilibrium, fields are stationary, and, by assumption, the equilibrium plasma velocity is negligibly small. The current density, $J_{ {\rm eq} }$![]() , is assumed to be uniform up to an elliptical boundary with minor semi-axis $a$
, is assumed to be uniform up to an elliptical boundary with minor semi-axis $a$![]() and major semi-axis $b$
and major semi-axis $b$![]() , and to drop to zero beyond that boundary, where vacuum is assumed. Clearly, the elliptical boundary must be a magnetic flux surface, which lies necessarily within the region bounded by the magnetic separatrix. In elliptical coordinates $( \mu,\theta )$
, and to drop to zero beyond that boundary, where vacuum is assumed. Clearly, the elliptical boundary must be a magnetic flux surface, which lies necessarily within the region bounded by the magnetic separatrix. In elliptical coordinates $( \mu,\theta )$![]() , where $x= A \sinh ( \mu ) \cos ( \theta )$
, where $x= A \sinh ( \mu ) \cos ( \theta )$![]() and $y = A \cosh ( \mu ) \sin ( \theta )$
and $y = A \cosh ( \mu ) \sin ( \theta )$![]() , with $A = \sqrt { { b }^{ 2 } - { a }^{ 2 } }$
, with $A = \sqrt { { b }^{ 2 } - { a }^{ 2 } }$![]() , the elliptical boundary corresponds to $\mu = { \mu }_{ b }$
, the elliptical boundary corresponds to $\mu = { \mu }_{ b }$![]() , such that $a = A\sinh {\mu _b}$
, such that $a = A\sinh {\mu _b}$![]() and $b = A\cosh {\mu _b}$
and $b = A\cosh {\mu _b}$![]() . The equilibrium current density is ${ J }_{ {\rm eq} }( \mu ) = 2 H( { \mu }_{ b } - \mu )$
. The equilibrium current density is ${ J }_{ {\rm eq} }( \mu ) = 2 H( { \mu }_{ b } - \mu )$![]() , where $H(x)$
, where $H(x)$![]() is the Heaviside unit step function.
is the Heaviside unit step function.
According to the analysis of Porcelli & Yolbarsop (Reference Porcelli and Yolbarsop2019), in the plasma region inside the elliptical boundary, where $\mu < { \mu }_{ b }$![]() and $\psi = { \psi }_{ {\rm eq} }^{ - }$
and $\psi = { \psi }_{ {\rm eq} }^{ - }$![]() , the solution of ${ \nabla }^{ 2 } { \psi }_{ {\rm eq} }^{ - }=2$
, the solution of ${ \nabla }^{ 2 } { \psi }_{ {\rm eq} }^{ - }=2$![]() that is well behaved on the magnetic axis and that reduces to a constant on the elliptical boundary is best written in terms of Cartesian components
that is well behaved on the magnetic axis and that reduces to a constant on the elliptical boundary is best written in terms of Cartesian components
In the vacuum region outside the elliptical boundary, where $\mu > { \mu }_{ b }$![]() , the equilibrium flux $\psi _{ {\rm eq} } = { \psi }_{ {\rm eq} }^{ + }$
, the equilibrium flux $\psi _{ {\rm eq} } = { \psi }_{ {\rm eq} }^{ + }$![]() satisfies ${ \nabla }^{ 2 } { \psi }_{ m }^{ + }=0$
satisfies ${ \nabla }^{ 2 } { \psi }_{ m }^{ + }=0$![]() . Here, and in the following, the superscripts ‘$-$
. Here, and in the following, the superscripts ‘$-$![]() ’ and ‘$+$
’ and ‘$+$![]() ’ indicate the plasma and vacuum regions, respectively. As we assume no equilibrium current sheets, $\psi _{{\rm eq}}$
’ indicate the plasma and vacuum regions, respectively. As we assume no equilibrium current sheets, $\psi _{{\rm eq}}$![]() and its derivative along the normal to the boundary must be continuous across the boundary. The relevant analytic solution is
and its derivative along the normal to the boundary must be continuous across the boundary. The relevant analytic solution is
with $\alpha ^{2} = ab/r_0^{2}$![]() and ${ e }_{ 0 }$
and ${ e }_{ 0 }$![]() the ellipticity parameter defined in (2.2). Magnetic flux surfaces $\psi _{ eq }(\mu, \theta ) = {\rm {const}}.$
the ellipticity parameter defined in (2.2). Magnetic flux surfaces $\psi _{ eq }(\mu, \theta ) = {\rm {const}}.$![]() exhibit a magnetic separatrix at $\psi _{ {\rm eq} }(\mu, \theta ) = \psi _X = { \mu }_{ b } \, { \alpha }^{ 2 }$
exhibit a magnetic separatrix at $\psi _{ {\rm eq} }(\mu, \theta ) = \psi _X = { \mu }_{ b } \, { \alpha }^{ 2 }$![]() , with X-points located at $\mu = \mu _X =2\mu _b$
, with X-points located at $\mu = \mu _X =2\mu _b$![]() and $\theta = \theta _X = {\rm \pi}/2 \pm n{\rm \pi}$
and $\theta = \theta _X = {\rm \pi}/2 \pm n{\rm \pi}$![]() .
.
The equilibrium plasma density profile is also assumed to be uniform up to the elliptical boundary $\mu = \mu _b$![]() , i.e. $\varrho _{ {\rm eq} } = H( { \mu }_{ b } - \mu )$
, i.e. $\varrho _{ {\rm eq} } = H( { \mu }_{ b } - \mu )$![]() . Thus, this model equilibrium, where the plasma terminates well before the magnetic separatrix, and a wall is present, resembles more closely a limiter tokamak scenario, with the equilibrium magnetic X-points that may lie either outside the plasma containment chamber, or in the vacuum region inside the chamber.
. Thus, this model equilibrium, where the plasma terminates well before the magnetic separatrix, and a wall is present, resembles more closely a limiter tokamak scenario, with the equilibrium magnetic X-points that may lie either outside the plasma containment chamber, or in the vacuum region inside the chamber.
Two main reasons justify the choice of this particular equilibrium. First, we intend to carry out a fully analytic treatment of the normal-mode problem, which can be done if the starting point is a relatively simple equilibrium. The second is that, based on previous studies of the vertical stability problem, effects associated with gradients of the equilibrium plasma current density are not expected to play an important role. Furthermore, the equilibrium adopted in this article is the same as that used in Laval et al. (Reference Laval, Pellat and Soule1974). On the other hand, equilibrium flows are neglected in this article and ought to be considered in future studies.
For stability considerations, set $\psi ( \mu,\theta, t) = \psi _{{\rm eq}}( \mu, \theta ) + \tilde {\psi }( \mu, \theta )\,{\rm e}^{\gamma \,t}$![]() and $\varphi ( \mu,\theta, t ) = \tilde {\phi }( \mu, \theta )\,{\rm e}^{\gamma t}$
and $\varphi ( \mu,\theta, t ) = \tilde {\phi }( \mu, \theta )\,{\rm e}^{\gamma t}$![]() , where the over-tilde denotes small perturbed quantities and $\gamma = -{\rm i}\omega$
, where the over-tilde denotes small perturbed quantities and $\gamma = -{\rm i}\omega$![]() . The linearized versions of (3.1) and (3.2) are
. The linearized versions of (3.1) and (3.2) are
In the region $\mu < { \mu }_{ b }$![]() , the streamfunction corresponding to a rigid vertical shift is represented in elliptical coordinates by
, the streamfunction corresponding to a rigid vertical shift is represented in elliptical coordinates by
where $\xi$![]() is the vertical displacement of the plasma column. From the flux freezing condition (3.5) we obtain the corresponding perturbed magnetic flux
is the vertical displacement of the plasma column. From the flux freezing condition (3.5) we obtain the corresponding perturbed magnetic flux
Since $\tilde { U }$![]() , $\tilde { J }$
, $\tilde { J }$![]() , $\boldsymbol {\nabla } \varrho _{ {\rm eq} }$
, $\boldsymbol {\nabla } \varrho _{ {\rm eq} }$![]() and $\boldsymbol {\nabla } J_{ {\rm eq} }$
and $\boldsymbol {\nabla } J_{ {\rm eq} }$![]() all vanish inside the elliptical boundary, (3.6) is trivially satisfied. Note that in elliptical coordinates, ${\nabla }^{ 2 }\chi = h^{ -2 }(\partial ^{2} \chi /\partial \mu ^{2} + \partial ^{2} \chi /\partial \theta ^{2} )$
all vanish inside the elliptical boundary, (3.6) is trivially satisfied. Note that in elliptical coordinates, ${\nabla }^{ 2 }\chi = h^{ -2 }(\partial ^{2} \chi /\partial \mu ^{2} + \partial ^{2} \chi /\partial \theta ^{2} )$![]() , where $h = 1 / | \boldsymbol {\nabla } \mu | = 1 / | \boldsymbol {\nabla } \theta |$
, where $h = 1 / | \boldsymbol {\nabla } \mu | = 1 / | \boldsymbol {\nabla } \theta |$![]() is a scale factor, with $h^{2} = A^{2}(\cosh {2\mu }+\cos {2\theta })/2$
is a scale factor, with $h^{2} = A^{2}(\cosh {2\mu }+\cos {2\theta })/2$![]() .
.
When an ideal or resistive wall is present, the rigid-shift solutions (3.7) and (3.8) for the streamfunction and the perturbed flux in the plasma region retain their validity, while, in the vacuum region, the perturbed flux satisfies $\nabla ^{2}\tilde {\psi }^{+} =0$![]() , whose solution can be best represented as
, whose solution can be best represented as
In this expression, $\xi _\infty$![]() is the amplitude of the rigid vertical displacement in the limit where the wall is moved to infinity, and the term proportional to $\xi _{{\rm ext}}$
is the amplitude of the rigid vertical displacement in the limit where the wall is moved to infinity, and the term proportional to $\xi _{{\rm ext}}$![]() represents the contribution to the perturbed flux due to the image currents that form on the wall when this is at a finite distance from the plasma boundary. Continuity of flux at the plasma boundary requires that $\xi = \xi _\infty - \xi _{{\rm ext}}$
represents the contribution to the perturbed flux due to the image currents that form on the wall when this is at a finite distance from the plasma boundary. Continuity of flux at the plasma boundary requires that $\xi = \xi _\infty - \xi _{{\rm ext}}$![]() , and so the actual vertical displacement $\xi$
, and so the actual vertical displacement $\xi$![]() is reduced, as compared with the no-wall case, by the amount $\xi _{{\rm ext}}$
is reduced, as compared with the no-wall case, by the amount $\xi _{{\rm ext}}$![]() . A perturbed current sheet forms at the plasma boundary
. A perturbed current sheet forms at the plasma boundary

where $\delta (x)$![]() is the Dirac delta function. A staightforward calculation yields the elliptical-angle modulation of the current sheet
is the Dirac delta function. A staightforward calculation yields the elliptical-angle modulation of the current sheet
Note that $\tilde { j }_b ( \theta )$![]() depends only on $\xi _\infty$
depends only on $\xi _\infty$![]() and not on $\xi _{{\rm ext}}$
and not on $\xi _{{\rm ext}}$![]() , as the current sheet at the plasma boundary does not depend on the wall image currents.
, as the current sheet at the plasma boundary does not depend on the wall image currents.
4. Dispersion relation and quadratic forms
In this section, with the help of quadratic forms, we derive a dispersion relation for $n=0$![]() vertical modes, which depends on geometrical parameters, $a$
vertical modes, which depends on geometrical parameters, $a$![]() and $b$
and $b$![]() , and on a function, $D_w(\gamma )$
, and on a function, $D_w(\gamma )$![]() , determined by the geometry and the resistivity of the wall, which becomes independent of $\gamma$
, determined by the geometry and the resistivity of the wall, which becomes independent of $\gamma$![]() in the ideal wall limit.
in the ideal wall limit.
Let us introduce the auxiliary streamfunction $\tilde {\varphi }^{{\dagger} }$![]() , such that it equals the complex-conjugate streamfunction in the volume occupied by the plasma (up to $\mu = \mu _b + \epsilon$
, such that it equals the complex-conjugate streamfunction in the volume occupied by the plasma (up to $\mu = \mu _b + \epsilon$![]() , i.e. including the perturbed current sheet at the plasma boundary), that we denote by the symbol $\varOmega$
, i.e. including the perturbed current sheet at the plasma boundary), that we denote by the symbol $\varOmega$![]() , while $\tilde {\varphi }^{{\dagger} }$
, while $\tilde {\varphi }^{{\dagger} }$![]() equals zero in the vacuum region. We multiply the perturbed plasma equation of motion (3.6) by $\tilde {\varphi }^{{\dagger} }/2\gamma ^{*}$
equals zero in the vacuum region. We multiply the perturbed plasma equation of motion (3.6) by $\tilde {\varphi }^{{\dagger} }/2\gamma ^{*}$![]() and integrate it over the whole volume extending to infinity. After standard manipulations, we obtain
and integrate it over the whole volume extending to infinity. After standard manipulations, we obtain
where $\boldsymbol {\xi } ={\boldsymbol {e}}_z\times \boldsymbol {\nabla } \tilde {\varphi }/\gamma$![]() is the displacement vector. Thus, the dispersion relation can be written as
is the displacement vector. Thus, the dispersion relation can be written as
where
and
with $\boldsymbol {F}(\boldsymbol {\xi }) = [ (\tilde {\boldsymbol {J}}\times {\boldsymbol {B}}_{{\rm eq}}) + ({\boldsymbol {J}}_{{\rm eq}}\times \tilde {\boldsymbol {B}})]$![]() the force density operator in the limit where $\beta$
the force density operator in the limit where $\beta$![]() effects are negligibly small. Note that, even though the potential energy integral is extended to the volume occupied by the plasma, wall effects are included in $\delta W$
effects are negligibly small. Note that, even though the potential energy integral is extended to the volume occupied by the plasma, wall effects are included in $\delta W$![]() through the perturbed magnetic flux, which depends also on the contribution due to image currents that flow on the wall as the plasma boundary is displaced. As it will be shown in the following, $\delta W$
through the perturbed magnetic flux, which depends also on the contribution due to image currents that flow on the wall as the plasma boundary is displaced. As it will be shown in the following, $\delta W$![]() is a real quantity, independent of the mode frequency, in the limit of an ideal wall, but it becomes frequency dependent when the wall is resistive.
is a real quantity, independent of the mode frequency, in the limit of an ideal wall, but it becomes frequency dependent when the wall is resistive.
Straightforward algebra, using ${\rm d}^{3}x = h^{2}\,{\rm d}\theta \,{\rm d}\mu \,{\rm d} z$![]() , leads to
, leads to
where $L_z$![]() is the length of the straight tokamak. Without loss of generality, we can take $\xi$
is the length of the straight tokamak. Without loss of generality, we can take $\xi$![]() to be real and to correspond to the amplitude of the vertical displacement introduced in the previous section. The perturbed energy integral is
to be real and to correspond to the amplitude of the vertical displacement introduced in the previous section. The perturbed energy integral is
The last term can be further manipulated, using the results for the perturbed streamfunction and the perturbed magnetic flux obtained in § 3. $\delta W$![]() is written as the sum of two terms. The first term is
is written as the sum of two terms. The first term is

The second term can be expressed as

It is convenient to introduce the quantity
where $\hat {e}_0=e_0b/(a+b)$![]() . Then, combining (4.7), (4.8) and (4.9), remembering that $\xi = \xi _{\infty }-\xi _{ext}$
. Then, combining (4.7), (4.8) and (4.9), remembering that $\xi = \xi _{\infty }-\xi _{ext}$![]() , we obtain
, we obtain
Thus, (4.2) yields the dispersion relation
This dispersion relation is ‘general’, in the sense that it can be applied to the three cases of interest, i.e. the no-wall limit, the ideal wall case and the resistive-wall case, as wall effects are included in (4.11) through the single stability function, $D_w$![]() . In (4.11), parameters $a$
. In (4.11), parameters $a$![]() and $b$
and $b$![]() are normalized to the scale length $r_0$
are normalized to the scale length $r_0$![]() defined below (3.2). Reintroducing dimensions, the dispersion relation (4.11) takes the form
defined below (3.2). Reintroducing dimensions, the dispersion relation (4.11) takes the form
Thus, the mode's stability depends on the quantity $D_w$![]() , which is determined once the location of the wall and its nature, whether ideal or resistive, is decided. As shown in §§ 4.1 and 4.2, if the wall is perfectly conducting, $D_w$
, which is determined once the location of the wall and its nature, whether ideal or resistive, is decided. As shown in §§ 4.1 and 4.2, if the wall is perfectly conducting, $D_w$![]() is a real quantity, independent of $\gamma$
is a real quantity, independent of $\gamma$![]() , that reduces to the parameter $D$
, that reduces to the parameter $D$![]() introduced in the heuristic model of S 2. In this case, the relevant dispersion relation is quadratic in $\gamma$
introduced in the heuristic model of S 2. In this case, the relevant dispersion relation is quadratic in $\gamma$![]() , and the sign of $\gamma ^{2}$
, and the sign of $\gamma ^{2}$![]() , which depends on the sign of $1-D$
, which depends on the sign of $1-D$![]() , determines the stability of vertical displacements in the ideal-MHD limit. However, if a resistive wall is considered, then $D_w = D_w(\gamma )$
, determines the stability of vertical displacements in the ideal-MHD limit. However, if a resistive wall is considered, then $D_w = D_w(\gamma )$![]() and the dispersion relation becomes cubic in $\gamma$
and the dispersion relation becomes cubic in $\gamma$![]() , as discussed in § 4.3.
, as discussed in § 4.3.
4.1. Wall at infinity
The first case we investigate is the no-wall limit, or equivalently, the case where the wall is moved to infinity. The analysis of § 3 shows that, in this case, $\xi _{{\rm ext}} = 0$![]() , hence $D_w=0$
, hence $D_w=0$![]() . The vertical mode is unstable, with $\gamma ^{2}$
. The vertical mode is unstable, with $\gamma ^{2}$![]() a positive real value (for $b>a$
a positive real value (for $b>a$![]() ), which reduces to zero in the circular limit, $a=b$
), which reduces to zero in the circular limit, $a=b$![]() . The mode growth rate is
. The mode growth rate is
and $\gamma ^{2}$![]() can also be written in terms of the ellipticity parameter,
can also be written in terms of the ellipticity parameter,
We remark that this result is valid for arbitrary values of $e_0$![]() in the interval $0 \leqslant e_0 \leqslant 1$
in the interval $0 \leqslant e_0 \leqslant 1$![]() . In the limit of small ellipticity, $\gamma _\infty$
. In the limit of small ellipticity, $\gamma _\infty$![]() reduces to $\gamma _H$
reduces to $\gamma _H$![]() in (2.3) and the mode growth rate agrees perfectly well with the heuristic result of § 2.
in (2.3) and the mode growth rate agrees perfectly well with the heuristic result of § 2.
4.2. Passive feedback stabilization: ideal wall
Assume that the wall is represented by an elliptical coordinate surface, $\mu = \mu _w$![]() , confocal to the elliptical plasma boundary at $\mu = \mu _b$
, confocal to the elliptical plasma boundary at $\mu = \mu _b$![]() , with $\mu _w \geqslant \mu _b$
, with $\mu _w \geqslant \mu _b$![]() . If the wall is ideal, the perturbed flux in (3.9) must vanish at $\mu = \mu _w$
. If the wall is ideal, the perturbed flux in (3.9) must vanish at $\mu = \mu _w$![]() , i.e. $\tilde {\psi }^{+}(\mu _w , \theta ) = 0$
, i.e. $\tilde {\psi }^{+}(\mu _w , \theta ) = 0$![]() . It follows that
. It follows that
Now, let us use
where $A = \sqrt {b_w^{2} - a_w^{2}} = \sqrt {b^{2} - a^{2}}$![]() , with $b_w$
, with $b_w$![]() and $a_w$
and $a_w$![]() the major and minor semi-axes of the elliptical wall, respectively. It follows that
the major and minor semi-axes of the elliptical wall, respectively. It follows that
Using (4.15)–(4.19) and the definition of $D_w$![]() in (4.9), we obtain
in (4.9), we obtain
Note that, as the wall is moved further away from the plasma boundary, it becomes more and more ‘circular’, due to the assumption of confocality with the elliptical plasma boundary. Therefore, as $b_w/b\to \infty$![]() , $b_w\to a_w$
, $b_w\to a_w$![]() and $D\to 0$
and $D\to 0$![]() , as it should. We also observe that, apart from the extra term $\hat {e}_0D$
, as it should. We also observe that, apart from the extra term $\hat {e}_0D$![]() in the denominator of (4.11), the dispersion relation (4.11) with $D_w = D$
in the denominator of (4.11), the dispersion relation (4.11) with $D_w = D$![]() agrees very well with the heuristic dispersion relation obtained in § 2. We can conclude that, if $D>1$
agrees very well with the heuristic dispersion relation obtained in § 2. We can conclude that, if $D>1$![]() , $\gamma ^{2}$
, $\gamma ^{2}$![]() is negative, and thus the vertical mode oscillates with a real frequency
is negative, and thus the vertical mode oscillates with a real frequency

which reduces to $\omega _H$![]() defined in (2.6) in the limit of small ellipticity. The dispersion relation is quadratic and the only solutions that can be extracted, in the limit $D>1$
defined in (2.6) in the limit of small ellipticity. The dispersion relation is quadratic and the only solutions that can be extracted, in the limit $D>1$![]() , are the VDOM solutions. Thus, an ideal elliptical wall, confocal with the elliptical plasma boundary, can provide passive feedback stabilization of the vertical instability when $D_w = D>1$
, are the VDOM solutions. Thus, an ideal elliptical wall, confocal with the elliptical plasma boundary, can provide passive feedback stabilization of the vertical instability when $D_w = D>1$![]() .
.
The term $\hat {e}_0D$![]() can be neglected if it is small as compared with unity, but in fact it plays an important role if the wall coincides with the plasma boundary. Indeed, $D$
can be neglected if it is small as compared with unity, but in fact it plays an important role if the wall coincides with the plasma boundary. Indeed, $D$![]() reaches its maximum value in this limit, where $\mu _w = \mu _b$
reaches its maximum value in this limit, where $\mu _w = \mu _b$![]() , $D=D_{\max }=(a+b)/(e_0b) = 1/\hat {e}_0$
, $D=D_{\max }=(a+b)/(e_0b) = 1/\hat {e}_0$![]() and the denominator in (4.21) vanishes. Therefore, in this special limit, the oscillation frequency goes to infinity, but also, the amplitude of the displacement, $\xi = \xi _\infty - \xi _{{\rm ext}}$
and the denominator in (4.21) vanishes. Therefore, in this special limit, the oscillation frequency goes to infinity, but also, the amplitude of the displacement, $\xi = \xi _\infty - \xi _{{\rm ext}}$![]() , goes to zero, as $\xi _{{\rm ext}}\to \xi _\infty$
, goes to zero, as $\xi _{{\rm ext}}\to \xi _\infty$![]() . As a numerical example, take $a_w = a$
. As a numerical example, take $a_w = a$![]() , $b_w = b$
, $b_w = b$![]() and $b/a = 1.8$
and $b/a = 1.8$![]() . In this case, $D_{\max }\approx 2.9$
. In this case, $D_{\max }\approx 2.9$![]() . As the wall is placed further away from the plasma boundary, the value of $D$
. As the wall is placed further away from the plasma boundary, the value of $D$![]() decreases monotonically, and a purely oscillatory solution is found for as long as $D$
decreases monotonically, and a purely oscillatory solution is found for as long as $D$![]() remains larger than unity.
remains larger than unity.
It can be easily checked, using (4.15)–(4.19), that the marginally stable value, $D=1$![]() , is obtained when $\mu _w = 2\mu _b$
, is obtained when $\mu _w = 2\mu _b$![]() , which corresponds to the elliptical wall intercepting the X-points. Thus, our model indicates that values of $D<1$
, which corresponds to the elliptical wall intercepting the X-points. Thus, our model indicates that values of $D<1$![]() , for which no passive feedback stabilization is possible, are found when the X-points lie inside the volume bounded by the wall. We point out that this result is in perfect agreement with that obtained by Laval et al. (Reference Laval, Pellat and Soule1974) on the basis of the ideal-MHD energy principle. However, this result holds true for the special case of confocal wall and plasma boundaries. For different wall shapes that fit more tightly with the plasma boundary, passive feedback stabilization due to the ideal wall does not necessarily require that the X-points lie beyond the wall. Furthermore, in real tokamak plasmas, additional coils and/or short-circuited plates located inside the vacuum chamber can contribute to passive feedback stabilization (Albanese et al. Reference Albanese, Mattei and Villone2004; Portone Reference Portone2017).
, for which no passive feedback stabilization is possible, are found when the X-points lie inside the volume bounded by the wall. We point out that this result is in perfect agreement with that obtained by Laval et al. (Reference Laval, Pellat and Soule1974) on the basis of the ideal-MHD energy principle. However, this result holds true for the special case of confocal wall and plasma boundaries. For different wall shapes that fit more tightly with the plasma boundary, passive feedback stabilization due to the ideal wall does not necessarily require that the X-points lie beyond the wall. Furthermore, in real tokamak plasmas, additional coils and/or short-circuited plates located inside the vacuum chamber can contribute to passive feedback stabilization (Albanese et al. Reference Albanese, Mattei and Villone2004; Portone Reference Portone2017).
Finally, we point out that, as shown in Yolbarsop et al. (Reference Yolbarsop, Porcelli and Fitzpatrick2021, Reference Yolbarsop, Porcelli, Liu and Fitzpatrick2022), if the plasma extends to the magnetic separatrix, as is normally the case for a divertor tokamak plasma, axisymmetric plasma currents associated with vertical displacement perturbations are driven in the vicinity of the magnetic X-points. As a consequence, these currents can also contribute to passive feedback stabilization of the vertical instability.
4.3. Passive feedback stabilization: resistive wall
Lastly, we consider the more realistic case of a resistive wall. In this situation the perturbed magnetic flux is not zero at the wall, but can diffuse across on the resistive-wall time scale. We identify three different regions: inside the elliptical boundary, $\mu \leqslant \mu _b$![]() , where the perturbed flux $\tilde {\psi }$
, where the perturbed flux $\tilde {\psi }$![]() equals $\tilde {\psi }^{-}$
equals $\tilde {\psi }^{-}$![]() given by (3.8); the vacuum region between the plasma boundary and the wall, $\mu _b \leqslant \mu \leqslant \mu _w$
given by (3.8); the vacuum region between the plasma boundary and the wall, $\mu _b \leqslant \mu \leqslant \mu _w$![]() , where $\tilde {\psi }$
, where $\tilde {\psi }$![]() equals $\tilde {\psi }^{+}$
equals $\tilde {\psi }^{+}$![]() given by (3.9); and the vacuum outside the wall, where $\tilde {\psi }=\tilde {\psi }_{{\rm out}}$
given by (3.9); and the vacuum outside the wall, where $\tilde {\psi }=\tilde {\psi }_{{\rm out}}$![]() is the solution of $\nabla ^{2}\tilde {\psi }_{{\rm out}} = 0$
is the solution of $\nabla ^{2}\tilde {\psi }_{{\rm out}} = 0$![]() that decays to zero at infinity. Focusing on vertical displacements with elliptical mode number $m=1$
that decays to zero at infinity. Focusing on vertical displacements with elliptical mode number $m=1$![]() , the relevant solution is
, the relevant solution is
where $\delta _{w}$![]() is a small parameter representing the average width of the thin wall.
is a small parameter representing the average width of the thin wall.
Two conditions at the wall determine the parameter $\psi _{0}$![]() and $D_w$
and $D_w$![]() ; the latter will turn out to be a function of complex $\gamma$
; the latter will turn out to be a function of complex $\gamma$![]() . The first condition is continuity of flux at the wall, $\tilde {\psi }^{+}(\mu _w,\theta ) = \tilde {\psi }_{{\rm out}}(\mu _w,\theta )$
. The first condition is continuity of flux at the wall, $\tilde {\psi }^{+}(\mu _w,\theta ) = \tilde {\psi }_{{\rm out}}(\mu _w,\theta )$![]() , which gives
, which gives
The second condition involves the current flowing along the wall. Consider the resistive Ohm's law for the perturbed magnetic flux within the wall, $\partial {\psi }_{w}/\partial t = (\eta c^{2}/4{\rm \pi} )\nabla ^{2}{\psi }_{w}$![]() , where $\eta$
, where $\eta$![]() is the wall resistivity. After proper normalization, we obtain
is the wall resistivity. After proper normalization, we obtain
where $\varepsilon _{\eta } = (\eta \tau _A c^{2})/(4{\rm \pi} r_0^{2})$![]() is the inverse of the relevant dimensionless Lundquist number. Since the wall is relatively thin, we can neglect the dependence on $\mu$
is the inverse of the relevant dimensionless Lundquist number. Since the wall is relatively thin, we can neglect the dependence on $\mu$![]() of the perturbed flux at the right-hand side of (4.24). This approximation is similar to the standard constant-$\psi$
of the perturbed flux at the right-hand side of (4.24). This approximation is similar to the standard constant-$\psi$![]() approximation used in magnetic reconnection theory. Set $\tilde {\psi } = \hat {\psi }(\mu )\sin {\theta }$
approximation used in magnetic reconnection theory. Set $\tilde {\psi } = \hat {\psi }(\mu )\sin {\theta }$![]() . We assume the ordering $\partial _\mu ^{2}\hat {\psi } \sim \hat {\psi }/\mu _w\delta _w \gg \hat {\psi }$
. We assume the ordering $\partial _\mu ^{2}\hat {\psi } \sim \hat {\psi }/\mu _w\delta _w \gg \hat {\psi }$![]() . Then, (4.24) can be approximated as
. Then, (4.24) can be approximated as
Integrating across the thin wall,

The scale factor $h$![]() is defined below (3.8). Strictly speaking, $h$
is defined below (3.8). Strictly speaking, $h$![]() depends on both $\mu$
depends on both $\mu$![]() and $\theta$
and $\theta$![]() . However, in the limit of small wall ellipticity, which is assumed in the following, the $\theta$
. However, in the limit of small wall ellipticity, which is assumed in the following, the $\theta$![]() modulation of $h$
modulation of $h$![]() along the wall is small, so that we can approximate $h(\mu _w , \theta ) \approx b_w$
along the wall is small, so that we can approximate $h(\mu _w , \theta ) \approx b_w$![]() . Carrying out the integration, we find
. Carrying out the integration, we find

or equivalently
Equations (4.23) and (4.28) are two equations that can be used to determine the two parameters, $\psi _0\propto \xi _\infty$![]() , and $\xi _{ext}/\xi _\infty \propto D_w$
, and $\xi _{ext}/\xi _\infty \propto D_w$![]() , cf. (4.9). After straightforward algebra, we obtain
, cf. (4.9). After straightforward algebra, we obtain
and
In these equations, $D$![]() was defined in (4.15), and $\tau _{\eta } = [b_w^{3}/(a_w+b_w)]\delta _{w} / \varepsilon _{\eta }$
was defined in (4.15), and $\tau _{\eta } = [b_w^{3}/(a_w+b_w)]\delta _{w} / \varepsilon _{\eta }$![]() is the resistive-wall time (normalized to the relevant Alfvén time). Notice that the stability parameter $D_w$
is the resistive-wall time (normalized to the relevant Alfvén time). Notice that the stability parameter $D_w$![]() depends on $\gamma$
depends on $\gamma$![]() due to finite wall resistivity. In the ideal wall limit, $\tau _\eta \rightarrow \infty$
due to finite wall resistivity. In the ideal wall limit, $\tau _\eta \rightarrow \infty$![]() , $D_w(\gamma )\to D$
, $D_w(\gamma )\to D$![]() reduces to the parameter $D$
reduces to the parameter $D$![]() discussed in § 4.2. Also, (4.30) shows that the perturbed flux at the wall goes to zero in the ideal wall limit, as it should.
discussed in § 4.2. Also, (4.30) shows that the perturbed flux at the wall goes to zero in the ideal wall limit, as it should.
Substituting $D_w(\gamma )$![]() in (4.11), one obtains the dispersion relation for vertical displacements in the case of feedback stabilization via a resistive wall
in (4.11), one obtains the dispersion relation for vertical displacements in the case of feedback stabilization via a resistive wall
with $\omega _{0}$![]() defined in (4.21). It is reassuring that (4.31) agrees very well with the dispersion relation found heuristically in § 2, cf. (2.10). This is particularly true in the small ellipticity limit, where the term $\hat {e}_0D$
defined in (4.21). It is reassuring that (4.31) agrees very well with the dispersion relation found heuristically in § 2, cf. (2.10). This is particularly true in the small ellipticity limit, where the term $\hat {e}_0D$![]() can be neglected and the frequency $\omega _0$
can be neglected and the frequency $\omega _0$![]() reduces to $\omega _H$
reduces to $\omega _H$![]() , cf. (2.6).
, cf. (2.6).
The three roots of this cubic dispersion relation are easily determined in the realistic limit $\omega _0 \tau _{\eta } \gg 1$![]() . After straightforward algebra, for $D>1$
. After straightforward algebra, for $D>1$![]() , one obtains two damped oscillatory roots and an unstable growing solution ($\gamma = -{\rm i}\omega$
, one obtains two damped oscillatory roots and an unstable growing solution ($\gamma = -{\rm i}\omega$![]() )
)
The two oscillatory, weakly damped roots of (4.32) correspond to the two VDOM that oscillate with a frequency slightly below the poloidal Alfvén frequency, as already found in § 4.2. The effect of a resistive wall is to introduce a small damping rate of the order of the inverse resistive-wall time. The third root, (4.33), corresponds to an unstable mode, growing on the resistive-wall time scale. Typical values of the resistive wall time in tokamak devices are of the order of a few milliseconds. As we have already pointed out in § 2, due to its slow growth, this non-rotating, unstable mode is normally suppressed by means of active feedback control systems (Albanese et al. Reference Albanese, Mattei and Villone2004).
5. Conclusions
In this article, the dispersion relation for vertical plasma displacement normal modes has been derived analytically. Vertical displacements are axisymmetric modes of a toroidal tokamak plasma, with toroidal mode number $n=0$![]() . They cause an up–down motion of the entire plasma column, and as such are dominated by Fourier components with elliptical mode number $m=1$
. They cause an up–down motion of the entire plasma column, and as such are dominated by Fourier components with elliptical mode number $m=1$![]() . The up–down symmetry implies that the perturbed streamfunction is an even function of the elliptical angle $\theta$
. The up–down symmetry implies that the perturbed streamfunction is an even function of the elliptical angle $\theta$![]() ($\theta =0$
($\theta =0$![]() corresponds to the horizontal direction), while the perturbed magnetic flux is an odd function of $\theta$
corresponds to the horizontal direction), while the perturbed magnetic flux is an odd function of $\theta$![]() . Our derivation is based on the reduced ideal-MHD model and on a simple, ‘straight-tokamak’ equilibrium, that assumes an elliptical plasma boundary and a uniform current density profile. This assumption is motivated by two considerations. Firstly, it is known that the stability and growth rate of vertical displacements depends on plasma shaping and on the total plasma current, but not on details of the current density profiles. Secondly, the assumed equilibrium is essentially the same as that used in the pioneering article by Laval et al. (Reference Laval, Pellat and Soule1974). In that article, vertical stability was analysed based on the ideal-MHD energy principle. In our analysis, we carry out the complete normal mode analysis, which provides a solution for the mode structure and for the relevant dispersion relation, given by (4.12).
. Our derivation is based on the reduced ideal-MHD model and on a simple, ‘straight-tokamak’ equilibrium, that assumes an elliptical plasma boundary and a uniform current density profile. This assumption is motivated by two considerations. Firstly, it is known that the stability and growth rate of vertical displacements depends on plasma shaping and on the total plasma current, but not on details of the current density profiles. Secondly, the assumed equilibrium is essentially the same as that used in the pioneering article by Laval et al. (Reference Laval, Pellat and Soule1974). In that article, vertical stability was analysed based on the ideal-MHD energy principle. In our analysis, we carry out the complete normal mode analysis, which provides a solution for the mode structure and for the relevant dispersion relation, given by (4.12).
The method of quadratic forms, adopted in this article, together with the normal-mode solution for the mode structure, are shown to be an expedient way to obtain the relevant dispersion relation. The latter contains a parameter, $D_w(\gamma )$![]() , which is a function of the complex mode eigenvalue, $\gamma = -{\rm i}\omega$
, which is a function of the complex mode eigenvalue, $\gamma = -{\rm i}\omega$![]() , for the case of plasma confined by a resistive wall, see (4.29); $D_w$
, for the case of plasma confined by a resistive wall, see (4.29); $D_w$![]() reduces to a constant $D$
reduces to a constant $D$![]() parameter in the limit of an ideal wall, see (4.20). Furthermore, when the wall is moved to infinity (the no-wall case), $D\to 0$
parameter in the limit of an ideal wall, see (4.20). Furthermore, when the wall is moved to infinity (the no-wall case), $D\to 0$![]() . Consequently, the relevant dispersion relation is quadratic in $\gamma$
. Consequently, the relevant dispersion relation is quadratic in $\gamma$![]() for the case of an ideal wall (including the no-wall limit), while it is cubic in $\gamma$
for the case of an ideal wall (including the no-wall limit), while it is cubic in $\gamma$![]() for the case of a resistive wall. Thus, an additional root (compared with the ideal wall limit) is found for the resistive-wall case. This root corresponds to a zero frequency, purely growing mode, with a growth time of the order of the resistive-wall time. Active feedback control systems applied to tokamak experiments concentrate on the suppression of this purely growing mode (Albanese et al. Reference Albanese, Mattei and Villone2004).
for the case of a resistive wall. Thus, an additional root (compared with the ideal wall limit) is found for the resistive-wall case. This root corresponds to a zero frequency, purely growing mode, with a growth time of the order of the resistive-wall time. Active feedback control systems applied to tokamak experiments concentrate on the suppression of this purely growing mode (Albanese et al. Reference Albanese, Mattei and Villone2004).
The other two roots, that we have dubbed VDOM, are purely oscillatory for the case of an ideal wall, provided the parameter $D$![]() is larger than unity, which sets a condition on the distance of the ideal wall from the plasma. These oscillatory modes are actually weakly damped by wall resistivity, see (4.32). Therefore, if their oscillation frequency is sufficiently well separated from the bandwidth of the vertical stabilization closed loop, these modes do not have a significant impact on the active feedback control systems. Nevertheless, we would like to bring the attention of the tokamak physics community on the importance of these oscillatory solutions. As we have shown in this article (see also Porcelli et al. Reference Porcelli, Yolbarsop, Barberis and Fitzpatrick2021; Barberis et al. Reference Barberis, Porcelli and Yolbarsop2022), their oscillation frequency is slightly below the poloidal Alfvén frequency, which makes these modes immune to Alfvén continuum damping. Thus, these modes are only weakly damped by wall resistivity. On the other hand, they can interact resonantly with fast ion populations, which are present in a tokamak plasma due to auxiliary heating and/or as fusion reaction products. Under special circumstances, discussed in some detail in Barberis et al. (Reference Barberis, Porcelli and Yolbarsop2022), this resonant interaction may drive the VDOM unstable.
is larger than unity, which sets a condition on the distance of the ideal wall from the plasma. These oscillatory modes are actually weakly damped by wall resistivity, see (4.32). Therefore, if their oscillation frequency is sufficiently well separated from the bandwidth of the vertical stabilization closed loop, these modes do not have a significant impact on the active feedback control systems. Nevertheless, we would like to bring the attention of the tokamak physics community on the importance of these oscillatory solutions. As we have shown in this article (see also Porcelli et al. Reference Porcelli, Yolbarsop, Barberis and Fitzpatrick2021; Barberis et al. Reference Barberis, Porcelli and Yolbarsop2022), their oscillation frequency is slightly below the poloidal Alfvén frequency, which makes these modes immune to Alfvén continuum damping. Thus, these modes are only weakly damped by wall resistivity. On the other hand, they can interact resonantly with fast ion populations, which are present in a tokamak plasma due to auxiliary heating and/or as fusion reaction products. Under special circumstances, discussed in some detail in Barberis et al. (Reference Barberis, Porcelli and Yolbarsop2022), this resonant interaction may drive the VDOM unstable.
Indeed, the theory presented in this article is motivated in part by the observation of saturated $n=0$![]() fluctuations, with a frequency of the order of the poloidal Alfvén frequency, in recent JET experiments where fast ions are produced by auxiliary heating (Oliver et al. Reference Oliver, Sharapov, Breizman and Zheng2017; Kiptily et al. Reference Kiptily, Fitzgerald, Kazakov, Ongena, Nocente, Sharapov, Dreval, Štancar, Craciunescu and Garcia2021). In those articles, the observations were tentatively interpreted in terms of a saturated $n=0$
fluctuations, with a frequency of the order of the poloidal Alfvén frequency, in recent JET experiments where fast ions are produced by auxiliary heating (Oliver et al. Reference Oliver, Sharapov, Breizman and Zheng2017; Kiptily et al. Reference Kiptily, Fitzgerald, Kazakov, Ongena, Nocente, Sharapov, Dreval, Štancar, Craciunescu and Garcia2021). In those articles, the observations were tentatively interpreted in terms of a saturated $n=0$![]() global Alfvén eigenmode (GAE) (Villard & Vaclavik Reference Villard and Vaclavik1997). It is early for us to conclude whether, in fact, the mode observed at JET is a VDOM driven unstable by the fast ion resonance, rather than a GAE: more experiments are required, but also, the theory presented here ought to be developed further. Nevertheless, we can indicate the main points of distinction between GAE and VDOM that may facilitate the experimental identification. These are basically three. First, the GAE mode frequency for $n=0$
global Alfvén eigenmode (GAE) (Villard & Vaclavik Reference Villard and Vaclavik1997). It is early for us to conclude whether, in fact, the mode observed at JET is a VDOM driven unstable by the fast ion resonance, rather than a GAE: more experiments are required, but also, the theory presented here ought to be developed further. Nevertheless, we can indicate the main points of distinction between GAE and VDOM that may facilitate the experimental identification. These are basically three. First, the GAE mode frequency for $n=0$![]() is given by (Villard & Vaclavik Reference Villard and Vaclavik1997) $\omega _{{\rm GAE}} = v_A/qR = \tau _A^{-1}$
is given by (Villard & Vaclavik Reference Villard and Vaclavik1997) $\omega _{{\rm GAE}} = v_A/qR = \tau _A^{-1}$![]() , where $\tau _A$
, where $\tau _A$![]() is the poloidal Alfvén time as defined below (2.3) of this article. On the other hand, the VDOM mode frequency is given by (4.32), and, taking the parameter $D$
is the poloidal Alfvén time as defined below (2.3) of this article. On the other hand, the VDOM mode frequency is given by (4.32), and, taking the parameter $D$![]() above unity, but anyway of order unity, it falls below the GAE mode frequency, since the ellipticity parameter $e_0$
above unity, but anyway of order unity, it falls below the GAE mode frequency, since the ellipticity parameter $e_0$![]() is typically small. Secondly, the VDOM frequency scales as the square root of $e_0$
is typically small. Secondly, the VDOM frequency scales as the square root of $e_0$![]() , while the $n=0$
, while the $n=0$![]() GAE mode frequency is independent of elongation. Indeed, the GAE would survive in the circular limit, while the VDOM would not. Thirdly, and perhaps most importantly, the VDOM mode structure is different from that of the GAE. The VDOM is a vertical mode, corresponding to a vertical oscillation of the plasma cross-section, with the relevant perturbed flux an odd function of the poloidal angle. This signature would be easily detected by magnetic perturbation coils placed on top and bottom of the plasma column. The GAE mode structure favours instead a ballooning type of parity, with the perturbed flux being an even function of the poloidal angle.
GAE mode frequency is independent of elongation. Indeed, the GAE would survive in the circular limit, while the VDOM would not. Thirdly, and perhaps most importantly, the VDOM mode structure is different from that of the GAE. The VDOM is a vertical mode, corresponding to a vertical oscillation of the plasma cross-section, with the relevant perturbed flux an odd function of the poloidal angle. This signature would be easily detected by magnetic perturbation coils placed on top and bottom of the plasma column. The GAE mode structure favours instead a ballooning type of parity, with the perturbed flux being an even function of the poloidal angle.
A numerical estimate of the VDOM frequency for realistic JET parameters can be provided as follows. Let us consider the JET discharges discussed in Oliver et al. (Reference Oliver, Sharapov, Breizman and Zheng2017), where saturated $n=0$![]() oscillations driven unstable by fast ions were observed. For these discharges, the main plasma species was deuterium, ion density $n_i\approx 4.0\times 10^{19}\ {\rm m}^{-3}$
oscillations driven unstable by fast ions were observed. For these discharges, the main plasma species was deuterium, ion density $n_i\approx 4.0\times 10^{19}\ {\rm m}^{-3}$![]() and $B_P^{\prime }\approx 1.0\ {\rm T}\ {\rm m}^{-1}$
and $B_P^{\prime }\approx 1.0\ {\rm T}\ {\rm m}^{-1}$![]() , yielding a poloidal Alfvén time $\tau _A\approx 0.4\ \mathrm {\mu } {\rm s}$
, yielding a poloidal Alfvén time $\tau _A\approx 0.4\ \mathrm {\mu } {\rm s}$![]() . The elongation parameter was $\kappa = b/a \approx 1.3$
. The elongation parameter was $\kappa = b/a \approx 1.3$![]() , corresponding to ellipticity $e_0\approx 0.26$
, corresponding to ellipticity $e_0\approx 0.26$![]() and to the no-wall growth rate $\gamma _\infty \approx 1.2\times 10^{6}\ {\rm s}^{-1}$
and to the no-wall growth rate $\gamma _\infty \approx 1.2\times 10^{6}\ {\rm s}^{-1}$![]() . In order to estimate the parameter $D$
. In order to estimate the parameter $D$![]() appearing in (4.21), let us take $a_w/a = 1.2$
appearing in (4.21), let us take $a_w/a = 1.2$![]() and $b_w/b = 1.1$
and $b_w/b = 1.1$![]() (since, for confocal ellipses, $b_w^{2}- a_w^{2} = b^{2} - a^{2}$
(since, for confocal ellipses, $b_w^{2}- a_w^{2} = b^{2} - a^{2}$![]() ). Then, $D\approx 5.2$
). Then, $D\approx 5.2$![]() , $\hat {e}_0D\approx 0.77$
, $\hat {e}_0D\approx 0.77$![]() and $\omega _0 \approx 4 \gamma _\infty \approx 5\times 10^{6}\ {\rm s}^{-1}$
and $\omega _0 \approx 4 \gamma _\infty \approx 5\times 10^{6}\ {\rm s}^{-1}$![]() , or $\omega _0 \approx 800\ {\rm kHz}$
, or $\omega _0 \approx 800\ {\rm kHz}$![]() , which is within a factor of two of the observed frequency of saturated $n=0$
, which is within a factor of two of the observed frequency of saturated $n=0$![]() modes in the mentioned JET experiment. However, JET plasmas are bounded by the divertor separatrix and a more appropriate estimate of the theoretical mode frequency should take into account X-point effects, as argued in Yolbarsop et al. (Reference Yolbarsop, Porcelli and Fitzpatrick2021). Clearly, an accurate determination of the theoretical VDOM frequency also requires more realistic equilibrium profiles and numerical work.
modes in the mentioned JET experiment. However, JET plasmas are bounded by the divertor separatrix and a more appropriate estimate of the theoretical mode frequency should take into account X-point effects, as argued in Yolbarsop et al. (Reference Yolbarsop, Porcelli and Fitzpatrick2021). Clearly, an accurate determination of the theoretical VDOM frequency also requires more realistic equilibrium profiles and numerical work.
It is reassuring to see that the dispersion relation derived in this article, (4.12), agrees fairly well with the heuristic result of § 2, see (2.9), in the limit where the $\hat {e}_0D$![]() appearing in the expression for $\omega _0$
appearing in the expression for $\omega _0$![]() is small.
is small.
Finally, the case where a magnetic divertor separatrix limits the plasma was not discussed in this article, but was treated in some detail in Yolbarsop et al. (Reference Yolbarsop, Porcelli and Fitzpatrick2021, Reference Yolbarsop, Porcelli, Liu and Fitzpatrick2022). The main result of that work is that, even for the no-wall case, axisymmetric current sheets localized in the vicinity of the magnetic X-point(s) on the divertor separatrix, induced by vertical displacement perturbations, lead to passive feedback stabilization. The reason is that X-points are resonant points for ideal-MHD perturbations with toroidal mode number $n=0$![]() . As a result, flux pile-up will occur in the presence of ideal-MHD flows having the appropriate symmetry around the resonant points, and this is indeed the symmetry of interest for vertical displacements. Flux pile-up is the reason for the occurrence of current sheets, which have the appropriate sign and magnitude to ‘push back’ the plasma drifting vertically towards a magnetic X-point. In this sense, these X-point currents have the same effect on the plasma as that of currents induced by vertical displacements on an ideal (or nearly ideal) wall. It remains to be seen what will happen to the zero-frequency unstable root resonating on magnetic X-points when the effect of finite plasma resistivity is taken into account.
. As a result, flux pile-up will occur in the presence of ideal-MHD flows having the appropriate symmetry around the resonant points, and this is indeed the symmetry of interest for vertical displacements. Flux pile-up is the reason for the occurrence of current sheets, which have the appropriate sign and magnitude to ‘push back’ the plasma drifting vertically towards a magnetic X-point. In this sense, these X-point currents have the same effect on the plasma as that of currents induced by vertical displacements on an ideal (or nearly ideal) wall. It remains to be seen what will happen to the zero-frequency unstable root resonating on magnetic X-points when the effect of finite plasma resistivity is taken into account.
Acknowledgements
The authors acknowledge useful discussions with F. Villone (University of Naples ‘Federico II’) on methods used for active feedback control of the vertical instability. The authors would also like to thank the authors of Oliver et al. (Reference Oliver, Sharapov, Breizman and Zheng2017), J. Oliver, B. Breizman and S. Sharapov, for useful discussions on numerical simulations and the interpretation of saturated $n=0$![]() oscillations observed at JET.
oscillations observed at JET.
Editor Peter Catto thanks the referees for their advice in evaluating this article.
Funding
This work was partially supported by the National Natural Science Foundation of China under Grant No. 11775220 and the National Magnetic Confinement Fusion Energy Development Program of China under Grant No. 2017YFE0301702. This work has been carried out within the framework of the EUROfusion Consortium and has received funding from the Euratom Research and Training Programme (Grant Agreement No 101052200 EUROfusion). Views and opinions expressed are, however, those of the authors only and do not necessarily reflect those of the European Union or the European Commission. Neither the European Union nor the European Commission can be held responsible for them.
Declaration of interests
The authors report no conflict of interest.