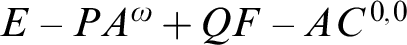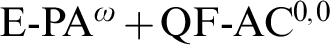Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Fujiwara, Makoto
2020.
Beyond the Horizon of Computability.
Vol. 12098,
Issue. ,
p.
38.
Dzhafarov, Damir D.
Hirschfeldt, Denis R.
and
Reitzes, Sarah
2022.
Reduction games, provability and compactness.
Journal of Mathematical Logic,
Vol. 22,
Issue. 03,
Pradic, Cécilia
and
Price, Ian
2025.
Crossroads of Computability and Logic: Insights, Inspirations, and Innovations.
Vol. 15764,
Issue. ,
p.
395.