Article contents
Forcing isomorphism
Published online by Cambridge University Press: 12 March 2014
Extract
If two models of a first-order theory are isomorphic, then they remain isomorphic in any forcing extension of the universe of sets. In general however, such a forcing extension may create new isomorphisms. For example, any forcing that collapses cardinals may easily make formerly nonisomorphic models isomorphic. However, if we place restrictions on the partially-ordered set to ensure that the forcing extension preserves certain invariants, then the ability to force nonisomorphic models of some theory T to be isomorphic implies that the invariants are not sufficient to characterize the models of T.
A countable first-order theory is said to be classifiable if it is superstable and does not have either the dimensional order property (DOP) or the omitting types order property (OTOP). If T is not classifiable, Shelah has shown in [5] that sentences in L∞,λ do not characterize models of T of power λ. By contrast, in [8] Shelah showed that if a theory T is classifiable, then each model of cardinality λ is described by a sentence of L∞,λ. In fact, this sentence can be chosen in the 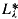 . (
. (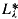 is the result of enriching the language
is the result of enriching the language 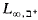 by adding for each μ < λ a quantifier saying the dimension of a dependence structure is greater than μ) Further work ([3], [2]) shows that ⊐+ can be replaced by ℵ1.
by adding for each μ < λ a quantifier saying the dimension of a dependence structure is greater than μ) Further work ([3], [2]) shows that ⊐+ can be replaced by ℵ1.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1993
References
REFERENCES
- 2
- Cited by

