We will consider some partition properties of the following type: given a function F: ωω →2, is there a sequence H0, H1, … of subsets of ω such that F is constant on ΠiεωHi? The answer is obviously positive if we allow all the Hi's to have exactly one element, but the problem is nontrivial if we require the Hi's to have at least two elements. The axiom of choice contradicts the statement “for all F: ωω→ 2 there is a sequence H0, H1, H2,… of subsets of ω such that {i|(Hi) ≥ 2} is infinite and F is constant on ΠHi”, but the infinite exponent partition relation ω(ω)ω implies it; so, this statement is relatively consistent with an inaccessible cardinal. (See [1] where these partition properties were considered.)
We will also consider partitions into any finite number of pieces, and we will prove some facts about partitions into ω-many pieces.
Given a partition F: ωω → k, we say that H0, H1…, a sequence of subsets of ω, is homogeneous for F if F is constant on ΠHi. We say the sequence H0, H1,… is nonoverlapping if, for all i ∈ ω, ∪Hi > ∩Hi+1.
The sequence 〈Hi: i ∈ ω〉 is of type 〈α0, α1,…〉 if, for every i ∈ ω, ∣Hi∣ = αi.
We will adopt the usual notation for polarized partition relations due to Erdös, Hajnal, and Rado.
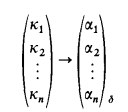
means that for every partition F: κ1 × κ2 × … × κn→δ there is a sequence H0, H1,…, Hn such that Hi ⊂ κi and ∣Hi∣ = αi for every i, 1 ≤ i ≤ n, and F is constant on H1 × H2 × … × Hn.