Article contents
Working below a high recursively enumerable degree
Published online by Cambridge University Press: 12 March 2014
Extract
In recent work, Cooper [3, 1990] has extended results of Jockusch and Shore [6, 1984] to show that the Turing jump is definable in the structure given by the Turing degrees and the ordering of Turing reducibility. In his definition of x′ from x, Cooper identifies an order-theoretic property shared by all of the degrees that are recursively enumerable in x and above x. He then shows that x′ is the least upper bound of all the degrees with this property. Thus, the jump of x is identified by comparing the recursively enumerable degrees with other degrees which are not recursively enumerable. Of course, once the jump operator is known to be definable, the relation of jump equivalence x′ = y′ is also known to be a definable relation on x and y. If we consider how much of the global theory of the Turing degrees is sufficient for Cooper's methods, it is immediately clear that his methods can be implemented to show that the jump operator and its weakening to the relation of jump equivalence are definable in any ideal closed under the Turing jump. However, his methods do not localize to 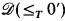 , the
, the 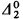 degrees, or to
degrees, or to 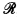 the recursively enumerable degrees.
the recursively enumerable degrees.
This paper fits, as do Shore and Slaman [16, 1990] and [17, to appear], within the general project to develop an understanding of the relationship between the local degree-theoretic properties of a recursively enumerable set A and its jump class. For an analysis of the possibility of defining jump equivalence in 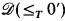 , consult Shore [15, to appear] who shows that the relation x(3) = y(3) is definable. In this paper, we will restrict our attention to definitions expressed completely in ℛ (Note: All sets and degrees discussed for the remainder of this paper will be recursively enumerable.) Ultimately, one would like to find some degree-theoretic properties definable in terms of the ordering of Turing reducibility and quantifiers over the recursively enumerable degrees that would define the relation of jump equivalence or define one or more of the jump classes Hn = {w∣ wn = 0n+1} or Ln = {w ∣ wn = 0n}. Such a result could very likely then be used as a springboard to other general definability results for the recursively enumerable degrees. It would be especially interesting to know whether every recursively enumerable degree is definable and whether every arithmetical degree-invariant property of the recursively enumerable sets is definable in
, consult Shore [15, to appear] who shows that the relation x(3) = y(3) is definable. In this paper, we will restrict our attention to definitions expressed completely in ℛ (Note: All sets and degrees discussed for the remainder of this paper will be recursively enumerable.) Ultimately, one would like to find some degree-theoretic properties definable in terms of the ordering of Turing reducibility and quantifiers over the recursively enumerable degrees that would define the relation of jump equivalence or define one or more of the jump classes Hn = {w∣ wn = 0n+1} or Ln = {w ∣ wn = 0n}. Such a result could very likely then be used as a springboard to other general definability results for the recursively enumerable degrees. It would be especially interesting to know whether every recursively enumerable degree is definable and whether every arithmetical degree-invariant property of the recursively enumerable sets is definable in 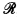 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1993
References
REFERENCES
- 17
- Cited by

