Article contents
Gentzenizations of relevant logics without distribution. I
Published online by Cambridge University Press: 12 March 2014
Extract
The history of the Gentzenization of relevant logics goes back to Kripke [17], who in 1959 Gentzenized R→ and went on to prove its decidability. Formulae were separated by commas on the left side of the turnstile, the commas just representing nested implications. Kripke employed just a singleton formula to the right of the turnstile. He also considered adding negation, as well as other connectives, but it was not until 1961 that Belnap and Wallace, in [5], Gentzenized 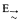 and proved its decidability, though their Gentzenization employed commas on both sides of the turnstile. Subsequently, in 1966, the logic R without distribution, now called LR (for lattice R), was Gentzenized in a similar style by Meyer in [20]. He also went on to show decidability for LR by extending Kripke's argument. Later, in 1969, Dunn Gentzenized R+ (published in [1], pp. 381–391) using two structural connectives (commas and semicolons) to the left of the turnstile, and with a single formula to the right. Here, the commas represent conjunction and the semicolons represent an intensional conjunction, called “fusion”. This is all nicely set out in McRobbie [19], where he also introduces left-handed Gentzenizations and analytic tableaux for a number of fragments of relevant logics. In 1979, further work on distributionless logic was done by Grishin, in a series of papers, including [16], in which he produced a Gentzenization of quantified RW without distribution (which we will call LRWQ), and used it to prove the decidability of this quantified logic.
and proved its decidability, though their Gentzenization employed commas on both sides of the turnstile. Subsequently, in 1966, the logic R without distribution, now called LR (for lattice R), was Gentzenized in a similar style by Meyer in [20]. He also went on to show decidability for LR by extending Kripke's argument. Later, in 1969, Dunn Gentzenized R+ (published in [1], pp. 381–391) using two structural connectives (commas and semicolons) to the left of the turnstile, and with a single formula to the right. Here, the commas represent conjunction and the semicolons represent an intensional conjunction, called “fusion”. This is all nicely set out in McRobbie [19], where he also introduces left-handed Gentzenizations and analytic tableaux for a number of fragments of relevant logics. In 1979, further work on distributionless logic was done by Grishin, in a series of papers, including [16], in which he produced a Gentzenization of quantified RW without distribution (which we will call LRWQ), and used it to prove the decidability of this quantified logic.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1996
References
REFERENCES
- 7
- Cited by

