This paper is a continuation of Zakharyaschev [25], where the following basic results on modal logics with transitive frames were obtained:
• With every finite rooted transitive frame 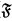 and every set
and every set 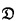 of antichains (which were called closed domains) in
of antichains (which were called closed domains) in 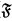 two formulas α (
two formulas α (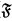 ,
, 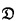 , ⊥) and α(
, ⊥) and α(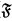 ,
, 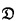 ) were associated. We called them the canonical and negation free canonical formulas, respectively, and proved the Refutability Criterion characterizing the constitution of their refutation general frames in terms of subreduction (alias partial p-morphism), the cofinality condition and the closed domain condition.
) were associated. We called them the canonical and negation free canonical formulas, respectively, and proved the Refutability Criterion characterizing the constitution of their refutation general frames in terms of subreduction (alias partial p-morphism), the cofinality condition and the closed domain condition.
• We proved also the Completeness Theorem for the canonical formulas providing us with an algorithm which, given a modal formula φ, returns canonical formulas α(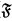 i,
i, 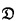 i), ⊥), for i = 1,…, n, such that
i), ⊥), for i = 1,…, n, such that
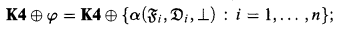
if φ is negation free then the algorithm instead of α(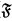 i,
i, 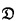 i, ⊥) can use the negation free canonical formulas α(
i, ⊥) can use the negation free canonical formulas α(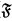 i,
i, 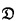 i). Thus, every normal modal logic containing K4 can be axiomatized by a set of canonical formulas.
i). Thus, every normal modal logic containing K4 can be axiomatized by a set of canonical formulas.
In this Part we apply the apparatus of the canonical formulas for establishing a number of results on the decidability, finite model property, elementarity and some other properties of modal logics within the field of K4.
Our attention will be focused on the class of logics which can be axiomatized by canonical formulas without closed domains, i.e., on the logics of the form
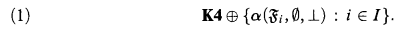
Adapting the terminology of Fine [11], we call them the cofinal subframe logics and denote this class by 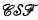 . As was shown in Part I, almost all standard modal logics are in
. As was shown in Part I, almost all standard modal logics are in 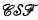 .
.