Article contents
INFORMATION IN PROPOSITIONAL PROOFS AND ALGORITHMIC PROOF SEARCH
Published online by Cambridge University Press: 27 September 2021
Abstract
We study from the proof complexity perspective the (informal) proof search problem (cf. [17, Sections 1.5 and 21.5]):
• Is there an optimal way to search for propositional proofs?
We note that, as a consequence of Levin’s universal search, for any fixed proof system there exists a time-optimal proof search algorithm. Using classical proof complexity results about reflection principles we prove that a time-optimal proof search algorithm exists without restricting proof systems iff a p-optimal proof system exists.
To characterize precisely the time proof search algorithms need for individual formulas we introduce a new proof complexity measure based on algorithmic information concepts. In particular, to a proof system P we attach information-efficiency function 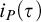 $i_P(\tau )$ assigning to a tautology a natural number, and we show that:
$i_P(\tau )$ assigning to a tautology a natural number, and we show that:
•
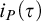 $i_P(\tau )$ characterizes time any P-proof search algorithm has to use on
$i_P(\tau )$ characterizes time any P-proof search algorithm has to use on 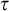 $\tau $,
$\tau $,• for a fixed P there is such an information-optimal algorithm (informally: it finds proofs of minimal information content),
• a proof system is information-efficiency optimal (its information-efficiency function is minimal up to a multiplicative constant) iff it is p-optimal,
• for non-automatizable systems P there are formulas
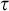 $\tau $ with short proofs but having large information measure
$\tau $ with short proofs but having large information measure 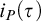 $i_P(\tau )$.
$i_P(\tau )$.
We isolate and motivate the problem to establish unconditional super-logarithmic lower bounds for 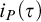 $i_P(\tau )$ where no super-polynomial size lower bounds are known. We also point out connections of the new measure with some topics in proof complexity other than proof search.
$i_P(\tau )$ where no super-polynomial size lower bounds are known. We also point out connections of the new measure with some topics in proof complexity other than proof search.
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic
References
- 2
- Cited by


