Hostname: page-component-8448b6f56d-sxzjt Total loading time: 0 Render date: 2024-04-24T21:19:18.979Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON DERIVABILITY CONDITIONS

Part of: Proof theory and constructive mathematics

Published online by Cambridge University Press:  07 September 2020

TAISHI KURAHASHI
TAISHI KURAHASHI*
Affiliation:
GRADUATE SCHOOL OF SYSTEM INFORMATICS KOBE UNIVERSITY 1-1 ROKKODAI, NADA KOBE 657-8501, JAPANE-mail: kurahashi@people.kobe-u.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate relationships between versions of derivability conditions for provability predicates. We show several implications and non-implications between the conditions, and we discuss unprovability of consistency statements induced by derivability conditions. First, we classify already known versions of the second incompleteness theorem, and exhibit some new sets of conditions which are sufficient for unprovability of Hilbert–Bernays’ consistency statement. Secondly, we improve Buchholz’s schematic proof of provable 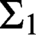$\Sigma_1$ -completeness. Then among other things, we show that Hilbert–Bernays’ conditions and Löb’s conditions are mutually incomparable. We also show that neither Hilbert–Bernays’ conditions nor Löb’s conditions accomplish Gödel’s original statement of the second incompleteness theorem.

Keywords

the second incompleteness theoremderivability conditionsprovability predicates

MSC classification

Primary: 03F30: First-order arithmetic and fragments
Secondary: 03F40: Gödel numberings and issues of incompleteness
Type
Articles
Information
The Journal of Symbolic Logic , Volume 85 , Issue 3 , September 2020 , pp. 1224 - 1253
Check for updates
Copyright
© The Association for Symbolic Logic 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Arai, T., Derivability conditions on Rosser’s provability predicates . Notre Dame Journal of Formal Logic , vol. 31 (1990), no. 4, pp. 487–497.CrossRefGoogle Scholar
Artemov, S. N. and Beklemishev, L. D., Provability logic, Handbook of Philosophical Logic , vol. 13, second ed., Springer, Dordrecht, 2005, pp. 189–360.Google Scholar
Beklemishev, L. D., Independent enumerations of theories and recursive progressions. Sibirskii Matematichskii Zhurnal , vol. 33 (1992), no. 5, pp. 22–46, English translation is in Siberian Mathematical Journal, 33(5), 760–783, 1992.Google Scholar
Bernardi, C. and Montagna, F., Equivalence relations induced by extensional formulae: classification by means of a new fixed point property. Fundamenta Mathematicae , vol. 124 (1984), no. 3, pp. 221–233.CrossRefGoogle Scholar
Boolos, G., The Logic of Provability , Cambridge University Press, Cambridge, 1993.Google Scholar
Buchholz, W., Mathematische Logik II, 1993. Available at http://www.mathematik.uni-muenchen.de/~buchholz/articles/LogikII.ps.Google Scholar
Feferman, S., Arithmetization of metamathematics in a general setting . Fundamenta Mathematicae , vol. 49 (1960), pp. 35–92.CrossRefGoogle Scholar
Gödel, K., Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I . (in German), Monatshefte für Mathematik und Physik , vol. 38 (1931), no. 1, pp. 173–198, English translation in Kurt Gödel, Collected Works, Vol. 1 (pp. 145–195).CrossRefGoogle Scholar
Hájek, P. and Pudlák, P., Metamathematics of First-Order Arithmetic , Perspectives in Mathematical Logic, Springer-Verlag, Berlin, Germany, 1993.Google Scholar
Hilbert, D. and Bernays, P., Grundlagen der Mathematik , vol. II, Springer, Berlin, 1939.Google Scholar
Hughes, G. E. and Cresswell, M. J., A New Introduction to Modal Logic , Routledge, London, 1996.CrossRefGoogle Scholar
Japaridze, G. and de Jongh, D., The logic of provability , Handbook of Proof Theory (Buss, S.R., editor), Studies in Logic and the Foundations of Mathematics, vol. 137, North-Holland, Amsterdam, 1998, pp. 475–546.CrossRefGoogle Scholar
Jeroslow, R. G., Redundancies in the Hilbert-Bernays derivability conditions for Gödel’s second incompleteness theorem , this Journal, vol. 38 (1973), no. 3, pp. 359–367.Google Scholar
Kaye, R., Models of Peano Arithmetic , Oxford Logic Guides, vol. 15, Oxford Science Publications, New York, 1991.Google Scholar
Kreisel, G. and Takeuti, G., Formally self-referential propositions for cut free classical analysis and related systems . Dissertationes Mathematicae (Rozprawy Matematyczne) , vol. 118 (1974).Google Scholar
Kurahashi, T., Rosser provability and the second incompleteness theorem, Symposium on Advances in Mathematical Logic 2018 Proceedings , accepted.Google Scholar
Lindström, P., Aspects of Incompleteness , 2nd ed., Lecture Notes in Logic, vol. 10, Association for Symbolic Logic, Urbana, IL, 2003.Google Scholar
Löb, M. H., Solution of a problem of Leon Henkin , this Journal, vol. 20 (1955), no. 2, pp. 115–118.Google Scholar
Montagna, F., On the formulas of Peano arithmetic which are provably closed under modus ponens . Bollettino dell’Unione Matematica Italiana , vol. 16 (1979), no. B5, pp. 196–211.Google Scholar
Mostowski, A., Thirty Years of Foundational Studies: Lectures on the Development of Mathematical Logic and the Study of the Foundations of Mathematics in 1930–1964 , Acta philosophica Fennica, no. 17, Barnes & Noble, Inc., New York, 1965.Google Scholar
Rautenberg, W., A Concise Introduction to Mathematical Logic , third ed., Universitext, Springer, New York, 2010.CrossRefGoogle Scholar
Smoryński, C., Self-Reference and Modal Logic , Universitext, Springer-Verlag, New York, 1985.CrossRefGoogle Scholar
Tarski, A., Mostowski, A., and Robinson, R. M., Undecidable Theories , Studies in Logic and the Foundations of Mathematics, vol. 13, North-Holland Publishing, Amsterdam, 1953.Google Scholar
Visser, A., Transductions in arithmetic . Annals of Pure and Applied Logic , vol. 167 (2016), no. 3, pp. 211–234.CrossRefGoogle Scholar
Visser, A., The absorption law, or how to Kreisel a Hilbert-Bernays-Löb, 2018, arXiv: 1804.07465.Google Scholar
von Bülow, C., A remark on equivalent Rosser sentences . Annals of Pure and Applied Logic , vol. 151 (2008), no. 1, pp. 62–67.CrossRefGoogle Scholar