Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-17T11:40:41.290Z Has data issue: false hasContentIssue false
  • English
  • Français

On the number of automorphisms of uncountable models

Published online by Cambridge University Press:  12 March 2014

Saharon Shelah ,
Heikki Tuuri  and
Jouko Väänänen
Saharon Shelah
Affiliation:
Department of Mathematics, Hebrew University of Jerusalem, Jerusalem, Israel
Heikki Tuuri
Affiliation:
Department of Mathematics, University of Helsinki, 00100 Helsinki, Finland
Jouko Väänänen
Affiliation:
Department of Mathematics, University of Helsinki, 00100 Helsinki, Finland
Get access Rights & Permissions [Opens in a new window]

Abstract

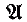Let σ() denote the number of automorphisms of a model 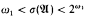of power ω1. We derive a necessary and sufficient condition in terms of trees for the existence of an with . We study the sufficiency of some conditions for 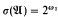. These conditions are analogous to conditions studied by D. Kueker in connection with countable models.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 58 , Issue 4 , December 1993 , pp. 1402 - 1418
Copyright
Copyright © Association for Symbolic Logic 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Galvin, F., Jech, T. and Magidor, M., An ideal game, this Journal, vol. 43 (1978), pp. 284–292.Google Scholar
[2]Hodges, W. and Shelah, S., Infinite games and reduced products, Annals of Mathematical Logic, vol. 20 (1981), pp. 77–108.CrossRefGoogle Scholar
[3]Hyttinen, T., Games and infinitary languages, Annales Academiae Scientarum Fennicae, Series A I, Mathematica Dissertationes, vol. 64, Academiae Scientarum Fennica, Helsinki, 1987.Google Scholar
[4]Hyttinen, T., Model theory for infinite quantifier languages, Fundamenta Mathematicae, vol. 134 (1990), pp. 125–142.CrossRefGoogle Scholar
[5]Jech, T., Automorphisms of ω 1-trees, Transactions of the American Mathematical Society, vol. 173 (1972), pp. 57–70.Google Scholar
[6]Jech, T., Set theory, Academic Press, New York, 1978.Google Scholar
[7]Karttunen, M., Model theory for infinitely deep languages, Annales Academiae Scientarum Fennicae, Series A I, Mathematica Dissertationes, vol. 50, Academiae Scientarum Fennica, Helsinki, 1984.Google Scholar
[8]Kueker, D., Definability, automorphisms and infinitary languages, The syntax and semantics of infinitary languages (Barwise, J., editor), Springer-Verlag, New York, 1968.Google Scholar
[9]Nadel, M. and Stavi, J., L∞λ-equivalence, isomorphism and potential isomorphism, Transactions of the American Mathematical Society, vol. 236 (1978), pp. 51–74.Google Scholar
[10]Oikkonen, J., How to obtain interpolation for , Logic colloquium '86 (Drake, and Truss, , editors), North-Holland, Amsterdam, 1988.Google Scholar
[11]Väänänen, J., Games and trees in infinitary logic: A survey, Quantifiers (Krynicki, M., Mostowski, M., and Szczerba, L., editors) (to appear).Google Scholar