Article contents
Pointwise compact and stable sets of measurable functions
Published online by Cambridge University Press: 12 March 2014
Extract
In a series of papers culminating in [9], M. Talagrand, the second author, and others investigated at length the properties and structure of pointwise compact sets of measurable functions. A number of problems, interesting in themselves and important for the theory of Pettis integration, were solved subject to various special axioms. It was left unclear just how far the special axioms were necessary. In particular, several results depended on the fact that it is consistent to suppose that every countable relatively pointwise compact set of Lebesgue measurable functions is ‘stable’ in Talagrand's sense, the point being that stable sets are known to have a variety of properties not shared by all pointwise compact sets. In the present paper we present a model of set theory in which there is a countable relatively pointwise compact set of Lebesgue measurable functions which is not stable and discuss the significance of this model in relation to the original questions. A feature of our model which may be of independent interest is the following: in it, there is a closed negligible set Q ⊆ [0, 1]2 such that whenever D ⊆ [0,1] has outer measure 1, then
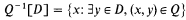
has inner measure 1 (see 2G below).
We embark immediately on the central ideas of this paper, setting out a construction of a partially ordered set which forces a fairly technical proposition in measure theory (IS below); the relevance of this proposition to pointwise compact sets will be discussed in §2.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1993
References
REFERENCES
- 2
- Cited by

