Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Komjáth, Péter
2013.
Another proof of a result of Jech and Shelah.
Czechoslovak Mathematical Journal,
Vol. 63,
Issue. 3,
p.
577.

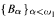 of sets of countable ordinals such that:
of sets of countable ordinals such that: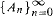 of
of 