Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kanovei, Vladimir
1998.
Ulm Classification of Analytic Equivalence Relations in Generic Universes.
Mathematical Logic Quarterly,
Vol. 44,
Issue. 3,
p.
287.
Kanovei, Vladimir
2000.
Linearization of definable order relations.
Annals of Pure and Applied Logic,
Vol. 102,
Issue. 1-2,
p.
69.
Kanovei, Vladimir
and
Reeken, Michael
2003.
A theorem on ROD‐hypersmooth equivalence relations in the Solovay model.
Mathematical Logic Quarterly,
Vol. 49,
Issue. 3,
p.
299.
Кановей, Владимир Григорьевич
Kanovei, Vladimir Grigor'evich
Реекен, М
and
Reeken, M
2003.
Некоторые новые результаты о борелевской несводимости отношений эквивалентности.
Известия Российской академии наук. Серия математическая,
Vol. 67,
Issue. 1,
p.
59.
2004.
2003 European Summer Meeting of the Association for Symbolic Logic. Logic Colloquim '03.
Bulletin of Symbolic Logic,
Vol. 10,
Issue. 02,
p.
234.
Friedman, Sy-David
and
Kanovei, Vladimir
2008.
Some natural equivalence relations in the Solovay model.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 78,
Issue. 1,
p.
91.
Kanovei, V. G.
and
Lyubetsky, V. A.
2015.
On effective σ-boundedness and σ-compactness in Solovay’s model.
Mathematical Notes,
Vol. 98,
Issue. 1-2,
p.
273.
Kanovei, Vladimir Grigorevich
and
Lyubetskii, Vasilii Aleksandrovich
2015.
Об эффективной $\sigma$-ограниченности и $\sigma$-компактности в модели Соловея.
Математические заметки,
Vol. 98,
Issue. 2,
p.
247.
Golshani, Mohammad
Kanovei, Vladimir
and
Lyubetsky, Vassily
2017.
A Groszek‐Laver pair of undistinguishable ‐classes.
Mathematical Logic Quarterly,
Vol. 63,
Issue. 1-2,
p.
19.
Kanovei, Vladimir
and
Lyubetsky, Vassily
2018.
Countable OD sets of reals belong to the ground model.
Archive for Mathematical Logic,
Vol. 57,
Issue. 3-4,
p.
285.
Kanovei, Vladimir
and
Lyubetsky, Vassily
2020.
Models of Set Theory in which Nonconstructible Reals First Appear at a Given Projective Level.
Mathematics,
Vol. 8,
Issue. 6,
p.
910.
Kanovei, Vladimir
and
Lyubetsky, Vassily
2020.
On the
Δ
n
1
Problem of Harvey Friedman.
Mathematics,
Vol. 8,
Issue. 9,
p.
1477.
Enayat, Ali
Kanovei, Vladimir
and
Lyubetsky, Vassily
2021.
On Effectively Indiscernible Projective Sets and the Leibniz-Mycielski Axiom.
Mathematics,
Vol. 9,
Issue. 14,
p.
1670.
Kanovei, Vladimir Grigorevich
and
Lyubetskii, Vasilii Aleksandrovich
2021.
Модели теории множеств, в которых теорема отделимости неверна.
Известия Российской академии наук. Серия математическая,
Vol. 85,
Issue. 6,
p.
164.
Kanovei, V. G.
and
Lyubetsky, V. A.
2021.
Models of set theory in which the separation theorem fails.
Izvestiya: Mathematics,
Vol. 85,
Issue. 6,
p.
1181.
Andretta, Alessandro
and
Motto Ros, Luca
2022.
Souslin quasi-orders and bi-embeddability of uncountable structures.
Memoirs of the American Mathematical Society,
Vol. 277,
Issue. 1365,
Kanovei, Vladimir
and
Lyubetsky, Vassily
2024.
Jensen Δn1 Reals by Means of ZFC and Second-Order Peano Arithmetic.
Axioms,
Vol. 13,
Issue. 2,
p.
96.
Kanovei, Vladimir
and
Lyubetsky, Vassily
2025.
On the Uniform Projection and Covering Problems in Descriptive Set Theory Under the Axiom of Constructibility.
Mathematics,
Vol. 13,
Issue. 3,
p.
409.


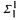 (resp.
(resp.  ) relation then the reduction above can be chosen in the class of all
) relation then the reduction above can be chosen in the class of all 