In the twenties Brouwer established the well-known continuity theorem “every real function is locally uniformly continuous,” [3, 2, 5]. From this theorem one immediately concludes that the continuum is indecomposable (unzerlegbar), i.e., if ℝ = A ∪ B and A ∩ B = ∅ (denoted by ℝ = A + B), then ℝ = A or ℝ = B.
Brouwer deduced the indecomposability directly from the fan theorem (cf. the 1927 Berline Lectures, [7, p. 49]).
The theorem was published for the first time in [6], it was used to refute the principle of the excluded middle: ¬∀x ∈ ℝ (x ∈ ℚ ∨ ¬x ∈ ℚ).
The indecomposability of ℝ is a peculiar feature of constructive universa, it shows that ℝ is much more closely knit in constructive mathematics, than in classically mathematics. The classically comparable fact is the topological connectedness of ℝ. In a way this characterizes the position of ℝ: the only (classically) connected subsets of ℝ are the various kinds of segments. In intuitionistic mathematics the situation is different; the continuum has, as it were, a syrupy nature, one cannot simply take away one point. In the classical continuum one can, thanks to the principle of the excluded third, do so. To put it picturesquely, the classical continuum is the frozen intuitionistic continuum. If one removes one point from the intuitionistic continuum, there still are all those points for which it is unknown whether or not they belong to the remaining part.
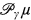 can be precipitous
can be precipitous