Fix an abelian group 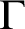$\Gamma $ and an injective endomorphism 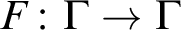$F\colon \Gamma \to \Gamma $. Improving on the results of [2], new characterizations are here obtained for the existence of spanning sets, F-automaticity, and F-sparsity. The model theoretic status of these sets is also investigated, culminating with a combinatorial description of the F-sparse sets that are stable in 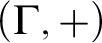$(\Gamma ,+)$, and a proof that the expansion of 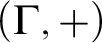$(\Gamma ,+)$ by any F-sparse set is NIP. These methods are also used to show for prime 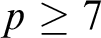$p\ge 7$ that the expansion of 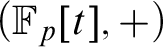$(\mathbb {F}_p[t],+)$ by multiplication restricted to 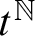$t^{\mathbb {N}}$ is NIP.