Hostname: page-component-65f69f4695-bd75b Total loading time: 0 Render date: 2025-06-30T04:36:47.965Z Has data issue: false hasContentIssue false
  • English
  • Français

EXTENSIONAL REALIZABILITY AND CHOICE FOR DEPENDENT TYPES IN INTUITIONISTIC SET THEORY

Part of: Proof theory and constructive mathematics

Published online by Cambridge University Press:  20 July 2022

EMANUELE FRITTAION Open the ORCID record for EMANUELE FRITTAION [Opens in a new window]
EMANUELE FRITTAION*
Affiliation:
DEPARTMENT OF MATHEMATICS TECHNISCHE UNIVERSITÄT DARMSTADT DARMSTADT, GERMANY
*
E-mail: frittaion@mathematik.tu-darmstadt.de
Get access Rights & Permissions [Opens in a new window]

Abstract

In [17], we introduced an extensional variant of generic realizability [22], where realizers act extensionally on realizers, and showed that this form of realizability provides inner models of 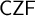$\mathsf {CZF}$ (constructive Zermelo–Fraenkel set theory) and $\mathsf {IZF}$ (intuitionistic Zermelo–Fraenkel set theory), that further validate 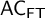$\mathsf {AC}_{\mathsf {FT}}$ (the axiom of choice in all finite types). In this paper, we show that extensional generic realizability validates several choice principles for dependent types, all exceeding 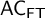$\mathsf {AC}_{\mathsf {FT}}$. We then show that adding such choice principles does not change the arithmetic part of either 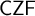$\mathsf {CZF}$ or $\mathsf {IZF}$.

Keywords

intuitionisticconstructiveset theoryrealizabilityextensionalitydependent types

MSC classification

Primary: 03F50: Metamathematics of constructive systems
Secondary: 03F25: Relative consistency and interpretations 03F55: Intuitionistic mathematics

Information

Type
Article
Information
The Journal of Symbolic Logic , Volume 88 , Issue 3 , September 2023 , pp. 1138 - 1169
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Aczel, P., The type theoretic interpretation of constructive set theory , Logic Colloquium ’77 (A. Macintyre, L. Pacholski, and J. Paris, editors), Studies in Logic and the Foundations of Mathematics, vol. 96, North-Holland, Amsterdam, 1978.Google Scholar
Aczel, P., The type theoretic interpretation of constructive set theory: Choice principles , The L. E. J. Brouwer Centenary Symposium (A. S. Troelstra and D. van Dalen, editors), Studies in Logic and the Foundations of Mathematics, vol. 110, North-Holland, Amsterdam, 1982, pp. 1–40.Google Scholar
Aczel, P., The type theoretic interpretation of constructive set theory: Inductive definitions , Logic, Methodology and Philosophy of Science, VII (Salzburg, 1983) (R. Barcan Marcus, G. J. W. Dorn, and P. Weingartner, editors), Studies in Logic and the Foundations of Mathematics, vol. 114, North-Holland, Amsterdam, 1986, pp. 17–49.Google Scholar
Aczel, P. and Rathjen, M., Notes on Constructive Set Theory, 2010. Available at http://www1.maths.leeds.ac.uk/~rathjen/book.pdf.Google Scholar
Beeson, M. J., Continuity in intuitionistic set theories , Logic Colloquium ’78 (M. Boffa, D. van Dalen, and K. McAloon, editors), Studies in Logic and the Foundations of Mathematics, vol. 97, North-Holland, Amsterdam, 1979, pp. 1–52.Google Scholar
Beeson, M. J., Goodman’s theorem and beyond . Pacific Journal of Mathematics , vol. 84 (1979), no. 1, pp. 1–16.10.2140/pjm.1979.84.1CrossRefGoogle Scholar
Beeson, M. J., Foundations of Constructive Mathematics , Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], vol. 6, Springer, Berlin, 1985.10.1007/978-3-642-68952-9CrossRefGoogle Scholar
van den Berg, B. and van Slooten, L., Arithmetical conservation results . Indagationes Mathematicae , vol. 29 (2018), no. 1, pp. 260–275.10.1016/j.indag.2017.07.009CrossRefGoogle Scholar
Bishop, E., Foundations of Constructive Analysis , vol. 60 , McGraw-Hill, New York, 1967.Google Scholar
Curry, H. B., Grundlagen der kombinatorischen Logik . American Journal of Mathematics , vol. 51 (1930), pp. 363–384.10.2307/2370728CrossRefGoogle Scholar
Diaconescu, R., Axiom of choice and complementation . Proceedings of the American Mathematical Society , vol. 51 (1975), no. 1, pp. 176–178.10.1090/S0002-9939-1975-0373893-XCrossRefGoogle Scholar
Feferman, S., A language and axioms for explicit mathematics , Algebra and Logic (J. N. Crossley, editor), Springer, Berlin, 1975, pp. 87–139.10.1007/BFb0062852CrossRefGoogle Scholar
Feferman, S., Constructive theories of functions and classes , Logic Colloquium ’78 (M. Boffa, D. van Dalen, and K. McAloon, editors), Studies in Logic and the Foundations of Mathematics, North-Holland, Amsterdam, 1979, pp. 159–224.Google Scholar
Friedman, H., Some applications of Kleene’s methods for intuitionistic systems , Cambridge Summer School in Mathematical Logic (A. R. D. Mathias and H. Rogers, editors), Springer, Berlin, 1973, pp. 113–170.10.1007/BFb0066773CrossRefGoogle Scholar
Friedman, H. and Ščedrov, A., Large sets in intuitionistic set theory . Annals of Pure and Applied Logic , vol. 27 (1984), pp. 1–24.10.1016/0168-0072(84)90033-2CrossRefGoogle Scholar
Frittaion, E., On Goodman realizability . Notre Dame Journal of Formal Logic , vol. 60 (2019), no. 3, pp. 523–550.10.1215/00294527-2019-0018CrossRefGoogle Scholar
Frittaion, E. and Rathjen, M., Extensional realizability for intuitionistic set theory . Journal of Logic and Computation , vol. 31 (2021), no. 2, pp. 630–653.10.1093/logcom/exaa087CrossRefGoogle Scholar
Goodman, N. D., The theory of the Gödel functionals, this Journal, vol. 41 (1976), no. 3, pp. 574–582.Google Scholar
Goodman, N. D., Relativized realizability in intuitionistic arithmetic of all finite types, this Journal, vol. 43 (1978), no. 1, pp. 23–44.Google Scholar
Gordeev, L., Proof-theoretical analysis of weak systems of functions and classes . Annals of Pure and Applied Logic , vol. 38 (1988), pp. 1–121.10.1016/0168-0072(88)90055-3CrossRefGoogle Scholar
Kreisel, G. and Troelstra, A. S., Formal systems for some branches of intuitionistic analysis . Annals of Mathematical Logic , vol. 1 (1970), pp. 229–387.10.1016/0003-4843(70)90001-XCrossRefGoogle Scholar
McCarty, D. C., Realizability and recursive mathematics , Ph.D. thesis, The University of Edinburgh, 1985.Google Scholar
McCarty, D. C., Realizability and recursive set theory . Annals of Pure and Applied Logic , vol. 32 (1986), no. 2, pp. 153–183.10.1016/0168-0072(86)90050-3CrossRefGoogle Scholar
Myhill, J., Constructive set theory, this Journal, vol. 40 (1975), no. 3, pp. 347–382.Google Scholar
van Oosten, J., Extensional realizability . Annals of Pure and Applied Logic , vol. 84 (1997), no. 3, pp. 317–349.10.1016/S0168-0072(96)00050-4CrossRefGoogle Scholar
van Oosten, J., Realizability: An Introduction to Its Categorical Side , Studies in Logic and the Foundations of Mathematics, vol. 152, Elsevier, Amsterdam, 2008.Google Scholar
Rathjen, M., Constructive set theory and Brouwerian principles . Journal of Universal Computer Science , vol. 11 (2005), no. 12, pp. 2008–2033.Google Scholar
Rathjen, M., Choice principles in constructive and classical set theories , Logic Colloquium ’02 (Z. Chatzidakis, P. Koepke, and W. Pohlers, editors), Lecture Notes in Logic, vol. 27, Association for Symbolic Logic, La Jolla, 2006, pp. 299–326.Google Scholar
Rathjen, M., The formulae-as-classes interpretation of constructive set theory , Proof Technology and Computation (H. Schwichtenberg and K. Spies, editors), NATO Science Series, III: Computer and Systems Sciences, vol. 200, IOS, Amsterdam, 2006, pp. 279–322.Google Scholar
Rathjen, M.. Realizability for constructive Zermelo–Fraenkel set theory , Logic Colloquium ’03 (J. Väänänen, editor), Lecture Notes in Logic, vol. 24, Association for Symbolic Logic, La Jolla, 2006, pp. 282–314.10.1201/9781439865835-14CrossRefGoogle Scholar
Schönfinkel, M., Über die Bausteine der mathematischen Logik . Mathematische Annalen , vol. 92 (1924), pp. 305–316.10.1007/BF01448013CrossRefGoogle Scholar
Troelstra, A. S., Metamathematical Investigation of Intuitionistic Arithmetic and Analysis , Lecture Notes in Mathematics, vol. 344, Springer, Berlin, 1973.10.1007/BFb0066739CrossRefGoogle Scholar
Troelstra, A. S., Realizability , Handbook of Proof Theory (S. R. Buss, editor), Studies in Logic and the Foundations of Mathematics, vol. 137, North-Holland, Amsterdam, 1998, pp. 407–473.10.1016/S0049-237X(98)80021-9CrossRefGoogle Scholar
Troelstra, A. S. and van Dalen, D., Constructivism in Mathematics: An Introduction , vol. II , Studies in Logic and the Foundations of Mathematics, 123, North-Holland, Amsterdam, 1988.Google Scholar