1 Introduction
The first-order logic of a theory T consists of those first-order formulas for which all substitution instances are provable in T. A classical result of Friedman and Ščedrov [Reference Friedman and Ščedrov7] is that very few axioms suffice for a set theory to exceed the logical strength of intuitionistic first-order logic:
Theorem (Friedman and Ščedrov (1986))
Let T be a set theory based on intuitionistic first-order logic that contains the axioms of extensionality, pairing and (finite) union, as well as the separation schema. Then the first-order logic of T exceeds the strength of intuitionistic first-order logic.
This result applies to intuitionistic Zermelo–Fraenkel Set Theory (
![]() $\mathrm {IZF}$
) but not to constructive Zermelo–Fraenkel set theory (
$\mathrm {IZF}$
) but not to constructive Zermelo–Fraenkel set theory (
![]() $\mathrm {CZF}$
) because the separation schema of
$\mathrm {CZF}$
) because the separation schema of
![]() $\mathrm {CZF}$
is restricted to
$\mathrm {CZF}$
is restricted to
![]() $\Delta _0$
-formulas. It has, thus, been a long-standing open question whether the first-order logic of
$\Delta _0$
-formulas. It has, thus, been a long-standing open question whether the first-order logic of
![]() $\mathrm {CZF}$
exceeds the strength of intuitionistic logic as well. We give an answer to this question:
$\mathrm {CZF}$
exceeds the strength of intuitionistic logic as well. We give an answer to this question:
Theorem (see Corollary 5.15)
The first-order logic of
![]() $\mathrm {CZF}$
is intuitionistic first-order logic.
$\mathrm {CZF}$
is intuitionistic first-order logic.
We prove this result by developing a realisability semantics for
![]() $\mathrm {CZF}$
based on a new model of transfinite computation, the so-called Set Register Machines (
$\mathrm {CZF}$
based on a new model of transfinite computation, the so-called Set Register Machines (
![]() $\mathrm {SRM}$
s). Related notions of realisability had earlier been studied by Rathjen [Reference Rathjen, Schwichtenberg and Spies22] and Tharp [Reference Tharp23]. Our main result is obtained by adapting a technique that van Oosten [Reference van Oosten19] had developed for Heyting arithmetic: we combine the resulting notion of
$\mathrm {SRM}$
s). Related notions of realisability had earlier been studied by Rathjen [Reference Rathjen, Schwichtenberg and Spies22] and Tharp [Reference Tharp23]. Our main result is obtained by adapting a technique that van Oosten [Reference van Oosten19] had developed for Heyting arithmetic: we combine the resulting notion of
![]() $\mathrm {SRM}$
-realisability with Beth semantics to obtain a model of
$\mathrm {SRM}$
-realisability with Beth semantics to obtain a model of
![]() $\mathrm {CZF}$
that matches logical truth in a universal Beth model.
$\mathrm {CZF}$
that matches logical truth in a universal Beth model.
Carl, Galeotti, and Passmann [Reference Carl, Galeotti and Passmann4] gave a first proof-theoretic application of transfinite computability and provided a realisability interpretation for (infinitary)
![]() $\mathrm {IKP}$
set theory using OTMs. In particular, they proved that the propositional admissible rules of
$\mathrm {IKP}$
set theory using OTMs. In particular, they proved that the propositional admissible rules of
![]() $\mathrm {IKP}$
are exactly the admissible rules of intuitionistic propositional logic. On the way to proving our main result, we will prove the same result for
$\mathrm {IKP}$
are exactly the admissible rules of intuitionistic propositional logic. On the way to proving our main result, we will prove the same result for
![]() $\mathrm {CZF}$
. Our motivation for introducing SRMs instead of working with OTMs is that the former are easier adapted for realising stronger set theories than
$\mathrm {CZF}$
. Our motivation for introducing SRMs instead of working with OTMs is that the former are easier adapted for realising stronger set theories than
![]() $\mathrm {IKP}$
. This work is thus another fruitful application of techniques of transfinite computability to proof-theoretic questions.
$\mathrm {IKP}$
. This work is thus another fruitful application of techniques of transfinite computability to proof-theoretic questions.
1.1 Overview
After recalling some preliminaries in Section 2, we will begin, in Section 3, with introducing our new notion of transfinite machines, the so-called set register machines (
![]() $\mathrm {SRM}$
s). The main result of this section will be a generalisation of a classical result by Kleene and Post about the existence of mutually irreducible degrees of computability. In Section 4, we introduce a realisability semantics based on
$\mathrm {SRM}$
s). The main result of this section will be a generalisation of a classical result by Kleene and Post about the existence of mutually irreducible degrees of computability. In Section 4, we introduce a realisability semantics based on
![]() $\mathrm {SRM}$
s and show that (a certain extension of) these machines allows to realise
$\mathrm {SRM}$
s and show that (a certain extension of) these machines allows to realise
![]() $\mathrm {CZF}$
set theory. It also serves as a preparation for Section 5, in which we will combine our realisability semantics with Beth models to prove our main result.
$\mathrm {CZF}$
set theory. It also serves as a preparation for Section 5, in which we will combine our realisability semantics with Beth models to prove our main result.
2 Preliminaries
2.1 Constructive set theory
We will be concerned with constructive Zermelo–Fraenkel set theory,
![]() $\mathrm {CZF}$
, and now recall its definition and some basic facts. First, recall the axiom schemes of strong collection,
$\mathrm {CZF}$
, and now recall its definition and some basic facts. First, recall the axiom schemes of strong collection,
for all formulas
![]() $\phi $
, in which b is not free, and subset collection,
$\phi $
, in which b is not free, and subset collection,
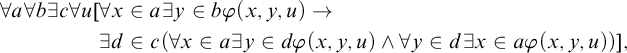 $$ \begin{align*} \forall a \forall b \exists c \forall u [&\forall x \in a \exists y \in b \phi(x,y,u) \rightarrow \\ & \exists d \in c (\forall x \in a \exists y \in d \phi(x,y,u) \wedge \forall y \in d \exists x \in a \phi(x,y,u)) ], \end{align*} $$
$$ \begin{align*} \forall a \forall b \exists c \forall u [&\forall x \in a \exists y \in b \phi(x,y,u) \rightarrow \\ & \exists d \in c (\forall x \in a \exists y \in d \phi(x,y,u) \wedge \forall y \in d \exists x \in a \phi(x,y,u)) ], \end{align*} $$
for all formulas
![]() $\phi $
, in which c is not free. By
$\phi $
, in which c is not free. By
![]() $\Delta _0$
-separation we denote the restriction of the separation schema to
$\Delta _0$
-separation we denote the restriction of the separation schema to
![]() $\Delta _0$
-formulas.
$\Delta _0$
-formulas.
Definition 2.1. Constructive Zermelo–Fraenkel Set Theory,
![]() $\mathrm {CZF}$
, is based on intuitionistic first-order logic in the language of set theory and consists of the following axioms and axiom schemes: extensionality, pairing, union, empty set, infinity,
$\mathrm {CZF}$
, is based on intuitionistic first-order logic in the language of set theory and consists of the following axioms and axiom schemes: extensionality, pairing, union, empty set, infinity,
![]() $\Delta _0$
-separation, strong collection, subset collection, and
$\Delta _0$
-separation, strong collection, subset collection, and
![]() $\in $
-induction.
$\in $
-induction.
We denote
![]() $\mathrm {CZF}$
without the subset collection schema by
$\mathrm {CZF}$
without the subset collection schema by
![]() $\mathrm {CZF}^-$
. The exponentiation axiom states that function sets exists:
$\mathrm {CZF}^-$
. The exponentiation axiom states that function sets exists:
The following is well known (consult, e.g., Aczel and Rathjen [Reference Aczel and Rathjen1]).
Fact 2.2. In
![]() $\mathrm {CZF}^-$
, the power set axiom implies the subset collection axiom. Moreover, in
$\mathrm {CZF}^-$
, the power set axiom implies the subset collection axiom. Moreover, in
![]() $\mathrm {CZF}^-$
, the subset collection scheme implies the exponentiation axiom.
$\mathrm {CZF}^-$
, the subset collection scheme implies the exponentiation axiom.
2.2 Logics and De Jongh’s theorem
Given a theory T, based on intuitionistic logic, the logically valid principles of T may exceed those valid in intuitionistic logic. The most well-known example of this phenomenon is probably the following consequence of what is known as Diaconescu’s theorem (see Diaconescu [Reference Diaconescu5] and Goodman and Myhill [Reference Goodman and Myhill8]):
![]() $\mathrm {IZF}$
extended with the axiom of choice implies the law of excluded middle, i.e.,
$\mathrm {IZF}$
extended with the axiom of choice implies the law of excluded middle, i.e.,
![]() $\mathrm {IZF} + \mathrm {AC} \vdash \phi \vee \neg \phi $
for all set-theoretic formulas
$\mathrm {IZF} + \mathrm {AC} \vdash \phi \vee \neg \phi $
for all set-theoretic formulas
![]() $\phi $
. This suggests that it is incorrect to say that the logic of
$\phi $
. This suggests that it is incorrect to say that the logic of
![]() $\mathrm {IZF} + \mathrm {AC}$
is intuitionistic: after all, the law of excluded middle is valid! For this reason, we define the propositional and first-order logics of a theory T as follows, in terms of translations.
$\mathrm {IZF} + \mathrm {AC}$
is intuitionistic: after all, the law of excluded middle is valid! For this reason, we define the propositional and first-order logics of a theory T as follows, in terms of translations.
Definition 2.3. Let T be a theory in a language
![]() $\mathcal {L}_T$
. A propositional translation is a function
$\mathcal {L}_T$
. A propositional translation is a function
![]() $\tau $
assigning
$\tau $
assigning
![]() $\mathcal {L}_T$
-sentences to propositional formulas such that:
$\mathcal {L}_T$
-sentences to propositional formulas such that:
-
(i)
 $\tau (p)$
is an
$\tau (p)$
is an
 $\mathcal {L}_T$
-sentence for every propositional letter p,
$\mathcal {L}_T$
-sentence for every propositional letter p, -
(ii)
 $\tau (\bot ) = \bot $
, and
$\tau (\bot ) = \bot $
, and -
(iii)
 $\tau (A \circ B) = \tau (A) \circ \tau (B)$
for
$\tau (A \circ B) = \tau (A) \circ \tau (B)$
for
 $\circ \in \{ \wedge ,\vee ,\rightarrow \}$
.
$\circ \in \{ \wedge ,\vee ,\rightarrow \}$
.
As customary with translations, we will often write
![]() $A^\tau $
instead of
$A^\tau $
instead of
![]() $\tau (A)$
.
$\tau (A)$
.
Definition 2.4. The propositional logic of T,
![]() $\mathbf {PL}(T)$
, consists of all propositional formulas A such that
$\mathbf {PL}(T)$
, consists of all propositional formulas A such that
![]() $T \vdash A^\tau $
for all propositional translations
$T \vdash A^\tau $
for all propositional translations
![]() $\tau $
.
$\tau $
.
A result concerning the first-order logic of Heyting arithmetic was proved by de Jongh in his doctoral dissertation [Reference de Jongh14, Reference de Jongh15]. We denote intuitionistic propositional logic by
![]() $\mathbf {IPC}$
and intuitionistic first-order logic by
$\mathbf {IPC}$
and intuitionistic first-order logic by
![]() $\mathbf {IQC}$
.
$\mathbf {IQC}$
.
Theorem 2.5 (de Jongh (1970))
The propositional logic of Heyting arithmetic is intuitionistic propositional logic,
![]() $\mathbf {PL}(\mathrm {HA}) = \mathbf {IPC}$
.
$\mathbf {PL}(\mathrm {HA}) = \mathbf {IPC}$
.
This result is now known as de Jongh’s theorem, and, in general, we say that a theory T satisfies de Jongh’s theorem whenever
![]() $\mathbf {PL}(T) = \mathbf {IPC}$
.
$\mathbf {PL}(T) = \mathbf {IPC}$
.
Definition 2.6. Let T be a theory in a language
![]() $\mathcal {L}_T$
. A first-order translation is a function
$\mathcal {L}_T$
. A first-order translation is a function
![]() $\tau $
assigning
$\tau $
assigning
![]() $\mathcal {L}_T$
-formulas to propositional formulas such that:
$\mathcal {L}_T$
-formulas to propositional formulas such that:
-
(i)
 $\tau (R(x_1,\dots ,x_n))$
is an
$\tau (R(x_1,\dots ,x_n))$
is an
 $\mathcal {L}_T$
-formula
$\mathcal {L}_T$
-formula
 $\phi $
with free variables among
$\phi $
with free variables among
 $x_1,\dots ,x_n$
,
$x_1,\dots ,x_n$
, -
(ii)
 $\tau (\bot ) = \bot $
,
$\tau (\bot ) = \bot $
, -
(iii)
 $\tau (A \circ B) = \tau (A) \circ \tau (B)$
for
$\tau (A \circ B) = \tau (A) \circ \tau (B)$
for
 $\circ \in \{ \wedge ,\vee ,\rightarrow \}$
, and
$\circ \in \{ \wedge ,\vee ,\rightarrow \}$
, and -
(iv)
 $\tau (\mathcal {Q} x A(x)) = \mathcal {Q} x \tau (A(x))$
for
$\tau (\mathcal {Q} x A(x)) = \mathcal {Q} x \tau (A(x))$
for
 $\mathcal {Q} \in \{ \forall ,\exists \}$
.
$\mathcal {Q} \in \{ \forall ,\exists \}$
.
Definition 2.7. The first-order logic of T,
![]() $\mathbf {QL}(T)$
, consists of all first-order formulas A such that
$\mathbf {QL}(T)$
, consists of all first-order formulas A such that
![]() $T \vdash A^\tau $
for all first-order translations
$T \vdash A^\tau $
for all first-order translations
![]() $\tau $
.
$\tau $
.
Since de Jongh’s initial work, many notable results have been obtained in this area. Leivant [Reference Leivant18] showed that
![]() $\mathbf {QL}(\mathrm {HA}) = \mathbf {IQC}$
; van Oosten [Reference van Oosten19] gave a semantic proof of this fact (the idea of his construction will reappear in our construction in Section 5). De Jongh, Verbrugge, and Visser [Reference de Jongh, Verbrugge and Visser16] consider a generalised version of de Jongh’s theorem: given a (propositional or first-order) logic J and a theory T, we can consider the theory
$\mathbf {QL}(\mathrm {HA}) = \mathbf {IQC}$
; van Oosten [Reference van Oosten19] gave a semantic proof of this fact (the idea of his construction will reappear in our construction in Section 5). De Jongh, Verbrugge, and Visser [Reference de Jongh, Verbrugge and Visser16] consider a generalised version of de Jongh’s theorem: given a (propositional or first-order) logic J and a theory T, we can consider the theory
![]() $T(J)$
obtained by closing T under J. We then say that T satisfies the de Jongh property for J if
$T(J)$
obtained by closing T under J. We then say that T satisfies the de Jongh property for J if
![]() $\mathbf {PL}(T(J)) = J$
(or,
$\mathbf {PL}(T(J)) = J$
(or,
![]() $\mathbf {QL}(T(J)) = J$
if J is a first-order logic).
$\mathbf {QL}(T(J)) = J$
if J is a first-order logic).
The main negative result concerning logics of set theory is due to Friedman and Ščedrov [Reference Friedman and Ščedrov7], and was also mentioned in the introduction. Here is a reformulation based on the terminology just introduced.
Theorem 2.8 (Friedman and Ščedrov (1986))
Let T be a set theory based on intuitionistic first-order logic that contains the axioms of extensionality, pairing and (finite) union, as well as the separation scheme. Then,
![]() $\mathbf {IQC} \subsetneq \mathbf {QL}(T)$
.
$\mathbf {IQC} \subsetneq \mathbf {QL}(T)$
.
Passmann [Reference Passmann, Fernández and Muscholl20] showed that
![]() $\mathbf {PL}(\mathrm {IZF}) = \mathbf {IPC}$
, and consequently,
$\mathbf {PL}(\mathrm {IZF}) = \mathbf {IPC}$
, and consequently,
![]() $\mathbf {PL}(\mathrm {CZF}) = \mathbf {IPC}$
. Iemhoff and Passmann [Reference Iemhoff and Passmann11] analysed the logical structure of
$\mathbf {PL}(\mathrm {CZF}) = \mathbf {IPC}$
. Iemhoff and Passmann [Reference Iemhoff and Passmann11] analysed the logical structure of
![]() $\mathrm {IKP}$
and proved, among other things, that
$\mathrm {IKP}$
and proved, among other things, that
![]() $\mathbf {QL}(\mathrm {IKP}) = \mathbf {IQC}$
.
$\mathbf {QL}(\mathrm {IKP}) = \mathbf {IQC}$
.
2.3 Admissible rules
We can further generalise our analysis of the logical structure of a given theory by not only considering its logically valid principles but also by determining its admissible rules.
Definition 2.9. Let T be a theory in a language
![]() $\mathcal {L}_T$
, and let A and B be propositional formulas. We say that a propositional rule
$\mathcal {L}_T$
, and let A and B be propositional formulas. We say that a propositional rule
![]() $A / B$
is admissible in T, written
$A / B$
is admissible in T, written
![]() , if and only if
, if and only if
![]() $T \vdash A^\tau $
implies
$T \vdash A^\tau $
implies
![]() $T \vdash B^\tau $
for all propositional translations
$T \vdash B^\tau $
for all propositional translations
![]() $\tau $
.
$\tau $
.
We say that a theory T has the disjunction property if
![]() $T \vdash \phi \vee \psi $
implies
$T \vdash \phi \vee \psi $
implies
![]() $T \vdash \phi $
or
$T \vdash \phi $
or
![]() $T \vdash \psi $
. The restricted Visser’s rules
$T \vdash \psi $
. The restricted Visser’s rules
![]() $\{ V_n \}_{n < \omega }$
are defined as follows and play a special role for admissibility (Iemhoff [Reference Iemhoff9] proved that they form a so-called basis of the admissible rules of intuitionistic propositional logic):
$\{ V_n \}_{n < \omega }$
are defined as follows and play a special role for admissibility (Iemhoff [Reference Iemhoff9] proved that they form a so-called basis of the admissible rules of intuitionistic propositional logic):
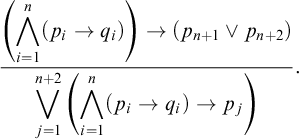
Denote by
![]() $V_n^a$
the antecedent and by
$V_n^a$
the antecedent and by
![]() $V_n^c$
the consequent of the rule. We will make use of the following result of Iemhoff [Reference Iemhoff10] to determine admissible rules.
$V_n^c$
the consequent of the rule. We will make use of the following result of Iemhoff [Reference Iemhoff10] to determine admissible rules.
Theorem 2.10 (Iemhoff [Reference Iemhoff10, Theorem 3.9 and Corollary 3.10])
Let T be a theory with the disjunction property. If the restricted Visser’s rules are propositional admissible in T, then the propositional admissible rules of T are exactly the propositional admissible rules of intuitionistic propositional logic,
![]() .
.
Visser [Reference Visser25] proved that the propositional admissible rules of Heyting Arithmetic
![]() $\mathrm {HA}$
are exactly the admissible rules of intuitionistic propositional logic
$\mathrm {HA}$
are exactly the admissible rules of intuitionistic propositional logic
![]() $\mathbf {IPC}$
. Using realisability techniques, Carl, Galeotti, and Passmann [Reference Carl, Galeotti and Passmann4] determined the propositional admissible rules of
$\mathbf {IPC}$
. Using realisability techniques, Carl, Galeotti, and Passmann [Reference Carl, Galeotti and Passmann4] determined the propositional admissible rules of
![]() $\mathrm {IKP}$
to be exactly the admissible rules of propositional intuitionistic logic. Iemhoff and Passmann [Reference Iemhoff and Passmann12] proved that the propositional admissible rules of
$\mathrm {IKP}$
to be exactly the admissible rules of propositional intuitionistic logic. Iemhoff and Passmann [Reference Iemhoff and Passmann12] proved that the propositional admissible rules of
![]() $\mathrm {CZF}_{\mathrm {ER}}$
and
$\mathrm {CZF}_{\mathrm {ER}}$
and
![]() $\mathrm {IZF}_{\mathrm {R}}$
are the admissible rules of intuitionistic propositional logic by using a modification of the so-called blended models (earlier introduced by Passmann [Reference Passmann, Fernández and Muscholl20]).Footnote
1
It is possible to consider first-order admissible rules; van den Berg and Moerdijk [Reference van den Berg and Moerdijk2] show that certain constructive principles are first-order admissible rules of
$\mathrm {IZF}_{\mathrm {R}}$
are the admissible rules of intuitionistic propositional logic by using a modification of the so-called blended models (earlier introduced by Passmann [Reference Passmann, Fernández and Muscholl20]).Footnote
1
It is possible to consider first-order admissible rules; van den Berg and Moerdijk [Reference van den Berg and Moerdijk2] show that certain constructive principles are first-order admissible rules of
![]() $\mathrm {CZF}$
(calling them derived rules).
$\mathrm {CZF}$
(calling them derived rules).
3 Set register machines
3.1 Definitions and basic properties
Let us begin with some intuition for set register machines (
![]() $\mathrm {SRM}$
s). A set register machine has a finite set of registers
$\mathrm {SRM}$
s). A set register machine has a finite set of registers
![]() $R_0,\dots ,R_n$
on which it conducts computations. However, the registers do not contain natural numbers (as in the case of register machines) or ordinal numbers (as in the case of ordinal register or Turing machines) but rather arbitrary sets. Accordingly,
$R_0,\dots ,R_n$
on which it conducts computations. However, the registers do not contain natural numbers (as in the case of register machines) or ordinal numbers (as in the case of ordinal register or Turing machines) but rather arbitrary sets. Accordingly,
![]() $\mathrm {SRM}$
s use a different set of operations: for example, adding a set contained in a register to another register, or removing a member of a set contained in a certain register.
$\mathrm {SRM}$
s use a different set of operations: for example, adding a set contained in a register to another register, or removing a member of a set contained in a certain register.
We assume that
![]() $<_\tau $
is a global well-ordering such that
$<_\tau $
is a global well-ordering such that
![]() $\operatorname {\mathrm {rank}}(x) < \operatorname {\mathrm {rank}}(y)$
implies
$\operatorname {\mathrm {rank}}(x) < \operatorname {\mathrm {rank}}(y)$
implies
![]() $x <_\tau y$
.Footnote
2
This means that we are working under the assumption of the global axiom of choice and extend our set-theoretical language with the symbol
$x <_\tau y$
.Footnote
2
This means that we are working under the assumption of the global axiom of choice and extend our set-theoretical language with the symbol
![]() $<_\tau $
. Note that this extended theory is conservative over
$<_\tau $
. Note that this extended theory is conservative over
![]() $\mathrm {ZFC}$
(see Fraenkel [Reference Fraenkel, Bar-Hillel and Levy6, pp. 72–73]). The reason for using this theory as our meta-theory is that we want SRM-computations to be deterministic, and assuming a global well-ordering is a convenient way to achieve this. For a discussion of alternatives see Remark 3.3.
$\mathrm {ZFC}$
(see Fraenkel [Reference Fraenkel, Bar-Hillel and Levy6, pp. 72–73]). The reason for using this theory as our meta-theory is that we want SRM-computations to be deterministic, and assuming a global well-ordering is a convenient way to achieve this. For a discussion of alternatives see Remark 3.3.
We will now first define programs by giving the permissible operations, and then computations for set register machines. While defining the permissible operations, we will directly give an intuitive description of what the operation does.
Definition 3.1. A set register program p is a finite sequence
![]() $p = (p_0, \dots , p_{n-1})$
, where each
$p = (p_0, \dots , p_{n-1})$
, where each
![]() $p_i$
is one of the following commands:
$p_i$
is one of the following commands:
-
(i) “
 $R_i := \emptyset $
”: replace the content of the ith register with the empty set.
$R_i := \emptyset $
”: replace the content of the ith register with the empty set. -
(ii) “
 $\mathtt {ADD}(i,j)$
”: replace the content of the jth register with
$\mathtt {ADD}(i,j)$
”: replace the content of the jth register with
 $R_j \cup \{ R_i \}$
.
$R_j \cup \{ R_i \}$
. -
(iii) “
 $\mathtt {COPY}(i,j)$
”: replace the content of the jth register with
$\mathtt {COPY}(i,j)$
”: replace the content of the jth register with
 $R_i$
.
$R_i$
. -
(iv) “
 $\mathtt {TAKE}(i,j)$
”: replace the content of the jth register with the
$\mathtt {TAKE}(i,j)$
”: replace the content of the jth register with the
 $<_\tau $
-least set contained in
$<_\tau $
-least set contained in
 $R_i$
, if
$R_i$
, if
 $R_i$
is non-empty.
$R_i$
is non-empty. -
(v) “
 $\mathtt {REMOVE}(i,j)$
”: replace the content of the jth register with the set
$\mathtt {REMOVE}(i,j)$
”: replace the content of the jth register with the set
 $R_j \setminus \{ R_i \}$
.
$R_j \setminus \{ R_i \}$
. -
(vi) “
 $\mathtt {IF} \ R_i = \emptyset \ \mathtt {THEN \ GO \ TO} \ k$
”: check whether the ith register is empty; if so, move to program line k, and, if not, move to the next line.
$\mathtt {IF} \ R_i = \emptyset \ \mathtt {THEN \ GO \ TO} \ k$
”: check whether the ith register is empty; if so, move to program line k, and, if not, move to the next line. -
(vii) “
 $\mathtt {IF} \ R_i \in R_j \ \mathtt {THEN \ GO \ TO} \ k$
”: check whether
$\mathtt {IF} \ R_i \in R_j \ \mathtt {THEN \ GO \ TO} \ k$
”: check whether
 $R_i \in R_j$
; if so, move to program line k, and, if not, move to the next line.
$R_i \in R_j$
; if so, move to program line k, and, if not, move to the next line. -
(viii) “
 $\mathtt {POW}(i,j)$
”: replace the content of the jth register with the power set of
$\mathtt {POW}(i,j)$
”: replace the content of the jth register with the power set of
 $R_i$
.
$R_i$
.
Definition 3.2. Let p be a set register program and
![]() $k < \omega $
be the highest register index appearing in p. A configuration of p is a sequence
$k < \omega $
be the highest register index appearing in p. A configuration of p is a sequence
![]() $(l,r_0,\dots ,r_k)$
consisting of the active program line
$(l,r_0,\dots ,r_k)$
consisting of the active program line
![]() $l < \omega $
and the current content
$l < \omega $
and the current content
![]() $r_i$
of register
$r_i$
of register
![]() $R_i$
. If
$R_i$
. If
![]() $c = (l,r_0,\dots ,r_k)$
is a configuration of p, then its successor configuration
$c = (l,r_0,\dots ,r_k)$
is a configuration of p, then its successor configuration
![]() $c^+ = (l^+,r_0^+,\dots ,r_k^+)$
is obtained as follows:
$c^+ = (l^+,r_0^+,\dots ,r_k^+)$
is obtained as follows:
-
(i) If
 $p_l$
is
$p_l$
is
 $\text {"} R_i := \emptyset\text {"},$
then let
$\text {"} R_i := \emptyset\text {"},$
then let
 $r_i^+ = \emptyset $
,
$r_i^+ = \emptyset $
,
 $r_n^+ = r_n$
for
$r_n^+ = r_n$
for
 $n \neq i$
, and
$n \neq i$
, and
 $l^+ = l + 1$
.
$l^+ = l + 1$
. -
(ii) If
 $p_l$
is
$p_l$
is
 $\text {"} \mathtt {ADD}(i,j)\text {"},$
then let
$\text {"} \mathtt {ADD}(i,j)\text {"},$
then let
 $r_j^+ = r_j \cup \{ r_i \}$
,
$r_j^+ = r_j \cup \{ r_i \}$
,
 $r_n^+ = r_n$
for
$r_n^+ = r_n$
for
 $n \neq j$
, and
$n \neq j$
, and
 $l^+ = l + 1$
.
$l^+ = l + 1$
. -
(iii) If
 $p_l$
is
$p_l$
is
 $\text {"} \mathtt {COPY}(i,j)\text {"},$
then let
$\text {"} \mathtt {COPY}(i,j)\text {"},$
then let
 $r_j^+ = r_i$
,
$r_j^+ = r_i$
,
 $r_n^+ = r_n$
for
$r_n^+ = r_n$
for
 $n \neq j$
, and
$n \neq j$
, and
 $l^+ = l + 1$
.
$l^+ = l + 1$
. -
(iv) If
 $p_l$
is
$p_l$
is
 $\text {"} \mathtt {TAKE}(i,j)\text {"},$
then let
$\text {"} \mathtt {TAKE}(i,j)\text {"},$
then let
 $r_j^+$
be the
$r_j^+$
be the
 $<_\tau $
-minimal element of
$<_\tau $
-minimal element of
 $r_i$
(if that exists; if
$r_i$
(if that exists; if
 $r_i = \emptyset $
, then
$r_i = \emptyset $
, then
 $r_j^+ = r_j$
),
$r_j^+ = r_j$
),
 $r_n^+ = r_n$
for
$r_n^+ = r_n$
for
 $n \neq j$
, and
$n \neq j$
, and
 $l^+ = l + 1$
.
$l^+ = l + 1$
. -
(v) If
 $p_l$
is
$p_l$
is
 $\text {"} \mathtt {REMOVE}(i,j)\text {"},$
then let
$\text {"} \mathtt {REMOVE}(i,j)\text {"},$
then let
 $r_j^+ = r_j \setminus \{ r_i \}$
,
$r_j^+ = r_j \setminus \{ r_i \}$
,
 $r_n^+ = r_n$
for
$r_n^+ = r_n$
for
 $n \neq j$
, and
$n \neq j$
, and
 $l^+ = l + 1$
.
$l^+ = l + 1$
. -
(vi) If
 $p_l$
is
$p_l$
is
 $\text {"} \mathtt {IF} \ R_i = \emptyset \ \mathtt {THEN \ GO \ TO} \ m\text {"},$
then
$\text {"} \mathtt {IF} \ R_i = \emptyset \ \mathtt {THEN \ GO \ TO} \ m\text {"},$
then
 $r_i^+ = r_i$
for all
$r_i^+ = r_i$
for all
 $i \leq k$
; and, if
$i \leq k$
; and, if
 $r_i = \emptyset $
, then
$r_i = \emptyset $
, then
 $l^+ = m$
; if
$l^+ = m$
; if
 $r_i \neq \emptyset $
, then
$r_i \neq \emptyset $
, then
 $l^+ = l + 1$
.
$l^+ = l + 1$
. -
(vii) If
 $p_l$
is
$p_l$
is
 $\text {"} \mathtt {IF} \ R_i \in R_j \ \mathtt {THEN \ GO \ TO} \ m\text {"},$
then
$\text {"} \mathtt {IF} \ R_i \in R_j \ \mathtt {THEN \ GO \ TO} \ m\text {"},$
then
 $r_i^+ = r_i$
for all
$r_i^+ = r_i$
for all
 $i \leq k$
; and, if
$i \leq k$
; and, if
 $r_i \in r_j$
, then
$r_i \in r_j$
, then
 $l^+ = m$
; if
$l^+ = m$
; if
 $r_i \notin r_j$
, then
$r_i \notin r_j$
, then
 $l^+ = l + 1$
.
$l^+ = l + 1$
. -
(viii) If
 $p_l$
is “
$p_l$
is “
 $\mathtt {POW}(i,j)$
”, then
$\mathtt {POW}(i,j)$
”, then
 $r_j^+ = \mathcal {P}(r_i)$
,
$r_j^+ = \mathcal {P}(r_i)$
,
 $r_n^+ = r_n$
for all
$r_n^+ = r_n$
for all
 $n \neq i$
, and
$n \neq i$
, and
 $l^+ = l + 1$
.
$l^+ = l + 1$
.
A computation of p with input
![]() $x_0,\dots ,x_j$
is a sequence d of ordinal length
$x_0,\dots ,x_j$
is a sequence d of ordinal length
![]() $\alpha + 1$
consisting of configurations of p such that:
$\alpha + 1$
consisting of configurations of p such that:
-
(i)
 $d_0 = (1,x_0, \dots , x_j, \emptyset , \dots , \emptyset )$
,
$d_0 = (1,x_0, \dots , x_j, \emptyset , \dots , \emptyset )$
, -
(ii) if
 $\beta < \alpha $
, then
$\beta < \alpha $
, then
 $d_{\beta + 1} = d_\beta ^+$
,
$d_{\beta + 1} = d_\beta ^+$
, -
(iii) if
 $\beta < \alpha $
is a limit, then
$\beta < \alpha $
is a limit, then
 $l_\beta = \liminf _{\gamma < \beta } l_\gamma $
, and
$l_\beta = \liminf _{\gamma < \beta } l_\gamma $
, and
 $r_\beta = \liminf _{\gamma < \beta } r_\gamma $
, where the limes inferior of a sequence of sets is the set obtained from the limes inferior of the characteristic functions, and
$r_\beta = \liminf _{\gamma < \beta } r_\gamma $
, where the limes inferior of a sequence of sets is the set obtained from the limes inferior of the characteristic functions, and -
(iv)
 $d_\alpha ^+$
is undefined (i.e.,
$d_\alpha ^+$
is undefined (i.e.,
 $l_\alpha> m$
).
$l_\alpha> m$
).
The notion of computability obtained by restricting Definitions 3.1 and 3.2 to clauses (i)–(vii) will be referred to as
![]() $\mathrm {SRM}$
; the full notion will be referred to as
$\mathrm {SRM}$
; the full notion will be referred to as
![]() $\mathrm {SRM}^+$
. In other words,
$\mathrm {SRM}^+$
. In other words,
![]() $\mathrm {SRM}^+$
is obtained from
$\mathrm {SRM}^+$
is obtained from
![]() $\mathrm {SRM}$
by adding the power set operation. We allow
$\mathrm {SRM}$
by adding the power set operation. We allow
![]() $\mathrm {SRM}$
s and
$\mathrm {SRM}$
s and
![]() $\mathrm {SRM}^+$
s to make use of finitely many set parameters which will be treated as additional input in a fixed register as specified in the program code.
$\mathrm {SRM}^+$
s to make use of finitely many set parameters which will be treated as additional input in a fixed register as specified in the program code.
Remark 3.3. There are several alternatives for working with a global well-ordering function
![]() $<_\tau $
: first, it is possible to develop a theory of non-deterministic SRMs, where the
$<_\tau $
: first, it is possible to develop a theory of non-deterministic SRMs, where the
![]() $\mathtt {TAKE}$
-command takes an arbitrary set. Second, SRMs could work on well-ordered sets (i.e., sets equipped with a well-order). This approach is not useful for
$\mathtt {TAKE}$
-command takes an arbitrary set. Second, SRMs could work on well-ordered sets (i.e., sets equipped with a well-order). This approach is not useful for
![]() $\mathrm {SRM}^+$
as there is no canonical way in extending the well-ordering of a set to its power set (i.e., a certain degree of non-determinateness is introduced again). A third approach is to make computations dependent on a large enough well-ordering of some initial
$\mathrm {SRM}^+$
as there is no canonical way in extending the well-ordering of a set to its power set (i.e., a certain degree of non-determinateness is introduced again). A third approach is to make computations dependent on a large enough well-ordering of some initial
![]() $V_\alpha $
. Finally, one could work in the constructible universe
$V_\alpha $
. Finally, one could work in the constructible universe
![]() $\mathrm {L}$
where we have a
$\mathrm {L}$
where we have a
![]() $\Sigma _1$
-definable well-ordering
$\Sigma _1$
-definable well-ordering
![]() $<_{\mathrm {L}}$
. We will, in fact, consider this approach in Section 3.3 but for different reasons: for our main application, we need computations to be definable in the language of set theory without an additional symbol for the global well-ordering.
$<_{\mathrm {L}}$
. We will, in fact, consider this approach in Section 3.3 but for different reasons: for our main application, we need computations to be definable in the language of set theory without an additional symbol for the global well-ordering.
Definition 3.4. A function f is
![]() $\mathrm {SRM}^{(+)}$
-computable if there is an
$\mathrm {SRM}^{(+)}$
-computable if there is an
![]() $\mathrm {SRM}^{(+)}$
-program p, possibly with parameters, which computes
$\mathrm {SRM}^{(+)}$
-program p, possibly with parameters, which computes
![]() $f(x)$
on input x. A predicate is called
$f(x)$
on input x. A predicate is called
![]() $\mathrm {SRM}^{(+)}$
-computable if its characteristic function is
$\mathrm {SRM}^{(+)}$
-computable if its characteristic function is
![]() $\mathrm {SRM}^{(+)}$
-computable.
$\mathrm {SRM}^{(+)}$
-computable.
Note that every function with set-sized domain is
![]() $\mathrm {SRM}$
-computable. Clearly, if a function or predicate is
$\mathrm {SRM}$
-computable. Clearly, if a function or predicate is
![]() $\mathrm {SRM}$
-computable, then it is also
$\mathrm {SRM}$
-computable, then it is also
![]() $\mathrm {SRM}^+$
-computable. The converse does not hold: consider, for example, the power set operation.
$\mathrm {SRM}^+$
-computable. The converse does not hold: consider, for example, the power set operation.
Proposition 3.5. Equality of sets is
![]() $\mathrm {SRM}$
-computable.
$\mathrm {SRM}$
-computable.
Proof The following SRM-program computes whether the sets contained in registers
![]() $R_0$
and
$R_0$
and
![]() $R_1$
are equal: the program successively takes elements of the first set, checks whether they are contained in the second set, and removes the element from both sets. If both registers
$R_1$
are equal: the program successively takes elements of the first set, checks whether they are contained in the second set, and removes the element from both sets. If both registers
![]() $R_0$
and
$R_0$
and
![]() $R_1$
are empty at the same time, then the original sets must have been equal. Otherwise, the original sets were not equal.
$R_1$
are empty at the same time, then the original sets must have been equal. Otherwise, the original sets were not equal.
1:
![]() $\mathtt {IF} \ R_0 = \emptyset \ \mathtt {THEN \ GO \ TO} \ 3$
$\mathtt {IF} \ R_0 = \emptyset \ \mathtt {THEN \ GO \ TO} \ 3$
2:
![]() $\mathtt {GO \ TO} \ 5$
$\mathtt {GO \ TO} \ 5$
3:
![]() $\mathtt {IF} \ R_1 = \emptyset \ \mathtt {THEN \ GO \ TO} \ 11$
$\mathtt {IF} \ R_1 = \emptyset \ \mathtt {THEN \ GO \ TO} \ 11$
4:
![]() $\mathtt {GO \ TO} \ 14$
$\mathtt {GO \ TO} \ 14$
5:
![]() $\mathtt {TAKE}(0,2)$
$\mathtt {TAKE}(0,2)$
6:
![]() $\mathtt {REMOVE}(2,0)$
$\mathtt {REMOVE}(2,0)$
7:
![]() $\mathtt {IF} \ R_2 \in R_1 \ \mathtt {THEN \ GO \ TO} \ 9$
$\mathtt {IF} \ R_2 \in R_1 \ \mathtt {THEN \ GO \ TO} \ 9$
8:
![]() $\mathtt {GO \ TO} \ 14$
$\mathtt {GO \ TO} \ 14$
9:
![]() $\mathtt {REMOVE}(2,1)$
$\mathtt {REMOVE}(2,1)$
10:
![]() $\mathtt {GO \ TO} \ 1$
$\mathtt {GO \ TO} \ 1$
11:
![]() $R_0 := \emptyset $
$R_0 := \emptyset $
12:
![]() $\mathtt {ADD}(0,0)$
$\mathtt {ADD}(0,0)$
13:
![]() $\mathtt {GO \ TO} \ 15$
$\mathtt {GO \ TO} \ 15$
14:
![]() $R_0 := \emptyset $
$R_0 := \emptyset $
Note that the operation “
![]() $\mathtt {GO \ TO} \ i$
” is a shortcut for “
$\mathtt {GO \ TO} \ i$
” is a shortcut for “
![]() $\mathtt {IF} \ R_j = \emptyset \ \mathtt {THEN \ GO \ TO} \ i$
” where j is chosen in such a way that the register
$\mathtt {IF} \ R_j = \emptyset \ \mathtt {THEN \ GO \ TO} \ i$
” where j is chosen in such a way that the register
![]() $R_j$
is not mentioned in any other instruction of the program.
$R_j$
is not mentioned in any other instruction of the program.
In view of this proposition, we can use an operation “
![]() $\mathtt {IF} \ R_i = R_j \ \mathtt {THEN \ GO \ TO} \ k$
” by implementing the program of the proof of the proposition as a subroutine. The following lemma shows that many basic operations and predicates are
$\mathtt {IF} \ R_i = R_j \ \mathtt {THEN \ GO \ TO} \ k$
” by implementing the program of the proof of the proposition as a subroutine. The following lemma shows that many basic operations and predicates are
![]() $\mathrm {SRM}^+$
-computable.
$\mathrm {SRM}^+$
-computable.
Lemma 3.6. The following functions and predicates are
![]() $\mathrm {SRM}^+$
-computable
$\mathrm {SRM}^+$
-computable
![]() $:$
$:$
-
(i) the binary union function
 $(x,y) \mapsto x \cup y$
,
$(x,y) \mapsto x \cup y$
, -
(ii) the intersection function
 $(x,y) \mapsto x \cap y$
,
$(x,y) \mapsto x \cap y$
, -
(iii) the singleton and pairing functions,
 $x \mapsto \{ x \}$
and
$x \mapsto \{ x \}$
and
 $(x,y) \mapsto \{ x,y \}$
,
$(x,y) \mapsto \{ x,y \}$
, -
(iv) the ordered pairing function
 $(x,y) \mapsto \langle x,y \rangle $
,
$(x,y) \mapsto \langle x,y \rangle $
, -
(v) the first and second projections
 $\langle x,y \rangle \mapsto x$
,
$\langle x,y \rangle \mapsto x$
,
 $\langle x,y \rangle \mapsto y$
,
$\langle x,y \rangle \mapsto y$
, -
(vi) the predicate “x is an ordered pair,”
-
(vii) the predicate “x is a function,”
-
(viii) the union of a set,
 $x \mapsto \bigcup x$
,
$x \mapsto \bigcup x$
, -
(ix) the intersection of a set,
 $x \mapsto \bigcap x$
,
$x \mapsto \bigcap x$
, -
(x) the function mapping a function to its domain
 $f \mapsto \operatorname {\mathrm {dom}}(f)$
,
$f \mapsto \operatorname {\mathrm {dom}}(f)$
, -
(xi) function application
 $(f, x) \mapsto f(x)$
,
$(f, x) \mapsto f(x)$
, -
(xii) the predicate “x is an ordinal,”
-
(xiii) the predicate “x is a sequence of ordinal length,”
-
(xiv) the function computing the
 $<_\tau $
-least element
$<_\tau $
-least element
 $x \in y$
satisfying an
$x \in y$
satisfying an
 $\mathrm {SRM}^+$
-computable predicate
$\mathrm {SRM}^+$
-computable predicate
 $P(x)$
,
$P(x)$
, -
(xv) the
 $\alpha $
th projection on a sequence,
$\alpha $
th projection on a sequence,
 $\langle x_i \, | \, i < \beta \rangle \mapsto x_\alpha $
,
$\langle x_i \, | \, i < \beta \rangle \mapsto x_\alpha $
, -
(xvi) the power set function,
 $x \mapsto \mathcal {P}(x)$
,
$x \mapsto \mathcal {P}(x)$
, -
(xvii) the predicate “x is the power set of
 $y,$
”
$y,$
” -
(xviii) the limes inferior of a sequence of sets.
Proof We will give explicit programs for the first few cases and then move to increasingly abstract descriptions of the desired programs:
-
(i) Observe that the following program computes the union of the sets in registers
 $R_0$
and
$R_0$
and
 $R_1$
by adding all elements of
$R_1$
by adding all elements of
 $R_1$
to
$R_1$
to
 $R_0$
:
$R_0$
:1:
 $\mathtt {IF} \ R_1 = \emptyset \ \mathtt {THEN \ GO \ TO} \ 6$
$\mathtt {IF} \ R_1 = \emptyset \ \mathtt {THEN \ GO \ TO} \ 6$
2:
 $\mathtt {TAKE}(1,2)$
$\mathtt {TAKE}(1,2)$
3:
 $\mathtt {REMOVE}(2,1)$
$\mathtt {REMOVE}(2,1)$
4:
 $\mathtt {ADD}(2,0)$
$\mathtt {ADD}(2,0)$
5:
 $\mathtt {GO \ TO} \ 1$
$\mathtt {GO \ TO} \ 1$
-
(ii) Observe that the intersection of the sets contained in registers
 $R_0$
and
$R_0$
and
 $R_1$
can be computed as follows. Check for each element of
$R_1$
can be computed as follows. Check for each element of
 $R_1$
whether it is contained in
$R_1$
whether it is contained in
 $R_0$
and, if so, save it into a register for the intersection:
$R_0$
and, if so, save it into a register for the intersection:1:
 $\mathtt {IF} \ R_1 = \emptyset \ \mathtt {THEN \ GO \ TO} \ 8$
$\mathtt {IF} \ R_1 = \emptyset \ \mathtt {THEN \ GO \ TO} \ 8$
2:
 $\mathtt {TAKE}(1,2)$
$\mathtt {TAKE}(1,2)$
3:
 $\mathtt {REMOVE}(2,1)$
$\mathtt {REMOVE}(2,1)$
4:
 $\mathtt {IF} \ R_2 \in R_0 \ \mathtt {THEN \ GO \ TO} \ 6$
$\mathtt {IF} \ R_2 \in R_0 \ \mathtt {THEN \ GO \ TO} \ 6$
5:
 $\mathtt {GO \ TO} \ 1$
$\mathtt {GO \ TO} \ 1$
6:
 $\mathtt {ADD}(2,3)$
$\mathtt {ADD}(2,3)$
7:
 $\mathtt {GO \ TO} \ 1$
$\mathtt {GO \ TO} \ 1$
8:
 $\mathtt {COPY}(3,0)$
$\mathtt {COPY}(3,0)$
-
(iii) The functions of (iii) can be easily implemented.
-
(iv) Recall that
 $\langle x, y \rangle = \{ \{ x \},\{ x,y \} \}$
, and this can easily be computed.
$\langle x, y \rangle = \{ \{ x \},\{ x,y \} \}$
, and this can easily be computed. -
(v) Note that
 $\bigcap \langle x, y \rangle = x$
and
$\bigcap \langle x, y \rangle = x$
and
 $\bigcup \langle x, y \rangle = \{ x,y \}$
. So we can construct the desired programs by combining the procedures from (i) and (ii) in a straightforward way.
$\bigcup \langle x, y \rangle = \{ x,y \}$
. So we can construct the desired programs by combining the procedures from (i) and (ii) in a straightforward way. -
(vi) We have to implement a procedure that checks whether x is an ordered pair: use (v) to compute the first and second projections of x, say, y and z. Then compute
 $\langle y,z \rangle $
with (iv) and check whether this equals x.
$\langle y,z \rangle $
with (iv) and check whether this equals x. -
(vii) Check whether x consists of ordered pairs (using (vi)), and then check that x is functional with (v).
-
(viii) Use four registers:
 $R_0$
contains x,
$R_0$
contains x,
 $R_1$
for the union of x, and
$R_1$
for the union of x, and
 $R_2$
and
$R_2$
and
 $R_3$
as auxiliary registers. Then proceed as follows: as long as
$R_3$
as auxiliary registers. Then proceed as follows: as long as
 $R_0$
is non-empty, take a set from
$R_0$
is non-empty, take a set from
 $R_0$
and save it in
$R_0$
and save it in
 $R_2$
, then remove it from
$R_2$
, then remove it from
 $R_0$
. Then, as long as
$R_0$
. Then, as long as
 $R_2$
is non-empty, take an element of
$R_2$
is non-empty, take an element of
 $R_2$
and save it in
$R_2$
and save it in
 $R_3$
, then remove it from
$R_3$
, then remove it from
 $R_2$
and add it to
$R_2$
and add it to
 $R_1$
. Once
$R_1$
. Once
 $R_0$
is empty, we are done: copy our result from
$R_0$
is empty, we are done: copy our result from
 $R_1$
to
$R_1$
to
 $R_0$
, and stop.
$R_0$
, and stop. -
(ix) A similar procedure as in the previous item does the job.
-
(x) Take and remove elements from
 $R_0$
as long as it is non-empty. To each element, apply the first-projection from (v), and add it to
$R_0$
as long as it is non-empty. To each element, apply the first-projection from (v), and add it to
 $R_1$
. Once
$R_1$
. Once
 $R_0$
is empty,
$R_0$
is empty,
 $R_1$
contains the domain of x.
$R_1$
contains the domain of x. -
(xi) Search through f until a pair with first coordinate x is found. Then return the second projection of that pair.
-
(xii) Observe that it is straightforward to compute whether “x is a transitive set of transitive sets.”
-
(xiii) Check whether x is a function whose domain is an ordinal.
-
(xiv) Given a procedure for checking P, take and remove elements from y until some x is found satisfying
 $P(x)$
. By the definition of the
$P(x)$
. By the definition of the
 $\mathtt {TAKE}$
-operation, this will be the
$\mathtt {TAKE}$
-operation, this will be the
 $<_\tau $
-minimal element of y satisfying P.
$<_\tau $
-minimal element of y satisfying P. -
(xv) This is just function application.
-
(xvi) This is straightforward using the
 $\mathtt {POW}$
-operation.
$\mathtt {POW}$
-operation. -
(xvii) Again, straightforward using the
 $\mathtt {POW}$
-operation.
$\mathtt {POW}$
-operation. -
(xviii) Note that the limes inferior of a sequence of sets can be presented as follows:
This can be straightforwardly implemented by combining the previous items of this lemma. $$ \begin{align*}\liminf_{\gamma < \alpha} x_\gamma = \bigcup_{\beta < \alpha} \, \bigcap_{\gamma \in [\beta+1,\alpha)} x_\gamma. \end{align*} $$
$$ \begin{align*}\liminf_{\gamma < \alpha} x_\gamma = \bigcup_{\beta < \alpha} \, \bigcap_{\gamma \in [\beta+1,\alpha)} x_\gamma. \end{align*} $$
Lemma 3.7. Let
![]() $\phi (\bar x)$
be a
$\phi (\bar x)$
be a
![]() $\Delta _0$
-formula. Then there is an
$\Delta _0$
-formula. Then there is an
![]() $\mathrm {SRM}\ p$
such that
$\mathrm {SRM}\ p$
such that
![]() $p(\ulcorner \phi \urcorner ,\bar x) = 1$
if
$p(\ulcorner \phi \urcorner ,\bar x) = 1$
if
![]() $\mathrm {V} \vDash \phi (\bar x)$
and
$\mathrm {V} \vDash \phi (\bar x)$
and
![]() $p(\ulcorner \phi \urcorner ,\bar x) =0$
if
$p(\ulcorner \phi \urcorner ,\bar x) =0$
if
![]() $\mathrm {V} \vDash \neg \phi (\bar x)$
.
$\mathrm {V} \vDash \neg \phi (\bar x)$
.
Proof We construct a machine that recursively calls itself. For the base cases, let
![]() $p(\ulcorner x_i = x_j \urcorner ,\bar x)$
be the program that returns
$p(\ulcorner x_i = x_j \urcorner ,\bar x)$
be the program that returns
![]() $1$
if
$1$
if
![]() $x_i = x_j$
and
$x_i = x_j$
and
![]() $0$
if
$0$
if
![]() $x_i \neq x_j$
. Similarly, let
$x_i \neq x_j$
. Similarly, let
![]() $p(\ulcorner x_i \in x_j \urcorner ,\bar x)$
be the program that returns
$p(\ulcorner x_i \in x_j \urcorner ,\bar x)$
be the program that returns
![]() $1$
if
$1$
if
![]() $x_i \in x_j$
and
$x_i \in x_j$
and
![]() $0$
if
$0$
if
![]() $x_i \notin x_j$
. The cases for conjunction, disjunction, and implication are easily constructed by recursion. For the bounded existential quantifier,
$x_i \notin x_j$
. The cases for conjunction, disjunction, and implication are easily constructed by recursion. For the bounded existential quantifier,
![]() $\exists x \in a \, \phi (x)$
, the machine p conducts a search through a by consecutively taking and removing elements. If p finds some
$\exists x \in a \, \phi (x)$
, the machine p conducts a search through a by consecutively taking and removing elements. If p finds some
![]() $b \in a$
such that
$b \in a$
such that
![]() $p(\ulcorner \phi \urcorner ,\langle b,a,x \rangle )= 1$
, then p returns
$p(\ulcorner \phi \urcorner ,\langle b,a,x \rangle )= 1$
, then p returns
![]() $1$
. If no such b is found, then a does not contain a witness for
$1$
. If no such b is found, then a does not contain a witness for
![]() $\phi $
and p returns
$\phi $
and p returns
![]() $0$
. The bounded universal quantifier can be implemented similarly with a bounded search.
$0$
. The bounded universal quantifier can be implemented similarly with a bounded search.
The next theorem shows that moving from Ordinal Turing Machines to Set Register Machines does not increase the computational strength. We do not give a detailed proof since the result is not used in the remainder of this article.
Theorem 3.8. Ordinal Turing machines with parameters (OTMs) and set register machines with parameters (SRMs) can simulate each other.
Proof For the first direction, recall that OTMs and ordinal register machines (ORMs) can simulate each other (e.g., Carl [Reference Carl3]). It will, therefore, be enough to show that SRMs simulate ORMs but, in fact, more is true: it is straightforward to see that every ORM-program can be executed by an SRM.
The other direction can be shown by a straightforward but tedious coding argument by using a large enough fragment of the well-order
![]() $<_\tau $
as a parameter (Carl, Galeotti, and Passmann [Reference Carl, Galeotti and Passmann4] spell out a very similar argument in an appendix; Carl [Reference Carl3, Section 2.3.2 and Chapter 3] discusses codings as well).
$<_\tau $
as a parameter (Carl, Galeotti, and Passmann [Reference Carl, Galeotti and Passmann4] spell out a very similar argument in an appendix; Carl [Reference Carl3, Section 2.3.2 and Chapter 3] discusses codings as well).
3.2 Oracles and relative computability
As with other notions of computability, we can enrich
![]() $\mathrm {SRM}^+$
s with oracles. Let
$\mathrm {SRM}^+$
s with oracles. Let
![]() $O: \mathrm {V} \to \mathrm {V}$
be a partial class function. We obtain oracle
$O: \mathrm {V} \to \mathrm {V}$
be a partial class function. We obtain oracle
![]() $\mathrm {SRM}^{+,O}$
by extending Definition 3.1 with the following operation:
$\mathrm {SRM}^{+,O}$
by extending Definition 3.1 with the following operation:
“
![]() $\mathtt {ORACLE}(i,j)$
”: replace the contents of the jth register with the result of querying the oracle O with
$\mathtt {ORACLE}(i,j)$
”: replace the contents of the jth register with the result of querying the oracle O with
![]() $R_i$
.
$R_i$
.
We also extend Definition 3.2:
If
![]() $p_l$
is “
$p_l$
is “
![]() $\mathtt {ORACLE}(i,j)$
,” proceed as follows: if
$\mathtt {ORACLE}(i,j)$
,” proceed as follows: if
![]() $O(r_i)$
is defined, let
$O(r_i)$
is defined, let
![]() $r_j^+ = O(r_i)$
,
$r_j^+ = O(r_i)$
,
![]() $r_n^+ = r_n$
for all
$r_n^+ = r_n$
for all
![]() $n \neq i$
, and
$n \neq i$
, and
![]() $l^+ = l + 1$
. If
$l^+ = l + 1$
. If
![]() $O(r_i)$
is undefined, let
$O(r_i)$
is undefined, let
![]() $r_j^+ = r_j$
for all
$r_j^+ = r_j$
for all
![]() $j \leq k$
and
$j \leq k$
and
![]() $l^+ = l$
.
$l^+ = l$
.
The evaluation function is chosen like this to ensure that any
![]() $\mathrm {SRM}^{+,O}$
loops whenever the oracle is queried on undefined input. This entails that the oracle is only queried on its domain within a successful computation. Given oracles, we can define a relative notion of computability.
$\mathrm {SRM}^{+,O}$
loops whenever the oracle is queried on undefined input. This entails that the oracle is only queried on its domain within a successful computation. Given oracles, we can define a relative notion of computability.
Definition 3.9. We say that a function f is
![]() $\mathrm {SRM}^+$
-computable in g if and only if there is an
$\mathrm {SRM}^+$
-computable in g if and only if there is an
![]() $\mathrm {SRM}^{+,g}$
program p that computes f.
$\mathrm {SRM}^{+,g}$
program p that computes f.
A function is
![]() $\mathrm {SRM}^+$
-computable if and only if it is
$\mathrm {SRM}^+$
-computable if and only if it is
![]() $\mathrm {SRM}^+$
-computable in the empty function. In fact, a function is
$\mathrm {SRM}^+$
-computable in the empty function. In fact, a function is
![]() $\mathrm {SRM}^+$
-computable if and only if it is
$\mathrm {SRM}^+$
-computable if and only if it is
![]() $\mathrm {SRM}^+$
-computable in any set-sized function.
$\mathrm {SRM}^+$
-computable in any set-sized function.
We will now work towards generalising a result of Kleene and Post [Reference Kleene and Post17], which will be useful later but is also interesting in its own regard.
Proposition 3.10. The class function
![]() $V_{(\cdot )}: \mathrm {Ord} \to V, \alpha \mapsto V_\alpha $
is
$V_{(\cdot )}: \mathrm {Ord} \to V, \alpha \mapsto V_\alpha $
is
![]() $\mathrm {SRM}^+$
-computable.
$\mathrm {SRM}^+$
-computable.
Proof An
![]() $\mathrm {SRM}^+$
-program does this by starting with the empty set and consecutively computing power sets while keeping the current rank in an auxiliary register. The program keeps computing until it reaches the desired
$\mathrm {SRM}^+$
-program does this by starting with the empty set and consecutively computing power sets while keeping the current rank in an auxiliary register. The program keeps computing until it reaches the desired
![]() $\alpha $
.
$\alpha $
.
This procedure is implemented in the following program, where the input
![]() $\alpha $
is written into
$\alpha $
is written into
![]() $R_0$
; note that the initial configuration of all other registers is
$R_0$
; note that the initial configuration of all other registers is
![]() $\emptyset $
. We use
$\emptyset $
. We use
![]() $R_1$
to count our current stage
$R_1$
to count our current stage
![]() $\beta $
and
$\beta $
and
![]() $R_2$
to save the current
$R_2$
to save the current
![]() $V_\beta $
.
$V_\beta $
.
1:
![]() $\mathtt {IF} \ R_0 = R_1 \ \mathtt {THEN \ GO \ TO} \ 5$
$\mathtt {IF} \ R_0 = R_1 \ \mathtt {THEN \ GO \ TO} \ 5$
2:
![]() $\mathtt {POW}(2,2)$
$\mathtt {POW}(2,2)$
3:
![]() $\mathtt {ADD}(1,1)$
$\mathtt {ADD}(1,1)$
4:
![]() $\mathtt {GO \ TO} \ 1$
$\mathtt {GO \ TO} \ 1$
Note that the register
![]() $R_0$
remains unchanged, and the registers
$R_0$
remains unchanged, and the registers
![]() $R_1$
and
$R_1$
and
![]() $R_2$
are monotonically increasing. Therefore, the program does the job also at limit stages.
$R_2$
are monotonically increasing. Therefore, the program does the job also at limit stages.
The following proposition can be anticipated from how the evaluation of the
![]() $\mathtt {TAKE}$
-operation was defined.
$\mathtt {TAKE}$
-operation was defined.
Proposition 3.11. The global well-ordering
![]() $<_\tau $
is
$<_\tau $
is
![]() $\mathrm {SRM}^+$
-decidable.
$\mathrm {SRM}^+$
-decidable.
Proof This is implemented by an
![]() $\mathrm {SRM}^+$
that does the following: given a and b, check whether
$\mathrm {SRM}^+$
that does the following: given a and b, check whether
![]() $a = b$
. If so, we are done. If not, compute
$a = b$
. If so, we are done. If not, compute
![]() $\{ a,b \}$
and use the
$\{ a,b \}$
and use the
![]() $\mathtt {TAKE}$
-operation to take a set
$\mathtt {TAKE}$
-operation to take a set
![]() $c \in \{ a,b \}$
. By the definition of the
$c \in \{ a,b \}$
. By the definition of the
![]() $\mathtt {TAKE}$
-operation, either
$\mathtt {TAKE}$
-operation, either
![]() $c = a$
and then
$c = a$
and then
![]() $a <_\tau b$
, or
$a <_\tau b$
, or
![]() $c = b$
and then
$c = b$
and then
![]() $b <_\tau a$
.
$b <_\tau a$
.
By the
![]() $\alpha $
th element of V according to
$\alpha $
th element of V according to
![]() $<_\tau $
, we denote the unique x such that the order type of
$<_\tau $
, we denote the unique x such that the order type of
![]() $(\{ y \, | \, y <_\tau x \}, <_\tau )$
is
$(\{ y \, | \, y <_\tau x \}, <_\tau )$
is
![]() $\alpha $
.
$\alpha $
.
Proposition 3.12. The bijective class function
![]() $F_\tau : \mathrm {Ord} \to V$
mapping
$F_\tau : \mathrm {Ord} \to V$
mapping
![]() $\alpha $
to the
$\alpha $
to the
![]() $\alpha $
th element of V according to
$\alpha $
th element of V according to
![]() $<_\tau $
is
$<_\tau $
is
![]() $\mathrm {SRM}^+$
-computable and so is its inverse.
$\mathrm {SRM}^+$
-computable and so is its inverse.
Proof Recall our assumption that
![]() $\operatorname {\mathrm {rank}}(x) < \operatorname {\mathrm {rank}}(y)$
implies
$\operatorname {\mathrm {rank}}(x) < \operatorname {\mathrm {rank}}(y)$
implies
![]() $x <_\tau y$
. Therefore, computing
$x <_\tau y$
. Therefore, computing
![]() $<_\tau $
on some
$<_\tau $
on some
![]() $V_\alpha $
means to compute an initial segment of
$V_\alpha $
means to compute an initial segment of
![]() $<_\tau $
. We can therefore proceed as follows.
$<_\tau $
. We can therefore proceed as follows.
For the forward direction, use the
![]() $\mathtt {POW}$
-operation to compute
$\mathtt {POW}$
-operation to compute
![]() $V_{\alpha +1}$
. Then take and remove elements from
$V_{\alpha +1}$
. Then take and remove elements from
![]() $V_{\alpha +1}$
while running a counter until it reaches
$V_{\alpha +1}$
while running a counter until it reaches
![]() $\alpha $
. The last element taken is the set we were looking for.
$\alpha $
. The last element taken is the set we were looking for.
For the other direction, given
![]() $a \in V$
, compute a
$a \in V$
, compute a
![]() $V_\beta $
such that
$V_\beta $
such that
![]() $a \in V_\beta $
. Then start a counter and successively take and remove elements from
$a \in V_\beta $
. Then start a counter and successively take and remove elements from
![]() $V_\beta $
until a is reached. The value of the counter is the ordinal
$V_\beta $
until a is reached. The value of the counter is the ordinal
![]() $\alpha $
we are looking for.
$\alpha $
we are looking for.
Proposition 3.13. Let O be a
![]() $($
partial
$($
partial
![]() $)$
class function. The
$)$
class function. The
![]() $\mathrm {SRM}^{+,O}$
halting problem is
$\mathrm {SRM}^{+,O}$
halting problem is
![]() $\mathrm {SRM}^{+,O}$
undecidable.
$\mathrm {SRM}^{+,O}$
undecidable.
Proof This is proved by contradiction with the usual diagonal argument. Assume that there is a machine p such that
![]() $p(x) = 1$
if and only if x is an
$p(x) = 1$
if and only if x is an
![]() $\mathrm {SRM}^+$
that halts, and
$\mathrm {SRM}^+$
that halts, and
![]() $p(x) = 0$
otherwise. Then define a machine q such that
$p(x) = 0$
otherwise. Then define a machine q such that
![]() $q(x)$
does not halt if and only if
$q(x)$
does not halt if and only if
![]() $p(x) = 1$
. Then,
$p(x) = 1$
. Then,
![]() $p(q) = 1$
if and only if
$p(q) = 1$
if and only if
![]() $q(q)$
does not halt if and only if
$q(q)$
does not halt if and only if
![]() $p(q) = 0$
. A contradiction.
$p(q) = 0$
. A contradiction.
Proposition 3.14. Let O be a
![]() $($
partial
$($
partial
![]() $)$
class function. Then there is an oracle
$)$
class function. Then there is an oracle
![]() $\tilde O$
such that there is an
$\tilde O$
such that there is an
![]() $\mathrm {SRM}^{+,\tilde O}$
-program u which is universal for
$\mathrm {SRM}^{+,\tilde O}$
-program u which is universal for
![]() $\mathrm {SRM}^{+,O}$
, i.e.,
$\mathrm {SRM}^{+,O}$
, i.e.,
![]() $u(p,x)$
and
$u(p,x)$
and
![]() $p(x)$
are both defined and equal whenever at least one of them is defined. Moreover, there is an
$p(x)$
are both defined and equal whenever at least one of them is defined. Moreover, there is an
![]() $\mathrm {SRM}^{+,\tilde O}$
-program c such that
$\mathrm {SRM}^{+,\tilde O}$
-program c such that
![]() $c(p,x) = 1$
if x is a successful computation of p and
$c(p,x) = 1$
if x is a successful computation of p and
![]() $c(p,x) = 0$
otherwise. In particular, if O is the empty function, then
$c(p,x) = 0$
otherwise. In particular, if O is the empty function, then
![]() $\tilde O$
can be taken empty as well.
$\tilde O$
can be taken empty as well.
Proof Let
![]() $\tilde O$
be the function such that
$\tilde O$
be the function such that
![]() $\tilde O(x) = \langle 1,O(x) \rangle $
whenever
$\tilde O(x) = \langle 1,O(x) \rangle $
whenever
![]() $O(x)$
is defined and
$O(x)$
is defined and
![]() $\tilde O(x) = \langle 0,0 \rangle $
whenever
$\tilde O(x) = \langle 0,0 \rangle $
whenever
![]() $O(x)$
is undefined. Using Lemma 3.6 and
$O(x)$
is undefined. Using Lemma 3.6 and
![]() $\tilde O$
, it is straightforward (but tedious) to construct a program c such that
$\tilde O$
, it is straightforward (but tedious) to construct a program c such that
![]() $c(p,x) = 1$
if x is a successful computation of p and
$c(p,x) = 1$
if x is a successful computation of p and
![]() $c(p,x) = 0$
otherwise. Then note that
$c(p,x) = 0$
otherwise. Then note that
![]() $p(x)$
is defined if and only if there is a successful computation of p on input x. For this reason, the universal machine can be implemented as an unbounded search through
$p(x)$
is defined if and only if there is a successful computation of p on input x. For this reason, the universal machine can be implemented as an unbounded search through
![]() $\mathrm {V}$
that stops if a successful computation for p on input x is found, and returns
$\mathrm {V}$
that stops if a successful computation for p on input x is found, and returns
![]() $p(x)$
. In the case where O is the empty function, we can take
$p(x)$
. In the case where O is the empty function, we can take
![]() $\tilde O$
to be the empty function as well because all
$\tilde O$
to be the empty function as well because all
![]() $\mathrm {SRM}^+$
-operations are
$\mathrm {SRM}^+$
-operations are
![]() $\mathrm {SRM}^+$
-decidable.
$\mathrm {SRM}^+$
-decidable.
It is possible to construct an
![]() $\mathrm {SRM}^{+,O}$
-universal machine for
$\mathrm {SRM}^{+,O}$
-universal machine for
![]() $\mathrm {SRM}^{+,O}$
, if one changes the definition of oracle evaluation in such a way that the universal machine can query the oracle without the risk of not halting.
$\mathrm {SRM}^{+,O}$
, if one changes the definition of oracle evaluation in such a way that the universal machine can query the oracle without the risk of not halting.
Let
![]() $D(x,y)$
be a binary predicate in the language of set theory. Adapting from Kleene and Post [Reference Kleene and Post17], we write
$D(x,y)$
be a binary predicate in the language of set theory. Adapting from Kleene and Post [Reference Kleene and Post17], we write
![]() $D_z(x) := D(x,z)$
and define
$D_z(x) := D(x,z)$
and define
![]() $D^z$
to be the join of all
$D^z$
to be the join of all
![]() $D_{y}$
with
$D_{y}$
with
![]() $y \neq z$
, as follows:
$y \neq z$
, as follows:
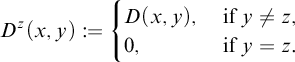 $$ \begin{align*}D^z(x,y) := \begin{cases} D(x,y), & \text{ if } y \neq z, \\ 0, & \text{ if } y = z. \end{cases} \end{align*} $$
$$ \begin{align*}D^z(x,y) := \begin{cases} D(x,y), & \text{ if } y \neq z, \\ 0, & \text{ if } y = z. \end{cases} \end{align*} $$
The proof of the following theorem is a generalisation of a result by Kleene and Post [Reference Kleene and Post17, Theorem 2]; our proof will be a generalisation of their diagonal argument to the case of
![]() $\mathrm {SRM}^+$
.
$\mathrm {SRM}^+$
.
Theorem 3.15. There is a set-theoretic predicate
![]() $D(x,y)$
such that
$D(x,y)$
such that
![]() $D_z$
is not
$D_z$
is not
![]() $\mathrm {SRM}^+$
-computable in
$\mathrm {SRM}^+$
-computable in
![]() $D^z$
.
$D^z$
.
Proof We define the predicate by informally describing a total
![]() $\mathrm {SRM}^{+,H}$
-program that makes use of an oracle H for the
$\mathrm {SRM}^{+,H}$
-program that makes use of an oracle H for the
![]() $\mathrm {SRM}^+$
-halting problem.
$\mathrm {SRM}^+$
-halting problem.
Let
![]() $R_{init}$
be an auxiliary register which is used to save an initial segment of the predicate we are defining. Let
$R_{init}$
be an auxiliary register which is used to save an initial segment of the predicate we are defining. Let
![]() $R_{stage}$
be an auxiliary register that contains an ordinal representing the current stage of the construction.
$R_{stage}$
be an auxiliary register that contains an ordinal representing the current stage of the construction.
To ensure the non-computability desired in the theorem, we have to satisfy class-many conditions, for each
![]() $\mathrm {SRM}^+$
-program e (possibly with parameters) and set z:
$\mathrm {SRM}^+$
-program e (possibly with parameters) and set z:
Apply the inverse of the Gödel pairing function to
![]() $R_{stage}$
to obtain ordinals
$R_{stage}$
to obtain ordinals
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
. By Proposition 3.12, calculate
$\beta $
. By Proposition 3.12, calculate
![]() $e := F_\tau ^{-1}(\alpha )$
and
$e := F_\tau ^{-1}(\alpha )$
and
![]() $z := F_\tau ^{-1}(\beta )$
. We want to extend
$z := F_\tau ^{-1}(\beta )$
. We want to extend
![]() $R_{init}$
in such a way that
$R_{init}$
in such a way that
![]() $P_{e,z}$
will hold. To this end, let x be the
$P_{e,z}$
will hold. To this end, let x be the
![]() $<_\tau $
-least set for which
$<_\tau $
-least set for which
![]() $R_{init}(x,z)$
is undefined. For convenience, let us say that E is a z-extension of
$R_{init}(x,z)$
is undefined. For convenience, let us say that E is a z-extension of
![]() $R_{init}$
if
$R_{init}$
if
![]() $R_{init} \subseteq E$
and if
$R_{init} \subseteq E$
and if
![]() $R_{init}(w,z)$
is undefined for some w then so is
$R_{init}(w,z)$
is undefined for some w then so is
![]() $E(w,z)$
. There are two cases to consider.
$E(w,z)$
. There are two cases to consider.
Case 1: There is a z-extension
![]() $D_{init}$
of
$D_{init}$
of
![]() $R_{init}$
such that there is a successful computation of e on input
$R_{init}$
such that there is a successful computation of e on input
![]() $(x,z)$
using
$(x,z)$
using
![]() $D_{init}^z$
as an oracle, i.e., the oracle is the predicate obtained from
$D_{init}^z$
as an oracle, i.e., the oracle is the predicate obtained from
![]() $D_{init}$
by taking
$D_{init}$
by taking
![]() $D_{init}^z(w,y) = D_{init}(w,y)$
if
$D_{init}^z(w,y) = D_{init}(w,y)$
if
![]() $y \neq z$
, and
$y \neq z$
, and
![]() $D_{init}^z(w,z) = 0$
for all w. Note that our machine can decide whether such an extension exists by using the oracle for the
$D_{init}^z(w,z) = 0$
for all w. Note that our machine can decide whether such an extension exists by using the oracle for the
![]() $\mathrm {SRM}^+$
-halting problem. Let
$\mathrm {SRM}^+$
-halting problem. Let
![]() $y \in \{ 0,1 \}$
be the result of this computation. As
$y \in \{ 0,1 \}$
be the result of this computation. As
![]() $D_{init}$
is a z-extension of
$D_{init}$
is a z-extension of
![]() $R_{init}$
, it must be that
$R_{init}$
, it must be that
![]() $D_{init}(x,z)$
is undefined. We can therefore set
$D_{init}(x,z)$
is undefined. We can therefore set
![]() $R_{init} := D_{init} \cup \{ ((x,z), 1 - y) \}$
. This choice ensures that e does not witness that
$R_{init} := D_{init} \cup \{ ((x,z), 1 - y) \}$
. This choice ensures that e does not witness that
![]() $D_z$
is computable in
$D_z$
is computable in
![]() $D^z$
.
$D^z$
.
Case 2: For all z-extensions
![]() $D_{init}$
of
$D_{init}$
of
![]() $R_{init}$
there is no successful computation of e on input
$R_{init}$
there is no successful computation of e on input
![]() $(x,z)$
with
$(x,z)$
with
![]() $D_{init}^z$
as oracle. In this case, we let
$D_{init}^z$
as oracle. In this case, we let
![]() $R_{init} := R_{init} \cup \{ ((x,y),0) \}$
. This (arbitrary) choice works because the final predicate D will be such that there is no successful computation of e on input
$R_{init} := R_{init} \cup \{ ((x,y),0) \}$
. This (arbitrary) choice works because the final predicate D will be such that there is no successful computation of e on input
![]() $(x,z)$
with oracle
$(x,z)$
with oracle
![]() $D^z$
: for contradiction, suppose there was such a successful computation c and consider the z-extension
$D^z$
: for contradiction, suppose there was such a successful computation c and consider the z-extension
![]() $D_{init}$
of
$D_{init}$
of
![]() $R_{init}$
given by
$R_{init}$
given by
![]() $D_{init}(x,y) = D(x,y)$
for all
$D_{init}(x,y) = D(x,y)$
for all
![]() $(x,y)$
,
$(x,y)$
,
![]() $y \neq z$
, for which the oracle is called during the computation c. As
$y \neq z$
, for which the oracle is called during the computation c. As
![]() $D_{init}^z(w,z)$
is defined for all w, all oracle calls during the computation c are still the same when using
$D_{init}^z(w,z)$
is defined for all w, all oracle calls during the computation c are still the same when using
![]() $D_{init}^z$
instead of
$D_{init}^z$
instead of
![]() $D^z$
. Hence, there is a successful computation c of e on input
$D^z$
. Hence, there is a successful computation c of e on input
![]() $(x,z)$
with oracle
$(x,z)$
with oracle
![]() $D_{init}^z$
. But that is in contradiction to the assumption of this case.
$D_{init}^z$
. But that is in contradiction to the assumption of this case.
The program defined this way will eventually give rise to a completely defined predicate D on
![]() $V \times V$
. The value of
$V \times V$
. The value of
![]() $D(x,y)$
can be computed by running the procedure above until the value for
$D(x,y)$
can be computed by running the procedure above until the value for
![]() $(x,y)$
is known.
$(x,y)$
is known.
Note that the program described in the proof above does not use any parameters and can thus be coded as a natural number.
Remark 3.16. In fact, Kleene and Post prove a stronger result which allows to locate D between any two Turing degrees. A similar result is possible here but we leave the proof to the interested reader as we do not need it.
3.3 Constructible SRMs
For our applications to the first-order logic of CZF, it will be important that we can express the predicate “
![]() $D(x,y)$
holds” in a way that only uses the language of set theory without introducing an extra relation symbol into our language to refer to the global well-order. This means that we have to circumvent referring to
$D(x,y)$
holds” in a way that only uses the language of set theory without introducing an extra relation symbol into our language to refer to the global well-order. This means that we have to circumvent referring to
![]() $<_\tau $
as this is an extra symbol that cannot be defined in terms of a set-theoretic formula. Due to the following well-known fact, we will restrict our attention to constructible sets (for reference see, e.g., Jech [Reference Jech13, Theorem 13.18 and Lemma 13.19]):
$<_\tau $
as this is an extra symbol that cannot be defined in terms of a set-theoretic formula. Due to the following well-known fact, we will restrict our attention to constructible sets (for reference see, e.g., Jech [Reference Jech13, Theorem 13.18 and Lemma 13.19]):
Fact 3.17. There is a
![]() $\Sigma _1$
-definable well-ordering
$\Sigma _1$
-definable well-ordering
![]() $<_{\mathrm {L}}$
of the constructible universe
$<_{\mathrm {L}}$
of the constructible universe
![]() $\mathrm {L}$
.
$\mathrm {L}$
.
So if we restrict our attention to
![]() $\mathrm {SRM}^+$
s that work only on constructible sets, we can replace
$\mathrm {SRM}^+$
s that work only on constructible sets, we can replace
![]() $<_\tau $
with
$<_\tau $
with
![]() $<_{\mathrm {L}}$
in Definition 3.2. The resulting notion of
$<_{\mathrm {L}}$
in Definition 3.2. The resulting notion of
![]() $\mathrm {SRM}$
will be called constructible
$\mathrm {SRM}$
will be called constructible
![]() $\mathrm {SRM}^+$
and denoted, in short, by
$\mathrm {SRM}^+$
and denoted, in short, by
![]() $\mathrm {SRM}^+_{\mathrm {L}}$
. Note that all of the results obtained so far about
$\mathrm {SRM}^+_{\mathrm {L}}$
. Note that all of the results obtained so far about
![]() $\mathrm {SRM}^+$
s can be relativised to
$\mathrm {SRM}^+$
s can be relativised to
![]() $\mathrm {L}$
and thus transferred to
$\mathrm {L}$
and thus transferred to
![]() $\mathrm {SRM}^+_{\mathrm {L}}$
. In particular, we get the following versions of Lemma 3.7 and Theorem 3.15:
$\mathrm {SRM}^+_{\mathrm {L}}$
. In particular, we get the following versions of Lemma 3.7 and Theorem 3.15:
Lemma 3.18. Let
![]() $\phi (\bar x)$
be a
$\phi (\bar x)$
be a
![]() $\Delta _0$
-formula. There is an
$\Delta _0$
-formula. There is an
![]() $\mathrm {SRM}_{\mathrm {L}}$
-program p such that
$\mathrm {SRM}_{\mathrm {L}}$
-program p such that
![]() $p(\ulcorner \phi \urcorner ,\bar x) = 1$
if
$p(\ulcorner \phi \urcorner ,\bar x) = 1$
if
![]() $L \vDash \phi $
and
$L \vDash \phi $
and
![]() $p(\ulcorner \phi \urcorner ,\bar x) =0$
if
$p(\ulcorner \phi \urcorner ,\bar x) =0$
if
![]() $L \vDash \neg \phi $
.
$L \vDash \neg \phi $
.
Corollary 3.19. There exists a non-
![]() $\mathrm {SRM}^+_{\mathrm {L}}$
-computable set-theoretic predicate
$\mathrm {SRM}^+_{\mathrm {L}}$
-computable set-theoretic predicate
![]() $D(x,y)$
, expressible in the language of set theory, such that
$D(x,y)$
, expressible in the language of set theory, such that
![]() $D_z$
is not
$D_z$
is not
![]() $\mathrm {SRM}^+_{\mathrm {L}}$
-computable in
$\mathrm {SRM}^+_{\mathrm {L}}$
-computable in
![]() $D^z$
.
$D^z$
.
4 Realisability
We will now define a notion of realisability based on
![]() $\mathrm {SRM}^+$
s, and observe a few proof-theoretic consequences for
$\mathrm {SRM}^+$
s, and observe a few proof-theoretic consequences for
![]() $\mathrm {CZF}$
.
$\mathrm {CZF}$
.
Definition 4.1. We define the realisability relation
![]() $\Vdash $
for an
$\Vdash $
for an
![]() $\mathrm {SRM}^{(+),(O)}_{(\mathrm {L})} r$
recursively as follows:
$\mathrm {SRM}^{(+),(O)}_{(\mathrm {L})} r$
recursively as follows:
-
(i)
 $r \Vdash a \in b$
if and only if
$r \Vdash a \in b$
if and only if
 $a \in b$
;
$a \in b$
; -
(ii)
 $r \Vdash a = b$
if and only if
$r \Vdash a = b$
if and only if
 $a = b$
;
$a = b$
; -
(iii)
 $r \Vdash \phi _0 \wedge \phi _1$
if and only if
$r \Vdash \phi _0 \wedge \phi _1$
if and only if
 $r(0) \Vdash \phi _0$
and
$r(0) \Vdash \phi _0$
and
 $r(1) \Vdash \phi _1$
;
$r(1) \Vdash \phi _1$
; -
(iv)
 $r \Vdash \phi _0 \vee \phi _1$
if and only if
$r \Vdash \phi _0 \vee \phi _1$
if and only if
 $r(1) \Vdash \phi _{r(0)}$
;
$r(1) \Vdash \phi _{r(0)}$
; -
(v)
 $r \Vdash \phi _0 \rightarrow \phi _1$
if and only if whenever
$r \Vdash \phi _0 \rightarrow \phi _1$
if and only if whenever
 $s \Vdash \phi _0$
, then
$s \Vdash \phi _0$
, then
 $r(s) \Vdash \phi _1$
;
$r(s) \Vdash \phi _1$
; -
(vi)
 $r \Vdash \exists x \phi (x)$
if and only if
$r \Vdash \exists x \phi (x)$
if and only if
 $r(1) \Vdash \phi (r(0))$
;
$r(1) \Vdash \phi (r(0))$
; -
(vii)
 $r \Vdash \forall x \phi (x)$
if and only if
$r \Vdash \forall x \phi (x)$
if and only if
 $r(a) \Vdash \phi (a)$
for every set a.
$r(a) \Vdash \phi (a)$
for every set a.
We say that
![]() $\phi $
is
$\phi $
is
![]() $\mathrm {SRM}$
-realisable if and only if there is an
$\mathrm {SRM}$
-realisable if and only if there is an
![]() $\mathrm {SRM}$
realising
$\mathrm {SRM}$
realising
![]() $\phi $
. Similarly, we say that
$\phi $
. Similarly, we say that
![]() $\phi $
is
$\phi $
is
![]() $\mathrm {SRM}^+$
-realisable if and only if there is an
$\mathrm {SRM}^+$
-realisable if and only if there is an
![]() $\mathrm {SRM}^+$
realising
$\mathrm {SRM}^+$
realising
![]() $\phi $
; and so for
$\phi $
; and so for
![]() $\mathrm {SRM}^{+,O}$
,
$\mathrm {SRM}^{+,O}$
,
![]() $\mathrm {SRM}^+_{\mathrm {L}}$
, and
$\mathrm {SRM}^+_{\mathrm {L}}$
, and
![]() $\mathrm {SRM}^{+,O}_{\mathrm {L}}$
.
$\mathrm {SRM}^{+,O}_{\mathrm {L}}$
.
This could be extended to infinitary languages as done by Carl, Galeotti, and Passmann [Reference Carl, Galeotti and Passmann4]. Analogously to (i) and (ii), one could give realisability semantics to the global well-order
![]() $<_\tau $
.
$<_\tau $
.
Theorem 4.2.
![]() $\mathrm {SRM}^{(+),(O)}_{(\mathrm {L})}$
-realisability is sound for intuitionistic logic.
$\mathrm {SRM}^{(+),(O)}_{(\mathrm {L})}$
-realisability is sound for intuitionistic logic.
Proof This is a standard argument and can be established, for example, by providing a realiser for every axiom in a Hilbert-style formalisation of
![]() $\mathbf {IQC}$
and showing that modus ponens is valid. The latter follows immediately from the definition of the realisability relation.
$\mathbf {IQC}$
and showing that modus ponens is valid. The latter follows immediately from the definition of the realisability relation.
Lemma 4.3. Let
![]() $\phi (\bar x)$
be a
$\phi (\bar x)$
be a
![]() $\Sigma _1$
-formula. Then there is some realiser
$\Sigma _1$
-formula. Then there is some realiser
![]() $r \Vdash \phi (\bar x)$
if and only if
$r \Vdash \phi (\bar x)$
if and only if
![]() $\mathrm {V} \vDash \phi (\bar x)$
.
$\mathrm {V} \vDash \phi (\bar x)$
.
Proof This is a straightforward induction on
![]() $\Sigma _1$
-formulas. We will prove a more intricate version of this lemma below (see Lemma 5.8).
$\Sigma _1$
-formulas. We will prove a more intricate version of this lemma below (see Lemma 5.8).
Theorem 4.4. The axioms
![]() $($
and schemes
$($
and schemes
![]() $)$
of extensionality, pairing, union, infinity, collection,
$)$
of extensionality, pairing, union, infinity, collection,
![]() $\in $
-induction, and
$\in $
-induction, and
![]() $\Delta _0$
-separation are
$\Delta _0$
-separation are
![]() $\mathrm {SRM}$
-realisable. The axiom of choice,
$\mathrm {SRM}$
-realisable. The axiom of choice,
![]() $\mathrm {AC}$
, is
$\mathrm {AC}$
, is
![]() $\mathrm {SRM}$
-realisable. The axioms of power set and strong collection are
$\mathrm {SRM}$
-realisable. The axioms of power set and strong collection are
![]() $\mathrm {SRM}^+$
-realisable. In conclusion,
$\mathrm {SRM}^+$
-realisable. In conclusion,
![]() $\mathrm {IKP} + \mathrm {AC}$
is
$\mathrm {IKP} + \mathrm {AC}$
is
![]() $\mathrm {SRM}$
-realisable, and
$\mathrm {SRM}$
-realisable, and
![]() $\mathrm {CZF} + \mathrm {PowerSet} + \mathrm {AC}$
is
$\mathrm {CZF} + \mathrm {PowerSet} + \mathrm {AC}$
is
![]() $\mathrm {SRM}^+$
-realisable. Moreover,
$\mathrm {SRM}^+$
-realisable. Moreover,
![]() $\mathrm {IKP} + \mathrm {AC}$
is
$\mathrm {IKP} + \mathrm {AC}$
is
![]() $\mathrm {SRM}_{\mathrm {L}}$
-realisable, and
$\mathrm {SRM}_{\mathrm {L}}$
-realisable, and
![]() $\mathrm {CZF} + \mathrm {PowerSet} + \mathrm {AC}$
is
$\mathrm {CZF} + \mathrm {PowerSet} + \mathrm {AC}$
is
![]() $\mathrm {SRM}^+_{\mathrm {L}}$
-realisable.
$\mathrm {SRM}^+_{\mathrm {L}}$
-realisable.
Proof It is straightforward to construct a realiser for the extensionality axiom. For the empty set axiom, let r be an
![]() $\mathrm {SRM}$
that returns the empty set on input
$\mathrm {SRM}$
that returns the empty set on input
![]() $0$
and the identity function on input
$0$
and the identity function on input
![]() $1$
. Then
$1$
. Then
![]() $r(1) \Vdash \forall y (y \in r(0) \rightarrow \bot )$
because
$r(1) \Vdash \forall y (y \in r(0) \rightarrow \bot )$
because
![]() $\not \Vdash _w y \in \emptyset $
for all
$\not \Vdash _w y \in \emptyset $
for all
![]() $w \in P$
and
$w \in P$
and
![]() $y \in \mathrm {V}$
. Hence,
$y \in \mathrm {V}$
. Hence,
![]() $r \Vdash \exists x \forall y (y \notin x)$
. A realiser for the union axiom is an
$r \Vdash \exists x \forall y (y \notin x)$
. A realiser for the union axiom is an
![]() $\mathrm {SRM} r$
such that, for every
$\mathrm {SRM} r$
such that, for every
![]() $a \in \mathrm {V}$
,
$a \in \mathrm {V}$
,
![]() $r(a)(0) = \bigcup a$
, using Lemma 3.6,
$r(a)(0) = \bigcup a$
, using Lemma 3.6,
![]() $r(a)(1)(x)(0) = \mathrm {id}$
, and
$r(a)(1)(x)(0) = \mathrm {id}$
, and
![]() $r(a)(1)(x)(1) = \mathrm {id}$
for every x. The infinity axiom is realised by an
$r(a)(1)(x)(1) = \mathrm {id}$
for every x. The infinity axiom is realised by an
![]() $\mathrm {SRM} r$
with
$\mathrm {SRM} r$
with
![]() $r(0) = \omega $
,
$r(0) = \omega $
,
![]() $r(1)(x)(0) = \mathrm {id}$
, and
$r(1)(x)(0) = \mathrm {id}$
, and
![]() $r(1)(x)(1) = \mathrm {id}$
for every
$r(1)(x)(1) = \mathrm {id}$
for every
![]() $x \in \mathrm {V}$
. Using the power set operation provided by
$x \in \mathrm {V}$
. Using the power set operation provided by
![]() $\mathrm {SRM}^+$
-programs, it is straightforward to construct a realiser of the power set axiom. Note that the subset collection schema is a consequence of the power set axiom.
$\mathrm {SRM}^+$
-programs, it is straightforward to construct a realiser of the power set axiom. Note that the subset collection schema is a consequence of the power set axiom.
Let us consider
![]() $\Delta _0$
-separation next, i.e., the schema consisting of
$\Delta _0$
-separation next, i.e., the schema consisting of
where
![]() $\phi (x)$
is a
$\phi (x)$
is a
![]() $\Delta _0$
-formula. By combining Lemmas 3.18 and 4.3, we know that
$\Delta _0$
-formula. By combining Lemmas 3.18 and 4.3, we know that
![]() $\Vdash \phi (x)$
if and only if
$\Vdash \phi (x)$
if and only if
![]() $p(\ulcorner \phi \urcorner ,x) = 1$
, and
$p(\ulcorner \phi \urcorner ,x) = 1$
, and
![]() $p(\ulcorner \phi \urcorner ,x) = 0$
in case
$p(\ulcorner \phi \urcorner ,x) = 0$
in case
![]() $\not \Vdash \phi (x)$
. Hence, we can compute the witnessing set y by conducting a bounded search through x and collecting all
$\not \Vdash \phi (x)$
. Hence, we can compute the witnessing set y by conducting a bounded search through x and collecting all
![]() $z \in x$
such that
$z \in x$
such that
![]() $p(\ulcorner \phi \urcorner ,z) = 1$
. It is then trivial to realise
$p(\ulcorner \phi \urcorner ,z) = 1$
. It is then trivial to realise
![]() $\forall z (z \in y \leftrightarrow z \in x \wedge \phi (x))$
because
$\forall z (z \in y \leftrightarrow z \in x \wedge \phi (x))$
because
![]() $\phi $
is a
$\phi $
is a
![]() $\Delta _0$
-formula.
$\Delta _0$
-formula.
Consider the schema of
![]() $\in $
-induction next:
$\in $
-induction next:
An
![]() $\mathrm {SRM} r$
is a realiser for this if and only if, if
$\mathrm {SRM} r$
is a realiser for this if and only if, if
![]() $s \Vdash \forall x (\forall y \in x \phi (z) \rightarrow \phi (x))$
, then
$s \Vdash \forall x (\forall y \in x \phi (z) \rightarrow \phi (x))$
, then
![]() $r(s) \Vdash \forall x \phi (x)$
. Now, in this situation, s allows us to iteratively construct realisers for every
$r(s) \Vdash \forall x \phi (x)$
. Now, in this situation, s allows us to iteratively construct realisers for every
![]() $x \in \mathrm {V}$
by successively building realisers for every
$x \in \mathrm {V}$
by successively building realisers for every
![]() $\mathrm {V}_\alpha $
. Hence, given
$\mathrm {V}_\alpha $
. Hence, given
![]() $x \in \mathrm {V}$
, we just compute realisers until we reach x and then output the realiser for
$x \in \mathrm {V}$
, we just compute realisers until we reach x and then output the realiser for
![]() $\phi (x)$
.
$\phi (x)$
.
Next, we consider the strong collection schema:
for all formulas
![]() $\phi (x,y)$
for which w is not free. Given
$\phi (x,y)$
for which w is not free. Given
![]() $x \in \mathrm {V}$
, let
$x \in \mathrm {V}$
, let
![]() $r(x)(s)$
, for
$r(x)(s)$
, for
![]() $s \Vdash \forall y \in x \exists z \phi (z,y)$
, be an
$s \Vdash \forall y \in x \exists z \phi (z,y)$
, be an
![]() $\mathrm {SRM}$
that computes a set consisting of all
$\mathrm {SRM}$
that computes a set consisting of all
![]() $s(y)(0)$
for every
$s(y)(0)$
for every
![]() $y \in x$
, and returns this set on input
$y \in x$
, and returns this set on input
![]() $0$
. Using s, it is straightforward to construct a realiser
$0$
. Using s, it is straightforward to construct a realiser
![]() $r(x)(s)(1) \Vdash \forall y \in x \exists z \in r(x)(s)(0) \ \phi (y,z) \wedge \forall z \in r(x)(s)(0) \exists y \in x \phi (y,z))$
.
$r(x)(s)(1) \Vdash \forall y \in x \exists z \in r(x)(s)(0) \ \phi (y,z) \wedge \forall z \in r(x)(s)(0) \exists y \in x \phi (y,z))$
.
Finally, consider the axiom of choice,
This axiom states that whenever x consists of non-empty sets, then there is a choice function f on x. Using Lemma 3.6, it is straightforward to construct an
![]() $\mathrm {SRM}$
that computes such a choice function: for every element of
$\mathrm {SRM}$
that computes such a choice function: for every element of
![]() $y \in x$
, use the
$y \in x$
, use the
![]() $\mathtt {TAKE}$
-operation to obtain some
$\mathtt {TAKE}$
-operation to obtain some
![]() $z \in y$
. Then add
$z \in y$
. Then add
![]() $(x,y)$
to the register in which we build the choice function.
$(x,y)$
to the register in which we build the choice function.
The corresponding results for
![]() $\mathrm {SRM}_{\mathrm {L}}$
and
$\mathrm {SRM}_{\mathrm {L}}$
and
![]() $\mathrm {SRM}^+_{\mathrm {L}}$
are obtained through relativisation and absoluteness properties (or by observing that the exact same realisers still do the job).
$\mathrm {SRM}^+_{\mathrm {L}}$
are obtained through relativisation and absoluteness properties (or by observing that the exact same realisers still do the job).
It turns out that
![]() $\mathrm {IZF}$
is not
$\mathrm {IZF}$
is not
![]() $\mathrm {SRM}^+$
-realisable.
$\mathrm {SRM}^+$
-realisable.
Theorem 4.5. There is an instance of the separation axiom that is not
![]() $\mathrm {SRM}^+$
-realisable. In conclusion,
$\mathrm {SRM}^+$
-realisable. In conclusion,
![]() $\mathrm {IZF}$
is not
$\mathrm {IZF}$
is not
![]() $\mathrm {SRM}^+$
-realisable.
$\mathrm {SRM}^+$
-realisable.
Proof Consider the predicate
![]() $H(x,y)$
expressing that “x is an
$H(x,y)$
expressing that “x is an
![]() $\mathrm {SRM}^+$
that halts on input y.” One can easily construct a formula
$\mathrm {SRM}^+$
that halts on input y.” One can easily construct a formula
![]() $\phi (x,y)$
such that
$\phi (x,y)$
such that
![]() $\phi (x,y)$
is realised if and only if
$\phi (x,y)$
is realised if and only if
![]() $H(x,y)$
is true (see also the proof of Lemma 5.11 for a similar argument). Then let s be a realiser of the following instance of the separation axiom:
$H(x,y)$
is true (see also the proof of Lemma 5.11 for a similar argument). Then let s be a realiser of the following instance of the separation axiom:
We can then construct an
![]() $\mathrm {SRM} r$
that does the following. Given x and y, compute
$\mathrm {SRM} r$
that does the following. Given x and y, compute
![]() $w := s(x)(y)(1)(0)$
and return the result. By construction,
$w := s(x)(y)(1)(0)$
and return the result. By construction,
![]() $r(x,y) = 1$
just in case
$r(x,y) = 1$
just in case
![]() $H(x,y)$
holds, and
$H(x,y)$
holds, and
![]() $r(x,y) = 0$
otherwise. So r is an
$r(x,y) = 0$
otherwise. So r is an
![]() $\mathrm {SRM}^+$
solving the
$\mathrm {SRM}^+$
solving the
![]() $\mathrm {SRM}^+$
halting problem but this is impossible (see Proposition 3.13).
$\mathrm {SRM}^+$
halting problem but this is impossible (see Proposition 3.13).
In fact, we have just seen that
![]() $\mathrm {CZF} + \mathrm {PowerSet}$
is
$\mathrm {CZF} + \mathrm {PowerSet}$
is
![]() $\mathrm {SRM}^+$
-realisable. The following proposition shows that we cannot be more fine-grained: if there is an
$\mathrm {SRM}^+$
-realisable. The following proposition shows that we cannot be more fine-grained: if there is an
![]() $\mathrm {SRM}$
realising the exponentiation axiom (possibly using an oracle), then we can already compute power sets. Recall that the axiom of exponentiation is a consequence of subset collection (Fact 2.2).
$\mathrm {SRM}$
realising the exponentiation axiom (possibly using an oracle), then we can already compute power sets. Recall that the axiom of exponentiation is a consequence of subset collection (Fact 2.2).
Proposition 4.6. Let r be an
![]() $\mathrm {SRM}$
, possibly using an oracle, such that r realises the axiom of exponentiation, then there is an
$\mathrm {SRM}$
, possibly using an oracle, such that r realises the axiom of exponentiation, then there is an
![]() $\mathrm {SRM}$
, using r as an oracle, that computes power sets.
$\mathrm {SRM}$
, using r as an oracle, that computes power sets.
Proof Let r be a realiser of the axiom of exponentiation:
where “f is a function from x to y” is expressed as a
![]() $\Delta _0$
-formula. Then, given a set a, the set
$\Delta _0$
-formula. Then, given a set a, the set
![]() $b := r(a)(\{ 0,1 \})(0)$
contains all f for which there is a realiser of “f is a function from x to y.” As this is a
$b := r(a)(\{ 0,1 \})(0)$
contains all f for which there is a realiser of “f is a function from x to y.” As this is a
![]() $\Delta _0$
-formula, Lemma 4.3 implies that b consists of all functions from a to
$\Delta _0$
-formula, Lemma 4.3 implies that b consists of all functions from a to
![]() $2$
. It is now easy to compute the power set of a as follows: for each element f of b, compute the set consisting of exactly those
$2$
. It is now easy to compute the power set of a as follows: for each element f of b, compute the set consisting of exactly those
![]() $x \in a$
for which
$x \in a$
for which
![]() $f(a) = 1$
. This results in the power set of a because each subset of a gives rise to its characteristic function contained in b.
$f(a) = 1$
. This results in the power set of a because each subset of a gives rise to its characteristic function contained in b.
Our realisability semantics also allow to give an upper bound for
![]() $\Pi _2$
-formulas provable in
$\Pi _2$
-formulas provable in
![]() $\mathrm {CZF}$
in terms of the computable strength of
$\mathrm {CZF}$
in terms of the computable strength of
![]() $\mathrm {SRM}^+$
.
$\mathrm {SRM}^+$
.
Theorem 4.7. Let
![]() $\phi $
be a
$\phi $
be a
![]() $\Sigma _1$
-formula. If
$\Sigma _1$
-formula. If
![]() $\mathrm {CZF} \vdash \forall x \exists y \phi (x,y)$
, then there is an
$\mathrm {CZF} \vdash \forall x \exists y \phi (x,y)$
, then there is an
![]() $\mathrm {SRM}^+ p$
such that
$\mathrm {SRM}^+ p$
such that
![]() $\mathrm {V} \vDash \phi (x,p(x))$
.
$\mathrm {V} \vDash \phi (x,p(x))$
.
Proof If
![]() $\mathrm {CZF} \vdash \forall x \exists y \phi (x,y)$
, then, by Theorem 4.4, there exists an
$\mathrm {CZF} \vdash \forall x \exists y \phi (x,y)$
, then, by Theorem 4.4, there exists an
![]() $\mathrm {SRM}^+ r \Vdash \forall x \exists y \phi (x,y)$
. Take
$\mathrm {SRM}^+ r \Vdash \forall x \exists y \phi (x,y)$
. Take
![]() $p(x)$
to be the
$p(x)$
to be the
![]() $\mathrm {SRM}^+$
to compute
$\mathrm {SRM}^+$
to compute
![]() $r(x)(0)$
. Then, for all x,
$r(x)(0)$
. Then, for all x,
![]() $\phi (x,p(x))$
is realisable. As
$\phi (x,p(x))$
is realisable. As
![]() $\phi $
is a
$\phi $
is a
![]() $\Sigma _1$
-formula, it follows with Lemma 4.3 that
$\Sigma _1$
-formula, it follows with Lemma 4.3 that
![]() $\mathrm {V} \vDash \phi (x,p(x))$
.
$\mathrm {V} \vDash \phi (x,p(x))$
.
Finally, we can use
![]() $\mathrm {SRM}^+$
-realisability to easily determine the admissible rules of
$\mathrm {SRM}^+$
-realisability to easily determine the admissible rules of
![]() $\mathrm {CZF}$
. A proof of Carl, Galeotti, and Passmann [Reference Carl, Galeotti and Passmann4, Theorem 56] can be adapted to work here.
$\mathrm {CZF}$
. A proof of Carl, Galeotti, and Passmann [Reference Carl, Galeotti and Passmann4, Theorem 56] can be adapted to work here.
Theorem 4.8. The propositional admissible rules of
![]() $\mathrm {CZF}$
are exactly those of intuitionistic logic.
$\mathrm {CZF}$
are exactly those of intuitionistic logic.
Proof Using the fact that
![]() $\mathrm {CZF}$
is
$\mathrm {CZF}$
is
![]() $\mathrm {SRM}^+$
-realisable, we can prove this with glued realisability using Theorem 2.10; almost exactly as we did in earlier joint work with Carl, Galeotti, and Passmann [Reference Carl, Galeotti and Passmann4].
$\mathrm {SRM}^+$
-realisable, we can prove this with glued realisability using Theorem 2.10; almost exactly as we did in earlier joint work with Carl, Galeotti, and Passmann [Reference Carl, Galeotti and Passmann4].
5 Beth realisability models
5.1 Fallible Beth models
In this section, we will make use of so-called fallible Beth models because they satisfy a particular handy universal model theorem.
Definition 5.1. A fallible Beth frame
![]() $(P,U)$
consists of a tree P and an upwards closed set
$(P,U)$
consists of a tree P and an upwards closed set
![]() $U \subseteq P$
such that if every path through
$U \subseteq P$
such that if every path through
![]() $p \in P$
meets U, then
$p \in P$
meets U, then
![]() $p \in U$
.
$p \in U$
.
Definition 5.2 (Fallible Beth model)
A fallible Beth model
![]() $(P,U,D,I)$
for first-order logic consists of a fallible Beth tree
$(P,U,D,I)$
for first-order logic consists of a fallible Beth tree
![]() $(P,U)$
, domains
$(P,U)$
, domains
![]() $D_p$
for
$D_p$
for
![]() $p \in P$
, and an interpretation
$p \in P$
, and an interpretation
![]() $I_p$
of the language of first-order logic for each
$I_p$
of the language of first-order logic for each
![]() $p \in P$
such that:
$p \in P$
such that:
-
(i)
 $I_v(R) \subseteq I_w(R)$
for all
$I_v(R) \subseteq I_w(R)$
for all
 $w \geq v$
,
$w \geq v$
, -
(ii)
 $I_v(R) = D_v$
for all
$I_v(R) = D_v$
for all
 $v \in U$
, and
$v \in U$
, and -
(iii) if R is an n-ary relation symbol,
 $\bar x \in D_v^n$
and on every path through v there is some w such that
$\bar x \in D_v^n$
and on every path through v there is some w such that
 $\bar x \in I_w(R)$
, then
$\bar x \in I_w(R)$
, then
 $\bar x \in I_v(R)$
.
$\bar x \in I_v(R)$
.
A Beth model is a fallible Beth model where
![]() $U = \emptyset $
. If
$U = \emptyset $
. If
![]() $p \in P$
, then a bar for p is a set
$p \in P$
, then a bar for p is a set
![]() $B \subseteq P$
such that every path through p meets B. A U-bar for p is a set
$B \subseteq P$
such that every path through p meets B. A U-bar for p is a set
![]() $B \subseteq P$
such that
$B \subseteq P$
such that
![]() $B \cup U$
is a bar for p.
$B \cup U$
is a bar for p.
Definition 5.3. Let
![]() $(P,U,D,I)$
be a fallible Beth model and
$(P,U,D,I)$
be a fallible Beth model and
![]() $v \in P$
. We define by recursion on sentences in the language of first-order logic:
$v \in P$
. We define by recursion on sentences in the language of first-order logic:
-
(i)
 $v \Vdash \bot $
if and only if
$v \Vdash \bot $
if and only if
 $v \in U$
;
$v \in U$
; -
(ii)
 $v \Vdash R(d_1,\dots ,d_n)$
if and only if
$v \Vdash R(d_1,\dots ,d_n)$
if and only if
 $(d_1,\dots ,d_n) \in I_v(R)$
;
$(d_1,\dots ,d_n) \in I_v(R)$
; -
(iii)
 $v \Vdash A_0 \wedge A_1$
if and only if
$v \Vdash A_0 \wedge A_1$
if and only if
 $v \Vdash A_0$
and
$v \Vdash A_0$
and
 $v \Vdash A_1$
;
$v \Vdash A_1$
; -
(iv)
 $v \Vdash A_0 \vee A_1$
if and only if there is a bar B for v such that for every
$v \Vdash A_0 \vee A_1$
if and only if there is a bar B for v such that for every
 $w \in B$
,
$w \in B$
,
 $w \Vdash A_0$
or
$w \Vdash A_0$
or
 $w \Vdash A_1$
;
$w \Vdash A_1$
; -
(v)
 $v \Vdash A_0 \rightarrow A_1$
if and only if for every
$v \Vdash A_0 \rightarrow A_1$
if and only if for every
 $w \geq v$
, if
$w \geq v$
, if
 $w \Vdash A_0$
, then
$w \Vdash A_0$
, then
 $w \Vdash A_1$
;
$w \Vdash A_1$
; -
(vi)
 $v \Vdash \exists x A(x)$
if and only if there is a bar B for v such that for all
$v \Vdash \exists x A(x)$
if and only if there is a bar B for v such that for all
 $w \in B$
, there is some
$w \in B$
, there is some
 $a \in D_w$
with
$a \in D_w$
with
 $w \Vdash A(a)$
;
$w \Vdash A(a)$
; -
(vii)
 $v \Vdash \forall x A(x)$
if and only if for every
$v \Vdash \forall x A(x)$
if and only if for every
 $w \geq v$
and
$w \geq v$
and
 $a \in D_w$
,
$a \in D_w$
,
 $w \Vdash A(a)$
.
$w \Vdash A(a)$
.
Note that, by this definition, if
![]() $v \in U$
, then v forces every formula trivially, i.e., the relation
$v \in U$
, then v forces every formula trivially, i.e., the relation
![]() $\Vdash $
trivialises in U. By definition of U, it follows that if
$\Vdash $
trivialises in U. By definition of U, it follows that if
![]() $v \notin U$
and B is a U-bar for v, then
$v \notin U$
and B is a U-bar for v, then
![]() $B \setminus U$
is non-empty. The following result of Troelstra and van Dalen [Reference Troelstra and van Dalen24, Chapter 13, Remark 2.6 and Theorem 2.8] will be a crucial ingredient of our proof.
$B \setminus U$
is non-empty. The following result of Troelstra and van Dalen [Reference Troelstra and van Dalen24, Chapter 13, Remark 2.6 and Theorem 2.8] will be a crucial ingredient of our proof.
Theorem 5.4. Let J be a recursively enumerable theory in intuitionistic first-order logic. Then there is a fallible Beth model
![]() $\mathcal {B}_J$
with constant domain
$\mathcal {B}_J$
with constant domain
![]() $\omega $
, based on the full binary tree of height
$\omega $
, based on the full binary tree of height
![]() $\omega $
, such that
$\omega $
, such that
![]() $\mathcal {B} \Vdash A$
if and only if
$\mathcal {B} \Vdash A$
if and only if
![]() $J \vdash A$
for every sentence A of first-order logic.
$J \vdash A$
for every sentence A of first-order logic.
In what follows, we will refer to
![]() $\mathcal {B}_J$
as the universal Beth model for J.
$\mathcal {B}_J$
as the universal Beth model for J.
5.2 Beth realisability models
Inspired by van Oosten [Reference van Oosten19], we now combine our notion of
![]() $\mathrm {SRM}^{+,O}_{\mathrm {L}}$
-realisability with Beth semantics. To make coherent use of oracles, we need the following definition.
$\mathrm {SRM}^{+,O}_{\mathrm {L}}$
-realisability with Beth semantics. To make coherent use of oracles, we need the following definition.
Definition 5.5. Let P be a partial order. A system of oracles
![]() $(O_v)_{v \in P}$
consists of partial class functions
$(O_v)_{v \in P}$
consists of partial class functions
![]() $O_v: \mathrm {V} \to \mathrm {V}$
such that, for all
$O_v: \mathrm {V} \to \mathrm {V}$
such that, for all
![]() $w \geq v$
, we have that
$w \geq v$
, we have that
![]() $\operatorname {\mathrm {dom}}(O_v) \subseteq \operatorname {\mathrm {dom}}(O_w)$
and
$\operatorname {\mathrm {dom}}(O_v) \subseteq \operatorname {\mathrm {dom}}(O_w)$
and
![]() $O_v(x) = O_w(x)$
for all
$O_v(x) = O_w(x)$
for all
![]() $x \in \operatorname {\mathrm {dom}}(O_v)$
.
$x \in \operatorname {\mathrm {dom}}(O_v)$
.
We need some notation to work with oracles. Given an
![]() $\mathrm {SRM}^{+,O}_{\mathrm {L}}$
-program r, we write
$\mathrm {SRM}^{+,O}_{\mathrm {L}}$
-program r, we write
![]() $r(x_1,\dots ,x_n;O)$
for the result of the successful computation (if it exists) of r on input
$r(x_1,\dots ,x_n;O)$
for the result of the successful computation (if it exists) of r on input
![]() $x_1,\dots ,x_n$
and oracle O. If we work with a system of oracles
$x_1,\dots ,x_n$
and oracle O. If we work with a system of oracles
![]() $(O_v)_{v \in P}$
, we also write
$(O_v)_{v \in P}$
, we also write
![]() $r(x_1,\dots ,x_n;v)$
to mean
$r(x_1,\dots ,x_n;v)$
to mean
![]() $r(x_1,\dots ,x_n;O_v)$
. Finally, we write
$r(x_1,\dots ,x_n;O_v)$
. Finally, we write
![]() $r(x_1,\dots ,x_n)$
to mean
$r(x_1,\dots ,x_n)$
to mean
![]() $r(x_1,\dots ,x_n;\emptyset )$
, i.e., the output (if it exists) of r run with the empty oracle.
$r(x_1,\dots ,x_n;\emptyset )$
, i.e., the output (if it exists) of r run with the empty oracle.
Definition 5.6. Let
![]() $(P,U)$
be a fallible Beth frame,
$(P,U)$
be a fallible Beth frame,
![]() $(O_v)_{v \in P}$
be a system of oracles. We define recursively for sentences
$(O_v)_{v \in P}$
be a system of oracles. We define recursively for sentences
![]() $\phi $
and
$\phi $
and
![]() $\psi $
in the language of set theory, for
$\psi $
in the language of set theory, for
![]() $a,b \in \mathrm {L}$
,
$a,b \in \mathrm {L}$
,
![]() $v \in P$
and an
$v \in P$
and an
![]() $\mathrm {SRM}^{+,O}_{\mathrm {L}}$
-program r:
$\mathrm {SRM}^{+,O}_{\mathrm {L}}$
-program r:
-
(i)
 $r \Vdash _v \bot $
if and only if
$r \Vdash _v \bot $
if and only if
 $v \in U$
;
$v \in U$
; -
(ii)
 $r \Vdash _v a = b$
if and only if
$r \Vdash _v a = b$
if and only if
 $a = b$
or
$a = b$
or
 $v \in U$
;
$v \in U$
; -
(iii)
 $r \Vdash _v a \in b$
if and only if
$r \Vdash _v a \in b$
if and only if
 $a \in b$
or
$a \in b$
or
 $v \in U$
;
$v \in U$
; -
(iv)
 $r \Vdash _v \phi \wedge \psi $
if and only if
$r \Vdash _v \phi \wedge \psi $
if and only if
 $r(0;v) \Vdash _v \phi $
and
$r(0;v) \Vdash _v \phi $
and
 $r(1;v) \Vdash _v \psi $
;
$r(1;v) \Vdash _v \psi $
; -
(v)
 $r \Vdash _v \phi \vee \psi $
if and only if there is a U-bar B for v such that, for every
$r \Vdash _v \phi \vee \psi $
if and only if there is a U-bar B for v such that, for every
 $w \in B$
, either
$w \in B$
, either
 $r(0;w) = 0$
and
$r(0;w) = 0$
and
 $r(1;w) \Vdash _w \phi $
, or
$r(1;w) \Vdash _w \phi $
, or
 $r(0;w) = 1$
and
$r(0;w) = 1$
and
 $r(1;w) \Vdash \psi $
;
$r(1;w) \Vdash \psi $
; -
(vi)
 $r \Vdash _v \phi \rightarrow \psi $
if and only if for every
$r \Vdash _v \phi \rightarrow \psi $
if and only if for every
 $w \geq v$
, if
$w \geq v$
, if
 $s \Vdash _w \phi $
, then
$s \Vdash _w \phi $
, then
 $r(s;w) \Vdash _w \psi $
;
$r(s;w) \Vdash _w \psi $
; -
(vii)
 $r \Vdash _v \exists x \phi (x)$
if and only if there is a U-bar B for v such that for all
$r \Vdash _v \exists x \phi (x)$
if and only if there is a U-bar B for v such that for all
 $w \in B$
,
$w \in B$
,
 $r(1;w) \Vdash _w \phi (r(0;w))$
;
$r(1;w) \Vdash _w \phi (r(0;w))$
; -
(viii)
 $r \Vdash _v \forall x \phi (x)$
if and only if for every a,
$r \Vdash _v \forall x \phi (x)$
if and only if for every a,
 $r(a;v) \Vdash _v \phi (a)$
.
$r(a;v) \Vdash _v \phi (a)$
.
If
![]() $v \in U$
, then
$v \in U$
, then
![]() $r \Vdash _v \phi $
for every realiser r and set-theoretic sentence
$r \Vdash _v \phi $
for every realiser r and set-theoretic sentence
![]() $\phi $
. The following is established by a standard argument.
$\phi $
. The following is established by a standard argument.
Theorem 5.7. Beth-realisability is sound for the axioms and rules of intuitionistic first-order logic.
Lemma 5.8. Let
![]() $\phi (\bar x)$
be a
$\phi (\bar x)$
be a
![]() $\Sigma _1$
-formula and
$\Sigma _1$
-formula and
![]() $v \notin U$
. Then there is some realiser
$v \notin U$
. Then there is some realiser
![]() $r \Vdash _v \phi (\bar x)$
if and only if
$r \Vdash _v \phi (\bar x)$
if and only if
![]() $L \vDash \phi (\bar x)$
.
$L \vDash \phi (\bar x)$
.
Proof As
![]() $v \notin U$
, we know that any U-bar B for v satisfies
$v \notin U$
, we know that any U-bar B for v satisfies
![]() $B \setminus U \neq \emptyset $
. We prove this by induction. The cases for equality and set-membership are trivial.
$B \setminus U \neq \emptyset $
. We prove this by induction. The cases for equality and set-membership are trivial.
Suppose that
![]() $\Vdash _v \phi (\bar a) \wedge \psi (\bar a)$
. By definition, this is equivalent to
$\Vdash _v \phi (\bar a) \wedge \psi (\bar a)$
. By definition, this is equivalent to
![]() $\Vdash _v \phi (\bar a)$
and
$\Vdash _v \phi (\bar a)$
and
![]() $\Vdash _v \psi (\bar a)$
. Applying the induction hypothesis, this holds if and only if
$\Vdash _v \psi (\bar a)$
. Applying the induction hypothesis, this holds if and only if
![]() $\mathrm {L} \vDash \phi (\bar a)$
and
$\mathrm {L} \vDash \phi (\bar a)$
and
![]() $\mathrm {L} \vDash \psi (\bar a)$
. This is, of course, equivalent to
$\mathrm {L} \vDash \psi (\bar a)$
. This is, of course, equivalent to
![]() $\mathrm {L} \vDash \phi (\bar a) \wedge \psi (\bar a)$
.
$\mathrm {L} \vDash \phi (\bar a) \wedge \psi (\bar a)$
.
For disjunction, first suppose that
![]() $r \Vdash _v \phi (\bar a) \vee \psi (\bar a)$
. By definition, this means that there is a U-bar B for v such that for all
$r \Vdash _v \phi (\bar a) \vee \psi (\bar a)$
. By definition, this means that there is a U-bar B for v such that for all
![]() $w \in B$
we have either
$w \in B$
we have either
![]() $r(0;w) = 0$
and
$r(0;w) = 0$
and
![]() $r(1;w) \Vdash _w \phi (\bar a)$
, or
$r(1;w) \Vdash _w \phi (\bar a)$
, or
![]() $r(0;w) = 1$
and
$r(0;w) = 1$
and
![]() $r(1;w) \Vdash _w \psi (\bar a)$
. Recall that
$r(1;w) \Vdash _w \psi (\bar a)$
. Recall that
![]() $B \setminus U$
is non-empty. So take any
$B \setminus U$
is non-empty. So take any
![]() $w \in B \setminus U$
, then
$w \in B \setminus U$
, then
![]() $\Vdash _w \phi (\bar a)$
or
$\Vdash _w \phi (\bar a)$
or
![]() $\Vdash _w \psi (\bar a)$
. By induction hypothesis,
$\Vdash _w \psi (\bar a)$
. By induction hypothesis,
![]() $\mathrm {L} \vDash \phi (\bar a)$
or
$\mathrm {L} \vDash \phi (\bar a)$
or
![]() $\mathrm {L} \vDash \psi (\bar a)$
. Hence
$\mathrm {L} \vDash \psi (\bar a)$
. Hence
![]() $\mathrm {L} \vDash \phi (\bar a ) \vee \psi (\bar a)$
. Conversely, assume that
$\mathrm {L} \vDash \phi (\bar a ) \vee \psi (\bar a)$
. Conversely, assume that
![]() $\mathrm {L} \vDash \phi (\bar a) \vee \psi (\bar a)$
. Then
$\mathrm {L} \vDash \phi (\bar a) \vee \psi (\bar a)$
. Then
![]() $\mathrm {L} \vDash \phi (\bar a)$
or
$\mathrm {L} \vDash \phi (\bar a)$
or
![]() $\mathrm {L} \vDash \psi (\bar a)$
. It follows, by induction hypothesis, that
$\mathrm {L} \vDash \psi (\bar a)$
. It follows, by induction hypothesis, that
![]() $\Vdash _v \phi (\bar a)$
or
$\Vdash _v \phi (\bar a)$
or
![]() $\Vdash _v \psi (\bar a)$
, but then
$\Vdash _v \psi (\bar a)$
, but then
![]() $\Vdash _v \phi (\bar a) \vee \psi (\bar a)$
.
$\Vdash _v \phi (\bar a) \vee \psi (\bar a)$
.
For implication, assume that
![]() $r \Vdash _v \phi \rightarrow \psi $
. If
$r \Vdash _v \phi \rightarrow \psi $
. If
![]() $\mathrm {L} \not \vDash \phi $
, then trivially
$\mathrm {L} \not \vDash \phi $
, then trivially
![]() $\mathrm {L} \vDash \phi \rightarrow \psi $
. So assume that
$\mathrm {L} \vDash \phi \rightarrow \psi $
. So assume that
![]() $\mathrm {L} \vDash \phi $
. By induction hypothesis, we know that there is a realiser
$\mathrm {L} \vDash \phi $
. By induction hypothesis, we know that there is a realiser
![]() $s \Vdash _v \phi $
. Hence,
$s \Vdash _v \phi $
. Hence,
![]() $r(s) \Vdash _v \psi $
. Applying the induction hypothesis once more, we get
$r(s) \Vdash _v \psi $
. Applying the induction hypothesis once more, we get
![]() $\mathrm {L} \vDash \psi $
. Conversely, assume that
$\mathrm {L} \vDash \psi $
. Conversely, assume that
![]() $\mathrm {L} \vDash \phi \rightarrow \psi $
. If
$\mathrm {L} \vDash \phi \rightarrow \psi $
. If
![]() $\mathrm {L} \not \vDash \phi $
, then, by induction hypothesis,
$\mathrm {L} \not \vDash \phi $
, then, by induction hypothesis,
![]() $\not \Vdash _w \phi $
for all
$\not \Vdash _w \phi $
for all
![]() $w \geq v$
. So
$w \geq v$
. So
![]() $\Vdash _v \phi \rightarrow \psi $
holds trivially. If
$\Vdash _v \phi \rightarrow \psi $
holds trivially. If
![]() $\mathrm {L} \vDash \phi $
, then
$\mathrm {L} \vDash \phi $
, then
![]() $\mathrm {L} \vDash \psi $
. So, by induction hypothesis, there is a realiser
$\mathrm {L} \vDash \psi $
. So, by induction hypothesis, there is a realiser
![]() $s \Vdash _v \psi $
. Hence, a realiser for
$s \Vdash _v \psi $
. Hence, a realiser for
![]() $\phi \rightarrow \psi $
is the
$\phi \rightarrow \psi $
is the
![]() $\mathrm {SRM}\ p$
that returns s on any input.
$\mathrm {SRM}\ p$
that returns s on any input.
For bounded universal quantification, assume that
![]() $\mathrm {L} \vDash \forall x \in y \phi (x)$
. Then, by induction hypothesis, we can find a function
$\mathrm {L} \vDash \forall x \in y \phi (x)$
. Then, by induction hypothesis, we can find a function
![]() $f: y \to \mathrm {L}$
such that
$f: y \to \mathrm {L}$
such that
![]() $f(z) \Vdash _v \phi (z)$
. Let p be the
$f(z) \Vdash _v \phi (z)$
. Let p be the
![]() $\mathrm {SRM}$
with parameter f that returns
$\mathrm {SRM}$
with parameter f that returns
![]() $f(z)$
on input z. Then
$f(z)$
on input z. Then
![]() $p \Vdash _v \forall x \in y \phi (x)$
. Conversely, note that
$p \Vdash _v \forall x \in y \phi (x)$
. Conversely, note that
![]() $\Vdash _v \forall x \in y \phi (x)$
entails that
$\Vdash _v \forall x \in y \phi (x)$
entails that
![]() $\Vdash _v \phi (x)$
for every
$\Vdash _v \phi (x)$
for every
![]() $x \in y$
. An application of the induction hypothesis yields
$x \in y$
. An application of the induction hypothesis yields
![]() $\mathrm {L} \vDash \forall x \in y \phi (x)$
.
$\mathrm {L} \vDash \forall x \in y \phi (x)$
.
For unbounded existential quantification, assume that
![]() $\mathrm {L} \vDash \exists x \phi (x)$
. Then there is some
$\mathrm {L} \vDash \exists x \phi (x)$
. Then there is some
![]() $a \in \mathrm {L}$
such that
$a \in \mathrm {L}$
such that
![]() $\mathrm {L} \vDash \phi (a)$
. By induction hypothesis, there is a realiser
$\mathrm {L} \vDash \phi (a)$
. By induction hypothesis, there is a realiser
![]() $s \Vdash _v \phi (a)$
. Let p be an
$s \Vdash _v \phi (a)$
. Let p be an
![]() $\mathrm {SRM}$
such that
$\mathrm {SRM}$
such that
![]() $p(1) = s$
and
$p(1) = s$
and
![]() $p(0) = a$
(by using, if necessary, parameter a). Then
$p(0) = a$
(by using, if necessary, parameter a). Then
![]() $p \Vdash _v \exists x \phi (x)$
. Conversely, if
$p \Vdash _v \exists x \phi (x)$
. Conversely, if
![]() $p \Vdash _v \exists x \phi (x)$
, then there is a U-bar B for v such that for all
$p \Vdash _v \exists x \phi (x)$
, then there is a U-bar B for v such that for all
![]() $w \in B$
,
$w \in B$
,
![]() $p(1;w) \Vdash _w \phi (p(0;w))$
. Take any
$p(1;w) \Vdash _w \phi (p(0;w))$
. Take any
![]() $w \in B$
and the induction hypothesis implies that
$w \in B$
and the induction hypothesis implies that
![]() $\mathrm {L} \vDash \phi (p(0;w))$
, and, hence,
$\mathrm {L} \vDash \phi (p(0;w))$
, and, hence,
![]() $\mathrm {L} \vDash \exists x \phi (x)$
.
$\mathrm {L} \vDash \exists x \phi (x)$
.
Theorem 5.9. The Beth realisability model satisfies
![]() $\mathrm {CZF} + \mathrm {PowerSet} + \mathrm {AC}$
.
$\mathrm {CZF} + \mathrm {PowerSet} + \mathrm {AC}$
.
Proof Realisers for the axioms and schemas can be constructed (almost exactly) as in the proof of Theorem 4.4. For the case of
![]() $\Delta _0$
-separation, observe that the use of Lemma 4.3 has to be replaced with Lemma 5.8. (Note that we only need to consider the cases for
$\Delta _0$
-separation, observe that the use of Lemma 4.3 has to be replaced with Lemma 5.8. (Note that we only need to consider the cases for
![]() $v \notin U$
, as the other case is trivial.)
$v \notin U$
, as the other case is trivial.)
5.3 Constructing a model for a given logic
The goal of this section is to construct a Beth-realisability model that matches the truth in the universal Beth model
![]() $\mathcal {B}_J = (P,U, D,I)$
for a given logic J. To begin with, we define the two systems of oracles
$\mathcal {B}_J = (P,U, D,I)$
for a given logic J. To begin with, we define the two systems of oracles
![]() $(F_v)_{v \in P}$
and
$(F_v)_{v \in P}$
and
![]() $(G_v)_{v \in P}$
. If a is a set, let
$(G_v)_{v \in P}$
. If a is a set, let
![]() $\operatorname {\mathrm {rank}}_{\omega }(a)$
be the unique natural number such that
$\operatorname {\mathrm {rank}}_{\omega }(a)$
be the unique natural number such that
![]() $\operatorname {\mathrm {rank}}(a) = \alpha + \operatorname {\mathrm {rank}}_{\omega }(a)$
for a maximal (possibly
$\operatorname {\mathrm {rank}}(a) = \alpha + \operatorname {\mathrm {rank}}_{\omega }(a)$
for a maximal (possibly
![]() $0$
) limit ordinal
$0$
) limit ordinal
![]() $\alpha $
.
$\alpha $
.
-
(i) We define
 $F_v: \mathrm {V} \times \mathrm {V} \to \mathrm {V}$
by recursion on
$F_v: \mathrm {V} \times \mathrm {V} \to \mathrm {V}$
by recursion on
 $v \in P$
(P being the binary tree of height
$v \in P$
(P being the binary tree of height
 $\omega $
) such that:
$\omega $
) such that:  $$ \begin{align*}\hspace{-2pc}F_v(m,\langle b_0,\dots,b_n \rangle) = \begin{cases} a, & \text{if } m = \ulcorner \exists x A(x,y_0,\dots,y_n) \urcorner \\ &\phantom{if} \text{and } w \leq v \text{ is least such that } \\ &\phantom{if} a \in \omega \text{ is least with } \\ &\phantom{if} \mathcal{B}_J, w \Vdash A(a,\operatorname{\mathrm{rank}}_\omega(b_0),\dots,\operatorname{\mathrm{rank}}_\omega(b_n)), \\ i, & \text{if } m = \ulcorner (A_0 \vee A_1)(y_0,\dots,y_n) \urcorner \\ &\phantom{if} \text{and } w \leq v \text{ is least such that } \\ &\phantom{if} i \in \omega \text{ is least with } \\ &\phantom{if} \mathcal{B}_J, w \Vdash A_i(\operatorname{\mathrm{rank}}_\omega(b_0),\dots,\operatorname{\mathrm{rank}}_\omega(b_n)), \\ \text{undefined}, & \text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*}\hspace{-2pc}F_v(m,\langle b_0,\dots,b_n \rangle) = \begin{cases} a, & \text{if } m = \ulcorner \exists x A(x,y_0,\dots,y_n) \urcorner \\ &\phantom{if} \text{and } w \leq v \text{ is least such that } \\ &\phantom{if} a \in \omega \text{ is least with } \\ &\phantom{if} \mathcal{B}_J, w \Vdash A(a,\operatorname{\mathrm{rank}}_\omega(b_0),\dots,\operatorname{\mathrm{rank}}_\omega(b_n)), \\ i, & \text{if } m = \ulcorner (A_0 \vee A_1)(y_0,\dots,y_n) \urcorner \\ &\phantom{if} \text{and } w \leq v \text{ is least such that } \\ &\phantom{if} i \in \omega \text{ is least with } \\ &\phantom{if} \mathcal{B}_J, w \Vdash A_i(\operatorname{\mathrm{rank}}_\omega(b_0),\dots,\operatorname{\mathrm{rank}}_\omega(b_n)), \\ \text{undefined}, & \text{otherwise.} \end{cases} \end{align*} $$
-
(ii) We define
 $G_v: \mathrm {V} \times \mathrm {V} \to \mathrm {V}$
such that:
$G_v: \mathrm {V} \times \mathrm {V} \to \mathrm {V}$
such that:  $$ \begin{align*}G_v(a,b) = \begin{cases} 1, & \text{if } b = \langle i,b_0,\dots,b_n \rangle, \\& \phantom{if} \ \mathcal{B}_J, v \Vdash P_i(\operatorname{\mathrm{rank}}_\omega(b_0),\dots,\operatorname{\mathrm{rank}}_\omega(b_n)), \\& \phantom{if} \text{ and } D(a,b) = 1, \\ 0, & \text{if } b = \langle i,b_0,\dots,b_n \rangle, \\& \phantom{if} \ \mathcal{B}_J, v \Vdash P_i(\operatorname{\mathrm{rank}}_\omega(b_0),\dots,\operatorname{\mathrm{rank}}_\omega(b_n)), \\& \phantom{if} \text{ and } D(a,b) = 0, \\ \text{undefined,} & \text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*}G_v(a,b) = \begin{cases} 1, & \text{if } b = \langle i,b_0,\dots,b_n \rangle, \\& \phantom{if} \ \mathcal{B}_J, v \Vdash P_i(\operatorname{\mathrm{rank}}_\omega(b_0),\dots,\operatorname{\mathrm{rank}}_\omega(b_n)), \\& \phantom{if} \text{ and } D(a,b) = 1, \\ 0, & \text{if } b = \langle i,b_0,\dots,b_n \rangle, \\& \phantom{if} \ \mathcal{B}_J, v \Vdash P_i(\operatorname{\mathrm{rank}}_\omega(b_0),\dots,\operatorname{\mathrm{rank}}_\omega(b_n)), \\& \phantom{if} \text{ and } D(a,b) = 0, \\ \text{undefined,} & \text{otherwise.} \end{cases} \end{align*} $$
Lemma 5.10. The sequences
![]() $(F_v)_{v \in P}$
and
$(F_v)_{v \in P}$
and
![]() $(G_v)_{v \in P}$
form systems of oracles.
$(G_v)_{v \in P}$
form systems of oracles.
From now on, we consider the Beth-realisability based on these systems of oracles. Note that, without loss of generality, we can combine two systems of oracles into one by, e.g., taking
![]() $O_v(\langle 0,x \rangle ) = F_v(x)$
and
$O_v(\langle 0,x \rangle ) = F_v(x)$
and
![]() $O_v(\langle 1,x \rangle ) = G_v(x)$
for all
$O_v(\langle 1,x \rangle ) = G_v(x)$
for all
![]() $v \in P$
.
$v \in P$
.
Lemma 5.11. Let
![]() $v \notin U$
. There is a negative formula
$v \notin U$
. There is a negative formula
![]() $\psi (x,y)$
such that there is a realiser
$\psi (x,y)$
such that there is a realiser
![]() $r \Vdash _v \psi (x,y)$
is realised if and only if
$r \Vdash _v \psi (x,y)$
is realised if and only if
![]() $D(x,y) = 1$
.
$D(x,y) = 1$
.
Proof Except for the power set case, every clause of the definition of successful computation (Definition 3.2), adapted for
![]() $\mathrm {SRM}^+_{\mathrm {L}}$
, can be written as a
$\mathrm {SRM}^+_{\mathrm {L}}$
, can be written as a
![]() $\Sigma _1$
-formula. For the
$\Sigma _1$
-formula. For the
![]() $\mathtt {TAKE}$
-operation, recall that
$\mathtt {TAKE}$
-operation, recall that
![]() $<_{\mathrm {L}}$
is
$<_{\mathrm {L}}$
is
![]() $\Sigma _1$
-definable. Now consider the predicate “
$\Sigma _1$
-definable. Now consider the predicate “
![]() $x = \mathcal {P}(y)$
” which is needed for the
$x = \mathcal {P}(y)$
” which is needed for the
![]() $\mathtt {POW}$
-operation and can be formalised as “
$\mathtt {POW}$
-operation and can be formalised as “
![]() $\forall z (z \in x \leftrightarrow \forall w \in z \, w \in y)$
.” As the part in brackets is a
$\forall z (z \in x \leftrightarrow \forall w \in z \, w \in y)$
.” As the part in brackets is a
![]() $\Delta _0$
-formula, it follows with Lemma 5.8 that this predicate is realised if and only if it is true. Note, in particular, that also the successor case for the halting problem oracle is realised if and only if it is true in
$\Delta _0$
-formula, it follows with Lemma 5.8 that this predicate is realised if and only if it is true. Note, in particular, that also the successor case for the halting problem oracle is realised if and only if it is true in
![]() $\mathrm {L}$
. This is because the existence of a successful computation is absolute, as we have just seen.
$\mathrm {L}$
. This is because the existence of a successful computation is absolute, as we have just seen.
Applying Lemma 5.8 once more, these observations show that we can construct a formula
![]() $\chi $
expressing “c is a successful computation of
$\chi $
expressing “c is a successful computation of
![]() $D(x,y)$
with result
$D(x,y)$
with result
![]() $0$
” such that
$0$
” such that
![]() $\chi (c,x,y)$
is realised if and only if it is true in
$\chi (c,x,y)$
is realised if and only if it is true in
![]() $\mathrm {L}$
. Take
$\mathrm {L}$
. Take
![]() $\psi (x,y)$
to be
$\psi (x,y)$
to be
![]() $\neg \exists c \chi (c,x,y)$
. It follows that
$\neg \exists c \chi (c,x,y)$
. It follows that
![]() $\psi (x,y)$
is realised if and only if
$\psi (x,y)$
is realised if and only if
![]() $D(x,y) = 1$
because D halts on every input with either
$D(x,y) = 1$
because D halts on every input with either
![]() $0$
or
$0$
or
![]() $1$
as output.
$1$
as output.
Lemma 5.12. Let
![]() $P_i(y_0,\dots ,y_n)$
be a predicate in the language of first-order logic. There is a set-theoretic formula
$P_i(y_0,\dots ,y_n)$
be a predicate in the language of first-order logic. There is a set-theoretic formula
![]() $\phi _i(y_0,\dots ,y_n)$
and a realiser r such that for all
$\phi _i(y_0,\dots ,y_n)$
and a realiser r such that for all
![]() $b_0,\dots ,b_n \in \mathrm {L}$
,
$b_0,\dots ,b_n \in \mathrm {L}$
,
![]() $r(b_0,\dots ,b_n) \Vdash _v \phi _i(b_0,\dots ,b_n)$
if and only if
$r(b_0,\dots ,b_n) \Vdash _v \phi _i(b_0,\dots ,b_n)$
if and only if
![]() $\mathcal {B}_J, v \Vdash P_i(\operatorname {\mathrm {rank}}_{\omega }(b_0),\dots ,\operatorname {\mathrm {rank}}_{\omega }(b_n))$
.
$\mathcal {B}_J, v \Vdash P_i(\operatorname {\mathrm {rank}}_{\omega }(b_0),\dots ,\operatorname {\mathrm {rank}}_{\omega }(b_n))$
.
Proof Let
![]() $\psi (x,y)$
be the negative formula from Lemma 5.11 expressing that
$\psi (x,y)$
be the negative formula from Lemma 5.11 expressing that
![]() $D(x,y) = 1$
. As
$D(x,y) = 1$
. As
![]() $\psi $
is negative, we know that, for every v and
$\psi $
is negative, we know that, for every v and
![]() $a, b \in \mathrm {L}$
, either
$a, b \in \mathrm {L}$
, either
![]() $\Vdash _v \psi (a,b)$
or
$\Vdash _v \psi (a,b)$
or
![]() $\Vdash _v \neg \psi (a,b)$
. Then take:
$\Vdash _v \neg \psi (a,b)$
. Then take:
Suppose there was a realiser
![]() $r \Vdash _v \phi _i(b_0,\dots ,b_n)$
but we also have that
$r \Vdash _v \phi _i(b_0,\dots ,b_n)$
but we also have that
![]() $\mathcal {B}_J, v \not \Vdash P_i(\operatorname {\mathrm {rank}}_\omega (b_0),\dots ,\operatorname {\mathrm {rank}}_\omega (b_n))$
. In this situation, we can decide
$\mathcal {B}_J, v \not \Vdash P_i(\operatorname {\mathrm {rank}}_\omega (b_0),\dots ,\operatorname {\mathrm {rank}}_\omega (b_n))$
. In this situation, we can decide
![]() $D_{\langle i,b_0,\dots ,b_n \rangle }$
from r for every a: if
$D_{\langle i,b_0,\dots ,b_n \rangle }$
from r for every a: if
![]() $r(a,b_0,\dots ,b_n)$
returns a realiser for
$r(a,b_0,\dots ,b_n)$
returns a realiser for
![]() $\psi (a,\langle i,b_0,\dots ,b_n \rangle )$
, then
$\psi (a,\langle i,b_0,\dots ,b_n \rangle )$
, then
![]() $D_{\langle i,b_0,\dots ,b_n \rangle }(a) = 1$
; if
$D_{\langle i,b_0,\dots ,b_n \rangle }(a) = 1$
; if
![]() $r(a,b_0,\dots ,b_n)$
returns a realiser for
$r(a,b_0,\dots ,b_n)$
returns a realiser for
![]() $\neg \psi (a,\langle i,b_0,\dots ,b_n \rangle )$
, then
$\neg \psi (a,\langle i,b_0,\dots ,b_n \rangle )$
, then
![]() $D_{\langle i,b_0,\dots ,b_n \rangle }(a) = 0$
. However, by our assumption,
$D_{\langle i,b_0,\dots ,b_n \rangle }(a) = 0$
. However, by our assumption,
![]() $G_v(c,\langle i,b_0,\dots ,b_n \rangle )$
is undefined for all
$G_v(c,\langle i,b_0,\dots ,b_n \rangle )$
is undefined for all
![]() $c \in \mathrm {L}$
. This means that r cannot query the oracle
$c \in \mathrm {L}$
. This means that r cannot query the oracle
![]() $G_v$
on elements of the form
$G_v$
on elements of the form
![]() $(c,\langle i,b_0,\dots ,b_n \rangle )$
because then the computation would not be successful. Hence, using r, we can construct a witnesses that
$(c,\langle i,b_0,\dots ,b_n \rangle )$
because then the computation would not be successful. Hence, using r, we can construct a witnesses that
![]() $D_{\langle i,b_0,\dots ,b_n \rangle }$
is computable in
$D_{\langle i,b_0,\dots ,b_n \rangle }$
is computable in
![]() $D^{\langle i,b_0,\dots ,b_n \rangle }$
but that is a contradiction to Theorem 3.19. (Note that F does not matter here because the information contained in F could be saved in a set-sized parameter.)
$D^{\langle i,b_0,\dots ,b_n \rangle }$
but that is a contradiction to Theorem 3.19. (Note that F does not matter here because the information contained in F could be saved in a set-sized parameter.)
Conversely, assume that
![]() $\mathcal {B}_J, v \Vdash P_i(\operatorname {\mathrm {rank}}_\omega (b_0),\dots ,\operatorname {\mathrm {rank}}_\omega (b_n))$
. By definition of G, it follows that
$\mathcal {B}_J, v \Vdash P_i(\operatorname {\mathrm {rank}}_\omega (b_0),\dots ,\operatorname {\mathrm {rank}}_\omega (b_n))$
. By definition of G, it follows that
![]() $G_v(a, \langle i,b_0,\dots ,b_n \rangle )$
is defined for all
$G_v(a, \langle i,b_0,\dots ,b_n \rangle )$
is defined for all
![]() $a \in \mathrm {L}$
. Hence, a realiser for
$a \in \mathrm {L}$
. Hence, a realiser for
![]() $\phi _i$
can be easily obtained by querying the oracle
$\phi _i$
can be easily obtained by querying the oracle
![]() $G(a, \langle i,b_0,\dots ,b_n \rangle )$
: if the result is
$G(a, \langle i,b_0,\dots ,b_n \rangle )$
: if the result is
![]() $1$
, then return a realiser of
$1$
, then return a realiser of
![]() $\psi (a, \langle i,b_0,\dots ,b_n \rangle )$
. If the result is
$\psi (a, \langle i,b_0,\dots ,b_n \rangle )$
. If the result is
![]() $0$
, then return a realiser of
$0$
, then return a realiser of
![]() $\neg \psi (a,\langle i,b_0,\dots ,b_n \rangle )$
. In both cases, the computation of the corresponding realiser is trivial because the formulas are negative.
$\neg \psi (a,\langle i,b_0,\dots ,b_n \rangle )$
. In both cases, the computation of the corresponding realiser is trivial because the formulas are negative.
Let
![]() $\tau (P_i) = \phi _i$
and extend
$\tau (P_i) = \phi _i$
and extend
![]() $\tau $
to a translation of all formulas in the language of first-order logic in the obvious way. Note that the formulas
$\tau $
to a translation of all formulas in the language of first-order logic in the obvious way. Note that the formulas
![]() $\phi _i$
are
$\phi _i$
are
![]() $\Pi _3$
-formulas.
$\Pi _3$
-formulas.
Lemma 5.13. Let
![]() $A(y_0,\dots ,y_n)$
be a formula in the language of first-order logic. Then
$A(y_0,\dots ,y_n)$
be a formula in the language of first-order logic. Then
![]() $:$
$:$
-
(i) If there is a realiser
 $r \Vdash _v A^\tau (b_0,\dots ,b_n)$
, then
$r \Vdash _v A^\tau (b_0,\dots ,b_n)$
, then  $$ \begin{align*}\mathcal{B}_J,v \Vdash A(\operatorname{\mathrm{rank}}_\omega(b_0),\dots,\operatorname{\mathrm{rank}}_\omega(b_n)).\end{align*} $$
$$ \begin{align*}\mathcal{B}_J,v \Vdash A(\operatorname{\mathrm{rank}}_\omega(b_0),\dots,\operatorname{\mathrm{rank}}_\omega(b_n)).\end{align*} $$
-
(ii) There is a realiser
 $r_A$
such that for all
$r_A$
such that for all
 $b_0,\dots ,b_n \in \mathrm {L}$
, if then
$b_0,\dots ,b_n \in \mathrm {L}$
, if then $$ \begin{align*}\mathcal{B}_J, v \Vdash A(\operatorname{\mathrm{rank}}_\omega(b_0),\dots,\operatorname{\mathrm{rank}}_\omega(b_n)),\end{align*} $$
$$ \begin{align*}\mathcal{B}_J, v \Vdash A(\operatorname{\mathrm{rank}}_\omega(b_0),\dots,\operatorname{\mathrm{rank}}_\omega(b_n)),\end{align*} $$
 $$ \begin{align*}r_A(b_0,\dots,b_n) \Vdash_v A^\tau(b_0,\dots,b_n).\end{align*} $$
$$ \begin{align*}r_A(b_0,\dots,b_n) \Vdash_v A^\tau(b_0,\dots,b_n).\end{align*} $$
Proof We prove (i) and (ii) simultaneously by induction so that both directions are available in the induction hypothesis. We begin with proving the cases for (i). The base case follows from Lemma 5.12. For conjunction,
![]() $A \wedge B$
, note that
$A \wedge B$
, note that
![]() $\Vdash _v A^\tau \wedge B^\tau $
entails
$\Vdash _v A^\tau \wedge B^\tau $
entails
![]() $\Vdash _v A^\tau $
and
$\Vdash _v A^\tau $
and
![]() $\Vdash _v B^\tau $
. Hence, by induction hypothesis,
$\Vdash _v B^\tau $
. Hence, by induction hypothesis,
![]() $\mathcal {B}_J, v \Vdash A$
and
$\mathcal {B}_J, v \Vdash A$
and
![]() $\mathcal {B}_J, v \Vdash B$
. So,
$\mathcal {B}_J, v \Vdash B$
. So,
![]() $\mathcal {B}_J, v \Vdash A \land B$
. For disjunction,
$\mathcal {B}_J, v \Vdash A \land B$
. For disjunction,
![]() $A \vee B$
, we have that
$A \vee B$
, we have that
![]() $r \Vdash _v A^\tau \lor B^\tau $
entails that there is a U-bar B for v such that for every
$r \Vdash _v A^\tau \lor B^\tau $
entails that there is a U-bar B for v such that for every
![]() $w \in B$
, either
$w \in B$
, either
![]() $r^w(0) = 0$
and
$r^w(0) = 0$
and
![]() $r^w(1) \Vdash _w A^\tau $
or
$r^w(1) \Vdash _w A^\tau $
or
![]() $r^w(0) = 1$
and
$r^w(0) = 1$
and
![]() $r^w(1) \Vdash _w B^\tau $
. By induction hypothesis, this means that there is a U-bar B for v such that for every
$r^w(1) \Vdash _w B^\tau $
. By induction hypothesis, this means that there is a U-bar B for v such that for every
![]() $w \in B$
,
$w \in B$
,
![]() $w \Vdash A$
or
$w \Vdash A$
or
![]() $w \Vdash B$
. Hence
$w \Vdash B$
. Hence
![]() $v \Vdash A \lor B$
. The case for implication is similar (making use of (ii) as well), and the cases for universal and existential quantification follow with the induction hypothesis.
$v \Vdash A \lor B$
. The case for implication is similar (making use of (ii) as well), and the cases for universal and existential quantification follow with the induction hypothesis.
Regarding the cases for (ii), we recursively construct the required realisers
![]() $r_A(b_0,\dots ,b_n)$
, uniform in
$r_A(b_0,\dots ,b_n)$
, uniform in
![]() $b_0,\dots ,b_n \in \mathrm {L}$
, for each formula A. Once more, the base case,
$b_0,\dots ,b_n \in \mathrm {L}$
, for each formula A. Once more, the base case,
![]() $r_{P_i}(y_0,\dots ,y_n)$
, was established in Lemma 5.12. To keep notation light, we will write
$r_{P_i}(y_0,\dots ,y_n)$
, was established in Lemma 5.12. To keep notation light, we will write
![]() $\bar y$
for
$\bar y$
for
![]() $y_0,\dots ,y_n$
(or, potentially, a subsequence of this), and similarly for
$y_0,\dots ,y_n$
(or, potentially, a subsequence of this), and similarly for
![]() $\bar b$
.
$\bar b$
.
For conjunction
![]() $(A \land B)(\bar y)$
, take
$(A \land B)(\bar y)$
, take
![]() $r_{(A \land B)(\bar y)}(\bar b)(0) = r_A(\bar b)$
and
$r_{(A \land B)(\bar y)}(\bar b)(0) = r_A(\bar b)$
and
![]() $r_{(A \land B)(\bar y)}(\bar b)(1) = r_B(\bar b)$
. An application of the induction hypothesis shows that
$r_{(A \land B)(\bar y)}(\bar b)(1) = r_B(\bar b)$
. An application of the induction hypothesis shows that
![]() $r_{(A \land B)(\bar y)}$
does the job.
$r_{(A \land B)(\bar y)}$
does the job.
For implication
![]() $(A \rightarrow B)(\bar y)$
, we know by our induction hypothesis—for both (i) and (ii)—that
$(A \rightarrow B)(\bar y)$
, we know by our induction hypothesis—for both (i) and (ii)—that
![]() $r_{B(\bar y)}(\bar b) \Vdash _w B(\bar b)$
if and only if
$r_{B(\bar y)}(\bar b) \Vdash _w B(\bar b)$
if and only if
![]() $w \Vdash B(\bar b)$
for all
$w \Vdash B(\bar b)$
for all
![]() $w \geq v$
. Hence, let
$w \geq v$
. Hence, let
![]() $r_{A \rightarrow B(\bar y)}(\bar b,s) = r_{B}(\bar b)$
. It is straightforward to check that this does the job.
$r_{A \rightarrow B(\bar y)}(\bar b,s) = r_{B}(\bar b)$
. It is straightforward to check that this does the job.
For disjunction, define
![]() $r_{A \vee B}(\bar y)$
to be the
$r_{A \vee B}(\bar y)$
to be the
![]() $\mathrm {SRM}^{+,O}$
that, on input
$\mathrm {SRM}^{+,O}$
that, on input
![]() $\bar b$
, returns a code s for an
$\bar b$
, returns a code s for an
![]() $\mathrm {SRM}^{+,O}$
with parameters
$\mathrm {SRM}^{+,O}$
with parameters
![]() $\bar b$
that does the following. On input
$\bar b$
that does the following. On input
![]() $0$
, s calls the oracle F on
$0$
, s calls the oracle F on
![]() $(\ulcorner (A \vee B)(\bar y) \urcorner , \langle \bar b \rangle )$
and returns this value. On input
$(\ulcorner (A \vee B)(\bar y) \urcorner , \langle \bar b \rangle )$
and returns this value. On input
![]() $1$
, s returns
$1$
, s returns
![]() $r_A(\bar b)$
if
$r_A(\bar b)$
if
![]() $F(\ulcorner (A \vee B)(\bar y) \urcorner , \langle \bar b \rangle ) = 0$
and it returns
$F(\ulcorner (A \vee B)(\bar y) \urcorner , \langle \bar b \rangle ) = 0$
and it returns
![]() $r_B(\bar b)$
otherwise. To see that
$r_B(\bar b)$
otherwise. To see that
![]() $r_{(A \vee B)(\bar y)}$
does the job, assume that there is a U-bar B such that for every
$r_{(A \vee B)(\bar y)}$
does the job, assume that there is a U-bar B such that for every
![]() $w \in B$
,
$w \in B$
,
![]() $w \Vdash A(\bar b)$
or
$w \Vdash A(\bar b)$
or
![]() $w \Vdash B(\bar b)$
. Equivalently, by induction hypothesis, for every
$w \Vdash B(\bar b)$
. Equivalently, by induction hypothesis, for every
![]() $w \in B$
,
$w \in B$
,
![]() $r_A(\bar b;w) \Vdash _w A(\operatorname {\mathrm {rank}}_\omega (b_0),\dots ,\operatorname {\mathrm {rank}}_\omega (b_n))$
or
$r_A(\bar b;w) \Vdash _w A(\operatorname {\mathrm {rank}}_\omega (b_0),\dots ,\operatorname {\mathrm {rank}}_\omega (b_n))$
or
![]() $r_B(\bar b;w) \Vdash _w B(\operatorname {\mathrm {rank}}_\omega (b_0),\dots ,\operatorname {\mathrm {rank}}_\omega (b_n))$
. By definition of
$r_B(\bar b;w) \Vdash _w B(\operatorname {\mathrm {rank}}_\omega (b_0),\dots ,\operatorname {\mathrm {rank}}_\omega (b_n))$
. By definition of
![]() $r_{(A \vee B)(\bar y)}$
, it follows that
$r_{(A \vee B)(\bar y)}$
, it follows that
![]() $r_{(A \vee B)(\bar y)}(\bar b;w)(1) = r_A$
or
$r_{(A \vee B)(\bar y)}(\bar b;w)(1) = r_A$
or
![]() $r_{(A \vee B)(\bar y)}(\bar b;w)(1) = r_B$
. In conclusion,
$r_{(A \vee B)(\bar y)}(\bar b;w)(1) = r_B$
. In conclusion,
![]() $r_{(A \vee B)(\bar y)}(\bar b;w) \Vdash _w (A \vee B)(\bar b)$
.
$r_{(A \vee B)(\bar y)}(\bar b;w) \Vdash _w (A \vee B)(\bar b)$
.
For existential quantification, define
![]() $r_{\exists x A(x,\bar y)}$
to be the function that, on input
$r_{\exists x A(x,\bar y)}$
to be the function that, on input
![]() $\bar b$
, calls the oracle F on input
$\bar b$
, calls the oracle F on input
![]() $(\ulcorner \exists x A(x,y) \urcorner ,\langle \bar b \rangle )$
. Let the result of this query be
$(\ulcorner \exists x A(x,y) \urcorner ,\langle \bar b \rangle )$
. Let the result of this query be
![]() $n \in \omega $
. Then let
$n \in \omega $
. Then let
![]() $r_{\exists x A(x,\bar y)}(0) = n$
and
$r_{\exists x A(x,\bar y)}(0) = n$
and
![]() $r_{\exists x A(x,\bar y)}(1) = r_{A(n,\bar y)}$
. Note here that we do not require the use of parameters because the realiser
$r_{\exists x A(x,\bar y)}(1) = r_{A(n,\bar y)}$
. Note here that we do not require the use of parameters because the realiser
![]() $r_{A(n,\bar y)}$
is uniform in
$r_{A(n,\bar y)}$
is uniform in
![]() $n,\bar y$
. To check that
$n,\bar y$
. To check that
![]() $r_{\exists x A(x,\bar y)}$
does the job, let
$r_{\exists x A(x,\bar y)}$
does the job, let
![]() $\bar b \in \mathrm {L}$
and assume that there is a U-bar B for v such that, for every
$\bar b \in \mathrm {L}$
and assume that there is a U-bar B for v such that, for every
![]() $w \in B$
, there is some
$w \in B$
, there is some
![]() $n_w \in \omega $
such that
$n_w \in \omega $
such that
![]() $w \Vdash A(n_w, \operatorname {\mathrm {rank}}_\omega (\bar b))$
. By induction hypothesis, it follows that
$w \Vdash A(n_w, \operatorname {\mathrm {rank}}_\omega (\bar b))$
. By induction hypothesis, it follows that
![]() $r_{A(n_w,\bar y)}(\bar b;w) \Vdash _w A^\tau (n_w,\bar b)$
(as
$r_{A(n_w,\bar y)}(\bar b;w) \Vdash _w A^\tau (n_w,\bar b)$
(as
![]() $\mathcal {B}_J$
has constant domain
$\mathcal {B}_J$
has constant domain
![]() $\omega $
and
$\omega $
and
![]() $\operatorname {\mathrm {rank}}_\omega (n_w) = n_w$
), i.e.,
$\operatorname {\mathrm {rank}}_\omega (n_w) = n_w$
), i.e.,
![]() $r_{\exists x A(x,\bar y)}(\bar b, 0; w) \Vdash _w A^\tau (r_{\exists x A(x,\bar y)}(\bar b, 1; w),\bar b)$
. Hence,
$r_{\exists x A(x,\bar y)}(\bar b, 0; w) \Vdash _w A^\tau (r_{\exists x A(x,\bar y)}(\bar b, 1; w),\bar b)$
. Hence,
![]() $r_{\exists x A(x,\bar y)}(\bar b; v) \Vdash _v \exists x A^\tau (x, \bar b)$
.
$r_{\exists x A(x,\bar y)}(\bar b; v) \Vdash _v \exists x A^\tau (x, \bar b)$
.
For universal quantification, define
![]() $r_{\forall x A(x,\bar y)}(\bar y)$
to be the function that returns
$r_{\forall x A(x,\bar y)}(\bar y)$
to be the function that returns
![]() $r_{A(x,\bar y)}(x,\bar y)$
.
$r_{A(x,\bar y)}(x,\bar y)$
.
If J is a set of formulas in first-order logic, we write
![]() $J^\tau $
for the image of J under
$J^\tau $
for the image of J under
![]() $\tau $
(i.e.,
$\tau $
(i.e.,
![]() $J^\tau = \tau [J]$
).
$J^\tau = \tau [J]$
).
Theorem 5.14. Let J be a recursively enumerable theory in intuitionistic first-order logic, and
![]() $T \subseteq \mathrm {CZF} + \mathrm {PowerSet} + \mathrm {AC}$
. Then
$T \subseteq \mathrm {CZF} + \mathrm {PowerSet} + \mathrm {AC}$
. Then
![]() $T + J^\tau \vdash A^\tau $
if and only if
$T + J^\tau \vdash A^\tau $
if and only if
![]() $J \vdash _{\mathbf {IQC}} A$
.
$J \vdash _{\mathbf {IQC}} A$
.
Proof The backwards direction is straightforward with the soundness of the Beth realisability model. For the forward direction, assume that
![]() $J \not \vdash A$
. Then, by Theorem 5.4, we know that
$J \not \vdash A$
. Then, by Theorem 5.4, we know that
![]() $\mathcal {B}_J \not \vdash A$
. In this situation, Lemma 5.13 implies that there is no realiser of
$\mathcal {B}_J \not \vdash A$
. In this situation, Lemma 5.13 implies that there is no realiser of
![]() $A^\tau $
. But the same lemma implies that
$A^\tau $
. But the same lemma implies that
![]() $B^\tau $
is realised for every
$B^\tau $
is realised for every
![]() $B \in J$
. Hence,
$B \in J$
. Hence,
![]() $T + J^\tau \not \vdash A^\tau $
.
$T + J^\tau \not \vdash A^\tau $
.
The following corollary follows immediately by taking
![]() $J = \emptyset $
.
$J = \emptyset $
.
Corollary 5.15. Let
![]() $T \subseteq \mathrm {CZF} + \mathrm {PowerSet} + \mathrm {AC}$
be a set theory. Then the first-order logic of T is intuitionistic first-order logic,
$T \subseteq \mathrm {CZF} + \mathrm {PowerSet} + \mathrm {AC}$
be a set theory. Then the first-order logic of T is intuitionistic first-order logic,
![]() $\mathbf {QL}(T) = \mathbf {IQC}$
. In particular,
$\mathbf {QL}(T) = \mathbf {IQC}$
. In particular,
![]() $\mathbf {QL}(\mathrm {CZF}) = \mathbf {IQC}$
.
$\mathbf {QL}(\mathrm {CZF}) = \mathbf {IQC}$
.
Remark 5.16. Rathjen [Reference Rathjen, Chatzidakis, Koepke and Pohlers21] points out that “the combination of
![]() $\mathrm {CZF}$
and the general axiom of choice has no constructive justification in Martin-Löf type theory.” In contrast, our results show that the combination of
$\mathrm {CZF}$
and the general axiom of choice has no constructive justification in Martin-Löf type theory.” In contrast, our results show that the combination of
![]() $\mathrm {CZF}$
and the axiom of choice is innocent on a logical level in that adding the axiom of choice does not result in an increase of logical strength:
$\mathrm {CZF}$
and the axiom of choice is innocent on a logical level in that adding the axiom of choice does not result in an increase of logical strength:
![]() $\mathbf {QL}(\mathrm {CZF} + \mathsf {AC}) = \mathbf {QL}(\mathrm {CZF}) = \mathbf {IQC}$
. Note, of course, that
$\mathbf {QL}(\mathrm {CZF} + \mathsf {AC}) = \mathbf {QL}(\mathrm {CZF}) = \mathbf {IQC}$
. Note, of course, that
![]() $\mathrm {CZF} + \mathrm {AC}$
satisfies the law of excluded middle for
$\mathrm {CZF} + \mathrm {AC}$
satisfies the law of excluded middle for
![]() $\Delta _0$
-formulas. This follows from the proof of Diaconescu’s theorem (see Section 2) which only requires
$\Delta _0$
-formulas. This follows from the proof of Diaconescu’s theorem (see Section 2) which only requires
![]() $\Delta _0$
-separation to prove the law of excluded middle for
$\Delta _0$
-separation to prove the law of excluded middle for
![]() $\Delta _0$
-formulas. Such theories satisfying the law of excluded middle for
$\Delta _0$
-formulas. Such theories satisfying the law of excluded middle for
![]() $\Delta _0$
-formulas but not in general are sometimes called semi-intuitionistic.
$\Delta _0$
-formulas but not in general are sometimes called semi-intuitionistic.
Acknowledgments
I am thankful for the very helpful remarks of an anonymous reviewer. Moreover, I would like to thank Merlin Carl, Lorenzo Galeotti, Rosalie Iemhoff, Benedikt Löwe, Benno van den Berg, and Ned Wontner for helpful discussions. I thank Daniël Otten for spotting a few typos. This research was supported by a doctoral scholarship of the Studienstiftung des deutschen Volkes (German Academic Scholarship Foundation).





