In this paper we extend the models for the “logic of categories” to a wider class of categories than is usually considered. We consider two kinds of logic, a restricted first-order logic and the full higher-order logic of elementary topoi.

The restricted first-order logic has as its only logical symbols ∧, ∃, Τ, and =. We interpret this logic in a category with finite limits equipped with a factorization system (in the sense of [4]). We require to satisfy two additional conditions: 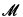⊆ Monos, and any pullback of an arrow in 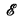is again in 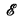. A category with a factorization system satisfying these conditions will be called an EM-category.

The interpretation of the restricted logic in EM-categories is given in §1. In §2 we give an axiomatization for the logic, and in §§3 and 5 we give two completeness proofs for this axiomatization. The first completeness proof constructs an EM-category out of the logic, in the spirit of Makkai and Reyes [8], though the construction used here differs from theirs. The second uses Boolean-valued models and shows that the restricted logic is exactly the ∧, ∃-fragment of classical first-order logic (adapted to categories). Some examples of EM-categories are given in §4.

The restricted logic is powerful enough to handle relations, and in §6 we assign to each EM-category 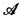a bicategory of relations Rel(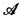) and a category of “functional relations” 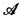fr. 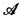fr is shown to be a regular category, and it turns out that Rel( 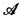and Rel(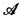fr) are biequivalent bicategories. In §7 we study complete objects in an EM-category 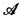where an object 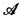of 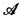is called complete if every functional relation into 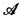is yielded by a unique morphism into 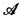. We write 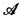c for the full subcategory of 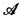consisting of the complete objects. Complete objects have some, but not all, of the properties that sheaves have in a category of presheaves.