1 Introduction
By space we mean an infinite topological Tychonoff space. A space X is Menger if for any sequence
![]() $\mathcal {U}_0, \mathcal {U}_1, \dotsc $
of open covers of X, there are finite families
$\mathcal {U}_0, \mathcal {U}_1, \dotsc $
of open covers of X, there are finite families
![]() $\mathcal {F}_0\subseteq \mathcal {U}_0, \mathcal {F}_1\subseteq \mathcal {U}_1,\dotsc $
such that the family
$\mathcal {F}_0\subseteq \mathcal {U}_0, \mathcal {F}_1\subseteq \mathcal {U}_1,\dotsc $
such that the family
![]() $\bigcup _{n\in \omega }\mathcal {F}_n$
covers X. Every
$\bigcup _{n\in \omega }\mathcal {F}_n$
covers X. Every
![]() $\sigma $
-compact space is Menger and every Menger space is Lindelöf. The Menger conjecture asserts that every subset of the real line with the Menger property is
$\sigma $
-compact space is Menger and every Menger space is Lindelöf. The Menger conjecture asserts that every subset of the real line with the Menger property is
![]() $\sigma $
-compact. By a result of Fremlin and Miller [Reference Fremlin and Miller11, Theorem 4], this conjecture is false in ZFC. This opened a wide stream of investigations in the realm of special subsets of the real line. The Menger property is a subject of research in the combinatorial covering properties theory but also appears in other branches of mathematics as local properties of function spaces [Reference Just, Miller, Scheepers and Szeptycki14], forcing theory [Reference Chodounský, Guzman and Hrusak8, Reference Chodounský, Repovš and Zdomskyy9] or additive Ramsey theory in algebra [Reference Szewczak23, Reference Tsaban26].
$\sigma $
-compact. By a result of Fremlin and Miller [Reference Fremlin and Miller11, Theorem 4], this conjecture is false in ZFC. This opened a wide stream of investigations in the realm of special subsets of the real line. The Menger property is a subject of research in the combinatorial covering properties theory but also appears in other branches of mathematics as local properties of function spaces [Reference Just, Miller, Scheepers and Szeptycki14], forcing theory [Reference Chodounský, Guzman and Hrusak8, Reference Chodounský, Repovš and Zdomskyy9] or additive Ramsey theory in algebra [Reference Szewczak23, Reference Tsaban26].
The Menger property is closely related to infinite combinatorics. Let
![]() $a,b\in {\omega ^{\omega }}$
. We write
$a,b\in {\omega ^{\omega }}$
. We write
![]() $a\le ^* b$
if the set
$a\le ^* b$
if the set
![]() $\{\,n : a(n)>b(n)\,\}$
is finite. In such a case we say that the function a is dominated by the function b. A set
$\{\,n : a(n)>b(n)\,\}$
is finite. In such a case we say that the function a is dominated by the function b. A set
![]() $D\subseteq {\omega ^{\omega }}$
is dominating if any function in
$D\subseteq {\omega ^{\omega }}$
is dominating if any function in
![]() ${\omega ^{\omega }}$
is dominated by some function from D. Let
${\omega ^{\omega }}$
is dominated by some function from D. Let
![]() $\mathfrak {d}$
be the minimal cardinality of a dominating subset of
$\mathfrak {d}$
be the minimal cardinality of a dominating subset of
![]() ${\omega ^{\omega }}$
. The Menger property can be characterized in terms of continuous images, as follows: a set
${\omega ^{\omega }}$
. The Menger property can be characterized in terms of continuous images, as follows: a set
![]() $X\subseteq {2^\omega }$
is Menger if and only if no continuous image of X into
$X\subseteq {2^\omega }$
is Menger if and only if no continuous image of X into
![]() ${\omega ^{\omega }}$
is dominating. This characterization was proved by Hurewicz [Reference Hurewicz12, Section 5] and then much later but independently by Recław [Reference Recław18, Proposition 3], so we call it the Hurewicz–Recław characterization of the Menger property. It follows that any subset of
${\omega ^{\omega }}$
is dominating. This characterization was proved by Hurewicz [Reference Hurewicz12, Section 5] and then much later but independently by Recław [Reference Recław18, Proposition 3], so we call it the Hurewicz–Recław characterization of the Menger property. It follows that any subset of
![]() $2^\omega $
with cardinality smaller than
$2^\omega $
with cardinality smaller than
![]() $\mathfrak {d}$
is Menger and there is a non-Menger set of cardinality
$\mathfrak {d}$
is Menger and there is a non-Menger set of cardinality
![]() $\mathfrak {d}$
.
$\mathfrak {d}$
.
The above mentioned result of Fremlin and Miller is dichotomic, i.e., it splits ZFC into two cases using undecidable statements. Bartoszyński and Tsaban provided in [Reference Bartoszyński and Tsaban1] a uniform ZFC counterexample to the Menger conjecture. By set with a given topological property we mean a space homeomorphic with a subspace of
![]() ${2^\omega }$
. A set is totally imperfect if it does not contain a homeomorphic copy of
${2^\omega }$
. A set is totally imperfect if it does not contain a homeomorphic copy of
![]() ${2^\omega }$
.
${2^\omega }$
.
Theorem 1.1 (Bartoszyński, Tsaban [Reference Bartoszyński and Tsaban1, Theorem 16]).
There is a totally imperfect Menger set of cardinality
![]() $\mathfrak {d}$
.
$\mathfrak {d}$
.
In the first part of the paper we consider the following problem.
Problem 1.2. Is there a totally imperfect Menger set of cardinality
![]() $\mathfrak {c}$
?
$\mathfrak {c}$
?
By Theorem 1.1, it suffices to consider the case
![]() $\mathfrak {d}<\mathfrak {c}$
. In Section 2, we introduce a game characterization of the Menger property, which is one of the main tools needed in Section 3. We show that adding iteratively
$\mathfrak {d}<\mathfrak {c}$
. In Section 2, we introduce a game characterization of the Menger property, which is one of the main tools needed in Section 3. We show that adding iteratively
![]() $\omega _2$
Sacks reals to a ground model satisfying CH, we get a model where
$\omega _2$
Sacks reals to a ground model satisfying CH, we get a model where
![]() $\mathfrak {d}<\mathfrak {c}$
and the answer to Problem 1.2 is negative. In Section 7 we also prove that
$\mathfrak {d}<\mathfrak {c}$
and the answer to Problem 1.2 is negative. In Section 7 we also prove that
![]() $\mathfrak {d}<\mathfrak {c}$
is consistent with the existence of a totally imperfect Menger set of cardinality
$\mathfrak {d}<\mathfrak {c}$
is consistent with the existence of a totally imperfect Menger set of cardinality
![]() $\mathfrak {c}$
.
$\mathfrak {c}$
.
In the second part of the paper we analyze the structure of Hurewicz and consonant subsets of
![]() ${2^\omega }$
. Recall that a space X is Hurewicz if for any sequence
${2^\omega }$
. Recall that a space X is Hurewicz if for any sequence
![]() $\mathcal {U}_0, \mathcal {U}_1, \dotsc $
of open covers of X, there are finite families
$\mathcal {U}_0, \mathcal {U}_1, \dotsc $
of open covers of X, there are finite families
![]() $\mathcal {F}_0\subseteq \mathcal {U}_0, \mathcal {F}_1\subseteq \mathcal {U}_1,\dotsc $
such that the family
$\mathcal {F}_0\subseteq \mathcal {U}_0, \mathcal {F}_1\subseteq \mathcal {U}_1,\dotsc $
such that the family
![]() $\{\bigcup \mathcal {F}_n: n\in \omega \}$
is a
$\{\bigcup \mathcal {F}_n: n\in \omega \}$
is a
![]() $\gamma $
-cover of X, i.e., the sets
$\gamma $
-cover of X, i.e., the sets
![]() $\{\,n : x\in \bigcup \mathcal {F}_n\,\}$
are cofinite for all
$\{\,n : x\in \bigcup \mathcal {F}_n\,\}$
are cofinite for all
![]() $x\in X$
. Obviously, every
$x\in X$
. Obviously, every
![]() $\sigma $
-compact space is Hurewicz and every Hurewicz space is Menger. Similarly to the Menger property, the Hurewicz property can be characterized in terms of continuous images, as follows. A set
$\sigma $
-compact space is Hurewicz and every Hurewicz space is Menger. Similarly to the Menger property, the Hurewicz property can be characterized in terms of continuous images, as follows. A set
![]() $A\subseteq {\omega ^{\omega }}$
is bounded if there is a function
$A\subseteq {\omega ^{\omega }}$
is bounded if there is a function
![]() $b\in {\omega ^{\omega }}$
such that
$b\in {\omega ^{\omega }}$
such that
![]() $a\le ^* b$
for all
$a\le ^* b$
for all
![]() $a\in A$
. A set
$a\in A$
. A set
![]() $X\subseteq {2^\omega }$
is Hurewicz if and only if every continuous image of X into
$X\subseteq {2^\omega }$
is Hurewicz if and only if every continuous image of X into
![]() ${\omega ^{\omega }}$
is bounded. This characterization was proved independently by Hurewicz [Reference Hurewicz12, Section 5] and Recław [Reference Recław18, Proposition 1], so we again call it the Hurewicz–Recław characterization of the Hurewicz property.
${\omega ^{\omega }}$
is bounded. This characterization was proved independently by Hurewicz [Reference Hurewicz12, Section 5] and Recław [Reference Recław18, Proposition 1], so we again call it the Hurewicz–Recław characterization of the Hurewicz property.
Consonant spaces were introduced by Dolecki, Greco, and Lechicki [Reference Dolecki, Greco and Lechicki10] and characterized by Jordan [Reference Jordan13, Corollary 11] in the following way. Let
![]() $X\subseteq {2^\omega }$
. A cover of X is a k-cover if any compact subset of X is contained in some set from the cover. A game
$X\subseteq {2^\omega }$
. A cover of X is a k-cover if any compact subset of X is contained in some set from the cover. A game
![]() $\mathsf {G}_1(\mathcal {K},\mathcal {O})$
played on X is a game for two players, Alice and Bob. For a natural number n, in round n: Alice picks an open k-cover
$\mathsf {G}_1(\mathcal {K},\mathcal {O})$
played on X is a game for two players, Alice and Bob. For a natural number n, in round n: Alice picks an open k-cover
![]() $\mathcal {U}_n$
of X and Bob picks a set
$\mathcal {U}_n$
of X and Bob picks a set
![]() $U_n\in \mathcal {U}_n$
. Bob wins the game if the family
$U_n\in \mathcal {U}_n$
. Bob wins the game if the family
![]() $\{\,U_n : n\in \omega \,\}$
is a cover of X, and Alice wins otherwise. A set
$\{\,U_n : n\in \omega \,\}$
is a cover of X, and Alice wins otherwise. A set
![]() $Y\subseteq 2^\omega $
is consonant if and only if Alice has no winning strategy in the game
$Y\subseteq 2^\omega $
is consonant if and only if Alice has no winning strategy in the game
![]() $\mathsf {G}_1(\mathcal {K},\mathcal {O})$
played on
$\mathsf {G}_1(\mathcal {K},\mathcal {O})$
played on
![]() $2^\omega \setminus Y$
. We treat here this characterization as a definition of consonant sets.
$2^\omega \setminus Y$
. We treat here this characterization as a definition of consonant sets.
Consonant spaces have close connections to combinatorial covering properties. Let
![]() $Y\subseteq {2^\omega }$
. It follows from the game characterization of the Menger property given below that if the set Y is consonant, then the set
$Y\subseteq {2^\omega }$
. It follows from the game characterization of the Menger property given below that if the set Y is consonant, then the set
![]() ${2^\omega }\setminus Y$
is Menger. A space X is Rothberger if for any sequence
${2^\omega }\setminus Y$
is Menger. A space X is Rothberger if for any sequence
![]() $\mathcal {U}_0, \mathcal {U}_1, \dotsc $
of open covers of X, there are sets
$\mathcal {U}_0, \mathcal {U}_1, \dotsc $
of open covers of X, there are sets
![]() $U_0\in \mathcal {U}_0, U_1\in \mathcal {U}_1,\dotsc $
such that the family
$U_0\in \mathcal {U}_0, U_1\in \mathcal {U}_1,\dotsc $
such that the family
![]() $\{\,U_n : n\in \omega \,\}$
is a cover of X. Using a game characterization of the Rothberger property given by Pawlikowski [Reference Pawlikowski16], if the set
$\{\,U_n : n\in \omega \,\}$
is a cover of X. Using a game characterization of the Rothberger property given by Pawlikowski [Reference Pawlikowski16], if the set
![]() ${2^\omega }\setminus Y$
is totally imperfect, then Y is consonant if and only if the set
${2^\omega }\setminus Y$
is totally imperfect, then Y is consonant if and only if the set
![]() ${2^\omega }\setminus Y$
is Rothberger. Indeed, if
${2^\omega }\setminus Y$
is Rothberger. Indeed, if
![]() $2^\omega \setminus Y$
is Rothberger, then Alice does not even have a winning strategy in the game
$2^\omega \setminus Y$
is Rothberger, then Alice does not even have a winning strategy in the game
![]() $\mathsf {G}_1(\mathcal O,\mathcal O)$
on
$\mathsf {G}_1(\mathcal O,\mathcal O)$
on
![]() $2^\omega \setminus Y$
, hence
$2^\omega \setminus Y$
, hence
![]() $ Y$
is consonant. Assuming now that Y is consonant and
$ Y$
is consonant. Assuming now that Y is consonant and
![]() $2^\omega \setminus Y$
is totally imperfect, we shall show that
$2^\omega \setminus Y$
is totally imperfect, we shall show that
![]() $2^\omega \setminus Y$
is Rothberger. Let
$2^\omega \setminus Y$
is Rothberger. Let
![]() $\mathcal U_{n,m}$
be an open cover of
$\mathcal U_{n,m}$
be an open cover of
![]() $2^\omega \setminus Y$
for all
$2^\omega \setminus Y$
for all
![]() $\langle n,m\rangle \in \omega \times \omega $
. Set
$\langle n,m\rangle \in \omega \times \omega $
. Set
![]() $\mathcal W_n=\{\bigcup _{m\in \omega }U_{n,m}: U_{n,m}\in \mathcal U_{n,m} $
for all
$\mathcal W_n=\{\bigcup _{m\in \omega }U_{n,m}: U_{n,m}\in \mathcal U_{n,m} $
for all
![]() $m\in \omega \}$
. Since each compact subset of
$m\in \omega \}$
. Since each compact subset of
![]() $2^\omega \setminus Y$
is countable, each
$2^\omega \setminus Y$
is countable, each
![]() $\mathcal W_n$
is a k-cover of
$\mathcal W_n$
is a k-cover of
![]() $2^\omega \setminus Y$
. Since Alice has no winning strategy in the game
$2^\omega \setminus Y$
. Since Alice has no winning strategy in the game
![]() $\mathsf {G}_1(\mathcal K,\mathcal O)$
on
$\mathsf {G}_1(\mathcal K,\mathcal O)$
on
![]() $2^\omega \setminus Y$
, we conclude that
$2^\omega \setminus Y$
, we conclude that
![]() $2^\omega \setminus Y$
is
$2^\omega \setminus Y$
is
![]() $\mathsf {S}_1(\mathcal K,\mathcal O)$
, and hence there are
$\mathsf {S}_1(\mathcal K,\mathcal O)$
, and hence there are
![]() $W_n\in \mathcal W_n$
,
$W_n\in \mathcal W_n$
,
![]() $n\in \omega $
, such that
$n\in \omega $
, such that
![]() $\bigcup _{n\in \omega }W_n=2^\omega \setminus Y$
. For each
$\bigcup _{n\in \omega }W_n=2^\omega \setminus Y$
. For each
![]() $n,m$
let
$n,m$
let
![]() $U_{n,m}\in \mathcal U_{n,m}$
be such that
$U_{n,m}\in \mathcal U_{n,m}$
be such that
![]() $W_n=\bigcup _{m\in \omega }U_{n,m}$
. Then
$W_n=\bigcup _{m\in \omega }U_{n,m}$
. Then
![]() $2^\omega \setminus Y=\bigcup _{n,m\in \omega }U_{n,m}$
, which shows that
$2^\omega \setminus Y=\bigcup _{n,m\in \omega }U_{n,m}$
, which shows that
![]() $2^\omega \setminus Y$
is Rothberger.Footnote
1
$2^\omega \setminus Y$
is Rothberger.Footnote
1
In Section 5 we introduce a topological game which allows us to analyze the structure of Hurewicz and consonant spaces in
![]() ${2^\omega }$
. We show that in the Sacks model, mentioned above, each consonant (Hurewicz) set
${2^\omega }$
. We show that in the Sacks model, mentioned above, each consonant (Hurewicz) set
![]() $X\subseteq {2^\omega }$
and its complement
$X\subseteq {2^\omega }$
and its complement
![]() ${2^\omega }\setminus X$
are unions of
${2^\omega }\setminus X$
are unions of
![]() $\omega _1$
compact sets. This approach allows us also to capture a result of Miller [Reference Miller15, Section 5] that in this model, every perfectly meager subset of
$\omega _1$
compact sets. This approach allows us also to capture a result of Miller [Reference Miller15, Section 5] that in this model, every perfectly meager subset of
![]() ${2^\omega }$
, i.e., a set which is meager in any perfect subset of
${2^\omega }$
, i.e., a set which is meager in any perfect subset of
![]() ${2^\omega }$
, has size at most
${2^\omega }$
, has size at most
![]() $\omega _1$
.
$\omega _1$
.
The main tools used in our investigations are game characterizations of the considered properties. Let X be a space. The Menger game played on X is a game for two players, Alice and Bob. For a natural number n, in round n: Alice picks an open cover
![]() $\mathcal {U}_n$
of X and Bob picks a finite family
$\mathcal {U}_n$
of X and Bob picks a finite family
![]() $\mathcal {F}_n\subseteq \mathcal {U}_n$
. Bob wins the game if the family
$\mathcal {F}_n\subseteq \mathcal {U}_n$
. Bob wins the game if the family
![]() $\bigcup _{n\in \omega }\mathcal {F}_n$
covers X, and Alice wins otherwise. For more details about this game, we refer to the works of Scheepers [Reference Scheepers21, Theorem 13] or Tsaban and the second named author [Reference Szewczak and Tsaban24]. Similarly to the Menger property, the Hurewicz property can also be characterized using a topological game. The Hurewicz game played on X is a game for two players, Alice and Bob. For a natural number n, in round n: Alice picks an open cover
$\bigcup _{n\in \omega }\mathcal {F}_n$
covers X, and Alice wins otherwise. For more details about this game, we refer to the works of Scheepers [Reference Scheepers21, Theorem 13] or Tsaban and the second named author [Reference Szewczak and Tsaban24]. Similarly to the Menger property, the Hurewicz property can also be characterized using a topological game. The Hurewicz game played on X is a game for two players, Alice and Bob. For a natural number n, in round n: Alice picks an open cover
![]() $\mathcal {U}_n$
of X and Bob picks a finite family
$\mathcal {U}_n$
of X and Bob picks a finite family
![]() $\mathcal {F}_n\subseteq \mathcal {U}_n$
. Bob wins the game if the family
$\mathcal {F}_n\subseteq \mathcal {U}_n$
. Bob wins the game if the family
![]() $\{\,\bigcup \mathcal {F}_n : n\in \omega \,\}$
is a
$\{\,\bigcup \mathcal {F}_n : n\in \omega \,\}$
is a
![]() $\gamma $
-cover of X, and Alice wins otherwise.
$\gamma $
-cover of X, and Alice wins otherwise.
Remark 1.3. In the definition of the Menger and Hurewicz games we could assume, in addition, that none of the
![]() $\mathcal U_n$
’s contains a finite subcover, and get an equivalent definition. Indeed, if X is compact, then Alice has no legal moves, and we standardly adopt the convention that the player having no moves loses. Thus, Bob has a “trivial” winning strategy. On the other hand, if X is not compact, then it has a cover
$\mathcal U_n$
’s contains a finite subcover, and get an equivalent definition. Indeed, if X is compact, then Alice has no legal moves, and we standardly adopt the convention that the player having no moves loses. Thus, Bob has a “trivial” winning strategy. On the other hand, if X is not compact, then it has a cover
![]() $\mathcal U_{*}$
without finite subcovers, and there is no loss of generality in assuming that Alice always plays refinements of
$\mathcal U_{*}$
without finite subcovers, and there is no loss of generality in assuming that Alice always plays refinements of
![]() $\mathcal U_{*}$
. Similar comments apply to the definitions of the Menger and Hurewicz properties.
$\mathcal U_{*}$
. Similar comments apply to the definitions of the Menger and Hurewicz properties.
Theorem 1.4 (Hurewicz).
A set
![]() $X\subseteq {2^\omega }$
is Menger if and only if Alice has no winning strategy in the Menger game played on X.
$X\subseteq {2^\omega }$
is Menger if and only if Alice has no winning strategy in the Menger game played on X.
Theorem 1.5 (Scheepers [Reference Scheepers21, Theorem 27]).
A set
![]() $X\subseteq {2^\omega }$
is Hurewicz if and only if Alice has no winning strategy in the Hurewicz game played on X.
$X\subseteq {2^\omega }$
is Hurewicz if and only if Alice has no winning strategy in the Hurewicz game played on X.
2 Menger game and perfect sets
Now we shall address some specific instances of perfect spaces and families of their clopen subsets. Suppose that
![]() ${\langle \, F_n : n\in \omega \,\rangle }$
is a non-decreasing sequence of finite subsets of some well-ordered set
${\langle \, F_n : n\in \omega \,\rangle }$
is a non-decreasing sequence of finite subsets of some well-ordered set
![]() $\langle S,<\rangle $
such that
$\langle S,<\rangle $
such that
![]() $S=\bigcup _{n\in \omega }F_n$
, and
$S=\bigcup _{n\in \omega }F_n$
, and
![]() ${\langle \, k_n : n\in \omega \,\rangle }$
is a strictly increasing sequence of natural numbers. For each
${\langle \, k_n : n\in \omega \,\rangle }$
is a strictly increasing sequence of natural numbers. For each
![]() $n\in \omega $
let
$n\in \omega $
let
![]() $\Sigma _n\subseteq (2^{k_n})^{F_n}$
. Fix natural numbers
$\Sigma _n\subseteq (2^{k_n})^{F_n}$
. Fix natural numbers
![]() $n,m$
with
$n,m$
with
![]() $n<m$
. For
$n<m$
. For
![]() $\nu \in \Sigma _n$
and
$\nu \in \Sigma _n$
and
![]() $\sigma \in \Sigma _m$
, we write
$\sigma \in \Sigma _m$
, we write
![]() $\nu \prec \sigma $
if
$\nu \prec \sigma $
if
![]() $\nu $
is extended by
$\nu $
is extended by
![]() $\sigma $
, i.e.,
$\sigma $
, i.e.,
![]() $\sigma (\beta )\upharpoonright k_n=\nu (\beta )$
for all
$\sigma (\beta )\upharpoonright k_n=\nu (\beta )$
for all
![]() $\beta \in F_n$
. Let
$\beta \in F_n$
. Let
![]() $C\subseteq \Sigma _n$
. A map
$C\subseteq \Sigma _n$
. A map
![]() $e\colon C\to \Sigma _m$
such that
$e\colon C\to \Sigma _m$
such that
![]() $\nu \prec e(\nu )$
for all
$\nu \prec e(\nu )$
for all
![]() $\nu \in C$
, is coherent, if for any
$\nu \in C$
, is coherent, if for any
![]() $\nu ,\nu '\in C$
, letting
$\nu ,\nu '\in C$
, letting
![]() $\beta \in F_{n}$
be the minimal element of
$\beta \in F_{n}$
be the minimal element of
![]() $F_{n}$
with
$F_{n}$
with
![]() $\nu (\beta )\neq \nu '(\beta )$
, we have
$\nu (\beta )\neq \nu '(\beta )$
, we have
![]() $e(\nu )\upharpoonright (F_{m}\cap \beta )=e(\nu ')\upharpoonright (F_{m}\cap \beta )$
. In what follows we shall assume that
$e(\nu )\upharpoonright (F_{m}\cap \beta )=e(\nu ')\upharpoonright (F_{m}\cap \beta )$
. In what follows we shall assume that
-
(e f ) For every
 $C\subset \Sigma _n$
, coherent
$C\subset \Sigma _n$
, coherent
 $e_0:C\to \Sigma _m$
, and
$e_0:C\to \Sigma _m$
, and
 $\nu \in \Sigma _n\setminus C$
, there exist two different coherent maps
$\nu \in \Sigma _n\setminus C$
, there exist two different coherent maps
 $e,e'\colon (C\cup \{\nu \}) \to \Sigma _m$
such that
$e,e'\colon (C\cup \{\nu \}) \to \Sigma _m$
such that
 $e{\kern-1pt}\upharpoonright{\kern-1pt} C{\kern-1pt}={\kern-1pt}e'{\kern-1pt}\upharpoonright{\kern-1pt} C{\kern-1pt}={\kern-1pt}e_0$
.
$e{\kern-1pt}\upharpoonright{\kern-1pt} C{\kern-1pt}={\kern-1pt}e'{\kern-1pt}\upharpoonright{\kern-1pt} C{\kern-1pt}={\kern-1pt}e_0$
.
Note that
![]() $(e_f)$
applied to
$(e_f)$
applied to
![]() $C=\emptyset $
yields that for every
$C=\emptyset $
yields that for every
![]() $\nu \in \Sigma _n$
there exists at least two
$\nu \in \Sigma _n$
there exists at least two
![]() $\sigma \in \Sigma _m$
such that
$\sigma \in \Sigma _m$
such that
![]() $\nu \prec \sigma .$
Moreover, using
$\nu \prec \sigma .$
Moreover, using
![]() $(e_f)$
iteratively for all natural numbers
$(e_f)$
iteratively for all natural numbers
![]() $n,m$
with
$n,m$
with
![]() $n<m$
, set
$n<m$
, set
![]() $C\subseteq \Sigma _n$
, elements
$C\subseteq \Sigma _n$
, elements
![]() $\nu \in C$
and
$\nu \in C$
and
![]() $\sigma \in \Sigma _m$
with
$\sigma \in \Sigma _m$
with
![]() $\nu \prec \sigma $
, there is a coherent map
$\nu \prec \sigma $
, there is a coherent map
![]() $e\colon C\to \Sigma _m$
with
$e\colon C\to \Sigma _m$
with
![]() $e(\nu )=\sigma $
.
$e(\nu )=\sigma $
.
The objects defined above give rise to the perfect subset
![]() $K\subseteq (2^\omega )^S$
consisting of those x such that for every n there exists
$K\subseteq (2^\omega )^S$
consisting of those x such that for every n there exists
![]() $\nu \in \Sigma _n$
such that
$\nu \in \Sigma _n$
such that
![]() $x\in [\nu ]$
, where
$x\in [\nu ]$
, where
For every
![]() $\beta \leq S$
, let
$\beta \leq S$
, let
![]() $\mathrm {pr}_\beta \colon K\to (2^\omega )^\beta $
be the projection map. For a set
$\mathrm {pr}_\beta \colon K\to (2^\omega )^\beta $
be the projection map. For a set
![]() $C\subseteq \Sigma _n$
, a map
$C\subseteq \Sigma _n$
, a map
![]() $E\colon C\to K$
is a coherent selection if for every
$E\colon C\to K$
is a coherent selection if for every
![]() $\nu \in C$
we have
$\nu \in C$
we have
![]() $E(\nu )\in [\nu ]$
and for every
$E(\nu )\in [\nu ]$
and for every
![]() $\nu ,\nu '\in C$
and
$\nu ,\nu '\in C$
and
![]() $\beta \in F_{n}$
, which is the minimal element in
$\beta \in F_{n}$
, which is the minimal element in
![]() $F_{n}$
with
$F_{n}$
with
![]() $\nu (\beta )\neq \nu '(\beta )$
, we have
$\nu (\beta )\neq \nu '(\beta )$
, we have
![]() $\mathrm {pr}_\beta (E(\nu ))=\mathrm {pr}_\beta (E(\nu '))$
.
$\mathrm {pr}_\beta (E(\nu ))=\mathrm {pr}_\beta (E(\nu '))$
.
Lemma 2.1. In the notation above, if a set
![]() $X\subseteq K$
is totally imperfect, then for every n there exists a coherent selection
$X\subseteq K$
is totally imperfect, then for every n there exists a coherent selection
![]() $E\colon \Sigma _n\to K$
such that
$E\colon \Sigma _n\to K$
such that
![]() $E[\Sigma _n]\subseteq K\setminus X$
.
$E[\Sigma _n]\subseteq K\setminus X$
.
Proof. Fix n and enumerate
![]() $\Sigma _n$
injectively as
$\Sigma _n$
injectively as
![]() $\{\nu _0,\ldots ,\nu _N\}$
. Since
$\{\nu _0,\ldots ,\nu _N\}$
. Since
![]() $[\nu _0]\cap K$
is perfect by
$[\nu _0]\cap K$
is perfect by
![]() $(e_f)$
, we can pick
$(e_f)$
, we can pick
![]() $E_0(\nu _0)\in ([\nu _0]\cap K)\setminus X$
. Fix a number
$E_0(\nu _0)\in ([\nu _0]\cap K)\setminus X$
. Fix a number
![]() $k<N$
and put
$k<N$
and put
![]() $C:=\{\nu _i:i\leq k\}$
. Assume that we have already defined a coherent map
$C:=\{\nu _i:i\leq k\}$
. Assume that we have already defined a coherent map
![]() $E_k:C\to K\setminus X$
. Then for every
$E_k:C\to K\setminus X$
. Then for every
![]() $m>n$
and
$m>n$
and
![]() $\nu _i\in C$
, there is
$\nu _i\in C$
, there is
![]() $e^m_0(\nu _i)\in \Sigma _m$
such that
$e^m_0(\nu _i)\in \Sigma _m$
such that
![]() $E_k(\nu _i)\in [e^m_0(\nu _i)]$
. In that way we define a map
$E_k(\nu _i)\in [e^m_0(\nu _i)]$
. In that way we define a map
![]() $e^m_0\colon C\to \Sigma _m$
. It is clear that this map is coherent. By
$e^m_0\colon C\to \Sigma _m$
. It is clear that this map is coherent. By
![]() $(e_f)$
there are
$(e_f)$
there are
![]() $\mu _{\langle 0\rangle }\neq \mu _{\langle 1\rangle }\in \Sigma _{n+1}$
such that both
$\mu _{\langle 0\rangle }\neq \mu _{\langle 1\rangle }\in \Sigma _{n+1}$
such that both
![]() $e^{n+1}_{\langle 0\rangle }=e^{n+1}_0\cup \{\langle \nu _{k+1}, \mu _{\langle 0\rangle }\rangle \}$
and
$e^{n+1}_{\langle 0\rangle }=e^{n+1}_0\cup \{\langle \nu _{k+1}, \mu _{\langle 0\rangle }\rangle \}$
and
![]() $e^{n+1}_{\langle 1\rangle }=e^{n+1}_0\cup \{\langle \nu _{k+1}, \mu _{\langle 1\rangle }\rangle \}$
are coherent as maps from
$e^{n+1}_{\langle 1\rangle }=e^{n+1}_0\cup \{\langle \nu _{k+1}, \mu _{\langle 1\rangle }\rangle \}$
are coherent as maps from
![]() $C\cup \{\nu _{k+1}\}$
to
$C\cup \{\nu _{k+1}\}$
to
![]() $\Sigma _{n+1}$
.
$\Sigma _{n+1}$
.
Suppose that for some
![]() $m>n$
we have defined mutually different
$m>n$
we have defined mutually different
![]() $\{\mu _s:s\in 2^{m-n}\}\subseteq \Sigma _m\setminus e_0^m[C]$
such that
$\{\mu _s:s\in 2^{m-n}\}\subseteq \Sigma _m\setminus e_0^m[C]$
such that
![]() $e^{m}_{ s}=e^{m}_0\cup \{\langle \nu _{k+1}, \mu _{ s}\rangle \}$
is coherent as a map from
$e^{m}_{ s}=e^{m}_0\cup \{\langle \nu _{k+1}, \mu _{ s}\rangle \}$
is coherent as a map from
![]() $C\cup \{\nu _{k+1}\}$
to
$C\cup \{\nu _{k+1}\}$
to
![]() $\Sigma _{m}$
for all
$\Sigma _{m}$
for all
![]() $s\in 2^{m-n}$
. By
$s\in 2^{m-n}$
. By
![]() $(e_f)$
for every
$(e_f)$
for every
![]() $s\in 2^{m-n}$
there are
$s\in 2^{m-n}$
there are
![]() $\mu _{ s\hat {\ \ } 0}\neq \mu _{ s\hat {\ \ }1}\in \Sigma _{m+1}$
such that
$\mu _{ s\hat {\ \ } 0}\neq \mu _{ s\hat {\ \ }1}\in \Sigma _{m+1}$
such that
is coherent as a map from
![]() $\Sigma _m$
to
$\Sigma _m$
to
![]() $\Sigma _{m+1}$
for all
$\Sigma _{m+1}$
for all
![]() $j\in 2$
. It follows that
$j\in 2$
. It follows that
is coherent as a map from
![]() $C\cup \{\nu _{k+1}\}\to \Sigma _{m+1}$
for all
$C\cup \{\nu _{k+1}\}\to \Sigma _{m+1}$
for all
![]() $s\in 2^{m-n}$
and
$s\in 2^{m-n}$
and
![]() $j\in s$
, which completes our construction of the maps
$j\in s$
, which completes our construction of the maps
![]() $e^m_s$
and elements
$e^m_s$
and elements
![]() $\mu _s$
as above for all
$\mu _s$
as above for all
![]() $m>n$
and
$m>n$
and
![]() $s\in 2^{m-n}$
.
$s\in 2^{m-n}$
.
For every
![]() $t\in 2^\omega $
let
$t\in 2^\omega $
let
![]() $z_t\in K$
be the unique element in
$z_t\in K$
be the unique element in
![]() $\bigcap _{m>n}[\mu _ {t\upharpoonright (m-n)}]$
and note that
$\bigcap _{m>n}[\mu _ {t\upharpoonright (m-n)}]$
and note that
![]() $z_t\neq z_{t'}$
for any
$z_t\neq z_{t'}$
for any
![]() $t\neq t'$
in
$t\neq t'$
in
![]() $2^\omega $
. Since the set
$2^\omega $
. Since the set
![]() $\{\,z_t : t\in 2^\omega \,\}$
is perfect, there exists t with
$\{\,z_t : t\in 2^\omega \,\}$
is perfect, there exists t with
![]() $z_t\not \in X$
. It suffices to observe that
$z_t\not \in X$
. It suffices to observe that
![]() $E_{k+1}:=E_k\cup \{\langle \nu _{k+1},z_t\rangle \}$
is a coherent map whose range is disjoint from X, which allows us to complete our proof by induction on
$E_{k+1}:=E_k\cup \{\langle \nu _{k+1},z_t\rangle \}$
is a coherent map whose range is disjoint from X, which allows us to complete our proof by induction on
![]() $k<N$
.
$k<N$
.
Lemma 2.2. In the notation used above, let
![]() $X\subseteq K$
be a totally imperfect Menger set. Then there exists a sequence
$X\subseteq K$
be a totally imperfect Menger set. Then there exists a sequence
![]() ${\langle \, \langle i_n,j_n,C_n\rangle : n\in \omega \,\rangle }$
such that
${\langle \, \langle i_n,j_n,C_n\rangle : n\in \omega \,\rangle }$
such that
-
(1)
 ${\langle \, i_n : n\in \omega \,\rangle }$
is a strictly increasing sequence of natural numbers;
${\langle \, i_n : n\in \omega \,\rangle }$
is a strictly increasing sequence of natural numbers; -
(2)
 $C_n\subseteq \Sigma _{i_n}$
;
$C_n\subseteq \Sigma _{i_n}$
; -
(3) for every
 $n\in \omega $
, we have
$n\in \omega $
, we have
 $j_n\in [i_n,i_{n+1})$
, and for every
$j_n\in [i_n,i_{n+1})$
, and for every
 $\nu \in C_n$
there exists
$\nu \in C_n$
there exists
 $e_n(\nu )\in \Sigma _{j_n}$
extending
$e_n(\nu )\in \Sigma _{j_n}$
extending
 $\nu $
, such that
$\nu $
, such that  $$ \begin{align*}C_{n+1}=\bigcup_{\nu\in C_n}\{\sigma\in\Sigma_{i_{n+1}}\: :\: \sigma \succ e_n(\nu)\};\end{align*} $$
$$ \begin{align*}C_{n+1}=\bigcup_{\nu\in C_n}\{\sigma\in\Sigma_{i_{n+1}}\: :\: \sigma \succ e_n(\nu)\};\end{align*} $$
-
(4) the maps
 $e_n\colon C_n\to \Sigma _{j_n}$
are coherent; and
$e_n\colon C_n\to \Sigma _{j_n}$
are coherent; and -
(5)
 $\bigcap _{n\in \omega }\bigcup _{\nu \in C_n}[\nu ]\cap X=\emptyset $
.
$\bigcap _{n\in \omega }\bigcup _{\nu \in C_n}[\nu ]\cap X=\emptyset $
.
Proof. We shall describe a strategy
![]() $\S $
for Alice in the Menger game played on X such that each play lost by Alice gives rise to the objects whose existence we need to establish. For every
$\S $
for Alice in the Menger game played on X such that each play lost by Alice gives rise to the objects whose existence we need to establish. For every
![]() $n\in \omega $
, let
$n\in \omega $
, let
![]() $E_n\colon \Sigma _n\to K$
be a coherent selection from Lemma 2.1. Put
$E_n\colon \Sigma _n\to K$
be a coherent selection from Lemma 2.1. Put
For every
![]() $j\geq i_0$
and
$j\geq i_0$
and
![]() $\nu \in \Sigma _{i_0}$
, let
$\nu \in \Sigma _{i_0}$
, let
![]() $ \sigma _{0,j}(\nu )$
be the unique element of
$ \sigma _{0,j}(\nu )$
be the unique element of
![]() $\Sigma _j$
such that
$\Sigma _j$
such that
![]() $E_{i_0}(\nu )\in [\sigma _{0,j}(\nu )]$
. Then,
$E_{i_0}(\nu )\in [\sigma _{0,j}(\nu )]$
. Then,
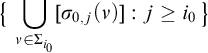 $$\begin{align*}{\big\{\,\bigcup_{\nu\in\Sigma_{i_0}}[\sigma_{0,j}(\nu)] : j\geq i_0\,\big\}} \end{align*}$$
$$\begin{align*}{\big\{\,\bigcup_{\nu\in\Sigma_{i_0}}[\sigma_{0,j}(\nu)] : j\geq i_0\,\big\}} \end{align*}$$
is a decreasing family of clopen sets in
![]() $(2^\omega )^S$
, whose intersection is equal to the set
$(2^\omega )^S$
, whose intersection is equal to the set
![]() $Z_0$
. Since
$Z_0$
. Since
![]() $Z_0\subseteq K\setminus X$
, the family
$Z_0\subseteq K\setminus X$
, the family
![]() $\mathcal {U}_0$
of all sets
$\mathcal {U}_0$
of all sets
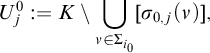 $$\begin{align*}U^0_j:=K\setminus \bigcup_{\nu\in\Sigma_{i_0}}[\sigma_{0,j}(\nu)], \end{align*}$$
$$\begin{align*}U^0_j:=K\setminus \bigcup_{\nu\in\Sigma_{i_0}}[\sigma_{0,j}(\nu)], \end{align*}$$
where
![]() $j\geq i_0$
, is an increasing open cover of X. Now,
$j\geq i_0$
, is an increasing open cover of X. Now,
![]() $\S $
instructs Alice to start the play with
$\S $
instructs Alice to start the play with
![]() $\mathcal {U}_0$
.
$\mathcal {U}_0$
.
Suppose that Bob chooses
![]() $U^0_{j_0}$
for some
$U^0_{j_0}$
for some
![]() $j_0\geq i_0$
. For each
$j_0\geq i_0$
. For each
![]() $\nu \in \Sigma _{i_0}$
, let
$\nu \in \Sigma _{i_0}$
, let
![]() $e_0(\nu ):=\sigma _{0,j_0}(\nu )$
, an element of
$e_0(\nu ):=\sigma _{0,j_0}(\nu )$
, an element of
![]() $\Sigma _{j_0}$
. Since
$\Sigma _{j_0}$
. Since
![]() $E_{i_0}$
is a coherent selection, the map
$E_{i_0}$
is a coherent selection, the map
![]() $e_0\colon C_0\to \Sigma _{j_0}$
is coherent.
$e_0\colon C_0\to \Sigma _{j_0}$
is coherent.
Then we put
Suppose that a natural number
![]() $i_n$
and a set
$i_n$
and a set
![]() $C_n\subseteq \Sigma _{i_n}$
have already been defined for some
$C_n\subseteq \Sigma _{i_n}$
have already been defined for some
![]() $n>0$
. Let
$n>0$
. Let
![]() $Z_n:=E_{i_n}[C_{n}]\subseteq K\setminus X$
. For every
$Z_n:=E_{i_n}[C_{n}]\subseteq K\setminus X$
. For every
![]() $j\geq i_n$
and
$j\geq i_n$
and
![]() $\nu \in C_n$
, let
$\nu \in C_n$
, let
![]() $ \sigma _{n,j}(\nu )$
be the unique element of
$ \sigma _{n,j}(\nu )$
be the unique element of
![]() $\Sigma _j$
such that
$\Sigma _j$
such that
![]() $E_{i_n}(\nu )\in [\sigma _{n,j}(\nu )]$
. Then,
$E_{i_n}(\nu )\in [\sigma _{n,j}(\nu )]$
. Then,
is a decreasing family of clopen sets in
![]() $(2^\omega )^S$
, whose intersection is equal to the set
$(2^\omega )^S$
, whose intersection is equal to the set
![]() $Z_n$
. Since
$Z_n$
. Since
![]() $Z_n\subseteq K\setminus X$
, the family
$Z_n\subseteq K\setminus X$
, the family
![]() $\mathcal {U}_0$
of all sets
$\mathcal {U}_0$
of all sets
where
![]() $j\geq i_n$
, is an increasing open cover of X. Now,
$j\geq i_n$
, is an increasing open cover of X. Now,
![]() $\S $
instructs Alice to play the family
$\S $
instructs Alice to play the family
![]() $\mathcal {U}_n$
.
$\mathcal {U}_n$
.
Suppose that Bob chooses
![]() $U^n_{j_n}$
for some
$U^n_{j_n}$
for some
![]() $j_n\geq i_n$
. Since
$j_n\geq i_n$
. Since
![]() $E_{i_n}$
is a coherent selection, the map
$E_{i_n}$
is a coherent selection, the map
![]() $e_n\colon C_n\to \Sigma _{j_n}$
is coherent. Then we put
$e_n\colon C_n\to \Sigma _{j_n}$
is coherent. Then we put
This completes our definition of the strategy
![]() $\S $
for Alice such that each infinite play in the Menger game on X in which Alice uses
$\S $
for Alice such that each infinite play in the Menger game on X in which Alice uses
![]() $\S $
gives rise to a sequence
$\S $
gives rise to a sequence
as described above. In particular, conditions
![]() $(1)$
–
$(1)$
–
![]() $(4)$
are satisfied by the construction. By Theorem 1.4, there is a play, where Alice uses the strategy
$(4)$
are satisfied by the construction. By Theorem 1.4, there is a play, where Alice uses the strategy
![]() $\S $
and the play is won by Bob. Then
$\S $
and the play is won by Bob. Then
![]() $X\subseteq \bigcup _{n\in \omega }U^n_{j_n}$
, i.e.,
$X\subseteq \bigcup _{n\in \omega }U^n_{j_n}$
, i.e.,
For each n, we have
and thus
It follows that condition
![]() $(5)$
is also satisfied.
$(5)$
is also satisfied.
3 Combinatorics of conditions in the iterated Sacks forcing
Here we deal with countable support iterations of the forcing notion introduced by Sacks [Reference Sacks and Scott19]. We do not prove any essentially new results about these iterations in this section, but rather “tailor” several results established in [Reference Baumgartner and Laver3, Reference Miller15] and perhaps somewhere else for the purposes we have in Sections 4 and 6. We try to follow notations used in [Reference Baumgartner and Laver3].
Let
![]() $2^{<\omega }:=\bigcup _{n\in \omega }2^n$
. For elements
$2^{<\omega }:=\bigcup _{n\in \omega }2^n$
. For elements
![]() $s,t\in 2^{<\omega }$
, we write
$s,t\in 2^{<\omega }$
, we write
![]() $s\subseteq t$
if the sequence s is an initial segment of the sequence t, i.e.,
$s\subseteq t$
if the sequence s is an initial segment of the sequence t, i.e.,
![]() $s(i)=t(i)$
for all
$s(i)=t(i)$
for all
![]() $i\in \operatorname {dom}(s)$
. A Sacks tree is a set
$i\in \operatorname {dom}(s)$
. A Sacks tree is a set
![]() $p\subseteq 2^{<\omega }$
such that for every
$p\subseteq 2^{<\omega }$
such that for every
![]() $s\in p$
and a natural number n, we have
$s\in p$
and a natural number n, we have
![]() $s \restriction n\in p$
and there are elements
$s \restriction n\in p$
and there are elements
![]() $t,u\in p$
with
$t,u\in p$
with
![]() $s\subseteq t$
,
$s\subseteq t$
,
![]() $s\subseteq u$
,
$s\subseteq u$
,
![]() $t\not \subseteq u$
and
$t\not \subseteq u$
and
![]() $t\not \subseteq u$
. For Sacks trees p and q, a condition q is stronger than p which we write
$t\not \subseteq u$
. For Sacks trees p and q, a condition q is stronger than p which we write
![]() $q\geq p$
if
$q\geq p$
if
![]() $q\subseteq p$
. The Sacks poset
$q\subseteq p$
. The Sacks poset
![]() $\mathbb {S}$
is the set of all Sacks trees ordered by
$\mathbb {S}$
is the set of all Sacks trees ordered by
![]() $\geq $
. For
$\geq $
. For
![]() $p,q\in \mathbb {S}$
and natural numbers
$p,q\in \mathbb {S}$
and natural numbers
![]() $m>n$
, we write
$m>n$
, we write
![]() $(q,m)\geq (p,n)$
if
$(q,m)\geq (p,n)$
if
![]() $q\subseteq p$
and for every
$q\subseteq p$
and for every
![]() $s\in p\cap 2^n$
, there are different elements
$s\in p\cap 2^n$
, there are different elements
![]() $t,u\in q\cap 2^m$
such that
$t,u\in q\cap 2^m$
such that
![]() $s\subseteq t$
and
$s\subseteq t$
and
![]() $s \subseteq u$
. For
$s \subseteq u$
. For
![]() $p\in \mathbb {S}$
and
$p\in \mathbb {S}$
and
![]() $s\in p$
, let
$s\in p$
, let
![]() $p_s:=\{\,t\in p : t\subseteq s\text { or }s\subseteq t\,\}$
.
$p_s:=\{\,t\in p : t\subseteq s\text { or }s\subseteq t\,\}$
.
Let
![]() $\alpha $
be an ordinal number and
$\alpha $
be an ordinal number and
![]() $\mathbb S_\alpha $
be an iterated forcing of length
$\mathbb S_\alpha $
be an iterated forcing of length
![]() $\alpha $
with countable support, where each iterand is a Sacks poset. For
$\alpha $
with countable support, where each iterand is a Sacks poset. For
![]() $p,q\in \mathbb S_\alpha $
, let
$p,q\in \mathbb S_\alpha $
, let
![]() $q\geq p$
if
$q\geq p$
if
![]() $\operatorname {supp}(q)\supseteq \operatorname {supp}(p)$
and for every
$\operatorname {supp}(q)\supseteq \operatorname {supp}(p)$
and for every
![]() $\beta \in \operatorname {supp}(p)$
, we have
$\beta \in \operatorname {supp}(p)$
, we have
![]() $q\upharpoonright \beta \Vdash _\beta q(\beta )\geq p(\beta )$
.
$q\upharpoonright \beta \Vdash _\beta q(\beta )\geq p(\beta )$
.
Let
![]() $p\in \mathbb S_\alpha $
,
$p\in \mathbb S_\alpha $
,
![]() $F\subseteq \alpha $
be a finite set, n a natural number and
$F\subseteq \alpha $
be a finite set, n a natural number and
![]() $\sigma \colon F\to 2^n$
a map. If
$\sigma \colon F\to 2^n$
a map. If
![]() $F=\emptyset $
, then the map
$F=\emptyset $
, then the map
![]() $\sigma $
is consistent with p and
$\sigma $
is consistent with p and
![]() $p|\sigma :=p$
. Assume that
$p|\sigma :=p$
. Assume that
![]() $\beta $
is the greatest element in F, the map
$\beta $
is the greatest element in F, the map
![]() $\sigma \upharpoonright \beta $
is consistent with p and the condition
$\sigma \upharpoonright \beta $
is consistent with p and the condition
![]() $p|(\sigma \upharpoonright \beta )$
has already been defined. If
$p|(\sigma \upharpoonright \beta )$
has already been defined. If
then the map
![]() $\sigma $
is consistent with p and we define
$\sigma $
is consistent with p and we define
![]() $p|\sigma (\gamma )$
to be the following
$p|\sigma (\gamma )$
to be the following
![]() $\mathbb S_\gamma $
-name
$\mathbb S_\gamma $
-name
![]() $\tau $
:
$\tau $
:
-
•
 $p|(\sigma \upharpoonright \beta )(\gamma ),$
if
$p|(\sigma \upharpoonright \beta )(\gamma ),$
if
 $\gamma <\beta $
;
$\gamma <\beta $
; -
• If
 $\gamma =\beta $
, then
$\gamma =\beta $
, then
 $\big (p|(\sigma \upharpoonright \beta )\big )\upharpoonright \beta \Vdash _\beta \tau =p(\beta )_{\sigma (\beta )}$
and
$\big (p|(\sigma \upharpoonright \beta )\big )\upharpoonright \beta \Vdash _\beta \tau =p(\beta )_{\sigma (\beta )}$
and
 $r\Vdash _\beta \tau =p(\beta )$
for
$r\Vdash _\beta \tau =p(\beta )$
for
 $r\in \mathbb S_\beta $
incompatible with
$r\in \mathbb S_\beta $
incompatible with
 $\big (p|(\sigma \upharpoonright \beta )\big )\upharpoonright \beta $
; and
$\big (p|(\sigma \upharpoonright \beta )\big )\upharpoonright \beta $
; and -
•
 $p(\gamma )$
, otherwise.
$p(\gamma )$
, otherwise.
The following fact can be established by induction on
![]() $|F|$
in a rather straightforward way.
$|F|$
in a rather straightforward way.
Observation 3.1. In the notation above, if
![]() $\sigma $
is consistent with p, then
$\sigma $
is consistent with p, then
![]() $\sigma \upharpoonright \beta $
is consistent with both
$\sigma \upharpoonright \beta $
is consistent with both
![]() $p\upharpoonright \beta $
and p, and
$p\upharpoonright \beta $
and p, and
![]() $\big (p|(\sigma \upharpoonright \beta )\big )\upharpoonright \beta =(p\upharpoonright \beta )|(\sigma \upharpoonright \beta )$
.
$\big (p|(\sigma \upharpoonright \beta )\big )\upharpoonright \beta =(p\upharpoonright \beta )|(\sigma \upharpoonright \beta )$
.
A condition
![]() $p\in \mathbb S_\alpha $
is
$p\in \mathbb S_\alpha $
is
![]() $(F,n)$
-determined, where
$(F,n)$
-determined, where
![]() $F\subseteq \alpha $
and
$F\subseteq \alpha $
and
![]() $n\in \omega $
, if every map
$n\in \omega $
, if every map
![]() $\sigma \colon F\to 2^n$
is either consistent with p, or there is
$\sigma \colon F\to 2^n$
is either consistent with p, or there is
![]() $\beta \in F$
such that
$\beta \in F$
such that
![]() $\sigma \upharpoonright \beta $
is consistent with p and
$\sigma \upharpoonright \beta $
is consistent with p and
![]() $(p\upharpoonright \beta )|(\sigma \upharpoonright \beta )\Vdash _\beta \sigma (\beta )\notin p(\beta )$
. For
$(p\upharpoonright \beta )|(\sigma \upharpoonright \beta )\Vdash _\beta \sigma (\beta )\notin p(\beta )$
. For
![]() $q\in \mathbb S_\alpha $
and a natural number
$q\in \mathbb S_\alpha $
and a natural number
![]() $m>n$
, we write
$m>n$
, we write
![]() $(q,m)\geq _F(p,n)$
if
$(q,m)\geq _F(p,n)$
if
![]() $q\geq p$
and for every
$q\geq p$
and for every
![]() $\beta \in F$
, we have
$\beta \in F$
, we have
![]() $q\upharpoonright \beta \Vdash _\beta (q(\beta ),m)\geq (p(\beta ),n)$
.
$q\upharpoonright \beta \Vdash _\beta (q(\beta ),m)\geq (p(\beta ),n)$
.
Let p be an
![]() $(F,n)$
-determined condition. We write
$(F,n)$
-determined condition. We write
![]() $(q,n)\geq _F (p,n)$
if
$(q,n)\geq _F (p,n)$
if
![]() $q\geq p$
and every map
$q\geq p$
and every map
![]() $\sigma \colon F\to 2^n$
consistent with p, is also consistent with q. Next, we collect rather straightforward facts about the notions introduced above, these are used in nearly all works investigating iterations of the Sacks forcing or similar posets consisting of trees.
$\sigma \colon F\to 2^n$
consistent with p, is also consistent with q. Next, we collect rather straightforward facts about the notions introduced above, these are used in nearly all works investigating iterations of the Sacks forcing or similar posets consisting of trees.
Observation 3.2. Let
![]() $p\in \mathbb S_\alpha $
be an
$p\in \mathbb S_\alpha $
be an
![]() $(F,n)$
-determined condition,
$(F,n)$
-determined condition,
![]() $\Sigma $
the set of all maps
$\Sigma $
the set of all maps
![]() $\nu \colon F\to 2^n$
consistent with p and
$\nu \colon F\to 2^n$
consistent with p and
![]() $\beta <\alpha $
. Then the following assertions hold.
$\beta <\alpha $
. Then the following assertions hold.
-
(1) If
 $(q,n)\geq _F (p,n)$
, then q is also
$(q,n)\geq _F (p,n)$
, then q is also
 $(F,n)$
-determined;
$(F,n)$
-determined; -
(2) If
 $\sigma \in \Sigma $
, then
$\sigma \in \Sigma $
, then
 $p|(\sigma \upharpoonright \beta )$
is
$p|(\sigma \upharpoonright \beta )$
is
 $(F\setminus \beta , n)$
-determined, and
$(F\setminus \beta , n)$
-determined, and
 $\nu \in (2^n)^{F\setminus \beta }$
is consistent with
$\nu \in (2^n)^{F\setminus \beta }$
is consistent with
 $p|(\sigma \upharpoonright \beta )$
iff
$p|(\sigma \upharpoonright \beta )$
iff
 $(\sigma \upharpoonright \beta )\cup \nu \in \Sigma $
;
$(\sigma \upharpoonright \beta )\cup \nu \in \Sigma $
; -
(3) The set
 $\{\,p|\sigma : \sigma \in \Sigma \,\}$
is a maximal antichain above p;
$\{\,p|\sigma : \sigma \in \Sigma \,\}$
is a maximal antichain above p; -
(4) p is
 $(F\cap \beta ,n)$
-determined and
$(F\cap \beta ,n)$
-determined and
 $\{\sigma \upharpoonright (F\cap \beta ):\sigma \in \Sigma \}$
is the family of all functions from
$\{\sigma \upharpoonright (F\cap \beta ):\sigma \in \Sigma \}$
is the family of all functions from
 $F\cap \beta $
to
$F\cap \beta $
to
 $2^n$
consistent with p;
$2^n$
consistent with p; -
(5) If
 $\sigma \in \Sigma $
and
$\sigma \in \Sigma $
and
 $r\geq p|\sigma $
, then there exists
$r\geq p|\sigma $
, then there exists
 $q\in \mathbb S_\alpha $
with
$q\in \mathbb S_\alpha $
with
 $(q,n)\geq _F(p,n)$
and
$(q,n)\geq _F(p,n)$
and
 ${q|\sigma =r;}$
${q|\sigma =r;}$
-
(6) If
 $D\subseteq \mathbb S_\alpha $
is open and dense, then there exists
$D\subseteq \mathbb S_\alpha $
is open and dense, then there exists
 $q\in \mathbb S_\alpha $
with
$q\in \mathbb S_\alpha $
with
 $(q,n)\geq _F(p,n)$
and
$(q,n)\geq _F(p,n)$
and
 $q|\sigma \in D$
for all
$q|\sigma \in D$
for all
 $\sigma \in \Sigma $
; and
$\sigma \in \Sigma $
; and -
(7) If
 $\tau $
is an
$\tau $
is an
 $\mathbb S_\alpha $
-name for a real, then for each natural number l there is a condition
$\mathbb S_\alpha $
-name for a real, then for each natural number l there is a condition
 $q\in \mathbb S_\alpha $
and a family
$q\in \mathbb S_\alpha $
and a family
 $\{y_\sigma :\sigma \in \Sigma \}\subseteq 2^l$
such that
$\{y_\sigma :\sigma \in \Sigma \}\subseteq 2^l$
such that
 $(q,n)\geq _F (p,n)$
and
$(q,n)\geq _F (p,n)$
and
 $q|\sigma \Vdash \tau \upharpoonright l= y_\sigma $
for all
$q|\sigma \Vdash \tau \upharpoonright l= y_\sigma $
for all
 $\sigma \in \Sigma $
.
$\sigma \in \Sigma $
.
The last three items of Observation 3.2 imply the following easy fact.
Lemma 3.3 (Miller [Reference Miller15, Lemma 2]).
Let
![]() $p\in \mathbb S_\alpha $
be an
$p\in \mathbb S_\alpha $
be an
![]() $(F,n)$
-determined condition and
$(F,n)$
-determined condition and
![]() $\tau $
an
$\tau $
an
![]() $\mathbb S_\alpha $
-name for a real such that
$\mathbb S_\alpha $
-name for a real such that
![]() $p\Vdash \tau \in {2^\omega }\setminus V$
. Then for each finite set
$p\Vdash \tau \in {2^\omega }\setminus V$
. Then for each finite set
![]() $Y\subseteq {2^\omega }\cap V$
, there is a finite set
$Y\subseteq {2^\omega }\cap V$
, there is a finite set
![]() $X\subseteq {2^\omega }\cap V$
disjoint from Y such that
$X\subseteq {2^\omega }\cap V$
disjoint from Y such that
![]() $|X|\leq 2^{n\cdot |F|}$
, and for each natural number l, there is a condition
$|X|\leq 2^{n\cdot |F|}$
, and for each natural number l, there is a condition
![]() $q\in \mathbb S_\alpha $
such that
$q\in \mathbb S_\alpha $
such that
![]() $(q,n)\geq _F (p,n)$
and
$(q,n)\geq _F (p,n)$
and
Let
![]() $\dot {G}_{\alpha }$
be an
$\dot {G}_{\alpha }$
be an
![]() $\mathbb S_\alpha $
-name for a
$\mathbb S_\alpha $
-name for a
![]() $\mathbb S_\alpha $
-generic filter, and for
$\mathbb S_\alpha $
-generic filter, and for
![]() $\beta <\alpha $
let
$\beta <\alpha $
let
![]() $\mathbb S_{\beta ,\alpha }$
be an
$\mathbb S_{\beta ,\alpha }$
be an
![]() $\mathbb S_\beta $
-name for the iteration from (including)
$\mathbb S_\beta $
-name for the iteration from (including)
![]() $\beta $
to
$\beta $
to
![]() $\alpha $
, so that
$\alpha $
, so that
![]() $\mathbb S_\alpha $
is forcing equivalent to
$\mathbb S_\alpha $
is forcing equivalent to
![]() $\mathbb S_\beta *\mathbb S_{\beta ,\alpha }$
. Whenever we work in the forcing extension
$\mathbb S_\beta *\mathbb S_{\beta ,\alpha }$
. Whenever we work in the forcing extension
![]() $V[G_\beta ]$
for some
$V[G_\beta ]$
for some
![]() $\mathbb S_\beta $
-generic filter
$\mathbb S_\beta $
-generic filter
![]() $G_\beta $
, we denote by
$G_\beta $
, we denote by
![]() $\dot {G}_{\beta ,\alpha }$
a
$\dot {G}_{\beta ,\alpha }$
a
![]() $\mathbb S_{\beta ,\alpha }^{G_\beta }$
-name for a
$\mathbb S_{\beta ,\alpha }^{G_\beta }$
-name for a
![]() $\mathbb S_{\beta ,\alpha }^{G_\beta }$
-generic filter over
$\mathbb S_{\beta ,\alpha }^{G_\beta }$
-generic filter over
![]() $V[G_\beta ]$
. We shall need the following easy observation, we use the notation from the above.
$V[G_\beta ]$
. We shall need the following easy observation, we use the notation from the above.
Observation 3.4. Suppose that p is
![]() $(F,n)$
-determined,
$(F,n)$
-determined,
![]() $\beta \leq \alpha $
, and
$\beta \leq \alpha $
, and
![]() $p\upharpoonright \beta \in G_\beta $
. Then in
$p\upharpoonright \beta \in G_\beta $
. Then in
![]() $V[G_\beta ]$
,
$V[G_\beta ]$
,
![]() $p\upharpoonright [\beta ,\alpha )^{G_\beta }\in \mathbb S_{\beta ,\alpha }^{G_\beta }$
is
$p\upharpoonright [\beta ,\alpha )^{G_\beta }\in \mathbb S_{\beta ,\alpha }^{G_\beta }$
is
![]() $(F\setminus \beta ,n)$
-determined.
$(F\setminus \beta ,n)$
-determined.
Moreover, if
![]() $\sigma \in (2^n)^F$
is consistent with p and
$\sigma \in (2^n)^F$
is consistent with p and
![]() $(p|(\sigma \upharpoonright \beta ))\upharpoonright \beta \in G_\beta $
, then
$(p|(\sigma \upharpoonright \beta ))\upharpoonright \beta \in G_\beta $
, then
![]() $\sigma \upharpoonright (F\setminus \beta )$
is consistent with
$\sigma \upharpoonright (F\setminus \beta )$
is consistent with
![]() $p\upharpoonright [\beta ,\alpha )^{G_\beta }$
in
$p\upharpoonright [\beta ,\alpha )^{G_\beta }$
in
![]() $V[G_\beta ]$
; and if
$V[G_\beta ]$
; and if
![]() $(p|(\sigma \upharpoonright \beta ))\upharpoonright \beta \in G_\beta $
and
$(p|(\sigma \upharpoonright \beta ))\upharpoonright \beta \in G_\beta $
and
![]() $\nu \in (2^n)^{F\setminus \beta }$
is consistent with
$\nu \in (2^n)^{F\setminus \beta }$
is consistent with
![]() $p\upharpoonright [\beta ,\alpha )^{G_\beta }$
in
$p\upharpoonright [\beta ,\alpha )^{G_\beta }$
in
![]() $V[G_\beta ]$
, then
$V[G_\beta ]$
, then
![]() $(\sigma \upharpoonright \beta )\cup \nu \in (2^n)^F$
is consistent with p.
$(\sigma \upharpoonright \beta )\cup \nu \in (2^n)^F$
is consistent with p.
Lemma 3.5 (Miller [Reference Miller15, Lemma 5]).
Let
![]() $p\in \mathbb S_\alpha $
be an
$p\in \mathbb S_\alpha $
be an
![]() $(F,n)$
-determined condition and
$(F,n)$
-determined condition and
![]() $\tau $
be an
$\tau $
be an
![]() $\mathbb S_\alpha $
-name for a real such that
$\mathbb S_\alpha $
-name for a real such that
Then for any
![]() $k\in \omega $
there exist a condition
$k\in \omega $
there exist a condition
![]() $q\in \mathbb S_\alpha $
, a natural number
$q\in \mathbb S_\alpha $
, a natural number
![]() $l>k$
, and elements
$l>k$
, and elements
![]() $y_{\sigma }\in 2^{l}$
, for all maps
$y_{\sigma }\in 2^{l}$
, for all maps
![]() $\sigma \colon F\to 2^n$
consistent with p, with the following properties:
$\sigma \colon F\to 2^n$
consistent with p, with the following properties:
-
(1)
 $(q, n) \geq _F (p, n)$
,
$(q, n) \geq _F (p, n)$
, -
(2)
 $q|\sigma \Vdash \tau \upharpoonright l= y_{\sigma }$
,
$q|\sigma \Vdash \tau \upharpoonright l= y_{\sigma }$
, -
(3) the maps
 $y_{\sigma }$
are pairwise different.
$y_{\sigma }$
are pairwise different.
Proof. Let
![]() $\xi =\min (F)$
and note that the fact that p is
$\xi =\min (F)$
and note that the fact that p is
![]() $(F,n)$
-determined yields
$(F,n)$
-determined yields
![]() $N\leq 2^n$
and
$N\leq 2^n$
and
![]() $\{s_i:i<N\}\subseteq 2^n$
such that
$\{s_i:i<N\}\subseteq 2^n$
such that
![]() $p\upharpoonright \xi $
forces
$p\upharpoonright \xi $
forces
![]() $p(\xi )\cap 2^n=\{s_i:i<N\}$
. For every
$p(\xi )\cap 2^n=\{s_i:i<N\}$
. For every
![]() $i<N$
let
$i<N$
let
![]() $\mu _i$
be the map
$\mu _i$
be the map
![]() $\{\langle \xi ,s_i\rangle \}$
and note that
$\{\langle \xi ,s_i\rangle \}$
and note that
![]() $\mu _i$
is consistent with p.
$\mu _i$
is consistent with p.
By induction on
![]() $i<N$
, using Lemma 3.3 and Observation 3.2(2), we can find mutually disjoint finite sets
$i<N$
, using Lemma 3.3 and Observation 3.2(2), we can find mutually disjoint finite sets
![]() $X_i\subseteq {2^\omega }\cap V$
,
$X_i\subseteq {2^\omega }\cap V$
,
![]() $i<N$
, such that
$i<N$
, such that
![]() $|X_i|\leq 2^{n\cdot (|F|-1)}$
, and for each natural number l there is a condition
$|X_i|\leq 2^{n\cdot (|F|-1)}$
, and for each natural number l there is a condition
![]() $u^l_i\in \mathbb S_\alpha $
with
$u^l_i\in \mathbb S_\alpha $
with
![]() $u^l_j\upharpoonright \xi \geq u^l_i\upharpoonright \xi $
for all
$u^l_j\upharpoonright \xi \geq u^l_i\upharpoonright \xi $
for all
![]() $i<j\leq N$
,
$i<j\leq N$
,
![]() $u^l_0\upharpoonright \xi \geq p\upharpoonright \xi $
,
$u^l_0\upharpoonright \xi \geq p\upharpoonright \xi $
,
![]() $(u^l_i,n)\geq _{F\setminus \{\xi \}} (p|\mu _i,n)$
and
$(u^l_i,n)\geq _{F\setminus \{\xi \}} (p|\mu _i,n)$
and
Pick a natural number
![]() $l_{*}>k$
such that
$l_{*}>k$
such that
![]() $x\upharpoonright l_{*}\neq x'\upharpoonright l_{*}$
for any distinct
$x\upharpoonright l_{*}\neq x'\upharpoonright l_{*}$
for any distinct
![]() $x,x'$
in
$x,x'$
in
![]() $\bigcup _{i<N} X_i$
. As a result, the elements of the family
$\bigcup _{i<N} X_i$
. As a result, the elements of the family
![]() $\{\,X_i\upharpoonright l_{*} : i<N\,\}$
are mutually disjoint.
$\{\,X_i\upharpoonright l_{*} : i<N\,\}$
are mutually disjoint.
Now we proceed by induction on the cardinality of F. If
![]() $F=\{\xi \}$
, then
$F=\{\xi \}$
, then
![]() $|X_i|=1$
for all
$|X_i|=1$
for all
![]() $i<N$
(because
$i<N$
(because
![]() $ 2^{n\cdot (|F|-1)}=1$
), i.e.,
$ 2^{n\cdot (|F|-1)}=1$
), i.e.,
![]() $X_i=\{x_i\}$
for some
$X_i=\{x_i\}$
for some
![]() $x_i\in 2^\omega $
. Put
$x_i\in 2^\omega $
. Put
![]() $y_{\mu _i}:=x_i\upharpoonright l_{*}$
for all
$y_{\mu _i}:=x_i\upharpoonright l_{*}$
for all
![]() $i<N$
and let
$i<N$
and let
![]() $r\in \mathbb S_\alpha $
be a condition such that
$r\in \mathbb S_\alpha $
be a condition such that
![]() $r\upharpoonright \xi =u^{l_{*}}_{N-1}\upharpoonright \xi $
,
$r\upharpoonright \xi =u^{l_{*}}_{N-1}\upharpoonright \xi $
,
![]() $r\upharpoonright \xi $
forces
$r\upharpoonright \xi $
forces
![]() $r(\xi )$
to be
$r(\xi )$
to be
![]() $\bigcup \{\,u^{l_{*}}_i(\xi ) : i<N\,\}$
, and
$\bigcup \{\,u^{l_{*}}_i(\xi ) : i<N\,\}$
, and
![]() $(r|\mu _i)\upharpoonright \beta $
forces
$(r|\mu _i)\upharpoonright \beta $
forces
![]() $r(\beta )=u^{l_{*}}_i(\beta )$
for all
$r(\beta )=u^{l_{*}}_i(\beta )$
for all
![]() $\beta>\xi $
. It follows from the above that
$\beta>\xi $
. It follows from the above that
![]() $r|\mu _i\geq u^{l_{*}}_i$
and hence
$r|\mu _i\geq u^{l_{*}}_i$
and hence
![]() $r|\mu _i$
forces
$r|\mu _i$
forces
![]() $\tau \upharpoonright l_{*}=x_i\upharpoonright l_{*}=y_{\mu _i}$
, hence
$\tau \upharpoonright l_{*}=x_i\upharpoonright l_{*}=y_{\mu _i}$
, hence
![]() $q:=r$
and
$q:=r$
and
![]() $l:=l_{*}$
are as required.
$l:=l_{*}$
are as required.
Now assume that
![]() $\left |F\right |>1$
and the statement holds for each set of cardinality smaller than
$\left |F\right |>1$
and the statement holds for each set of cardinality smaller than
![]() $\left |F\right |$
. Let
$\left |F\right |$
. Let
![]() $\xi ,l_{*},r$
be as above and note that by the construction we have
$\xi ,l_{*},r$
be as above and note that by the construction we have
for all
![]() $i<N$
, and hence
$i<N$
, and hence
![]() $(r,n)\geq _F (p,n)$
. Fix
$(r,n)\geq _F (p,n)$
. Fix
![]() $i<N$
and let G be an
$i<N$
and let G be an
![]() $\mathbb {S}_{\xi +1}$
-generic filter containing
$\mathbb {S}_{\xi +1}$
-generic filter containing
![]() $(r|\mu _i)\upharpoonright (\xi +1)$
. Work in
$(r|\mu _i)\upharpoonright (\xi +1)$
. Work in
![]() $V[G]$
. Then
$V[G]$
. Then
is
![]() $(F\setminus \{\xi \},n)$
-determined by Observation 3.2(1) because
$(F\setminus \{\xi \},n)$
-determined by Observation 3.2(1) because
by the construction, and
![]() $\big (u^{l_{*}}_i\upharpoonright [\xi +1,\alpha )\big )^{G}$
is
$\big (u^{l_{*}}_i\upharpoonright [\xi +1,\alpha )\big )^{G}$
is
![]() $(F\setminus \{\xi \},n)$
-determined by Observation 3.4. Note that
$(F\setminus \{\xi \},n)$
-determined by Observation 3.4. Note that
because
![]() $r^{\prime }_i\geq p\upharpoonright [\xi +1,\alpha )^G$
and
$r^{\prime }_i\geq p\upharpoonright [\xi +1,\alpha )^G$
and
![]() $p\restriction (\xi +1)\in G$
. By the inductive assumption, there exist a condition
$p\restriction (\xi +1)\in G$
. By the inductive assumption, there exist a condition
![]() $r^{\prime \prime }_i\in \mathbb {S}_{\xi +1,\alpha }^{G} $
, a natural number
$r^{\prime \prime }_i\in \mathbb {S}_{\xi +1,\alpha }^{G} $
, a natural number
![]() $l_i>l_{*}$
and pairwise different elements
$l_i>l_{*}$
and pairwise different elements
![]() $t_{\sigma '}\in 2^{l_i}$
for all maps
$t_{\sigma '}\in 2^{l_i}$
for all maps
![]() $\sigma '\colon F\setminus \{\xi \}\to 2^n$
consistent with
$\sigma '\colon F\setminus \{\xi \}\to 2^n$
consistent with
![]() $r_i^{\prime \prime }$
, such that
$r_i^{\prime \prime }$
, such that
![]() $(r_i^{\prime \prime },n)\geq _{F\setminus \{\xi \}}(r_i^{\prime },n)$
and
$(r_i^{\prime \prime },n)\geq _{F\setminus \{\xi \}}(r_i^{\prime },n)$
and
![]() $r_i^{\prime \prime }|\sigma '\Vdash \tau \upharpoonright l_i = t_{\sigma '}$
. Let
$r_i^{\prime \prime }|\sigma '\Vdash \tau \upharpoonright l_i = t_{\sigma '}$
. Let
![]() $\Sigma ^{\prime }_i$
be the set of all maps
$\Sigma ^{\prime }_i$
be the set of all maps
![]() $\sigma '\colon F\setminus \{\xi \}\to 2^n$
consistent with
$\sigma '\colon F\setminus \{\xi \}\to 2^n$
consistent with
![]() $r_i^{\prime \prime }$
.
$r_i^{\prime \prime }$
.
Now we work in V. Let
![]() $\Sigma $
be the set of all maps
$\Sigma $
be the set of all maps
![]() $\sigma \colon F\to 2^n$
consistent with p. Let
$\sigma \colon F\to 2^n$
consistent with p. Let ![]() ,
, ![]() ,
, ![]() and
and ![]() be
be
![]() $\mathbb {S}_{\xi +1}$
-names for the condition
$\mathbb {S}_{\xi +1}$
-names for the condition
![]() $r_i^{\prime \prime }$
, the set
$r_i^{\prime \prime }$
, the set
![]() $\Sigma ^{\prime }_i$
, natural number
$\Sigma ^{\prime }_i$
, natural number
![]() $l_i$
and finite sequences
$l_i$
and finite sequences
![]() $t_{\sigma '}$
, respectively. Note that
$t_{\sigma '}$
, respectively. Note that
by the second part of Observation 3.4. By induction on
![]() $i<N$
pick a condition
$i<N$
pick a condition
![]() $r_i\in \mathbb S_{\xi +1}$
stronger than
$r_i\in \mathbb S_{\xi +1}$
stronger than
![]() $(r|\mu _i)\upharpoonright (\xi +1)$
and such that
$(r|\mu _i)\upharpoonright (\xi +1)$
and such that
![]() $r_j\upharpoonright \xi \geq r_i\upharpoonright \xi $
for all
$r_j\upharpoonright \xi \geq r_i\upharpoonright \xi $
for all
![]() $i<j<N$
,
$i<j<N$
,
![]() $r_0\upharpoonright \xi \geq r\upharpoonright \xi $
, and which forces all the above properties, and also decides all the names mentioned in the previous sentences. More precisely, there exist
$r_0\upharpoonright \xi \geq r\upharpoonright \xi $
, and which forces all the above properties, and also decides all the names mentioned in the previous sentences. More precisely, there exist
![]() $l_i>l_{*}$
,
$l_i>l_{*}$
,
![]() $t^i_\sigma \in 2^{l_i}$
for all
$t^i_\sigma \in 2^{l_i}$
for all
![]() $\sigma \in \Sigma $
with
$\sigma \in \Sigma $
with
![]() $\sigma (\xi )=s_i$
, and
$\sigma (\xi )=s_i$
, and
![]() $r_i^{\prime \prime }\in \mathbb S_{\xi +1,\alpha }$
such that
$r_i^{\prime \prime }\in \mathbb S_{\xi +1,\alpha }$
such that
![]() $r_i$
forces that
$r_i$
forces that ![]() ,
, ![]() and
and ![]() for all maps
for all maps
![]() $\sigma \in \Sigma $
with
$\sigma \in \Sigma $
with
![]() $\sigma (\xi )=s_i$
. Thus the elements
$\sigma (\xi )=s_i$
. Thus the elements
![]() $t^i_{\sigma }$
are pairwise different for all maps
$t^i_{\sigma }$
are pairwise different for all maps
![]() $\sigma \in \Sigma $
with
$\sigma \in \Sigma $
with
![]() $\sigma (\xi )=s_i$
.
$\sigma (\xi )=s_i$
.
Let
![]() $w\in \mathbb S_\alpha $
be a condition such that
$w\in \mathbb S_\alpha $
be a condition such that
![]() $w\upharpoonright \xi =r_{N-1}\upharpoonright \xi $
,
$w\upharpoonright \xi =r_{N-1}\upharpoonright \xi $
,
and for every ordinal number
![]() $\beta $
with
$\beta $
with
![]() $\xi <\beta <\alpha $
and natural number
$\xi <\beta <\alpha $
and natural number
![]() $i<N$
, we have
$i<N$
, we have
It follows that
for all
![]() $\sigma \in \Sigma $
with
$\sigma \in \Sigma $
with
![]() $\sigma (\xi )=s_i$
because
$\sigma (\xi )=s_i$
because
Let
![]() $\sigma ,\nu \in \Sigma $
be different maps. Assume that
$\sigma ,\nu \in \Sigma $
be different maps. Assume that
![]() $\sigma (\xi )\neq \nu (\xi )$
. Then there are different natural numbers
$\sigma (\xi )\neq \nu (\xi )$
. Then there are different natural numbers
![]() $i,j$
such that
$i,j$
such that
![]() $\sigma (\xi )=s_i$
and
$\sigma (\xi )=s_i$
and
![]() $\nu (\xi )=s_j$
. Since
$\nu (\xi )=s_j$
. Since
![]() $w|\sigma \geq w|\mu _i\geq u^{l_{*}}_i$
and
$w|\sigma \geq w|\mu _i\geq u^{l_{*}}_i$
and
![]() $w|\nu \geq w|\mu _j\geq u^{l_{*}}_j$
, we have
$w|\nu \geq w|\mu _j\geq u^{l_{*}}_j$
, we have
and
The sets
![]() $\{\,x\upharpoonright l_{*} : x\in X_i\,\}$
and
$\{\,x\upharpoonright l_{*} : x\in X_i\,\}$
and
![]() $\{\,x\upharpoonright l_{*} : x\in X_j\,\}$
are disjoint, and thus
$\{\,x\upharpoonright l_{*} : x\in X_j\,\}$
are disjoint, and thus
![]() $t^i_\sigma \upharpoonright l_{*}\neq t^j_\nu \upharpoonright l_{*}$
. Now assume that there is a natural number i such that
$t^i_\sigma \upharpoonright l_{*}\neq t^j_\nu \upharpoonright l_{*}$
. Now assume that there is a natural number i such that
![]() $\sigma (\xi )=\nu (\xi )=s_i$
. Then
$\sigma (\xi )=\nu (\xi )=s_i$
. Then
![]() $\sigma \upharpoonright F\setminus \{\xi \}\neq \nu \upharpoonright F\setminus \{\xi \}$
and the condition
$\sigma \upharpoonright F\setminus \{\xi \}\neq \nu \upharpoonright F\setminus \{\xi \}$
and the condition
![]() $(w|\mu _i)\upharpoonright (\xi +1)$
forces that
$(w|\mu _i)\upharpoonright (\xi +1)$
forces that ![]() and
and ![]() because
because
![]() $(w|\mu _i)\upharpoonright (\xi +1)\geq r_i$
, while
$(w|\mu _i)\upharpoonright (\xi +1)\geq r_i$
, while
![]() $t^i_\sigma \neq t^i_\nu $
. Summarizing, if
$t^i_\sigma \neq t^i_\nu $
. Summarizing, if
![]() $\nu (\xi )=\sigma (\xi )=s_i$
, then
$\nu (\xi )=\sigma (\xi )=s_i$
, then
![]() $t^i_\sigma \neq t^i_\nu $
, and if
$t^i_\sigma \neq t^i_\nu $
, and if
![]() $\nu (\xi )=s_j\neq s_i=\sigma (\xi )$
, then
$\nu (\xi )=s_j\neq s_i=\sigma (\xi )$
, then
![]() $t^i_\sigma \upharpoonright l_{*}\neq t^j_\nu \upharpoonright l_{*}$
.
$t^i_\sigma \upharpoonright l_{*}\neq t^j_\nu \upharpoonright l_{*}$
.
Finally, applying Observation 3.2(7) to
![]() $l=\max _{i<N}l_i$
and w which is
$l=\max _{i<N}l_i$
and w which is
![]() $(F,n)$
-determined (because
$(F,n)$
-determined (because
![]() $(w,n)\geq _F(p,n)$
by the construction), we get a condition q such that
$(w,n)\geq _F(p,n)$
by the construction), we get a condition q such that
![]() $(q,n)\geq _F (w,n)$
, and for every
$(q,n)\geq _F (w,n)$
, and for every
![]() $\sigma \in \Sigma $
a sequence
$\sigma \in \Sigma $
a sequence
![]() $y_\sigma \in 2^l$
such that
$y_\sigma \in 2^l$
such that
![]() $q|\sigma \Vdash \tau \upharpoonright l=y_\sigma $
. Since
$q|\sigma \Vdash \tau \upharpoonright l=y_\sigma $
. Since
![]() $q|\sigma \geq w|\sigma ,$
we have
$q|\sigma \geq w|\sigma ,$
we have
![]() $y_\sigma \upharpoonright l_i=t^i_\sigma $
for all
$y_\sigma \upharpoonright l_i=t^i_\sigma $
for all
![]() $\sigma \in \Sigma $
with
$\sigma \in \Sigma $
with
![]() $\sigma (\xi )=s_i$
. It follows from the above that the
$\sigma (\xi )=s_i$
. It follows from the above that the
![]() $y_\sigma $
’s are mutually different: if
$y_\sigma $
’s are mutually different: if
![]() $\nu (\xi )=\sigma (\xi )=s_i$
, then
$\nu (\xi )=\sigma (\xi )=s_i$
, then
![]() $y_\sigma \upharpoonright l_i =t^i_\sigma \neq t^i_\nu =y_\nu \upharpoonright l_i$
; and if
$y_\sigma \upharpoonright l_i =t^i_\sigma \neq t^i_\nu =y_\nu \upharpoonright l_i$
; and if
![]() $\nu (\xi )=s_j\neq s_i= \sigma (\xi )$
, then
$\nu (\xi )=s_j\neq s_i= \sigma (\xi )$
, then
![]() $y_\sigma \upharpoonright l_{*}=t^i_\sigma \upharpoonright l_{*}\neq t^j_\nu \upharpoonright l_{*}=y_\nu \upharpoonright l_{*}$
.
$y_\sigma \upharpoonright l_{*}=t^i_\sigma \upharpoonright l_{*}\neq t^j_\nu \upharpoonright l_{*}=y_\nu \upharpoonright l_{*}$
.
The following fact is reminiscent of [Reference Baumgartner and Laver3, Lemma 2.3(i)], and we use a rather similar approach to the proof, which we present for the sake of completeness.
Lemma 3.6. Let
![]() $\alpha $
be an ordinal,
$\alpha $
be an ordinal,
![]() $p\in \mathbb S_\alpha $
,
$p\in \mathbb S_\alpha $
,
![]() $n\in \omega $
and
$n\in \omega $
and
![]() $F\subseteq \alpha $
a nonempty finite set. Then there are a natural number
$F\subseteq \alpha $
a nonempty finite set. Then there are a natural number
![]() $k>n$
and an
$k>n$
and an
![]() $(F,k)$
-determined condition
$(F,k)$
-determined condition
![]() $q\in \mathbb S_\alpha $
such that
$q\in \mathbb S_\alpha $
such that
![]() $(q,k)\geq _F (p,n)$
.
$(q,k)\geq _F (p,n)$
.
Proof. We proceed by induction on
![]() $|F|$
. Suppose that
$|F|$
. Suppose that
![]() $F=\{\beta \}$
for some
$F=\{\beta \}$
for some
![]() $\beta <\alpha $
and pick
$\beta <\alpha $
and pick
![]() $r\in \mathbb S_\beta $
,
$r\in \mathbb S_\beta $
,
![]() $r\geq p\upharpoonright \beta $
which decides
$r\geq p\upharpoonright \beta $
which decides
![]() $k>n$
and
$k>n$
and
![]() $p(\beta )\cap 2^k$
(and hence also decides
$p(\beta )\cap 2^k$
(and hence also decides
![]() $p(\beta )\cap 2^n$
), so that each element
$p(\beta )\cap 2^n$
), so that each element
![]() $s\in p(\beta )\cap 2^n$
has at least 2 extensions in
$s\in p(\beta )\cap 2^n$
has at least 2 extensions in
![]() $p(\beta )\cap 2^k$
. Then
$p(\beta )\cap 2^k$
. Then
![]() $q:=r\cup p\upharpoonright [\beta ,\alpha )$
is as required.
$q:=r\cup p\upharpoonright [\beta ,\alpha )$
is as required.
Now assume that
![]() $|F|>1$
and let
$|F|>1$
and let
![]() $\beta =\max (F)$
. By the inductive assumption there exists
$\beta =\max (F)$
. By the inductive assumption there exists
![]() $r\in \mathbb S_\beta $
and
$r\in \mathbb S_\beta $
and
![]() $k_0>n$
such that r is
$k_0>n$
such that r is
![]() $(F\cap \beta ,k_0)$
-determined and
$(F\cap \beta ,k_0)$
-determined and
![]() $(r,k_0)\geq _{F\cap \beta } (p\upharpoonright \beta ,n)$
. Let
$(r,k_0)\geq _{F\cap \beta } (p\upharpoonright \beta ,n)$
. Let
![]() $\Sigma $
be the family of all
$\Sigma $
be the family of all
![]() $\sigma :F\cap \beta \to 2^{k_0}$
consistent with r. Let
$\sigma :F\cap \beta \to 2^{k_0}$
consistent with r. Let
![]() $N=|\Sigma |$
and write
$N=|\Sigma |$
and write
![]() $\Sigma $
in the form
$\Sigma $
in the form
![]() $\{\sigma _i:i<N\}$
. By induction on
$\{\sigma _i:i<N\}$
. By induction on
![]() $i<N$
let us construct a sequence
$i<N$
let us construct a sequence
where
![]() $r^0_{-1}=r$
and
$r^0_{-1}=r$
and
![]() $r^0_i\in \mathbb S_\beta $
for all
$r^0_i\in \mathbb S_\beta $
for all
![]() $i<N$
, as follows: Given
$i<N$
, as follows: Given
![]() $r^0_{i-1}$
for some
$r^0_{i-1}$
for some
![]() $i<N$
, let
$i<N$
, let
![]() $\mathbb S_\beta \ni u^0_i\geq r^0_{i-1}|\sigma _i$
be a condition such that there exists
$\mathbb S_\beta \ni u^0_i\geq r^0_{i-1}|\sigma _i$
be a condition such that there exists
![]() $T^0_i\subseteq 2^{l_i}$
for some
$T^0_i\subseteq 2^{l_i}$
for some
![]() $l_i\geq k_0$
such that
$l_i\geq k_0$
such that
![]() $u^0_i$
forces
$u^0_i$
forces
![]() $p(\beta )\cap 2^{l_i}=T^0_i$
, and for every
$p(\beta )\cap 2^{l_i}=T^0_i$
, and for every
![]() $s\in T^0_i\upharpoonright n$
there exists at least two
$s\in T^0_i\upharpoonright n$
there exists at least two
![]() $t\in T^0_i$
extending s. Now, let
$t\in T^0_i$
extending s. Now, let
![]() $r^0_i\in \mathbb S_\beta $
be such that
$r^0_i\in \mathbb S_\beta $
be such that
![]() $(r^0_i,k_0)\geq _{F\cap \beta }(r^0_{i-1},k_0)$
and
$(r^0_i,k_0)\geq _{F\cap \beta }(r^0_{i-1},k_0)$
and
![]() $r^0_i|\sigma _i=u^0_i$
, by Observation 3.2(5).
$r^0_i|\sigma _i=u^0_i$
, by Observation 3.2(5).
Let
![]() $k=\max _{i<N}l_i$
and set
$k=\max _{i<N}l_i$
and set
![]() $r^1_{-1}=r^0_{N-1}$
. By induction on
$r^1_{-1}=r^0_{N-1}$
. By induction on
![]() $i<N$
let us construct a sequence
$i<N$
let us construct a sequence
where
![]() $r^1_i\in \mathbb S_\beta $
for all
$r^1_i\in \mathbb S_\beta $
for all
![]() $i<N$
, as follows: Given
$i<N$
, as follows: Given
![]() $r^1_{i-1}$
for some
$r^1_{i-1}$
for some
![]() $i<N$
, let
$i<N$
, let
![]() $\mathbb S_\beta \ni u^1_i\geq r^1_{i-1}|\sigma _i$
be a condition such that there exists
$\mathbb S_\beta \ni u^1_i\geq r^1_{i-1}|\sigma _i$
be a condition such that there exists
![]() $T^1_i\subseteq 2^{k}$
for which
$T^1_i\subseteq 2^{k}$
for which
![]() $u^1_i$
forces
$u^1_i$
forces
![]() $p(\beta )\cap 2^{k}=T^1_i$
. Now, let
$p(\beta )\cap 2^{k}=T^1_i$
. Now, let
![]() $r^1_i\in \mathbb S_\beta $
be such that
$r^1_i\in \mathbb S_\beta $
be such that
![]() $(r^1_i,k_0)\geq _{F\cap \beta }(r^1_{i-1},k_0)$
and
$(r^1_i,k_0)\geq _{F\cap \beta }(r^1_{i-1},k_0)$
and
![]() $r^1_i|\sigma _i=u^1_i$
. Note that
$r^1_i|\sigma _i=u^1_i$
. Note that
![]() $T^0_i=\{t\upharpoonright l_i:t\in T^1_i\}$
.
$T^0_i=\{t\upharpoonright l_i:t\in T^1_i\}$
.
Set
![]() $r^2_{-1}=r^1_{N-1}$
. By induction on
$r^2_{-1}=r^1_{N-1}$
. By induction on
![]() $i<N$
let us construct a sequence
$i<N$
let us construct a sequence
where
![]() $r^2_i\in \mathbb S_\beta $
for all
$r^2_i\in \mathbb S_\beta $
for all
![]() $i<N$
, as follows: Given
$i<N$
, as follows: Given
![]() $r^2_{i-1}$
for some
$r^2_{i-1}$
for some
![]() $i<N$
, let
$i<N$
, let
![]() $\mathbb S_\beta \ni u^2_i\geq r^2_{i-1}|\sigma _i$
be a condition such that for every
$\mathbb S_\beta \ni u^2_i\geq r^2_{i-1}|\sigma _i$
be a condition such that for every
![]() $\gamma \in F\cap \beta $
there exists
$\gamma \in F\cap \beta $
there exists
![]() $\nu _i(\gamma )\in 2^k$
such that
$\nu _i(\gamma )\in 2^k$
such that
![]() $\sigma _i(\gamma )=\nu _i(\gamma )\upharpoonright k_0$
and
$\sigma _i(\gamma )=\nu _i(\gamma )\upharpoonright k_0$
and
![]() $u^2_i\upharpoonright \gamma $
forces that
$u^2_i\upharpoonright \gamma $
forces that
![]() $\nu _i(\gamma )$
is an initial segment of the stem of
$\nu _i(\gamma )$
is an initial segment of the stem of
![]() $u^2_i(\gamma )$
. Such an
$u^2_i(\gamma )$
. Such an
![]() $u^2_i$
can be constructed recursively over
$u^2_i$
can be constructed recursively over
![]() $\gamma \in F\cap \beta $
, moving from the bigger to smaller elements. Now, let
$\gamma \in F\cap \beta $
, moving from the bigger to smaller elements. Now, let
![]() $r^2_i\in \mathbb S_\beta $
be such that
$r^2_i\in \mathbb S_\beta $
be such that
![]() $(r^2_i,k_0)\geq _{F\cap \beta }(r^2_{i-1},k_0)$
and
$(r^2_i,k_0)\geq _{F\cap \beta }(r^2_{i-1},k_0)$
and
![]() $r^1_i|\sigma _i=u^2_i$
.
$r^1_i|\sigma _i=u^2_i$
.
We claim that
![]() $q=r^2_{N-1}\cup p\upharpoonright [\beta ,\alpha )$
and k are as required. Indeed, we have that
$q=r^2_{N-1}\cup p\upharpoonright [\beta ,\alpha )$
and k are as required. Indeed, we have that
![]() $(q\upharpoonright \beta ,k)\geq _{F\cap \beta } (p\upharpoonright \beta ,n)$
because
$(q\upharpoonright \beta ,k)\geq _{F\cap \beta } (p\upharpoonright \beta ,n)$
because
![]() $q\upharpoonright \beta =r^2_{N-1}$
,
$q\upharpoonright \beta =r^2_{N-1}$
,
![]() $k\geq k_0$
, and
$k\geq k_0$
, and
![]() $(r^2_{N-1},k_0)\geq _{F\cap \beta } (r,k_0)\geq _{F\cap \beta } (p\upharpoonright \beta ,n)$
. Moreover, since
$(r^2_{N-1},k_0)\geq _{F\cap \beta } (r,k_0)\geq _{F\cap \beta } (p\upharpoonright \beta ,n)$
. Moreover, since
![]() $r^2_{N-1}|\sigma _i\geq u^0_i$
, we have that
$r^2_{N-1}|\sigma _i\geq u^0_i$
, we have that
![]() $r^2_{N-1}|\sigma _i$
decides
$r^2_{N-1}|\sigma _i$
decides
![]() $p(\beta )\cap 2^k$
as
$p(\beta )\cap 2^k$
as
![]() $T^1_i$
, which has the property that any
$T^1_i$
, which has the property that any
![]() $s\in T^1_i\upharpoonright n$
has at least two extensions in
$s\in T^1_i\upharpoonright n$
has at least two extensions in
![]() $T^1_i$
(because
$T^1_i$
(because
![]() $T^0_i=T^1_i\upharpoonright l_i$
has this property). It follows that
$T^0_i=T^1_i\upharpoonright l_i$
has this property). It follows that
![]() $r^2_{N-1}|\sigma _i$
forces
$r^2_{N-1}|\sigma _i$
forces
![]() $q(\beta )=p(\beta ) $
and
$q(\beta )=p(\beta ) $
and
![]() $(p(\beta ),k)\geq (p(\beta ),n)$
. Since
$(p(\beta ),k)\geq (p(\beta ),n)$
. Since
![]() $\{r^2_{N-1}|\sigma _i:i<N\}$
is dense above
$\{r^2_{N-1}|\sigma _i:i<N\}$
is dense above
![]() $r^2_{N-1}$
, we conclude that
$r^2_{N-1}$
, we conclude that
![]() $r^2_{N-1}=q\upharpoonright \beta $
forces
$r^2_{N-1}=q\upharpoonright \beta $
forces
![]() $(q(\beta ),k)\geq (p(\beta ),n)$
, and therefore
$(q(\beta ),k)\geq (p(\beta ),n)$
, and therefore
![]() $(q,k)\geq (p,n)$
.
$(q,k)\geq (p,n)$
.
Finally, by the construction of
![]() $r^2_{N-1}$
we have that q is
$r^2_{N-1}$
we have that q is
![]() $(F,k)$
-determined, with
$(F,k)$
-determined, with
being the family of those
![]() $\nu :F\to 2^k$
which are consistent with q.
$\nu :F\to 2^k$
which are consistent with q.
Lemma 3.7 (Miller [Reference Miller15, Lemma 6]).
Let
![]() $\alpha $
be an ordinal number,
$\alpha $
be an ordinal number,
![]() $p_0\in \mathbb S_\alpha $
, and
$p_0\in \mathbb S_\alpha $
, and
![]() $\tau $
an
$\tau $
an
![]() $\mathbb S_\alpha $
-name for a real such that
$\mathbb S_\alpha $
-name for a real such that
Then there exist a condition
![]() $p\geq p_0$
, an increasing sequence
$p\geq p_0$
, an increasing sequence
![]() ${\langle \, F_n : n\in \omega \,\rangle }$
of finite subsets of
${\langle \, F_n : n\in \omega \,\rangle }$
of finite subsets of
![]() $\alpha $
, increasing sequences of natural numbers
$\alpha $
, increasing sequences of natural numbers
![]() ${\langle \, k_n : n\in \omega \,\rangle }$
,
${\langle \, k_n : n\in \omega \,\rangle }$
,
![]() ${\langle \, l_n : n\in \omega \,\rangle }$
, and elements
${\langle \, l_n : n\in \omega \,\rangle }$
, and elements
![]() $y_{\sigma }\in 2^{l_n}$
for all maps
$y_{\sigma }\in 2^{l_n}$
for all maps
![]() $\sigma \colon F_n\to 2^{k_n}$
consistent with p, with the following properties:
$\sigma \colon F_n\to 2^{k_n}$
consistent with p, with the following properties:
-
(1)
 $\bigcup _{n\in \omega }F_n=\operatorname {supp}(p)$
,
$\bigcup _{n\in \omega }F_n=\operatorname {supp}(p)$
, -
(2) p is
 $(F_n,k_n)$
-determined,
$(F_n,k_n)$
-determined, -
(3)
 $(p, k_{n+1}) \geq _{F_n} (p, k_n)$
,
$(p, k_{n+1}) \geq _{F_n} (p, k_n)$
, -
(4)
 $p|\sigma \Vdash \tau \upharpoonright l_n= y_{\sigma }$
for all
$p|\sigma \Vdash \tau \upharpoonright l_n= y_{\sigma }$
for all
 $\sigma \in (2^{k_n})^{F_n}$
consistent with p, and
$\sigma \in (2^{k_n})^{F_n}$
consistent with p, and -
(5) the maps
 $y_{\sigma }$
, where
$y_{\sigma }$
, where
 $\sigma $
is as above, are mutually different.
$\sigma $
is as above, are mutually different.
Proof. The choice of the
![]() $F_n$
’s is standard and thus will not be specified, except that we set
$F_n$
’s is standard and thus will not be specified, except that we set
![]() $F_0=\{0\}$
. Set also
$F_0=\{0\}$
. Set also
![]() $k_0=0$
. Trivially,
$k_0=0$
. Trivially,
![]() $p_0$
is
$p_0$
is
![]() $(F_0,k_0)$
-determined since the unique map
$(F_0,k_0)$
-determined since the unique map
![]() $\{\langle 0,\emptyset \rangle \} $
in
$\{\langle 0,\emptyset \rangle \} $
in
![]() $(2^{k_0})^{F_0}$
is consistent with
$(2^{k_0})^{F_0}$
is consistent with
![]() $p_0$
. By Lemma 3.5, there are a condition
$p_0$
. By Lemma 3.5, there are a condition
![]() $q_0\in \mathbb S_\alpha $
, a natural number
$q_0\in \mathbb S_\alpha $
, a natural number
![]() $l_0$
and pairwise different elements
$l_0$
and pairwise different elements
![]() $y_{\sigma }\in 2^{l_0}$
for all mapsFootnote
2
$y_{\sigma }\in 2^{l_0}$
for all mapsFootnote
2
![]() $\sigma \colon F_0\to 2^{k_0}$
consistent with
$\sigma \colon F_0\to 2^{k_0}$
consistent with
![]() $p_0$
such that
$p_0$
such that
![]() $(q_0,k_0)\geq _{F_0}(p_0,k_0)$
and
$(q_0,k_0)\geq _{F_0}(p_0,k_0)$
and
![]() $q_0|\sigma \Vdash \tau \upharpoonright l_0=y_{\sigma }$
.
$q_0|\sigma \Vdash \tau \upharpoonright l_0=y_{\sigma }$
.
Let
![]() $k_1>k_0$
be a natural number and
$k_1>k_0$
be a natural number and
![]() $p_1\in \mathbb S_\alpha $
a condition from Lemma 3.6, applied to the set
$p_1\in \mathbb S_\alpha $
a condition from Lemma 3.6, applied to the set
![]() $F_1$
and the condition
$F_1$
and the condition
![]() $q_0$
. Then
$q_0$
. Then
![]() $p_1$
is
$p_1$
is
![]() $(F_1,k_1)$
-determined and
$(F_1,k_1)$
-determined and
![]() $(p_1,k_1)\geq _{F_0}(p_0,k_0)$
.
$(p_1,k_1)\geq _{F_0}(p_0,k_0)$
.
Fix a natural number
![]() $n\geq 1$
and assume that a set
$n\geq 1$
and assume that a set
![]() $F_n$
, natural number
$F_n$
, natural number
![]() $k_n$
, and an
$k_n$
, and an
![]() $(F_n,k_n)$
-determined condition
$(F_n,k_n)$
-determined condition
![]() $p_n\in \mathbb S_\alpha $
with
$p_n\in \mathbb S_\alpha $
with
![]() $(p_n,k_n)\geq _{F_{n-1}}(q_{n-1},k_{n-1})$
have already been defined. By Lemma 3.5, there are a condition
$(p_n,k_n)\geq _{F_{n-1}}(q_{n-1},k_{n-1})$
have already been defined. By Lemma 3.5, there are a condition
![]() $q_n\in \mathbb S_\alpha $
, a natural number
$q_n\in \mathbb S_\alpha $
, a natural number
![]() $l_n>l_{n-1}$
and pairwise different elements
$l_n>l_{n-1}$
and pairwise different elements
![]() $y_{\sigma }\in 2^{l_n}$
for all maps
$y_{\sigma }\in 2^{l_n}$
for all maps
![]() $\sigma \colon F_n\to 2^{k_n}$
consistent with
$\sigma \colon F_n\to 2^{k_n}$
consistent with
![]() $p_n$
such that
$p_n$
such that
![]() $(q_n,k_n)\geq _{F_n}(p_n,k_n)$
and
$(q_n,k_n)\geq _{F_n}(p_n,k_n)$
and
![]() $q_n|\sigma \Vdash \tau \upharpoonright l_n=y_{\sigma }$
.
$q_n|\sigma \Vdash \tau \upharpoonright l_n=y_{\sigma }$
.
Let p be the fusion of the sequence
![]() ${\langle \, (p_n,k_n,F_n) : n\in \omega \,\rangle }$
[Reference Baumgartner and Laver3, Lemma 1.2] and note that it is as required.
${\langle \, (p_n,k_n,F_n) : n\in \omega \,\rangle }$
[Reference Baumgartner and Laver3, Lemma 1.2] and note that it is as required.
Let F be a subset of H,
![]() $n\leq m$
be natural numbers, and
$n\leq m$
be natural numbers, and
![]() $\nu \colon F\to 2^n$
,
$\nu \colon F\to 2^n$
,
![]() $\sigma \colon H\to 2^m$
be maps. Following our convention at the beginning of Section 2, the map
$\sigma \colon H\to 2^m$
be maps. Following our convention at the beginning of Section 2, the map
![]() $\sigma $
is an extension of
$\sigma $
is an extension of
![]() $\nu $
(we denote this by
$\nu $
(we denote this by
![]() $\nu \prec \sigma $
) if
$\nu \prec \sigma $
) if
![]() $\nu (\beta )=\sigma (\beta )\upharpoonright n$
for all
$\nu (\beta )=\sigma (\beta )\upharpoonright n$
for all
![]() $\beta \in F$
. The next fact is standard.
$\beta \in F$
. The next fact is standard.
Observation 3.8. In the notation above, if
![]() $F,H\subseteq \alpha $
,
$F,H\subseteq \alpha $
,
![]() $p\in \mathbb S_\alpha $
,
$p\in \mathbb S_\alpha $
,
![]() $\nu ,\sigma $
are consistent with p and
$\nu ,\sigma $
are consistent with p and
![]() $\nu \prec \sigma $
, then
$\nu \prec \sigma $
, then
![]() $p|\sigma \geq p|\nu $
.
$p|\sigma \geq p|\nu $
.
Lemma 3.9. Let
![]() $p\in \mathbb S_\alpha $
be an
$p\in \mathbb S_\alpha $
be an
![]() $(F,n)$
-determined condition and
$(F,n)$
-determined condition and
![]() $\Sigma _n$
be the set of all maps
$\Sigma _n$
be the set of all maps
![]() $\nu \colon F\to 2^n$
consistent with p. Then for every
$\nu \colon F\to 2^n$
consistent with p. Then for every
![]() $G\subseteq F$
and
$G\subseteq F$
and
![]() $k\leq n$
, if p is
$k\leq n$
, if p is
![]() $(G,k)$
-determined and
$(G,k)$
-determined and
![]() $\mu :G\to 2^k$
is consistent with p, then there exists
$\mu :G\to 2^k$
is consistent with p, then there exists
![]() $\nu \in \Sigma _n$
extending
$\nu \in \Sigma _n$
extending
![]() $\mu $
.
$\mu $
.
Moreover, if
![]() $H\subseteq \alpha $
is a finite set with
$H\subseteq \alpha $
is a finite set with
![]() $F\subseteq H$
,
$F\subseteq H$
,
![]() $\beta \in F$
,
$\beta \in F$
,
![]() $m>n$
is a natural number, p is also
$m>n$
is a natural number, p is also
![]() $(H,m)$
-determined,
$(H,m)$
-determined,
![]() $\Sigma _m$
is the set of all maps
$\Sigma _m$
is the set of all maps
![]() $\sigma \colon H\to 2^m$
consistent with p, and
$\sigma \colon H\to 2^m$
consistent with p, and
![]() $(p,m)\geq _F (p,n)$
, then the following assertions hold.
$(p,m)\geq _F (p,n)$
, then the following assertions hold.
-
(1) For every
 $\nu \in \Sigma _n$
and
$\nu \in \Sigma _n$
and
 $\sigma \in \Sigma _m$
such that
$\sigma \in \Sigma _m$
such that
 $\sigma \upharpoonright (H\cap \beta )$
extends
$\sigma \upharpoonright (H\cap \beta )$
extends
 $\nu \upharpoonright (F\cap \beta )$
, there are
$\nu \upharpoonright (F\cap \beta )$
, there are
 $\sigma _1,\sigma _2\in \Sigma _m$
extending
$\sigma _1,\sigma _2\in \Sigma _m$
extending
 $\nu $
with
$\nu $
with
 $\sigma _1\upharpoonright (H\cap \beta )=\sigma _2\upharpoonright (H\cap \beta )=\sigma \upharpoonright (H\cap \beta )$
, and such that
$\sigma _1\upharpoonright (H\cap \beta )=\sigma _2\upharpoonright (H\cap \beta )=\sigma \upharpoonright (H\cap \beta )$
, and such that
 $\sigma _1(\beta ), \sigma _2(\beta )$
are distinct extensions of
$\sigma _1(\beta ), \sigma _2(\beta )$
are distinct extensions of
 $\nu (\beta )$
.
$\nu (\beta )$
. -
(2) For every
 $\nu \in \Sigma _n$
and
$\nu \in \Sigma _n$
and
 $\rho :H\cap \beta \to 2^m$
consistent with p, if
$\rho :H\cap \beta \to 2^m$
consistent with p, if
 $\rho $
extends
$\rho $
extends
 $\nu \upharpoonright (F\cap \beta )$
, then there are
$\nu \upharpoonright (F\cap \beta )$
, then there are
 $\sigma _1,\sigma _2\in \Sigma _m$
extending
$\sigma _1,\sigma _2\in \Sigma _m$
extending
 $\nu $
with
$\nu $
with
 $\sigma _1\upharpoonright (H\cap \beta )=\sigma _2\upharpoonright (H\cap \beta )=\rho $
and such that
$\sigma _1\upharpoonright (H\cap \beta )=\sigma _2\upharpoonright (H\cap \beta )=\rho $
and such that
 $\sigma _1(\beta ), \sigma _2(\beta )$
are distinct extensions of
$\sigma _1(\beta ), \sigma _2(\beta )$
are distinct extensions of
 $\nu (\beta )$
.
$\nu (\beta )$
. -
(3) For every
 $C\subset \Sigma _n$
, coherent
$C\subset \Sigma _n$
, coherent
 $e_0:C\to \Sigma _m$
, and
$e_0:C\to \Sigma _m$
, and
 $\nu _{*}\in \Sigma _n\setminus C$
, there exist two different coherent maps
$\nu _{*}\in \Sigma _n\setminus C$
, there exist two different coherent maps
 $e,e'\colon (C\cup \{\nu _{*}\}) \to \Sigma _m$
such that
$e,e'\colon (C\cup \{\nu _{*}\}) \to \Sigma _m$
such that
 $e\upharpoonright C=e'\upharpoonright C=e_0$
.
$e\upharpoonright C=e'\upharpoonright C=e_0$
.
Proof. We start with proving the first part. Proceed by induction on
![]() $|G|$
. If
$|G|$
. If
![]() $G=\emptyset $
, then there is nothing to prove. Let
$G=\emptyset $
, then there is nothing to prove. Let
![]() $\gamma :=\max G$
and assume that the statement holds for
$\gamma :=\max G$
and assume that the statement holds for
![]() $G':=G\setminus \{\gamma \}$
. Fix a map
$G':=G\setminus \{\gamma \}$
. Fix a map
![]() $\mu \colon G\to 2^k$
consistent with p and let
$\mu \colon G\to 2^k$
consistent with p and let
![]() $\mu ':=\mu \upharpoonright G'$
. By Observation 3.2(4), p is both
$\mu ':=\mu \upharpoonright G'$
. By Observation 3.2(4), p is both
![]() $(F\cap \gamma ,n)$
- and
$(F\cap \gamma ,n)$
- and
![]() $(G\cap \gamma ,k)$
-determined, and hence there exists
$(G\cap \gamma ,k)$
-determined, and hence there exists
![]() $\nu ':(F\cap \gamma )\to 2^n$
consistent with p such that
$\nu ':(F\cap \gamma )\to 2^n$
consistent with p such that
![]() $\nu '\succ \mu '$
. Since
$\nu '\succ \mu '$
. Since
![]() $(p\upharpoonright \gamma )|\mu '\Vdash \mu (\gamma )\in p(\gamma ),$
the condition
$(p\upharpoonright \gamma )|\mu '\Vdash \mu (\gamma )\in p(\gamma ),$
the condition
![]() $(p\upharpoonright \gamma )|\nu '$
also forces this because
$(p\upharpoonright \gamma )|\nu '$
also forces this because
![]() $(p\upharpoonright \gamma )|\nu '\geq (p\upharpoonright \gamma )|\mu '$
by Observation 3.8. Strengthening the latter condition to some r if necessary, we may find
$(p\upharpoonright \gamma )|\nu '\geq (p\upharpoonright \gamma )|\mu '$
by Observation 3.8. Strengthening the latter condition to some r if necessary, we may find
![]() $t\in 2^n$
extending
$t\in 2^n$
extending
![]() $\mu (\gamma )$
such that
$\mu (\gamma )$
such that
![]() $r\Vdash t\in p(\gamma )$
. Since p is
$r\Vdash t\in p(\gamma )$
. Since p is
![]() $(F,n)$
-determined, we conclude that
$(F,n)$
-determined, we conclude that
![]() $(p\upharpoonright \gamma )|\nu '\Vdash t\in p(\gamma ).$
It follows that
$(p\upharpoonright \gamma )|\nu '\Vdash t\in p(\gamma ).$
It follows that
![]() $\nu '\cup \{(\gamma ,t)\}\in (2^n)^F$
is consistent with p and extends
$\nu '\cup \{(\gamma ,t)\}\in (2^n)^F$
is consistent with p and extends
![]() $\mu $
.
$\mu $
.
The second part of the lemma is rather straightforward. Item
![]() $(2)$
is an equivalent reformulation of
$(2)$
is an equivalent reformulation of
![]() $(1)$
, by Observation 3.2(2). We shall present the proof of
$(1)$
, by Observation 3.2(2). We shall present the proof of
![]() $(3)$
, because we find it the least obvious one.
$(3)$
, because we find it the least obvious one.
Proceed by induction on
![]() $|F|$
. Assume that
$|F|$
. Assume that
![]() $F=\{\beta \}$
. Let
$F=\{\beta \}$
. Let
![]() $\nu \in C$
and
$\nu \in C$
and
![]() $\sigma := e_0(\nu )$
. Choose some distinct
$\sigma := e_0(\nu )$
. Choose some distinct
![]() $\mu ,\mu '\in \Sigma _m$
such that
$\mu ,\mu '\in \Sigma _m$
such that
![]() $\mu ,\mu '\succ \nu _{*}$
and
$\mu ,\mu '\succ \nu _{*}$
and
![]() $\mu \restriction (H \cap \beta ) = \sigma \restriction (H \cap \beta ) = \mu ' \restriction (H \cap \beta )$
, which is possible by (1). Then the maps
$\mu \restriction (H \cap \beta ) = \sigma \restriction (H \cap \beta ) = \mu ' \restriction (H \cap \beta )$
, which is possible by (1). Then the maps
![]() $e=e_0\cup \{\langle \nu _{*},\mu \rangle \}$
and
$e=e_0\cup \{\langle \nu _{*},\mu \rangle \}$
and
![]() $e'=e_0\cup \{\langle \nu _{*},\mu '\rangle \}$
are easily seen to be as required.
$e'=e_0\cup \{\langle \nu _{*},\mu '\rangle \}$
are easily seen to be as required.
Now assume that
![]() $|F|>1$
and
$|F|>1$
and
![]() $(3)$
holds for any finite subset of the support of p of cardinality smaller than
$(3)$
holds for any finite subset of the support of p of cardinality smaller than
![]() $\left |F\right |$
. Set
$\left |F\right |$
. Set
![]() $\beta =\max F$
,
$\beta =\max F$
,
![]() $C^-=\{\nu \upharpoonright (F\cap \beta ):\nu \in C\}$
,
$C^-=\{\nu \upharpoonright (F\cap \beta ):\nu \in C\}$
,
![]() $e^-_0(\nu \upharpoonright (F\cap \beta ))= e_0(\nu )\upharpoonright (H\cap \beta )$
for all
$e^-_0(\nu \upharpoonright (F\cap \beta ))= e_0(\nu )\upharpoonright (H\cap \beta )$
for all
![]() $\nu \in C$
, and
$\nu \in C$
, and
![]() $\nu ^-_{*}=\nu _{*}\upharpoonright (F\cap \beta )$
. Let also
$\nu ^-_{*}=\nu _{*}\upharpoonright (F\cap \beta )$
. Let also
![]() $\Sigma _m^-$
be the family of all maps
$\Sigma _m^-$
be the family of all maps
![]() $\sigma :H\cap \beta \to 2^m$
consistent with p. By the inductive assumption applied to the objects defined above we can get a coherent
$\sigma :H\cap \beta \to 2^m$
consistent with p. By the inductive assumption applied to the objects defined above we can get a coherent
![]() $e^-:C^-\cup \{\nu ^-_{*}\}\to \Sigma ^-_m $
such that
$e^-:C^-\cup \{\nu ^-_{*}\}\to \Sigma ^-_m $
such that
![]() $e^-\upharpoonright C^-= e^-_0$
. (Actually, we could get even two different such
$e^-\upharpoonright C^-= e^-_0$
. (Actually, we could get even two different such
![]() $e^-$
if
$e^-$
if
![]() $\nu ^-_{*}\not \in C^-$
, but thus irrelevant here.)
$\nu ^-_{*}\not \in C^-$
, but thus irrelevant here.)
By
![]() $(2)$
applied to
$(2)$
applied to
![]() $\nu _{*}$
and
$\nu _{*}$
and
![]() $\rho =e^-(\nu ^-_{*})$
we can find distinct
$\rho =e^-(\nu ^-_{*})$
we can find distinct
![]() $\sigma ,\sigma '\in \Sigma _m$
such that
$\sigma ,\sigma '\in \Sigma _m$
such that
It suffices to show that
![]() $e=e_0\cup \{\langle \nu _{*},\sigma \rangle \}$
and
$e=e_0\cup \{\langle \nu _{*},\sigma \rangle \}$
and
![]() $e'=e_0\cup \{\langle \nu _{*},\sigma '\rangle \}$
are both coherent. We shall check this for e, the case of
$e'=e_0\cup \{\langle \nu _{*},\sigma '\rangle \}$
are both coherent. We shall check this for e, the case of
![]() $e'$
is analogous. Pick
$e'$
is analogous. Pick
![]() $\nu \in C$
and let
$\nu \in C$
and let
![]() $\gamma \in F$
be the minimal element with
$\gamma \in F$
be the minimal element with
![]() $\nu (\gamma )\neq \nu _{*}(\gamma )$
. Such an ordinal
$\nu (\gamma )\neq \nu _{*}(\gamma )$
. Such an ordinal
![]() $\gamma $
must exist because
$\gamma $
must exist because
![]() $\nu \neq \nu _{*}$
as
$\nu \neq \nu _{*}$
as
![]() $\nu \in C\not \ni \nu _{*}$
. Fix
$\nu \in C\not \ni \nu _{*}$
. Fix
![]() $\beta \geq \gamma $
. In the assertions from the cases below we use the fact that
$\beta \geq \gamma $
. In the assertions from the cases below we use the fact that
and
![]() $e(\nu _{*})=\sigma $
.
$e(\nu _{*})=\sigma $
.
If
![]() $\gamma <\beta $
, then
$\gamma <\beta $
, then
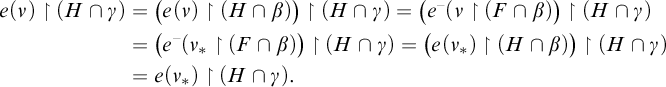 $$ \begin{align*} e(\nu)\upharpoonright (H\cap\gamma) &= \big(e(\nu)\upharpoonright (H\cap\beta)\big) \upharpoonright (H\cap\gamma)= \big(e^-(\nu\upharpoonright (F\cap\beta)\big) \upharpoonright (H\cap\gamma) \\ & = \big(e^-(\nu_{*}\upharpoonright (F\cap\beta)\big) \upharpoonright (H\cap\gamma)= \big(e(\nu_{*})\upharpoonright (H\cap\beta)\big) \upharpoonright (H\cap\gamma) \\ &= e(\nu_{*})\upharpoonright(H\cap\gamma). \end{align*} $$
$$ \begin{align*} e(\nu)\upharpoonright (H\cap\gamma) &= \big(e(\nu)\upharpoonright (H\cap\beta)\big) \upharpoonright (H\cap\gamma)= \big(e^-(\nu\upharpoonright (F\cap\beta)\big) \upharpoonright (H\cap\gamma) \\ & = \big(e^-(\nu_{*}\upharpoonright (F\cap\beta)\big) \upharpoonright (H\cap\gamma)= \big(e(\nu_{*})\upharpoonright (H\cap\beta)\big) \upharpoonright (H\cap\gamma) \\ &= e(\nu_{*})\upharpoonright(H\cap\gamma). \end{align*} $$
If
![]() $\gamma =\beta $
, then
$\gamma =\beta $
, then
Lemma 3.10. We use notation from the formulation of Lemma 3.7. Set
![]() $S=\mathrm {supp}(p)$
,
$S=\mathrm {supp}(p)$
,
![]() $\Sigma _n=\{\nu \in (2^{k_n})^{F_n}:\nu $
is consistent with
$\Sigma _n=\{\nu \in (2^{k_n})^{F_n}:\nu $
is consistent with
![]() $p\}$
, and suppose that
$p\}$
, and suppose that
![]() ${\langle \, \langle i_n,j_n,C_n \rangle : n\in \omega \,\rangle }$
is a sequence such that items
${\langle \, \langle i_n,j_n,C_n \rangle : n\in \omega \,\rangle }$
is a sequence such that items
![]() $(1)$
–
$(1)$
–
![]() $(4)$
of Lemma 2.2 are satisfied. Then there exists
$(4)$
of Lemma 2.2 are satisfied. Then there exists
![]() $q\geq p$
such that
$q\geq p$
such that
![]() $\{p|\sigma :\sigma \in C_n\}$
is predense above q for all
$\{p|\sigma :\sigma \in C_n\}$
is predense above q for all
![]() $n\in \omega $
.
$n\in \omega $
.
Proof. For each natural number n, let
![]() $q_n\geq p$
be such that for every
$q_n\geq p$
be such that for every
![]() $\beta <\alpha $
and
$\beta <\alpha $
and
![]() $\nu \in C_n$
we have
$\nu \in C_n$
we have
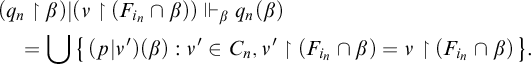 $$\begin{align*} & (q_n\upharpoonright\beta)|(\nu\upharpoonright (F_{i_n}\cap \beta))\Vdash_\beta q_n(\beta) \\ &\quad = \bigcup {\big\{\,(p|\nu')(\beta) : \nu'\in C_n,\nu'\upharpoonright (F_{i_n}\cap \beta)= \nu\upharpoonright (F_{i_n}\cap \beta)\,\big\}}. \end{align*}$$
$$\begin{align*} & (q_n\upharpoonright\beta)|(\nu\upharpoonright (F_{i_n}\cap \beta))\Vdash_\beta q_n(\beta) \\ &\quad = \bigcup {\big\{\,(p|\nu')(\beta) : \nu'\in C_n,\nu'\upharpoonright (F_{i_n}\cap \beta)= \nu\upharpoonright (F_{i_n}\cap \beta)\,\big\}}. \end{align*}$$
The correctness of this definition formally requires to prove by recursion over
![]() $\beta \leq \alpha $
, along with defining
$\beta \leq \alpha $
, along with defining
![]() $q_n$
, that each
$q_n$
, that each
![]() $\nu \upharpoonright (F_{i_n}\cap \beta )$
is consistent with
$\nu \upharpoonright (F_{i_n}\cap \beta )$
is consistent with
![]() $q_n\upharpoonright \beta $
, where
$q_n\upharpoonright \beta $
, where
![]() $\nu \in C_n$
, and the set
$\nu \in C_n$
, and the set
is a maximal antichain above
![]() $q_n\upharpoonright \beta $
, but this is rather easy and standard. As a result, the set
$q_n\upharpoonright \beta $
, but this is rather easy and standard. As a result, the set
![]() $ \{\,q_n|\nu : \nu \in C_n\,\}$
is a maximal antichain above
$ \{\,q_n|\nu : \nu \in C_n\,\}$
is a maximal antichain above
![]() $q_n$
.
$q_n$
.
It remains to show that
for all
![]() $n\in \omega $
, and then let q be the fusion of the
$n\in \omega $
, and then let q be the fusion of the
![]() $q_n$
’s. Suppose that for some
$q_n$
’s. Suppose that for some
![]() $\beta \in F_{i_n}$
we have already shown that
$\beta \in F_{i_n}$
we have already shown that
and we will prove that
This boils down to proving that for every
![]() $\sigma \in C_{n+1}$
, if
$\sigma \in C_{n+1}$
, if
![]() $\nu (\gamma ):=\sigma (\gamma )\upharpoonright k_n$
for all
$\nu (\gamma ):=\sigma (\gamma )\upharpoonright k_n$
for all
![]() $\gamma \in F_{i_n}$
, then
$\gamma \in F_{i_n}$
, then
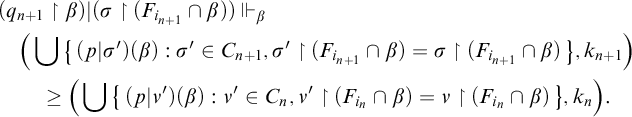 $$ \begin{align*} & (q_{n+1}\upharpoonright\beta)|(\sigma\upharpoonright (F_{i_{n+1}}\cap \beta))\Vdash_\beta \\ &\quad \Big(\bigcup {\big\{\,(p|\sigma')(\beta) : \sigma'\in C_{n+1},\sigma'\upharpoonright (F_{i_{n+1}}\cap \beta)= \sigma\upharpoonright (F_{i_{n+1}}\cap \beta)\,\big\}}, k_{n+1}\Big) \\ &\qquad \geq \Big(\bigcup{\big\{\,(p|\nu')(\beta) : \nu'\in C_n,\nu'\upharpoonright (F_{i_n}\cap \beta)= \nu\upharpoonright (F_{i_n}\cap \beta)\,\big\}},k_n\Big). \end{align*} $$
$$ \begin{align*} & (q_{n+1}\upharpoonright\beta)|(\sigma\upharpoonright (F_{i_{n+1}}\cap \beta))\Vdash_\beta \\ &\quad \Big(\bigcup {\big\{\,(p|\sigma')(\beta) : \sigma'\in C_{n+1},\sigma'\upharpoonright (F_{i_{n+1}}\cap \beta)= \sigma\upharpoonright (F_{i_{n+1}}\cap \beta)\,\big\}}, k_{n+1}\Big) \\ &\qquad \geq \Big(\bigcup{\big\{\,(p|\nu')(\beta) : \nu'\in C_n,\nu'\upharpoonright (F_{i_n}\cap \beta)= \nu\upharpoonright (F_{i_n}\cap \beta)\,\big\}},k_n\Big). \end{align*} $$
Fix
![]() $s\in 2^{k_n}$
such that there exists
$s\in 2^{k_n}$
such that there exists
![]() $\nu '\in C_n$
with
$\nu '\in C_n$
with
![]() $\nu '(\beta )=s$
and
$\nu '(\beta )=s$
and
![]() $\nu '\upharpoonright (F_{i_n}\cap \beta )=\nu \upharpoonright (F_{i_n}\cap \beta )$
. By Lemma 2.2(4), we have
$\nu '\upharpoonright (F_{i_n}\cap \beta )=\nu \upharpoonright (F_{i_n}\cap \beta )$
. By Lemma 2.2(4), we have
![]() $e(\nu )\upharpoonright (F_{j_n}\cap \beta )= e(\nu ')\upharpoonright (F_{j_n}\cap \beta )$
. By Lemma 3.9(1), there are
$e(\nu )\upharpoonright (F_{j_n}\cap \beta )= e(\nu ')\upharpoonright (F_{j_n}\cap \beta )$
. By Lemma 3.9(1), there are
![]() $\sigma _1,\sigma _2\in \Sigma _{i_{n+1}}$
, both extending
$\sigma _1,\sigma _2\in \Sigma _{i_{n+1}}$
, both extending
![]() $e(\nu ')$
(and hence
$e(\nu ')$
(and hence
![]() $\sigma _1,\sigma _2\in C_{n+1}$
) such that
$\sigma _1,\sigma _2\in C_{n+1}$
) such that
![]() $\sigma _1(\beta )\neq \sigma _2(\beta )$
and
$\sigma _1(\beta )\neq \sigma _2(\beta )$
and
It follows that
and
![]() $\sigma _1(\beta ),\sigma _2(\beta )$
are distinct extensions of
$\sigma _1(\beta ),\sigma _2(\beta )$
are distinct extensions of
![]() $e(\nu ')(\beta ),$
which in its turn extends
$e(\nu ')(\beta ),$
which in its turn extends
![]() $\nu '(\beta )=s$
.
$\nu '(\beta )=s$
.
4 Totally imperfect Menger sets and Sacks forcing
By V we mean a ground model of ZFC and
![]() $G_{\omega _2}$
is an
$G_{\omega _2}$
is an
![]() $\mathbb S_{\omega _2}$
-generic filter over V.
$\mathbb S_{\omega _2}$
-generic filter over V.
Theorem 4.1. In
![]() $V[G_{\omega _2}]$
, every totally imperfect Menger set
$V[G_{\omega _2}]$
, every totally imperfect Menger set
![]() $X\subseteq 2^\omega $
has size at most
$X\subseteq 2^\omega $
has size at most
![]() $\omega _1$
.
$\omega _1$
.
For the proof of Theorem 4.1, we need the following auxiliary result, whose proof is rather standard (see, e.g., [Reference Blass and Shelah5, Lemma 5.10] for a similar argument) and is left to the reader.
Lemma 4.2. In
![]() $V[G_{\omega _2}]$
, let
$V[G_{\omega _2}]$
, let
![]() $X\subseteq 2^\omega $
. Then there exists
$X\subseteq 2^\omega $
. Then there exists
![]() $\alpha <\omega _2$
of cofinality
$\alpha <\omega _2$
of cofinality
![]() $\omega _1$
such that
$\omega _1$
such that
-
(1)
 $X\cap V[G_\alpha ]\in V[G_\alpha ]$
and if
$X\cap V[G_\alpha ]\in V[G_\alpha ]$
and if
 $K,K'\subseteq 2^\omega $
are closed crowded sets and coded in
$K,K'\subseteq 2^\omega $
are closed crowded sets and coded in
 $V[G_\alpha ]$
, and
$V[G_\alpha ]$
, and
 $K'\subseteq K\setminus (X\cap V[G_\alpha ])$
, then
$K'\subseteq K\setminus (X\cap V[G_\alpha ])$
, then
 $K'\subseteq K\setminus X$
.
$K'\subseteq K\setminus X$
.
Moreover, if X is a totally imperfect Menger set in
![]() $V[G_{\omega _2}]$
, then
$V[G_{\omega _2}]$
, then
-
(2)
 $X\cap V[G_\alpha ]$
is a totally imperfect Menger set in
$X\cap V[G_\alpha ]$
is a totally imperfect Menger set in
 $V[G_\alpha ]$
.
$V[G_\alpha ]$
.
In what follows we use the same notation for a Borel (typically closed) subset of
![]() $ 2^\omega $
in the ground model as well as for its reinterpretation in the forcing extensions we consider, it will be always clear in which set-theoretic universe we work.
$ 2^\omega $
in the ground model as well as for its reinterpretation in the forcing extensions we consider, it will be always clear in which set-theoretic universe we work.
Proof of Theorem 4.1.
Let
![]() $\alpha $
be such as in Lemma 4.2. Working in
$\alpha $
be such as in Lemma 4.2. Working in
![]() $V[G_{\omega _2}]$
, we claim that
$V[G_{\omega _2}]$
, we claim that
![]() $X\subseteq V[G_\alpha ]$
. Since in
$X\subseteq V[G_\alpha ]$
. Since in
![]() $V[G_\alpha ]$
the remainder
$V[G_\alpha ]$
the remainder
![]() $\mathbb S_{\alpha ,\omega _2}$
is order-isomorphic to
$\mathbb S_{\alpha ,\omega _2}$
is order-isomorphic to
![]() $\mathbb S_{\omega _2}$
, there is no loss of generality in assuming that
$\mathbb S_{\omega _2}$
, there is no loss of generality in assuming that
![]() $\alpha =0$
, i.e., that
$\alpha =0$
, i.e., that
![]() $V=V[G_\alpha ]$
.
$V=V[G_\alpha ]$
.
Let us pick
![]() $z\in X\setminus V$
and let
$z\in X\setminus V$
and let
![]() $\gamma $
be the minimal ordinal with
$\gamma $
be the minimal ordinal with
![]() $z\in V[G_\gamma ]$
. Next, we work in V. Let
$z\in V[G_\gamma ]$
. Next, we work in V. Let
![]() $p_0\in G_{\gamma }$
and
$p_0\in G_{\gamma }$
and
![]() $\tau \in V^{\mathbb S_\gamma }$
be such that
$\tau \in V^{\mathbb S_\gamma }$
be such that
![]() $\tau ^{G_\gamma }=z$
and
$\tau ^{G_\gamma }=z$
and
We shall find
![]() $q\geq p_0$
,
$q\geq p_0$
,
![]() $q \in \mathbb {S}_\gamma $
such that
$q \in \mathbb {S}_\gamma $
such that
![]() $q\Vdash _{\omega _2}\tau \not \in X$
. This would accomplish the proof: The genericity of
$q\Vdash _{\omega _2}\tau \not \in X$
. This would accomplish the proof: The genericity of
![]() $G_{\gamma }$
implies that there is q as above which lies in
$G_{\gamma }$
implies that there is q as above which lies in
![]() $G_{\gamma } \subseteq G_{\omega _2}$
, which would yield
$G_{\gamma } \subseteq G_{\omega _2}$
, which would yield
![]() $z=\tau ^{G_\gamma }=\tau ^{G_{\omega _2}}\not \in X$
.
$z=\tau ^{G_\gamma }=\tau ^{G_{\omega _2}}\not \in X$
.
Take p and
![]() $F_n,k_n,l_n, y_{\sigma _n}$
from Lemma 3.7, applied to
$F_n,k_n,l_n, y_{\sigma _n}$
from Lemma 3.7, applied to
![]() $p_0$
and
$p_0$
and
![]() $\tau $
. Note also that Lemma 3.9(3) ensures that
$\tau $
. Note also that Lemma 3.9(3) ensures that
![]() $S=\mathrm {supp}(p)$
and the sequences
$S=\mathrm {supp}(p)$
and the sequences
![]() ${\langle \, k_n : n\in \omega \,\rangle }, {\langle \, F_n : n\in \omega \,\rangle }, {\langle \, \Sigma _n : n\in \omega \,\rangle }$
satisfy
${\langle \, k_n : n\in \omega \,\rangle }, {\langle \, F_n : n\in \omega \,\rangle }, {\langle \, \Sigma _n : n\in \omega \,\rangle }$
satisfy
![]() $(e_f)$
from the first paragraph of Section 2. Let K and
$(e_f)$
from the first paragraph of Section 2. Let K and
![]() $[\sigma ]$
for
$[\sigma ]$
for
![]() $\sigma \in \bigcup _{n\in \omega }\Sigma _n$
be defined in the same way as in the first paragraph of Section 2.
$\sigma \in \bigcup _{n\in \omega }\Sigma _n$
be defined in the same way as in the first paragraph of Section 2.
Fix an element
![]() $x\in K$
and let
$x\in K$
and let
![]() $\sigma _n\in \Sigma _n$
be such that
$\sigma _n\in \Sigma _n$
be such that
![]() $\{x\}=\bigcap _{n\in \omega }[\sigma _n]$
. Fix a natural number n. We have
$\{x\}=\bigcap _{n\in \omega }[\sigma _n]$
. Fix a natural number n. We have
![]() $\sigma _n(\beta )\subseteq \sigma _{n+1}(\beta )$
for all
$\sigma _n(\beta )\subseteq \sigma _{n+1}(\beta )$
for all
![]() $\beta \in F_n$
, i.e.,
$\beta \in F_n$
, i.e.,
![]() $\sigma _n \prec \sigma _{n+1}$
. Then
$\sigma _n \prec \sigma _{n+1}$
. Then
![]() $p|\sigma _{n+1}\geq p|\sigma _n$
and it follows from Lemma 3.7(4) that
$p|\sigma _{n+1}\geq p|\sigma _n$
and it follows from Lemma 3.7(4) that
which gives
![]() $y_{\sigma _n}\subseteq y_{\sigma _{n+1}}$
. Thus, the map
$y_{\sigma _n}\subseteq y_{\sigma _{n+1}}$
. Thus, the map
![]() $h\colon K\to {2^\omega }$
such that
$h\colon K\to {2^\omega }$
such that
for all
![]() $x\in K$
, is well defined. By Lemma 3.7(5), the map h is a continuous injection. Consequently, the map
$x\in K$
, is well defined. By Lemma 3.7(5), the map h is a continuous injection. Consequently, the map
![]() $h\colon K\to h[K]$
is a homeomorphism, and hence
$h\colon K\to h[K]$
is a homeomorphism, and hence
![]() $h[K]$
is perfect.
$h[K]$
is perfect.
Fix a natural number n. By Lemma 3.7(2) and Observation 3.2(3), the set
![]() $\{\,p|\sigma : \sigma \in \Sigma _n\,\}$
is a maximal antichain above p. Applying Lemma 3.7(4), we have that
$\{\,p|\sigma : \sigma \in \Sigma _n\,\}$
is a maximal antichain above p. Applying Lemma 3.7(4), we have that
It follows from the above and from the definition of the function h that
![]() $p\Vdash \tau \in h[K].$
$p\Vdash \tau \in h[K].$
By our assumption on
![]() $\alpha =0$
, the set
$\alpha =0$
, the set
![]() $h[K]\cap X\cap V$
is an element of V and it is totally imperfect and Menger in V. Let
$h[K]\cap X\cap V$
is an element of V and it is totally imperfect and Menger in V. Let
![]() ${\langle \, \langle i_n,j_n,C_n\rangle : n\in \omega \,\rangle }$
be a sequence from Lemma 2.2, applied to
${\langle \, \langle i_n,j_n,C_n\rangle : n\in \omega \,\rangle }$
be a sequence from Lemma 2.2, applied to
![]() $S:=\mathrm {supp}(p)$
and
$S:=\mathrm {supp}(p)$
and
![]() $h^{-1}[X\cap V]\subseteq K$
. Lemma 2.2(5) yields
$h^{-1}[X\cap V]\subseteq K$
. Lemma 2.2(5) yields
and therefore,
![]() $h[K']\subseteq h[K]\setminus (X\cap V)$
. Since
$h[K']\subseteq h[K]\setminus (X\cap V)$
. Since
![]() $K,K',h$
are all coded in V, we conclude that
$K,K',h$
are all coded in V, we conclude that
![]() $h[K']\subseteq h[K]\setminus X$
holds in
$h[K']\subseteq h[K]\setminus X$
holds in
![]() $V[G_{\omega _2}]$
by Lemma 4.2(2).
$V[G_{\omega _2}]$
by Lemma 4.2(2).
Let
![]() $q\geq p$
be a condition given by Lemma 3.10. Since the sets
$q\geq p$
be a condition given by Lemma 3.10. Since the sets
![]() $\{p|\nu :\nu \in C_n\}$
are predense above q for all
$\{p|\nu :\nu \in C_n\}$
are predense above q for all
![]() $n\in \omega $
, we have
$n\in \omega $
, we have
![]() $q\Vdash \tau \restriction l_{i_n} \in \{\,y_{\nu } : \nu \in C_n\,\}$
, and thus
$q\Vdash \tau \restriction l_{i_n} \in \{\,y_{\nu } : \nu \in C_n\,\}$
, and thus
![]() $q\Vdash \tau \in h[K']$
. We conclude that
$q\Vdash \tau \in h[K']$
. We conclude that
![]() $q\Vdash \tau \not \in X$
.
$q\Vdash \tau \not \in X$
.
5 A modification of the Menger game and consonant spaces
Let
![]() $X\subseteq {2^\omega }$
. We introduce a modification of the Menger game played on X, which we call grouped Menger game played on X.
$X\subseteq {2^\omega }$
. We introduce a modification of the Menger game played on X, which we call grouped Menger game played on X.
Round 0: Alice selects a natural number
![]() $l_0>0$
, and then the players play the usual Menger game
$l_0>0$
, and then the players play the usual Menger game
![]() $l_0$
subrounds, thus constructing a partial play
$l_0$
subrounds, thus constructing a partial play
where
![]() $\mathcal {F}_i$
is a finite subfamily of
$\mathcal {F}_i$
is a finite subfamily of
![]() $\mathcal {U}_i$
for all natural numbers
$\mathcal {U}_i$
for all natural numbers
![]() $i<l_0$
.
$i<l_0$
.
Round 1: Alice selects a natural number
![]() $l_1>0$
, and then the players play the usual Menger game additional
$l_1>0$
, and then the players play the usual Menger game additional
![]() $l_1$
subrounds, thus constructing a partial play
$l_1$
subrounds, thus constructing a partial play
where
![]() $\mathcal {F}_i$
is a finite subfamily of
$\mathcal {F}_i$
is a finite subfamily of
![]() $\mathcal {U}_i$
for all natural numbers
$\mathcal {U}_i$
for all natural numbers
![]() $i<l_0+l_1$
.
$i<l_0+l_1$
.
Fix a natural number
![]() $n>0$
and assume that natural numbers
$n>0$
and assume that natural numbers
![]() $l_0,\dotsc ,l_{n-1}>0$
and
$l_0,\dotsc ,l_{n-1}>0$
and
![]() $n-1$
rounds of the game have been defined.
$n-1$
rounds of the game have been defined.
Round n: Alice selects a natural number
![]() $l_n>0$
, and then the players play the usual Menger game additional
$l_n>0$
, and then the players play the usual Menger game additional
![]() $l_n$
subrounds, thus constructing a partial play
$l_n$
subrounds, thus constructing a partial play
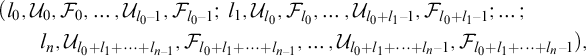 $$ \begin{align*} & (l_0,\mathcal U_0,\mathcal{F}_0,\dotsc,\mathcal U_{l_0-1}, \mathcal F_{l_0-1};\ l_1, \mathcal U_{l_0},\mathcal F_{l_0},\dotsc,\mathcal U_{l_0+l_1-1},\mathcal F_{l_0+l_1-1};\dotsc \nonumber ;\\ & \qquad l_n, \mathcal U_{l_0+l_1+\cdots+l_{n-1}},\mathcal F_{l_0+l_1+\cdots+l_{n-1}},\ldots, \mathcal U_{l_0+l_1+\cdots+l_{n}-1},\mathcal F_{l_0+l_1+\cdots+l_{n}-1}), \end{align*} $$
$$ \begin{align*} & (l_0,\mathcal U_0,\mathcal{F}_0,\dotsc,\mathcal U_{l_0-1}, \mathcal F_{l_0-1};\ l_1, \mathcal U_{l_0},\mathcal F_{l_0},\dotsc,\mathcal U_{l_0+l_1-1},\mathcal F_{l_0+l_1-1};\dotsc \nonumber ;\\ & \qquad l_n, \mathcal U_{l_0+l_1+\cdots+l_{n-1}},\mathcal F_{l_0+l_1+\cdots+l_{n-1}},\ldots, \mathcal U_{l_0+l_1+\cdots+l_{n}-1},\mathcal F_{l_0+l_1+\cdots+l_{n}-1}), \end{align*} $$
where
![]() $\mathcal {F}_i$
is a finite subfamily of
$\mathcal {F}_i$
is a finite subfamily of
![]() $\mathcal {U}_i$
for all natural numbers
$\mathcal {U}_i$
for all natural numbers
![]() $i<l_0+\dotsb +l_{n}$
.
$i<l_0+\dotsb +l_{n}$
.
Let
![]() $L_0:=0$
and
$L_0:=0$
and
![]() $L_{n+1}:=l_0+l_1+\dotsb +l_n$
for all natural numbers n. Bob wins the game if
$L_{n+1}:=l_0+l_1+\dotsb +l_n$
for all natural numbers n. Bob wins the game if
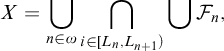 $$\begin{align*}X=\bigcup_{n\in\omega}\bigcap_{i\in [L_n,L_{n+1})}\bigcup\mathcal F_n, \end{align*}$$
$$\begin{align*}X=\bigcup_{n\in\omega}\bigcap_{i\in [L_n,L_{n+1})}\bigcup\mathcal F_n, \end{align*}$$
and Alice wins otherwise.
Remark 5.1. In the grouped Menger game played on a set
![]() $X\subseteq {2^\omega }$
, there is no loss of generality if we assume that covers given by Alice in each step are countable and increasing and the families
$X\subseteq {2^\omega }$
, there is no loss of generality if we assume that covers given by Alice in each step are countable and increasing and the families
![]() $\mathcal {F}_n$
chosen by Bob are singletons.
$\mathcal {F}_n$
chosen by Bob are singletons.
We are interested in sets
![]() $X\subseteq 2^\omega $
for which Alice has no winning strategy in the grouped Menger game played on X. They include two important classes of subspaces of the Cantor space: Hurewicz spaces and those ones whose complement is consonant.
$X\subseteq 2^\omega $
for which Alice has no winning strategy in the grouped Menger game played on X. They include two important classes of subspaces of the Cantor space: Hurewicz spaces and those ones whose complement is consonant.
The following observation is an immediate consequence of Theorem 1.5.
Observation 5.2. If
![]() $X\subseteq 2^\omega $
is Hurewicz, then Alice has no winning strategy in the grouped Menger game played on X.
$X\subseteq 2^\omega $
is Hurewicz, then Alice has no winning strategy in the grouped Menger game played on X.
Proposition 5.3. If
![]() $Y\subseteq 2^\omega $
is consonant, then Alice has no winning strategy in the grouped Menger game played on
$Y\subseteq 2^\omega $
is consonant, then Alice has no winning strategy in the grouped Menger game played on
![]() $2^\omega \setminus Y$
.
$2^\omega \setminus Y$
.
Proof. Let
![]() $\sigma $
be a strategy for Alice in the grouped Menger game played on
$\sigma $
be a strategy for Alice in the grouped Menger game played on
![]() $X:={2^\omega }\setminus Y$
. By Remark 5.1, we may assume that each family given by Alice according to the strategy
$X:={2^\omega }\setminus Y$
. By Remark 5.1, we may assume that each family given by Alice according to the strategy
![]() $\sigma $
is countable and increasing and Bob chooses one set from the families given by Alice. We shall define a strategy
$\sigma $
is countable and increasing and Bob chooses one set from the families given by Alice. We shall define a strategy
![]() $\S $
for Alice in the game
$\S $
for Alice in the game
![]() $\mathsf {G}_1(\mathcal {K},\mathcal {O})$
played on X such that each play in
$\mathsf {G}_1(\mathcal {K},\mathcal {O})$
played on X such that each play in
![]() $\mathsf {G}_1(\mathcal {K},\mathcal {O})$
played according to
$\mathsf {G}_1(\mathcal {K},\mathcal {O})$
played according to
![]() $\S $
and lost by Alice, gives rise to a play in the grouped Menger game on X in which Alice uses
$\S $
and lost by Alice, gives rise to a play in the grouped Menger game on X in which Alice uses
![]() $\sigma $
and loses.
$\sigma $
and loses.
Suppose that
![]() $\sigma $
instructs Alice to start round
$\sigma $
instructs Alice to start round
![]() $0$
by selecting a natural number
$0$
by selecting a natural number
![]() $l_0>0$
. Let
$l_0>0$
. Let
![]() $L_0:=0$
and
$L_0:=0$
and
![]() $L_1:=l_0$
. Then
$L_1:=l_0$
. Then
![]() $\S $
instructs Alice to play the family of all sets
$\S $
instructs Alice to play the family of all sets
 $$\begin{align*}\bigcap_{i\in[L_0,L_1)}U_i, \end{align*}$$
$$\begin{align*}\bigcap_{i\in[L_0,L_1)}U_i, \end{align*}$$
where
is a play, where Alice uses the strategy
![]() $\sigma $
. Note that the family of all the intersections as above is indeed an open k-cover of X. Suppose that Bob replies in
$\sigma $
. Note that the family of all the intersections as above is indeed an open k-cover of X. Suppose that Bob replies in
![]() $\mathsf {G}_1(\mathcal {K},\mathcal {O})$
by selecting
$\mathsf {G}_1(\mathcal {K},\mathcal {O})$
by selecting
![]() $\bigcap _{i\in [L_0,L_1)}U_i$
for some sequence
$\bigcap _{i\in [L_0,L_1)}U_i$
for some sequence
![]() $(\mathcal U_0,U_0,\dotsc ,\mathcal U_{l_0-1},U_{l_0-1})$
as above. The strategy
$(\mathcal U_0,U_0,\dotsc ,\mathcal U_{l_0-1},U_{l_0-1})$
as above. The strategy
![]() $\sigma $
instructs Alice to proceed in round
$\sigma $
instructs Alice to proceed in round
![]() $1$
by selecting a natural number
$1$
by selecting a natural number
![]() $l_1>0$
. Let
$l_1>0$
. Let
![]() $L_2:=l_0+l_1$
. Then
$L_2:=l_0+l_1$
. Then
![]() $\S $
instructs Alice to play the family of all sets
$\S $
instructs Alice to play the family of all sets
 $$\begin{align*}\bigcap_{i\in[L_1,L_2)}U_i, \end{align*}$$
$$\begin{align*}\bigcap_{i\in[L_1,L_2)}U_i, \end{align*}$$
where
is a play in which Alice uses
![]() $\sigma $
, an open k-cover of X. Suppose that Bob replies in
$\sigma $
, an open k-cover of X. Suppose that Bob replies in
![]() $\mathsf {G}_1(\mathcal {K},\mathcal {O})$
by selecting
$\mathsf {G}_1(\mathcal {K},\mathcal {O})$
by selecting
![]() $\bigcap _{i\in [L_1,L_2)}U_i$
for some sequence
$\bigcap _{i\in [L_1,L_2)}U_i$
for some sequence
![]() $(\mathcal U_0,\mathcal F_0,\dotsc ,\mathcal U_{l_0-1},U_{l_0-1};\: \mathcal U_{l_0},U_{l_0},\ldots , \mathcal U_{l_0+l_1-1},U_{l_0+l_1-1})$
as above.
$(\mathcal U_0,\mathcal F_0,\dotsc ,\mathcal U_{l_0-1},U_{l_0-1};\: \mathcal U_{l_0},U_{l_0},\ldots , \mathcal U_{l_0+l_1-1},U_{l_0+l_1-1})$
as above.
In general, let
![]() $\sigma $
instruct Alice to start round n by selecting a natural number
$\sigma $
instruct Alice to start round n by selecting a natural number
![]() $ l_n>0$
. Let
$ l_n>0$
. Let
![]() $L_{n+1}:=l_0+l_1+\dotsb +l_n$
. Then the next move of Alice in
$L_{n+1}:=l_0+l_1+\dotsb +l_n$
. Then the next move of Alice in
![]() $\mathsf {G}_1(\mathcal {K},\mathcal {O})$
according to
$\mathsf {G}_1(\mathcal {K},\mathcal {O})$
according to
![]() $\S $
is, by the definition, the family of all sets
$\S $
is, by the definition, the family of all sets
 $$\begin{align*}\bigcap_{i\in[L_n,L_{n+1})} U_i, \end{align*}$$
$$\begin{align*}\bigcap_{i\in[L_n,L_{n+1})} U_i, \end{align*}$$
where
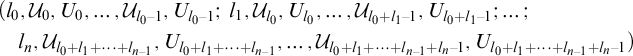 $$ \begin{align*} & ( l_0,\mathcal U_0,U_0,\ldots, \mathcal U_{ l_0-1},U_{ l_0-1};\ l_1, \mathcal U_{ l_0},U_{ l_0},\ldots,\mathcal U_{ l_0+ l_1-1},U_{ l_0+ l_1-1};\ldots ;\\ &\quad l_n, \mathcal U_{ l_0+ l_1+\cdots+ l_{n-1}},U_{ l_0+ l_1+\dotsb+ l_{n-1}},\ldots, \mathcal U_{ l_0+ l_1+\dotsb+ l_{n-1}+ l_n-1},U_{ l_0+ l_1+\dotsb+ l_{n-1}+ l_n -1}) \end{align*} $$
$$ \begin{align*} & ( l_0,\mathcal U_0,U_0,\ldots, \mathcal U_{ l_0-1},U_{ l_0-1};\ l_1, \mathcal U_{ l_0},U_{ l_0},\ldots,\mathcal U_{ l_0+ l_1-1},U_{ l_0+ l_1-1};\ldots ;\\ &\quad l_n, \mathcal U_{ l_0+ l_1+\cdots+ l_{n-1}},U_{ l_0+ l_1+\dotsb+ l_{n-1}},\ldots, \mathcal U_{ l_0+ l_1+\dotsb+ l_{n-1}+ l_n-1},U_{ l_0+ l_1+\dotsb+ l_{n-1}+ l_n -1}) \end{align*} $$
is a play in which Alice uses
![]() $\sigma $
, an open k-cover of X.
$\sigma $
, an open k-cover of X.
Since the strategy
![]() $\S $
is not winning, there is a play in
$\S $
is not winning, there is a play in
![]() $\mathsf {G}_1(\mathcal {K},\mathcal {O})$
in which Alice uses
$\mathsf {G}_1(\mathcal {K},\mathcal {O})$
in which Alice uses
![]() $\S $
and loses, which gives rise to an infinite play
$\S $
and loses, which gives rise to an infinite play
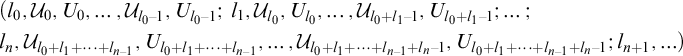 $$ \begin{align*} & ( l_0,\mathcal U_0, U_0,\ldots, \mathcal U_{ l_0-1},U_{ l_0-1};\ l_1, \mathcal U_{ l_0},U_{ l_0},\ldots,\mathcal U_{ l_0+ l_1-1},U_{ l_0+ l_1-1}; \ldots;\\ &l_n, \mathcal U_{ l_0+ l_1+\cdots+ l_{n-1}},U_{ l_0+ l_1+\cdots+ l_{n-1}},\ldots, \mathcal U_{ l_0+ l_1+\cdots+ l_{n-1}+ l_n-1},U_{ l_0+ l_1+\cdots+ l_{n-1}+ l_n -1}; l_{n+1},\ldots) \end{align*} $$
$$ \begin{align*} & ( l_0,\mathcal U_0, U_0,\ldots, \mathcal U_{ l_0-1},U_{ l_0-1};\ l_1, \mathcal U_{ l_0},U_{ l_0},\ldots,\mathcal U_{ l_0+ l_1-1},U_{ l_0+ l_1-1}; \ldots;\\ &l_n, \mathcal U_{ l_0+ l_1+\cdots+ l_{n-1}},U_{ l_0+ l_1+\cdots+ l_{n-1}},\ldots, \mathcal U_{ l_0+ l_1+\cdots+ l_{n-1}+ l_n-1},U_{ l_0+ l_1+\cdots+ l_{n-1}+ l_n -1}; l_{n+1},\ldots) \end{align*} $$
in which Alice uses
![]() $\sigma $
and
$\sigma $
and
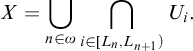 $$\begin{align*}X=\bigcup_{n\in\omega}\bigcap_{i\in[L_n,L_{n+1})} U_i. \end{align*}$$
$$\begin{align*}X=\bigcup_{n\in\omega}\bigcap_{i\in[L_n,L_{n+1})} U_i. \end{align*}$$
This means that the strategy
![]() $\sigma $
is not winning as well.
$\sigma $
is not winning as well.
5.1 Menger game versus the grouped Menger game
Let
![]() $\mathcal {GM}$
be the class of all subspaces X of
$\mathcal {GM}$
be the class of all subspaces X of
![]() $2^\omega $
such that Alice has no winning strategy in the grouped Menger game played on X. Obviously,
$2^\omega $
such that Alice has no winning strategy in the grouped Menger game played on X. Obviously,
![]() $\mathcal {GM}$
is contained in the class of all Menger subspaces of
$\mathcal {GM}$
is contained in the class of all Menger subspaces of
![]() $2^\omega $
. As we established in Section 5,
$2^\omega $
. As we established in Section 5,
![]() $\mathcal {GM} $
includes Hurewicz subspaces and subspaces with consonant complement, and hence also all Rothberger subspaces of
$\mathcal {GM} $
includes Hurewicz subspaces and subspaces with consonant complement, and hence also all Rothberger subspaces of
![]() $2^\omega $
(see the discussion at the end of Section 1 in the work of Jordan [Reference Jordan13]). Our next result gives a consistent example of a Menger space which does not belong to
$2^\omega $
(see the discussion at the end of Section 1 in the work of Jordan [Reference Jordan13]). Our next result gives a consistent example of a Menger space which does not belong to
![]() $\mathcal {GM}$
.
$\mathcal {GM}$
.
Proposition 5.4. The class
![]() $\mathcal {GM}$
contains no ultrafilters.
$\mathcal {GM}$
contains no ultrafilters.
Proof. Given an ultrafilter X on
![]() $\omega $
, we shall describe a winning strategy
$\omega $
, we shall describe a winning strategy
![]() $\sigma $
for Alice in the grouped Menger game played on X. For natural numbers
$\sigma $
for Alice in the grouped Menger game played on X. For natural numbers
![]() $n<k$
, let
$n<k$
, let
Then the families
![]() $\mathcal U_n:=\{\,U_{[n,k)} : k> n\,\}$
are increasing open covers of X for all
$\mathcal U_n:=\{\,U_{[n,k)} : k> n\,\}$
are increasing open covers of X for all
![]() $n\in \omega $
. Playing according to the strategy
$n\in \omega $
. Playing according to the strategy
![]() $\sigma $
, Alice chooses
$\sigma $
, Alice chooses
![]() $ l_n=2$
for all
$ l_n=2$
for all
![]() $n\in \omega $
. The strategy
$n\in \omega $
. The strategy
![]() $\sigma $
instructs Alice to play some cover
$\sigma $
instructs Alice to play some cover
![]() $\mathcal {U}_m$
. Then if the set chosen by Bob is of the form
$\mathcal {U}_m$
. Then if the set chosen by Bob is of the form
![]() $U_{[m,k)}$
, then Alice plays the family
$U_{[m,k)}$
, then Alice plays the family
![]() $\mathcal {U}_k$
. Each play where Alice uses
$\mathcal {U}_k$
. Each play where Alice uses
![]() $\sigma $
has the following form
$\sigma $
has the following form
where
![]() ${\langle \, i_n : i\in \omega \,\rangle }$
is an increasing sequence of natural numbers with
${\langle \, i_n : i\in \omega \,\rangle }$
is an increasing sequence of natural numbers with
![]() $i_0=0$
. Since the sets
$i_0=0$
. Since the sets
are disjoint and
![]() $a\cup b=\omega $
, exactly one of them is a member of X. Assume that
$a\cup b=\omega $
, exactly one of them is a member of X. Assume that
![]() $a\in X$
. Since
$a\in X$
. Since
![]() $a\notin \bigcup _{k\in \omega } U_{[i_{2k+1},i_{2k+2})}$
, we have
$a\notin \bigcup _{k\in \omega } U_{[i_{2k+1},i_{2k+2})}$
, we have
Combining [Reference Chodounský, Repovš and Zdomskyy9, Theorem 1.1] and [Reference Canjar6, Theorem 10], we conclude that
![]() $\mathfrak d=\mathfrak c$
implies the existence of a Menger ultrafilter.
$\mathfrak d=\mathfrak c$
implies the existence of a Menger ultrafilter.
Corollary 5.5. Assume that
![]() $\mathfrak d=\mathfrak c$
. There exists a Menger subspace X of
$\mathfrak d=\mathfrak c$
. There exists a Menger subspace X of
![]() $2^\omega $
such that Alice has a winning strategy in the grouped Menger game on X, i.e.,
$2^\omega $
such that Alice has a winning strategy in the grouped Menger game on X, i.e.,
![]() $X\not \in \mathcal {GM}$
.
$X\not \in \mathcal {GM}$
.
Let us note that there are models of ZFC without Menger ultrafilters. Indeed, every Menger ultrafilter is a P-point, see, e.g., [Reference Bella, Tokgoz and Zdomskyy4, Observation 3.4]. According to a result of Shelah published in [Reference Wimmers27] (see also [Reference Chodounský and Guzman7]), consistently there are no P-points.
Next, we introduce a variation of the grouped Menger game which is “harder” for Alice since her choices are more restricted, i.e., are not arbitrary open covers of the space in question. Let
![]() $K\subseteq {2^\omega }$
be a perfect set. For
$K\subseteq {2^\omega }$
be a perfect set. For
![]() $y\in K$
, let
$y\in K$
, let
![]() $\mathcal {U}_y$
be a countable increasing family of clopen sets in K such that
$\mathcal {U}_y$
be a countable increasing family of clopen sets in K such that
![]() $\bigcup \mathcal {U}_y=K\setminus \{y\}$
. Let
$\bigcup \mathcal {U}_y=K\setminus \{y\}$
. Let
![]() $X\subseteq K$
be a set such that
$X\subseteq K$
be a set such that
![]() $K\setminus X$
is dense in K. The weak grouped Menger game played on X in K (
$K\setminus X$
is dense in K. The weak grouped Menger game played on X in K (
![]() $\operatorname {wgM}(K,X)$
in short) is played as follows: In round
$\operatorname {wgM}(K,X)$
in short) is played as follows: In round
![]() $0$
Alice selects a natural number
$0$
Alice selects a natural number
![]() $ l_0>0$
, and Bob selects a closed nowhere dense subset
$ l_0>0$
, and Bob selects a closed nowhere dense subset
![]() $K_0$
of K. Let
$K_0$
of K. Let
![]() $L_0:=0$
and
$L_0:=0$
and
![]() $L_1:=l_0$
. Then the players play the usual Menger game
$L_1:=l_0$
. Then the players play the usual Menger game
![]() $ l_0$
subrounds, with the following restrictions. In each subround
$ l_0$
subrounds, with the following restrictions. In each subround
![]() $i\in [L_0,L_1)$
, Alice chooses
$i\in [L_0,L_1)$
, Alice chooses
![]() $y_i\in K\setminus (X\cup K_0)$
and plays the family
$y_i\in K\setminus (X\cup K_0)$
and plays the family
![]() $\mathcal {U}_i:=\mathcal {U}_{y_i}$
. Then Bob replies by choosing a set
$\mathcal {U}_i:=\mathcal {U}_{y_i}$
. Then Bob replies by choosing a set
![]() $U_i\in \mathcal U_i$
with
$U_i\in \mathcal U_i$
with
![]() $K_0\subseteq U_i$
.
$K_0\subseteq U_i$
.
Afterwards, in round
![]() $1$
Alice selects a natural number
$1$
Alice selects a natural number
![]() $ l_1>0$
, and Bob selects a closed nowhere dense set
$ l_1>0$
, and Bob selects a closed nowhere dense set
![]() $K_1\subseteq K$
. Let
$K_1\subseteq K$
. Let
![]() $L_2:=l_0+l_1$
. Then the players play the Menger game further
$L_2:=l_0+l_1$
. Then the players play the Menger game further
![]() $ l_1$
subrounds with the restriction given above, i.e., in each subround
$ l_1$
subrounds with the restriction given above, i.e., in each subround
![]() $i\in [L_1,L_2)$
Alice chooses
$i\in [L_1,L_2)$
Alice chooses
![]() $y_i\in K\setminus (X\cup K_1)$
and plays the family
$y_i\in K\setminus (X\cup K_1)$
and plays the family
![]() $\mathcal U_i:=\mathcal {U}_{y_i}$
. Then Bob replies by choosing a set
$\mathcal U_i:=\mathcal {U}_{y_i}$
. Then Bob replies by choosing a set
![]() $U_i\in \mathcal U_i$
with
$U_i\in \mathcal U_i$
with
![]() $K_1\subseteq U_i$
.
$K_1\subseteq U_i$
.
In round n Alice selects a natural number
![]() $ l_n>0$
, and Bob selects a closed nowhere dense set
$ l_n>0$
, and Bob selects a closed nowhere dense set
![]() $K_n\subseteq K$
. Let
$K_n\subseteq K$
. Let
![]() $L_{n+1}:=l_0+l_1+\dotsb +l_n$
. Then the players play the Menger game further
$L_{n+1}:=l_0+l_1+\dotsb +l_n$
. Then the players play the Menger game further
![]() $ l_n$
subrounds such that in each subround
$ l_n$
subrounds such that in each subround
![]() $i\in [L_n,L_{n+1})$
Alice chooses
$i\in [L_n,L_{n+1})$
Alice chooses
![]() $y_i\in K\setminus (X\cup K_n)$
and plays the family
$y_i\in K\setminus (X\cup K_n)$
and plays the family
![]() $\mathcal U_i:=\mathcal {U}_{y_i}$
. Then Bob replies by choosing a set
$\mathcal U_i:=\mathcal {U}_{y_i}$
. Then Bob replies by choosing a set
![]() $U_i\in \mathcal U_i$
with
$U_i\in \mathcal U_i$
with
![]() $K_n\subseteq U_i$
.
$K_n\subseteq U_i$
.
Bob wins the game if
 $$\begin{align*}X=\bigcup_{n\in\omega}\bigcap_{i\in [L_n,L_{n+1})}U_i , \end{align*}$$
$$\begin{align*}X=\bigcup_{n\in\omega}\bigcap_{i\in [L_n,L_{n+1})}U_i , \end{align*}$$
and Alice wins otherwise.
Remark 5.8. Let X be a subset of a perfect set
![]() $K\subseteq {2^\omega }$
such that
$K\subseteq {2^\omega }$
such that
![]() $K\setminus X$
is dense in K. If Alice has a winning strategy in the weak grouped Menger game played on X in K, then Alice has a winning strategy in the grouped Menger game played on X.
$K\setminus X$
is dense in K. If Alice has a winning strategy in the weak grouped Menger game played on X in K, then Alice has a winning strategy in the grouped Menger game played on X.
A set
![]() $X\subseteq {2^\omega }$
is perfectly meager if for any perfect set
$X\subseteq {2^\omega }$
is perfectly meager if for any perfect set
![]() $K\subseteq {2^\omega }$
, the intersection
$K\subseteq {2^\omega }$
, the intersection
![]() $X\cap K$
is meager in K.
$X\cap K$
is meager in K.
Proposition 5.9. Let
![]() $K\subseteq {2^\omega }$
be a perfect set and
$K\subseteq {2^\omega }$
be a perfect set and
![]() $X\subseteq {2^\omega }$
be a perfectly meager set. Then Bob has a winning strategy in the weak grouped Menger game played on
$X\subseteq {2^\omega }$
be a perfectly meager set. Then Bob has a winning strategy in the weak grouped Menger game played on
![]() $X\cap K$
in K.
$X\cap K$
in K.
Proof. For each natural number n let
![]() $K_n\subseteq K$
be a closed nowhere dense subset of K such that
$K_n\subseteq K$
be a closed nowhere dense subset of K such that
![]() $X\cap K\subseteq \bigcup _{n\in \omega }K_n\subseteq K$
. Then any strategy for Bob in the weak grouped Menger game played on
$X\cap K\subseteq \bigcup _{n\in \omega }K_n\subseteq K$
. Then any strategy for Bob in the weak grouped Menger game played on
![]() $X\cap K$
in K, where in each round n, Bob plays the set
$X\cap K$
in K, where in each round n, Bob plays the set
![]() $K_n$
, is a winning strategy.
$K_n$
, is a winning strategy.
Let
![]() $K\subseteq {2^\omega }$
be a perfect set and
$K\subseteq {2^\omega }$
be a perfect set and
![]() $X\subseteq {2^\omega }$
. The diagram below presents the relations between the considered properties. By
$X\subseteq {2^\omega }$
. The diagram below presents the relations between the considered properties. By
![]() $\mathrm {A}\not \uparrow \operatorname {wgM}(K,X\cap K)$
we mean that Alice has no winning strategy and by
$\mathrm {A}\not \uparrow \operatorname {wgM}(K,X\cap K)$
we mean that Alice has no winning strategy and by
![]() $\mathrm {B}\uparrow \operatorname {wgM}(K,X\cap K)$
we mean that Bob has a winning strategy in the game
$\mathrm {B}\uparrow \operatorname {wgM}(K,X\cap K)$
we mean that Bob has a winning strategy in the game
![]() $\operatorname {wgM}(K,X\cap K)$
. Note that co-consonant spaces are preserved by closed subspaces.
$\operatorname {wgM}(K,X\cap K)$
. Note that co-consonant spaces are preserved by closed subspaces.
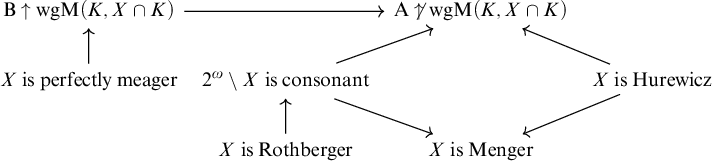
The next fact is similar to Lemma 2.2.
Lemma 5.10. We use the notation and objects described in Section 2. Suppose that X is a subset of the perfect set
![]() $K\subseteq ({2^\omega })^S$
such that
$K\subseteq ({2^\omega })^S$
such that
![]() $K\setminus X$
is dense in K and Alice has no winning strategy in
$K\setminus X$
is dense in K and Alice has no winning strategy in
![]() $\operatorname {wgM}(K,X)$
.
$\operatorname {wgM}(K,X)$
.
Then there exists a sequence
![]() ${\langle \, \langle i_n,j_n,C_n\rangle : n\in \omega \,\rangle }$
such that
${\langle \, \langle i_n,j_n,C_n\rangle : n\in \omega \,\rangle }$
such that
-
(1)
 ${\langle \, i_n : n\in \omega \,\rangle }$
is a strictly increasing sequence of natural numbers;
${\langle \, i_n : n\in \omega \,\rangle }$
is a strictly increasing sequence of natural numbers; -
(2)
 $C_n\subseteq \Sigma _{i_n}$
;
$C_n\subseteq \Sigma _{i_n}$
; -
(3) for every
 $n\in \omega $
, we have
$n\in \omega $
, we have
 $j_n\in [i_n,i_{n+1})$
, and for every
$j_n\in [i_n,i_{n+1})$
, and for every
 $\nu \in C_n$
there exists
$\nu \in C_n$
there exists
 $e_n(\nu )\in \Sigma _{j_n}$
extending
$e_n(\nu )\in \Sigma _{j_n}$
extending
 $\nu $
, such that
$\nu $
, such that  $$ \begin{align*}C_{n+1}=\bigcup_{\nu\in C_n}\{\sigma\in\Sigma_{i_{n+1}}\: :\: \sigma \succ e_n(\nu)\};\end{align*} $$
$$ \begin{align*}C_{n+1}=\bigcup_{\nu\in C_n}\{\sigma\in\Sigma_{i_{n+1}}\: :\: \sigma \succ e_n(\nu)\};\end{align*} $$
-
(4) the maps
 $e_n\colon C_n\to \Sigma _{j_n}$
are coherent; and
$e_n\colon C_n\to \Sigma _{j_n}$
are coherent; and -
(5)
 $\bigcap _{n\in \omega }\bigcup _{\nu \in C_n}[\nu ]\cap X=\emptyset $
.
$\bigcap _{n\in \omega }\bigcup _{\nu \in C_n}[\nu ]\cap X=\emptyset $
.
Proof. We shall describe a strategy
![]() $\S $
for Alice in the weak grouped Menger game played on X in K such that each play lost Alice gives rise to the objects whose existence we need to establish.
$\S $
for Alice in the weak grouped Menger game played on X in K such that each play lost Alice gives rise to the objects whose existence we need to establish.
Round 0. Let
![]() $C_0:=\Sigma _0$
and
$C_0:=\Sigma _0$
and
![]() $i_0:=0$
. Alice declares that the
$i_0:=0$
. Alice declares that the
![]() $0$
th group will have length
$0$
th group will have length
![]() $ l_0:=|C_0|$
. Let
$ l_0:=|C_0|$
. Let
![]() $\{\nu _j:j< l_0\}\subseteq \Sigma _0$
be an enumeration of
$\{\nu _j:j< l_0\}\subseteq \Sigma _0$
be an enumeration of
![]() $C_0$
. Suppose that Bob plays a closed nowhere dense
$C_0$
. Suppose that Bob plays a closed nowhere dense
![]() $K_0\subseteq K$
.
$K_0\subseteq K$
.
Subround
![]() $\langle 0,0\rangle $
. By density of
$\langle 0,0\rangle $
. By density of
![]() $K\setminus X$
, Alice picks
$K\setminus X$
, Alice picks
![]() $y_{\langle 0,0\rangle }\in [\nu _0]\setminus (X\cup K_0)$
and she plays the family
$y_{\langle 0,0\rangle }\in [\nu _0]\setminus (X\cup K_0)$
and she plays the family
![]() $\mathcal U_{\langle 0,0\rangle }:=\mathcal {U}_{y_{\langle 0,0\rangle }}$
. Suppose that Bob replies by choosing
$\mathcal U_{\langle 0,0\rangle }:=\mathcal {U}_{y_{\langle 0,0\rangle }}$
. Suppose that Bob replies by choosing
![]() $U_{\langle 0,0\rangle }\in \mathcal U_{\langle 0,0\rangle }$
with
$U_{\langle 0,0\rangle }\in \mathcal U_{\langle 0,0\rangle }$
with
![]() $K_0\subseteq U_{\langle 0,0\rangle }$
. Take
$K_0\subseteq U_{\langle 0,0\rangle }$
. Take
![]() $j_{\langle 0,0\rangle }>i_0$
and
$j_{\langle 0,0\rangle }>i_0$
and
![]() $\nu _{\langle 0,0\rangle }\in \Sigma _{j_{\langle 0,0\rangle }}$
with
$\nu _{\langle 0,0\rangle }\in \Sigma _{j_{\langle 0,0\rangle }}$
with
![]() $\nu _{\langle 0,0\rangle }\succ \nu _0$
such that
$\nu _{\langle 0,0\rangle }\succ \nu _0$
such that
![]() $y_{\langle 0,0\rangle }\in [\nu _{\langle 0,0\rangle }]$
and
$y_{\langle 0,0\rangle }\in [\nu _{\langle 0,0\rangle }]$
and
![]() $[\nu _{\langle 0,0\rangle }]\cap U_{\langle 0,0\rangle }=\emptyset $
. Let
$[\nu _{\langle 0,0\rangle }]\cap U_{\langle 0,0\rangle }=\emptyset $
. Let
![]() $e_{\langle 0,0\rangle }\colon C_0\to \Sigma _{j_{\langle 0,0\rangle }}$
be a coherent map such that
$e_{\langle 0,0\rangle }\colon C_0\to \Sigma _{j_{\langle 0,0\rangle }}$
be a coherent map such that
![]() $e_{\langle 0,0\rangle }(\nu _0)=\nu _{\langle 0,0\rangle }$
. Fix a natural number a with
$e_{\langle 0,0\rangle }(\nu _0)=\nu _{\langle 0,0\rangle }$
. Fix a natural number a with
![]() $0<a< l_0$
and assume that the players have already defined the following sequences:
$0<a< l_0$
and assume that the players have already defined the following sequences:
-
•
 ${\langle \, y_{\langle 0,b\rangle } : 0\leq b<a\,\rangle }$
of elements
${\langle \, y_{\langle 0,b\rangle } : 0\leq b<a\,\rangle }$
of elements
 $y_{\langle 0,b\rangle }\in K\setminus (X\cup K_0)$
,
$y_{\langle 0,b\rangle }\in K\setminus (X\cup K_0)$
, -
•
 ${\langle \, \mathcal U_{\langle 0,b\rangle } : 0\leq b<a\,\rangle }$
of covers of X by clopen subsets of K such that
${\langle \, \mathcal U_{\langle 0,b\rangle } : 0\leq b<a\,\rangle }$
of covers of X by clopen subsets of K such that
 $\mathcal {U}_{\langle 0, b\rangle }=\mathcal {U}_{y_{\langle 0, b\rangle }}$
,
$\mathcal {U}_{\langle 0, b\rangle }=\mathcal {U}_{y_{\langle 0, b\rangle }}$
, -
•
 ${\langle \, U_{\langle 0,b\rangle } : 0\leq b<a\,\rangle }$
of sets
${\langle \, U_{\langle 0,b\rangle } : 0\leq b<a\,\rangle }$
of sets
 $U_{\langle 0,b\rangle }\in \mathcal U_{\langle 0,b\rangle }$
with
$U_{\langle 0,b\rangle }\in \mathcal U_{\langle 0,b\rangle }$
with
 $K_0\subseteq U_{\langle 0,b\rangle }$
,
$K_0\subseteq U_{\langle 0,b\rangle }$
, -
•
 ${\langle \, j_{\langle 0,b\rangle } : 0\leq b<a\,\rangle }\in \omega ^{\uparrow a}$
with
${\langle \, j_{\langle 0,b\rangle } : 0\leq b<a\,\rangle }\in \omega ^{\uparrow a}$
with
 $i_0<j_{\langle 0,0\rangle }$
,
$i_0<j_{\langle 0,0\rangle }$
, -
•
 ${\langle \, \nu _{\langle 0,b\rangle } : 0\leq b<a\,\rangle }$
of maps
${\langle \, \nu _{\langle 0,b\rangle } : 0\leq b<a\,\rangle }$
of maps
 $\nu _{\langle 0,b\rangle }\in \Sigma _{j_{\langle 0,b\rangle }}$
such that
$\nu _{\langle 0,b\rangle }\in \Sigma _{j_{\langle 0,b\rangle }}$
such that
 $y_{\langle 0,b\rangle }\in [\nu _{\langle 0,b\rangle }]$
,
$y_{\langle 0,b\rangle }\in [\nu _{\langle 0,b\rangle }]$
,
 $\nu _b\prec \nu _{\langle 0,b\rangle }$
and
$\nu _b\prec \nu _{\langle 0,b\rangle }$
and
 $[\nu _{\langle 0,b\rangle }]\cap U_{\langle 0,b\rangle }=\emptyset $
,
$[\nu _{\langle 0,b\rangle }]\cap U_{\langle 0,b\rangle }=\emptyset $
, -
•
 ${\langle \, e_{\langle 0,b\rangle } : 0\leq b<a\,\rangle }$
of coherent maps
${\langle \, e_{\langle 0,b\rangle } : 0\leq b<a\,\rangle }$
of coherent maps
 $e_{\langle 0,b\rangle }\colon C_0\to \Sigma _{j_{\langle 0,b\rangle }}$
with
$e_{\langle 0,b\rangle }\colon C_0\to \Sigma _{j_{\langle 0,b\rangle }}$
with
 $e_{\langle 0,b\rangle }(\nu _b)=\nu _{\langle 0,b\rangle }$
and for every
$e_{\langle 0,b\rangle }(\nu _b)=\nu _{\langle 0,b\rangle }$
and for every
 $0\leq b_0<b_1<a$
and
$0\leq b_0<b_1<a$
and
 $j< l_0$
we have
$j< l_0$
we have
 $e_{\langle 0,b_0\rangle }(\nu _{j})\prec e_{\langle 0,b_1\rangle }(\nu _{j})$
.
$e_{\langle 0,b_0\rangle }(\nu _{j})\prec e_{\langle 0,b_1\rangle }(\nu _{j})$
.
Subround
![]() $\langle 0,a\rangle $
: Alice picks
$\langle 0,a\rangle $
: Alice picks
![]() $y_{\langle 0,a\rangle }\in [e_{\langle 0,a-1\rangle }(\nu _a)]\setminus (X\cup K_0)$
and she plays the family
$y_{\langle 0,a\rangle }\in [e_{\langle 0,a-1\rangle }(\nu _a)]\setminus (X\cup K_0)$
and she plays the family
![]() $\mathcal U_{\langle 0,a\rangle }:=\mathcal {U}_{y_{\langle 0, a\rangle }}$
. Suppose that Bob replies by choosing
$\mathcal U_{\langle 0,a\rangle }:=\mathcal {U}_{y_{\langle 0, a\rangle }}$
. Suppose that Bob replies by choosing
![]() $U_{\langle 0,a\rangle }\in \mathcal U_{\langle 0,a\rangle }$
with
$U_{\langle 0,a\rangle }\in \mathcal U_{\langle 0,a\rangle }$
with
![]() $K_0\subseteq U_{\langle 0,a\rangle }$
. Take
$K_0\subseteq U_{\langle 0,a\rangle }$
. Take
![]() $j_{\langle 0,a\rangle }>j_{\langle 0,a-1\rangle }$
and
$j_{\langle 0,a\rangle }>j_{\langle 0,a-1\rangle }$
and
![]() $\nu _{\langle 0,a\rangle }\in \Sigma _{j_{\langle 0,a\rangle }}$
with
$\nu _{\langle 0,a\rangle }\in \Sigma _{j_{\langle 0,a\rangle }}$
with
![]() $\nu _{\langle 0,a\rangle }\succ e_{\langle 0,a-1\rangle }(\nu _a)$
such that
$\nu _{\langle 0,a\rangle }\succ e_{\langle 0,a-1\rangle }(\nu _a)$
such that
![]() $y_{\langle 0,a\rangle }\in [\nu _{\langle 0,a\rangle }]$
and
$y_{\langle 0,a\rangle }\in [\nu _{\langle 0,a\rangle }]$
and
![]() $[\nu _{\langle 0,a\rangle }]\cap U_{\langle 0,a\rangle }=\emptyset $
. Let
$[\nu _{\langle 0,a\rangle }]\cap U_{\langle 0,a\rangle }=\emptyset $
. Let
![]() $e^{\prime }_{\langle 0,a\rangle }\colon e_{\langle 0,a-1\rangle }[ C_0]\to \Sigma _{j_{\langle 0,a\rangle }}$
be a coherent map such that
$e^{\prime }_{\langle 0,a\rangle }\colon e_{\langle 0,a-1\rangle }[ C_0]\to \Sigma _{j_{\langle 0,a\rangle }}$
be a coherent map such that
![]() $e^{\prime }_{\langle 0,a\rangle }(e_{\langle 0,a-1\rangle }(\nu _a))=\nu _{\langle 0,a\rangle }$
. Put
$e^{\prime }_{\langle 0,a\rangle }(e_{\langle 0,a-1\rangle }(\nu _a))=\nu _{\langle 0,a\rangle }$
. Put
![]() $e_{\langle 0,a\rangle }:=e^{\prime }_{\langle 0,a\rangle }\circ e_{\langle 0,a-1\rangle }$
.
$e_{\langle 0,a\rangle }:=e^{\prime }_{\langle 0,a\rangle }\circ e_{\langle 0,a-1\rangle }$
.
After subround
![]() $\langle 0, l_0-1\rangle $
, the last subround of round 0, we set
$\langle 0, l_0-1\rangle $
, the last subround of round 0, we set
Fix a natural number
![]() $n>0$
and assume that the elements of the sequence
$n>0$
and assume that the elements of the sequence
satisfy all relevant instances of
![]() $(1)$
–
$(1)$
–
![]() $(4)$
.
$(4)$
.
Round n. Alice declares that the nth group will have length
![]() $ l_{n}:=|C_{n}|$
. Let
$ l_{n}:=|C_{n}|$
. Let
![]() $\{\nu _j:j< l_{n}\}\subseteq \Sigma _{i_{n}}$
be an enumerationFootnote
3
of
$\{\nu _j:j< l_{n}\}\subseteq \Sigma _{i_{n}}$
be an enumerationFootnote
3
of
![]() $C_{n}$
. Suppose that Bob plays a closed nowhere dense subset
$C_{n}$
. Suppose that Bob plays a closed nowhere dense subset
![]() $K_{n}\subseteq K$
.
$K_{n}\subseteq K$
.
Subround
![]() $\langle n,0\rangle $
: Alice picks
$\langle n,0\rangle $
: Alice picks
![]() $y_{\langle n,0\rangle }\in [\nu _0]\setminus (X\cup K_{n})$
and she plays the family
$y_{\langle n,0\rangle }\in [\nu _0]\setminus (X\cup K_{n})$
and she plays the family
![]() $\mathcal U_{\langle n,0\rangle }:=\mathcal {U}_{y_{\langle n,0\rangle }}$
. Suppose that Bob replies by choosing
$\mathcal U_{\langle n,0\rangle }:=\mathcal {U}_{y_{\langle n,0\rangle }}$
. Suppose that Bob replies by choosing
![]() $U_{\langle n,0\rangle }\in \mathcal U_{\langle n,0\rangle }$
with
$U_{\langle n,0\rangle }\in \mathcal U_{\langle n,0\rangle }$
with
![]() $K_n\subseteq U_{\langle n, 0\rangle }$
. Take
$K_n\subseteq U_{\langle n, 0\rangle }$
. Take
![]() $j_{\langle n,0\rangle }>i_{n}$
and
$j_{\langle n,0\rangle }>i_{n}$
and
![]() $\nu _{\langle n,0\rangle }\in \Sigma _{j_{\langle n,0\rangle }}$
with
$\nu _{\langle n,0\rangle }\in \Sigma _{j_{\langle n,0\rangle }}$
with
![]() $\nu _{\langle n,0\rangle }\succ \nu _0$
such that
$\nu _{\langle n,0\rangle }\succ \nu _0$
such that
![]() $y_{\langle n,0\rangle }\in [\nu _{\langle n,0\rangle }]$
and
$y_{\langle n,0\rangle }\in [\nu _{\langle n,0\rangle }]$
and
![]() $[\nu _{\langle n,0\rangle }]\cap U_{\langle n,0\rangle }=\emptyset $
. Let
$[\nu _{\langle n,0\rangle }]\cap U_{\langle n,0\rangle }=\emptyset $
. Let
![]() $e_{\langle n,0\rangle }\colon C_{n}\to \Sigma _{j_{\langle n,0\rangle }}$
be a coherent map such that
$e_{\langle n,0\rangle }\colon C_{n}\to \Sigma _{j_{\langle n,0\rangle }}$
be a coherent map such that
![]() $e_{\langle n,0\rangle }(\nu _0)=\nu _{\langle n,0\rangle }$
.
$e_{\langle n,0\rangle }(\nu _0)=\nu _{\langle n,0\rangle }$
.
Fix a natural number a with
![]() $0<a< l_{n}$
and assume that the players have already defined the following sequences:
$0<a< l_{n}$
and assume that the players have already defined the following sequences:
-
•
 ${\langle \, y_{\langle n,b\rangle } : 0\leq b<a\,\rangle }$
of elements
${\langle \, y_{\langle n,b\rangle } : 0\leq b<a\,\rangle }$
of elements
 $y_{\langle n,b\rangle }\in K\setminus (X\cup K_{n})$
;
$y_{\langle n,b\rangle }\in K\setminus (X\cup K_{n})$
; -
•
 ${\langle \, \mathcal U_{\langle n,b\rangle } : 0\leq b<a\,\rangle }$
of covers of X by clopen subsets of K such that
${\langle \, \mathcal U_{\langle n,b\rangle } : 0\leq b<a\,\rangle }$
of covers of X by clopen subsets of K such that
 $\mathcal U_{\langle n,b\rangle }=\mathcal {U}_{y_{\langle n,b\rangle }}$
;
$\mathcal U_{\langle n,b\rangle }=\mathcal {U}_{y_{\langle n,b\rangle }}$
; -
•
 ${\langle \, U_{\langle n,b\rangle } : 0\leq b<a\,\rangle }$
of sets
${\langle \, U_{\langle n,b\rangle } : 0\leq b<a\,\rangle }$
of sets
 $U_{\langle n,b\rangle }\in \mathcal U_{\langle n,b\rangle }$
with
$U_{\langle n,b\rangle }\in \mathcal U_{\langle n,b\rangle }$
with
 $K_{n}\subseteq U_{\langle n,b\rangle }$
;
$K_{n}\subseteq U_{\langle n,b\rangle }$
; -
•
 ${\langle \, j_{\langle n,b\rangle } : 0\leq b<a\,\rangle }$
which is an increasing sequence with
${\langle \, j_{\langle n,b\rangle } : 0\leq b<a\,\rangle }$
which is an increasing sequence with
 $j_{\langle n,0\rangle }>i_{n}$
;
$j_{\langle n,0\rangle }>i_{n}$
; -
•
 ${\langle \, \nu _{\langle n,b\rangle } : 0\leq b<a\,\rangle }$
of maps
${\langle \, \nu _{\langle n,b\rangle } : 0\leq b<a\,\rangle }$
of maps
 $\nu _{\langle n,b\rangle }\in \Sigma _{j_{\langle n,b\rangle }}$
such that
$\nu _{\langle n,b\rangle }\in \Sigma _{j_{\langle n,b\rangle }}$
such that
 $y_{\langle n,b\rangle }\in [\nu _{\langle n,b\rangle }]$
,
$y_{\langle n,b\rangle }\in [\nu _{\langle n,b\rangle }]$
,
 $\nu _b\prec \nu _{\langle n,b\rangle }$
and
$\nu _b\prec \nu _{\langle n,b\rangle }$
and
 $[\nu _{\langle n,b\rangle }]\cap U_{\langle n,b\rangle }=\emptyset $
;
$[\nu _{\langle n,b\rangle }]\cap U_{\langle n,b\rangle }=\emptyset $
; -
•
 ${\langle \, e_{\langle n,b\rangle } : 0\leq b<a\,\rangle }$
of coherent maps
${\langle \, e_{\langle n,b\rangle } : 0\leq b<a\,\rangle }$
of coherent maps
 $e_{\langle n,b\rangle }\colon C_{n}\to \Sigma _{j_{\langle n,b\rangle }}$
with
$e_{\langle n,b\rangle }\colon C_{n}\to \Sigma _{j_{\langle n,b\rangle }}$
with
 $e_{\langle n,b\rangle }(\nu _b)=\nu _{\langle n,b\rangle }$
and for every
$e_{\langle n,b\rangle }(\nu _b)=\nu _{\langle n,b\rangle }$
and for every
 $0\leq b_0<b_1<a$
and
$0\leq b_0<b_1<a$
and
 $j< l_{n}$
we have
$j< l_{n}$
we have
 $e_{\langle n,b_0\rangle }(\nu _{j})\prec e_{\langle n,b_1\rangle }(\nu _{j})$
.
$e_{\langle n,b_0\rangle }(\nu _{j})\prec e_{\langle n,b_1\rangle }(\nu _{j})$
.
Subround
![]() $\langle n,a\rangle $
: Alice picks
$\langle n,a\rangle $
: Alice picks
![]() $y_{\langle n,a\rangle }\in [e_{\langle n,a-1\rangle }(\nu _a)]\setminus (X\cup K_{n})$
and she plays the family
$y_{\langle n,a\rangle }\in [e_{\langle n,a-1\rangle }(\nu _a)]\setminus (X\cup K_{n})$
and she plays the family
![]() $\mathcal U_{\langle n,a\rangle }:=\mathcal {U}_{y_{\langle n,a\rangle }}$
. Suppose that Bob replies by choosing
$\mathcal U_{\langle n,a\rangle }:=\mathcal {U}_{y_{\langle n,a\rangle }}$
. Suppose that Bob replies by choosing
![]() $U_{\langle n,a\rangle }\in \mathcal U_{\langle n,a\rangle }$
such that
$U_{\langle n,a\rangle }\in \mathcal U_{\langle n,a\rangle }$
such that
![]() $K_n\subseteq U_{\langle n,a\rangle }$
. Take
$K_n\subseteq U_{\langle n,a\rangle }$
. Take
![]() $j_{\langle n,a\rangle }>j_{\langle n,a-1\rangle }$
and
$j_{\langle n,a\rangle }>j_{\langle n,a-1\rangle }$
and
![]() $\nu _{\langle n,a\rangle }\in \Sigma _{j_{\langle n,a\rangle }}$
with
$\nu _{\langle n,a\rangle }\in \Sigma _{j_{\langle n,a\rangle }}$
with
![]() $\nu _{\langle n,a\rangle }\succ e_{\langle n,a-1\rangle }(\nu _a)$
such that
$\nu _{\langle n,a\rangle }\succ e_{\langle n,a-1\rangle }(\nu _a)$
such that
![]() $y_{\langle n,a\rangle }\in [\nu _{\langle n,a\rangle }]$
and
$y_{\langle n,a\rangle }\in [\nu _{\langle n,a\rangle }]$
and
![]() $[\nu _{\langle n,a\rangle }]\cap U_{\langle n,a\rangle }=\emptyset $
. Let
$[\nu _{\langle n,a\rangle }]\cap U_{\langle n,a\rangle }=\emptyset $
. Let
![]() $e^{\prime }_{\langle n,a\rangle }\colon e_{\langle n,a-1\rangle }[ C_{n}]\to \Sigma _{j_{\langle n,a\rangle }}$
be a coherent map such that
$e^{\prime }_{\langle n,a\rangle }\colon e_{\langle n,a-1\rangle }[ C_{n}]\to \Sigma _{j_{\langle n,a\rangle }}$
be a coherent map such that
![]() $e^{\prime }_{\langle n,a\rangle }(e_{\langle n,a-1\rangle }(\nu _a))=\nu _{\langle n,a\rangle }$
. Put
$e^{\prime }_{\langle n,a\rangle }(e_{\langle n,a-1\rangle }(\nu _a))=\nu _{\langle n,a\rangle }$
. Put
![]() $e_{\langle n,a\rangle }:=e^{\prime }_{\langle n,a\rangle }\circ e_{\langle n,a-1\rangle }$
.
$e_{\langle n,a\rangle }:=e^{\prime }_{\langle n,a\rangle }\circ e_{\langle n,a-1\rangle }$
.
After subround
![]() $\langle n, l_{n}-1\rangle $
, the last subround of round n, we set
$\langle n, l_{n}-1\rangle $
, the last subround of round n, we set
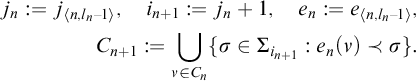 $$\begin{align*}\begin{aligned} j_{n}:=j_{\langle n, l_{n}-1\rangle},\quad i_{n+1}:=j_{n}+1,\quad e_{n}:=e_{\langle n, l_{n}-1\rangle},\\ C_{n+1}:=\bigcup_{\nu\in C_{n}}\{\sigma\in\Sigma_{i_{n+1}}:e_{n}(\nu)\prec\sigma\}. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} j_{n}:=j_{\langle n, l_{n}-1\rangle},\quad i_{n+1}:=j_{n}+1,\quad e_{n}:=e_{\langle n, l_{n}-1\rangle},\\ C_{n+1}:=\bigcup_{\nu\in C_{n}}\{\sigma\in\Sigma_{i_{n+1}}:e_{n}(\nu)\prec\sigma\}. \end{aligned} \end{align*}$$
This completes the definition of the strategy
![]() $\S $
in the weak grouped Menger game played on X. It remains to notice that any play in this game in which Alice uses
$\S $
in the weak grouped Menger game played on X. It remains to notice that any play in this game in which Alice uses
![]() $\S $
gives a sequence of objects we require in our lemma, such that conditions
$\S $
gives a sequence of objects we require in our lemma, such that conditions
![]() $(1)$
–
$(1)$
–
![]() $(4)$
are satisfied, and if Alice loses (and such a play exists because
$(4)$
are satisfied, and if Alice loses (and such a play exists because
![]() $\S $
cannot be winning), then also
$\S $
cannot be winning), then also
![]() $(5)$
is satisfied.
$(5)$
is satisfied.
6 The weak grouped Menger game and Sacks forcing
Again, by V we mean a ground model of ZFC and
![]() $G_{\omega _2}$
is an
$G_{\omega _2}$
is an
![]() $\mathbb S_{\omega _2}$
-generic filter over V.
$\mathbb S_{\omega _2}$
-generic filter over V.
Theorem 6.1. Assume that V satisfies CH. In
![]() $V[G_{\omega _2}]$
, suppose that
$V[G_{\omega _2}]$
, suppose that
![]() $X\subseteq 2^\omega $
and for any perfect set
$X\subseteq 2^\omega $
and for any perfect set
![]() $K\subseteq 2^\omega $
such that
$K\subseteq 2^\omega $
such that
![]() $K\setminus X$
is dense in K Alice has no winning strategy in the weak grouped Menger game played on
$K\setminus X$
is dense in K Alice has no winning strategy in the weak grouped Menger game played on
![]() $X\cap K$
in K. Then both X and
$X\cap K$
in K. Then both X and
![]() $2^\omega \setminus X$
are unions of
$2^\omega \setminus X$
are unions of
![]() $\omega _1$
compact sets.
$\omega _1$
compact sets.
For the proof of Theorem 6.1, we need the following auxiliary result. Similarly to Lemma 4.2, it can be proved in the same way as [Reference Blass and Shelah5, Lemma 5.10], a rather standard argument is left to the reader.
Lemma 6.2. In
![]() $V[G_{\omega _2}]$
, let
$V[G_{\omega _2}]$
, let
![]() $X\subseteq {2^\omega }$
. Then there exists a limit ordinal
$X\subseteq {2^\omega }$
. Then there exists a limit ordinal
![]() $\alpha <\omega _2$
of cofinality
$\alpha <\omega _2$
of cofinality
![]() $\omega _1$
such that
$\omega _1$
such that
-
(1)
 $X\cap V[G_\alpha ]\in V[G_\alpha ]$
, and if
$X\cap V[G_\alpha ]\in V[G_\alpha ]$
, and if
 $K,K'\subseteq 2^\omega $
are closed crowded sets and coded in
$K,K'\subseteq 2^\omega $
are closed crowded sets and coded in
 $V[G_\alpha ]$
, and
$V[G_\alpha ]$
, and
 $K'\subseteq K\setminus (X\cap V[G_\alpha ])$
, then
$K'\subseteq K\setminus (X\cap V[G_\alpha ])$
, then
 $K'\subseteq K\setminus X$
;
$K'\subseteq K\setminus X$
; -
(2) There is a function in
 $V[G_\alpha ]$
which assigns to every perfect set
$V[G_\alpha ]$
which assigns to every perfect set
 $K\subseteq {2^\omega }$
, coded in
$K\subseteq {2^\omega }$
, coded in
 $V[G_\alpha ]$
, such that
$V[G_\alpha ]$
, such that
 $K\setminus X$
is not dense in K, a nonempty clopen subset O of
$K\setminus X$
is not dense in K, a nonempty clopen subset O of
 $2^\omega $
withFootnote
4
$2^\omega $
withFootnote
4
 $\emptyset \neq K\cap O\subseteq K\cap X$
.
$\emptyset \neq K\cap O\subseteq K\cap X$
.
Moreover, if for each perfect set
![]() $K\subseteq {2^\omega }$
such that
$K\subseteq {2^\omega }$
such that
![]() $K\setminus X$
is dense in K, Alice has no winning strategy in the weak grouped Menger game played on
$K\setminus X$
is dense in K, Alice has no winning strategy in the weak grouped Menger game played on
![]() $X\cap K$
in K, then we can in addition assume that
$X\cap K$
in K, then we can in addition assume that
-
(3) in
 $V[G_\alpha ]$
, for each perfect set
$V[G_\alpha ]$
, for each perfect set
 $K\subseteq {2^\omega }$
such that
$K\subseteq {2^\omega }$
such that
 $K\setminus (X\cap V[G_\alpha ])$
is dense in K, Alice has no winning strategy in the weak grouped Menger game played on
$K\setminus (X\cap V[G_\alpha ])$
is dense in K, Alice has no winning strategy in the weak grouped Menger game played on
 $X\cap K\cap V[G_\alpha ]$
in K.
$X\cap K\cap V[G_\alpha ]$
in K.
Proof of Theorem 6.1.
Let
![]() $\alpha $
be such as in Lemma 6.2. Working in
$\alpha $
be such as in Lemma 6.2. Working in
![]() $V[G_{\omega _2}]$
, we claim that
$V[G_{\omega _2}]$
, we claim that
Since in
![]() $V[G_\alpha ]$
the remainder
$V[G_\alpha ]$
the remainder
![]() $\mathbb S_{\alpha ,\omega _2}$
is order-isomorphic to
$\mathbb S_{\alpha ,\omega _2}$
is order-isomorphic to
![]() $\mathbb S_{\omega _2}$
, there is no loss of generality in assuming that
$\mathbb S_{\omega _2}$
, there is no loss of generality in assuming that
![]() $\alpha =0$
, i.e., that
$\alpha =0$
, i.e., that
![]() $V=V[G_\alpha ]$
.
$V=V[G_\alpha ]$
.
First we prove (6.2.1). Let us pick
![]() $z\in X$
and let
$z\in X$
and let
![]() $\gamma $
be the minimal ordinal with
$\gamma $
be the minimal ordinal with
![]() $z\in V[G_\gamma ]$
. From now on, whenever we do not specify that we work in some other model, we work in V. Let
$z\in V[G_\gamma ]$
. From now on, whenever we do not specify that we work in some other model, we work in V. Let
![]() $r\in G_{\omega _2}$
and
$r\in G_{\omega _2}$
and
![]() $\tau \in V^{\mathbb S_\gamma }$
be such that
$\tau \in V^{\mathbb S_\gamma }$
be such that
![]() $\tau ^{G_\gamma }=z$
and
$\tau ^{G_\gamma }=z$
and
![]() $r\Vdash \tau \in X$
. Let
$r\Vdash \tau \in X$
. Let
![]() $p_0 \geq r \restriction \gamma $
be such that
$p_0 \geq r \restriction \gamma $
be such that
![]() $p_0\in G_{\gamma }$
and
$p_0\in G_{\gamma }$
and
We shall find
![]() $q\geq p_0$
,
$q\geq p_0$
,
![]() $q \in \mathbb {S}_\gamma $
and a compact set
$q \in \mathbb {S}_\gamma $
and a compact set
![]() $L\subseteq X$
coded in V such that
$L\subseteq X$
coded in V such that
![]() $q\Vdash _{\omega _2}\tau \in L$
. This would accomplish the proof: The genericity of
$q\Vdash _{\omega _2}\tau \in L$
. This would accomplish the proof: The genericity of
![]() $G_{\gamma }$
implies that there is a condition q as above which lies in
$G_{\gamma }$
implies that there is a condition q as above which lies in
![]() $G_\gamma \subseteq G_{\omega _2}$
. Then
$G_\gamma \subseteq G_{\omega _2}$
. Then
![]() $z = \tau ^{G_\gamma } = \tau ^{G_{\omega _2}}\in L$
.
$z = \tau ^{G_\gamma } = \tau ^{G_{\omega _2}}\in L$
.
Take p and
![]() $F_n,k_n,l_n, y_{\sigma _n}$
from Lemma 3.7, applied to
$F_n,k_n,l_n, y_{\sigma _n}$
from Lemma 3.7, applied to
![]() $p_0$
and
$p_0$
and
![]() $\tau $
. Let
$\tau $
. Let
![]() $\Sigma _n$
be the set of all maps
$\Sigma _n$
be the set of all maps
![]() $\sigma \colon F_n\to 2^{k_n}$
consistent with p, where
$\sigma \colon F_n\to 2^{k_n}$
consistent with p, where
![]() $n\in \omega $
. By Lemma 3.9(1), for each map
$n\in \omega $
. By Lemma 3.9(1), for each map
![]() $\sigma \in \Sigma _n$
, there are maps
$\sigma \in \Sigma _n$
, there are maps
![]() $\sigma '\neq \sigma "\in \Sigma _{n+1}$
extending
$\sigma '\neq \sigma "\in \Sigma _{n+1}$
extending
![]() $\sigma $
, which implies
$\sigma $
, which implies
![]() $[\sigma ']\cap [\sigma "]=\emptyset $
. For
$[\sigma ']\cap [\sigma "]=\emptyset $
. For
![]() $S:=\operatorname {supp}(p)$
, define a perfect set K, exactly in the same way as before Lemma 2.1, i.e.,
$S:=\operatorname {supp}(p)$
, define a perfect set K, exactly in the same way as before Lemma 2.1, i.e.,
Then the family of all sets
![]() $[\sigma ]$
, where
$[\sigma ]$
, where
![]() $\sigma \in \bigcup _{n\in \omega }\Sigma _n$
, is a basis for K. Note also that Lemma 3.9(3) ensures that S and the sequence
$\sigma \in \bigcup _{n\in \omega }\Sigma _n$
, is a basis for K. Note also that Lemma 3.9(3) ensures that S and the sequence
![]() ${\langle \, k_n,F_n,\Sigma _n : n\in \omega \,\rangle }$
satisfy
${\langle \, k_n,F_n,\Sigma _n : n\in \omega \,\rangle }$
satisfy
![]() $(e_f)$
stated at the beginning of Section 2.
$(e_f)$
stated at the beginning of Section 2.
Let
![]() $h:K\to 2^\omega $
be defined in the same way as in the proof of Theorem 4.1. Thus
$h:K\to 2^\omega $
be defined in the same way as in the proof of Theorem 4.1. Thus
![]() $h\colon K\to h[K]$
is a homeomorphism, and hence
$h\colon K\to h[K]$
is a homeomorphism, and hence
![]() $h[K]$
is perfect. Fix a natural number n. By Lemma 3.7(2) and Observation 3.2(3), the set
$h[K]$
is perfect. Fix a natural number n. By Lemma 3.7(2) and Observation 3.2(3), the set
![]() $\{\,p|\sigma _n : \sigma _n\in \Sigma _n\,\}$
is a maximal antichain above p. Applying Lemma 3.7(4), we have that
$\{\,p|\sigma _n : \sigma _n\in \Sigma _n\,\}$
is a maximal antichain above p. Applying Lemma 3.7(4), we have that
It follows from the above and from the definition of the function h that
![]() $p\Vdash \tau \in h[K].$
$p\Vdash \tau \in h[K].$
Assume that in
![]() $V[G_{\omega _2}]$
, the set
$V[G_{\omega _2}]$
, the set
![]() $h[K]\setminus X$
is dense in
$h[K]\setminus X$
is dense in
![]() $h[K]$
. We shall show that this is impossible. By the assumption, Alice has no winning strategy in
$h[K]$
. We shall show that this is impossible. By the assumption, Alice has no winning strategy in
![]() $\operatorname {wgM}(h[K], X\cap h[K])$
. We proceed in V. By Lemma 6.2(3) we have that Alice has no winning strategy in
$\operatorname {wgM}(h[K], X\cap h[K])$
. We proceed in V. By Lemma 6.2(3) we have that Alice has no winning strategy in
![]() $\operatorname {wgM}(h[K],h[K]\cap X\cap V)$
. Since h is a homeomorphism and
$\operatorname {wgM}(h[K],h[K]\cap X\cap V)$
. Since h is a homeomorphism and
![]() $h^{-1}[X\cap V]=h^{-1}[X]\cap V=h^{-1}[X]\cap V\cap K$
(because h is defined in V and its domain is K), Alice has no winning strategy in
$h^{-1}[X\cap V]=h^{-1}[X]\cap V=h^{-1}[X]\cap V\cap K$
(because h is defined in V and its domain is K), Alice has no winning strategy in
![]() $\operatorname {wgM}(K,h^{-1}[X]\cap V)$
. Applying Lemma 5.10 to
$\operatorname {wgM}(K,h^{-1}[X]\cap V)$
. Applying Lemma 5.10 to
![]() $S=\mathrm {supp}(p)$
and
$S=\mathrm {supp}(p)$
and
![]() $h^{-1}[X]\cap V\subseteq K$
, we can get a sequence
$h^{-1}[X]\cap V\subseteq K$
, we can get a sequence
![]() ${\langle \, \langle i_n,j_n,C_n\rangle : n\in \omega \,\rangle }$
satisfying the conclusion of Lemma 5.10. Lemma 5.10(5) yields
${\langle \, \langle i_n,j_n,C_n\rangle : n\in \omega \,\rangle }$
satisfying the conclusion of Lemma 5.10. Lemma 5.10(5) yields
and therefore
![]() $h[K']\subseteq h[K]\setminus (X\cap V)$
, both of these inclusions holding in V. Applying Lemma 6.2(1) we conclude that
$h[K']\subseteq h[K]\setminus (X\cap V)$
, both of these inclusions holding in V. Applying Lemma 6.2(1) we conclude that
![]() $h[K']\subseteq h[K]\setminus X$
holds in
$h[K']\subseteq h[K]\setminus X$
holds in
![]() $V[G_{\omega _2}]$
.
$V[G_{\omega _2}]$
.
Let
![]() $q\geq p$
be a condition given by Lemma 3.10. Note that
$q\geq p$
be a condition given by Lemma 3.10. Note that
![]() $q\Vdash \tau \restriction l_{i_n} \in \{\,y_{\nu } : \nu \in C_n\,\}$
because
$q\Vdash \tau \restriction l_{i_n} \in \{\,y_{\nu } : \nu \in C_n\,\}$
because
![]() $\{p|\nu :\nu \in C_n\}$
is predense above q, for all
$\{p|\nu :\nu \in C_n\}$
is predense above q, for all
![]() $n\in \omega $
, which implies
$n\in \omega $
, which implies
![]() $q\Vdash \tau \in h[K']$
. It follows from the above that
$q\Vdash \tau \in h[K']$
. It follows from the above that
![]() $q\Vdash \tau \not \in X$
, which is impossible since
$q\Vdash \tau \not \in X$
, which is impossible since
![]() $q^\frown r \restriction [\gamma ,\omega _2) \Vdash \tau \in X$
.
$q^\frown r \restriction [\gamma ,\omega _2) \Vdash \tau \in X$
.
Now assume that in
![]() $V[G_{\omega _2}]$
, we have
$V[G_{\omega _2}]$
, we have
![]() $\operatorname {\mathrm {Int}}_{h[K]}(h[K]\cap X)\neq \emptyset $
. Since
$\operatorname {\mathrm {Int}}_{h[K]}(h[K]\cap X)\neq \emptyset $
. Since
![]() $h[K]$
is coded in V, there is a clopen set O (namely the one assigned to
$h[K]$
is coded in V, there is a clopen set O (namely the one assigned to
![]() $h[K]$
by the function given by Lemma 6.2(2)) such that
$h[K]$
by the function given by Lemma 6.2(2)) such that
![]() $\emptyset \neq h[K]\cap O\subseteq X$
. It follows from the definition of h that there exist
$\emptyset \neq h[K]\cap O\subseteq X$
. It follows from the definition of h that there exist
![]() $n\in \omega $
and
$n\in \omega $
and
![]() $\sigma \in \Sigma _n$
with
$\sigma \in \Sigma _n$
with
![]() $h[[\sigma ]\cap K]\subseteq O$
, and hence
$h[[\sigma ]\cap K]\subseteq O$
, and hence
![]() $h[[\sigma ]\cap K]\subseteq X$
. Let
$h[[\sigma ]\cap K]\subseteq X$
. Let
![]() $q:=p|\sigma $
. Since
$q:=p|\sigma $
. Since
![]() $q\Vdash \tau \in h[[\sigma ]\cap K]$
, the set
$q\Vdash \tau \in h[[\sigma ]\cap K]$
, the set
![]() $L:=h[[\sigma ]\cap K]$
is a perfect set coded in V which is a subset of X and
$L:=h[[\sigma ]\cap K]$
is a perfect set coded in V which is a subset of X and
![]() $q\Vdash \tau \in L$
. This completes the proof of Equation 6.2.1.
$q\Vdash \tau \in L$
. This completes the proof of Equation 6.2.1.
Next, we prove (6.2.2). The argument is very similar to that of (6.2.1), but we anyway give it for the sake of completeness. As above, let
![]() $r\in G_{\omega _2}$
,
$r\in G_{\omega _2}$
,
![]() $p_0 \geq r \restriction \gamma $
,
$p_0 \geq r \restriction \gamma $
,
![]() $p_0\in G_{\gamma }$
and
$p_0\in G_{\gamma }$
and
![]() $\tau \in V^{\mathbb S_\gamma }$
be such that
$\tau \in V^{\mathbb S_\gamma }$
be such that
![]() $r\Vdash \tau \in 2^\omega \setminus X$
and
$r\Vdash \tau \in 2^\omega \setminus X$
and
We shall find
![]() $q\geq p_0$
,
$q\geq p_0$
,
![]() $q \in \mathbb {S}_\gamma $
and a compact set
$q \in \mathbb {S}_\gamma $
and a compact set
![]() $L\subseteq 2^\omega \setminus X$
coded in V such that
$L\subseteq 2^\omega \setminus X$
coded in V such that
![]() $q\Vdash _{\omega _2} \tau \in L$
. As in the case of (6.2.1), this would accomplish the proof.
$q\Vdash _{\omega _2} \tau \in L$
. As in the case of (6.2.1), this would accomplish the proof.
Again, take p and
![]() $F_n,k_n,l_n, y_{\sigma _n}$
from Lemma 3.7, applied to
$F_n,k_n,l_n, y_{\sigma _n}$
from Lemma 3.7, applied to
![]() $p_0$
and
$p_0$
and
![]() $\tau $
. Let
$\tau $
. Let
![]() $\Sigma _n$
,
$\Sigma _n$
,
![]() $[\sigma ]$
for
$[\sigma ]$
for
![]() $\sigma \in \Sigma _n$
, K, and
$\sigma \in \Sigma _n$
, K, and
![]() $h:K\to 2^\omega $
be defined in the same way as in the proof of (6.2.1). We have
$h:K\to 2^\omega $
be defined in the same way as in the proof of (6.2.1). We have
![]() $p\Vdash \tau \in h[K].$
$p\Vdash \tau \in h[K].$
Assume that in
![]() $V[G_{\omega _2}]$
, we have
$V[G_{\omega _2}]$
, we have
![]() $\operatorname {\mathrm {Int}}_{h[K]}(h[K]\cap X)\neq \emptyset $
. We shall show that this case is impossible. Since
$\operatorname {\mathrm {Int}}_{h[K]}(h[K]\cap X)\neq \emptyset $
. We shall show that this case is impossible. Since
![]() $h[K]$
is coded in V, there is a clopen set O such that
$h[K]$
is coded in V, there is a clopen set O such that
![]() $\emptyset \neq h[K]\cap O\subseteq X$
. It follows from the above that there exist
$\emptyset \neq h[K]\cap O\subseteq X$
. It follows from the above that there exist
![]() $n\in \omega $
and
$n\in \omega $
and
![]() $\sigma \in \Sigma _n$
with
$\sigma \in \Sigma _n$
with
![]() $h[[\sigma ]\cap K]\subseteq O$
, and hence
$h[[\sigma ]\cap K]\subseteq O$
, and hence
![]() $h[[\sigma ]\cap K]\subseteq X$
. Let
$h[[\sigma ]\cap K]\subseteq X$
. Let
![]() $q:=p|\sigma $
. Since
$q:=p|\sigma $
. Since
![]() $q\Vdash \tau \in h[[\sigma ]\cap K]$
, the set
$q\Vdash \tau \in h[[\sigma ]\cap K]$
, the set
![]() $L:=h[[\sigma ]\cap K]$
is a perfect set coded in V which is a subset of X and
$L:=h[[\sigma ]\cap K]$
is a perfect set coded in V which is a subset of X and
![]() $q\Vdash \tau \in L$
. Consequently,
$q\Vdash \tau \in L$
. Consequently,
![]() $q\Vdash \tau \in X$
, a contradiction to
$q\Vdash \tau \in X$
, a contradiction to
![]() $r\Vdash \tau \in 2^\omega \setminus X$
.
$r\Vdash \tau \in 2^\omega \setminus X$
.
Now assume that in
![]() $V[G_{\omega _2}]$
, the set
$V[G_{\omega _2}]$
, the set
![]() $h[K]\setminus X$
is dense in
$h[K]\setminus X$
is dense in
![]() $h[K]$
. In V, we have that
$h[K]$
. In V, we have that
![]() $h[K]\setminus (X\cap V)$
is dense in
$h[K]\setminus (X\cap V)$
is dense in
![]() $h[K]$
: If there were a clopen
$h[K]$
: If there were a clopen
![]() $K'\subseteq 2^\omega $
with
$K'\subseteq 2^\omega $
with
then we would get
![]() $K'\cap h[K]\subseteq h[K]\setminus X$
holding in
$K'\cap h[K]\subseteq h[K]\setminus X$
holding in
![]() $V[G_{\omega _2}]$
by Lemma 6.2(1).
$V[G_{\omega _2}]$
by Lemma 6.2(1).
By the assumption, Alice has no winning strategy in the game
![]() $\operatorname {wgM}(h[K],X\cap h[K])$
. By Lemma 6.2(3), in
$\operatorname {wgM}(h[K],X\cap h[K])$
. By Lemma 6.2(3), in
![]() $V,$
Alice has no winning strategy in
$V,$
Alice has no winning strategy in
![]() $\operatorname {wgM}(h[K],X\cap h[K]\cap V)$
. Since h is a homeomorphism, Alice has no winning strategy in
$\operatorname {wgM}(h[K],X\cap h[K]\cap V)$
. Since h is a homeomorphism, Alice has no winning strategy in
![]() $\operatorname {wgM}(K,h^{-1}[X]\cap K\cap V)$
. Now let
$\operatorname {wgM}(K,h^{-1}[X]\cap K\cap V)$
. Now let
![]() ${\langle \, \langle i_n,j_n,C_n\rangle : n\in \omega \,\rangle }$
,
${\langle \, \langle i_n,j_n,C_n\rangle : n\in \omega \,\rangle }$
,
![]() $K'$
and q be the same as in the proof of (6.2.1). Again, since
$K'$
and q be the same as in the proof of (6.2.1). Again, since
![]() $K'\subseteq K\setminus (h^{-1}[X]\cap V)$
holds in V, we have
$K'\subseteq K\setminus (h^{-1}[X]\cap V)$
holds in V, we have
![]() $K'\subseteq K\setminus h^{-1}[X]$
in
$K'\subseteq K\setminus h^{-1}[X]$
in
![]() $V[G_{\omega _2}]$
by Lemma 6.2(1), or equivalently
$V[G_{\omega _2}]$
by Lemma 6.2(1), or equivalently
![]() $h[K']\subseteq h[K]\setminus X$
. Repeating our previous arguments we get
$h[K']\subseteq h[K]\setminus X$
. Repeating our previous arguments we get
It follows from the above that the set
![]() $L:=h[K']$
is a perfect subset of
$L:=h[K']$
is a perfect subset of
![]() $2^\omega \setminus X$
and
$2^\omega \setminus X$
and
![]() $q\Vdash \tau \in L$
, which completes the proof of (6.2.2).
$q\Vdash \tau \in L$
, which completes the proof of (6.2.2).
Combining Theorem 6.1 with Proposition 5.3, Remark 5.8, and Proposition 5.9, we get the following result.
Corollary 6.3. Assume that V satisfies GCH. In
![]() $V[G_{\omega _2}]$
, the following assertions hold.
$V[G_{\omega _2}]$
, the following assertions hold.
-
(1) Each consonant (Hurewicz) subset of
 ${2^\omega }$
as well as its complement are unions of
${2^\omega }$
as well as its complement are unions of
 $\mathfrak {d}=\omega _1$
many compact subspaces. In particular, there are
$\mathfrak {d}=\omega _1$
many compact subspaces. In particular, there are
 $\mathfrak c=\omega _2$
consonant (Hurewicz) subspaces of
$\mathfrak c=\omega _2$
consonant (Hurewicz) subspaces of
 $2^\omega $
.
$2^\omega $
. -
(2) Each perfectly meager subset of
 ${2^\omega }$
has cardinality at most
${2^\omega }$
has cardinality at most
 $\mathfrak {d}=\omega _1$
, and its complement is a union of
$\mathfrak {d}=\omega _1$
, and its complement is a union of
 $\omega _1$
compact sets.
$\omega _1$
compact sets.
The first half of Corollary 6.3(2), namely that all perfectly meager subsets of
![]() ${2^\omega }$
have cardinality at most
${2^\omega }$
have cardinality at most
![]() $\omega _1$
in the Sacks model, was established by Miller [Reference Miller15, Section 5].
$\omega _1$
in the Sacks model, was established by Miller [Reference Miller15, Section 5].
Remark 6.4. In
![]() $V[G_{\omega _2}]$
, considered in the above corollary, there is a Luzin subset of
$V[G_{\omega _2}]$
, considered in the above corollary, there is a Luzin subset of
![]() ${2^\omega }$
, i.e., an uncountable set whose intersection with any meager set is at most countable, which is totally imperfect and Menger [Reference Hurewicz12], but it is not (perfectly) meager. There is also a perfectly meager set that is not Menger: Since
${2^\omega }$
, i.e., an uncountable set whose intersection with any meager set is at most countable, which is totally imperfect and Menger [Reference Hurewicz12], but it is not (perfectly) meager. There is also a perfectly meager set that is not Menger: Since
![]() $\mathfrak {d}=\omega _1$
in
$\mathfrak {d}=\omega _1$
in
![]() $V[G_{\omega _2}]$
, there is a dominating set
$V[G_{\omega _2}]$
, there is a dominating set
![]() $X=\{\,x_\alpha : \alpha <\omega _1\,\}$
in
$X=\{\,x_\alpha : \alpha <\omega _1\,\}$
in
![]() ${[\omega ]^{\omega }}$
, where
${[\omega ]^{\omega }}$
, where
![]() $x_\beta \le ^* x_\alpha $
for all ordinal numbers
$x_\beta \le ^* x_\alpha $
for all ordinal numbers
![]() $\beta <\alpha <\omega _1$
. This set is not Menger. The set
$\beta <\alpha <\omega _1$
. This set is not Menger. The set
![]() $X\cup \mathrm {Fin}$
satisfies the Hurewicz covering property [Reference Bartoszyński and Tsaban1, Theorem 10], and any totally imperfect set with this property is perfectly meager [Reference Just, Miller, Scheepers and Szeptycki14, Theorem 5.5]. Thus, the set X is perfectly meager, too. Alternatively, we could use here the main result of [Reference Plewik17], which implies directly that X is perfectly meager since
$X\cup \mathrm {Fin}$
satisfies the Hurewicz covering property [Reference Bartoszyński and Tsaban1, Theorem 10], and any totally imperfect set with this property is perfectly meager [Reference Just, Miller, Scheepers and Szeptycki14, Theorem 5.5]. Thus, the set X is perfectly meager, too. Alternatively, we could use here the main result of [Reference Plewik17], which implies directly that X is perfectly meager since
![]() $\leq ^*$
is a Borel subset of
$\leq ^*$
is a Borel subset of
![]() $\omega ^\omega \times \omega ^\omega $
.
$\omega ^\omega \times \omega ^\omega $
.
Theorems 4.1 and 6.1 motivate the following problem.
Problem 6.5. In the Sacks model:
-
(1) Is every Menger space
 $X\subseteq 2^\omega $
a union of
$X\subseteq 2^\omega $
a union of
 $\omega _1$
-many of its compact subspaces?
$\omega _1$
-many of its compact subspaces? -
(2) Is the complement
 $2^\omega \setminus X$
of a Menger set
$2^\omega \setminus X$
of a Menger set
 $X\subseteq 2^\omega $
a union of
$X\subseteq 2^\omega $
a union of
 $\omega _1$
-many of its compact subspaces?
$\omega _1$
-many of its compact subspaces? -
(3) Are there only
 $\omega _2$
-many Menger subsets of
$\omega _2$
-many Menger subsets of
 $2^\omega $
?
$2^\omega $
? -
(4) Is the complement
 $2^\omega \setminus X$
of a totally imperfect Menger set
$2^\omega \setminus X$
of a totally imperfect Menger set
 $X\subseteq 2^\omega $
a union of
$X\subseteq 2^\omega $
a union of
 $\omega _1$
-many of its compact subspaces?
$\omega _1$
-many of its compact subspaces?
Regarding the last item of Problem 5.6, we do not know the answer even to the following question.
Problem 6.6. In the Sacks model, is the complement
![]() $2^\omega \setminus X$
of any set
$2^\omega \setminus X$
of any set
![]() $X\subseteq {2^\omega }$
with
$X\subseteq {2^\omega }$
with
![]() $\left |X\right |=\omega _1$
a union of
$\left |X\right |=\omega _1$
a union of
![]() $\omega _1$
-many of its compact subspaces? In particular, is
$\omega _1$
-many of its compact subspaces? In particular, is
![]() $2^\omega \setminus (2^\omega \cap V)$
a union of
$2^\omega \setminus (2^\omega \cap V)$
a union of
![]() $\omega _1$
-many of its compact subspaces?
$\omega _1$
-many of its compact subspaces?
7 Menger sets and Hechler forcing
The results from the previous section lead to the question, whether
![]() $\mathfrak {d}<\mathfrak {c}$
implies that any totally imperfect Menger subset of
$\mathfrak {d}<\mathfrak {c}$
implies that any totally imperfect Menger subset of
![]() ${2^\omega }$
has cardinality at most
${2^\omega }$
has cardinality at most
![]() $\mathfrak {d}$
. We address this problem, showing that this is not the case. We also provide a consistent result that the size of the family of all Hurewicz subsets of
$\mathfrak {d}$
. We address this problem, showing that this is not the case. We also provide a consistent result that the size of the family of all Hurewicz subsets of
![]() ${2^\omega }$
can be equal
${2^\omega }$
can be equal
![]() $2^{\mathfrak {c}}$
even if
$2^{\mathfrak {c}}$
even if
![]() $\mathfrak {d}<\mathfrak {c}$
. Let
$\mathfrak {d}<\mathfrak {c}$
. Let
![]() $\mathbb {P}$
be a definable ccc forcing notion of size
$\mathbb {P}$
be a definable ccc forcing notion of size
![]() $\mathfrak c$
which adds dominating reals over a ground model (e.g., the poset defined in [Reference Baumgartner and Dordal2, p. 95], nowadays commonly named Hechler forcing) and
$\mathfrak c$
which adds dominating reals over a ground model (e.g., the poset defined in [Reference Baumgartner and Dordal2, p. 95], nowadays commonly named Hechler forcing) and
![]() $\mathbb {P}_{\omega _1}$
be an iterated forcing of length
$\mathbb {P}_{\omega _1}$
be an iterated forcing of length
![]() $\omega _1$
with finite support, where each iterand is equal to
$\omega _1$
with finite support, where each iterand is equal to
![]() $\mathbb {P}$
. In this section, by
$\mathbb {P}$
. In this section, by
![]() $G_{\omega _1}$
we mean a
$G_{\omega _1}$
we mean a
![]() $\mathbb {P}_{\omega _1}$
-generic filter over a ground model V of ZFC.
$\mathbb {P}_{\omega _1}$
-generic filter over a ground model V of ZFC.
Proposition 7.1. In
![]() $V[G_{\omega _1}]$
, each subset of
$V[G_{\omega _1}]$
, each subset of
![]() ${2^\omega }\cap V$
is Hurewicz.
${2^\omega }\cap V$
is Hurewicz.
Proof. Let
![]() $X\subseteq {2^\omega }\cap V$
and
$X\subseteq {2^\omega }\cap V$
and
![]() $\phi \colon X\to {[\omega ]^{\omega }}$
be a continuous function. The function
$\phi \colon X\to {[\omega ]^{\omega }}$
be a continuous function. The function
![]() $\phi $
can be extended to a continuous function
$\phi $
can be extended to a continuous function
![]() $\Phi $
defined on a
$\Phi $
defined on a
![]() $G_\delta $
-set A, containing X. Then there is an ordinal number
$G_\delta $
-set A, containing X. Then there is an ordinal number
![]() $\alpha <\omega _1$
such that the function
$\alpha <\omega _1$
such that the function
![]() $\Phi $
and the set A are coded in
$\Phi $
and the set A are coded in
![]() $V[G_\alpha ]$
. It follows that
$V[G_\alpha ]$
. It follows that
![]() $\Phi [X]\subseteq V[G_\alpha ]$
. Since there exists a function
$\Phi [X]\subseteq V[G_\alpha ]$
. Since there exists a function
![]() $g_\alpha $
, added in step
$g_\alpha $
, added in step
![]() $\alpha $
, which dominates any real from
$\alpha $
, which dominates any real from
![]() $V[G_\alpha ]$
, the set
$V[G_\alpha ]$
, the set
![]() $\Phi [X]$
is bounded in
$\Phi [X]$
is bounded in
![]() $V[G_{\omega _1}]$
. By the Hurewicz–Recław characterization of the Hurewicz property [Reference Recław18, Proposition 1], the set X is HurewiczFootnote
5
in
$V[G_{\omega _1}]$
. By the Hurewicz–Recław characterization of the Hurewicz property [Reference Recław18, Proposition 1], the set X is HurewiczFootnote
5
in
![]() $V[G_{\omega _1}]$
.
$V[G_{\omega _1}]$
.
Theorem 7.2. Assume that V satisfies
![]() $\neg $
CH. In
$\neg $
CH. In
![]() $V[G_{\omega _1}]$
, we have
$V[G_{\omega _1}]$
, we have
![]() $\mathfrak {d}<\mathfrak {c}$
and the following assertions hold.
$\mathfrak {d}<\mathfrak {c}$
and the following assertions hold.
-
(1) There is a totally imperfect Hurewicz and Rothberger (and thus Menger) subset of
 ${2^\omega }$
with cardinality
${2^\omega }$
with cardinality
 $\mathfrak {c}$
.
$\mathfrak {c}$
. -
(2) There are
 $2^{\mathfrak {c}}$
-many Hurewicz and Rothberger (and thus consonant) subsets of
$2^{\mathfrak {c}}$
-many Hurewicz and Rothberger (and thus consonant) subsets of
 ${2^\omega }$
.
${2^\omega }$
.
Proof. Since
![]() $\mathbb {P}_{\omega _1}$
adds
$\mathbb {P}_{\omega _1}$
adds
![]() $\omega _1$
dominating reals to the ground model, we have
$\omega _1$
dominating reals to the ground model, we have
![]() $\mathfrak {d}=\omega _1<\mathfrak {c}$
in
$\mathfrak {d}=\omega _1<\mathfrak {c}$
in
![]() $V[G_{\omega _1}]$
. Since the forcing
$V[G_{\omega _1}]$
. Since the forcing
![]() $\mathbb {P}$
is ccc, the forcing
$\mathbb {P}$
is ccc, the forcing
![]() $\mathbb {P}_{\omega _1}$
is ccc, too. Since
$\mathbb {P}_{\omega _1}$
is ccc, too. Since
![]() $\mathbb {P}_{\omega _1}$
adds reals to the ground model, any subset of
$\mathbb {P}_{\omega _1}$
adds reals to the ground model, any subset of
![]() ${2^\omega }\cap V$
is totally imperfect in
${2^\omega }\cap V$
is totally imperfect in
![]() $V[G_{\omega _1}]$
. By Proposition 7.1, any subset of
$V[G_{\omega _1}]$
. By Proposition 7.1, any subset of
![]() ${2^\omega }\cap V$
is Hurewicz in
${2^\omega }\cap V$
is Hurewicz in
![]() $V[G_{\omega _1}]$
.
$V[G_{\omega _1}]$
.
Since Cohen reals are added by any tail of the considered iteration, any subset of
![]() $2^\omega \cap V$
is also Rothberger in
$2^\omega \cap V$
is also Rothberger in
![]() $V[G_{\omega _1}]$
, by virtue of an argument similar to that in the proof of Proposition 7.1, more details could be found in the proof of [Reference Scheepers and Tall22, Theorem 11].
$V[G_{\omega _1}]$
, by virtue of an argument similar to that in the proof of Proposition 7.1, more details could be found in the proof of [Reference Scheepers and Tall22, Theorem 11].
8 Comments and open problems
Let
![]() ${\operatorname {P}(\omega )}$
be the power set of
${\operatorname {P}(\omega )}$
be the power set of
![]() $\omega $
, the set of natural numbers. We identify each element of
$\omega $
, the set of natural numbers. We identify each element of
![]() ${\operatorname {P}(\omega )}$
with its characteristic function, an element of
${\operatorname {P}(\omega )}$
with its characteristic function, an element of
![]() ${2^\omega }$
. In that way we introduce a topology on
${2^\omega }$
. In that way we introduce a topology on
![]() ${\operatorname {P}(\omega )}$
. Let
${\operatorname {P}(\omega )}$
. Let
![]() ${[\omega ]^{\omega }}$
be the family of all infinite sets in
${[\omega ]^{\omega }}$
be the family of all infinite sets in
![]() ${\operatorname {P}(\omega )}$
. Each set in
${\operatorname {P}(\omega )}$
. Each set in
![]() ${[\omega ]^{\omega }}$
we identify with an increasing enumeration of its elements, a function in the Baire space
${[\omega ]^{\omega }}$
we identify with an increasing enumeration of its elements, a function in the Baire space
![]() ${\omega ^{\omega }}$
. We have
${\omega ^{\omega }}$
. We have
![]() ${[\omega ]^{\omega }}\subseteq {\omega ^{\omega }}$
and topologies in
${[\omega ]^{\omega }}\subseteq {\omega ^{\omega }}$
and topologies in
![]() ${[\omega ]^{\omega }}$
induced from
${[\omega ]^{\omega }}$
induced from
![]() ${\operatorname {P}(\omega )}$
and
${\operatorname {P}(\omega )}$
and
![]() ${\omega ^{\omega }}$
are the same. Let
${\omega ^{\omega }}$
are the same. Let
![]() $\mathrm {Fin}$
be the family of all finite sets in
$\mathrm {Fin}$
be the family of all finite sets in
![]() ${\operatorname {P}(\omega )}$
. A totally imperfect Menger set constructed by Bartoszyński and Tsaban, mentioned in Theorem 1.1 is a set the form
${\operatorname {P}(\omega )}$
. A totally imperfect Menger set constructed by Bartoszyński and Tsaban, mentioned in Theorem 1.1 is a set the form
![]() $X\cup \mathrm {Fin}\subseteq {\operatorname {P}(\omega )}$
of size
$X\cup \mathrm {Fin}\subseteq {\operatorname {P}(\omega )}$
of size
![]() $\mathfrak {d}$
, such that for any function
$\mathfrak {d}$
, such that for any function
![]() $d\in {[\omega ]^{\omega }}$
, we have
$d\in {[\omega ]^{\omega }}$
, we have
![]() $\left |\{\,x\in X : x\le ^* d \,\}\right |<\mathfrak {d}$
. In fact, any set with these properties is totally imperfect and Menger [Reference Bartoszyński and Tsaban1, Remark 18]. It has also a stronger covering property
$\left |\{\,x\in X : x\le ^* d \,\}\right |<\mathfrak {d}$
. In fact, any set with these properties is totally imperfect and Menger [Reference Bartoszyński and Tsaban1, Remark 18]. It has also a stronger covering property
![]() ${\mathsf {S}_1(\Gamma ,\mathrm {O})}$
, described in details in Section 8.2.
${\mathsf {S}_1(\Gamma ,\mathrm {O})}$
, described in details in Section 8.2.
Proposition 8.1. There are at least
![]() $2^{\mathfrak {d}}$
-many totally imperfect Menger subsets of
$2^{\mathfrak {d}}$
-many totally imperfect Menger subsets of
![]() ${2^\omega }$
.
${2^\omega }$
.
Proof. Let
![]() $X\subseteq {[\omega ]^{\omega }}$
be a set of size
$X\subseteq {[\omega ]^{\omega }}$
be a set of size
![]() $\mathfrak {d}$
such that all coordinates of elements in X are even numbers and for any function
$\mathfrak {d}$
such that all coordinates of elements in X are even numbers and for any function
![]() $d\in {[\omega ]^{\omega }}$
, we have
$d\in {[\omega ]^{\omega }}$
, we have
![]() $\left |\{\,x\in X : x\le ^* d \,\}\right |<\mathfrak {d}$
. Let
$\left |\{\,x\in X : x\le ^* d \,\}\right |<\mathfrak {d}$
. Let
![]() $\{\,x_\alpha : \alpha <\mathfrak {d}\,\}$
be a bijective enumeration of elements in X. Fix a function
$\{\,x_\alpha : \alpha <\mathfrak {d}\,\}$
be a bijective enumeration of elements in X. Fix a function
![]() $y\colon \mathfrak {d}\to {2^\omega }$
. For each ordinal number
$y\colon \mathfrak {d}\to {2^\omega }$
. For each ordinal number
![]() $\alpha <\mathfrak {d}$
, let
$\alpha <\mathfrak {d}$
, let
![]() $x_\alpha +y_\alpha $
be the function such that
$x_\alpha +y_\alpha $
be the function such that
![]() $(x_\alpha +y_\alpha )(n):=x_\alpha (n)+y_\alpha (n)$
for all n. Then
$(x_\alpha +y_\alpha )(n):=x_\alpha (n)+y_\alpha (n)$
for all n. Then
![]() $x_\alpha +y_\alpha \in {[\omega ]^{\omega }}$
and
$x_\alpha +y_\alpha \in {[\omega ]^{\omega }}$
and
![]() $x_\alpha \le ^* x_\alpha +y_\alpha $
for all ordinal numbers
$x_\alpha \le ^* x_\alpha +y_\alpha $
for all ordinal numbers
![]() $\alpha <\mathfrak {d}$
. Thus, for any function
$\alpha <\mathfrak {d}$
. Thus, for any function
![]() $d\in {[\omega ]^{\omega }}$
, we have
$d\in {[\omega ]^{\omega }}$
, we have
![]() $\{\,\alpha : x_\alpha +y_\alpha \le ^* d\,\}\subseteq \{\,\alpha : x_\alpha \le ^* d\,\}$
, and the latter set has size smaller than
$\{\,\alpha : x_\alpha +y_\alpha \le ^* d\,\}\subseteq \{\,\alpha : x_\alpha \le ^* d\,\}$
, and the latter set has size smaller than
![]() $\mathfrak {d}$
. Then the set
$\mathfrak {d}$
. Then the set
![]() $\{\,x_\alpha +y_\alpha : \alpha <\mathfrak {d}\,\}\cup \mathrm {Fin}$
is totally imperfect and Menger. It follows that for different functions
$\{\,x_\alpha +y_\alpha : \alpha <\mathfrak {d}\,\}\cup \mathrm {Fin}$
is totally imperfect and Menger. It follows that for different functions
![]() $y\colon \mathfrak {d}\to {2^\omega }$
, we get different totally imperfect Menger sets.
$y\colon \mathfrak {d}\to {2^\omega }$
, we get different totally imperfect Menger sets.
8.1 Menger versus property
 ${\mathsf {S}_1(\Gamma ,\mathrm {O})}$
${\mathsf {S}_1(\Gamma ,\mathrm {O})}$
A cover of a space is a
![]() $\gamma $
-cover if it is infinite and any point of the space belongs to all but finitely many sets in the cover. A space satisfies property
$\gamma $
-cover if it is infinite and any point of the space belongs to all but finitely many sets in the cover. A space satisfies property
![]() ${\mathsf {S}_1(\Gamma ,\mathrm {O})}$
if for any sequence
${\mathsf {S}_1(\Gamma ,\mathrm {O})}$
if for any sequence
![]() $\mathcal {U}_0, \mathcal {U}_1, \dotsc $
of open
$\mathcal {U}_0, \mathcal {U}_1, \dotsc $
of open
![]() $\gamma $
-covers of the space there are sets
$\gamma $
-covers of the space there are sets
![]() $U_0\in \mathcal {U}_0, U_1\in \mathcal {U}_1,\dotsc $
such that the family
$U_0\in \mathcal {U}_0, U_1\in \mathcal {U}_1,\dotsc $
such that the family
![]() $\{\,U_n : n\in \omega \,\}$
covers the space. This property implies the Menger property. By the result of Just, Miller, Scheepers, and Szeptycki [Reference Just, Miller, Scheepers and Szeptycki14, Theorem 2.3] (see also the work of Sakai [Reference Sakai20, Lemma 2.1]), any subset of
$\{\,U_n : n\in \omega \,\}$
covers the space. This property implies the Menger property. By the result of Just, Miller, Scheepers, and Szeptycki [Reference Just, Miller, Scheepers and Szeptycki14, Theorem 2.3] (see also the work of Sakai [Reference Sakai20, Lemma 2.1]), any subset of
![]() ${2^\omega }$
satisfying
${2^\omega }$
satisfying
![]() ${\mathsf {S}_1(\Gamma ,\mathrm {O})}$
is totally imperfect. The following questions are one of the major open problems in the combinatorial covering properties theory.
${\mathsf {S}_1(\Gamma ,\mathrm {O})}$
is totally imperfect. The following questions are one of the major open problems in the combinatorial covering properties theory.
Problem 8.2.
-
(1) Is there a ZFC example of a totally imperfect Menger subset of
 ${2^\omega }$
which does not satisfy
${2^\omega }$
which does not satisfy
 ${\mathsf {S}_1(\Gamma ,\mathrm {O})}$
?
${\mathsf {S}_1(\Gamma ,\mathrm {O})}$
? -
(2) Is there a subset of
 ${2^\omega }$
whose continuous images into
${2^\omega }$
whose continuous images into
 ${2^\omega }$
are totally imperfect and Menger, which does not satisfy
${2^\omega }$
are totally imperfect and Menger, which does not satisfy
 ${\mathsf {S}_1(\Gamma ,\mathrm {O})}$
?
${\mathsf {S}_1(\Gamma ,\mathrm {O})}$
?
In the first item of the problem above we ask about ZFC examples because under CH there exists even a Hurewicz totally imperfect subspace of
![]() $2^\omega $
which can be mapped continuously onto
$2^\omega $
which can be mapped continuously onto
![]() $2^\omega $
, see [Reference Szewczak, Weiss and Zdomskyy25]. The second item of Problem 8.2 is motivated by the fact that the property
$2^\omega $
, see [Reference Szewczak, Weiss and Zdomskyy25]. The second item of Problem 8.2 is motivated by the fact that the property
![]() ${\mathsf {S}_1(\Gamma ,\mathrm {O})}$
is preserved by continuous functions. By the results from Section 2, we can put this problem in a more specific context.
${\mathsf {S}_1(\Gamma ,\mathrm {O})}$
is preserved by continuous functions. By the results from Section 2, we can put this problem in a more specific context.
Problem 8.3. Let
![]() $G_{\omega _2}$
ba an
$G_{\omega _2}$
ba an
![]() $\mathbb {S}_{\omega _2}$
-generic filter over a ground model V. In
$\mathbb {S}_{\omega _2}$
-generic filter over a ground model V. In
![]() $V[G_{\omega _2}]$
, does any Menger set of cardinality
$V[G_{\omega _2}]$
, does any Menger set of cardinality
![]() $\omega _1$
satisfy
$\omega _1$
satisfy
![]() ${\mathsf {S}_1(\Gamma ,\mathrm {O})}$
?
${\mathsf {S}_1(\Gamma ,\mathrm {O})}$
?
8.2 Other problems
The following problem is motivated by Remark 6.4.
Problem 8.4. Is any perfectly meager subset of
![]() ${2^\omega }$
contained in a Menger totally imperfect set?
${2^\omega }$
contained in a Menger totally imperfect set?
We do not know whether the conclusion of Corollary 5.5 holds in ZFC.
Problem 8.5. Is it consistent that
![]() $\mathcal {GM}$
coincides with the family of all Menger subspaces of
$\mathcal {GM}$
coincides with the family of all Menger subspaces of
![]() $2^\omega $
? In other words, is it consistent that for every Menger
$2^\omega $
? In other words, is it consistent that for every Menger
![]() $X\subseteq 2^\omega $
Alice has no winning strategy in the grouped Menger game on X?
$X\subseteq 2^\omega $
Alice has no winning strategy in the grouped Menger game on X?
Funding
The research of the first and the third authors was funded in whole by the Austrian Science Fund (FWF) [10.55776/I5930 and 10.55776/PAT5730424]. The research of the second author was funded by the National Science Center, Poland Weave-UNISONO call in the Weave programme Project: Set-theoretic aspects of topological selections 2021/03/Y/ST1/00122.


