Hostname: page-component-76fb5796d-vfjqv Total loading time: 0 Render date: 2024-04-26T06:30:29.477Z Has data issue: false hasContentIssue false
  • English
  • Français

NEW RELATIONS AND SEPARATIONS OF CONJECTURES ABOUT INCOMPLETENESS IN THE FINITE DOMAIN

Part of: Computability and recursion theory Theory of computing Proof theory and constructive mathematics

Published online by Cambridge University Press:  22 November 2021

ERFAN KHANIKI
ERFAN KHANIKI*
Affiliation:
DEPARTMENT OF MATHEMATICAL SCIENCES SHARIF UNIVERSITY OF TECHNOLOGYTEHRAN, IRANE-mail:e.khaniki@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

In [20] Krajíček and Pudlák discovered connections between problems in computational complexity and the lengths of first-order proofs of finite consistency statements. Later Pudlák [25] studied more statements that connect provability with computational complexity and conjectured that they are true. All these conjectures are at least as strong as 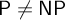$\mathsf {P}\neq \mathsf {NP}$ [23–25].One of the problems concerning these conjectures is to find out how tightly they are connected with statements about computational complexity classes. Results of this kind had been proved in [20, 22].In this paper, we generalize and strengthen these results. Another question that we address concerns the dependence between these conjectures. We construct two oracles that enable us to answer questions about relativized separations asked in [19, 25] (i.e., for the pairs of conjectures mentioned in the questions, we construct oracles such that one conjecture from the pair is true in the relativized world and the other is false and vice versa). We also show several new connections between the studied conjectures. In particular, we show that the relation between the finite reflection principle and proof systems for existentially quantified Boolean formulas is similar to the one for finite consistency statements and proof systems for non-quantified propositional tautologies.

Keywords

finite consistencypropositional proof systemsdisjoint NE-setsTFNP classoraclesrelativized worlds

MSC classification

Primary: 03F20: Complexity of proofs
Secondary: 03D15: Complexity of computation (including implicit computational complexity) 68Q15: Complexity classes (hierarchies, relations among complexity classes, etc.) 03F30: First-order arithmetic and fragments 03F40: Gödel numberings and issues of incompleteness 68Q17: Computational difficulty of problems (lower bounds, completeness, difficulty of approximation, etc.)
Type
Article
Information
The Journal of Symbolic Logic , Volume 87 , Issue 3 , September 2022 , pp. 912 - 937
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ajtai, M., ${\varSigma}_1^1$ -formulae on finite structures. Annals of Pure and Applied Logic, vol. 24 (1983), pp. 1–48.CrossRefGoogle Scholar
Ajtai, M., The complexity of the pigeonhole principle. Combinatorica, vol. 14 (1994), no. 4, 417–433.CrossRefGoogle Scholar
Ben-David, S. and Gringauze, A., On the existence of propositional proof systems and oracle-relativized propositional logic, ECCC technical report no. TR98-021, 1998.Google Scholar
Beyersdorff, O. and Sadowski, Z., Characterizing the existence of optimal proof systems and complete sets for promise classes, Computer Science – Theory and Applications: Fourth International Computer Science Symposium in Russia, CSR 2009, Springer,Berlin, 2009, pp. 47–58.CrossRefGoogle Scholar
Buhrman, H., Fenner, S., Fortnow, L., and van Melkebeek, D., Optimal proof systems and sparse sets, STACS 2000: 17th Annual Symposium on Theoretical Aspects of Computer Science, Springer,Berlin, 2000, pp. 407–418.CrossRefGoogle Scholar
Buhrman, H., Fortnow, L., Koucký, M., Rogers, J. D., and Vereshchagin, N., Does the polynomial hierarchy collapse if onto functions are invertible? Theory of Computing Systems, vol. 46 (2010), no. 1, pp. 143–156.CrossRefGoogle Scholar
Buss, S., Kabanets, V., Kolokolova, A., and Koucký, M., Expander construction in ${VNC}^1$ . Annals of Pure and Applied Logic, vol. 171 (2020), no. 7, p. 39.CrossRefGoogle Scholar
Buss, S. R., Bounded Arithmetic, Bibliopolis,Napoli, 1986.Google Scholar
Buss, S. R., Bounded arithmetic and propositional proof complexity, Logic of Computation, Proceedings of the NATO ASI, Springer,Berlin, 1997, pp. 67–121.CrossRefGoogle Scholar
Chen, Y. and Flum, J., On $p$ -optimal proof systems and logics for PTIME, Automata, Languages and Programming: 37th international colloquium, ICALP 2010, Springer,Berlin, 2010, pp. 321–332.CrossRefGoogle Scholar
Cook, S. A. and Reckhow, R. A., The relative efficiency of propositional proof systems, this Journal, vol. 44 (1979), pp. 36–50.Google Scholar
Dose, T., An oracle separating conjectures about incompleteness in the finite domain. Theoretical Computer Science, vol. 809 (2020), pp. 466–481.CrossRefGoogle Scholar
Fenner, S., Fortnow, L., Kurtz, S. A., and Li, L., An oracle builder’s toolkit. Information and Computation, vol. 182 (2003), no. 2, pp. 95–136.CrossRefGoogle Scholar
Fenner, S. A., Fortnow, L., Naik, A. V., and Rogers, J. D., Inverting onto functions. Information and Computation, vol. 186 (2003), no. 1, pp. 90–103.CrossRefGoogle Scholar
Glasser, C., Selman, A. L., Sengupta, S., and Zhang, L., Disjoint NP-pairs. SIAM Journal on Computing, vol. 33 (2004), no. 6, pp. 1369–1416.CrossRefGoogle Scholar
Hájek, P. and Pudlák, P., Metamathematics of First-Order Arithmetic, Springer-Verlag,Berlin, 1993.CrossRefGoogle Scholar
Khaniki, E., New relations and separations of conjectures about incompleteness in the finite domain, preprint, 2019, arXiv:1904.01362.Google Scholar
Krajíček, J., Forcing with Random Variables and Proof Complexity, London Mathematical Society Lecture Notes Series, vol. 382, Cambridge University Press,Cambridge, 2011.Google Scholar
Krajíček, J., Proof Complexity, Encyclopedia of Mathematics and its Applications, vol. 170, Cambridge University Press,Cambridge, 2019.CrossRefGoogle Scholar
Krajíček, J. and Pudlák, P., Propositional proof systems, the consistency of first order theories and the complexity of computations. this Journal, vol. 54 (1989), no. 3, pp. 1063–1079.Google Scholar
Kurtz, S. A., Sparse sets in NP-P: relativizations. SIAM Journal on Computing, vol. 14 (1985), pp. 113–119.CrossRefGoogle Scholar
Messner, J. and Torán, J., Optimal proof systems for propositional logic and complete sets, STACS 98, Springer,Berlin, 1998, pp. 477–487.CrossRefGoogle Scholar
Pudlák, P.. Logical Foundations of Mathematics and Computational Complexity: A Gentle Introduction, Springer,Cham, 2013.CrossRefGoogle Scholar
Pudlák, P., On the complexity of finding falsifying assignments for Herbrand disjunctions. Archive for Mathematical Logic, vol. 54 (2015), nos. (7–8), pp. 769–783.CrossRefGoogle Scholar
Pudlák, P., Incompleteness in the finite domain. The Bulletin of Symbolic Logic, vol. 23 (2017), no. 4, pp. 405–441.CrossRefGoogle Scholar
Riis, S., Count $(q)$ versus the pigeon-hole principle. Archive for Mathematical Logic, vol. 36 (1997), no. 3, pp. 157–188.CrossRefGoogle Scholar