Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-23T14:47:05.762Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on Mathematics of infinity

Published online by Cambridge University Press:  12 March 2014

Erik Palmgren
Erik Palmgren*
Affiliation:
Department of Mathematics, Uppsala University, S-751 06 Uppsala, Sweden, E-mail: Erik.Palmgren@math.uu.se
Get access Rights & Permissions [Opens in a new window]

Extract

In the paper Mathematics of infinity, Martin-Löf extends his intuitionistic type theory with fixed “choice sequences”. The simplest, and most important instance, is given by adding the axioms

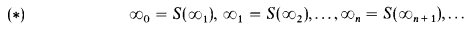
to the type of natural numbers. Martin-Löf's type theory can be regarded as an extension of Heyting arithmetic (HA). In this note we state and prove Martin-Löf's main result for this choice sequence, in the simpler setting of HA and other arithmetical theories based on intuitionistic logic (Theorem A). We also record some remarkable properties of the resulting systems; in general, these lack the disjunction property and may or may not have the explicit definability property. Moreover, they represent all recursive functions by terms.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 58 , Issue 4 , December 1993 , pp. 1195 - 1200
Copyright
Copyright © Association for Symbolic Logic 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Kreisel, G., Mathematical significance of consistency proofs, this Journal, vol. 23 (1958), pp. 155–182.Google Scholar
[2]Laugwitz, D., Ω-calculus as a generalization of field extension—An alternative approach to nonstandard analysis, Nonstandard analysis—Recent developments (Hurd, A. E., editor), Lecture Notes in Mathematics, vol. 983, Springer-Verlag, Berlin and New York, 1983.Google Scholar
[3]Liu, S.-C., A proof-theoretic approach to nonstandard analysis with emphasis on distinguishing between constructive and nonconstructive results, The Kleene symposium (Barwise, J., Keisler, H. J., and Kunen, K., editors), North-Holland, Amsterdam, 1980, pp. 391–414.CrossRefGoogle Scholar
[4]Martin-Löf, P., Mathematics of infinity, COLOG-88 computer logic (Martin-Löf, P. and Mints, G. E., editors), Lecture Notes in Computer Science, vol. 417, Springer-Verlag, Berlin and New York, 1989.Google Scholar
[5]Mycielski, J., Analysis without actual infinity, this Journal, vol. 46 (1981), pp. 625–633.Google Scholar
[6]Troelstra, A. S. (editor), Metamathematical investigation of intuitionistic arithmetic and analysis, Lecture Notes in Mathematics, vol. 344, Springer-Verlag, Berlin and New York, 1973.CrossRefGoogle Scholar