Article contents
On the Σ2-theory of the upper semilattice of Turing degrees
Published online by Cambridge University Press: 12 March 2014
Extract
A first-order sentence Φ is Σ2 if there is a quantifier-free formula Θ such that Φ has the form 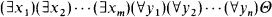 . The Σ2-theory of a structure
. The Σ2-theory of a structure 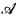 for a language ℒis the set of Σ2-sentences of ℒ true in
for a language ℒis the set of Σ2-sentences of ℒ true in 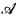 . It was shown independently by Lerman and Shore (see [Le, Theorem VII.4.4]) that the Σ2-theory of the structure
. It was shown independently by Lerman and Shore (see [Le, Theorem VII.4.4]) that the Σ2-theory of the structure 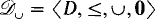 = 〈D, ≤ 〉 is decidable, where D is the set of degrees of unsolvability and ≤ is the standard ordering of D. This result is optimal in the sense that the Σ3-theory of
= 〈D, ≤ 〉 is decidable, where D is the set of degrees of unsolvability and ≤ is the standard ordering of D. This result is optimal in the sense that the Σ3-theory of 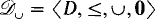 is undecidable, a result due to J. Schmerl. (For a proof, see [Le, Theorem VII.4.5]. As Lerman has pointed out, this proof should be corrected by defining θσ to be ∀xσ1(x) rather than ∀x(ψ(x)→ σ1(x)).) Nonetheless, in this paper we extend the decidability result of Lerman and Shore by showing that the Σ2-theory of
is undecidable, a result due to J. Schmerl. (For a proof, see [Le, Theorem VII.4.5]. As Lerman has pointed out, this proof should be corrected by defining θσ to be ∀xσ1(x) rather than ∀x(ψ(x)→ σ1(x)).) Nonetheless, in this paper we extend the decidability result of Lerman and Shore by showing that the Σ2-theory of 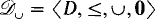 is decidable, where ⋃ is the least upper bound operator and 0 is the least degree. Of course ⋃ is definable in
is decidable, where ⋃ is the least upper bound operator and 0 is the least degree. Of course ⋃ is definable in 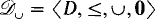 , but many interesting degree-theoretic results are expressible as Σ2-sentences in the language of
, but many interesting degree-theoretic results are expressible as Σ2-sentences in the language of 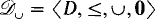 ∪ but not as Σ2-sentences in the language of
∪ but not as Σ2-sentences in the language of 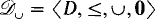 . For instance, Simpson observed that the Posner-Robinson cupping theorem could be used to show that for any nonzero degrees a, b, there is a degree g such that b ≤ a ⋃ g, and b ⋠ g (see [PR, Corollary 6]). However, the Posner-Robinson technique does not seem to suffice to decide the Σ2-theory of
. For instance, Simpson observed that the Posner-Robinson cupping theorem could be used to show that for any nonzero degrees a, b, there is a degree g such that b ≤ a ⋃ g, and b ⋠ g (see [PR, Corollary 6]). However, the Posner-Robinson technique does not seem to suffice to decide the Σ2-theory of 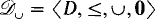 ∪. We introduce instead a new method for coding a set into the join of two other sets and use it to decide this theory.
∪. We introduce instead a new method for coding a set into the join of two other sets and use it to decide this theory.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1993
References
REFERENCES
- 8
- Cited by

