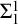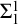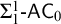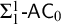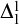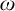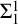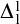1 Introduction
Reverse mathematics, as initiated by Friedman [Reference Friedman5] in the 1970s, is a program in the foundations of mathematics which aims to find the axioms or formal systems needed in order to carry out proofs of particular mathematical theorems. Early results by Friedman, Simpson, and others showed that several basic theorems of analysis, algebra, and combinatorics, when formalized in second-order arithmetic, are equivalent to one of five sets of axioms, now known as the “Big Five.” (The standard reference for subsystems of second-order arithmetic is [Reference Simpson15].) These equivalences were proved over the base theory
![]() $\mathsf {RCA}_0$
, which formalizes computable mathematics and is the weakest of the Big Five. Later work revealed several exceptions to the Big Five phenomenon, including theorems that lie strictly between consecutive levels of the Big Five, and theorems that are incomparable to some level of the Big Five (for instance, Ramsey’s theorem for pairs). In this paper, we study a weak form of the axiom of choice which lies strictly between consecutive levels of the Big Five, namely
$\mathsf {RCA}_0$
, which formalizes computable mathematics and is the weakest of the Big Five. Later work revealed several exceptions to the Big Five phenomenon, including theorems that lie strictly between consecutive levels of the Big Five, and theorems that are incomparable to some level of the Big Five (for instance, Ramsey’s theorem for pairs). In this paper, we study a weak form of the axiom of choice which lies strictly between consecutive levels of the Big Five, namely
![]() $\mathsf {ACA}_0$
and
$\mathsf {ACA}_0$
and
![]() $\mathsf {ATR}_0$
.
$\mathsf {ATR}_0$
.
The study of choice schemes in second-order arithmetic predates reverse mathematics. In 1962, Kreisel [Reference Kreisel8] introduced the
![]() $\Sigma ^1_1$
axiom of choice (
$\Sigma ^1_1$
axiom of choice (
![]() $\Sigma ^1_1$
-
$\Sigma ^1_1$
-
![]() $\mathsf {AC}$
), which asserts that
$\mathsf {AC}$
), which asserts that
for each formula
![]() $\varphi (n,X)$
in the language of second-order arithmetic which is arithmetical (i.e., has no set quantifiers). Equivalently,Footnote
1
it asserts that for any sequence of trees
$\varphi (n,X)$
in the language of second-order arithmetic which is arithmetical (i.e., has no set quantifiers). Equivalently,Footnote
1
it asserts that for any sequence of trees
![]() $(T_n)_n$
, each of which has a branch (i.e., a ray in the sense of graph theory), one can choose a branch from each
$(T_n)_n$
, each of which has a branch (i.e., a ray in the sense of graph theory), one can choose a branch from each
![]() $T_n$
.
$T_n$
.
Kreisel’s interest in
![]() $\Sigma ^1_1$
-
$\Sigma ^1_1$
-
![]() $\mathsf {AC}$
stemmed at least partially from its intimate connection with the hyperarithmetic sets. (For background on hyperarithmetic theory, see [Reference Sacks13].) This connection arises from studying the
$\mathsf {AC}$
stemmed at least partially from its intimate connection with the hyperarithmetic sets. (For background on hyperarithmetic theory, see [Reference Sacks13].) This connection arises from studying the
![]() $\omega $
-models (defined below) of
$\omega $
-models (defined below) of
![]() $\mathsf {RCA}_0 + \Sigma ^1_1$
-
$\mathsf {RCA}_0 + \Sigma ^1_1$
-
![]() $\mathsf {AC}$
, or
$\mathsf {AC}$
, or
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
for short.
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
for short.
A structure in the language of second-order arithmetic has the form
where
![]() $(N,+,\cdot ,<,0,1)$
is a structure in the language of first-order arithmetic (called the first-order part), S is a collection of subsets of N (called the second-order part), and
$(N,+,\cdot ,<,0,1)$
is a structure in the language of first-order arithmetic (called the first-order part), S is a collection of subsets of N (called the second-order part), and
![]() $\in $
is the membership relation between elements of N and elements of S. Such a structure is said to be an
$\in $
is the membership relation between elements of N and elements of S. Such a structure is said to be an
![]() $\omega $
-model if its first-order part is the standard natural numbers
$\omega $
-model if its first-order part is the standard natural numbers
![]() $\mathbb {N}$
and the symbols
$\mathbb {N}$
and the symbols
![]() $+$
,
$+$
,
![]() $\cdot $
, etc. have their standard interpretations. We identify an
$\cdot $
, etc. have their standard interpretations. We identify an
![]() $\omega $
-model with its second-order part.
$\omega $
-model with its second-order part.
Kreisel [Reference Kreisel8] showed that the
![]() $\omega $
-model
$\omega $
-model
![]() $\mathrm {HYP}$
consisting of all hyperarithmetical subsets of
$\mathrm {HYP}$
consisting of all hyperarithmetical subsets of
![]() $\mathbb {N}$
satisfies
$\mathbb {N}$
satisfies
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
, and furthermore,
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
, and furthermore,
![]() $\mathrm {HYP}$
is the minimum
$\mathrm {HYP}$
is the minimum
![]() $\omega $
-model of
$\omega $
-model of
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
. This is analogous to the well-known facts that
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
. This is analogous to the well-known facts that
![]() $\mathsf {ACA}_0$
has a minimum
$\mathsf {ACA}_0$
has a minimum
![]() $\omega $
-model ARITH consisting of all arithmetical subsets of
$\omega $
-model ARITH consisting of all arithmetical subsets of
![]() $\mathbb {N}$
, and
$\mathbb {N}$
, and
![]() $\mathsf {RCA}_0$
has a minimum
$\mathsf {RCA}_0$
has a minimum
![]() $\omega $
-model REC consisting of all recursive (a.k.a. computable) subsets of
$\omega $
-model REC consisting of all recursive (a.k.a. computable) subsets of
![]() $\mathbb {N}$
. In fact, Friedman [Reference Friedman5] observed that a subset of
$\mathbb {N}$
. In fact, Friedman [Reference Friedman5] observed that a subset of
![]() $\mathcal {P}(\mathbb {N})$
is a model of
$\mathcal {P}(\mathbb {N})$
is a model of
![]() $\mathsf {RCA}_0$
(
$\mathsf {RCA}_0$
(
![]() $\mathsf {ACA}_0$
, respectively) if and only if it is closed under (effective) join
$\mathsf {ACA}_0$
, respectively) if and only if it is closed under (effective) join
![]() $\oplus $
and Turing reduction
$\oplus $
and Turing reduction
![]() $\leq _T$
(and the Turing jump operator, respectively). In summary:
$\leq _T$
(and the Turing jump operator, respectively). In summary:

One might hope to fill in the final entry of the table with “
![]() $\oplus $
, hyperarithmetical reduction.” Every
$\oplus $
, hyperarithmetical reduction.” Every
![]() $\omega $
-model of
$\omega $
-model of
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
is closed under join and hyperarithmetical reduction [Reference Kreisel8]. However, not every subset of
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
is closed under join and hyperarithmetical reduction [Reference Kreisel8]. However, not every subset of
![]() $\mathcal {P}(\mathbb {N})$
which is closed under join and hyperarithmetical reduction satisfies
$\mathcal {P}(\mathbb {N})$
which is closed under join and hyperarithmetical reduction satisfies
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
. The issue is not that
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
. The issue is not that
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
is too strong; rather, there is no theory
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
is too strong; rather, there is no theory
![]() $\mathsf {T}$
such that the
$\mathsf {T}$
such that the
![]() $\omega $
-models of
$\omega $
-models of
![]() $\mathsf {T}$
are exactly those which are closed under join and hyperarithmetical reduction [Reference Van Wesep17, 2.2.2]. This motivated the following definition:
$\mathsf {T}$
are exactly those which are closed under join and hyperarithmetical reduction [Reference Van Wesep17, 2.2.2]. This motivated the following definition:
Definition 1.1 (Steel [Reference Steel16], Montalbán [Reference Montalbán9]).
A theory
![]() $\mathsf {T}$
is a theory of hyperarithmetic analysis (THA) if:
$\mathsf {T}$
is a theory of hyperarithmetic analysis (THA) if:
-
– every
 $\omega $
-model of
$\omega $
-model of
 $\mathsf {T}$
is closed under join and hyperarithmetic reduction, and
$\mathsf {T}$
is closed under join and hyperarithmetic reduction, and -
–
 $\mathsf {T}$
holds in
$\mathsf {T}$
holds in
 $\mathrm {HYP}(Y)$
for every
$\mathrm {HYP}(Y)$
for every
 $Y \subseteq \mathbb {N}$
(here
$Y \subseteq \mathbb {N}$
(here
 $\mathrm {HYP}(Y)$
consists of all subsets of
$\mathrm {HYP}(Y)$
consists of all subsets of
 $\mathbb {N}$
which are hyperarithmetically reducible to Y).
$\mathbb {N}$
which are hyperarithmetically reducible to Y).
Before we discuss examples of THAs, note that each THA
![]() $\mathsf {T}$
characterizes the notion of hyperarithmetic reduction in the following sense: A set
$\mathsf {T}$
characterizes the notion of hyperarithmetic reduction in the following sense: A set
![]() $X \subseteq \mathbb {N}$
is hyperarithmetically reducible to a set
$X \subseteq \mathbb {N}$
is hyperarithmetically reducible to a set
![]() $Y \subseteq \mathbb {N}$
if and only if every
$Y \subseteq \mathbb {N}$
if and only if every
![]() $\omega $
-model of
$\omega $
-model of
![]() $\mathsf {T}$
which contains Y also contains X.
$\mathsf {T}$
which contains Y also contains X.
The aforementioned results of Kreisel [Reference Kreisel8] relativize to show that
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
is a THA. In the 60s and 70s a number of THAs were identified and proved to be nonequivalent [Reference Friedman4, Reference Steel16, Reference Van Wesep17]. These THAs are natural fragments of well-studied axiom schemes such as choice schemes or comprehension schemes. In 2006, Montalbań [Reference Montalbán9] was the first to identify a THA which is a published theorem not stated using concepts from logic (such as first-order formulas). This THA, known as INDEC, is a result of Jullien (see [Reference Montalbán9]) about indecomposability of linear orderings. Other works on THAs include [Reference Conidis2, Reference Montalbán10–Reference Neeman12].
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
is a THA. In the 60s and 70s a number of THAs were identified and proved to be nonequivalent [Reference Friedman4, Reference Steel16, Reference Van Wesep17]. These THAs are natural fragments of well-studied axiom schemes such as choice schemes or comprehension schemes. In 2006, Montalbań [Reference Montalbán9] was the first to identify a THA which is a published theorem not stated using concepts from logic (such as first-order formulas). This THA, known as INDEC, is a result of Jullien (see [Reference Montalbán9]) about indecomposability of linear orderings. Other works on THAs include [Reference Conidis2, Reference Montalbán10–Reference Neeman12].
Recently Barnes, Goh, and Shore [Reference Barnes, Goh and Shore1] (hereafter BGS) identified several theorems of graph theory which are THAs. These theorems are variations of classical results of Halin [Reference Halin6] on disjoint rays in graphs. For simplicity we only discuss the oldest of these results (see [Reference Diestel3, Theorem 8.2.5(i)] for its statement), which we call Halin’s theorem. (Much of the discussion below applies to variations of Halin’s theorem as well; see [Reference Barnes, Goh and Shore1].) In their proof that Halin’s theorem is a THA, BGS [Reference Barnes, Goh and Shore1] showed that Halin’s theorem is provable using
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
, and conversely, Halin’s theorem implies the following weakening of
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
, and conversely, Halin’s theorem implies the following weakening of
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
(assuming additional induction axioms on top of what is available in
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
(assuming additional induction axioms on top of what is available in
![]() $\mathsf {RCA}_0$
):
$\mathsf {RCA}_0$
):
Definition 1.2 (BGS [Reference Barnes, Goh and Shore1]).
Finite-
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
consists of
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
consists of
![]() $\mathsf {RCA}_0$
and
$\mathsf {RCA}_0$
and
for each arithmetical formula
![]() $\varphi (n,X)$
. Formally, “
$\varphi (n,X)$
. Formally, “
![]() $(\exists $
nonzero finitely many
$(\exists $
nonzero finitely many
![]() $X)\varphi (n,X)$
” means that there is a nonempty sequence
$X)\varphi (n,X)$
” means that there is a nonempty sequence
![]() $(X_i)_{i<j}$
such that for each X,
$(X_i)_{i<j}$
such that for each X,
![]() $\varphi (n,X)$
holds if and only if
$\varphi (n,X)$
holds if and only if
![]() $X = X_i$
for some
$X = X_i$
for some
![]() $i < j$
.
$i < j$
.
Henceforth we will refer to finite-
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
as finite choice.
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
as finite choice.
In this paper we present implications and nonimplications between finite choice and other known THAs (Theorems 1.3 and 1.5). First we ought to discuss why finite choice is a THA. To show that a theory is a THA, it suffices to show that it is sandwiched between two THAs. Of course
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
implies finite choice. On the other hand, finite choice implies another known THA: unique-
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
implies finite choice. On the other hand, finite choice implies another known THA: unique-
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
, which asserts (in addition to
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
, which asserts (in addition to
![]() $\mathsf {RCA}_0$
) that
$\mathsf {RCA}_0$
) that
for each arithmetical formula
![]() $\varphi (n,X)$
. Unique-
$\varphi (n,X)$
. Unique-
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
has appeared in the literature with names such as arithmetical replacement
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
has appeared in the literature with names such as arithmetical replacement
![]() $\Pi ^0_{(\omega )}$
-
$\Pi ^0_{(\omega )}$
-
![]() $\mathsf {RA}$
[Reference Van Wesep17, p. 6],
$\mathsf {RA}$
[Reference Van Wesep17, p. 6],
![]() $\Pi ^1_0$
-replacement [Reference Steel16, p. 74], and most commonly weak-
$\Pi ^1_0$
-replacement [Reference Steel16, p. 74], and most commonly weak-
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
(e.g., [Reference Simpson15, VIII.4.12]). A proof that unique-
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
(e.g., [Reference Simpson15, VIII.4.12]). A proof that unique-
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
is a THA can be found in [Reference Simpson15, VIII.4.15–16].
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
is a THA can be found in [Reference Simpson15, VIII.4.15–16].
Since finite choice is sandwiched between
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
and unique-
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
and unique-
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
, we can calibrate its proof-theoretic complexity by comparing it with other THAs in this position. One such THA is the
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
, we can calibrate its proof-theoretic complexity by comparing it with other THAs in this position. One such THA is the
![]() $\Delta ^1_1$
-comprehension scheme (
$\Delta ^1_1$
-comprehension scheme (
![]() $\Delta ^1_1$
-
$\Delta ^1_1$
-
![]() $\mathsf {CA}_0$
), which asserts (in addition to
$\mathsf {CA}_0$
), which asserts (in addition to
![]() $\mathsf {RCA}_0$
) that
$\mathsf {RCA}_0$
) that
for any
![]() $\varphi (n)$
and
$\varphi (n)$
and
![]() $\psi (n)$
which are
$\psi (n)$
which are
![]() $\Sigma ^1_1$
. It is easy to see that
$\Sigma ^1_1$
. It is easy to see that
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0 \to \Delta ^1_1$
-
$\Sigma ^1_1\text {-}\mathsf {AC}_0 \to \Delta ^1_1$
-
![]() $\mathsf {CA}_0 \to $
unique-
$\mathsf {CA}_0 \to $
unique-
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
. In order to separate
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
. In order to separate
![]() $\Delta ^1_1$
-
$\Delta ^1_1$
-
![]() $\mathsf {CA}_0$
and
$\mathsf {CA}_0$
and
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
, Steel [Reference Steel16] introduced a new forcing notion and used it to construct an
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
, Steel [Reference Steel16] introduced a new forcing notion and used it to construct an
![]() $\omega $
-model which satisfies
$\omega $
-model which satisfies
![]() $\Delta ^1_1$
-
$\Delta ^1_1$
-
![]() $\mathsf {CA}_0$
but not
$\mathsf {CA}_0$
but not
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
. Van Wesep [Reference Van Wesep17] modified Steel’s methods to construct an
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
. Van Wesep [Reference Van Wesep17] modified Steel’s methods to construct an
![]() $\omega $
-model which satisfies unique-
$\omega $
-model which satisfies unique-
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
but not
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
but not
![]() $\Delta ^1_1$
-
$\Delta ^1_1$
-
![]() $\mathsf {CA}_0$
. Subsequently various modifications of Steel forcing have been used to separate THAs [Reference Conidis2, Reference Montalbán9–Reference Neeman12]. Using yet another variant of Steel forcing (Section 3.3), we shall prove the following:
$\mathsf {CA}_0$
. Subsequently various modifications of Steel forcing have been used to separate THAs [Reference Conidis2, Reference Montalbán9–Reference Neeman12]. Using yet another variant of Steel forcing (Section 3.3), we shall prove the following:
Theorem 1.3. There is an
![]() $\omega $
-model which satisfies
$\omega $
-model which satisfies
![]() $\Delta ^1_1$
-
$\Delta ^1_1$
-
![]() $\mathsf {CA}_0$
but not finite choice. Therefore
$\mathsf {CA}_0$
but not finite choice. Therefore
![]() $\Delta ^1_1$
-
$\Delta ^1_1$
-
![]() $\mathsf {CA}_0$
does not imply finite choice, even if additional induction axioms are assumed.
$\mathsf {CA}_0$
does not imply finite choice, even if additional induction axioms are assumed.
In particular, finite choice is strictly stronger than unique-
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
. Theorem 1.3 was used by BGS [Reference Barnes, Goh and Shore1] to show that Halin’s theorem and many of its variants cannot be proved using
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
. Theorem 1.3 was used by BGS [Reference Barnes, Goh and Shore1] to show that Halin’s theorem and many of its variants cannot be proved using
![]() $\Delta ^1_1$
-
$\Delta ^1_1$
-
![]() $\mathsf {CA}_0$
(even if additional induction axioms are assumed).
$\mathsf {CA}_0$
(even if additional induction axioms are assumed).
To show that finite choice is strictly weaker than
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
, we will establish a connection between finite choice and a known THA: the arithmetic Bolzano–Weierstrass theorem
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
, we will establish a connection between finite choice and a known THA: the arithmetic Bolzano–Weierstrass theorem
![]() $\mathsf {ABW}$
introduced by Friedman [Reference Friedman5]. Our statement of
$\mathsf {ABW}$
introduced by Friedman [Reference Friedman5]. Our statement of
![]() $\mathsf {ABW}$
below follows Conidis [Reference Conidis2, p. 4470].
$\mathsf {ABW}$
below follows Conidis [Reference Conidis2, p. 4470].
Definition 1.4. The arithmetic Bolzano–Weierstrass theorem (
![]() $\mathsf {ABW}$
) states that if
$\mathsf {ABW}$
) states that if
![]() $A(X)$
is an arithmetic predicate on
$A(X)$
is an arithmetic predicate on
![]() $2^N$
, then either
$2^N$
, then either
![]() $A(X)$
has finitely many solutions, or the set
$A(X)$
has finitely many solutions, or the set
![]() $\{X \in 2^N: A(X)\}$
of A-solutions has an accumulation point.
$\{X \in 2^N: A(X)\}$
of A-solutions has an accumulation point.
Friedman asserted that
![]() $\mathsf {ABW}$
follows from
$\mathsf {ABW}$
follows from
![]() $\Sigma ^1_1$
-
$\Sigma ^1_1$
-
![]() $\mathsf {AC}_0$
. Conidis [Reference Conidis2, Theorem 2.1(2)] furnished a proof of that statement. In addition, [Reference Conidis2, Theorem 2.1(4)] showed that
$\mathsf {AC}_0$
. Conidis [Reference Conidis2, Theorem 2.1(2)] furnished a proof of that statement. In addition, [Reference Conidis2, Theorem 2.1(4)] showed that
![]() $\mathsf {ABW}$
implies unique-
$\mathsf {ABW}$
implies unique-
![]() $\Sigma ^1_1$
-
$\Sigma ^1_1$
-
![]() $\mathsf {AC}_0$
over the base theory consisting of
$\mathsf {AC}_0$
over the base theory consisting of
![]() $\mathsf {RCA}_0$
and the induction scheme for
$\mathsf {RCA}_0$
and the induction scheme for
![]() $\Sigma ^1_1$
formulas (denoted
$\Sigma ^1_1$
formulas (denoted
![]() $\mathsf {I}\Sigma ^1_1$
). (To the best of our knowledge it is not known if
$\mathsf {I}\Sigma ^1_1$
). (To the best of our knowledge it is not known if
![]() $\mathsf {ABW}$
implies unique-
$\mathsf {ABW}$
implies unique-
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
over just
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
over just
![]() $\mathsf {RCA}_0$
. Nevertheless, as every
$\mathsf {RCA}_0$
. Nevertheless, as every
![]() $\omega $
-model satisfies
$\omega $
-model satisfies
![]() $\mathsf {I}\Sigma ^1_1$
, Conidis’s result shows that every
$\mathsf {I}\Sigma ^1_1$
, Conidis’s result shows that every
![]() $\omega $
-model of
$\omega $
-model of
![]() $\mathsf {RCA}_0+\mathsf {ABW}$
satisfies unique-
$\mathsf {RCA}_0+\mathsf {ABW}$
satisfies unique-
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
.) We will strengthen Conidis’s result by proving the following (Section 2):
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
.) We will strengthen Conidis’s result by proving the following (Section 2):
Theorem 1.5.
![]() $\mathsf {ABW}$
implies finite choice over
$\mathsf {ABW}$
implies finite choice over
![]() $\mathsf {RCA}_0 + \mathsf {I}\Sigma ^1_1$
.
$\mathsf {RCA}_0 + \mathsf {I}\Sigma ^1_1$
.
It follows that finite choice is strictly weaker than
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
, as
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
, as
![]() $\mathsf {RCA}_0 + \mathsf {I}\Sigma ^1_1 + \mathsf {ABW}$
does not imply
$\mathsf {RCA}_0 + \mathsf {I}\Sigma ^1_1 + \mathsf {ABW}$
does not imply
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
or even
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
or even
![]() $\Delta ^1_1$
-
$\Delta ^1_1$
-
![]() $\mathsf {CA}_0$
(as witnessed by Van Wesep’s model, see [Reference Van Wesep17, Lemma 1.4] and [Reference Conidis2, Theorem 4.7]).
$\mathsf {CA}_0$
(as witnessed by Van Wesep’s model, see [Reference Van Wesep17, Lemma 1.4] and [Reference Conidis2, Theorem 4.7]).
Having established a connection between
![]() $\mathsf {ABW}$
and finite choice (Theorem 1.5), our Theorem 1.3 gives an alternate, arguably simpler, proof of Conidis’s [Reference Conidis2, Theorem 3.1] result that
$\mathsf {ABW}$
and finite choice (Theorem 1.5), our Theorem 1.3 gives an alternate, arguably simpler, proof of Conidis’s [Reference Conidis2, Theorem 3.1] result that
![]() $\Delta ^1_1$
-
$\Delta ^1_1$
-
![]() $\mathsf {CA}_0$
does not imply
$\mathsf {CA}_0$
does not imply
![]() $\mathsf {ABW}$
. (See Remark 3.1.)
$\mathsf {ABW}$
. (See Remark 3.1.)
2 Arithmetic Bolzano–Weierstrass
We adapt a proof of Conidis [Reference Conidis2, Theorem 2.1(4)] to prove Theorem 1.5, which asserts that
![]() $\mathsf {RCA}_0 + \mathsf {I}\Sigma ^1_1 + \mathsf {ABW} \vdash \mathrm {finite}$
choice.
$\mathsf {RCA}_0 + \mathsf {I}\Sigma ^1_1 + \mathsf {ABW} \vdash \mathrm {finite}$
choice.
Proof of Theorem 1.5
Suppose that
![]() $\varphi (n,Y)$
is an arithmetical predicate which is an instance of finite choice, i.e., for each n,
$\varphi (n,Y)$
is an arithmetical predicate which is an instance of finite choice, i.e., for each n,
![]() $\varphi (n,Y)$
has finitely many solutions. Without loss of generality, we may assume that
$\varphi (n,Y)$
has finitely many solutions. Without loss of generality, we may assume that
![]() $\varphi (n,\emptyset )$
always fails.
$\varphi (n,\emptyset )$
always fails.
Define an arithmetical predicate A on
![]() $2^N$
as follows:
$2^N$
as follows:
![]() $A(\langle X_n \rangle _n)$
holds if
$A(\langle X_n \rangle _n)$
holds if
Using
![]() $\mathsf {I}\Sigma ^1_1$
and the assumption that for each n,
$\mathsf {I}\Sigma ^1_1$
and the assumption that for each n,
![]() $\varphi (n,Y)$
has a solution, we can show that for each
$\varphi (n,Y)$
has a solution, we can show that for each
![]() $n_0$
,
$n_0$
,
![]() $A(\langle X_n \rangle _n)$
has at least
$A(\langle X_n \rangle _n)$
has at least
![]() $n_0$
distinct solutions. (Note if
$n_0$
distinct solutions. (Note if
![]() $X_n$
is
$X_n$
is
![]() $\emptyset $
, then it does not code a solution to
$\emptyset $
, then it does not code a solution to
![]() $\varphi (n,\cdot )$
.) Hence
$\varphi (n,\cdot )$
.) Hence
![]() $A(\langle X_n \rangle _n)$
is an instance of
$A(\langle X_n \rangle _n)$
is an instance of
![]() $\mathsf {ABW}$
.
$\mathsf {ABW}$
.
By
![]() $\mathsf {ABW}$
, the set
$\mathsf {ABW}$
, the set
![]() $\{\langle X_n \rangle _n: A(\langle X_n \rangle _n)\}$
has an accumulation point Y. Interpret Y as a sequence
$\{\langle X_n \rangle _n: A(\langle X_n \rangle _n)\}$
has an accumulation point Y. Interpret Y as a sequence
![]() $\langle Y_n \rangle _n$
. We claim that for all n,
$\langle Y_n \rangle _n$
. We claim that for all n,
![]() $\varphi (n,Y_n)$
holds.
$\varphi (n,Y_n)$
holds.
Suppose towards a contradiction that
![]() $\varphi (k,Y_k)$
fails. Since
$\varphi (k,Y_k)$
fails. Since
![]() $\varphi (k,\cdot )$
has only finitely many solutions, there is some m sufficiently large such that
$\varphi (k,\cdot )$
has only finitely many solutions, there is some m sufficiently large such that
![]() $Y_k\restriction m \neq Y\restriction m$
for every Y such that
$Y_k\restriction m \neq Y\restriction m$
for every Y such that
![]() $\varphi (k,Y)$
holds.
$\varphi (k,Y)$
holds.
Now, by our choice of
![]() $\langle Y_n \rangle _n$
, there are infinitely many
$\langle Y_n \rangle _n$
, there are infinitely many
![]() $\langle X_n \rangle _n$
satisfying A such that
$\langle X_n \rangle _n$
satisfying A such that
![]() $X_k$
extends
$X_k$
extends
![]() $Y_k\restriction m$
. For any such
$Y_k\restriction m$
. For any such
![]() $\langle X_n \rangle _n$
,
$\langle X_n \rangle _n$
,
![]() $\varphi (k,X_k)$
fails, so by definition of A,
$\varphi (k,X_k)$
fails, so by definition of A,
![]() $X_n = \emptyset $
for all
$X_n = \emptyset $
for all
![]() $n \geq k$
.
$n \geq k$
.
But for each
![]() $n < k$
,
$n < k$
,
![]() $\varphi (n,\cdot )$
has only finitely many solutions, so there cannot be infinitely many
$\varphi (n,\cdot )$
has only finitely many solutions, so there cannot be infinitely many
![]() $\langle X_n \rangle _n$
satisfying the above conditions. Contradiction. We have showed that
$\langle X_n \rangle _n$
satisfying the above conditions. Contradiction. We have showed that
![]() $\langle Y_n \rangle _n$
is a finite choice solution to
$\langle Y_n \rangle _n$
is a finite choice solution to
![]() $\varphi (n,Y)$
.
$\varphi (n,Y)$
.
We do not know if finite choice implies
![]() $\mathsf {ABW}$
.
$\mathsf {ABW}$
.
3
 $\Delta ^1_1$
-comprehension does not imply finite choice
$\Delta ^1_1$
-comprehension does not imply finite choice
The rest of the paper is devoted to proving Theorem 1.3 using a new variant of Steel’s [Reference Steel16] tagged tree forcing. We assume familiarity with forcing in arithmetic (see, e.g., [Reference Shore14, Section 3]). A helpful reference for forcing in arithmetic over ramified languages is [Reference Sacks13, III.4 and IV.3].
We begin by fixing some notation regarding trees. By a tree we mean a subset of
![]() $\mathbb {N}^{<\mathbb {N}}$
which is closed under prefix. An element f of
$\mathbb {N}^{<\mathbb {N}}$
which is closed under prefix. An element f of
![]() $\mathbb {N}^{\mathbb {N}}$
is a branch through a tree T, written
$\mathbb {N}^{\mathbb {N}}$
is a branch through a tree T, written
![]() $f \in [T]$
, if every prefix of f lies in T. If some
$f \in [T]$
, if every prefix of f lies in T. If some
![]() $\sigma $
in T is a prefix of a branch through T, we say that
$\sigma $
in T is a prefix of a branch through T, we say that
![]() $\sigma $
is extendible in T. The empty string is denoted by
$\sigma $
is extendible in T. The empty string is denoted by
![]() $\emptyset $
. The length of a string
$\emptyset $
. The length of a string
![]() $\sigma $
is denoted by
$\sigma $
is denoted by
![]() $|\sigma |$
. If
$|\sigma |$
. If
![]() $\sigma $
is a prefix of
$\sigma $
is a prefix of
![]() $\tau $
(or a branch f), we write
$\tau $
(or a branch f), we write
![]() $\sigma \subseteq \tau $
(
$\sigma \subseteq \tau $
(
![]() $\sigma \subseteq f$
, respectively). If
$\sigma \subseteq f$
, respectively). If
![]() $\sigma $
is a nonempty string,
$\sigma $
is a nonempty string,
![]() $\sigma ^-$
denotes the prefix of
$\sigma ^-$
denotes the prefix of
![]() $\sigma $
of length
$\sigma $
of length
![]() $|\sigma |-1$
. If
$|\sigma |-1$
. If
![]() $\sigma $
is a string and T is a tree,
$\sigma $
is a string and T is a tree,
![]() $\sigma \cap T$
denotes the longest prefix of
$\sigma \cap T$
denotes the longest prefix of
![]() $\sigma $
which lies in T.
$\sigma $
which lies in T.
3.1 The model
We shall construct an
![]() $\omega $
-model
$\omega $
-model
![]() $M_\infty \subset \mathcal {P}(\mathbb {N})$
which satisfies
$M_\infty \subset \mathcal {P}(\mathbb {N})$
which satisfies
![]() $\Delta ^1_1$
-
$\Delta ^1_1$
-
![]() $\mathsf {CA}_0$
but not finite choice. The basic setup follows [Reference Montalbán10].
$\mathsf {CA}_0$
but not finite choice. The basic setup follows [Reference Montalbán10].
To define
![]() $M_\infty $
we will construct a generic object
$M_\infty $
we will construct a generic object
where
![]() $T^G$
is a tree, each
$T^G$
is a tree, each
![]() $f_i^G$
is a distinct branch through
$f_i^G$
is a distinct branch through
![]() $T^G$
, and
$T^G$
, and
![]() $h^G: T^G \to \omega _1^{CK} \cup \{\infty \}$
is the well-founded rank function on
$h^G: T^G \to \omega _1^{CK} \cup \{\infty \}$
is the well-founded rank function on
![]() $T^G$
, i.e., for all
$T^G$
, i.e., for all
![]() $\sigma $
in the well-founded part of
$\sigma $
in the well-founded part of
![]() $T^G$
, we have
$T^G$
, we have
![]() $h^G(\sigma ) = \sup \{h^G(\tau )+1: \tau \in T^G, \, \tau \supseteq \sigma \}$
, while for all
$h^G(\sigma ) = \sup \{h^G(\tau )+1: \tau \in T^G, \, \tau \supseteq \sigma \}$
, while for all
![]() $\sigma $
which is extendible in
$\sigma $
which is extendible in
![]() $T^G$
, we have
$T^G$
, we have
![]() $h^G(\sigma ) = \infty $
. Our convention is that
$h^G(\sigma ) = \infty $
. Our convention is that
![]() $\infty = \infty +1$
and
$\infty = \infty +1$
and
![]() $\infty> \infty > \alpha $
, so
$\infty> \infty > \alpha $
, so
![]() $h^G(\sigma ) = \sup \{h^G(\tau )+1: \tau \in T^G, \, \tau \supseteq \sigma \}$
for all
$h^G(\sigma ) = \sup \{h^G(\tau )+1: \tau \in T^G, \, \tau \supseteq \sigma \}$
for all
![]() $\sigma $
in
$\sigma $
in
![]() $T^G$
.
$T^G$
.
Then, for each finite
![]() $F \subset \mathbb {N}$
(written
$F \subset \mathbb {N}$
(written
![]() $F \subset _{\mathrm {f}} \mathbb {N}$
), we define
$F \subset _{\mathrm {f}} \mathbb {N}$
), we define
where
![]() $Y^{(\mu )}$
denotes the transfinite iteration of the Turing jump of Y up to level
$Y^{(\mu )}$
denotes the transfinite iteration of the Turing jump of Y up to level
![]() $\mu $
. (For background on transfinite iterations of the Turing jump, see [Reference Sacks13]. Later, we will express
$\mu $
. (For background on transfinite iterations of the Turing jump, see [Reference Sacks13]. Later, we will express
![]() $M_F$
as the sets which are computable in
$M_F$
as the sets which are computable in
![]() $H_{\mu ,F}$
for some
$H_{\mu ,F}$
for some
![]() $\mu < \omega _1^{CK}$
, defined below.) Notice that
$\mu < \omega _1^{CK}$
, defined below.) Notice that
![]() $\mu $
ranges over the computable ordinals, rather than the ordinals which are computable in
$\mu $
ranges over the computable ordinals, rather than the ordinals which are computable in
![]() $\omega _1^{T^G \oplus \langle f_i^G \rangle _{i \in F}}$
. Nonetheless we will show in Corollary 3.14 that
$\omega _1^{T^G \oplus \langle f_i^G \rangle _{i \in F}}$
. Nonetheless we will show in Corollary 3.14 that
![]() $M_F = \mathrm {HYP}(T^G \oplus \langle f_i^G \rangle _{i \in F})$
.
$M_F = \mathrm {HYP}(T^G \oplus \langle f_i^G \rangle _{i \in F})$
.
Finally, our desired
![]() $\omega $
-model is defined by
$\omega $
-model is defined by
Notice that
![]() $h^G$
does not appear in the definitions of
$h^G$
does not appear in the definitions of
![]() $M_F$
or
$M_F$
or
![]() $M_\infty $
. Nonetheless it will play a crucial role in showing that
$M_\infty $
. Nonetheless it will play a crucial role in showing that
![]() $M_\infty $
has the properties we desire.
$M_\infty $
has the properties we desire.
Let us sketch why finite choice fails in
![]() $M_\infty $
. We will show (Lemma 3.9) that for each
$M_\infty $
. We will show (Lemma 3.9) that for each
![]() $F \subset _{\mathrm {f}} \mathbb {N}$
,
$F \subset _{\mathrm {f}} \mathbb {N}$
,
![]() $M_F \cap [T^G] = \{f_i^G: i \in F\}$
. This implies that the branches through
$M_F \cap [T^G] = \{f_i^G: i \in F\}$
. This implies that the branches through
![]() $T^G$
in
$T^G$
in
![]() $M_\infty $
are exactly the branches
$M_\infty $
are exactly the branches
![]() $f_i^G$
, for
$f_i^G$
, for
![]() $i \in \mathbb {N}$
. This also implies that
$i \in \mathbb {N}$
. This also implies that
![]() $M_\infty $
does not contain any infinite sequence of distinct branches
$M_\infty $
does not contain any infinite sequence of distinct branches
![]() $f_i^G$
, for such a sequence has to lie in some
$f_i^G$
, for such a sequence has to lie in some
![]() $M_F$
, contradicting Lemma 3.9.
$M_F$
, contradicting Lemma 3.9.
This allows us to construct a failure of finite choice: For each n, let
![]() $T_n$
be the subtree of
$T_n$
be the subtree of
![]() $T^G$
passing through
$T^G$
passing through
![]() $\langle n \rangle $
. Our forcing will ensure that each
$\langle n \rangle $
. Our forcing will ensure that each
![]() $[T_n]$
contains (nonzero) finitely many
$[T_n]$
contains (nonzero) finitely many
![]() $f_i^G$
. Hence
$f_i^G$
. Hence
![]() $M_\infty $
thinks that
$M_\infty $
thinks that
![]() $\langle T_n \rangle _n$
is an instance of finite choice. Any finite choice solution to
$\langle T_n \rangle _n$
is an instance of finite choice. Any finite choice solution to
![]() $\langle T_n \rangle _n$
would be an infinite sequence of distinct branches
$\langle T_n \rangle _n$
would be an infinite sequence of distinct branches
![]() $f_i^G$
(they are distinct because the nth branch has first entry n), and hence would not lie in
$f_i^G$
(they are distinct because the nth branch has first entry n), and hence would not lie in
![]() $M_\infty $
, by the previous paragraph.
$M_\infty $
, by the previous paragraph.
In preparation for describing the forcing, we shall give every element of
![]() $M_\infty $
a name. Define by recursion on
$M_\infty $
a name. Define by recursion on
![]() $\mu < \omega _1^{CK}$
:
$\mu < \omega _1^{CK}$
:
 $$\begin{align*}H_{1,F} = T^G \oplus \langle f^G_i \rangle_{i \in F}, \quad S_{\mu,F,e} = W^{H_{\mu,F}}_e, \quad H_{\mu,F} = \bigoplus_{\nu<\mu,e \in \mathbb{N}} S_{\nu,F,e} \end{align*}$$
$$\begin{align*}H_{1,F} = T^G \oplus \langle f^G_i \rangle_{i \in F}, \quad S_{\mu,F,e} = W^{H_{\mu,F}}_e, \quad H_{\mu,F} = \bigoplus_{\nu<\mu,e \in \mathbb{N}} S_{\nu,F,e} \end{align*}$$
for
![]() $\mu < \omega _1^{CK}$
,
$\mu < \omega _1^{CK}$
,
![]() $F \subset _{\mathrm {f}} \mathbb {N}$
,
$F \subset _{\mathrm {f}} \mathbb {N}$
,
![]() $e \in \mathbb {N}$
. (Here
$e \in \mathbb {N}$
. (Here
![]() $W^Y_e$
is the eth computably enumerable set relative to the oracle Y.)
$W^Y_e$
is the eth computably enumerable set relative to the oracle Y.)
3.2 The forcing language
We consider a ramified language
![]() $\mathcal {L}_\infty $
which extends the language of second-order arithmetic with constants for each element of
$\mathcal {L}_\infty $
which extends the language of second-order arithmetic with constants for each element of
![]() $M_\infty $
, and various types of restricted set variables.
$M_\infty $
, and various types of restricted set variables.
In order to define
![]() $\mathcal {L}_\infty $
, we first define a language
$\mathcal {L}_\infty $
, we first define a language
![]() $\mathcal {L}_F$
for each
$\mathcal {L}_F$
for each
![]() $F \subset _{\mathrm {f}} \mathbb {N}$
.
$F \subset _{\mathrm {f}} \mathbb {N}$
.
![]() $\mathcal {L}_F$
consists of first-order formulas in the language of second-order arithmetic generated by the following set variables and constants: for each
$\mathcal {L}_F$
consists of first-order formulas in the language of second-order arithmetic generated by the following set variables and constants: for each
![]() $D \subseteq F$
, there are unranked set variables of the form
$D \subseteq F$
, there are unranked set variables of the form
![]() $X_D$
and ranked set variables of the form
$X_D$
and ranked set variables of the form
![]() $X^\lambda _D$
for each
$X^\lambda _D$
for each
![]() $\lambda < \omega _1^{CK}$
, while the constants are intended to name every element of
$\lambda < \omega _1^{CK}$
, while the constants are intended to name every element of
![]() $M_F$
:
$M_F$
:
-
–
 $\mathbf {T}$
,
$\mathbf {T}$
,
 $\mathbf {f}_i$
for
$\mathbf {f}_i$
for
 $i \in F$
;
$i \in F$
; -
– for each
 $\nu < \omega _1^{CK}$
,
$\nu < \omega _1^{CK}$
,
 $\mathbf {H}_{\nu ,F}$
and
$\mathbf {H}_{\nu ,F}$
and
 $\mathbf {S}_{\nu ,F,e}$
for each
$\mathbf {S}_{\nu ,F,e}$
for each
 $e \in \mathbb {N}$
.
$e \in \mathbb {N}$
.
Let
![]() $C_F$
denote the above set of constants. If
$C_F$
denote the above set of constants. If
![]() $\textbf {S}$
is of the form
$\textbf {S}$
is of the form
![]() $\textbf {S}_{\nu ,F,e}$
, we define
$\textbf {S}_{\nu ,F,e}$
, we define
![]() $\mathrm {dom}(\textbf {S})$
to be F. We define
$\mathrm {dom}(\textbf {S})$
to be F. We define
![]() $C^\mu $
to be the set of all constants of the form
$C^\mu $
to be the set of all constants of the form
![]() $\textbf {H}_{\nu ,F}$
or
$\textbf {H}_{\nu ,F}$
or
![]() $\textbf {S}_{\nu ,F,e}$
for some
$\textbf {S}_{\nu ,F,e}$
for some
![]() $\nu < \mu $
.
$\nu < \mu $
.
The language
![]() $\mathcal {L}_\infty $
consists of
$\mathcal {L}_\infty $
consists of
![]() $\bigcup _{F \subset _{\mathrm {f}} \mathbb {N}} \mathcal {L}_F$
, unranked set variables of the form X, and ranked set variables of the form
$\bigcup _{F \subset _{\mathrm {f}} \mathbb {N}} \mathcal {L}_F$
, unranked set variables of the form X, and ranked set variables of the form
![]() $X^\lambda $
for each
$X^\lambda $
for each
![]() $\lambda < \omega _1^{CK}$
.
$\lambda < \omega _1^{CK}$
.
Each formula
![]() $\psi $
of
$\psi $
of
![]() $\mathcal {L}_\infty $
can be assigned an ordinal rank as follows:
$\mathcal {L}_\infty $
can be assigned an ordinal rank as follows:
where:
-
–
 $u(\psi ) < \omega $
denotes the number of unranked quantifiers in
$u(\psi ) < \omega $
denotes the number of unranked quantifiers in
 $\psi $
;
$\psi $
; -
–
 $o(\psi ) < \omega _1^{CK}$
denotes the least upper bound of
$o(\psi ) < \omega _1^{CK}$
denotes the least upper bound of  $$ \begin{align*} &\{\nu: \nu \text{ is the superscript of a bound variable in }\psi\} \\ \cup \; &\{\nu+1: \text{ some constant of the form }\textbf{S}_{\nu,F,e} \text{ or } \textbf{H}_{\nu,F} \text{ occurs in }\psi\}; \end{align*} $$
$$ \begin{align*} &\{\nu: \nu \text{ is the superscript of a bound variable in }\psi\} \\ \cup \; &\{\nu+1: \text{ some constant of the form }\textbf{S}_{\nu,F,e} \text{ or } \textbf{H}_{\nu,F} \text{ occurs in }\psi\}; \end{align*} $$
-
–
 $r(\psi ) < \omega $
denotes the number of ranked set quantifiers in
$r(\psi ) < \omega $
denotes the number of ranked set quantifiers in
 $\psi $
;
$\psi $
; -
–
 $n(\psi ) < \omega $
denotes the number of connectives.
$n(\psi ) < \omega $
denotes the number of connectives.
We say that a formula
![]() $\psi $
of
$\psi $
of
![]() $\mathcal {L}_\infty $
is ranked if all of its bound variables are ranked, or equivalently, if
$\mathcal {L}_\infty $
is ranked if all of its bound variables are ranked, or equivalently, if
![]() $\mathrm {rk}(\psi ) < \omega _1^{CK}$
.
$\mathrm {rk}(\psi ) < \omega _1^{CK}$
.
A variable of the form
![]() $X^\lambda _D$
or
$X^\lambda _D$
or
![]() $X_D$
is F-restricted if
$X_D$
is F-restricted if
![]() $D \subseteq F$
. A constant of the form
$D \subseteq F$
. A constant of the form
![]() $H_{\mu ,D}$
or
$H_{\mu ,D}$
or
![]() $S_{\mu ,D,e}$
is F-restricted if
$S_{\mu ,D,e}$
is F-restricted if
![]() $D \subseteq F$
. A formula of
$D \subseteq F$
. A formula of
![]() $\mathcal {L}_\infty $
is F-restricted if all of its bound variables and constants are F-restricted.
$\mathcal {L}_\infty $
is F-restricted if all of its bound variables and constants are F-restricted.
A formula is
![]() $\Sigma $
-over-
$\Sigma $
-over-
![]() $\mathcal {L}_F$
if it is built up from ranked F-restricted formulas using
$\mathcal {L}_F$
if it is built up from ranked F-restricted formulas using
![]() $\land $
,
$\land $
,
![]() $\forall n$
, and
$\forall n$
, and
![]() $\exists X$
.
$\exists X$
.
For any formula
![]() $\psi $
and any
$\psi $
and any
![]() $\mu < \omega _1^{CK}$
, we define
$\mu < \omega _1^{CK}$
, we define
![]() $\psi ^\mu $
by replacing every unranked set variable in
$\psi ^\mu $
by replacing every unranked set variable in
![]() $\psi $
with its ranked counterpart, i.e., X is replaced by
$\psi $
with its ranked counterpart, i.e., X is replaced by
![]() $X^\mu $
and
$X^\mu $
and
![]() $X_F$
is replaced by
$X_F$
is replaced by
![]() $X^\mu _F$
.
$X^\mu _F$
.
3.3 The forcing notion
The forcing
![]() $\mathbb {P}$
consists of tuples
$\mathbb {P}$
consists of tuples
such that:
-
(C1)
 $T^p \subseteq \mathbb {N}^{<\mathbb {N}}$
is a finite tree;
$T^p \subseteq \mathbb {N}^{<\mathbb {N}}$
is a finite tree; -
(C2)
 $f^p$
is a finite partial function from
$f^p$
is a finite partial function from
 $\mathbb {N}$
to
$\mathbb {N}$
to
 $T^p\backslash \{\emptyset \}$
such that each
$T^p\backslash \{\emptyset \}$
such that each
 $\sigma \in T^p$
of length
$\sigma \in T^p$
of length
 $1$
is an initial segment of some
$1$
is an initial segment of some
 $f^p(i)$
$f^p(i)$
(we view
 $f^p$
as a finite collection of finite paths in
$f^p$
as a finite collection of finite paths in
 $T^p$
);
$T^p$
); -
(C3)
 $h^p: T^p \to \omega _1^{CK} \cup \{\infty \}$
satisfies the following:
$h^p: T^p \to \omega _1^{CK} \cup \{\infty \}$
satisfies the following:-
(a)
 $h^p$
is a rank function, i.e., if
$h^p$
is a rank function, i.e., if
 $\tau \subsetneq \sigma $
, then
$\tau \subsetneq \sigma $
, then
 $h^p(\tau )> h^p(\sigma )$
$h^p(\tau )> h^p(\sigma )$
(by fiat
 $\infty> \infty > \alpha $
for every
$\infty> \infty > \alpha $
for every
 $\alpha $
);
$\alpha $
); -
(b) for all
 $i \in \mathrm {dom}(f^p)$
,
$i \in \mathrm {dom}(f^p)$
,
 $h^p(f^p(i)) = \infty $
;
$h^p(f^p(i)) = \infty $
; -
(c)
 $h^p(\emptyset ) = \infty $
.
$h^p(\emptyset ) = \infty $
.
-
We think of
![]() $h^p$
as a labeling or tagging of nodes in
$h^p$
as a labeling or tagging of nodes in
![]() $T^p$
. Condition (C2) is novel; ordinary Steel forcing only requires that
$T^p$
. Condition (C2) is novel; ordinary Steel forcing only requires that
![]() $f^p$
is a finite partial function from
$f^p$
is a finite partial function from
![]() $\mathbb {N}$
to
$\mathbb {N}$
to
![]() $T^p$
. We impose (C2) in order to ensure that every node of length
$T^p$
. We impose (C2) in order to ensure that every node of length
![]() $1$
is extendible in the generic tree
$1$
is extendible in the generic tree
![]() $T^G$
. Note that by (C2) and (C3)(b), for each
$T^G$
. Note that by (C2) and (C3)(b), for each
![]() $\sigma $
in
$\sigma $
in
![]() $T^p$
of length
$T^p$
of length
![]() $1$
, we must have
$1$
, we must have
![]() $h^p(\sigma ) = \infty $
. Therefore, if
$h^p(\sigma ) = \infty $
. Therefore, if
![]() $T^p$
contains any node of length
$T^p$
contains any node of length
![]() $1$
, then (C3)(c) follows from (C2) and (C3)(b). There may be nodes
$1$
, then (C3)(c) follows from (C2) and (C3)(b). There may be nodes
![]() $\sigma $
(of length greater than
$\sigma $
(of length greater than
![]() $1$
) such that
$1$
) such that
![]() $h^p(\sigma ) = \infty $
yet there is no i such that
$h^p(\sigma ) = \infty $
yet there is no i such that
![]() $\sigma \subseteq f^p(i)$
.
$\sigma \subseteq f^p(i)$
.
We say that q extends p, written
![]() $q \leq p$
, if:
$q \leq p$
, if:
-
(E1)
 $T^q \supseteq T^p$
;
$T^q \supseteq T^p$
; -
(E2) for all
 $i \in \mathrm {dom}(f^p)$
,
$i \in \mathrm {dom}(f^p)$
,
 $f^q(i)$
is defined and
$f^q(i)$
is defined and
 $f^p(i) = f^q(i) \cap T^p$
$f^p(i) = f^q(i) \cap T^p$
(old paths cannot be extended in the old tree);
-
(E3) for all
 $i \in \mathrm {dom}(f^q)\backslash \mathrm {dom}(f^p)$
,
$i \in \mathrm {dom}(f^q)\backslash \mathrm {dom}(f^p)$
,
 $f^q(i) \cap T^p = \emptyset $
$f^q(i) \cap T^p = \emptyset $
(new paths can only intersect the old tree at the root);
-
(E4)
 $h^q \supseteq h^p$
.
$h^q \supseteq h^p$
.
Conditions (E2) and (E3) are needed for us to control the complexity of the forcing relation. Condition (E2) is present in ordinary Steel forcing [Reference Steel16, p. 68]. One could weaken (E2) by considering only conditions p where each
![]() $f^p(i)$
is a leaf in
$f^p(i)$
is a leaf in
![]() $T^p$
(such conditions are dense in the above forcing): In this case we could replace (E2) by “for all
$T^p$
(such conditions are dense in the above forcing): In this case we could replace (E2) by “for all
![]() $i \in \mathrm {dom}(f^p)$
,
$i \in \mathrm {dom}(f^p)$
,
![]() $f^q(i)$
is defined and
$f^q(i)$
is defined and
![]() $f^p(i) \subseteq f^q(i)$
.” Condition (E3) is not in [Reference Steel16] but needs to be added to it, as pointed out in [Reference Montalbán10, Section 2.2].
$f^p(i) \subseteq f^q(i)$
.” Condition (E3) is not in [Reference Steel16] but needs to be added to it, as pointed out in [Reference Montalbán10, Section 2.2].
Remark 3.1. Conidis [Reference Conidis2, Section 3.2] used a more complicated variant of Steel forcing (with locks on certain nodes of
![]() $T^p$
which can be toggled on and off) to prove that
$T^p$
which can be toggled on and off) to prove that
![]() $\Delta ^1_1$
-
$\Delta ^1_1$
-
![]() $\mathsf {CA}_0$
does not imply
$\mathsf {CA}_0$
does not imply
![]() $\mathsf {ABW}_0$
. Theorems 1.3 and 1.5 together provide an alternate proof of his result.
$\mathsf {ABW}_0$
. Theorems 1.3 and 1.5 together provide an alternate proof of his result.
We will take G to be a sufficiently
![]() $\mathbb {P}$
-generic filter (G must decide all
$\mathbb {P}$
-generic filter (G must decide all
![]() $\Sigma $
-over-
$\Sigma $
-over-
![]() $\mathcal {L}_F$
formulas for all
$\mathcal {L}_F$
formulas for all
![]() $F \subset _{\mathrm {f}} \mathbb {N}$
, as well as all formulas of the form
$F \subset _{\mathrm {f}} \mathbb {N}$
, as well as all formulas of the form
![]() $\forall n(\psi (n) \leftrightarrow \neg \varphi (n))$
, where
$\forall n(\psi (n) \leftrightarrow \neg \varphi (n))$
, where
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
are
$\psi $
are
![]() $\Sigma $
-over-
$\Sigma $
-over-
![]() $\mathcal {L}_F$
for some
$\mathcal {L}_F$
for some
![]() $F \subset _{\mathrm {f}} \mathbb {N}$
). Then we may define
$F \subset _{\mathrm {f}} \mathbb {N}$
). Then we may define
![]() $T^G = \bigcup _{p \in G} T^p$
,
$T^G = \bigcup _{p \in G} T^p$
,
![]() $f_i^G = \bigcup _{p \in G} f^p(i)$
for
$f_i^G = \bigcup _{p \in G} f^p(i)$
for
![]() $i \in \mathbb {N}$
, and
$i \in \mathbb {N}$
, and
![]() $h^G = \bigcup _{p \in G} h^p$
. By genericity, each
$h^G = \bigcup _{p \in G} h^p$
. By genericity, each
![]() $f_i^G$
is an infinite branch in
$f_i^G$
is an infinite branch in
![]() $T^G$
, the branches
$T^G$
, the branches
![]() $f_i^G$
are distinct, and
$f_i^G$
are distinct, and
![]() $h^G$
is the well-founded rank function on
$h^G$
is the well-founded rank function on
![]() $T^G$
.
$T^G$
.
We encode each condition as a number as follows. Fix a computable linear ordering with well-founded part
![]() $\omega _1^{CK}$
. (Such orderings are known as pseudo-well-orderings; see [Reference Harrison7].) We identify each
$\omega _1^{CK}$
. (Such orderings are known as pseudo-well-orderings; see [Reference Harrison7].) We identify each
![]() $\alpha < \omega _1^{CK}$
with its corresponding element in the well-founded part. When we write
$\alpha < \omega _1^{CK}$
with its corresponding element in the well-founded part. When we write
![]() $\alpha < \beta $
, we always refer to their order as ordinals rather than the natural number ordering. Using the above identification and standard pairing functions, we may encode
$\alpha < \beta $
, we always refer to their order as ordinals rather than the natural number ordering. Using the above identification and standard pairing functions, we may encode
![]() $\mathbb {P}$
as a
$\mathbb {P}$
as a
![]() $\Pi ^1_1$
subset of
$\Pi ^1_1$
subset of
![]() $\mathbb {N}$
. For each
$\mathbb {N}$
. For each
![]() $\alpha < \omega _1^{CK}$
, define
$\alpha < \omega _1^{CK}$
, define
![]() $\mathbb {P}_\alpha $
to be the set of all conditions p such that the range of
$\mathbb {P}_\alpha $
to be the set of all conditions p such that the range of
![]() $h^p$
is contained in
$h^p$
is contained in
![]() $\alpha \cup \{\infty \}$
. We have
$\alpha \cup \{\infty \}$
. We have
![]() $\mathbb {P} = \bigcup _{\alpha < \omega _1^{CK}} \mathbb {P}_\alpha $
. Each
$\mathbb {P} = \bigcup _{\alpha < \omega _1^{CK}} \mathbb {P}_\alpha $
. Each
![]() $\mathbb {P}_\alpha $
is computable, uniformly in
$\mathbb {P}_\alpha $
is computable, uniformly in
![]() $\alpha $
.
$\alpha $
.
3.4 The forcing relation
The forcing relation for formulas in
![]() $\mathcal {L}_\infty $
is defined by recursion as follows:
$\mathcal {L}_\infty $
is defined by recursion as follows:
-
(1) for quantifier-free formulas of arithmetic
 $\psi $
,
$\psi $
,
 $p \Vdash \psi $
if and only if
$p \Vdash \psi $
if and only if
 $\psi $
is true;
$\psi $
is true; -
(2)
 $p \Vdash \boldsymbol {\sigma } \in \mathbf {T}$
if either
$p \Vdash \boldsymbol {\sigma } \in \mathbf {T}$
if either
 $|\sigma | < 2$
and
$|\sigma | < 2$
and
 $\sigma \in T^p$
, or
$\sigma \in T^p$
, or
 $\sigma ^- \in T^p$
and
$\sigma ^- \in T^p$
and
 $h^p(\sigma ^-) \geq 1$
;
$h^p(\sigma ^-) \geq 1$
; -
(3)
 $p \Vdash \langle \mathbf {n},\mathbf {m} \rangle \in \textbf {f}_i$
if
$p \Vdash \langle \mathbf {n},\mathbf {m} \rangle \in \textbf {f}_i$
if
 $i \in \mathrm {dom}(f^p)$
and
$i \in \mathrm {dom}(f^p)$
and
 $f^p(i)(n) = m$
;
$f^p(i)(n) = m$
; -
(4)
 $p \Vdash \langle 0,\sigma \rangle \in \textbf {H}_{1,F}$
if
$p \Vdash \langle 0,\sigma \rangle \in \textbf {H}_{1,F}$
if
 $p \Vdash \boldsymbol {\sigma } \in \textbf {T}$
;
$p \Vdash \boldsymbol {\sigma } \in \textbf {T}$
; -
(5)
 $p \Vdash \langle 1,\langle \textbf {i},\langle \textbf {n},\textbf {m} \rangle \rangle \rangle \in \textbf {H}_{1,F}$
if
$p \Vdash \langle 1,\langle \textbf {i},\langle \textbf {n},\textbf {m} \rangle \rangle \rangle \in \textbf {H}_{1,F}$
if
 $i \in F$
and
$i \in F$
and
 $p \Vdash \langle \textbf {n},\textbf {m} \rangle \in \textbf {f}_i$
;
$p \Vdash \langle \textbf {n},\textbf {m} \rangle \in \textbf {f}_i$
; -
(6) for
 $\nu> 1$
,
$\nu> 1$
,
 $p \Vdash \mathbf {n} \in \mathbf {S}_{\nu ,F,e}$
if
$p \Vdash \mathbf {n} \in \mathbf {S}_{\nu ,F,e}$
if
 $p \Vdash \exists s R(\mathbf {H}_{\nu ,F}; \mathbf {e},s,\mathbf {n})$
where R codes a universal Turing machine;
$p \Vdash \exists s R(\mathbf {H}_{\nu ,F}; \mathbf {e},s,\mathbf {n})$
where R codes a universal Turing machine; -
(7) for
 $\nu> 1$
,
$\nu> 1$
,
 $p \Vdash \langle \mathbf {e},\mathbf {n},\mu \rangle \in \mathbf {H}_{\nu ,F}$
if
$p \Vdash \langle \mathbf {e},\mathbf {n},\mu \rangle \in \mathbf {H}_{\nu ,F}$
if
 $\mu < \nu $
and
$\mu < \nu $
and
 $p \Vdash \mathbf {n} \in \mathbf {S}_{\mu ,F,e}$
;
$p \Vdash \mathbf {n} \in \mathbf {S}_{\mu ,F,e}$
; -
(8)
 $p \Vdash \forall x\psi (x)$
if for all
$p \Vdash \forall x\psi (x)$
if for all
 $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
 $p \Vdash \psi (\mathbf {n})$
;
$p \Vdash \psi (\mathbf {n})$
; -
(9)
 $p \Vdash \forall X^\lambda _F \psi (X^\lambda _F)$
if for all
$p \Vdash \forall X^\lambda _F \psi (X^\lambda _F)$
if for all
 $\nu < \lambda $
,
$\nu < \lambda $
,
 $e \in \mathbb {N}$
,
$e \in \mathbb {N}$
,
 $p \Vdash \psi (\mathbf {S}_{\nu ,F,e})$
;
$p \Vdash \psi (\mathbf {S}_{\nu ,F,e})$
; -
(10)
 $p \Vdash \forall X^\lambda \psi (X^\lambda )$
if for all
$p \Vdash \forall X^\lambda \psi (X^\lambda )$
if for all
 $\nu <\lambda $
,
$\nu <\lambda $
,
 $e \in \mathbb {N}$
,
$e \in \mathbb {N}$
,
 $F \subset _{\mathrm {f}} \mathbb {N}$
,
$F \subset _{\mathrm {f}} \mathbb {N}$
,
 $p \Vdash \psi (\mathbf {S}_{\nu ,F,e})$
;
$p \Vdash \psi (\mathbf {S}_{\nu ,F,e})$
; -
(11)
 $p \Vdash \forall X_F \psi (X_F)$
if for all
$p \Vdash \forall X_F \psi (X_F)$
if for all
 $\nu < \omega _1^{CK}$
,
$\nu < \omega _1^{CK}$
,
 $e \in \mathbb {N}$
,
$e \in \mathbb {N}$
,
 $p \Vdash \psi (\mathbf {S}_{\nu ,F,e})$
;
$p \Vdash \psi (\mathbf {S}_{\nu ,F,e})$
; -
(12)
 $p \Vdash \forall X \psi (X)$
if for all
$p \Vdash \forall X \psi (X)$
if for all
 $\nu < \omega _1^{CK}$
,
$\nu < \omega _1^{CK}$
,
 $e \in \mathbb {N}$
,
$e \in \mathbb {N}$
,
 $F \subset _{\mathrm {f}} \mathbb {N}$
,
$F \subset _{\mathrm {f}} \mathbb {N}$
,
 $p \Vdash \psi (\mathbf {S}_{\nu ,F,e})$
;
$p \Vdash \psi (\mathbf {S}_{\nu ,F,e})$
; -
(13)
 $p \Vdash \varphi \land \psi $
if
$p \Vdash \varphi \land \psi $
if
 $p \Vdash \varphi $
and
$p \Vdash \varphi $
and
 $p \Vdash \psi $
;
$p \Vdash \psi $
; -
(14)
 $p \Vdash \neg \psi $
if for every
$p \Vdash \neg \psi $
if for every
 $q \leq p$
,
$q \leq p$
,
 $q \not \Vdash \psi $
.
$q \not \Vdash \psi $
.
Lemma 3.2. The following facts hold of
![]() $\Vdash $
:
$\Vdash $
:
-
(1) If
 $p \Vdash \psi $
, then for every sufficiently generic filter G which contains p,
$p \Vdash \psi $
, then for every sufficiently generic filter G which contains p,
 $M_\infty $
satisfies
$M_\infty $
satisfies
 $\psi $
.
$\psi $
. -
(2) If G is sufficiently generic and
 $M_\infty $
satisfies
$M_\infty $
satisfies
 $\psi $
, then there is some
$\psi $
, then there is some
 $p \in G$
such that
$p \in G$
such that
 $p \Vdash \psi $
.
$p \Vdash \psi $
.
Analogous facts hold for
![]() $\psi \in \mathcal {L}_F$
and each model
$\psi \in \mathcal {L}_F$
and each model
![]() $M_F$
.
$M_F$
.
Just as we encoded each forcing condition as a number, we may also encode each formula in
![]() $\mathcal {L}_\infty $
as a number. We will show that the forcing relation for certain classes of formulas (encoded as a relation on numbers) can be computed within
$\mathcal {L}_\infty $
as a number. We will show that the forcing relation for certain classes of formulas (encoded as a relation on numbers) can be computed within
![]() $M_\infty $
(Lemma 3.12).
$M_\infty $
(Lemma 3.12).
3.5 Analyzing the forcing relation for ranked formulas
In order to control the complexity of the forcing relation, we will show that conditions that are sufficiently similar to each other force the same formulas of sufficiently low complexity. The basic notion of similarity in Steel forcing is known as retagging:
Definition 3.3 [Reference Steel16, Definition 4].
Suppose
![]() $\mu < \omega _1^{CK}$
and
$\mu < \omega _1^{CK}$
and
![]() $F \subset _{\mathrm {f}} \mathbb {N}$
. If p and
$F \subset _{\mathrm {f}} \mathbb {N}$
. If p and
![]() $p^\ast $
are conditions, we say that they are
$p^\ast $
are conditions, we say that they are
![]() $\mu $
-F-retaggings if:
$\mu $
-F-retaggings if:
-
–
 $T^p = T^{p^\ast }$
and
$T^p = T^{p^\ast }$
and
 $f^p \restriction F = f^{p^\ast } \restriction F$
;
$f^p \restriction F = f^{p^\ast } \restriction F$
; -
–
 $h^p$
and
$h^p$
and
 $h^{p^\ast }$
agree on labels strictly smaller than
$h^{p^\ast }$
agree on labels strictly smaller than
 $\mu $
;
$\mu $
; -
– if
 $h^p(\sigma ) \geq \mu $
, then
$h^p(\sigma ) \geq \mu $
, then
 $h^{p^\ast }(\sigma ) \geq \mu $
.
$h^{p^\ast }(\sigma ) \geq \mu $
.
We make some observations:
-
–
 $\mu $
-F-retagging is an equivalence relation on conditions.
$\mu $
-F-retagging is an equivalence relation on conditions. -
– If p and
 $p^\ast $
are
$p^\ast $
are
 $\mu $
-F-retaggings, then for any
$\mu $
-F-retaggings, then for any
 $\mu ' \leq \mu $
and any
$\mu ' \leq \mu $
and any
 $F' \subseteq F$
, p and
$F' \subseteq F$
, p and
 $p^\ast $
are
$p^\ast $
are
 $\mu '$
-
$\mu '$
-
 $F'$
-retaggings as well.
$F'$
-retaggings as well.
Central to our analysis will be the ability to replace a quantifier over
![]() $\mathbb {P}$
with a quantifier over some subset
$\mathbb {P}$
with a quantifier over some subset
![]() $\mathbb {P}_\beta $
(recall that
$\mathbb {P}_\beta $
(recall that
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\Pi ^1_1$
while
$\Pi ^1_1$
while
![]() $\mathbb {P}_\beta $
is computable). Once we have established connections between retagging and the forcing relation, the following lemma will be useful for achieving the above:
$\mathbb {P}_\beta $
is computable). Once we have established connections between retagging and the forcing relation, the following lemma will be useful for achieving the above:
Lemma 3.4. For any
![]() $q \in \mathbb {P}$
and any
$q \in \mathbb {P}$
and any
![]() $\beta < \omega _1^{CK}$
, there is some
$\beta < \omega _1^{CK}$
, there is some
![]() $q^\ast \in \mathbb {P}_\beta $
such that:
$q^\ast \in \mathbb {P}_\beta $
such that:
-
– q and
 $q^\ast $
are
$q^\ast $
are
 $\beta $
-F-retaggings for every
$\beta $
-F-retaggings for every
 $F \subset _{\mathrm {f}} \mathbb {N}$
;
$F \subset _{\mathrm {f}} \mathbb {N}$
; -
– for every
 $p \in \mathbb {P}_\beta $
such that
$p \in \mathbb {P}_\beta $
such that
 $q \leq p$
, we have
$q \leq p$
, we have
 $q^\ast \leq p$
.
$q^\ast \leq p$
.
Proof Define
![]() $T^{q^\ast } = T^q$
,
$T^{q^\ast } = T^q$
,
![]() $f^{q^\ast } = f^q$
, and
$f^{q^\ast } = f^q$
, and
 $$\begin{align*}h^{q^\ast}(\tau) = \begin{cases} \infty, & h^q(\tau) \geq \beta, \\ h^q(\tau), & h^q(\tau) < \beta. \end{cases} \end{align*}$$
$$\begin{align*}h^{q^\ast}(\tau) = \begin{cases} \infty, & h^q(\tau) \geq \beta, \\ h^q(\tau), & h^q(\tau) < \beta. \end{cases} \end{align*}$$
It is easy to see that
![]() $q^\ast $
satisfies the desired properties.
$q^\ast $
satisfies the desired properties.
A cornerstone of the method of Steel forcing is the following basic retagging lemma.
Lemma 3.5. Let p and
![]() $p^\ast $
be
$p^\ast $
be
![]() $\omega \beta $
-F-retaggings. Then for all
$\omega \beta $
-F-retaggings. Then for all
![]() $q \leq p$
and all
$q \leq p$
and all
![]() $\gamma < \beta $
, there exists
$\gamma < \beta $
, there exists
![]() $q^\ast \leq p^\ast $
such that q and
$q^\ast \leq p^\ast $
such that q and
![]() $q^\ast $
are
$q^\ast $
are
![]() $\omega \gamma $
-F-retaggings. Furthermore, if
$\omega \gamma $
-F-retaggings. Furthermore, if
![]() $\mathrm {dom}(f^{p^\ast }) \subseteq F$
(and hence
$\mathrm {dom}(f^{p^\ast }) \subseteq F$
(and hence
![]() $f^{p^\ast } \subseteq f^p$
), then we can choose
$f^{p^\ast } \subseteq f^p$
), then we can choose
![]() $q^\ast $
such that
$q^\ast $
such that
![]() $f^{q^\ast } \subseteq f^q$
.
$f^{q^\ast } \subseteq f^q$
.
The first part of the lemma is identical in form to [Reference Montalbán10, Lemma 2.5]. The second part has no analog in [Reference Montalbán10], but its analog would follow immediately from the proof of [Reference Montalbán10, Lemma 2.5]. For our forcing we will construct
![]() $q^\ast $
(specifically
$q^\ast $
(specifically
![]() $f^{q^\ast }$
) slightly differently in order to prove the second part. The second part will be used in the proof of Lemma 3.11.
$f^{q^\ast }$
) slightly differently in order to prove the second part. The second part will be used in the proof of Lemma 3.11.
Proof Define
![]() $q^\ast $
as follows:
$q^\ast $
as follows:
-
–
 $T^{q^\ast } = T^q$
;
$T^{q^\ast } = T^q$
; -
– in general, we define
 $f^{q^\ast }$
to be the disjoint union of:
$f^{q^\ast }$
to be the disjoint union of:-
–
 $f^q\restriction F$
,
$f^q\restriction F$
, -
–
 $f^{p^\ast }\restriction (\mathrm {dom}(f^{p^\ast })\backslash (\mathrm {dom}(f^q) \cap F))$
, and
$f^{p^\ast }\restriction (\mathrm {dom}(f^{p^\ast })\backslash (\mathrm {dom}(f^q) \cap F))$
, and -
– a function g such that
 $\mathrm {dom}(g)$
is disjoint from
$\mathrm {dom}(g)$
is disjoint from
 $F \cup \mathrm {dom}(f^{p^\ast })$
and
$F \cup \mathrm {dom}(f^{p^\ast })$
and
 $\mathrm {range}(g) = \{\sigma \in T^{q^\ast }\backslash T^{p^\ast }: |\sigma | = 1\}$
;
$\mathrm {range}(g) = \{\sigma \in T^{q^\ast }\backslash T^{p^\ast }: |\sigma | = 1\}$
;
-
-
– if
 $\mathrm {dom}(f^{p^\ast }) \subseteq F$
and we want to satisfy the second part of the lemma, we define
$\mathrm {dom}(f^{p^\ast }) \subseteq F$
and we want to satisfy the second part of the lemma, we define
 $f^{q^\ast } = f^q\restriction (F \cup \{i: f^q(i) \cap T^p = \emptyset \})$
;
$f^{q^\ast } = f^q\restriction (F \cup \{i: f^q(i) \cap T^p = \emptyset \})$
; -
–
 $h^{q^\ast }$
is defined by cases: where
$h^{q^\ast }$
is defined by cases: where $$\begin{align*}h^{q^\ast}(\tau) = \begin{cases} h^{p^\ast}(\tau), & \text{if }\tau \in T^p, \\ \infty, & \text{if }\exists i(\tau \subseteq f^{q^\ast}(i)), \\ h^q(\tau), & \text{if }h^q(\tau) < \omega\gamma, \\ \omega\gamma+|\tau|_Q, &\text{otherwise}, \end{cases} \end{align*}$$
$$\begin{align*}h^{q^\ast}(\tau) = \begin{cases} h^{p^\ast}(\tau), & \text{if }\tau \in T^p, \\ \infty, & \text{if }\exists i(\tau \subseteq f^{q^\ast}(i)), \\ h^q(\tau), & \text{if }h^q(\tau) < \omega\gamma, \\ \omega\gamma+|\tau|_Q, &\text{otherwise}, \end{cases} \end{align*}$$
 $Q = \{\sigma \in T^q: h^q(\sigma ) \geq \omega \gamma \}$
and
$Q = \{\sigma \in T^q: h^q(\sigma ) \geq \omega \gamma \}$
and
 $|\tau |_Q \in \mathbb {N}$
denotes the rank of
$|\tau |_Q \in \mathbb {N}$
denotes the rank of
 $\tau $
in the finite tree Q.
$\tau $
in the finite tree Q.
![]() $h^{q^\ast }$
is well-defined. First, we show that the second and third cases in the definition of
$h^{q^\ast }$
is well-defined. First, we show that the second and third cases in the definition of
![]() $h^{q^\ast }$
are mutually exclusive. Suppose
$h^{q^\ast }$
are mutually exclusive. Suppose
![]() $\tau \subseteq f^{q^\ast }(i)$
for some i.
$\tau \subseteq f^{q^\ast }(i)$
for some i.
Case 1. If
![]() $f^{q^\ast }(i) = f^q(i)$
, then
$f^{q^\ast }(i) = f^q(i)$
, then
![]() $h^q(\tau ) = \infty> \omega \gamma $
.
$h^q(\tau ) = \infty> \omega \gamma $
.
Case 2. If
![]() $f^{q^\ast }(i) = f^{p^\ast }(i)$
, then
$f^{q^\ast }(i) = f^{p^\ast }(i)$
, then
![]() $\tau \in T^p$
and
$\tau \in T^p$
and
![]() $h^{p^\ast }(\tau ) = \infty $
. Since p and
$h^{p^\ast }(\tau ) = \infty $
. Since p and
![]() $p^\ast $
are
$p^\ast $
are
![]() $\omega \beta $
-F-retaggings, we have
$\omega \beta $
-F-retaggings, we have
![]() $h^p(\tau ) \geq \omega \beta $
. It follows that
$h^p(\tau ) \geq \omega \beta $
. It follows that
![]() $h^q(\tau ) = h^p(\tau ) \geq \omega \beta> \omega \gamma $
.
$h^q(\tau ) = h^p(\tau ) \geq \omega \beta> \omega \gamma $
.
Case 3. Otherwise,
![]() $|f^{q^\ast }(i)| = 1$
. Then
$|f^{q^\ast }(i)| = 1$
. Then
![]() $h^q(\tau ) = \infty> \omega \gamma $
.
$h^q(\tau ) = \infty> \omega \gamma $
.
Second, in order to show that the first and second cases in the definition of
![]() $h^{q^\ast }$
do not conflict, we shall show that if
$h^{q^\ast }$
do not conflict, we shall show that if
![]() $\tau \in T^p$
and
$\tau \in T^p$
and
![]() $\tau \subseteq f^{q^\ast }(i)$
for some i, then
$\tau \subseteq f^{q^\ast }(i)$
for some i, then
![]() $h^{p^\ast }(\tau ) = \infty $
.
$h^{p^\ast }(\tau ) = \infty $
.
Case 1. Suppose
![]() $f^{q^\ast }(i) = f^q(i)$
and
$f^{q^\ast }(i) = f^q(i)$
and
![]() $i \in F$
. 1a. If
$i \in F$
. 1a. If
![]() $f^q(i) \cap T^p = \emptyset $
, then
$f^q(i) \cap T^p = \emptyset $
, then
![]() $\tau = \emptyset $
so
$\tau = \emptyset $
so
![]() $h^{p^\ast }(\tau ) = \infty $
. 1b. Otherwise, by (E2) and (E3), we have
$h^{p^\ast }(\tau ) = \infty $
. 1b. Otherwise, by (E2) and (E3), we have
![]() $f^q(i) \cap T^p = f^p(i)$
. Since p and
$f^q(i) \cap T^p = f^p(i)$
. Since p and
![]() $p^\ast $
are
$p^\ast $
are
![]() $\omega \beta $
-F-retaggings, we have
$\omega \beta $
-F-retaggings, we have
![]() $f^{p^\ast }(i) = f^p(i)$
. It follows that
$f^{p^\ast }(i) = f^p(i)$
. It follows that
![]() $\tau \subseteq f^q(i) \cap T^p = f^p(i) = f^{p^\ast }(i)$
, implying
$\tau \subseteq f^q(i) \cap T^p = f^p(i) = f^{p^\ast }(i)$
, implying
![]() $h^{p^\ast }(\tau ) = \infty $
.
$h^{p^\ast }(\tau ) = \infty $
.
Case 2. If
![]() $f^{q^\ast }(i) = f^{p^\ast }(i)$
, then
$f^{q^\ast }(i) = f^{p^\ast }(i)$
, then
![]() $h^{p^\ast }(\tau ) \geq h^{p^\ast }(f^{p^\ast }(i)) = \infty $
.
$h^{p^\ast }(\tau ) \geq h^{p^\ast }(f^{p^\ast }(i)) = \infty $
.
Case 3. Otherwise,
![]() $|f^{q^\ast }(i)| = 1$
. Then
$|f^{q^\ast }(i)| = 1$
. Then
![]() $h^{p^\ast }(\tau ) = \infty $
.
$h^{p^\ast }(\tau ) = \infty $
.
To see that the first and third cases in the definition of
![]() $h^{q^\ast }$
do not conflict, suppose
$h^{q^\ast }$
do not conflict, suppose
![]() $\tau \in T^p$
and
$\tau \in T^p$
and
![]() $h^q(\tau ) < \omega \gamma $
. We have
$h^q(\tau ) < \omega \gamma $
. We have
![]() $h^p(\tau ) = h^q(\tau ) < \omega \gamma $
, so by retagging,
$h^p(\tau ) = h^q(\tau ) < \omega \gamma $
, so by retagging,
![]() $h^{p^\ast }(\tau ) = h^p(\tau ) = h^q(\tau )$
as desired. We have shown that
$h^{p^\ast }(\tau ) = h^p(\tau ) = h^q(\tau )$
as desired. We have shown that
![]() $h^{q^\ast }$
is well-defined.
$h^{q^\ast }$
is well-defined.
![]() $q^\ast $
satisfies (C2). We address the two definitions of
$q^\ast $
satisfies (C2). We address the two definitions of
![]() $f^{q^\ast }$
separately. Suppose
$f^{q^\ast }$
separately. Suppose
![]() $\sigma \in T^{q^\ast }$
has length
$\sigma \in T^{q^\ast }$
has length
![]() $1$
. We want to show that there is some i such that
$1$
. We want to show that there is some i such that
![]() $\sigma \subseteq f^{q^\ast }(i)$
.
$\sigma \subseteq f^{q^\ast }(i)$
.
We begin by considering the first definition of
![]() $f^{q^\ast }$
. First, consider the case
$f^{q^\ast }$
. First, consider the case
![]() $\sigma \in T^{p^\ast }$
. If there is some
$\sigma \in T^{p^\ast }$
. If there is some
![]() $i \in \mathrm {dom}(f^{p^\ast })\backslash (\mathrm {dom}(f^q) \cap F)$
such that
$i \in \mathrm {dom}(f^{p^\ast })\backslash (\mathrm {dom}(f^q) \cap F)$
such that
![]() $\sigma \subseteq f^{p^\ast }(i)$
, then we are done. Otherwise, since
$\sigma \subseteq f^{p^\ast }(i)$
, then we are done. Otherwise, since
![]() $p^\ast $
satisfies (C2), there is some
$p^\ast $
satisfies (C2), there is some
![]() $i \in \mathrm {dom}(f^{p^\ast }) \cap \mathrm {dom}(f^q) \cap F$
such that
$i \in \mathrm {dom}(f^{p^\ast }) \cap \mathrm {dom}(f^q) \cap F$
such that
![]() $\sigma \subseteq f^{p^\ast }(i)$
. Then
$\sigma \subseteq f^{p^\ast }(i)$
. Then
![]() $f^{q^\ast }(i) = f^q(i) \supseteq f^p(i) = f^{p^\ast }(i) \supseteq \sigma $
as desired.
$f^{q^\ast }(i) = f^q(i) \supseteq f^p(i) = f^{p^\ast }(i) \supseteq \sigma $
as desired.
Second, if
![]() $\sigma \in T^{q^\ast }\backslash T^{p^\ast }$
, then there is some
$\sigma \in T^{q^\ast }\backslash T^{p^\ast }$
, then there is some
![]() $i \in \mathrm {dom}(g)$
such that
$i \in \mathrm {dom}(g)$
such that
![]() $g(i) = \sigma $
. We have
$g(i) = \sigma $
. We have
![]() $f^{q^\ast }(i) = g(i) = \sigma $
as desired.
$f^{q^\ast }(i) = g(i) = \sigma $
as desired.
Next we consider the second definition of
![]() $f^{q^\ast }$
. Assume that
$f^{q^\ast }$
. Assume that
![]() $\mathrm {dom}(f^{p^\ast }) \subseteq F$
. If
$\mathrm {dom}(f^{p^\ast }) \subseteq F$
. If
![]() $\sigma \in T^{p^\ast }$
, then since
$\sigma \in T^{p^\ast }$
, then since
![]() $p^\ast $
satisfies (C2), there is some
$p^\ast $
satisfies (C2), there is some
![]() $i \in \mathrm {dom}(f^{p^\ast })$
such that
$i \in \mathrm {dom}(f^{p^\ast })$
such that
![]() $\sigma \subseteq f^{p^\ast }(i)$
. Such i lies in F by assumption, so
$\sigma \subseteq f^{p^\ast }(i)$
. Such i lies in F by assumption, so
![]() $f^{q^\ast }(i) = f^q(i) \supseteq f^p(i) = f^{p^\ast }(i) \supseteq \sigma $
as desired.
$f^{q^\ast }(i) = f^q(i) \supseteq f^p(i) = f^{p^\ast }(i) \supseteq \sigma $
as desired.
If
![]() $\sigma \in T^{q^\ast }\backslash T^{p^\ast }$
, then since q satisfies (C2), there is some
$\sigma \in T^{q^\ast }\backslash T^{p^\ast }$
, then since q satisfies (C2), there is some
![]() $i \in \mathrm {dom}(f^q)$
such that
$i \in \mathrm {dom}(f^q)$
such that
![]() $\sigma \subseteq f^q(i)$
. Since
$\sigma \subseteq f^q(i)$
. Since
![]() $\sigma \notin T^p$
and
$\sigma \notin T^p$
and
![]() $|\sigma | = 1$
, it follows that
$|\sigma | = 1$
, it follows that
![]() $f^q(i) \cap T^p = \emptyset $
. So i lies in
$f^q(i) \cap T^p = \emptyset $
. So i lies in
![]() $\mathrm {dom}(f^{q^\ast })$
. Hence
$\mathrm {dom}(f^{q^\ast })$
. Hence
![]() $f^{q^\ast }(i) = f^q(i) \supseteq \sigma $
as desired. This completes the proof that
$f^{q^\ast }(i) = f^q(i) \supseteq \sigma $
as desired. This completes the proof that
![]() $q^\ast $
satisfies (C2).
$q^\ast $
satisfies (C2).
To show that
![]() $q^\ast $
is a condition, it remains to check (C3). We omit the verification as it is exactly the same as that for ordinary Steel forcing.
$q^\ast $
is a condition, it remains to check (C3). We omit the verification as it is exactly the same as that for ordinary Steel forcing.
![]() $q^\ast $
extends
$q^\ast $
extends
![]() $p^\ast $
. (E1) and (E4) are immediate. To check (E2), consider any
$p^\ast $
. (E1) and (E4) are immediate. To check (E2), consider any
![]() $i \in \mathrm {dom}(f^{p^\ast })$
.
$i \in \mathrm {dom}(f^{p^\ast })$
.
Case 1. Suppose
![]() $i \in F$
. By retagging, we have
$i \in F$
. By retagging, we have
![]() $i \in \mathrm {dom}(f^p) \subseteq \mathrm {dom}(f^q)$
and
$i \in \mathrm {dom}(f^p) \subseteq \mathrm {dom}(f^q)$
and
![]() $f^{p^\ast }(i) = f^p(i)$
. In both definitions of
$f^{p^\ast }(i) = f^p(i)$
. In both definitions of
![]() $f^{q^\ast }$
we have
$f^{q^\ast }$
we have
![]() $f^{q^\ast }(i) = f^q(i)$
, so
$f^{q^\ast }(i) = f^q(i)$
, so
![]() $f^{q^\ast }(i) \cap T^{p^\ast } = f^q(i) \cap T^p = f^p(i) = f^{p^\ast }(i)$
(the second equality holds by (E2)).
$f^{q^\ast }(i) \cap T^{p^\ast } = f^q(i) \cap T^p = f^p(i) = f^{p^\ast }(i)$
(the second equality holds by (E2)).
Case 2. If
![]() $i \notin F$
, then we have
$i \notin F$
, then we have
![]() $\mathrm {dom}(f^{p^\ast }) \not \subseteq F$
. So we are only concerned with the first definition of
$\mathrm {dom}(f^{p^\ast }) \not \subseteq F$
. So we are only concerned with the first definition of
![]() $f^{q^\ast }$
. In this case
$f^{q^\ast }$
. In this case
![]() $f^{q^\ast }(i)$
is defined to be
$f^{q^\ast }(i)$
is defined to be
![]() $f^{p^\ast }(i)$
, which lies in
$f^{p^\ast }(i)$
, which lies in
![]() $T^{p^\ast }$
, so
$T^{p^\ast }$
, so
![]() $f^{q^\ast }(i) \cap T^{p^\ast } = f^{p^\ast }(i)$
.
$f^{q^\ast }(i) \cap T^{p^\ast } = f^{p^\ast }(i)$
.
To check (E3), consider any
![]() $i \in \mathrm {dom}(f^{q^\ast })\backslash \mathrm {dom}(f^{p^\ast })$
. We analyze the two definitions of
$i \in \mathrm {dom}(f^{q^\ast })\backslash \mathrm {dom}(f^{p^\ast })$
. We analyze the two definitions of
![]() $f^{q^\ast }$
separately.
$f^{q^\ast }$
separately.
We begin by considering the first definition of
![]() $f^{q^\ast }$
.
$f^{q^\ast }$
.
Case 1.
![]() $i \in \mathrm {dom}(f^q) \cap F$
and
$i \in \mathrm {dom}(f^q) \cap F$
and
![]() $f^{q^\ast }(i) = f^q(i)$
. Since
$f^{q^\ast }(i) = f^q(i)$
. Since
![]() $i \in F\backslash \mathrm {dom}(f^{p^\ast })$
, we have
$i \in F\backslash \mathrm {dom}(f^{p^\ast })$
, we have
![]() $i \notin \mathrm {dom}(f^p)$
by retagging. Hence by (E3) for
$i \notin \mathrm {dom}(f^p)$
by retagging. Hence by (E3) for
![]() $q \leq p$
, we have
$q \leq p$
, we have
![]() $f^q(i) \cap T^p = \emptyset $
as desired.
$f^q(i) \cap T^p = \emptyset $
as desired.
Case 2. Otherwise,
![]() $i \in \mathrm {dom}(g)$
and
$i \in \mathrm {dom}(g)$
and
![]() $f^{q^\ast }(i) = g(i)$
. In this case,
$f^{q^\ast }(i) = g(i)$
. In this case,
![]() $g(i) \notin T^{p^\ast }$
and
$g(i) \notin T^{p^\ast }$
and
![]() $|g(i)| = 1$
, so
$|g(i)| = 1$
, so
![]() $g(i) \cap T^{p^\ast } = \emptyset $
as desired.
$g(i) \cap T^{p^\ast } = \emptyset $
as desired.
Next we consider the second definition of
![]() $f^{q^\ast }$
. If
$f^{q^\ast }$
. If
![]() $i \in F$
, then the reasoning is identical to Case 1 above. Otherwise, by the definition of
$i \in F$
, then the reasoning is identical to Case 1 above. Otherwise, by the definition of
![]() $f^{q^\ast }$
, we have
$f^{q^\ast }$
, we have
![]() $f^{q^\ast }(i) \cap T^p = f^q(i) \cap T^p = \emptyset $
as desired. This completes the proof that
$f^{q^\ast }(i) \cap T^p = f^q(i) \cap T^p = \emptyset $
as desired. This completes the proof that
![]() $q^\ast $
extends
$q^\ast $
extends
![]() $p^\ast $
.
$p^\ast $
.
Finally, it is easy to check that q and
![]() $q^\ast $
are
$q^\ast $
are
![]() $\omega \gamma $
-F-retaggings.
$\omega \gamma $
-F-retaggings.
The following consequences of the basic retagging lemma are routine (see [Reference Montalbán10, Lemma 2.4 and Corollary 2.6]). We include their proofs for completeness.
Lemma 3.6. Let
![]() $\psi $
be a ranked formula in
$\psi $
be a ranked formula in
![]() $\mathcal {L}_F$
. Suppose that p and
$\mathcal {L}_F$
. Suppose that p and
![]() $p^\ast $
are
$p^\ast $
are
![]() $(\omega \cdot \mathrm {rk}(\psi ))$
-F-retaggings. Then
$(\omega \cdot \mathrm {rk}(\psi ))$
-F-retaggings. Then
![]() $p \Vdash \psi $
if and only if
$p \Vdash \psi $
if and only if
![]() $p^\ast \Vdash \psi $
.
$p^\ast \Vdash \psi $
.
Proof We proceed by induction on the rank of
![]() $\psi $
. The only nontrivial case is when
$\psi $
. The only nontrivial case is when
![]() $\psi $
is
$\psi $
is
![]() $\neg \varphi $
. Assuming that
$\neg \varphi $
. Assuming that
![]() $p^\ast $
and p are
$p^\ast $
and p are
![]() $(\omega \cdot \mathrm {rk}(\neg \varphi ))$
-F-retaggings and that
$(\omega \cdot \mathrm {rk}(\neg \varphi ))$
-F-retaggings and that
![]() $p^\ast \Vdash \neg \varphi $
, we want to show that
$p^\ast \Vdash \neg \varphi $
, we want to show that
![]() $p \Vdash \neg \varphi $
, i.e., for all
$p \Vdash \neg \varphi $
, i.e., for all
![]() $q \leq p$
, we have
$q \leq p$
, we have
![]() $q \not \Vdash \varphi $
. By Lemma 3.5, there is some
$q \not \Vdash \varphi $
. By Lemma 3.5, there is some
![]() $q^\ast \leq p^\ast $
such that
$q^\ast \leq p^\ast $
such that
![]() $q^\ast $
and q are
$q^\ast $
and q are
![]() $(\omega \cdot \mathrm {rk}(\varphi ))$
-F-retaggings. Since
$(\omega \cdot \mathrm {rk}(\varphi ))$
-F-retaggings. Since
![]() $p^\ast \Vdash \neg \varphi $
, we have
$p^\ast \Vdash \neg \varphi $
, we have
![]() $q^\ast \not \Vdash \varphi $
. Applying the inductive hypothesis to q and
$q^\ast \not \Vdash \varphi $
. Applying the inductive hypothesis to q and
![]() $q^\ast $
shows that
$q^\ast $
shows that
![]() $q \not \Vdash \varphi $
as desired.
$q \not \Vdash \varphi $
as desired.
Corollary 3.7. Suppose
![]() $p \in \mathbb {P}_\mu $
and
$p \in \mathbb {P}_\mu $
and
![]() $\psi \in \mathcal {L}_F$
. If there is some
$\psi \in \mathcal {L}_F$
. If there is some
![]() $q \leq p$
such that
$q \leq p$
such that
![]() $q \Vdash \psi $
, then there is some
$q \Vdash \psi $
, then there is some
![]() $q' \leq p$
in
$q' \leq p$
in
![]() $\mathbb {P}_{\max \{\mu ,\omega \cdot \mathrm {rk}(\psi )\}}$
such that
$\mathbb {P}_{\max \{\mu ,\omega \cdot \mathrm {rk}(\psi )\}}$
such that
![]() $q' \Vdash \psi $
. Therefore,
$q' \Vdash \psi $
. Therefore,
![]() $p \Vdash \neg \psi $
if and only if for all
$p \Vdash \neg \psi $
if and only if for all
![]() $q \leq p$
in
$q \leq p$
in
![]() $\mathbb {P}_{\max \{\mu ,\omega \cdot \mathrm {rk}(\psi )\}}$
,
$\mathbb {P}_{\max \{\mu ,\omega \cdot \mathrm {rk}(\psi )\}}$
,
![]() $q \not \Vdash \psi $
.
$q \not \Vdash \psi $
.
Proof Apply Lemma 3.4 to obtain some
![]() $q' \leq p$
in
$q' \leq p$
in
![]() $\mathbb {P}_{\max \{\mu ,\omega \cdot \mathrm {rk}(\psi )\}}$
such that q and
$\mathbb {P}_{\max \{\mu ,\omega \cdot \mathrm {rk}(\psi )\}}$
such that q and
![]() $q'$
are
$q'$
are
![]() $(\max \{\mu ,\omega \cdot \mathrm {rk}(\psi )\})$
-F-retaggings. By Lemma 3.6,
$(\max \{\mu ,\omega \cdot \mathrm {rk}(\psi )\})$
-F-retaggings. By Lemma 3.6,
![]() $q' \Vdash \psi $
.
$q' \Vdash \psi $
.
Corollary 3.8. For each condition p and each formula
![]() $\psi $
in
$\psi $
in
![]() $\mathcal {L}_F$
,
$\mathcal {L}_F$
,
![]() $\emptyset ^{(\mathrm {rk}(\psi ))}$
can decide whether
$\emptyset ^{(\mathrm {rk}(\psi ))}$
can decide whether
![]() $p \Vdash \psi $
uniformly in p and
$p \Vdash \psi $
uniformly in p and
![]() $\psi $
.
$\psi $
.
Proof Induction on
![]() $\mathrm {rk}(\psi )$
using Corollary 3.7.
$\mathrm {rk}(\psi )$
using Corollary 3.7.
We may now analyze which branches on
![]() $T^G$
lie in each
$T^G$
lie in each
![]() $M_F$
. The proof below follows [Reference Montalbán10, Lemma 2.7], with modifications in order to account for (C2).
$M_F$
. The proof below follows [Reference Montalbán10, Lemma 2.7], with modifications in order to account for (C2).
Lemma 3.9. For each
![]() $F \subset _{\mathrm {f}} \mathbb {N}$
,
$F \subset _{\mathrm {f}} \mathbb {N}$
,
![]() $M_F \cap [T^G] = \{f^G_i: i \in F\}$
. Hence
$M_F \cap [T^G] = \{f^G_i: i \in F\}$
. Hence
![]() $M_\infty \cap [T^G] = \{f^G_i: i \in \mathbb {N}\}$
, but no infinite sequence of distinct
$M_\infty \cap [T^G] = \{f^G_i: i \in \mathbb {N}\}$
, but no infinite sequence of distinct
![]() $f^G_i$
lies in
$f^G_i$
lies in
![]() $M_\infty $
.
$M_\infty $
.
Proof Suppose towards a contradiction that
![]() $S = S_{\nu ,F,e} \in [T^G]$
is not
$S = S_{\nu ,F,e} \in [T^G]$
is not
![]() $f^G_i$
for any
$f^G_i$
for any
![]() $i \in F$
. Then there is some prefix
$i \in F$
. Then there is some prefix
![]() $\sigma \subset S$
such that
$\sigma \subset S$
such that
![]() $\sigma \not \subset f^G_i$
for any
$\sigma \not \subset f^G_i$
for any
![]() $i \in F$
. For later purposes, fix such
$i \in F$
. For later purposes, fix such
![]() $\sigma $
with length greater than
$\sigma $
with length greater than
![]() $1$
. By Lemma 3.2, fix
$1$
. By Lemma 3.2, fix
![]() $p \in G$
such that
$p \in G$
such that
![]() $p \Vdash \varphi (\textbf {S})$
, where
$p \Vdash \varphi (\textbf {S})$
, where
![]() $\varphi (\textbf {S})$
is
$\varphi (\textbf {S})$
is
Note
![]() $\varphi (\textbf {S})$
is a ranked formula in
$\varphi (\textbf {S})$
is a ranked formula in
![]() $\mathcal {L}_F$
.
$\mathcal {L}_F$
.
By genericity, we may assume that
![]() $\sigma \in T^p$
. Next, fix
$\sigma \in T^p$
. Next, fix
![]() $\beta < \omega _1^{CK}$
large enough so that
$\beta < \omega _1^{CK}$
large enough so that
![]() $\beta> \omega \cdot \mathrm {rk}(\varphi (\textbf {S}))$
and
$\beta> \omega \cdot \mathrm {rk}(\varphi (\textbf {S}))$
and
![]() $p \in \mathbb {P}_\beta $
.
$p \in \mathbb {P}_\beta $
.
Since p forces that
![]() $\sigma $
is extendible in
$\sigma $
is extendible in
![]() $T^G$
, we have
$T^G$
, we have
![]() $h^p(\sigma ) = \infty $
(by Lemma 3.2). We now define
$h^p(\sigma ) = \infty $
(by Lemma 3.2). We now define
![]() $p^\ast $
which is a
$p^\ast $
which is a
![]() $\beta $
-F-retagging of p, such that
$\beta $
-F-retagging of p, such that
![]() $h^{p^\ast }(\sigma ) \in [\beta ,\omega _1^{CK})$
. Define
$h^{p^\ast }(\sigma ) \in [\beta ,\omega _1^{CK})$
. Define
![]() $T^{p^\ast } = T^p$
. Define
$T^{p^\ast } = T^p$
. Define
![]() $f^{p^\ast }$
to be the union of
$f^{p^\ast }$
to be the union of
![]() $f^p\restriction F$
and a function g such that
$f^p\restriction F$
and a function g such that
![]() $\mathrm {dom}(g)$
is disjoint from F and
$\mathrm {dom}(g)$
is disjoint from F and
![]() $\mathrm {range}(g) = \{\sigma \in T^p: |\sigma |=1\}$
. Finally, define
$\mathrm {range}(g) = \{\sigma \in T^p: |\sigma |=1\}$
. Finally, define
 $$\begin{align*}h^{p^\ast}(\tau) = \begin{cases} \beta+|\tau|_Q, & \text{if }\tau \supseteq \sigma \land h^p(\tau) = \infty, \\ h^p(\tau), & \text{otherwise}, \end{cases} \end{align*}$$
$$\begin{align*}h^{p^\ast}(\tau) = \begin{cases} \beta+|\tau|_Q, & \text{if }\tau \supseteq \sigma \land h^p(\tau) = \infty, \\ h^p(\tau), & \text{otherwise}, \end{cases} \end{align*}$$
where
![]() $Q = \{\tau : \tau \subseteq \sigma \lor (\tau \supseteq \sigma \land h^p(\tau ) = \infty )\}$
.
$Q = \{\tau : \tau \subseteq \sigma \lor (\tau \supseteq \sigma \land h^p(\tau ) = \infty )\}$
.
Since
![]() $h^p(\sigma ) = \infty $
and
$h^p(\sigma ) = \infty $
and
![]() $|\sigma |> 1$
, it is straightforward to check that
$|\sigma |> 1$
, it is straightforward to check that
![]() $h^{p^\ast }$
is a rank function and
$h^{p^\ast }$
is a rank function and
![]() $h^{p^\ast }(\emptyset ) = \infty $
. In order to show that
$h^{p^\ast }(\emptyset ) = \infty $
. In order to show that
![]() $p^\ast $
is a condition, it suffices to check that
$p^\ast $
is a condition, it suffices to check that
![]() $h^{p^\ast }(f^{p^\ast }(i)) = \infty $
for all
$h^{p^\ast }(f^{p^\ast }(i)) = \infty $
for all
![]() $i \in \mathrm {dom}(f^{p^\ast })$
. If
$i \in \mathrm {dom}(f^{p^\ast })$
. If
![]() $i \in F$
, we have
$i \in F$
, we have
![]() $\sigma \not \subseteq f^p(i) = f^{p^\ast }(i)$
, so
$\sigma \not \subseteq f^p(i) = f^{p^\ast }(i)$
, so
![]() $h^{p^\ast }(f^{p^\ast }(i)) = h^p(f^{p^\ast }(i)) = h^p(f^p(i)) = \infty $
. If
$h^{p^\ast }(f^{p^\ast }(i)) = h^p(f^{p^\ast }(i)) = h^p(f^p(i)) = \infty $
. If
![]() $i \in \mathrm {dom}(f^{p^\ast })\backslash F$
(that is,
$i \in \mathrm {dom}(f^{p^\ast })\backslash F$
(that is,
![]() $\mathrm {dom}(g)$
), then
$\mathrm {dom}(g)$
), then
![]() $f^{p^\ast }(i)$
has length
$f^{p^\ast }(i)$
has length
![]() $1$
, so
$1$
, so
![]() $h^{p^\ast }(f^{p^\ast }(i)) = h^p(f^{p^\ast }(i)) = \infty $
.
$h^{p^\ast }(f^{p^\ast }(i)) = h^p(f^{p^\ast }(i)) = \infty $
.
Finally, it is clear that
![]() $p^\ast $
is a
$p^\ast $
is a
![]() $\beta $
-F-retagging of p, and hence an
$\beta $
-F-retagging of p, and hence an
![]() $(\omega \cdot \mathrm {rk}(\varphi (\textbf {S})))$
-F-retagging of p. By Lemma 3.6 we have
$(\omega \cdot \mathrm {rk}(\varphi (\textbf {S})))$
-F-retagging of p. By Lemma 3.6 we have
which is impossible because
![]() $h^{p^\ast }(\sigma ) \neq \infty $
.
$h^{p^\ast }(\sigma ) \neq \infty $
.
The following lemma is new; (C2) was designed in order to prove it.
Lemma 3.10.
![]() $M_\infty $
does not satisfy finite choice.
$M_\infty $
does not satisfy finite choice.
Proof Consider the following arithmetical predicate
![]() $\varphi (n,X)$
(with parameter
$\varphi (n,X)$
(with parameter
![]() $T^G$
):
$T^G$
):
First, we claim that for each n, there is some
![]() $X \in M_\infty $
such that
$X \in M_\infty $
such that
![]() $\varphi (n,X)$
holds. By genericity, fix some
$\varphi (n,X)$
holds. By genericity, fix some
![]() $p \in G$
such that
$p \in G$
such that
![]() $\langle n \rangle \in T^p$
. By (C2), there is some i such that
$\langle n \rangle \in T^p$
. By (C2), there is some i such that
![]() $\langle n \rangle \subseteq f^p(i)$
. Then
$\langle n \rangle \subseteq f^p(i)$
. Then
![]() $\varphi (n,f^G_i)$
holds.
$\varphi (n,f^G_i)$
holds.
Second, we claim that for each n, there are at most finitely many
![]() $X \in M_\infty $
such that
$X \in M_\infty $
such that
![]() $\varphi (n,X)$
holds. By Lemma 3.9, it suffices to show that there are only finitely many i such that
$\varphi (n,X)$
holds. By Lemma 3.9, it suffices to show that there are only finitely many i such that
![]() $\varphi (n,f^G_i)$
holds. As above, fix
$\varphi (n,f^G_i)$
holds. As above, fix
![]() $p \in G$
such that
$p \in G$
such that
![]() $\langle n \rangle \in T^p$
. For each i, we claim that if
$\langle n \rangle \in T^p$
. For each i, we claim that if
![]() $i \notin \mathrm {dom}(f^p)$
, then
$i \notin \mathrm {dom}(f^p)$
, then
![]() $\langle n \rangle \not \subseteq f^G_i$
. Suppose to the contrary that there is some
$\langle n \rangle \not \subseteq f^G_i$
. Suppose to the contrary that there is some
![]() $i \notin \mathrm {dom}(f^p)$
such that
$i \notin \mathrm {dom}(f^p)$
such that
![]() $\langle n \rangle \subseteq f^G_i$
. Fix some
$\langle n \rangle \subseteq f^G_i$
. Fix some
![]() $q \in G$
such that
$q \in G$
such that
![]() $q \Vdash \langle \textbf {n} \rangle \subseteq \textbf {f}_i$
. Let
$q \Vdash \langle \textbf {n} \rangle \subseteq \textbf {f}_i$
. Let
![]() $r \in G$
be a common refinement of p and q. Then
$r \in G$
be a common refinement of p and q. Then
![]() $\langle n \rangle \subseteq f^r(i)$
. But then
$\langle n \rangle \subseteq f^r(i)$
. But then
![]() $f^r(i) \cap T^p \neq \emptyset $
, violating (E3) for
$f^r(i) \cap T^p \neq \emptyset $
, violating (E3) for
![]() $r \leq p$
.
$r \leq p$
.
This shows that
![]() $\varphi (n,X)$
is an instance of finite choice in
$\varphi (n,X)$
is an instance of finite choice in
![]() $M_\infty $
. By Lemma 3.9,
$M_\infty $
. By Lemma 3.9,
![]() $M_\infty $
does not contain any infinite sequence of distinct branches through
$M_\infty $
does not contain any infinite sequence of distinct branches through
![]() $T^G$
, so
$T^G$
, so
![]() $M_\infty $
does not contain any finite choice solution to
$M_\infty $
does not contain any finite choice solution to
![]() $\varphi (n,X)$
.
$\varphi (n,X)$
.
3.6 Analyzing the forcing relation for
 $\Sigma $
-over-
$\Sigma $
-over-
 $\mathcal {L}_F$
formulas
$\mathcal {L}_F$
formulas
In order to show that
![]() $M_\infty \models \Delta ^1_1$
-
$M_\infty \models \Delta ^1_1$
-
![]() $\mathsf {CA}_0$
(Section 3.7), we need to analyze the forcing relation for
$\mathsf {CA}_0$
(Section 3.7), we need to analyze the forcing relation for
![]() $\Sigma $
-over-
$\Sigma $
-over-
![]() $\mathcal {L}_F$
formulas
$\mathcal {L}_F$
formulas
![]() $\psi $
. We begin by considering formulas
$\psi $
. We begin by considering formulas
![]() $\psi ^\rho $
where
$\psi ^\rho $
where
![]() $\rho < \omega _1^{CK}$
. Note that such formulas may not lie in any
$\rho < \omega _1^{CK}$
. Note that such formulas may not lie in any
![]() $\mathcal {L}_{F'}$
because they may contain (existential) quantifiers over set variables of the form
$\mathcal {L}_{F'}$
because they may contain (existential) quantifiers over set variables of the form
![]() $X^\rho $
.
$X^\rho $
.
To this end we exploit automorphisms of
![]() $\mathbb {P}$
, as was done in [Reference Steel16, Lemma 10]. Each permutation
$\mathbb {P}$
, as was done in [Reference Steel16, Lemma 10]. Each permutation
![]() $\pi : \mathbb {N} \to \mathbb {N}$
induces an automorphism
$\pi : \mathbb {N} \to \mathbb {N}$
induces an automorphism
![]() $\hat {\pi }$
of
$\hat {\pi }$
of
![]() $\mathbb {P}$
by permuting the finite paths in each condition:
$\mathbb {P}$
by permuting the finite paths in each condition:
![]() $T^{\hat {\pi }(p)} = T^p$
,
$T^{\hat {\pi }(p)} = T^p$
,
![]() $h^{\hat {\pi }(p)} = h^p$
, and
$h^{\hat {\pi }(p)} = h^p$
, and
![]() $f^{\hat {\pi }(p)}(\pi (i)) = f^p(i)$
. Each permutation
$f^{\hat {\pi }(p)}(\pi (i)) = f^p(i)$
. Each permutation
![]() $\pi $
also induces an automorphism of
$\pi $
also induces an automorphism of
![]() $\mathcal {L}_\infty $
: For each formula
$\mathcal {L}_\infty $
: For each formula
![]() $\psi $
, let
$\psi $
, let
![]() $\pi \psi $
denote the formula obtained from
$\pi \psi $
denote the formula obtained from
![]() $\psi $
by replacing each
$\psi $
by replacing each
![]() $\textbf {f}_i$
by
$\textbf {f}_i$
by
![]() $\textbf {f}_{\pi (i)}$
and each
$\textbf {f}_{\pi (i)}$
and each
![]() $\textbf {S}_{\nu ,F,e}$
by
$\textbf {S}_{\nu ,F,e}$
by
![]() $\textbf {S}_{\nu ,\pi "F,e}$
. (In the proof below, we will denote
$\textbf {S}_{\nu ,\pi "F,e}$
. (In the proof below, we will denote
![]() $\textbf {S}_{\nu ,\pi "F,e}$
by
$\textbf {S}_{\nu ,\pi "F,e}$
by
![]() $\pi \textbf {S}_{\nu ,F,e}$
.) By induction on
$\pi \textbf {S}_{\nu ,F,e}$
.) By induction on
![]() $\mathrm {rk}(\psi )$
, one can show that
$\mathrm {rk}(\psi )$
, one can show that
![]() $p \Vdash \psi $
if and only if
$p \Vdash \psi $
if and only if
![]() $\hat {\pi }(p) \Vdash \pi \psi $
.
$\hat {\pi }(p) \Vdash \pi \psi $
.
Lemma 3.11. Suppose
![]() $\psi $
is
$\psi $
is
![]() $\Sigma $
-over-
$\Sigma $
-over-
![]() $\mathcal {L}_F$
,
$\mathcal {L}_F$
,
![]() $p \Vdash \psi ^\mu $
, and
$p \Vdash \psi ^\mu $
, and
![]() $\mathrm {dom}(f^p) \subseteq F$
. If p and
$\mathrm {dom}(f^p) \subseteq F$
. If p and
![]() $p^\ast $
are
$p^\ast $
are
![]() $(\omega \cdot \mathrm {rk}(\psi ^\mu )+\omega ^2)$
-F-retaggings, then
$(\omega \cdot \mathrm {rk}(\psi ^\mu )+\omega ^2)$
-F-retaggings, then
![]() $p^\ast \Vdash \psi ^\mu $
as well.
$p^\ast \Vdash \psi ^\mu $
as well.
Proof We prove by induction on k that if
![]() $\psi $
is built from ranked, F-restricted formulas using k steps and p is a condition such that
$\psi $
is built from ranked, F-restricted formulas using k steps and p is a condition such that
![]() $p \Vdash \psi ^\mu $
,
$p \Vdash \psi ^\mu $
,
![]() $\mathrm {dom}(f^p) \subseteq F$
, and p and
$\mathrm {dom}(f^p) \subseteq F$
, and p and
![]() $p^\ast $
are
$p^\ast $
are
![]() $(\omega \cdot \mathrm {rk}(\psi ^\mu )+\omega \cdot 2k)$
-F-retaggings, then
$(\omega \cdot \mathrm {rk}(\psi ^\mu )+\omega \cdot 2k)$
-F-retaggings, then
![]() $p^\ast \Vdash \psi ^\mu $
. The base case holds by Lemma 3.6.
$p^\ast \Vdash \psi ^\mu $
. The base case holds by Lemma 3.6.
The only nontrivial inductive step is if
![]() $\psi $
has the form
$\psi $
has the form
![]() $\exists X\varphi (X)$
. We want to prove that for all
$\exists X\varphi (X)$
. We want to prove that for all
![]() $q^\ast \leq p^\ast $
, there is some
$q^\ast \leq p^\ast $
, there is some
![]() $r^\ast \leq q^\ast $
and some
$r^\ast \leq q^\ast $
and some
![]() $\textbf {S} \in C^\mu $
such that
$\textbf {S} \in C^\mu $
such that
![]() $r^\ast \Vdash \varphi ^\mu (\textbf {S})$
. Our plan for doing so is illustrated in Figure 1.
$r^\ast \Vdash \varphi ^\mu (\textbf {S})$
. Our plan for doing so is illustrated in Figure 1.

Figure 1 Illustration of the proof of Lemma 3.11. Arrows correspond to extension in the forcing. Dotted lines correspond to retaggings.
Given
![]() $q^\ast \leq p^\ast $
, there is some
$q^\ast \leq p^\ast $
, there is some
![]() $q \leq p$
such that q and
$q \leq p$
such that q and
![]() $q^\ast $
are
$q^\ast $
are
![]() $(\omega \cdot \mathrm {rk}(\psi ^\mu ) + \omega \cdot (2k+1))$
-F-retaggings. Furthermore, since
$(\omega \cdot \mathrm {rk}(\psi ^\mu ) + \omega \cdot (2k+1))$
-F-retaggings. Furthermore, since
![]() $\mathrm {dom}(f^p) \subseteq F$
, we can choose such q with
$\mathrm {dom}(f^p) \subseteq F$
, we can choose such q with
![]() $f^q \subseteq f^{q^\ast }$
(by the second part of Lemma 3.5).
$f^q \subseteq f^{q^\ast }$
(by the second part of Lemma 3.5).
Since
![]() $p \Vdash \psi ^\mu $
and
$p \Vdash \psi ^\mu $
and
![]() $q \leq p$
, there is some
$q \leq p$
, there is some
![]() $r \leq q$
and some
$r \leq q$
and some
![]() $\textbf {S} \in C^\mu $
such that
$\textbf {S} \in C^\mu $
such that
![]() $r \Vdash \varphi ^\mu (\textbf {S})$
. By extending r, we may assume that
$r \Vdash \varphi ^\mu (\textbf {S})$
. By extending r, we may assume that
![]() $F \cup \mathrm {dom}(\textbf {S}) \subseteq \mathrm {dom}(f^r)$
. To complete the inductive step, we want to define
$F \cup \mathrm {dom}(\textbf {S}) \subseteq \mathrm {dom}(f^r)$
. To complete the inductive step, we want to define
![]() $r^\ast \leq q^\ast $
such that r and
$r^\ast \leq q^\ast $
such that r and
![]() $r^\ast $
are
$r^\ast $
are
![]() $(\omega \cdot \mathrm {rk}(\psi ^\mu )+\omega \cdot 2k)$
-
$(\omega \cdot \mathrm {rk}(\psi ^\mu )+\omega \cdot 2k)$
-
![]() $\mathrm {dom}(f^r)$
-retaggings. By inductive hypothesis, it would follow that
$\mathrm {dom}(f^r)$
-retaggings. By inductive hypothesis, it would follow that
![]() $r^\ast \Vdash \varphi ^\mu (\textbf {S})$
as desired.
$r^\ast \Vdash \varphi ^\mu (\textbf {S})$
as desired.
The naive definition of
![]() $r^\ast $
fails because there may be conflict between
$r^\ast $
fails because there may be conflict between
![]() $f^r$
and
$f^r$
and
![]() $f^{q^\ast }$
. In order to avoid this conflict, we use an automorphism of
$f^{q^\ast }$
. In order to avoid this conflict, we use an automorphism of
![]() $\mathbb {P}$
to permute r and
$\mathbb {P}$
to permute r and
![]() $\textbf {S}$
as follows. Consider a permutation
$\textbf {S}$
as follows. Consider a permutation
![]() $\pi $
which fixes
$\pi $
which fixes
![]() $F \cup \mathrm {dom}(f^q)$
and moves
$F \cup \mathrm {dom}(f^q)$
and moves
![]() $\mathrm {dom}(f^r)\backslash (F \cup \mathrm {dom}(f^q))$
to some set which is disjoint with
$\mathrm {dom}(f^r)\backslash (F \cup \mathrm {dom}(f^q))$
to some set which is disjoint with
![]() $\mathrm {dom}(f^{q^\ast })$
. Since
$\mathrm {dom}(f^{q^\ast })$
. Since
![]() $\pi $
fixes
$\pi $
fixes
![]() $\mathrm {dom}(f^q)$
, we have
$\mathrm {dom}(f^q)$
, we have
![]() $\hat {\pi } r \leq q$
. Since
$\hat {\pi } r \leq q$
. Since
![]() $\pi $
fixes F and
$\pi $
fixes F and
![]() $\varphi $
is
$\varphi $
is
![]() $\Sigma $
-over-
$\Sigma $
-over-
![]() $\mathcal {L}_F$
, we have
$\mathcal {L}_F$
, we have
![]() $\pi \varphi ^\mu = \varphi ^\mu $
. So
$\pi \varphi ^\mu = \varphi ^\mu $
. So
![]() $\hat {\pi } r \Vdash \varphi ^\mu (\pi \textbf {S})$
. Therefore, by replacing r and
$\hat {\pi } r \Vdash \varphi ^\mu (\pi \textbf {S})$
. Therefore, by replacing r and
![]() $\textbf {S}$
with
$\textbf {S}$
with
![]() $\hat {\pi } r$
and
$\hat {\pi } r$
and
![]() $\pi \textbf {S}$
, we may assume that
$\pi \textbf {S}$
, we may assume that
![]() $\mathrm {dom}(f^r)\backslash (F \cup \mathrm {dom}(f^q))$
and
$\mathrm {dom}(f^r)\backslash (F \cup \mathrm {dom}(f^q))$
and
![]() $\mathrm {dom}(f^{q^\ast })$
are disjoint.
$\mathrm {dom}(f^{q^\ast })$
are disjoint.
We claim that q and
![]() $q^\ast $
are
$q^\ast $
are
![]() $(\omega \cdot \mathrm {rk}(\psi ^\mu ) + \omega \cdot (2k+1))$
-
$(\omega \cdot \mathrm {rk}(\psi ^\mu ) + \omega \cdot (2k+1))$
-
![]() $\mathrm {dom}(f^r)$
-retaggings. Since
$\mathrm {dom}(f^r)$
-retaggings. Since
![]() $f^q \subseteq f^{q^\ast }$
, this reduces to showing that
$f^q \subseteq f^{q^\ast }$
, this reduces to showing that
![]() $\mathrm {dom}(f^{q^\ast }) \cap \mathrm {dom}(f^r) \subseteq \mathrm {dom}(f^q)$
. Suppose
$\mathrm {dom}(f^{q^\ast }) \cap \mathrm {dom}(f^r) \subseteq \mathrm {dom}(f^q)$
. Suppose
![]() $i \in \mathrm {dom}(f^{q^\ast }) \cap \mathrm {dom}(f^r)$
. By assumption on r, it follows that
$i \in \mathrm {dom}(f^{q^\ast }) \cap \mathrm {dom}(f^r)$
. By assumption on r, it follows that
![]() $i \in F \cup \mathrm {dom}(f^q)$
. If
$i \in F \cup \mathrm {dom}(f^q)$
. If
![]() $i \in \mathrm {dom}(f^q)$
, then we are done. Otherwise
$i \in \mathrm {dom}(f^q)$
, then we are done. Otherwise
![]() $i \in F$
, but since
$i \in F$
, but since
![]() $i \in \mathrm {dom}(f^{q^\ast })$
and q and
$i \in \mathrm {dom}(f^{q^\ast })$
and q and
![]() $q^\ast $
are
$q^\ast $
are
![]() $(\omega \cdot \mathrm {rk}(\psi ^\mu ) + \omega \cdot (2k+1))$
-F-retaggings, it follows that
$(\omega \cdot \mathrm {rk}(\psi ^\mu ) + \omega \cdot (2k+1))$
-F-retaggings, it follows that
![]() $i \in \mathrm {dom}(f^q)$
as well. This proves the claim.
$i \in \mathrm {dom}(f^q)$
as well. This proves the claim.
By Lemma 3.5, there is some
![]() $r^\ast \leq q^\ast $
such that r and
$r^\ast \leq q^\ast $
such that r and
![]() $r^\ast $
are
$r^\ast $
are
![]() $(\omega \cdot \mathrm {rk}(\psi ^\mu )+\omega \cdot 2k)$
-
$(\omega \cdot \mathrm {rk}(\psi ^\mu )+\omega \cdot 2k)$
-
![]() $\mathrm {dom}(f^r)$
-retaggings. Since
$\mathrm {dom}(f^r)$
-retaggings. Since
![]() $F \cup \mathrm {dom}(\textbf {S}) \subseteq \mathrm {dom}(f^r)$
, we may apply the inductive hypothesis and the fact that
$F \cup \mathrm {dom}(\textbf {S}) \subseteq \mathrm {dom}(f^r)$
, we may apply the inductive hypothesis and the fact that
![]() $r \Vdash \varphi ^\mu (\textbf {S})$
to conclude that
$r \Vdash \varphi ^\mu (\textbf {S})$
to conclude that
![]() $r^\ast \Vdash \varphi ^\mu (\textbf {S})$
as desired.
$r^\ast \Vdash \varphi ^\mu (\textbf {S})$
as desired.
The following lemma is not stated in [Reference Montalbán10] but some form of it is used in the proof of [Reference Montalbán10, Lemma 2.9(1)].
Lemma 3.12. Given a condition p, a formula
![]() $\psi $
which is
$\psi $
which is
![]() $\Sigma $
-over-
$\Sigma $
-over-
![]() $\mathcal {L}_F$
, and some
$\mathcal {L}_F$
, and some
![]() $\rho < \omega _1^{CK}$
,
$\rho < \omega _1^{CK}$
,
![]() $\emptyset ^{(\mathrm {rk}(\psi ^\rho ))}$
can decide whether
$\emptyset ^{(\mathrm {rk}(\psi ^\rho ))}$
can decide whether
![]() $p \Vdash \psi ^\rho $
uniformly in p,
$p \Vdash \psi ^\rho $
uniformly in p,
![]() $\psi $
, and
$\psi $
, and
![]() $\rho $
.
$\rho $
.
Proof We proceed by induction on the number of steps it takes to construct
![]() $\psi $
from ranked F-restricted formulas. The base case holds by Corollary 3.8.
$\psi $
from ranked F-restricted formulas. The base case holds by Corollary 3.8.
For the inductive step, the only nontrivial case is when
![]() $\psi $
has the form
$\psi $
has the form
![]() $\exists X\varphi (X)$
. Fix any
$\exists X\varphi (X)$
. Fix any
![]() $\mu \geq \omega \cdot \mathrm {rk}(\varphi ^\rho (\textbf {S})) + \omega ^2 + \omega $
such that
$\mu \geq \omega \cdot \mathrm {rk}(\varphi ^\rho (\textbf {S})) + \omega ^2 + \omega $
such that
![]() $p \in \mathbb {P}_\mu $
. We claim that
$p \in \mathbb {P}_\mu $
. We claim that
![]() $p \Vdash \exists X^\rho \psi ^\rho (X^\rho )$
if and only if for every
$p \Vdash \exists X^\rho \psi ^\rho (X^\rho )$
if and only if for every
![]() $q \leq p$
in
$q \leq p$
in
![]() $\mathbb {P}_\mu $
, there is some
$\mathbb {P}_\mu $
, there is some
![]() $r \leq q$
in
$r \leq q$
in
![]() $\mathbb {P}_\mu $
and some
$\mathbb {P}_\mu $
and some
![]() $\textbf {S} \in C^\rho $
such that
$\textbf {S} \in C^\rho $
such that
![]() $r \Vdash \varphi ^\rho (\textbf {S})$
. This claim suffices for proving this case of the inductive step.
$r \Vdash \varphi ^\rho (\textbf {S})$
. This claim suffices for proving this case of the inductive step.
To prove the forward direction, suppose we are given
![]() $q \leq p$
in
$q \leq p$
in
![]() $\mathbb {P}_\mu $
. By assumption, there is some
$\mathbb {P}_\mu $
. By assumption, there is some
![]() $r \leq q$
and some
$r \leq q$
and some
![]() $\textbf {S} \in C^\rho $
such that
$\textbf {S} \in C^\rho $
such that
![]() $r \Vdash \varphi ^\rho (\textbf {S})$
. We can retag r to some
$r \Vdash \varphi ^\rho (\textbf {S})$
. We can retag r to some
![]() $r^\ast \leq q$
in
$r^\ast \leq q$
in
![]() $\mathbb {P}_\mu $
such that r and
$\mathbb {P}_\mu $
such that r and
![]() $r^\ast $
are
$r^\ast $
are
![]() $\mu $
-
$\mu $
-
![]() $(F \cup \mathrm {dom}(f^r))$
-retaggings (Lemma 3.4). Since
$(F \cup \mathrm {dom}(f^r))$
-retaggings (Lemma 3.4). Since
![]() $\mu \geq \omega \cdot \mathrm {rk}(\varphi ^\rho (\textbf {S})) + \omega ^2$
, it follows from Lemma 3.11 that
$\mu \geq \omega \cdot \mathrm {rk}(\varphi ^\rho (\textbf {S})) + \omega ^2$
, it follows from Lemma 3.11 that
![]() $r^\ast \Vdash \varphi ^\rho (\textbf {S})$
as desired.
$r^\ast \Vdash \varphi ^\rho (\textbf {S})$
as desired.
To prove the backward direction, suppose we are given
![]() $q \leq p$
. In order to construct some
$q \leq p$
. In order to construct some
![]() $r \leq q$
and some
$r \leq q$
and some
![]() $\textbf {S} \in C^\rho $
such that
$\textbf {S} \in C^\rho $
such that
![]() $r \Vdash \varphi ^\rho (\textbf {S})$
, we follow Figure 2. We begin by retagging q to some
$r \Vdash \varphi ^\rho (\textbf {S})$
, we follow Figure 2. We begin by retagging q to some
![]() $q^\ast \leq p$
in
$q^\ast \leq p$
in
![]() $\mathbb {P}_\mu $
such that q and
$\mathbb {P}_\mu $
such that q and
![]() $q^\ast $
are
$q^\ast $
are
![]() $\mu $
-
$\mu $
-
![]() $F'$
-retaggings for every
$F'$
-retaggings for every
![]() $F' \subset _f \mathbb {N}$
(Lemma 3.4). By assumption, there is some
$F' \subset _f \mathbb {N}$
(Lemma 3.4). By assumption, there is some
![]() $r^\ast \leq q^\ast $
in
$r^\ast \leq q^\ast $
in
![]() $\mathbb {P}_\mu $
and some
$\mathbb {P}_\mu $
and some
![]() $\textbf {S} \in C^\rho $
such that
$\textbf {S} \in C^\rho $
such that
![]() $r^\ast \Vdash \varphi ^\rho (\textbf {S})$
.
$r^\ast \Vdash \varphi ^\rho (\textbf {S})$
.
To complete the proof of the backward direction, we want to produce some
![]() $r \leq q$
which is a retagging of
$r \leq q$
which is a retagging of
![]() $r^\ast $
. Define
$r^\ast $
. Define
![]() $F'$
to be the union of F,
$F'$
to be the union of F,
![]() $\mathrm {dom}(f^{r^\ast })$
and
$\mathrm {dom}(f^{r^\ast })$
and
![]() $\mathrm {dom}(\textbf {S})$
(recall that
$\mathrm {dom}(\textbf {S})$
(recall that
![]() $\mathrm {dom}(\textbf {S}_{\nu ,D,e})$
is defined to be D.) Then
$\mathrm {dom}(\textbf {S}_{\nu ,D,e})$
is defined to be D.) Then
![]() $\varphi ^\rho (\textbf {S})$
is
$\varphi ^\rho (\textbf {S})$
is
![]() $\Sigma $
-over-
$\Sigma $
-over-
![]() $\mathcal {L}_{F'}$
. Since
$\mathcal {L}_{F'}$
. Since
![]() $\mu \geq \omega \cdot \mathrm {rk}(\varphi ^\rho (\textbf {S})) + \omega ^2 + \omega $
, there is some
$\mu \geq \omega \cdot \mathrm {rk}(\varphi ^\rho (\textbf {S})) + \omega ^2 + \omega $
, there is some
![]() $r \leq q$
such that r and
$r \leq q$
such that r and
![]() $r^\ast $
are
$r^\ast $
are
![]() $(\omega \cdot \mathrm {rk}(\varphi ^\rho (\textbf {S})) + \omega ^2)$
-
$(\omega \cdot \mathrm {rk}(\varphi ^\rho (\textbf {S})) + \omega ^2)$
-
![]() $F'$
-retaggings (Lemma 3.5). It follows from Lemma 3.11 that
$F'$
-retaggings (Lemma 3.5). It follows from Lemma 3.11 that
![]() $r \Vdash \varphi ^\rho (\textbf {S})$
as desired.
$r \Vdash \varphi ^\rho (\textbf {S})$
as desired.
Next, we shall show that in order to understand the forcing relation for
![]() $\Sigma $
-over-
$\Sigma $
-over-
![]() $\mathcal {L}_F$
formulas
$\mathcal {L}_F$
formulas
![]() $\varphi $
, it suffices to consider formulas
$\varphi $
, it suffices to consider formulas
![]() $\varphi ^\rho $
where
$\varphi ^\rho $
where
![]() $\rho < \omega _1^{CK}$
. This will be useful for showing that
$\rho < \omega _1^{CK}$
. This will be useful for showing that
![]() $M_\infty \models \Delta ^1_1$
-
$M_\infty \models \Delta ^1_1$
-
![]() $\mathsf {CA}_0$
.
$\mathsf {CA}_0$
.
Lemma 3.13. Suppose
![]() $\psi $
is
$\psi $
is
![]() $\Sigma $
-over-
$\Sigma $
-over-
![]() $\mathcal {L}_F$
. If
$\mathcal {L}_F$
. If
![]() $p \Vdash \psi $
, then there is some
$p \Vdash \psi $
, then there is some
![]() $\mu < \omega _1^{CK}$
such that for all
$\mu < \omega _1^{CK}$
such that for all
![]() $\rho \in [\mu ,\omega _1^{CK})$
,
$\rho \in [\mu ,\omega _1^{CK})$
,
![]() $p \Vdash \psi ^\rho $
.
$p \Vdash \psi ^\rho $
.
Proof We proceed by induction on the number of steps it takes to construct
![]() $\psi $
from ranked F-restricted formulas. The base case is trivial. For the inductive step, the only nontrivial case is when
$\psi $
from ranked F-restricted formulas. The base case is trivial. For the inductive step, the only nontrivial case is when
![]() $\psi $
has the form
$\psi $
has the form
![]() $\exists X\varphi (X)$
. Since
$\exists X\varphi (X)$
. Since
![]() $p \Vdash \exists X \varphi (X)$
, for every
$p \Vdash \exists X \varphi (X)$
, for every
![]() $q \leq p$
, there exist
$q \leq p$
, there exist
![]() $r \leq q$
and
$r \leq q$
and
![]() $\textbf {S}$
such that
$\textbf {S}$
such that
![]() $r \Vdash \varphi (\textbf {S})$
. By the inductive hypothesis,
$r \Vdash \varphi (\textbf {S})$
. By the inductive hypothesis,
![]() $r \Vdash \varphi ^\rho (\textbf {S})$
for all sufficiently large
$r \Vdash \varphi ^\rho (\textbf {S})$
for all sufficiently large
![]() $\rho < \omega _1^{CK}$
.
$\rho < \omega _1^{CK}$
.
Hence, for each
![]() $q \leq p$
, there exist
$q \leq p$
, there exist
![]() $\gamma _q < \omega _1^{CK}$
, a condition
$\gamma _q < \omega _1^{CK}$
, a condition
![]() $r \leq q$
in
$r \leq q$
in
![]() $\mathbb {P}_{\gamma _q}$
, and
$\mathbb {P}_{\gamma _q}$
, and
![]() $\textbf {S} \in C^{\gamma _q}$
such that
$\textbf {S} \in C^{\gamma _q}$
such that
![]() $r \Vdash \varphi ^{\gamma _q}(\textbf {S})$
. By Lemma 3.12, we can hyperarithmetically search for the least such
$r \Vdash \varphi ^{\gamma _q}(\textbf {S})$
. By Lemma 3.12, we can hyperarithmetically search for the least such
![]() $\gamma _q$
, r and
$\gamma _q$
, r and
![]() $\textbf {S}$
.
$\textbf {S}$
.
By boundedness, for each
![]() $\beta < \omega _1^{CK}$
, there is some
$\beta < \omega _1^{CK}$
, there is some
![]() $\gamma < \omega _1^{CK}$
such that for every
$\gamma < \omega _1^{CK}$
such that for every
![]() $q \leq p$
in
$q \leq p$
in
![]() $\mathbb {P}_\beta $
, there exists
$\mathbb {P}_\beta $
, there exists
![]() $\gamma _q < \gamma $
as above. For later purposes, we will choose
$\gamma _q < \gamma $
as above. For later purposes, we will choose
![]() $\gamma < \omega _1^{CK}$
sufficiently large such that
$\gamma < \omega _1^{CK}$
sufficiently large such that
![]() $\omega \cdot \mathrm {rk}(\varphi ^{\gamma _q}(\textbf {S}))+\omega ^2+\omega \leq \gamma $
for every
$\omega \cdot \mathrm {rk}(\varphi ^{\gamma _q}(\textbf {S}))+\omega ^2+\omega \leq \gamma $
for every
![]() $q \leq p$
in
$q \leq p$
in
![]() $\mathbb {P}_\beta $
.
$\mathbb {P}_\beta $
.
Since we can find
![]() $\gamma $
from
$\gamma $
from
![]() $\beta $
hyperarithmetically, by boundedness, there is some limit
$\beta $
hyperarithmetically, by boundedness, there is some limit
![]() $\mu < \omega _1^{CK}$
such that (1)
$\mu < \omega _1^{CK}$
such that (1)
![]() $p \in \mathbb {P}_\mu $
; (2) for every
$p \in \mathbb {P}_\mu $
; (2) for every
![]() $\beta < \mu $
, there is some
$\beta < \mu $
, there is some
![]() $\gamma < \mu $
satisfying the previous paragraph.
$\gamma < \mu $
satisfying the previous paragraph.
We shall show that
![]() $p \Vdash \exists X^\mu \varphi ^\mu (X^\mu )$
. Given
$p \Vdash \exists X^\mu \varphi ^\mu (X^\mu )$
. Given
![]() $q \leq p$
, we want to construct
$q \leq p$
, we want to construct
![]() $r \leq q$
and
$r \leq q$
and
![]() $\textbf {S} \in C^\mu $
such that
$\textbf {S} \in C^\mu $
such that
![]() $r \Vdash \varphi ^\mu (\textbf {S})$
. Our plan for doing so is illustrated in Figure 2.
$r \Vdash \varphi ^\mu (\textbf {S})$
. Our plan for doing so is illustrated in Figure 2.
We begin by retagging q to some
![]() $q^\ast \leq p$
in
$q^\ast \leq p$
in
![]() $\mathbb {P}_\mu $
such that q and
$\mathbb {P}_\mu $
such that q and
![]() $q^\ast $
are
$q^\ast $
are
![]() $\mu $
-
$\mu $
-
![]() $F'$
-retaggings for every
$F'$
-retaggings for every
![]() $F' \subset _f \mathbb {N}$
(Lemma 3.4). Since
$F' \subset _f \mathbb {N}$
(Lemma 3.4). Since
![]() $\mu $
is a limit and
$\mu $
is a limit and
![]() $\mathrm {dom}(h^{q^\ast }) = T^{q^\ast }$
is finite, we have
$\mathrm {dom}(h^{q^\ast }) = T^{q^\ast }$
is finite, we have
![]() $q^\ast \in \mathbb {P}_\beta $
for some
$q^\ast \in \mathbb {P}_\beta $
for some
![]() $\beta < \mu $
. By construction of
$\beta < \mu $
. By construction of
![]() $\mu $
, there exist
$\mu $
, there exist
![]() $\gamma _{q^\ast } < \gamma < \mu $
, a condition
$\gamma _{q^\ast } < \gamma < \mu $
, a condition
![]() $r^\ast \leq q^\ast $
in
$r^\ast \leq q^\ast $
in
![]() $\mathbb {P}_{\gamma _{q^\ast }}$
, and
$\mathbb {P}_{\gamma _{q^\ast }}$
, and
![]() $\textbf {S} \in C^{\gamma _{q^\ast }}$
such that
$\textbf {S} \in C^{\gamma _{q^\ast }}$
such that
![]() $\omega \cdot \mathrm {rk}(\varphi ^{\gamma _{q^\ast }}(\textbf {S}))+\omega ^2+\omega \leq \gamma $
and
$\omega \cdot \mathrm {rk}(\varphi ^{\gamma _{q^\ast }}(\textbf {S}))+\omega ^2+\omega \leq \gamma $
and
![]() $r^\ast \Vdash \varphi ^{\gamma _{q^\ast }}(\textbf {S})$
.
$r^\ast \Vdash \varphi ^{\gamma _{q^\ast }}(\textbf {S})$
.
Define
![]() $F'$
to be the union of F,
$F'$
to be the union of F,
![]() $\mathrm {dom}(f^{r^\ast })$
, and
$\mathrm {dom}(f^{r^\ast })$
, and
![]() $\mathrm {dom}(\textbf {S})$
. Since
$\mathrm {dom}(\textbf {S})$
. Since
![]() $\omega \cdot \mathrm {rk}(\varphi ^{\gamma _{q^\ast }}(\textbf {S}))+\omega ^2+\omega \leq \gamma < \mu $
and q and
$\omega \cdot \mathrm {rk}(\varphi ^{\gamma _{q^\ast }}(\textbf {S}))+\omega ^2+\omega \leq \gamma < \mu $
and q and
![]() $q^\ast $
are
$q^\ast $
are
![]() $\mu $
-
$\mu $
-
![]() $F'$
-retaggings, by Lemma 3.5, there is some
$F'$
-retaggings, by Lemma 3.5, there is some
![]() $r \leq q$
such that r and
$r \leq q$
such that r and
![]() $r^\ast $
are
$r^\ast $
are
![]() $(\omega \cdot \mathrm {rk}(\varphi ^{\gamma _{q^\ast }}(\textbf {S}))+\omega ^2)$
-
$(\omega \cdot \mathrm {rk}(\varphi ^{\gamma _{q^\ast }}(\textbf {S}))+\omega ^2)$
-
![]() $F'$
-retaggings. By Lemma 3.11, we have
$F'$
-retaggings. By Lemma 3.11, we have
![]() $r \Vdash \varphi ^{\gamma _{q^\ast }}(\textbf {S})$
and so
$r \Vdash \varphi ^{\gamma _{q^\ast }}(\textbf {S})$
and so
![]() $r \Vdash \varphi ^\mu (\textbf {S})$
as desired.
$r \Vdash \varphi ^\mu (\textbf {S})$
as desired.
Following [Reference Montalbán10, Lemma 2.9(2)], we conclude the following corollary.
Corollary 3.14. For each
![]() $F \subset _f \mathbb {N}$
,
$F \subset _f \mathbb {N}$
,
![]() $M_F \models \Sigma ^1_1$
-
$M_F \models \Sigma ^1_1$
-
![]() $\mathsf {AC}_0$
. It follows that
$\mathsf {AC}_0$
. It follows that
![]() $M_F = \mathrm {HYP}(T^G \oplus \langle f_i^G \rangle _{i \in F})$
.
$M_F = \mathrm {HYP}(T^G \oplus \langle f_i^G \rangle _{i \in F})$
.
Proof Suppose that
![]() $M_F \models \forall n\exists X\varphi (n,X)$
, where
$M_F \models \forall n\exists X\varphi (n,X)$
, where
![]() $\varphi (n,X)$
is arithmetic with parameters from
$\varphi (n,X)$
is arithmetic with parameters from
![]() $M_F$
. Fix some
$M_F$
. Fix some
![]() $p \in G$
such that
$p \in G$
such that
![]() $p \Vdash \forall n \exists X\varphi (n,X)$
. By Lemma 3.13, fix some
$p \Vdash \forall n \exists X\varphi (n,X)$
. By Lemma 3.13, fix some
![]() $\mu < \omega _1^{CK}$
(greater than the rank of every constant symbol in
$\mu < \omega _1^{CK}$
(greater than the rank of every constant symbol in
![]() $\varphi $
) such that
$\varphi $
) such that
![]() $p \Vdash \forall n \exists X^\mu \varphi (n,X^\mu )$
. It follows that
$p \Vdash \forall n \exists X^\mu \varphi (n,X^\mu )$
. It follows that
![]() $M_F \models \forall n \exists X^\mu \varphi (n,X^\mu )$
.
$M_F \models \forall n \exists X^\mu \varphi (n,X^\mu )$
.
For each n, let
![]() $e_n$
be least such that
$e_n$
be least such that
![]() $M_F \models \varphi (n,S_{\mu ,F,e_n})$
. For each e,
$M_F \models \varphi (n,S_{\mu ,F,e_n})$
. For each e,
![]() $H_{\mu +\omega ,F}$
computes whether
$H_{\mu +\omega ,F}$
computes whether
![]() $M_F \models \varphi (n,S_{\mu ,F,e})$
, so
$M_F \models \varphi (n,S_{\mu ,F,e})$
, so
![]() $\langle S_{\mu ,F,e_n} \rangle _n$
is a
$\langle S_{\mu ,F,e_n} \rangle _n$
is a
![]() $\Sigma ^1_1\text {-}\mathsf {AC}_0$
solution which lies in
$\Sigma ^1_1\text {-}\mathsf {AC}_0$
solution which lies in
![]() $M_F$
.
$M_F$
.
We are ready to prove that
![]() $M_\infty $
satisfies
$M_\infty $
satisfies
![]() $\Delta ^1_1$
-
$\Delta ^1_1$
-
![]() $\mathsf {CA}_0$
. The overall strategy follows [Reference Steel16, Lemma 12], with modifications in order to account for (C2).
$\mathsf {CA}_0$
. The overall strategy follows [Reference Steel16, Lemma 12], with modifications in order to account for (C2).
3.7 Proof that
 $M_\infty $
satisfies
$M_\infty $
satisfies
 $\Delta ^1_1$
-comprehension
$\Delta ^1_1$
-comprehension
Suppose
![]() $\varphi (n)$
and
$\varphi (n)$
and
![]() $\psi (n)$
are
$\psi (n)$
are
![]() $\Sigma $
-over-
$\Sigma $
-over-
![]() $\mathcal {L}_F$
with only n free and
$\mathcal {L}_F$
with only n free and
![]() $M_\infty \models \forall n(\psi (n) \leftrightarrow \neg \varphi (n))$
. We want to define
$M_\infty \models \forall n(\psi (n) \leftrightarrow \neg \varphi (n))$
. We want to define
![]() $D \in M_\infty $
such that
$D \in M_\infty $
such that
A naive attempt is to consider
but there are two obstacles preventing us from showing that the above set lies in
![]() $M_\infty $
:
$M_\infty $
:
-
–
 $M_\infty $
does not contain G so we cannot search over
$M_\infty $
does not contain G so we cannot search over
 $q \in G$
;
$q \in G$
; -
– deciding whether
 $q \Vdash \psi (\mathbf {n})$
is not hyperarithmetic in general.
$q \Vdash \psi (\mathbf {n})$
is not hyperarithmetic in general.
The second obstacle is overcome using Lemma 3.13. To overcome the first obstacle, we shall use retagging to change the scope of our search to a class of conditions which look like they might lie in G, based on information from
![]() $T^G$
and finitely many branches
$T^G$
and finitely many branches
![]() $f^G_i$
(all of which lie in
$f^G_i$
(all of which lie in
![]() $M_\infty $
, unlike G).
$M_\infty $
, unlike G).
Recall that (by genericity)
![]() $h^G$
is the well-founded rank function of
$h^G$
is the well-founded rank function of
![]() $T^G$
. We say that a rank function
$T^G$
. We say that a rank function
![]() $h: T \to \omega _1^{CK} \cup \{\infty \}$
is
$h: T \to \omega _1^{CK} \cup \{\infty \}$
is
![]() $\nu $
-good if
$\nu $
-good if
![]() $T \subset T^G$
and for all
$T \subset T^G$
and for all
![]() $\sigma \in T$
:
$\sigma \in T$
:
 $$ \begin{align*} h^G(\sigma) < \nu \quad &\Rightarrow \quad h(\sigma) = h^G(\sigma), \\ h^G(\sigma) \geq \nu \quad &\Leftrightarrow \quad h(\sigma) \geq \nu. \end{align*} $$
$$ \begin{align*} h^G(\sigma) < \nu \quad &\Rightarrow \quad h(\sigma) = h^G(\sigma), \\ h^G(\sigma) \geq \nu \quad &\Leftrightarrow \quad h(\sigma) \geq \nu. \end{align*} $$
We will use the notion of
![]() $\nu $
-goodness in our definition of D.
$\nu $
-goodness in our definition of D.
We begin the proof by fixing
![]() $p \in G$
such that
$p \in G$
such that
![]() $p \Vdash \forall n(\psi (n) \leftrightarrow \neg \varphi (n))$
. By genericity and by expanding F if necessary, we may assume that
$p \Vdash \forall n(\psi (n) \leftrightarrow \neg \varphi (n))$
. By genericity and by expanding F if necessary, we may assume that
![]() $F = \mathrm {dom}(f^p)$
. Since
$F = \mathrm {dom}(f^p)$
. Since
![]() $p \Vdash \forall n(\psi (n) \lor \varphi (n))$
(which is
$p \Vdash \forall n(\psi (n) \lor \varphi (n))$
(which is
![]() $\Sigma $
-over-
$\Sigma $
-over-
![]() $\mathcal {L}_F$
), by Lemma 3.13, we may fix
$\mathcal {L}_F$
), by Lemma 3.13, we may fix
![]() $\mu < \omega _1^{CK}$
large enough such that
$\mu < \omega _1^{CK}$
large enough such that
![]() $p \Vdash \forall n(\psi ^\mu (n) \lor \varphi ^\mu (n))$
and
$p \Vdash \forall n(\psi ^\mu (n) \lor \varphi ^\mu (n))$
and
![]() $\mu $
is greater than the rank of any constant in
$\mu $
is greater than the rank of any constant in
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
. Since
$\psi $
. Since
![]() $p \Vdash \forall n(\neg \psi (n) \lor \neg \varphi (n))$
and
$p \Vdash \forall n(\neg \psi (n) \lor \neg \varphi (n))$
and
![]() $\mu $
is large enough, we also have
$\mu $
is large enough, we also have
![]() $p \Vdash \forall n(\neg \psi ^\mu (n) \lor \neg \varphi ^\mu (n))$
and so
$p \Vdash \forall n(\neg \psi ^\mu (n) \lor \neg \varphi ^\mu (n))$
and so
![]() $p \Vdash \forall n(\psi ^\mu (n) \leftrightarrow \varphi ^\mu (n))$
.
$p \Vdash \forall n(\psi ^\mu (n) \leftrightarrow \varphi ^\mu (n))$
.
Next, fix
![]() $\nu < \omega _1^{CK}$
large enough such that
$\nu < \omega _1^{CK}$
large enough such that
![]() $p \in \mathbb {P}_\nu $
and
$p \in \mathbb {P}_\nu $
and
![]() $\mathrm {rk}(\varphi ^\mu (\mathbf {d}) \lor \psi ^\mu (\mathbf {d})) < \nu $
for all
$\mathrm {rk}(\varphi ^\mu (\mathbf {d}) \lor \psi ^\mu (\mathbf {d})) < \nu $
for all
![]() $d \in \mathbb {N}$
. Now we define
$d \in \mathbb {N}$
. Now we define
![]() $D \subseteq \mathbb {N}$
as follows:
$D \subseteq \mathbb {N}$
as follows:
![]() $d \in D$
if and only if there is some
$d \in D$
if and only if there is some
![]() $q \in \mathbb {P}_{\omega \nu +\omega ^2+\omega }$
extending p such that:
$q \in \mathbb {P}_{\omega \nu +\omega ^2+\omega }$
extending p such that:
-
(1)
 $q \Vdash \psi ^\mu (\mathbf {d})$
;
$q \Vdash \psi ^\mu (\mathbf {d})$
; -
(2)
 $T^q \subset T^G$
(this is implied by (3) but we include it for emphasis);
$T^q \subset T^G$
(this is implied by (3) but we include it for emphasis); -
(3)
 $h^q$
is
$h^q$
is
 $(\omega \nu +\omega ^2+\omega )$
-good;
$(\omega \nu +\omega ^2+\omega )$
-good; -
(4)
 $\forall i \in F(f^q(i) = f^G_i \cap T^q)$
.
$\forall i \in F(f^q(i) = f^G_i \cap T^q)$
.
Note that if
![]() $q \in G$
, then q satisfies (2) (by (E1)) and (4) (by (E2)). (3) must hold as well, but even more is true: we must have
$q \in G$
, then q satisfies (2) (by (E1)) and (4) (by (E2)). (3) must hold as well, but even more is true: we must have
![]() $h^q \subseteq h^G$
. Since
$h^q \subseteq h^G$
. Since
![]() $M_\infty $
does not have access to
$M_\infty $
does not have access to
![]() $h^G$
, we make do with sufficiently good approximations. Observe that D is hyperarithmetic in
$h^G$
, we make do with sufficiently good approximations. Observe that D is hyperarithmetic in
![]() $T^G \oplus \langle f^G_i \rangle _{i \in F}$
, so
$T^G \oplus \langle f^G_i \rangle _{i \in F}$
, so
![]() $D \in M_F \subseteq M_\infty $
. It remains to show that
$D \in M_F \subseteq M_\infty $
. It remains to show that
![]() $M_\infty \models \psi (\mathbf {d})$
if and only if
$M_\infty \models \psi (\mathbf {d})$
if and only if
![]() $d \in D$
.
$d \in D$
.
The forward direction is straightforward: If
![]() $M_\infty \models \psi (\mathbf {d})$
, then
$M_\infty \models \psi (\mathbf {d})$
, then
![]() $M_\infty \models \psi ^\mu (\mathbf {d})$
, so we may fix
$M_\infty \models \psi ^\mu (\mathbf {d})$
, so we may fix
![]() $q' \in G$
extending p which forces
$q' \in G$
extending p which forces
![]() $\psi ^\mu (\mathbf {d})$
. Using
$\psi ^\mu (\mathbf {d})$
. Using
![]() $q'$
, we define q as we did in the proof of Lemma 3.4:
$q'$
, we define q as we did in the proof of Lemma 3.4:
![]() $T^q = T^{q'}$
,
$T^q = T^{q'}$
,
![]() $f^q = f^{q'}$
, and
$f^q = f^{q'}$
, and
 $$\begin{align*}h^q(\sigma) = \begin{cases} \infty, & \text{if }h^{q'}(\sigma) \geq \omega\nu+\omega^2+\omega, \\ h^{q'}(\sigma), & \text{otherwise}. \end{cases} \end{align*}$$
$$\begin{align*}h^q(\sigma) = \begin{cases} \infty, & \text{if }h^{q'}(\sigma) \geq \omega\nu+\omega^2+\omega, \\ h^{q'}(\sigma), & \text{otherwise}. \end{cases} \end{align*}$$
It is straightforward to check that q witnesses
![]() $d \in D$
(using Lemma 3.11 to show that
$d \in D$
(using Lemma 3.11 to show that
![]() $q \Vdash \psi ^\mu (\textbf {d})$
).
$q \Vdash \psi ^\mu (\textbf {d})$
).
To prove the backward direction, suppose
![]() $M_\infty \models \varphi (\mathbf {d})$
. Then
$M_\infty \models \varphi (\mathbf {d})$
. Then
![]() $M_\infty \models \varphi ^\mu (\mathbf {d})$
, so we may fix
$M_\infty \models \varphi ^\mu (\mathbf {d})$
, so we may fix
![]() $r \in G$
extending p which forces
$r \in G$
extending p which forces
![]() $\varphi ^\mu (\mathbf {d})$
. Suppose towards a contradiction that
$\varphi ^\mu (\mathbf {d})$
. Suppose towards a contradiction that
![]() $d \in D$
, as witnessed by some q. Our plan is to construct conditions
$d \in D$
, as witnessed by some q. Our plan is to construct conditions
![]() $q^\ast $
extending q,
$q^\ast $
extending q,
![]() $r^\ast $
extending r, and
$r^\ast $
extending r, and
![]() $s^\ast $
extending p, as illustrated in Figure 3.
$s^\ast $
extending p, as illustrated in Figure 3.
We begin by using an automorphism of
![]() $\mathbb {P}$
to avoid conflict between
$\mathbb {P}$
to avoid conflict between
![]() $f^q$
and
$f^q$
and
![]() $f^r$
. Consider a permutation
$f^r$
. Consider a permutation
![]() $\pi $
which fixes F and moves
$\pi $
which fixes F and moves
![]() $\mathrm {dom}(f^q)\backslash F$
to some set which is disjoint with
$\mathrm {dom}(f^q)\backslash F$
to some set which is disjoint with
![]() $\mathrm {dom}(f^r)$
. Since
$\mathrm {dom}(f^r)$
. Since
![]() $F = \mathrm {dom}(f^p)$
, we have
$F = \mathrm {dom}(f^p)$
, we have
![]() $\hat {\pi } q \leq p$
. It is straightforward to check that
$\hat {\pi } q \leq p$
. It is straightforward to check that
![]() $\hat {\pi } q$
witnesses
$\hat {\pi } q$
witnesses
![]() $d \in D$
. Therefore, by replacing q with
$d \in D$
. Therefore, by replacing q with
![]() $\hat {\pi } q$
, we may assume that
$\hat {\pi } q$
, we may assume that
![]() $\mathrm {dom}(f^q)\backslash F$
and
$\mathrm {dom}(f^q)\backslash F$
and
![]() $\mathrm {dom}(f^r)$
are disjoint. It follows that
$\mathrm {dom}(f^r)$
are disjoint. It follows that
![]() $\mathrm {dom}(f^q) \cap \mathrm {dom}(f^r) = F$
.
$\mathrm {dom}(f^q) \cap \mathrm {dom}(f^r) = F$
.
Next, fix finite partial functions
![]() $g_{q^\ast }$
and
$g_{q^\ast }$
and
![]() $g_{r^\ast }$
on
$g_{r^\ast }$
on
![]() $\mathbb {N}$
such that:
$\mathbb {N}$
such that:
-
–
 $\mathrm {dom}(g_{q^\ast })$
,
$\mathrm {dom}(g_{q^\ast })$
,
 $\mathrm {dom}(g_{r^\ast })$
, and
$\mathrm {dom}(g_{r^\ast })$
, and
 $\mathrm {dom}(f^q) \cup \mathrm {dom}(f^r)$
are pairwise disjoint;
$\mathrm {dom}(f^q) \cup \mathrm {dom}(f^r)$
are pairwise disjoint; -
–
 $\mathrm {range}(g_{q^\ast }) = \{\sigma \in T^r\backslash T^q: |\sigma | = 1\}$
;
$\mathrm {range}(g_{q^\ast }) = \{\sigma \in T^r\backslash T^q: |\sigma | = 1\}$
; -
–
 $\mathrm {range}(g_{r^\ast }) = \{\sigma \in T^q\backslash T^r: |\sigma | = 1\}$
.
$\mathrm {range}(g_{r^\ast }) = \{\sigma \in T^q\backslash T^r: |\sigma | = 1\}$
.
We may now define
![]() $q^\ast $
as follows:
$q^\ast $
as follows:
-
–
 $T^{q^\ast } = T^q \cup T^r$
;
$T^{q^\ast } = T^q \cup T^r$
; -
–
 $f^{q^\ast }(i) = \begin {cases} f^q(i), & \text {if }i \in \mathrm {dom}(f^q)\backslash F; \\ f^G_i \cap T^{q^\ast }, & \text {if }i \in F; \\ g_{q^\ast }(i), &\text {if }i \in \mathrm {dom}(g_{q^\ast }); \end {cases}$
$f^{q^\ast }(i) = \begin {cases} f^q(i), & \text {if }i \in \mathrm {dom}(f^q)\backslash F; \\ f^G_i \cap T^{q^\ast }, & \text {if }i \in F; \\ g_{q^\ast }(i), &\text {if }i \in \mathrm {dom}(g_{q^\ast }); \end {cases}$
-
–
 $h^{q^\ast }$
is defined by cases: where
$h^{q^\ast }$
is defined by cases: where $$\begin{align*}h^{q^\ast}(\tau) = \begin{cases} h^q(\tau), & \text{if }\tau \in T^q, \\ \infty, & \text{if }\exists i(\tau \subseteq f^{q^\ast}(i)), \\ h^r(\tau), & \text{if }h^r(\tau) < \omega\nu+\omega^2, \\ \omega\nu+\omega^2+|\tau|_Q, &\text{otherwise}, \end{cases} \end{align*}$$
$$\begin{align*}h^{q^\ast}(\tau) = \begin{cases} h^q(\tau), & \text{if }\tau \in T^q, \\ \infty, & \text{if }\exists i(\tau \subseteq f^{q^\ast}(i)), \\ h^r(\tau), & \text{if }h^r(\tau) < \omega\nu+\omega^2, \\ \omega\nu+\omega^2+|\tau|_Q, &\text{otherwise}, \end{cases} \end{align*}$$
 $Q = \{\sigma \in T^r\backslash T^q: h^r(\sigma ) \geq \omega \nu +\omega ^2\}$
.
$Q = \{\sigma \in T^r\backslash T^q: h^r(\sigma ) \geq \omega \nu +\omega ^2\}$
.
Figure 3 p and r lie in G, while q “looks like” it lies in G.
Next, define
![]() $r^\ast $
as follows:
$r^\ast $
as follows:
-
–
 $T^{r^\ast } = T^q \cup T^r$
;
$T^{r^\ast } = T^q \cup T^r$
; -
–
 $f^{r^\ast }(i) = \begin {cases} f^r(i), & \text {if }i \in \mathrm {dom}(f^r)\backslash F; \\ f^G_i \cap T^{r^\ast }, & \text {if }i \in F; \\ g_{r^\ast }(i), & \text {if } i \in \mathrm {dom}(g_{r^\ast }); \end {cases}$
$f^{r^\ast }(i) = \begin {cases} f^r(i), & \text {if }i \in \mathrm {dom}(f^r)\backslash F; \\ f^G_i \cap T^{r^\ast }, & \text {if }i \in F; \\ g_{r^\ast }(i), & \text {if } i \in \mathrm {dom}(g_{r^\ast }); \end {cases}$
-
–
 $h^{r^\ast } = h^G\restriction T^{r^\ast }$
.
$h^{r^\ast } = h^G\restriction T^{r^\ast }$
.
Finally, define
![]() $s^\ast $
as follows:
$s^\ast $
as follows:
-
–
 $T^{s^\ast } = T^q \cup T^r$
;
$T^{s^\ast } = T^q \cup T^r$
; -
–
 $f^{s^\ast } = f^{q^\ast } \cup f^{r^\ast }$
;
$f^{s^\ast } = f^{q^\ast } \cup f^{r^\ast }$
; -
–
 $h^{s^\ast }(\sigma ) = \begin {cases} h^G(\sigma ), &\text {if } h^G(\sigma ) < \omega \nu + \omega ^2; \\ \infty , &\text {otherwise.} \end {cases}$
$h^{s^\ast }(\sigma ) = \begin {cases} h^G(\sigma ), &\text {if } h^G(\sigma ) < \omega \nu + \omega ^2; \\ \infty , &\text {otherwise.} \end {cases}$
One may verify that:
-
–
 $q^\ast $
is a condition which extends q;
$q^\ast $
is a condition which extends q; -
–
 $r^\ast $
is a condition which extends r;
$r^\ast $
is a condition which extends r; -
–
 $s^\ast $
is a condition which extends p;
$s^\ast $
is a condition which extends p; -
–
 $q^\ast $
and
$q^\ast $
and
 $s^\ast $
are
$s^\ast $
are
 $(\omega \nu +\omega ^2)$
-
$(\omega \nu +\omega ^2)$
-
 $\mathrm {dom}(f^{q^\ast })$
-retaggings;
$\mathrm {dom}(f^{q^\ast })$
-retaggings; -
–
 $r^\ast $
and
$r^\ast $
and
 $s^\ast $
are
$s^\ast $
are
 $(\omega \nu +\omega ^2)$
-
$(\omega \nu +\omega ^2)$
-
 $\mathrm {dom}(f^{r^\ast })$
-retaggings.
$\mathrm {dom}(f^{r^\ast })$
-retaggings.
The verification is the same as that for ordinary Steel forcing, with minor additions in order to handle the new paths contributed by
![]() $g_{q^\ast }$
and
$g_{q^\ast }$
and
![]() $g_{r^\ast }$
. We only discuss
$g_{r^\ast }$
. We only discuss
![]() $g_{q^\ast }$
here; the argument for
$g_{q^\ast }$
here; the argument for
![]() $g_{r^\ast }$
is similar. First, note that
$g_{r^\ast }$
is similar. First, note that
![]() $g_{q^\ast }$
was defined to ensure that
$g_{q^\ast }$
was defined to ensure that
![]() $q^\ast $
satisfies (C2). Second, (E3) is satisfied for
$q^\ast $
satisfies (C2). Second, (E3) is satisfied for
![]() $q^\ast \leq q$
because for each
$q^\ast \leq q$
because for each
![]() $i \in \mathrm {dom}(f^{q^\ast })\backslash \mathrm {dom}(f^q)$
(
$i \in \mathrm {dom}(f^{q^\ast })\backslash \mathrm {dom}(f^q)$
(
![]() $=\mathrm {dom}(g_{q^\ast })$
), we have
$=\mathrm {dom}(g_{q^\ast })$
), we have
![]() $g_{q^\ast } \notin T^q$
and
$g_{q^\ast } \notin T^q$
and
![]() $|g_{q^\ast }(i)| = 1$
.
$|g_{q^\ast }(i)| = 1$
.
With the above facts, we may complete the proof that if
![]() $M_\infty \models \varphi (\textbf {d})$
, then
$M_\infty \models \varphi (\textbf {d})$
, then
![]() $d \notin D$
. Since
$d \notin D$
. Since
![]() $q^\ast \leq q$
and
$q^\ast \leq q$
and
![]() $q \Vdash \psi ^\mu (\textbf {d})$
, we have
$q \Vdash \psi ^\mu (\textbf {d})$
, we have
![]() $q^\ast \Vdash \psi ^\mu (\textbf {d})$
. It follows from Lemma 3.11 that
$q^\ast \Vdash \psi ^\mu (\textbf {d})$
. It follows from Lemma 3.11 that
![]() $s^\ast \Vdash \psi ^\mu (\textbf {d})$
(note
$s^\ast \Vdash \psi ^\mu (\textbf {d})$
(note
![]() $F \subseteq \mathrm {dom}(f^{q^\ast })$
so
$F \subseteq \mathrm {dom}(f^{q^\ast })$
so
![]() $\psi ^\mu (\mathbf {d})$
is
$\psi ^\mu (\mathbf {d})$
is
![]() $\Sigma $
-over-
$\Sigma $
-over-
![]() $\mathcal {L}_{\mathrm {dom}(f^{q^\ast })}$
). Similarly, we have
$\mathcal {L}_{\mathrm {dom}(f^{q^\ast })}$
). Similarly, we have
![]() $s^\ast \Vdash \varphi ^\mu (\mathbf {d})$
. But since
$s^\ast \Vdash \varphi ^\mu (\mathbf {d})$
. But since
![]() $M_\infty \models \forall n(\psi ^\mu (n) \to \psi (n))$
and
$M_\infty \models \forall n(\psi ^\mu (n) \to \psi (n))$
and
![]() $M_\infty \models \forall n(\varphi ^\mu (n) \to \varphi (n))$
, it follows that
$M_\infty \models \forall n(\varphi ^\mu (n) \to \varphi (n))$
, it follows that
![]() $s^\ast \Vdash \psi (\mathbf {d}) \land \varphi (\mathbf {d})$
. This contradicts the fact that
$s^\ast \Vdash \psi (\mathbf {d}) \land \varphi (\mathbf {d})$
. This contradicts the fact that
![]() $p \Vdash \forall n(\psi (n) \leftrightarrow \neg \varphi (n))$
and
$p \Vdash \forall n(\psi (n) \leftrightarrow \neg \varphi (n))$
and
![]() $s^\ast \leq p$
.
$s^\ast \leq p$
.
This completes the proof that
![]() $M_\infty $
satisfies
$M_\infty $
satisfies
![]() $\Delta ^1_1$
-
$\Delta ^1_1$
-
![]() $\mathsf {CA}_0$
.
$\mathsf {CA}_0$
.
Remark 3.15. We are unable to extend our proof to show that
![]() $M_\infty $
satisfies the
$M_\infty $
satisfies the
![]() $\Pi ^1_1$
-separation principle (studied by Montalbán [Reference Montalbán10]). We do not know if
$\Pi ^1_1$
-separation principle (studied by Montalbán [Reference Montalbán10]). We do not know if
![]() $\Pi ^1_1$
-separation implies finite choice. If there is a model of
$\Pi ^1_1$
-separation implies finite choice. If there is a model of
![]() $\Pi ^1_1$
-separation and
$\Pi ^1_1$
-separation and
![]() $\mathsf {I}\Sigma ^1_1$
(such as an
$\mathsf {I}\Sigma ^1_1$
(such as an
![]() $\omega $
-model of
$\omega $
-model of
![]() $\Pi ^1_1$
-separation) which does not satisfy finite choice, then we would obtain a negative answer to [Reference Conidis2, Question 1.11] (using Theorem 1.5).
$\Pi ^1_1$
-separation) which does not satisfy finite choice, then we would obtain a negative answer to [Reference Conidis2, Question 1.11] (using Theorem 1.5).
Acknowledgments
We thank Richard A. Shore, Antonio Montalbán, Linda Brown Westrick, James Barnes, and the anonymous referees for many useful discussions and suggestions.
Funding
This work was partially supported by National Science Foundation grant DMS-1161175.