Let 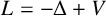$L=-\Delta +V$ be a Schrödinger operator in 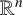${\mathbb R}^n$ with 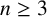$n\geq 3$, where 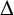$\Delta $ is the Laplace operator denoted by 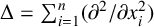$\Delta =\sum ^{n}_{i=1}({\partial ^{2}}/{\partial x_{i}^{2}})$ and the nonnegative potential V belongs to the reverse Hölder class $(RH)_{q}$ with 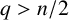$q>n/2$. For 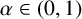$\alpha \in (0,1)$, we define the operator

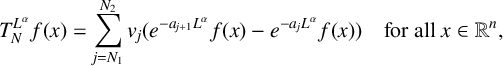$$ \begin{align*} T_N^{L^{\alpha}} f(x) =\sum_{j=N_1}^{N_2} v_j(e^{-a_{j+1}L^\alpha} f(x)-e^{-a_{j}L^\alpha} f(x)) \quad \mbox{for all }x\in \mathbb R^n, \end{align*} $$

where 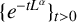$\{e^{-tL^\alpha } \}_{t>0}$ is the fractional heat semigroup of the operator L, 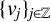$\{v_j\}_{j\in \mathbb Z}$ is a bounded real sequence and 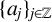$\{a_j\}_{j\in \mathbb Z}$ is an increasing real sequence.

We investigate the boundedness of the operator 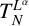$T_N^{L^{\alpha }}$ and the related maximal operator 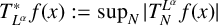$T^*_{L^{\alpha }}f(x):=\sup _N \vert T_N^{L^{\alpha }} f(x)\vert $ on the spaces 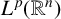$L^{p}(\mathbb {R}^{n})$ and 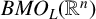$BMO_{L}(\mathbb {R}^{n})$, respectively. As extensions of 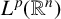$L^{p}(\mathbb {R}^{n})$, the boundedness of the operators 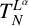$T_N^{L^{\alpha }}$ and 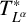$T^*_{L^{\alpha }}$ on the Morrey space 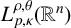$L^{\rho ,\theta }_{p,\kappa }(\mathbb {R}^{n})$ and the weak Morrey space 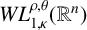$WL^{\rho ,\theta }_{1,\kappa }(\mathbb {R}^{n})$ has also been proved.