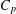Hostname: page-component-65f69f4695-thqfx Total loading time: 0 Render date: 2025-06-29T17:10:37.687Z Has data issue: false hasContentIssue false
  • English
  • Français

CONVOLUTION OF ORBITAL MEASURES ON SYMMETRIC SPACES OF TYPE $C_{p}$ AND 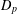$D_{p}$

Part of: Abstract harmonic analysis Lie algebras and Lie superalgebras Global differential geometry

Published online by Cambridge University Press:  11 November 2014

P. GRACZYK  and
P. SAWYER
P. GRACZYK
Affiliation:
Laboratoire de Mathématiques, LAREMA, Université d’Angers, 49045 Angers cedex 01, France email piotr.graczyk@univ-angers.fr
P. SAWYER*
Affiliation:
Department of Mathematics and Computer Science, Laurentian University, Sudbury, Ontario, Canada P3E 2C6 email psawyer@laurentian.ca
*
✉psawyer@laurentian.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the absolute continuity of the convolution 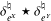${\it\delta}_{e^{X}}^{\natural }\star {\it\delta}_{e^{Y}}^{\natural }$ of two orbital measures on the symmetric spaces 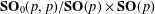$\mathbf{SO}_{0}(p,p)/\mathbf{SO}(p)\times \mathbf{SO}(p)$, 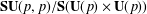$\mathbf{SU}(p,p)/\mathbf{S}(\mathbf{U}(p)\times \mathbf{U}(p))$ and 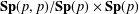$\mathbf{Sp}(p,p)/\mathbf{Sp}(p)\times \mathbf{Sp}(p)$. We prove sharp conditions on 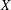$X$, 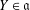$Y\in \mathfrak{a}$ for the existence of the density of the convolution measure. This measure intervenes in the product formula for the spherical functions.

Keywords

root systemsspherical functionssymmetric spacesnoncompact type

MSC classification

Primary: 43A90: Spherical functions
Secondary: 53C35: Symmetric spaces 17B05: Structure theory

Information

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 98 , Issue 2 , April 2015 , pp. 232 - 256
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Flensted-Jensen, M. and Koornwinder, T., ‘The convolution structure for Jacobi function expansions’, Ark. Mat. 11 (1973), 245–262.CrossRefGoogle Scholar
Friedberg, S. H., Insel, A. J. and Spence, L. E., Linear Algebra (Prentice-Hall, Upper Saddle River, NJ, 1997).Google Scholar
Graczyk, P., Loeb, J. J. and Zak, T., ‘Strong central limit theorem for isotropic random walks in Rd’, Probab. Theory Related Fields 151(1–2) (2011), 153–172.Google Scholar
Graczyk, P. and Sawyer, P., ‘The product formula for the spherical functions on symmetric spaces of noncompact type’, J. Lie Theory 13 (2003), 247–261.Google Scholar
Graczyk, P. and Sawyer, P., ‘Absolute continuity of convolutions of orbital measures on Riemannian symmetric spaces’, J. Funct. Anal. 259 (2010), 1759–1770.Google Scholar
Graczyk, P. and Sawyer, P., ‘A sharp criterion for the existence of the density in the product formula on symmetric spaces of type A n’, J. Lie Theory 20 (2010), 751–766.Google Scholar
Graczyk, P. and Sawyer, P., ‘On the product formula on noncompact Grassmannians’, Colloq. Math. 133 (2013), 145–167.Google Scholar
Helgason, S., Differential Geometry, Lie Groups, and Symmetric Spaces (Academic Press, New York, 1978).Google Scholar
Helgason, S., Groups and Geometric Analysis (Academic Press, Orlando, FL, 1984).Google Scholar
Helgason, S., Geometric Analysis on Symmetric Spaces, Mathematical Surveys and Monographs, 83 (American Mathematical Society, Providence, RI, 1994).Google Scholar
Jaworski, W., ‘Strong approximate transitivity, polynomial growth, and spread out random walks on locally compact groups’, Pacific J. Math. 170(2) (1995), 517–533.Google Scholar
Jaworski, W. and Raja, C. R. E., ‘The Choquet–Deny theorem and distal properties of totally disconnected locally compact groups of polynomial growth’, New York J. Math. 13 (2007), 159–174.Google Scholar
Koornwinder, T., ‘Jacobi polynomials. II. An analytic proof of the product formula’, SIAM J. Math. Anal. 5 (1974), 125–137.CrossRefGoogle Scholar
Lin, M. and Wittmann, R., ‘Convolution powers of spread-out probabilities’, Ann. Inst. Henri Poincaré Probab. Stat. 32(5) (1996), 661–667.Google Scholar
Ostrovskii, I. V., ‘Description of the I 0class in a special semigroup of probability measures’, Sov. Math. Dokl. 14 (1973), 525–529 (transl. Dokl. Akad. Nauk SSSR 209 (1973), 788–791).Google Scholar
Rösler, M., ‘Positive convolution structure for a class of Heckman–Opdam hypergeometric functions of type BC’, J. Funct. Anal. 258(8) (2010), 2779–2800.Google Scholar
Sawyer, P., ‘Spherical functions on SO0(p, q)∕SO(p) ×SO(q)’, Canad. Math. Bull. 42(4) (1999), 486–498.Google Scholar
Trukhina, I. P., ‘Arithmetic of spherically symmetric measures in Lobachevskij space’, Teor. Funkts. Funkts. Anal. Prilozh. 34 (1980), 136–146.Google Scholar
Voit, M., ‘Factorization of probability measures on symmetric hypergroups’, J. Aust. Math. Soc. 50(3) (1991), 417–467.Google Scholar