No CrossRef data available.
Article contents
EXPLICIT INTERPOLATION BOUNDS BETWEEN HARDY SPACE AND 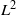 ${L}^{2} $
${L}^{2} $
Published online by Cambridge University Press: 18 July 2013
Abstract
Every bounded linear operator that maps 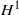 ${H}^{1} $ to
${H}^{1} $ to 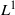 ${L}^{1} $ and
${L}^{1} $ and 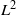 ${L}^{2} $ to
${L}^{2} $ to 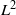 ${L}^{2} $ is bounded from
${L}^{2} $ is bounded from 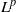 ${L}^{p} $ to
${L}^{p} $ to 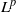 ${L}^{p} $ for each
${L}^{p} $ for each 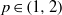 $p\in (1, 2)$, by a famous interpolation result of Fefferman and Stein. We prove
$p\in (1, 2)$, by a famous interpolation result of Fefferman and Stein. We prove 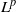 ${L}^{p} $-norm bounds that grow like
${L}^{p} $-norm bounds that grow like 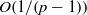 $O(1/ (p- 1))$ as
$O(1/ (p- 1))$ as 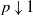 $p\downarrow 1$. This growth rate is optimal, and improves significantly on the previously known exponential bound
$p\downarrow 1$. This growth rate is optimal, and improves significantly on the previously known exponential bound 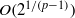 $O({2}^{1/ (p- 1)} )$. For
$O({2}^{1/ (p- 1)} )$. For 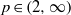 $p\in (2, \infty )$, we prove explicit
$p\in (2, \infty )$, we prove explicit 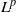 ${L}^{p} $ estimates on each bounded linear operator mapping
${L}^{p} $ estimates on each bounded linear operator mapping 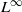 ${L}^{\infty } $ to bounded mean oscillation (
${L}^{\infty } $ to bounded mean oscillation (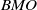 $\mathit{BMO}$) and
$\mathit{BMO}$) and 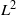 ${L}^{2} $ to
${L}^{2} $ to 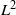 ${L}^{2} $. This
${L}^{2} $. This 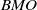 $\mathit{BMO}$ interpolation result implies the
$\mathit{BMO}$ interpolation result implies the 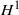 ${H}^{1} $ result above, by duality. In addition, we obtain stronger results by working with dyadic
${H}^{1} $ result above, by duality. In addition, we obtain stronger results by working with dyadic 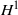 ${H}^{1} $ and dyadic
${H}^{1} $ and dyadic 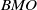 $\mathit{BMO}$. The proofs proceed by complex interpolation, after we develop an optimal dyadic ‘good lambda’ inequality for the dyadic
$\mathit{BMO}$. The proofs proceed by complex interpolation, after we develop an optimal dyadic ‘good lambda’ inequality for the dyadic  $\sharp $-maximal operator.
$\sharp $-maximal operator.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright ©2013 Australian Mathematical Publishing Association Inc.

