Hostname: page-component-848d4c4894-4rdrl Total loading time: 0 Render date: 2024-06-20T00:22:46.939Z Has data issue: false hasContentIssue false
  • English
  • Français

Finite Generation of the Extension Algebra Ext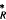(M, M)

Part of: Chain conditions, growth conditions, and other forms of finiteness Homological algebra Homological methods

Published online by Cambridge University Press:  09 April 2009

Rainer Schulz
Rainer Schulz
Affiliation:
Department of MathematicsNational University of SingaporeSingapore0511
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a module M Over an Artin algebra R, we discuss the question of whether the Yoneda extension algebra Ext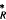(M, M) is finitely generated as an algebra. We give an answer for bounded modules M. (These are modules whose syzygies have direct summands of bounded lengths.)

MSC classification

Secondary: 16E40: (Co)homology of rings and algebras (e.g. Hochschild, cyclic, dihedral, etc.) 16P10: Finite rings and finite-dimensional algebras 18G15: Ext and Tor, generalizations, Künneth formula
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 59 , Issue 3 , December 1995 , pp. 366 - 374
Copyright
Copyright © Australian Mathematical Society 1995

References

[1]Anick, D. J., ‘A counterexample to a conjecture of Serre’, Ann. of Math. 115 (1982), 1–33.CrossRefGoogle Scholar
[2]Evens, L., ‘The cohomology ring of a finite group’, Trans. Amer. Math. Soc. 101 (1961), 224–239.Google Scholar
[3]Gasharov, V. N. and Peeva, I. V., ‘Boundedness versus periodicity over commutative local rings’, Trans. Amer. Math. Soc. 320 (1990), 569–580.CrossRefGoogle Scholar
[4]Gulliksen, T. and Levin, G., Homology of local rings, Queen's Papers in Pure and Applied Math. 20 (Queen's Univ., Kingston, 1969).Google Scholar
[5]Levin, G., ‘Two conjectures in the cohomology of local rings’, J. Algebra 30 (1974), 56–74.CrossRefGoogle Scholar
[6]Roos, J.-E., ‘Relation between the Poincaré-Betti series of loop spaces and local rings’, in: Lecture Notes in Math. 740 (Springer, Berlin, 1979)pp. 285–322.Google Scholar
[7]Rowen, L. H., Ring theory, I (Academic Press, Boston, 1988).Google Scholar
[8]Schulz, R., ‘Boundedness and periodicity of modules over QF rings’, J. Algebra 101 (1986), 450–469.Google Scholar
[9]Wilson, G. V., ‘Ultimately closed projective resolutions and rationality of Poincaré-Betti series’, Proc. Amer. Math. Soc. 88 (1983), 221–223.Google Scholar