Hostname: page-component-848d4c4894-wg55d Total loading time: 0 Render date: 2024-06-02T18:57:03.366Z Has data issue: false hasContentIssue false
  • English
  • Français

HARDY AND RELLICH INEQUALITIES ON THE COMPLEMENT OF CONVEX SETS

Part of: General theory in ordinary differential equations Partial differential equations Miscellaneous topics - Partial differential equations

Published online by Cambridge University Press:  21 December 2018

DEREK W. ROBINSON
DEREK W. ROBINSON*
Affiliation:
Mathematical Sciences Institute (CMA), Australian National University, Canberra, ACT 0200, Australia email derek.robinson@anu.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

We establish existence of weighted Hardy and Rellich inequalities on the spaces 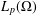$L_{p}(\unicode[STIX]{x1D6FA})$, where $\unicode[STIX]{x1D6FA}=\mathbf{R}^{d}\backslash K$ with 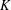$K$ a closed convex subset of 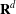$\mathbf{R}^{d}$. Let 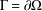$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$ denote the boundary of 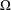$\unicode[STIX]{x1D6FA}$ and 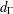$d_{\unicode[STIX]{x1D6E4}}$ the Euclidean distance to 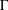$\unicode[STIX]{x1D6E4}$. We consider weighting functions 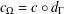$c_{\unicode[STIX]{x1D6FA}}=c\circ d_{\unicode[STIX]{x1D6E4}}$ with 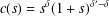$c(s)=s^{\unicode[STIX]{x1D6FF}}(1+s)^{\unicode[STIX]{x1D6FF}^{\prime }-\unicode[STIX]{x1D6FF}}$ and 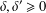$\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF}^{\prime }\geq 0$. Then the Hardy inequalities take the form

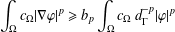$$\begin{eqnarray}\int _{\unicode[STIX]{x1D6FA}}c_{\unicode[STIX]{x1D6FA}}|\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D711}|^{p}\geq b_{p}\int _{\unicode[STIX]{x1D6FA}}c_{\unicode[STIX]{x1D6FA}}\,d_{\unicode[STIX]{x1D6E4}}^{-p}|\unicode[STIX]{x1D711}|^{p}\end{eqnarray}$$
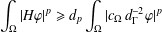and the Rellich inequalities are given by
$$\begin{eqnarray}\int _{\unicode[STIX]{x1D6FA}}|H\unicode[STIX]{x1D711}|^{p}\geq d_{p}\int _{\unicode[STIX]{x1D6FA}}|c_{\unicode[STIX]{x1D6FA}}\,d_{\unicode[STIX]{x1D6E4}}^{-2}\unicode[STIX]{x1D711}|^{p}\end{eqnarray}$$
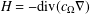 with $H=-\text{div}(c_{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D6FB})$. The constants 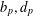$b_{p},d_{p}$ depend on the weighting parameters 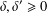$\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF}^{\prime }\geq 0$ and the Hausdorff dimension of the boundary. We compute the optimal constants in a broad range of situations.

Keywords

Hardy inequalityRellich inequality

MSC classification

Primary: 39B62: Functional inequalities, including subadditivity, convexity, etc.
Secondary: 34A40: Differential inequalities 35A23: Inequalities involving derivatives and differential and integral operators, inequalities for integrals 35R45: Partial differential inequalities
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 108 , Issue 1 , February 2020 , pp. 98 - 119
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avkhadiev, F. G., ‘Sharp constants in Hardy type inequalities’, Izv. Vyssh. Uchebn. Zaved. Mat. 2 (2015), 61–65.Google Scholar
Avkhadiev, F. G., ‘Hardy type L p-inequalities in r-close-to-convex domains’, Izv. Vyssh. Uchebn. Zaved. Mat. 2 (2015), 84–88.Google Scholar
Balinsky, A. A., Evans, W. D. and Lewis, R. L., The Analysis and Geometry of Hardy’s Inequality, Universitext (Springer, New York, 2015).Google Scholar
Barbatis, G., Filippas, S. and Tertikas, A., ‘A unified approach to improved L p Hardy inequalities’, Trans. Amer. Math. Soc. 356 (2004), 2169–2196.Google Scholar
Davies, E. B., ‘The Hardy constant’, Q. J. Math. 46 (1995), 417–431.Google Scholar
Davies, E. B. and Hinz, A. M., ‘Explicit constants for Rellich inequalities in L p(𝛺)’, Math. Z. 227 (1998), 511–523.Google Scholar
Evans, L. C. and Gariepy, R. F., Measure Theory and Fine Properties of Functions, Studies in Advanced Mathematics (CRC Press, Boca Raton, FL, 1992).Google Scholar
Hörmander, L., Notions of Convexity, Progress in Mathematics, 127 (Birkhäuser, Boston–Basel–Berlin, 1994).Google Scholar
Lehrbäck, J. and Robinson, D. W., ‘Uniqueness of diffusion on domains with rough boundaries’, Nonlinear Anal. Theory Methods Appl. 131 (2016), 60–80.Google Scholar
Lehrbäck, J. and Vähäkangas, A. V., ‘In between the inequalities of Sobolev and Hardy’, J. Funct. Anal. 271 (2016), 330–364.Google Scholar
Metafune, G., Sobajima, M. and Spina, C., ‘Weighted Calderón–Zygmund and Rellich inequalities in L p ’, Math. Ann. 361 (2015), 313–366.Google Scholar
Robinson, D. W., ‘Hardy inequalities, Rellich inequalities and local Dirichlet forms’, J. Evol. Equ. 18 (2018), 1521–1541.Google Scholar
Robinson, D. W. and Sikora, A., ‘Degenerate elliptic operators in one dimension’, J. Evol. Equ. 10 (2010), 731–759.Google Scholar
Simon, B., Convexity: An Analytic Viewpoint, Cambridge Tracts in Mathematics, 187 (Cambridge University Press, Cambridge, 2011).Google Scholar
Secchi, S., Smets, D. and Willem, M., ‘Remarks on a Hardy–Sobolev inequality’, C. R. Acad. Sci. Paris Sér. I 336 (2003), 811–815.Google Scholar
Ward, A. D., ‘On essential self-adjointness, confining potentials and the $L_{p}$ -Hardy inequality’, PhD Thesis, Massey University, Albany, New Zealand, 2014,http://hdl.handle.net/10179/5941.Google Scholar