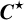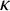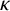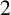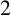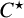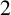1 Introduction
In [Reference Vdovina15], it was shown how to construct a two-dimensional CW-complex whose link at each vertex is a complete bipartite graph. In [Reference Kumjian and Pask6], generalising the work of [Reference Robertson and Steger10], certain combinatorial objects called higher-rank graphs were defined and then associated with a generalisation of a graph algebra [Reference Raeburn9, Ch. 1]. We combine these two methods to build an infinite family of
![]() $C^{\star }$
-algebras corresponding to complete bipartite graphs.
$C^{\star }$
-algebras corresponding to complete bipartite graphs.
We begin in Section 2 by detailing Vdovina’s construction of the CW-complexes, called tile complexes; the data we use to build these is called a tile system. In Sections 3 and 5, we associate adjacency matrices to the tile systems in two different ways: by considering the tiles as pointed and as unpointed geometrical objects, as in [Reference Konter and Vdovina5]. Since these adjacency matrices commute, they characterise the structure of a higher-rank graph, and induce a universal
![]() $C^{\star }$
-algebra: the higher-rank graph algebra. We use a result of [Reference Evans2] to calculate the K-groups of these algebras (Theorems 3.10 and 5.3).
$C^{\star }$
-algebra: the higher-rank graph algebra. We use a result of [Reference Evans2] to calculate the K-groups of these algebras (Theorems 3.10 and 5.3).
In Section 6, we show that the tile complexes have torsion-free homology groups given by
![]() $H_1 \cong \mathbb{Z}^{\alpha + \beta + 2},\ H_2 \cong \mathbb{Z}^{(\alpha - 1)(\beta - 1)}$
and
$H_1 \cong \mathbb{Z}^{\alpha + \beta + 2},\ H_2 \cong \mathbb{Z}^{(\alpha - 1)(\beta - 1)}$
and
![]() $H_n = 0$
otherwise.
$H_n = 0$
otherwise.
Finally, we explore extensions of these methods to
![]() $2t$
-gon systems, constructed analogously from two-dimensional complexes consisting entirely of
$2t$
-gon systems, constructed analogously from two-dimensional complexes consisting entirely of
![]() $2t$
-gons. In all, we associate
$2t$
-gons. In all, we associate
![]() $2$
-rank graph
$2$
-rank graph
![]() $C^{\star }$
-algebras to five systems, and compute their K-theory in the following theorems:
$C^{\star }$
-algebras to five systems, and compute their K-theory in the following theorems:
-
(1) pointed and unpointed tile systems (Theorems 3.10 and 5.3);
-
(2) pointed and unpointed
 $2t$
-gon systems for even t (Theorem 7.4 and Corollary 7.6);
$2t$
-gon systems for even t (Theorem 7.4 and Corollary 7.6); -
(3) pointed
 $2t$
-gon systems for arbitrary t (Theorem 7.11).
$2t$
-gon systems for arbitrary t (Theorem 7.11).
The respective systems in (2) directly generalise those in (1); however, there is another intuitive way of building
![]() $2t$
-gon systems from polyhedra, (3). We discuss the naturality of these generalisations in Section 7.
$2t$
-gon systems from polyhedra, (3). We discuss the naturality of these generalisations in Section 7.
Our approach differs from that of Robertson and Steger [Reference Robertson and Steger10], who focused on complexes with one vertex. Furthermore, we use the terminology of higher-rank graphs in order to demonstrate the large intersection between the fields of k-graphs and geometry.
Throughout this paper,
![]() $\alpha $
,
$\alpha $
,
![]() $\beta $
are positive integers, and
$\beta $
are positive integers, and
![]() $\kappa (\alpha ,\beta )$
denotes the complete connected bipartite graph on
$\kappa (\alpha ,\beta )$
denotes the complete connected bipartite graph on
![]() $\alpha $
white and
$\alpha $
white and
![]() $\beta $
black vertices.
$\beta $
black vertices.
2 The tile system associated to a bipartite graph
Definition 2.1. Let
![]() $t \in \mathbb {Z}$
satisfy
$t \in \mathbb {Z}$
satisfy
![]() $t \geq 2$
, and let
$t \geq 2$
, and let
![]() $A_1,\ldots ,A_n$
be a sequence of solid t-gons, with directed edges labelled from some set
$A_1,\ldots ,A_n$
be a sequence of solid t-gons, with directed edges labelled from some set
![]() $\mathcal {U}$
. By gluing together like-labelled edges (respecting their direction), we obtain a two-dimensional complex P. We call such a complex a t-polyhedron.
$\mathcal {U}$
. By gluing together like-labelled edges (respecting their direction), we obtain a two-dimensional complex P. We call such a complex a t-polyhedron.
The link at a vertex z of P is the graph obtained as the intersection of P with a small
![]() $2$
-sphere centred at z.
$2$
-sphere centred at z.
Theorem 2.2 (Vdovina [Reference Vdovina15])
Let G be a connected bipartite (undirected) graph on
![]() $\alpha $
white and
$\alpha $
white and
![]() $\beta $
black vertices, with edge set
$\beta $
black vertices, with edge set
![]() $E(G)$
. Then, for each
$E(G)$
. Then, for each
![]() $t \geq 1$
, we can construct a
$t \geq 1$
, we can construct a
![]() $2t$
-polyhedron
$2t$
-polyhedron
![]() $P(G)$
which has G as the link at each vertex.
$P(G)$
which has G as the link at each vertex.
We refer to [Reference Vdovina15], in which it was shown how to build such a
![]() $2t$
-polyhedron. The general method is as follows.
$2t$
-polyhedron. The general method is as follows.
Write
![]() $U'=\lbrace u_1 , \ldots , u_\alpha \rbrace $
for the set of white vertices of G, and
$U'=\lbrace u_1 , \ldots , u_\alpha \rbrace $
for the set of white vertices of G, and
![]() $V'=\lbrace v_1,\ldots , v_\beta \rbrace $
for the set of black vertices.
$V'=\lbrace v_1,\ldots , v_\beta \rbrace $
for the set of black vertices.
Let U be a set with
![]() $2t\alpha $
elements, indexed
$2t\alpha $
elements, indexed
![]() $u_i^1, u_i^2, \ldots , u_i^t, \bar {u}_i^1, \bar {u}_i^2,\ldots \bar {u}_i^t$
for each
$u_i^1, u_i^2, \ldots , u_i^t, \bar {u}_i^1, \bar {u}_i^2,\ldots \bar {u}_i^t$
for each
![]() $u_i \in U'$
, and let V be the corresponding set with
$u_i \in U'$
, and let V be the corresponding set with
![]() $2t\beta $
elements. Define fixed-point-free involutions
$2t\beta $
elements. Define fixed-point-free involutions
![]() $u_i^r \mapsto \bar {u}_i^r$
and
$u_i^r \mapsto \bar {u}_i^r$
and
![]() $v_i^r \mapsto \bar {v}_i^r$
in U and V, respectively.
$v_i^r \mapsto \bar {v}_i^r$
in U and V, respectively.
Each edge of the graph G joins an element of
![]() $U'$
to an element of
$U'$
to an element of
![]() $V'$
; for each edge
$V'$
; for each edge
![]() $e = u_p v_q$
, we construct a
$e = u_p v_q$
, we construct a
![]() $2t$
-gon
$2t$
-gon
![]() $A_e$
with a distinguished base vertex. Label the boundary of
$A_e$
with a distinguished base vertex. Label the boundary of
![]() $A_e$
anticlockwise, starting from the base, by the sequence
$A_e$
anticlockwise, starting from the base, by the sequence
![]() $u_p^1,v_q^1,u_p^2,v_q^2,\ldots , u_p^t,v_q^t$
, giving each side of the boundary a forward-directed arrow. We denote this pointed oriented
$u_p^1,v_q^1,u_p^2,v_q^2,\ldots , u_p^t,v_q^t$
, giving each side of the boundary a forward-directed arrow. We denote this pointed oriented
![]() $2t$
-gon by
$2t$
-gon by
![]() $A_e = [ u_p^1,v_q^1,\ldots , u_p^t,v_q^t ]$
. Then glue the
$A_e = [ u_p^1,v_q^1,\ldots , u_p^t,v_q^t ]$
. Then glue the
![]() $A_e$
together in the manner of Definition 2.1 in order to obtain a
$A_e$
together in the manner of Definition 2.1 in order to obtain a
![]() $2t$
-polyhedron
$2t$
-polyhedron
![]() $P(G)$
(Figure 1).
$P(G)$
(Figure 1).

Figure 1 Construction of a
![]() $2t$
-polyhedron. Give each side of a sequence of solid
$2t$
-polyhedron. Give each side of a sequence of solid
![]() $2t$
-gons a direction and a label from one of two sets U, V, and then glue together corresponding sides with respect to their direction.
$2t$
-gons a direction and a label from one of two sets U, V, and then glue together corresponding sides with respect to their direction.
Definition 2.3. In this paper, we mainly concern ourselves with
![]() $4$
-polyhedra, that is, those constructed by gluing together squares. We refer to
$4$
-polyhedra, that is, those constructed by gluing together squares. We refer to
![]() $4$
-polyhedra as tile complexes. For a connected bipartite graph G, write
$4$
-polyhedra as tile complexes. For a connected bipartite graph G, write
![]() $TC(G)$
for the tile complex
$TC(G)$
for the tile complex
![]() $P(G)$
, and define the set
$P(G)$
, and define the set
 $$ \begin{align} \mathcal{S}(G):= \lbrace A_e = \,&[ u_p^1, v_q^1, u_p^2, v_q^2 ], [ \bar{u}_p^1, \bar{v}_q^2, \bar{u}_p^2, \bar{v}_q^1 ], \nonumber\\ &[ u_p^2,v_q^2,u_p^1,v_q^1 ], [ \bar{u}_p^2, \bar{v}_q^1, \bar{u}_p^1, \bar{v}_q^2 ] \mid e = u_p v_q \in E(G) \rbrace. \end{align} $$
$$ \begin{align} \mathcal{S}(G):= \lbrace A_e = \,&[ u_p^1, v_q^1, u_p^2, v_q^2 ], [ \bar{u}_p^1, \bar{v}_q^2, \bar{u}_p^2, \bar{v}_q^1 ], \nonumber\\ &[ u_p^2,v_q^2,u_p^1,v_q^1 ], [ \bar{u}_p^2, \bar{v}_q^1, \bar{u}_p^1, \bar{v}_q^2 ] \mid e = u_p v_q \in E(G) \rbrace. \end{align} $$
We call the elements of
![]() $\mathcal {S}(G)$
pointed tiles. We define an equivalence relation which, for each
$\mathcal {S}(G)$
pointed tiles. We define an equivalence relation which, for each
![]() $A_e$
, identifies the four corresponding pointed tiles in (2-1). We denote by
$A_e$
, identifies the four corresponding pointed tiles in (2-1). We denote by
![]() $\mathcal {S}'(G)$
the quotient of
$\mathcal {S}'(G)$
the quotient of
![]() $\mathcal {S}(G)$
with respect to this relation, and we write
$\mathcal {S}(G)$
with respect to this relation, and we write
![]() $A_e' = ( u_p^1,v_q^1,u_p^2,v_q^2 )$
for the equivalence class of
$A_e' = ( u_p^1,v_q^1,u_p^2,v_q^2 )$
for the equivalence class of
![]() $A_e$
in
$A_e$
in
![]() $\mathcal {S}'(G)$
. Then
$\mathcal {S}'(G)$
. Then
![]() $\mathcal {S}'(G)$
is the set of geometric squares (that is, disregarding basepoint and orientation) in
$\mathcal {S}'(G)$
is the set of geometric squares (that is, disregarding basepoint and orientation) in
![]() $TC(G)$
. We call elements of
$TC(G)$
. We call elements of
![]() $\mathcal {S}'(G)$
unpointed tiles.
$\mathcal {S}'(G)$
unpointed tiles.
Notice that by placing the basepoint at the bottom-left vertex, we can arrange that the horizontal sides of each pointed tile are labelled by elements of U, and the vertical sides by elements of V, such that
![]() $\mathcal {S}(G) \subseteq U \times V \times U \times V$
. Indeed, the four tuples in (2-1) correspond to the four symmetries of a pointed tile that preserve this property (Figure 2).
$\mathcal {S}(G) \subseteq U \times V \times U \times V$
. Indeed, the four tuples in (2-1) correspond to the four symmetries of a pointed tile that preserve this property (Figure 2).
Note also that, by design, any two pointed tiles in
![]() $\mathcal {S}(G)$
are distinct, and any two adjacent sides of a tile uniquely determine the remaining two sides.
$\mathcal {S}(G)$
are distinct, and any two adjacent sides of a tile uniquely determine the remaining two sides.

Figure 2 Visualisation of tiles:
![]() $A=[x_1,y_1,x_2,y_2]$
,
$A=[x_1,y_1,x_2,y_2]$
,
![]() $B=[\bar {x}_1,\bar {y}_2,\bar {x}_2,\bar {y}_1]$
, and so on. These four pointed squares represent different pointed tiles, but the same unpointed tile.
$B=[\bar {x}_1,\bar {y}_2,\bar {x}_2,\bar {y}_1]$
, and so on. These four pointed squares represent different pointed tiles, but the same unpointed tile.
Definition 2.4. Let G be a connected bipartite graph on
![]() $\alpha $
white and
$\alpha $
white and
![]() $\beta $
black vertices. Let U, V be sets with
$\beta $
black vertices. Let U, V be sets with
![]() $|U| = 4\alpha $
,
$|U| = 4\alpha $
,
![]() $|V| = 4\beta $
, as constructed above, and let
$|V| = 4\beta $
, as constructed above, and let
![]() $\mathcal {S} = \mathcal {S}(G) \subseteq U \times V \times U \times V$
be the corresponding set of pointed tiles. We call the datum
$\mathcal {S} = \mathcal {S}(G) \subseteq U \times V \times U \times V$
be the corresponding set of pointed tiles. We call the datum
![]() $(G, U, V, \mathcal {S})$
a tile system.
$(G, U, V, \mathcal {S})$
a tile system.
This construction is closely related to, and indeed modelled on, that of a VH-datum, introduced in [Reference Wise16] and developed further in [Reference Burger and Mozes1].
3 The
 $C^{\star }$
-algebra corresponding to a tile system
$C^{\star }$
-algebra corresponding to a tile system
Definition 3.1. Let
![]() $(G, U, V, \mathcal {S})$
be a tile system, and
$(G, U, V, \mathcal {S})$
be a tile system, and
![]() $A=[x_1,y_1,x_2,y_2]$
and
$A=[x_1,y_1,x_2,y_2]$
and
![]() $B=[x_3,y_3,x_4,y_4]$
be pointed tiles in
$B=[x_3,y_3,x_4,y_4]$
be pointed tiles in
![]() $\mathcal {S}$
. We define two
$\mathcal {S}$
. We define two
![]() $4\alpha \beta \times 4\alpha \beta $
matrices
$4\alpha \beta \times 4\alpha \beta $
matrices
![]() $M_1,M_2$
with
$M_1,M_2$
with
![]() $AB$
th entry
$AB$
th entry
![]() $M_i(A,B)$
as follows:
$M_i(A,B)$
as follows:
 $$ \begin{align*} \begin{array}{r} M_1(A,B) = \left\{ \begin{array}{@{}l} 1 \quad \text{if}\ y_1 = \bar{y}_4\ \text{and}\ x_1 \neq \bar{x}_3, \\ 0 \quad \text{otherwise,} \end{array} \right.\\ \text{}\\ M_2(A,B) = \left\{ \begin{array}{@{}l} 1 \quad \text{if}\ x_2 = \bar{x}_3\ \text{and}\ y_1 \neq \bar{y}_3, \\ 0 \quad \text{otherwise,} \end{array} \right. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{r} M_1(A,B) = \left\{ \begin{array}{@{}l} 1 \quad \text{if}\ y_1 = \bar{y}_4\ \text{and}\ x_1 \neq \bar{x}_3, \\ 0 \quad \text{otherwise,} \end{array} \right.\\ \text{}\\ M_2(A,B) = \left\{ \begin{array}{@{}l} 1 \quad \text{if}\ x_2 = \bar{x}_3\ \text{and}\ y_1 \neq \bar{y}_3, \\ 0 \quad \text{otherwise,} \end{array} \right. \end{array} \end{align*} $$
as demonstrated in Figure 3. We call
![]() $M_1$
the horizontal adjacency matrix and
$M_1$
the horizontal adjacency matrix and
![]() $M_2$
the vertical adjacency matrix. If
$M_2$
the vertical adjacency matrix. If
![]() $M_i(A,B) = 1$
, we say that B is horizontally or vertically adjacent to A.
$M_i(A,B) = 1$
, we say that B is horizontally or vertically adjacent to A.

Figure 3 Horizontal and vertical adjacency: (a)
![]() $M_1(A,B) = 1$
, (b)
$M_1(A,B) = 1$
, (b)
![]() $M_2(A,B) = 1$
.
$M_2(A,B) = 1$
.
Definition 3.2. Let
![]() $(G, U, V, \mathcal {S})$
be a tile system, and let A, B, C be pointed tiles in
$(G, U, V, \mathcal {S})$
be a tile system, and let A, B, C be pointed tiles in
![]() $\mathcal {S}(G)$
such that
$\mathcal {S}(G)$
such that
![]() $M_1(A,B) = 1$
and
$M_1(A,B) = 1$
and
![]() $M_2(A,C) = 1$
. We say that the tile system
$M_2(A,C) = 1$
. We say that the tile system
![]() $(G, U, V, \mathcal {S})$
satisfies the unique common extension property (UCE property) if there exists a unique
$(G, U, V, \mathcal {S})$
satisfies the unique common extension property (UCE property) if there exists a unique
![]() $D \in \mathcal {S}$
such that
$D \in \mathcal {S}$
such that
![]() $M_2(B,D) = M_1(C,D) = 1$
.
$M_2(B,D) = M_1(C,D) = 1$
.
Proposition 3.3. Consider the complete bipartite graph
![]() $\kappa = \kappa (\alpha ,\beta )$
on
$\kappa = \kappa (\alpha ,\beta )$
on
![]() $\alpha \geq 2$
white and
$\alpha \geq 2$
white and
![]() $\beta \geq 2$
black vertices, and let
$\beta \geq 2$
black vertices, and let
![]() $(\kappa , U, V, \mathcal {S}(\kappa ))$
be a tile system with corresponding adjacency matrices
$(\kappa , U, V, \mathcal {S}(\kappa ))$
be a tile system with corresponding adjacency matrices
![]() $M_1$
,
$M_1$
,
![]() $M_2$
. Then:
$M_2$
. Then:
-
(1)
 $M_1$
and
$M_1$
and
 $M_2$
are symmetric and commute with each other;
$M_2$
are symmetric and commute with each other; -
(2) each row and column of
 $M_1$
and
$M_1$
and
 $M_2$
contains at least one nonzero element;
$M_2$
contains at least one nonzero element; -
(3)
 $(\kappa , U, V, \mathcal {S}(\kappa ))$
satisfies the UCE property.
$(\kappa , U, V, \mathcal {S}(\kappa ))$
satisfies the UCE property.
Proof. It is straightforward to verify that the matrices
![]() $M_1$
and
$M_1$
and
![]() $M_2$
are symmetric. Now, consider the pointed tile
$M_2$
are symmetric. Now, consider the pointed tile
![]() $A = [ u_i^1,v_j^1,u_i^2,v_j^2 ] \in \mathcal {S}(\kappa )$
(any other tiles may be dealt with in a similar manner), and let
$A = [ u_i^1,v_j^1,u_i^2,v_j^2 ] \in \mathcal {S}(\kappa )$
(any other tiles may be dealt with in a similar manner), and let
![]() $D = [ u_p^2,v_q^2,u_p^1,v_q^1 ] \in \mathcal {S}(\kappa )$
for some
$D = [ u_p^2,v_q^2,u_p^1,v_q^1 ] \in \mathcal {S}(\kappa )$
for some
![]() $p \neq i$
,
$p \neq i$
,
![]() $q \neq j$
. By the completeness of
$q \neq j$
. By the completeness of
![]() $\kappa $
and the fact that
$\kappa $
and the fact that
![]() $\alpha , \beta \geq 2$
, there are tiles
$\alpha , \beta \geq 2$
, there are tiles
![]() $B = [ \bar {u}_p^1, \bar {v}_j^2, \bar {u}_p^2, \bar {v}_j^1 ]$
and
$B = [ \bar {u}_p^1, \bar {v}_j^2, \bar {u}_p^2, \bar {v}_j^1 ]$
and
![]() $C = [ \bar {u}_i^2, \bar {v}_q^1, \bar {u}_i^1, \bar {v}_q^2 ]$
in
$C = [ \bar {u}_i^2, \bar {v}_q^1, \bar {u}_i^1, \bar {v}_q^2 ]$
in
![]() $\mathcal {S}(\kappa )$
such that
$\mathcal {S}(\kappa )$
such that
![]() $M_1(A,B) = M_2(B,D) = 1$
and
$M_1(A,B) = M_2(B,D) = 1$
and
![]() $M_2(A,C) = M_1(C,D) = 1$
(Figure 4), proving (2). Since any two adjacent sides of a tile determine the remaining sides, B and C are unique. So
$M_2(A,C) = M_1(C,D) = 1$
(Figure 4), proving (2). Since any two adjacent sides of a tile determine the remaining sides, B and C are unique. So
![]() $M_1 M_2 (A,D) = M_2 M_1 (A,D) \in \lbrace 0,1 \rbrace $
for all
$M_1 M_2 (A,D) = M_2 M_1 (A,D) \in \lbrace 0,1 \rbrace $
for all
![]() $A,D \in \mathcal {S}(\kappa )$
.
$A,D \in \mathcal {S}(\kappa )$
.

Figure 4 Proposition 3.3. Given tiles A and D as shown, tiles B and C are uniquely determined; hence,
![]() $M_1 M_2 = M_2 M_1$
. Likewise, given an initial tile A, a horizontally adjacent tile B and a vertically adjacent tile C, there is a unique tile D adjacent to both B and C: this is the UCE property.
$M_1 M_2 = M_2 M_1$
. Likewise, given an initial tile A, a horizontally adjacent tile B and a vertically adjacent tile C, there is a unique tile D adjacent to both B and C: this is the UCE property.
Similarly, given
![]() $A,B,C \in \mathcal {S}(\kappa )$
as above, D is the unique tile adjacent to both B and C, and so
$A,B,C \in \mathcal {S}(\kappa )$
as above, D is the unique tile adjacent to both B and C, and so
![]() $(\kappa , U, V, \mathcal {S}(\kappa ))$
has the UCE property.
$(\kappa , U, V, \mathcal {S}(\kappa ))$
has the UCE property.
We see shortly that a tile system is actually an example of a so-called k-rank graph (specifically a
![]() $2$
-rank graph), as introduced in [Reference Kumjian and Pask6] to build on work by [Reference Robertson and Steger10].
$2$
-rank graph), as introduced in [Reference Kumjian and Pask6] to build on work by [Reference Robertson and Steger10].
3.1 Higher-rank graphs
Definition 3.4. Let
![]() $\Lambda $
be a category such that
$\Lambda $
be a category such that
![]() $\operatorname {\mathrm {Ob}}(\Lambda )$
and
$\operatorname {\mathrm {Ob}}(\Lambda )$
and
![]() $\operatorname {\mathrm {Hom}}(\Lambda )$
are countable sets (that is, a countable small category), and identify
$\operatorname {\mathrm {Hom}}(\Lambda )$
are countable sets (that is, a countable small category), and identify
![]() $\operatorname {\mathrm {Ob}}(\Lambda )$
with the identity morphisms in
$\operatorname {\mathrm {Ob}}(\Lambda )$
with the identity morphisms in
![]() $\operatorname {\mathrm {Hom}}(\Lambda )$
. For a morphism
$\operatorname {\mathrm {Hom}}(\Lambda )$
. For a morphism
![]() $\lambda \in \operatorname {\mathrm {Hom}}_\Lambda (u,v)$
, we define range and source maps
$\lambda \in \operatorname {\mathrm {Hom}}_\Lambda (u,v)$
, we define range and source maps
![]() $r(\lambda ) = v$
and
$r(\lambda ) = v$
and
![]() $s(\lambda ) = u$
, respectively.
$s(\lambda ) = u$
, respectively.
Let
![]() $d : \Lambda \rightarrow \mathbb {N}^k$
be a functor, called the degree map, and let
$d : \Lambda \rightarrow \mathbb {N}^k$
be a functor, called the degree map, and let
![]() $\lambda \in \operatorname {\mathrm {Hom}}(\Lambda )$
. We call the pair
$\lambda \in \operatorname {\mathrm {Hom}}(\Lambda )$
. We call the pair
![]() $(\Lambda , d)$
a k-rank graph (or simply a k-graph) if, whenever
$(\Lambda , d)$
a k-rank graph (or simply a k-graph) if, whenever
![]() $d(\lambda ) = \mathbf {m} + \mathbf {n}$
for some
$d(\lambda ) = \mathbf {m} + \mathbf {n}$
for some
![]() $\mathbf {m},\mathbf {n} \in \mathbb {N}^k$
, we can find unique elements
$\mathbf {m},\mathbf {n} \in \mathbb {N}^k$
, we can find unique elements
![]() $\mu , \nu \in \operatorname {\mathrm {Hom}}(\Lambda )$
such that
$\mu , \nu \in \operatorname {\mathrm {Hom}}(\Lambda )$
such that
![]() $\lambda = \nu \mu $
, and
$\lambda = \nu \mu $
, and
![]() $d({\kern1.3pt}\mu )=\mathbf {m}$
,
$d({\kern1.3pt}\mu )=\mathbf {m}$
,
![]() $d(\nu ) = \mathbf {n}$
. Note that, for
$d(\nu ) = \mathbf {n}$
. Note that, for
![]() $\mu $
,
$\mu $
,
![]() $\nu $
to be composable, we must have
$\nu $
to be composable, we must have
![]() $r({\kern1.3pt}\mu ) = s(\nu )$
.
$r({\kern1.3pt}\mu ) = s(\nu )$
.
For
![]() $\mathbf {n} \in \mathbb {N}^k$
, we write
$\mathbf {n} \in \mathbb {N}^k$
, we write
![]() $\Lambda ^{\mathbf {n}} := d{}^{-1} (\mathbf {n})$
; by the above property,
$\Lambda ^{\mathbf {n}} := d{}^{-1} (\mathbf {n})$
; by the above property,
![]() $\Lambda ^{\mathbf {0}} = \operatorname {\mathrm {Ob}}(\Lambda )$
, and we call the elements of
$\Lambda ^{\mathbf {0}} = \operatorname {\mathrm {Ob}}(\Lambda )$
, and we call the elements of
![]() $\Lambda ^{\mathbf {0}}$
the vertices of
$\Lambda ^{\mathbf {0}}$
the vertices of
![]() $(\Lambda , d)$
; see [Reference Kumjian and Pask6].
$(\Lambda , d)$
; see [Reference Kumjian and Pask6].
We direct the reader to [Reference Sims, Raeburn and Yeend14], for example, for further details and standard examples of higher-rank graphs.
If E is a directed graph on n vertices, we can construct an
![]() $n \times n$
vertex matrix
$n \times n$
vertex matrix
![]() $M_E(i,j)$
with
$M_E(i,j)$
with
![]() $ij$
th entry
$ij$
th entry
![]() $1$
if there is an edge from i to j, and
$1$
if there is an edge from i to j, and
![]() $0$
otherwise.
$0$
otherwise.
If E, F are directed graphs with the same vertex set, whose associated vertex matrices
![]() $M_E$
,
$M_E$
,
![]() $M_F$
commute, then [Reference Kumjian and Pask6] showed that we can construct a
$M_F$
commute, then [Reference Kumjian and Pask6] showed that we can construct a
![]() $2$
-rank graph out of E and F. We use their method to prove the following proposition.
$2$
-rank graph out of E and F. We use their method to prove the following proposition.
Proposition 3.5. Let
![]() $\kappa = \kappa (\alpha ,\beta )$
be the complete bipartite graph on
$\kappa = \kappa (\alpha ,\beta )$
be the complete bipartite graph on
![]() $\alpha \geq 2$
white and
$\alpha \geq 2$
white and
![]() $\beta \geq 2$
black vertices, and let
$\beta \geq 2$
black vertices, and let
![]() $(\kappa , U, V, \mathcal {S}(\kappa ))$
be a tile system with adjacency matrices
$(\kappa , U, V, \mathcal {S}(\kappa ))$
be a tile system with adjacency matrices
![]() $M_1$
,
$M_1$
,
![]() $M_2$
. Then
$M_2$
. Then
![]() $(\kappa, U,V, \mathcal{S}(\kappa))$
has a 2-rank graph structure.
$(\kappa, U,V, \mathcal{S}(\kappa))$
has a 2-rank graph structure.
Proof. Following the method of Theorem 2.2, label the elements of the sets U, V
 $$ \begin{align*} U &= \lbrace u_1^1,u_1^2,\ldots , u_\alpha^1,u_\alpha^2, \bar{u}_1^1,\bar{u}_1^2,\ldots , \bar{u}_\alpha^1,\bar{u}_\alpha^2 \rbrace, \\ \quad V &= \lbrace v_1^1,v_1^2,\ldots , v_\beta^1,v_\beta^2, \bar{v}_1^1,\bar{v}_1^2, \ldots , \bar{v}_\beta^1,\bar{v}_\beta^2 \rbrace, \end{align*} $$
$$ \begin{align*} U &= \lbrace u_1^1,u_1^2,\ldots , u_\alpha^1,u_\alpha^2, \bar{u}_1^1,\bar{u}_1^2,\ldots , \bar{u}_\alpha^1,\bar{u}_\alpha^2 \rbrace, \\ \quad V &= \lbrace v_1^1,v_1^2,\ldots , v_\beta^1,v_\beta^2, \bar{v}_1^1,\bar{v}_1^2, \ldots , \bar{v}_\beta^1,\bar{v}_\beta^2 \rbrace, \end{align*} $$
where
![]() $u_1,\ldots , u_\alpha $
and
$u_1,\ldots , u_\alpha $
and
![]() $v_1,\ldots ,v_\beta $
are the white and black vertices of
$v_1,\ldots ,v_\beta $
are the white and black vertices of
![]() $\kappa $
, respectively. Construct the tile complex
$\kappa $
, respectively. Construct the tile complex
![]() $TC(\kappa )$
, and consider the set
$TC(\kappa )$
, and consider the set
![]() $\mathcal {S}(\kappa ) \subseteq U \times V \times U \times V$
of pointed tiles of
$\mathcal {S}(\kappa ) \subseteq U \times V \times U \times V$
of pointed tiles of
![]() $TC(\kappa )$
. Since
$TC(\kappa )$
. Since
![]() $\kappa $
is complete, there is for an edge joining each
$\kappa $
is complete, there is for an edge joining each
![]() $u_i$
and
$u_i$
and
![]() $v_j$
, thus:
$v_j$
, thus:
 $$ \begin{align*} \mathcal{S}(\kappa) = \lbrace &[ u_i^1,v_j^1,u_i^2,v_j^2 ], [ \bar{u}_i^1, \bar{v}_j^2, \bar{u}_i^2, \bar{v}_j^1 ], \\ &[ u_i^2,v_j^2,u_i^1,v_j^1 ], [ \bar{u}_i^2, \bar{v}_j^1, \bar{u}_i^1, \bar{v}_j^2 ] \mid\, 1 \leq i \leq \alpha, 1\leq j \leq \beta \rbrace. \end{align*} $$
$$ \begin{align*} \mathcal{S}(\kappa) = \lbrace &[ u_i^1,v_j^1,u_i^2,v_j^2 ], [ \bar{u}_i^1, \bar{v}_j^2, \bar{u}_i^2, \bar{v}_j^1 ], \\ &[ u_i^2,v_j^2,u_i^1,v_j^1 ], [ \bar{u}_i^2, \bar{v}_j^1, \bar{u}_i^1, \bar{v}_j^2 ] \mid\, 1 \leq i \leq \alpha, 1\leq j \leq \beta \rbrace. \end{align*} $$
Consider the corresponding adjacency matrices
![]() $M_1$
and
$M_1$
and
![]() $M_2$
as described in Definition 3.1, and note that they commute by Proposition 3.3. We can draw directed graphs E, F with the same vertex set
$M_2$
as described in Definition 3.1, and note that they commute by Proposition 3.3. We can draw directed graphs E, F with the same vertex set
![]() $E^0 = F^0 = \mathcal {S}(\kappa )$
. We draw a directed edge in E from A to B whenever
$E^0 = F^0 = \mathcal {S}(\kappa )$
. We draw a directed edge in E from A to B whenever
![]() $M_1(A,B) = 1$
, and in F from A to B whenever
$M_1(A,B) = 1$
, and in F from A to B whenever
![]() $M_2(A,B) = 1$
(Figure 5). Write
$M_2(A,B) = 1$
(Figure 5). Write
![]() $r_E$
,
$r_E$
,
![]() $s_E$
(respectively,
$s_E$
(respectively,
![]() $r_F$
,
$r_F$
,
![]() $s_F$
) for the maps describing the respective range and source of edges in
$s_F$
) for the maps describing the respective range and source of edges in
![]() $E^1$
(respectively,
$E^1$
(respectively,
![]() $F^1$
).
$F^1$
).

Figure 5 Visualisation of the tile system corresponding to the complete bipartite graph
![]() $\kappa (2,2)$
. Each vertex is labelled with an element of
$\kappa (2,2)$
. Each vertex is labelled with an element of
![]() $\mathcal {S}(\kappa )$
; a few labels have been shown here. A solid (dashed) arrow joins vertex A to B if and only if
$\mathcal {S}(\kappa )$
; a few labels have been shown here. A solid (dashed) arrow joins vertex A to B if and only if
![]() $M_1(A,B)=1$
(
$M_1(A,B)=1$
(
![]() $M_2(A,B)=1$
, respectively). Notice the commuting squares, giving the tile system a
$M_2(A,B)=1$
, respectively). Notice the commuting squares, giving the tile system a
![]() $2$
-rank graph structure: from any vertex A, follow a solid arrow, and then a dashed arrow to another vertex D, say. Then
$2$
-rank graph structure: from any vertex A, follow a solid arrow, and then a dashed arrow to another vertex D, say. Then
![]() $\theta $
defines a unique dashed-solid path from A to D. The
$\theta $
defines a unique dashed-solid path from A to D. The
![]() $1$
-skeleton of the
$1$
-skeleton of the
![]() $2$
-rank graph
$2$
-rank graph
![]() $\Lambda (\kappa (\alpha ,\beta ))$
is strongly connected only when
$\Lambda (\kappa (\alpha ,\beta ))$
is strongly connected only when
![]() $\alpha , \beta \geq 3$
.
$\alpha , \beta \geq 3$
.
Define the following edge sets:
![]() $E^1 \ast F^1 := \lbrace (\lambda ,\mu ) \in E^1 \times F^1 \mid r_E(\lambda ) = s_F({\kern1.3pt}\mu ) \rbrace $
and
$E^1 \ast F^1 := \lbrace (\lambda ,\mu ) \in E^1 \times F^1 \mid r_E(\lambda ) = s_F({\kern1.3pt}\mu ) \rbrace $
and
![]() $F^1 \ast E^1 := \lbrace ({\kern1.3pt}\mu ,\lambda ) \in F^1 \times E^1 \mid r_F({\kern1.3pt}\mu ) = s_E(\lambda ) \rbrace $
. Since
$F^1 \ast E^1 := \lbrace ({\kern1.3pt}\mu ,\lambda ) \in F^1 \times E^1 \mid r_F({\kern1.3pt}\mu ) = s_E(\lambda ) \rbrace $
. Since
![]() $M_1$
,
$M_1$
,
![]() $M_2$
commute, there is a unique bijection
$M_2$
commute, there is a unique bijection
![]() $\theta : E^1 \ast F^1 \rightarrow F^1 \ast E^1$
, mapping
$\theta : E^1 \ast F^1 \rightarrow F^1 \ast E^1$
, mapping
![]() $(\lambda ,\mu ) \mapsto ({\kern1.3pt}\mu ',\lambda ')$
such that
$(\lambda ,\mu ) \mapsto ({\kern1.3pt}\mu ',\lambda ')$
such that
![]() ${s_E(\lambda ) = s_F({\kern1.3pt}\mu ')}$
and
${s_E(\lambda ) = s_F({\kern1.3pt}\mu ')}$
and
![]() $r_F({\kern1.3pt}\mu ) = r_E(\lambda ')$
.
$r_F({\kern1.3pt}\mu ) = r_E(\lambda ')$
.
We construct a
![]() $2$
-rank graph
$2$
-rank graph
![]() $(\Lambda ,d)$
in the following way. Let
$(\Lambda ,d)$
in the following way. Let
![]() $\Lambda ^0 = \mathcal {S}(\kappa )$
, and for each
$\Lambda ^0 = \mathcal {S}(\kappa )$
, and for each
![]() $(m,n) \in \mathbb {N}^2$
, define the set
$(m,n) \in \mathbb {N}^2$
, define the set
![]() $W(m,n) := \lbrace (p,q) \in \mathbb {N}^2 \mid p \leq m, q \leq n \rbrace $
. Then an element of
$W(m,n) := \lbrace (p,q) \in \mathbb {N}^2 \mid p \leq m, q \leq n \rbrace $
. Then an element of
![]() $\Lambda ^{(m,n)}$
is a triple
$\Lambda ^{(m,n)}$
is a triple
![]() $(A,\lambda ,\mu ) = ((A(p,q))_{p,q},(\lambda (p,q))_{p,q},({\kern1.3pt}\mu (p,q))_{p,q})$
such that:
$(A,\lambda ,\mu ) = ((A(p,q))_{p,q},(\lambda (p,q))_{p,q},({\kern1.3pt}\mu (p,q))_{p,q})$
such that:
-
(a)
 $A(p,q) \in \mathcal {S}(\kappa )$
for some
$A(p,q) \in \mathcal {S}(\kappa )$
for some
 $(p,q) \in W(m,n)$
;
$(p,q) \in W(m,n)$
; -
(b)
 $\lambda (p,q) \in E^1$
for some
$\lambda (p,q) \in E^1$
for some
 $(p,q) \in W(m-1,n)$
;
$(p,q) \in W(m-1,n)$
; -
(c)
 $\mu (p,q) \in F^1$
for some
$\mu (p,q) \in F^1$
for some
 $(p,q) \in W(m,n-1)$
;
$(p,q) \in W(m,n-1)$
; -
(d)
 $s_E(\lambda (p,q)) = s_F({\kern1.3pt}\mu (p,q)) = A(p,q)$
;
$s_E(\lambda (p,q)) = s_F({\kern1.3pt}\mu (p,q)) = A(p,q)$
; -
(e)
 $r_E(\lambda (p,q)) = A(p+1,q)$
and
$r_E(\lambda (p,q)) = A(p+1,q)$
and
 $r_F({\kern1.3pt}\mu (p,q)) = A(p,q+1)$
;
$r_F({\kern1.3pt}\mu (p,q)) = A(p,q+1)$
; -
(f)
 $\theta (\lambda (p,q),\mu (p+1,q)) = ({\kern1.3pt}\mu (p,q),\lambda (p,q+1))$
,
$\theta (\lambda (p,q),\mu (p+1,q)) = ({\kern1.3pt}\mu (p,q),\lambda (p,q+1))$
,
whenever these conditions make sense. We write
![]() $\Lambda := \bigcup _{m,n \geq 0} \Lambda ^{(m,n)}$
, and define range and source maps
$\Lambda := \bigcup _{m,n \geq 0} \Lambda ^{(m,n)}$
, and define range and source maps
![]() $r(A,\lambda ,\mu ) := A(0,0)$
,
$r(A,\lambda ,\mu ) := A(0,0)$
,
![]() $s(A,\lambda ,\mu ):= A(m,n)$
, respectively. Note that two finite paths
$s(A,\lambda ,\mu ):= A(m,n)$
, respectively. Note that two finite paths
![]() $\mu $
,
$\mu $
,
![]() $\nu $
in such a directed graph E can be concatenated to give a path
$\nu $
in such a directed graph E can be concatenated to give a path
![]() $\nu \cdot \mu $
if and only if
$\nu \cdot \mu $
if and only if
![]() $s_E({\kern1.3pt}\mu ) = r_E(\nu )$
; consequently, ‘change the direction’ of the sources and ranges of the arrows here.
$s_E({\kern1.3pt}\mu ) = r_E(\nu )$
; consequently, ‘change the direction’ of the sources and ranges of the arrows here.
If
![]() $\varphi $
,
$\varphi $
,
![]() $\psi $
are paths of nonzero length m, n in E, F respectively, with
$\psi $
are paths of nonzero length m, n in E, F respectively, with
![]() $r_E(\varphi ) = s_F(\psi )$
, then there is a unique element
$r_E(\varphi ) = s_F(\psi )$
, then there is a unique element
![]() $\varphi \psi = (A,\lambda ,\mu ) \in \Lambda ^{(m,n)}$
such that
$\varphi \psi = (A,\lambda ,\mu ) \in \Lambda ^{(m,n)}$
such that
![]() $\varphi = \lambda (0,0) \cdots \lambda (m-1,0)$
and
$\varphi = \lambda (0,0) \cdots \lambda (m-1,0)$
and
![]() $\psi = \mu (m,0) \cdots \mu (m,n-1)$
. If, instead (or as well),
$\psi = \mu (m,0) \cdots \mu (m,n-1)$
. If, instead (or as well),
![]() $r_F(\psi ) = s_E(\varphi )$
, then there is a unique element
$r_F(\psi ) = s_E(\varphi )$
, then there is a unique element
![]() $\psi \varphi $
such that
$\psi \varphi $
such that
![]() $\varphi = \lambda (0,n) \cdots \lambda (m-1,n)$
and
$\varphi = \lambda (0,n) \cdots \lambda (m-1,n)$
and
![]() $\psi = \mu (0,0) \cdots \mu (0,n-1)$
(Figure 6).
$\psi = \mu (0,0) \cdots \mu (0,n-1)$
(Figure 6).

Figure 6 An element
![]() $(A,\lambda ,\mu )$
of
$(A,\lambda ,\mu )$
of
![]() $\Lambda ^{(m,n)}$
can be represented as an
$\Lambda ^{(m,n)}$
can be represented as an
![]() $m \times n$
grid. The isomorphism
$m \times n$
grid. The isomorphism
![]() $\theta $
defines commuting squares. Here is an element of
$\theta $
defines commuting squares. Here is an element of
![]() $\Lambda ^{(2,5)}$
.
$\Lambda ^{(2,5)}$
.
Then, given two elements
![]() $( A_1,\lambda _1,\mu _1) \in \Lambda ^{( m_1,n_1)}$
and
$( A_1,\lambda _1,\mu _1) \in \Lambda ^{( m_1,n_1)}$
and
![]() $( A_2,\lambda _2, \mu _2) \in \Lambda ^{( m_2,n_2)}$
such that
$( A_2,\lambda _2, \mu _2) \in \Lambda ^{( m_2,n_2)}$
such that
![]() $A_1 ( m_1,n_1) = A_2(0,0)$
, we can find a unique element
$A_1 ( m_1,n_1) = A_2(0,0)$
, we can find a unique element
![]() $( A_1,\lambda _1,\mu _1)( A_2,\lambda _2,\mu _2) = ( A_3,\lambda _3,\mu _3 )$
in
$( A_1,\lambda _1,\mu _1)( A_2,\lambda _2,\mu _2) = ( A_3,\lambda _3,\mu _3 )$
in
![]() $\Lambda ^{( m_1+m_2,n_1+n_2)}$
that satisfies
$\Lambda ^{( m_1+m_2,n_1+n_2)}$
that satisfies
-
(a)
 $A_3(p,q) = A_1(p,q)$
, and
$A_3(p,q) = A_1(p,q)$
, and
 $A_3(m+p,n+q) = A_2(p,q)$
;
$A_3(m+p,n+q) = A_2(p,q)$
; -
(b)
 $\lambda _3(p,q) = \lambda _1(p,q)$
, and
$\lambda _3(p,q) = \lambda _1(p,q)$
, and
 $\lambda _3(m+p,n+q) = \lambda _2(p,q)$
;
$\lambda _3(m+p,n+q) = \lambda _2(p,q)$
; -
(c)
 $\mu _3(p,q) = \mu _1(p,q)$
, and
$\mu _3(p,q) = \mu _1(p,q)$
, and
 $\mu _3(m+p,n+q) = \mu _2(p,q)$
,
$\mu _3(m+p,n+q) = \mu _2(p,q)$
,
whenever these conditions make sense. In this way, composition is defined in
![]() $\Lambda $
, and, by construction, we have associativity and the factorisation property of Definition 3.4. Thus
$\Lambda $
, and, by construction, we have associativity and the factorisation property of Definition 3.4. Thus
![]() $\Lambda $
, together with obvious degree functor
$\Lambda $
, together with obvious degree functor
![]() $d : (A,\lambda ,\mu ) \mapsto (m,n)$
for
$d : (A,\lambda ,\mu ) \mapsto (m,n)$
for
![]() $(A, \lambda , \mu ) \in \Lambda ^{(m,n)}$
, has the structure of a
$(A, \lambda , \mu ) \in \Lambda ^{(m,n)}$
, has the structure of a
![]() $2$
-rank graph, and we write
$2$
-rank graph, and we write
![]() $(\Lambda ,d) = \Lambda (\kappa )$
.
$(\Lambda ,d) = \Lambda (\kappa )$
.
Definition 3.6. Let
![]() $(\Lambda ,d)$
be a k-rank graph, let
$(\Lambda ,d)$
be a k-rank graph, let
![]() $\mathbf {n} \in \mathbb {N}^k$
, and let
$\mathbf {n} \in \mathbb {N}^k$
, and let
![]() $v \in \Lambda ^{\mathbf {0}}$
. Write
$v \in \Lambda ^{\mathbf {0}}$
. Write
![]() $\Lambda ^{\mathbf {n}}(v)$
for the set of morphisms in
$\Lambda ^{\mathbf {n}}(v)$
for the set of morphisms in
![]() $\Lambda ^{\mathbf {n}}$
which map onto v, that is,
$\Lambda ^{\mathbf {n}}$
which map onto v, that is,
![]() $\Lambda ^{\mathbf {n}}(v) := \lbrace \lambda \in \Lambda ^{\mathbf {n}} \mid r(\lambda ) = v\rbrace $
. We say that
$\Lambda ^{\mathbf {n}}(v) := \lbrace \lambda \in \Lambda ^{\mathbf {n}} \mid r(\lambda ) = v\rbrace $
. We say that
![]() $(\Lambda ,d)$
is row-finite if each set
$(\Lambda ,d)$
is row-finite if each set
![]() $\Lambda ^{\mathbf {n}}(v)$
is finite, and that
$\Lambda ^{\mathbf {n}}(v)$
is finite, and that
![]() $(\Lambda ,d)$
has no sources if each
$(\Lambda ,d)$
has no sources if each
![]() $\Lambda ^{\mathbf {n}}(v)$
is nonempty.
$\Lambda ^{\mathbf {n}}(v)$
is nonempty.
As an extension of the concept of a graph algebra (see [Reference Raeburn9]), we can associate a
![]() $C^{\star }$
-algebra to a k-rank graph.
$C^{\star }$
-algebra to a k-rank graph.
Definition 3.7. Let
![]() $\Lambda = (\Lambda ,d)$
be a row-finite k-rank graph with no sources. We define
$\Lambda = (\Lambda ,d)$
be a row-finite k-rank graph with no sources. We define
![]() $C^{\star }(\Lambda )$
to be the universal
$C^{\star }(\Lambda )$
to be the universal
![]() $C^{\star }$
-algebra generated by a family
$C^{\star }$
-algebra generated by a family
![]() $\lbrace s_\lambda \mid \lambda \in \Lambda \rbrace $
of partial isometries satisfying the following properties.
$\lbrace s_\lambda \mid \lambda \in \Lambda \rbrace $
of partial isometries satisfying the following properties.
-
(a) For all
 $u,v \in \Lambda^\mathbf{0}$
, we have
$u,v \in \Lambda^\mathbf{0}$
, we have
 $(s_v)^2 = s_v = s_v^*$
and
$(s_v)^2 = s_v = s_v^*$
and
 $s_us_v = 0$
whenever
$s_us_v = 0$
whenever
 $u \neq v$
.
$u \neq v$
. -
(b) If
 $r(\lambda ) = s({\kern1.3pt}\mu )$
for some
$r(\lambda ) = s({\kern1.3pt}\mu )$
for some
 $\lambda , \mu \in \Lambda $
, then
$\lambda , \mu \in \Lambda $
, then
 $s_{\mu \lambda } = s_\mu s_\lambda $
.
$s_{\mu \lambda } = s_\mu s_\lambda $
. -
(c) For all
 $\lambda \in \Lambda $
, we have
$\lambda \in \Lambda $
, we have
 $s_\lambda ^* s_\lambda = s_{s(\lambda )}$
.
$s_\lambda ^* s_\lambda = s_{s(\lambda )}$
. -
(d) For all vertices
 $v \in \Lambda ^{\mathbf {0}}$
and
$v \in \Lambda ^{\mathbf {0}}$
and
 $\mathbf {n} \in \mathbb {N}^k$
,
$\mathbf {n} \in \mathbb {N}^k$
,  $$ \begin{align*} s_v = \sum_{\lambda \in \Lambda^{\mathbf{n}}(v)} s_\lambda s_\lambda^*. \end{align*} $$
$$ \begin{align*} s_v = \sum_{\lambda \in \Lambda^{\mathbf{n}}(v)} s_\lambda s_\lambda^*. \end{align*} $$
Note that, without the row-finiteness condition, property (d) is not well defined.
Theorem 3.8 (Evans [Reference Evans2, Proposition 4.4])
Let
![]() $\Lambda $
be a row-finite
$\Lambda $
be a row-finite
![]() $2$
-graph with no sources, finite vertex set
$2$
-graph with no sources, finite vertex set
![]() $\Lambda ^{\mathbf {0}}$
, and vertex matrices
$\Lambda ^{\mathbf {0}}$
, and vertex matrices
![]() $M_E$
,
$M_E$
,
![]() $M_F$
. Then
$M_F$
. Then
 $$ \begin{align*} K_0 (C^{\star} (\Lambda)) &\cong \mathbb{Z}^{r_0} \oplus \operatorname{\mathrm{tor}}(\operatorname{\mathrm{coker}}(\mathbf{1}-M_E^T, \mathbf{1}-M_F^T)), \\ K_1(C^{\star} (\Lambda)) &\cong \mathbb{Z}^{r_1} \oplus \operatorname{\mathrm{tor}}(\operatorname{\mathrm{coker}}(\mathbf{1}-M_E, \mathbf{1}-M_F)), \end{align*} $$
$$ \begin{align*} K_0 (C^{\star} (\Lambda)) &\cong \mathbb{Z}^{r_0} \oplus \operatorname{\mathrm{tor}}(\operatorname{\mathrm{coker}}(\mathbf{1}-M_E^T, \mathbf{1}-M_F^T)), \\ K_1(C^{\star} (\Lambda)) &\cong \mathbb{Z}^{r_1} \oplus \operatorname{\mathrm{tor}}(\operatorname{\mathrm{coker}}(\mathbf{1}-M_E, \mathbf{1}-M_F)), \end{align*} $$
where
 $$ \begin{align*} r_0 &:= \operatorname{\mathrm{rk}}(\operatorname{\mathrm{coker}}(\mathbf{1}-M_E^T, \mathbf{1}-M_F^T)) + \operatorname{\mathrm{rk}}(\operatorname{\mathrm{coker}} (\mathbf{1}-M_E,\mathbf{1}-M_F) ), \\ r_1 &:= \operatorname{\mathrm{rk}}(\operatorname{\mathrm{coker}}(\mathbf{1}-M_E^T, \mathbf{1}-M_F^T)) + \operatorname{\mathrm{rk}}(\operatorname{\mathrm{coker}}(\mathbf{1}-M_E,\mathbf{1}-M_F) ), \end{align*} $$
$$ \begin{align*} r_0 &:= \operatorname{\mathrm{rk}}(\operatorname{\mathrm{coker}}(\mathbf{1}-M_E^T, \mathbf{1}-M_F^T)) + \operatorname{\mathrm{rk}}(\operatorname{\mathrm{coker}} (\mathbf{1}-M_E,\mathbf{1}-M_F) ), \\ r_1 &:= \operatorname{\mathrm{rk}}(\operatorname{\mathrm{coker}}(\mathbf{1}-M_E^T, \mathbf{1}-M_F^T)) + \operatorname{\mathrm{rk}}(\operatorname{\mathrm{coker}}(\mathbf{1}-M_E,\mathbf{1}-M_F) ), \end{align*} $$
![]() $| \Lambda ^{\mathbf {0}}| = n$
,
$| \Lambda ^{\mathbf {0}}| = n$
,
![]() $\mathbf {1}$
is the
$\mathbf {1}$
is the
![]() $n \times n$
identity matrix,
$n \times n$
identity matrix,
![]() $({}\ast {} ,{} \ast {})$
denotes the corresponding block
$({}\ast {} ,{} \ast {})$
denotes the corresponding block
![]() $n \times 2n$
matrix,
$n \times 2n$
matrix,
![]() $\operatorname {\mathrm {rk}}(\mathfrak {G})$
is the torsion-free rank of a finitely generated Abelian group
$\operatorname {\mathrm {rk}}(\mathfrak {G})$
is the torsion-free rank of a finitely generated Abelian group
![]() $\mathfrak {G}$
, and
$\mathfrak {G}$
, and
![]() $\operatorname {\mathrm {tor}}(\mathfrak {G})$
is the torsion part of
$\operatorname {\mathrm {tor}}(\mathfrak {G})$
is the torsion part of
![]() $\mathfrak {G}$
.
$\mathfrak {G}$
.
Corollary 3.9. Let
![]() $\kappa = \kappa (\alpha ,\beta )$
be the complete bipartite graph on
$\kappa = \kappa (\alpha ,\beta )$
be the complete bipartite graph on
![]() $\alpha \geq 2$
white and
$\alpha \geq 2$
white and
![]() $\beta \geq 2$
black vertices, and let
$\beta \geq 2$
black vertices, and let
![]() $(\kappa ,U,V,\mathcal {S}(\kappa ))$
be a tile system with adjacency matrices
$(\kappa ,U,V,\mathcal {S}(\kappa ))$
be a tile system with adjacency matrices
![]() $M_1$
,
$M_1$
,
![]() $M_2$
as in Definition 3.1. For simplicity, we write
$M_2$
as in Definition 3.1. For simplicity, we write
![]() $C^{\star }(\kappa ) = C^{\star }(\Lambda (\kappa ))$
. Then
$C^{\star }(\kappa ) = C^{\star }(\Lambda (\kappa ))$
. Then
where
![]() $r := \operatorname {\mathrm {rk}} (\operatorname {\mathrm {coker}}(\mathbf {1}-M_1^T, \mathbf {1}-M_2^T))$
.
$r := \operatorname {\mathrm {rk}} (\operatorname {\mathrm {coker}}(\mathbf {1}-M_1^T, \mathbf {1}-M_2^T))$
.
Proof. Firstly,
![]() $\alpha , \beta < \infty $
by assumption, and by the UCE property of the tile system (Proposition 3.3) we know that each row and column of
$\alpha , \beta < \infty $
by assumption, and by the UCE property of the tile system (Proposition 3.3) we know that each row and column of
![]() $M_1$
and
$M_1$
and
![]() $M_2$
has at least one nonzero element. Hence,
$M_2$
has at least one nonzero element. Hence,
![]() $\Lambda (\kappa )$
is row-finite, has no sources, and satisfies
$\Lambda (\kappa )$
is row-finite, has no sources, and satisfies
![]() $|\Lambda (\kappa )^{\mathbf {0}}| = 4\alpha \beta $
, whence the result follows from Theorem 3.8.
$|\Lambda (\kappa )^{\mathbf {0}}| = 4\alpha \beta $
, whence the result follows from Theorem 3.8.
Theorem 3.10 (K-groups for pointed tile systems)
Let
![]() $a,b \ge 0$
. Let
$a,b \ge 0$
. Let
![]() ${\kappa (a+2,b+2)}$
be the complete bipartite graph on
${\kappa (a+2,b+2)}$
be the complete bipartite graph on
![]() $a+2$
white and
$a+2$
white and
![]() $b+2$
black vertices. Without loss of generality, we assume that
$b+2$
black vertices. Without loss of generality, we assume that
![]() $a\leq b$
. Write
$a\leq b$
. Write
![]() $l := \operatorname {\mathrm {lcm}} ( a, b )$
, and
$l := \operatorname {\mathrm {lcm}} ( a, b )$
, and
![]() $g := \gcd ( a, b )$
. Then, for
$g := \gcd ( a, b )$
. Then, for
![]() $\epsilon = 0,1$
, we have the following assertions.
$\epsilon = 0,1$
, we have the following assertions.
-
(1) If
 $a=b=0$
, then
$a=b=0$
, then
 $K_\epsilon (C^{\star } (\kappa (a+2,b+2))) = K_\epsilon (C^{\star } (\kappa (2,2))) \cong \mathbb {Z}^8$
.
$K_\epsilon (C^{\star } (\kappa (a+2,b+2))) = K_\epsilon (C^{\star } (\kappa (2,2))) \cong \mathbb {Z}^8$
. -
(2) If
 $a=0,1$
and
$a=0,1$
and
 $b \geq 1$
, then
$b \geq 1$
, then  $$ \begin{align*} K_\epsilon (C^{\star} (\kappa (a+2,b+2))) \cong (\mathbb{Z}/b)^2 \oplus \mathbb{Z}^{4(b+1)}. \end{align*} $$
$$ \begin{align*} K_\epsilon (C^{\star} (\kappa (a+2,b+2))) \cong (\mathbb{Z}/b)^2 \oplus \mathbb{Z}^{4(b+1)}. \end{align*} $$
-
(3) If
 $a,b \geq 2$
and
$a,b \geq 2$
and
 $a,b$
are coprime, then
$a,b$
are coprime, then  $$ \begin{align*} K_\epsilon (C^{\star} (\kappa (a+2,b+2))) \cong (\mathbb{Z}/a)^{b-a} \oplus ( \mathbb{Z}/ab )^{a+1} \oplus \mathbb{Z}^{2(a+1)(b+1)}. \end{align*} $$
$$ \begin{align*} K_\epsilon (C^{\star} (\kappa (a+2,b+2))) \cong (\mathbb{Z}/a)^{b-a} \oplus ( \mathbb{Z}/ab )^{a+1} \oplus \mathbb{Z}^{2(a+1)(b+1)}. \end{align*} $$
-
(4) If
 $a,b \geq 2$
and
$a,b \geq 2$
and
 $a,b$
are not coprime, then where
$a,b$
are not coprime, then where $$ \begin{align*} K_\epsilon(C^{\star} (\kappa(a+2,b+2))) \cong (\mathbb{Z}/a)^{b-a} \oplus ( \mathbb{Z}/l )^{a+1} \oplus ( \mathbb{Z}/g)^{a+2} \oplus \mathbb{Z}^{2(a+1)(b+1)}, \end{align*} $$
$$ \begin{align*} K_\epsilon(C^{\star} (\kappa(a+2,b+2))) \cong (\mathbb{Z}/a)^{b-a} \oplus ( \mathbb{Z}/l )^{a+1} \oplus ( \mathbb{Z}/g)^{a+2} \oplus \mathbb{Z}^{2(a+1)(b+1)}, \end{align*} $$
 $(\mathbb {Z}/a)^0$
is defined to be the trivial group in the case that
$(\mathbb {Z}/a)^0$
is defined to be the trivial group in the case that
 $a=b$
.
$a=b$
.
Proof. We begin by proving (3) and (4), since (1) and (2) are special cases thereof.
Assume that
![]() $a,b \geq 2$
. Write
$a,b \geq 2$
. Write
![]() $\alpha = a+2$
and
$\alpha = a+2$
and
![]() $\beta = b+2$
, and for
$\beta = b+2$
, and for
![]() $1 \leq i \leq \alpha $
,
$1 \leq i \leq \alpha $
,
![]() $1 \leq j \leq \beta $
, let
$1 \leq j \leq \beta $
, let
![]() $A_{ij}$
denote the pointed tile
$A_{ij}$
denote the pointed tile
![]() $[ u_i^1,v_j^1,u_i^2,v_j^2] \in \mathcal {S}(\kappa )$
. Similarly, write
$[ u_i^1,v_j^1,u_i^2,v_j^2] \in \mathcal {S}(\kappa )$
. Similarly, write
![]() $B_{ij} := [ \bar {u}_i^1, \bar {v}_j^2, \bar {u}_i^2, \bar {v}_j^1 ]$
,
$B_{ij} := [ \bar {u}_i^1, \bar {v}_j^2, \bar {u}_i^2, \bar {v}_j^1 ]$
,
![]() $C_{ij} := [ \bar {u}_i^2, \bar {v}_j^1, \bar {u}_i^1, \bar {v}_j^2 ]$
,
$C_{ij} := [ \bar {u}_i^2, \bar {v}_j^1, \bar {u}_i^1, \bar {v}_j^2 ]$
,
![]() $D_{ij} := [ u_i^2,v_j^2,u_i^1,v_j^1 ]$
for the tiles with the same edge labels as the horizontal reflection, vertical reflection, and rotation by
$D_{ij} := [ u_i^2,v_j^2,u_i^1,v_j^1 ]$
for the tiles with the same edge labels as the horizontal reflection, vertical reflection, and rotation by
![]() $\pi $
of
$\pi $
of
![]() $A_{ij}$
, respectively. Then
$A_{ij}$
, respectively. Then
![]() $\mathcal {S}(\kappa ) = \lbrace A_{ij},B_{ij},C_{ij},D_{ij} \mid 1 \leq i \leq \alpha , 1 \leq j \leq \beta \rbrace $
, and
$\mathcal {S}(\kappa ) = \lbrace A_{ij},B_{ij},C_{ij},D_{ij} \mid 1 \leq i \leq \alpha , 1 \leq j \leq \beta \rbrace $
, and
 $$ \begin{align} \operatorname{\mathrm{coker}} = \bigg\langle S \in \mathcal{S}(\kappa) \bigg\vert\, S = \sum_{T \in \mathcal{S}(\kappa)} M_1(S,T)\cdot T = \sum_{T \in \mathcal{S}(\kappa)} M_2(S,T)\cdot T \bigg\rangle , \end{align} $$
$$ \begin{align} \operatorname{\mathrm{coker}} = \bigg\langle S \in \mathcal{S}(\kappa) \bigg\vert\, S = \sum_{T \in \mathcal{S}(\kappa)} M_1(S,T)\cdot T = \sum_{T \in \mathcal{S}(\kappa)} M_2(S,T)\cdot T \bigg\rangle , \end{align} $$
where
![]() $\operatorname {\mathrm {coker}} := \operatorname {\mathrm {coker}}(\mathbf {1}-M_1^T,\mathbf {1}-M_2^T)$
. Now fix some
$\operatorname {\mathrm {coker}} := \operatorname {\mathrm {coker}}(\mathbf {1}-M_1^T,\mathbf {1}-M_2^T)$
. Now fix some
![]() $p \in \lbrace 1 ,\ldots , \alpha \rbrace $
and
$p \in \lbrace 1 ,\ldots , \alpha \rbrace $
and
![]() $q \in \lbrace 1 , \ldots , \beta \rbrace $
, and notice that:
$q \in \lbrace 1 , \ldots , \beta \rbrace $
, and notice that:
-
•
 $M_1(A_{pq}, T) = 1$
if and only if
$M_1(A_{pq}, T) = 1$
if and only if
 $T = B_{iq}$
, and
$T = B_{iq}$
, and
 $M_1(B_{pq}, T) = 1$
if and only if
$M_1(B_{pq}, T) = 1$
if and only if
 $T = A_{iq}$
, for some
$T = A_{iq}$
, for some
 $i \neq p$
;
$i \neq p$
; -
•
 $M_1(C_{pq}, T) = 1$
if and only if
$M_1(C_{pq}, T) = 1$
if and only if
 $T = D_{iq}$
, and
$T = D_{iq}$
, and
 $M_1(D_{pq}, T) = 1$
if and only if
$M_1(D_{pq}, T) = 1$
if and only if
 $T = C_{iq}$
, for some
$T = C_{iq}$
, for some
 $i \neq p$
;
$i \neq p$
; -
•
 $M_2(A_{pq}, T) = 1$
if and only if
$M_2(A_{pq}, T) = 1$
if and only if
 $T = C_{pj}$
, and
$T = C_{pj}$
, and
 $M_2(B_{pq}, T) = 1$
if and only if
$M_2(B_{pq}, T) = 1$
if and only if
 $T = D_{pj}$
, for some
$T = D_{pj}$
, for some
 $j \neq q$
;
$j \neq q$
; -
•
 $M_2(C_{pq}, T) = 1$
if and only if
$M_2(C_{pq}, T) = 1$
if and only if
 $T = A_{pj}$
, and
$T = A_{pj}$
, and
 $M_2(D_{pq}, T) = 1$
if and only if
$M_2(D_{pq}, T) = 1$
if and only if
 $T = B_{pj}$
, for some
$T = B_{pj}$
, for some
 $j \neq q$
.
$j \neq q$
.
Hence, the relations of (3-1) are equations of the form
![]() $A_{pq} = \sum _{i \neq p} B_{iq} = \sum _{j \neq q} C_{pj}$
, and so on for each
$A_{pq} = \sum _{i \neq p} B_{iq} = \sum _{j \neq q} C_{pj}$
, and so on for each
![]() $B_{pq}$
,
$B_{pq}$
,
![]() $C_{pq}$
,
$C_{pq}$
,
![]() $D_{pq}$
. In particular, we can write
$D_{pq}$
. In particular, we can write
![]() $B_{pq} = \sum _{i \neq p} A_{iq}$
and
$B_{pq} = \sum _{i \neq p} A_{iq}$
and
![]() $C_{pq} = \sum _{j \neq q} A_{pj}$
so that
$C_{pq} = \sum _{j \neq q} A_{pj}$
so that
 $$ \begin{align*} A_{pq} = (\alpha - 1)A_{pq} + (\alpha - 2)\sum_{i \neq p}A_{iq} \quad\text{and}\quad A_{pq} = (\beta - 1)A_{pq} + (\beta - 2)\sum_{j \neq q}A_{pj}. \end{align*} $$
$$ \begin{align*} A_{pq} = (\alpha - 1)A_{pq} + (\alpha - 2)\sum_{i \neq p}A_{iq} \quad\text{and}\quad A_{pq} = (\beta - 1)A_{pq} + (\beta - 2)\sum_{j \neq q}A_{pj}. \end{align*} $$
Define
![]() $J_q := \sum _{i=1}^\alpha A_{iq}$
, and
$J_q := \sum _{i=1}^\alpha A_{iq}$
, and
![]() $I_p := \sum _{j=1}^\beta A_{pj}$
. Then
$I_p := \sum _{j=1}^\beta A_{pj}$
. Then
![]() $(\alpha - 2)J_q = (\beta - 2)I_p = 0$
, and, viewing the sum of all the tiles
$(\alpha - 2)J_q = (\beta - 2)I_p = 0$
, and, viewing the sum of all the tiles
![]() $A_{ij}$
both as the sum of all the
$A_{ij}$
both as the sum of all the
![]() $I_i$
and of the
$I_i$
and of the
![]() $J_j$
, we conclude that
$J_j$
, we conclude that
![]() $g\Sigma = 0$
, where
$g\Sigma = 0$
, where
![]() $\Sigma := \sum _{i,j} A_{ij}$
.
$\Sigma := \sum _{i,j} A_{ij}$
.
Now, we can also write
![]() $D_{pq}$
(and all of the relevant relations) in terms of the
$D_{pq}$
(and all of the relevant relations) in terms of the
![]() $A_{ij}$
, namely
$A_{ij}$
, namely
![]() $D_{pq} = \sum _{i \neq p} \sum _{j \neq q} A_{ij}$
. Hence, we can remove all the
$D_{pq} = \sum _{i \neq p} \sum _{j \neq q} A_{ij}$
. Hence, we can remove all the
![]() $B_{pq}$
,
$B_{pq}$
,
![]() $C_{pq}$
, and
$C_{pq}$
, and
![]() $D_{pq}$
from the list of generators of
$D_{pq}$
from the list of generators of
![]() $\operatorname {\mathrm {coker}}$
, yielding
$\operatorname {\mathrm {coker}}$
, yielding
 $$ \begin{align} \operatorname{\mathrm{coker}} &= \langle A_{pq} \mid\, (\alpha -2)J_q = (\beta -2)I_p = 0, J_q = \textstyle\sum_i A_{iq}, \nonumber\\ & \quad I_p = \textstyle\sum_j A_{pj}, \text{ for } 1 \leq p \leq \alpha, 1 \leq q \leq \beta \rangle. \end{align} $$
$$ \begin{align} \operatorname{\mathrm{coker}} &= \langle A_{pq} \mid\, (\alpha -2)J_q = (\beta -2)I_p = 0, J_q = \textstyle\sum_i A_{iq}, \nonumber\\ & \quad I_p = \textstyle\sum_j A_{pj}, \text{ for } 1 \leq p \leq \alpha, 1 \leq q \leq \beta \rangle. \end{align} $$
We have the following equalities:
 $$ \begin{align*} A_{p1} = I_p - \sum_{j=2}^\beta A_{pj},\quad A_{1q} = J_q - \sum_{i=2}^\alpha A_{iq},\quad I_1 = \Sigma - \sum_{i=2}^\alpha I_i,\quad J_1 = \Sigma - \sum_{j=2}^\beta J_j. \end{align*} $$
$$ \begin{align*} A_{p1} = I_p - \sum_{j=2}^\beta A_{pj},\quad A_{1q} = J_q - \sum_{i=2}^\alpha A_{iq},\quad I_1 = \Sigma - \sum_{i=2}^\alpha I_i,\quad J_1 = \Sigma - \sum_{j=2}^\beta J_j. \end{align*} $$
Furthermore,
![]() $A_{11}$
may be expressed in terms of
$A_{11}$
may be expressed in terms of
![]() $\Sigma $
,
$\Sigma $
,
![]() $I_p$
,
$I_p$
,
![]() $J_q$
, and
$J_q$
, and
![]() $A_{pq}$
for
$A_{pq}$
for
![]() $p,q \geq 2$
, and so, after a sequence of Tietze transformations on (3-2), we find that
$p,q \geq 2$
, and so, after a sequence of Tietze transformations on (3-2), we find that
where
![]() $g:= \gcd (\alpha -2,\beta -2)$
. This, after substituting
$g:= \gcd (\alpha -2,\beta -2)$
. This, after substituting
![]() $a = \alpha -2$
and
$a = \alpha -2$
and
![]() $b = \beta -2$
, gives a presentation for
$b = \beta -2$
, gives a presentation for
![]() $(\mathbb {Z}/b )^{a+1} \oplus ( \mathbb {Z}/a )^{b+1} \oplus ( \mathbb {Z}/g) \oplus \mathbb {Z}^{(a+1)(b+1)}$
. In particular, we have
$(\mathbb {Z}/b )^{a+1} \oplus ( \mathbb {Z}/a )^{b+1} \oplus ( \mathbb {Z}/g) \oplus \mathbb {Z}^{(a+1)(b+1)}$
. In particular, we have
![]() $a+1$
copies of
$a+1$
copies of
![]() $( \mathbb {Z}/b ) \oplus ( \mathbb {Z}/a )$
. It is well known that if a and b are not coprime,
$( \mathbb {Z}/b ) \oplus ( \mathbb {Z}/a )$
. It is well known that if a and b are not coprime,
![]() $( \mathbb {Z}/b ) \oplus ( \mathbb {Z}/a ) \cong ( \mathbb {Z}/l ) \oplus ( \mathbb {Z}/g )$
; in case (4), this, together with Corollary 3.9, immediately gives the desired result. In case (3), where a and b are coprime, we instead have that
$( \mathbb {Z}/b ) \oplus ( \mathbb {Z}/a ) \cong ( \mathbb {Z}/l ) \oplus ( \mathbb {Z}/g )$
; in case (4), this, together with Corollary 3.9, immediately gives the desired result. In case (3), where a and b are coprime, we instead have that
![]() $( \mathbb {Z}/b ) \oplus ( \mathbb {Z}/a ) \cong ( \mathbb {Z}/ab)$
, and we are done.
$( \mathbb {Z}/b ) \oplus ( \mathbb {Z}/a ) \cong ( \mathbb {Z}/ab)$
, and we are done.
Now consider case (1), where
![]() $\alpha = \beta = 2$
. Then, following the method above,
$\alpha = \beta = 2$
. Then, following the method above,
![]() $\operatorname {\mathrm {coker}}$
is generated by
$\operatorname {\mathrm {coker}}$
is generated by
![]() $\lbrace A_{pq} \mid p,q = 1,2 \rbrace $
with trivial relations, and so
$\lbrace A_{pq} \mid p,q = 1,2 \rbrace $
with trivial relations, and so
![]() $\operatorname {\mathrm {coker}} \cong \mathbb {Z}^4$
. Hence, by Corollary 3.9,
$\operatorname {\mathrm {coker}} \cong \mathbb {Z}^4$
. Hence, by Corollary 3.9,
![]() $K_\epsilon (C^{\star }(\kappa )) \cong \mathbb {Z}^8$
.
$K_\epsilon (C^{\star }(\kappa )) \cong \mathbb {Z}^8$
.
Similarly, when
![]() $\alpha = 2$
and
$\alpha = 2$
and
![]() $\beta \geq 3$
, it is straightforward to show that
$\beta \geq 3$
, it is straightforward to show that
and, when
![]() $\alpha = 3$
and
$\alpha = 3$
and
![]() $\beta \geq 3$
,
$\beta \geq 3$
,
both of which are presentations of
![]() $(\mathbb {Z}/(\beta - 2))^2 \oplus \mathbb {Z}^{2(\beta - 1)}$
; hence, by Corollary 3.9, (2) is proved.
$(\mathbb {Z}/(\beta - 2))^2 \oplus \mathbb {Z}^{2(\beta - 1)}$
; hence, by Corollary 3.9, (2) is proved.
Example 3.11. Recall the tile system corresponding to
![]() $\kappa (2,2)$
, given in Figure 5. From the diagram, we can see that the (
$\kappa (2,2)$
, given in Figure 5. From the diagram, we can see that the (
![]() $1$
-skeleton of the)
$1$
-skeleton of the)
![]() $2$
-rank graph
$2$
-rank graph
![]() $\Lambda (\kappa (2,2))$
comprises four connected components, each being the Cartesian product
$\Lambda (\kappa (2,2))$
comprises four connected components, each being the Cartesian product
![]() $C_2 \times C_2$
, depicted in Figure 7. It is well known that the k-graph
$C_2 \times C_2$
, depicted in Figure 7. It is well known that the k-graph
![]() $C^{\star }$
-algebra of
$C^{\star }$
-algebra of
![]() $C_2$
is isomorphic to
$C_2$
is isomorphic to
![]() $M_2(C(\mathbb {T}))$
. Furthermore, there is a natural isomorphism
$M_2(C(\mathbb {T}))$
. Furthermore, there is a natural isomorphism
![]() $C^{\star }(C_m \times C_n) \cong M_{mn}(C(\mathbb {T}^2))$
, and so
$C^{\star }(C_m \times C_n) \cong M_{mn}(C(\mathbb {T}^2))$
, and so
![]() $C^{\star }(\kappa (2,2)) \cong (M_4(C(\mathbb {T}^2)))^4$
. The K-groups of this
$C^{\star }(\kappa (2,2)) \cong (M_4(C(\mathbb {T}^2)))^4$
. The K-groups of this
![]() $C^{\star }$
-algebra are both
$C^{\star }$
-algebra are both
![]() $\mathbb {Z}^8$
, in agreement with Theorem 3.10.
$\mathbb {Z}^8$
, in agreement with Theorem 3.10.

Figure 7 The
![]() $2$
-graph
$2$
-graph
![]() $\Lambda (\kappa (2,2))$
, depicted in Figure 5, consists of four copies of
$\Lambda (\kappa (2,2))$
, depicted in Figure 5, consists of four copies of
![]() $C_2 \times C_2$
, where
$C_2 \times C_2$
, where
![]() $C_2$
is the cyclic
$C_2$
is the cyclic
![]() $1$
-graph with two vertices.
$1$
-graph with two vertices.
Theorem 3.12. Let
![]() $\alpha , \beta \geq 3$
, and let
$\alpha , \beta \geq 3$
, and let
![]() $\kappa = \kappa (\alpha , \beta )$
be the complete bipartite graph on
$\kappa = \kappa (\alpha , \beta )$
be the complete bipartite graph on
![]() $\alpha $
white and
$\alpha $
white and
![]() $\beta $
black vertices. Then the order of the class of the identity
$\beta $
black vertices. Then the order of the class of the identity
![]() $[\mathbf {1}]$
in
$[\mathbf {1}]$
in
![]() $K_0(C^{\star }(\Lambda (\kappa )))$
is equal to
$K_0(C^{\star }(\Lambda (\kappa )))$
is equal to
![]() $g := \gcd (\alpha - 2, \beta - 2)$
.
$g := \gcd (\alpha - 2, \beta - 2)$
.
Proof. From [Reference Kimberley and Robertson3], it follows that the order of
![]() $[\mathbf {1}]$
in
$[\mathbf {1}]$
in
![]() $K_0(C^{\star }(\kappa ))$
is equal to the order of the sum of pointed tiles in
$K_0(C^{\star }(\kappa ))$
is equal to the order of the sum of pointed tiles in
![]() $\mathcal {S}(\kappa )$
; by considerations in the proof of Theorem 3.10, we know this to be g.
$\mathcal {S}(\kappa )$
; by considerations in the proof of Theorem 3.10, we know this to be g.
4 Aperiodicity and Kirchberg–Phillips classification
Kumjian and Pask in [Reference Kumjian and Pask6] developed conditions under which the
![]() $C^{\star }$
-algebra of a k-rank graph is both simple and purely infinite. In this section we show that the conditions are satisfied by the algebras
$C^{\star }$
-algebra of a k-rank graph is both simple and purely infinite. In this section we show that the conditions are satisfied by the algebras
![]() $C^{\star }(\kappa )$
, and thus, by the Kirchberg and Phillips results [Reference Kirchberg4, Reference Phillips8], that the
$C^{\star }(\kappa )$
, and thus, by the Kirchberg and Phillips results [Reference Kirchberg4, Reference Phillips8], that the
![]() $C^{\star }(\kappa )$
are completely classified by their K-theory. We detail the following definitions from [Reference Kumjian and Pask6].
$C^{\star }(\kappa )$
are completely classified by their K-theory. We detail the following definitions from [Reference Kumjian and Pask6].
Let
![]() $k \geq 1$
, and let
$k \geq 1$
, and let
![]() $\Omega _k$
be the countable small category with object set
$\Omega _k$
be the countable small category with object set
![]() $\operatorname {\mathrm {Ob}}(\Omega _k) := \mathbb {N}_0^k$
and morphism set
$\operatorname {\mathrm {Ob}}(\Omega _k) := \mathbb {N}_0^k$
and morphism set
![]() $\operatorname {\mathrm {Hom}}(\Omega _k)$
given by
$\operatorname {\mathrm {Hom}}(\Omega _k)$
given by
We identify
![]() $\operatorname {\mathrm {Ob}}(\Omega _k)$
with the set of identity morphisms
$\operatorname {\mathrm {Ob}}(\Omega _k)$
with the set of identity morphisms
![]() $\lbrace (\mathbf {m}, \mathbf {m}) \mid \mathbf {m} \in \mathbb {N}_0^k \rbrace $
, and, hence, identify
$\lbrace (\mathbf {m}, \mathbf {m}) \mid \mathbf {m} \in \mathbb {N}_0^k \rbrace $
, and, hence, identify
![]() $\Omega _k$
with
$\Omega _k$
with
![]() $\operatorname {\mathrm {Hom}}(\Omega _k)$
. Define range and source maps
$\operatorname {\mathrm {Hom}}(\Omega _k)$
. Define range and source maps
![]() $r(\mathbf {m},\mathbf {n}) := \mathbf {m}$
and
$r(\mathbf {m},\mathbf {n}) := \mathbf {m}$
and
![]() $s(\mathbf {m},\mathbf {n}) := \mathbf {n}$
, respectively. Then
$s(\mathbf {m},\mathbf {n}) := \mathbf {n}$
, respectively. Then
![]() $\Omega _k$
, together with the degree map
$\Omega _k$
, together with the degree map
![]() $d(\mathbf {m},\mathbf {n}) := \mathbf {n} - \mathbf {m}$
, is a k-rank graph, which we can visualise as a nonnegative integer lattice in
$d(\mathbf {m},\mathbf {n}) := \mathbf {n} - \mathbf {m}$
, is a k-rank graph, which we can visualise as a nonnegative integer lattice in
![]() $\mathbb {R}^k$
(see Figure 6).
$\mathbb {R}^k$
(see Figure 6).
Definition 4.1. Let
![]() $\Lambda $
be a k-rank graph. We define the infinite path space
$\Lambda $
be a k-rank graph. We define the infinite path space
![]() $\Lambda ^\infty $
of
$\Lambda ^\infty $
of
![]() $\Lambda $
to be
$\Lambda $
to be
![]() $\Lambda ^\infty := \lbrace \varphi : \Omega _k \rightarrow \Lambda \mid \varphi \text { is a}\ k\text {-graph morphism} \rbrace $
.
$\Lambda ^\infty := \lbrace \varphi : \Omega _k \rightarrow \Lambda \mid \varphi \text { is a}\ k\text {-graph morphism} \rbrace $
.
Given a vertex
![]() $v \in \Lambda ^{\mathbf {0}}$
, we write
$v \in \Lambda ^{\mathbf {0}}$
, we write
![]() $\Lambda ^\infty (v)$
for the set of infinite paths that begin at v, that is,
$\Lambda ^\infty (v)$
for the set of infinite paths that begin at v, that is,
![]() $\Lambda ^\infty (v) := \lbrace \varphi \in \Lambda ^\infty \mid \varphi (\mathbf {0}) = v \rbrace $
.
$\Lambda ^\infty (v) := \lbrace \varphi \in \Lambda ^\infty \mid \varphi (\mathbf {0}) = v \rbrace $
.
Let
![]() $\mathbf {p} \in \mathbb {Z}^k$
, and let
$\mathbf {p} \in \mathbb {Z}^k$
, and let
![]() $\varphi \in \Lambda ^\infty $
. We say that
$\varphi \in \Lambda ^\infty $
. We say that
![]() $\mathbf {p}$
is a period for
$\mathbf {p}$
is a period for
![]() $\varphi $
if, for every
$\varphi $
if, for every
![]() $(\mathbf {m},\mathbf {n}) \in \Omega _k$
with
$(\mathbf {m},\mathbf {n}) \in \Omega _k$
with
![]() $\mathbf {m} + \mathbf {p} \geq \mathbf {0}$
, we have
$\mathbf {m} + \mathbf {p} \geq \mathbf {0}$
, we have
![]() $\varphi (\mathbf {m}+\mathbf {p}, \mathbf {n}+\mathbf {p}) = \varphi (\mathbf {m}, \mathbf {n})$
. We call
$\varphi (\mathbf {m}+\mathbf {p}, \mathbf {n}+\mathbf {p}) = \varphi (\mathbf {m}, \mathbf {n})$
. We call
![]() $\varphi $
periodic if we can find a nonzero period for
$\varphi $
periodic if we can find a nonzero period for
![]() $\varphi $
.
$\varphi $
.
Given
![]() $\mathbf {q} \in \mathbb {N}_0^k$
and a path
$\mathbf {q} \in \mathbb {N}_0^k$
and a path
![]() $\varphi \in \Lambda ^\infty $
, we write
$\varphi \in \Lambda ^\infty $
, we write
![]() $\varphi _{\mathbf {q}}(\mathbf {m},\mathbf {n}) := (\mathbf {m}+\mathbf {q}, \mathbf {n}+\mathbf {q})$
. We say that
$\varphi _{\mathbf {q}}(\mathbf {m},\mathbf {n}) := (\mathbf {m}+\mathbf {q}, \mathbf {n}+\mathbf {q})$
. We say that
![]() $\varphi $
is eventually periodic if we can find some nonzero
$\varphi $
is eventually periodic if we can find some nonzero
![]() $\mathbf {q} \in \mathbb {N}_0^k$
such that
$\mathbf {q} \in \mathbb {N}_0^k$
such that
![]() $\varphi _{\mathbf {q}}$
is periodic. We say that an infinite path
$\varphi _{\mathbf {q}}$
is periodic. We say that an infinite path
![]() $\varphi $
is aperiodic if it is neither periodic nor eventually periodic.
$\varphi $
is aperiodic if it is neither periodic nor eventually periodic.
We say that
![]() $\Lambda $
satisfies the aperiodicity condition (also referred to in the literature as Condition (A)) if, for every vertex
$\Lambda $
satisfies the aperiodicity condition (also referred to in the literature as Condition (A)) if, for every vertex
![]() $v \in \Lambda ^{\mathbf {0}}$
, we can find an aperiodic path
$v \in \Lambda ^{\mathbf {0}}$
, we can find an aperiodic path
![]() $\varphi \in \Lambda ^\infty (v)$
. We say that
$\varphi \in \Lambda ^\infty (v)$
. We say that
![]() $\Lambda $
is cofinal if, for every vertex
$\Lambda $
is cofinal if, for every vertex
![]() $v \in \Lambda ^{\mathbf {0}}$
and every infinite path
$v \in \Lambda ^{\mathbf {0}}$
and every infinite path
![]() $\varphi \in \Lambda ^\infty $
, we can find
$\varphi \in \Lambda ^\infty $
, we can find
![]() $\lambda \in \Lambda $
and
$\lambda \in \Lambda $
and
![]() $\mathbf {n} \in \mathbb {N}_0^k$
such that
$\mathbf {n} \in \mathbb {N}_0^k$
such that
![]() $r(\lambda ) = v$
and
$r(\lambda ) = v$
and
![]() $s(\lambda ) = \varphi (\mathbf {n})$
.
$s(\lambda ) = \varphi (\mathbf {n})$
.
The aperiodicity condition is a generalisation of the condition on
![]() $1$
-graphs that every cycle has an entrance. Similarly, cofinality is a generalisation of the property of
$1$
-graphs that every cycle has an entrance. Similarly, cofinality is a generalisation of the property of
![]() $1$
-graphs that every vertex be reachable from somewhere on every infinite path.
$1$
-graphs that every vertex be reachable from somewhere on every infinite path.
Lemma 4.2. Consider the complete bipartite graph
![]() $\kappa = \kappa (\alpha ,\beta )$
, where
$\kappa = \kappa (\alpha ,\beta )$
, where
![]() $\alpha ,\beta \geq 3$
, and let
$\alpha ,\beta \geq 3$
, and let
![]() $\Lambda (\kappa )$
be the corresponding
$\Lambda (\kappa )$
be the corresponding
![]() $2$
-rank graph as constructed in the proof of Proposition 3.5. Then
$2$
-rank graph as constructed in the proof of Proposition 3.5. Then
![]() $\Lambda (\kappa )$
satisfies the aperiodicity condition.
$\Lambda (\kappa )$
satisfies the aperiodicity condition.
In order to get a feeling as to why this is true, consider Figure 8, which shows a representation of
![]() $\Lambda (\kappa (3,3))$
. Each vertex is labelled by a pointed tile from
$\Lambda (\kappa (3,3))$
. Each vertex is labelled by a pointed tile from
![]() $\mathcal {S}(\kappa (3,3))$
, and since each tile is vertically adjacent to two others (and horizontally adjacent to two others), there are two solid arrows and two dashed arrows emanating from each vertex of
$\mathcal {S}(\kappa (3,3))$
, and since each tile is vertically adjacent to two others (and horizontally adjacent to two others), there are two solid arrows and two dashed arrows emanating from each vertex of
![]() $\Lambda (\kappa (3,3))$
. This suggests that, analogously to the
$\Lambda (\kappa (3,3))$
. This suggests that, analogously to the
![]() $1$
-graph condition, we can always find an entrance to any cycle in
$1$
-graph condition, we can always find an entrance to any cycle in
![]() $\Lambda $
, namely by stopping mid-cycle at a vertex, and diverting the path down the second of the two available edges. Hence, as long as
$\Lambda $
, namely by stopping mid-cycle at a vertex, and diverting the path down the second of the two available edges. Hence, as long as
![]() $\alpha , \beta \geq 3$
, there is enough choice at each vertex to be able to exit a cycle.
$\alpha , \beta \geq 3$
, there is enough choice at each vertex to be able to exit a cycle.

Figure 8 A representation of
![]() $\Lambda (\kappa (3,3))$
. It is always possible to exit a cycle.
$\Lambda (\kappa (3,3))$
. It is always possible to exit a cycle.
Proof. Firstly, write
![]() $\Lambda = \Lambda (\kappa )$
, and let
$\Lambda = \Lambda (\kappa )$
, and let
![]() $A \in \Lambda ^{\mathbf {0}}$
be an arbitrary vertex. We construct an aperiodic infinite path beginning from A in the following way.
$A \in \Lambda ^{\mathbf {0}}$
be an arbitrary vertex. We construct an aperiodic infinite path beginning from A in the following way.
Let
![]() $x:\Omega _1 \rightarrow \bigcup _{m \geq 0} \Lambda ^{(m,0)}$
be a
$x:\Omega _1 \rightarrow \bigcup _{m \geq 0} \Lambda ^{(m,0)}$
be a
![]() $1$
-graph morphism such that
$1$
-graph morphism such that
![]() $x(0) = A$
. The vertex A represents a pointed tile in
$x(0) = A$
. The vertex A represents a pointed tile in
![]() $\mathcal {S}(\kappa )$
, which is horizontally adjacent to
$\mathcal {S}(\kappa )$
, which is horizontally adjacent to
![]() $\beta - 1$
other pointed tiles. Hence, A is connected by bidirectional blue arrows to
$\beta - 1$
other pointed tiles. Hence, A is connected by bidirectional blue arrows to
![]() $\beta - 1$
other vertices in
$\beta - 1$
other vertices in
![]() $\Lambda $
. Choose two of these vertices,
$\Lambda $
. Choose two of these vertices,
![]() $B_1$
and
$B_1$
and
![]() $B_2$
, say, and let x be such that
$B_2$
, say, and let x be such that
 $$ \begin{align*} x(m,m) = \begin{cases} A & \text{if}\ m\ \text{is even,} \\ B_1 & \text{if}\ m = r^2 + r + 1\ \text{for some}\ r \geq 1, \\ B_2 & \text{otherwise,} \end{cases} \end{align*} $$
$$ \begin{align*} x(m,m) = \begin{cases} A & \text{if}\ m\ \text{is even,} \\ B_1 & \text{if}\ m = r^2 + r + 1\ \text{for some}\ r \geq 1, \\ B_2 & \text{otherwise,} \end{cases} \end{align*} $$
for all
![]() $m \in \mathbb {N}_0$
. Since
$m \in \mathbb {N}_0$
. Since
![]() $x$
forms an aperiodic sequence, there is no
$x$
forms an aperiodic sequence, there is no
![]() $p \in \mathbb {Z}$
such that
$p \in \mathbb {Z}$
such that
![]() $x(m,m) = x(m+p,m+p)$
for all m, nor any
$x(m,m) = x(m+p,m+p)$
for all m, nor any
![]() $q \in \mathbb {N}$
such that
$q \in \mathbb {N}$
such that
![]() $x_q$
is periodic; hence, x is an aperiodic path. Similarly, define
$x_q$
is periodic; hence, x is an aperiodic path. Similarly, define
![]() $y : \Omega _1 \rightarrow \bigcup _{n \geq 0} \Lambda ^{(0,n)}$
by
$y : \Omega _1 \rightarrow \bigcup _{n \geq 0} \Lambda ^{(0,n)}$
by
 $$ \begin{align*} y(n,n) = \begin{cases} A & \text{if}\ n\ \text{is even,} \\ C_1 & \text{if}\ n = s^2 + s + 1,\ \text{for some}\ s \geq 1, \\ C_2 & \text{otherwise,} \end{cases} \end{align*} $$
$$ \begin{align*} y(n,n) = \begin{cases} A & \text{if}\ n\ \text{is even,} \\ C_1 & \text{if}\ n = s^2 + s + 1,\ \text{for some}\ s \geq 1, \\ C_2 & \text{otherwise,} \end{cases} \end{align*} $$
for some vertices labelled by pointed tiles
![]() $C_1$
,
$C_1$
,
![]() $C_2$
that are vertically adjacent to A. Then y is also an aperiodic path. By the UCE property, x and y uniquely determine an infinite path
$C_2$
that are vertically adjacent to A. Then y is also an aperiodic path. By the UCE property, x and y uniquely determine an infinite path
![]() $\varphi : \Omega _2 \rightarrow \Lambda $
with
$\varphi : \Omega _2 \rightarrow \Lambda $
with
![]() $\varphi ((m,0),(m,0)) = x(m,m)$
and
$\varphi ((m,0),(m,0)) = x(m,m)$
and
![]() $\varphi ((0,n),(0,n)) = y(n,n)$
.
$\varphi ((0,n),(0,n)) = y(n,n)$
.
Denote by D the unique pointed tile (other than A) adjacent to both
![]() $B_1$
and
$B_1$
and
![]() $C_1$
. This cannot also be adjacent to
$C_1$
. This cannot also be adjacent to
![]() $B_2$
, nor to
$B_2$
, nor to
![]() $C_2$
, so
$C_2$
, so
![]() $\varphi ((m,n),(m,n)) = D$
precisely when
$\varphi ((m,n),(m,n)) = D$
precisely when
![]() $m = r^2+r+1$
and
$m = r^2+r+1$
and
![]() $n=s^2+s+1$
, for some
$n=s^2+s+1$
, for some
![]() $r,s \geq 1$
. As above, there is no
$r,s \geq 1$
. As above, there is no
![]() $\mathbf {p} \in \mathbb {Z}^2$
such that
$\mathbf {p} \in \mathbb {Z}^2$
such that
![]() $\varphi ((m,n),(m,n)) = \varphi ((m,n)+\mathbf {p},(m,n)+\mathbf {p})$
, nor any
$\varphi ((m,n),(m,n)) = \varphi ((m,n)+\mathbf {p},(m,n)+\mathbf {p})$
, nor any
![]() $\mathbf {q} \in \mathbb {N}_0^2$
such that
$\mathbf {q} \in \mathbb {N}_0^2$
such that
![]() $\varphi _{\mathbf {q}}$
is periodic. Since our initial vertex A was arbitrary, we are done.
$\varphi _{\mathbf {q}}$
is periodic. Since our initial vertex A was arbitrary, we are done.
The following definitions are required for the rest of the section. For the reader who desires more detail, we recommend [Reference Rørdam, Larsen and Laustsen11, Ch. 5].
Definition 4.3. Let
![]() $\mathcal {A}$
be a unital
$\mathcal {A}$
be a unital
![]() $C^{\star }$
-algebra, and let
$C^{\star }$
-algebra, and let
![]() $\mathcal {B} \subset \mathcal {A}$
be a
$\mathcal {B} \subset \mathcal {A}$
be a
![]() $C^{\star }$
-subalgebra. We say that
$C^{\star }$
-subalgebra. We say that
![]() $\mathcal {B}$
is hereditary if, for all
$\mathcal {B}$
is hereditary if, for all
![]() $a,b \in \mathcal {A}$
, if
$a,b \in \mathcal {A}$
, if
![]() $b \in \mathcal {B}$
and
$b \in \mathcal {B}$
and
![]() $a \leq b$
, then
$a \leq b$
, then
![]() $a \in \mathcal {B}$
.
$a \in \mathcal {B}$
.
We say that
![]() $\mathcal {A}$
is simple if it has no nontrivial closed two-sided ideals.
$\mathcal {A}$
is simple if it has no nontrivial closed two-sided ideals.
If
![]() $\mathcal {A}$
is simple, we say that it is purely infinite if every nonzero hereditary
$\mathcal {A}$
is simple, we say that it is purely infinite if every nonzero hereditary
![]() $C^{\star }$
-subalgebra of
$C^{\star }$
-subalgebra of
![]() $\mathcal {A}$
contains a projection which is Murray–von Neumann equivalent to a proper subprojection of itself. Equivalently,
$\mathcal {A}$
contains a projection which is Murray–von Neumann equivalent to a proper subprojection of itself. Equivalently,
![]() $\mathcal {A}$
is purely infinite if every nonzero hereditary
$\mathcal {A}$
is purely infinite if every nonzero hereditary
![]() $C^{\star }$
-subalgebra contains a projection equivalent to
$C^{\star }$
-subalgebra contains a projection equivalent to
![]() $\mathbf {1}$
.
$\mathbf {1}$
.
Theorem 4.4 (Kumjian and Pask [Reference Kumjian and Pask6])
Let
![]() $\Lambda $
be a k-rank graph that satisfies the aperiodicity condition. Then the associated universal
$\Lambda $
be a k-rank graph that satisfies the aperiodicity condition. Then the associated universal
![]() $C^{\star }$
-algebra
$C^{\star }$
-algebra
![]() $C^{\star }(\Lambda )$
is simple if and only if
$C^{\star }(\Lambda )$
is simple if and only if
![]() $\Lambda $
is cofinal.
$\Lambda $
is cofinal.
Theorem 4.5 (Kumjian and Pask [Reference Kumjian and Pask6], Sims [Reference Sims13, Proposition 8.8])
Let
![]() $\Lambda $
be a k-rank graph that is cofinal and satisfies the aperiodicity condition. Suppose that, for every
$\Lambda $
be a k-rank graph that is cofinal and satisfies the aperiodicity condition. Suppose that, for every
![]() $v \in \Lambda ^{\mathbf {0}}$
, we can find
$v \in \Lambda ^{\mathbf {0}}$
, we can find
![]() $\lambda \in \Lambda $
with
$\lambda \in \Lambda $
with
![]() $r(\lambda ) = v$
, and some cycle
$r(\lambda ) = v$
, and some cycle
![]() $\mu \in \Lambda $
with an entrance, such that
$\mu \in \Lambda $
with an entrance, such that
![]() $d({\kern1.3pt}\mu ) \neq \mathbf {0}$
, and
$d({\kern1.3pt}\mu ) \neq \mathbf {0}$
, and
![]() $s(\lambda ) = r({\kern1.3pt}\mu ) = s({\kern1.3pt}\mu )$
. Then
$s(\lambda ) = r({\kern1.3pt}\mu ) = s({\kern1.3pt}\mu )$
. Then
![]() $C^{\star }(\Lambda )$
is purely infinite.
$C^{\star }(\Lambda )$
is purely infinite.
Proposition 4.6. Consider
![]() $\kappa = \kappa (\alpha ,\beta )$
for
$\kappa = \kappa (\alpha ,\beta )$
for
![]() $\alpha ,\beta \geq 3$
, and let
$\alpha ,\beta \geq 3$
, and let
![]() $\Lambda (\kappa )$
be the corresponding
$\Lambda (\kappa )$
be the corresponding
![]() $2$
-rank graph. Then the
$2$
-rank graph. Then the
![]() $C^{\star }$
-algebra
$C^{\star }$
-algebra
![]() $C^{\star }(\kappa )$
from Definition 3.7 is simple and purely infinite.
$C^{\star }(\kappa )$
from Definition 3.7 is simple and purely infinite.
Proof. Firstly observe that
![]() $\Lambda (\kappa )$
is cofinal, since the
$\Lambda (\kappa )$
is cofinal, since the
![]() $1$
-skeleton of
$1$
-skeleton of
![]() $\Lambda (\kappa )$
is strongly connected. From Theorem 4.4 it follows that
$\Lambda (\kappa )$
is strongly connected. From Theorem 4.4 it follows that
![]() $C^{\star }(\kappa )$
is simple.
$C^{\star }(\kappa )$
is simple.
Now, let
![]() $A \in \Lambda (\kappa )^{\mathbf {0}}$
be an arbitrary vertex. Since each edge of the
$A \in \Lambda (\kappa )^{\mathbf {0}}$
be an arbitrary vertex. Since each edge of the
![]() $1$
-skeleton of
$1$
-skeleton of
![]() $\Lambda (\kappa )$
is bidirectional, we can set
$\Lambda (\kappa )$
is bidirectional, we can set
![]() $\mu $
to be a path that begins at A and traverses a single solid edge to some vertex B, before immediately returning to A. Then
$\mu $
to be a path that begins at A and traverses a single solid edge to some vertex B, before immediately returning to A. Then
![]() $d({\kern1.3pt}\mu ) = (2,0)$
, and, since
$d({\kern1.3pt}\mu ) = (2,0)$
, and, since
![]() $\alpha , \beta \geq 3$
, B is the range of some other solid edge, and so
$\alpha , \beta \geq 3$
, B is the range of some other solid edge, and so
![]() $\mu $
is a cycle with an entrance. Then, by strong-connectedness, the conditions of Theorem 4.5 are satisfied, and
$\mu $
is a cycle with an entrance. Then, by strong-connectedness, the conditions of Theorem 4.5 are satisfied, and
![]() $\Lambda (\kappa )$
is purely infinite.
$\Lambda (\kappa )$
is purely infinite.
In [Reference Evans2] it is shown that, given a row-finite k-rank graph
![]() $\Lambda $
with no sources, the
$\Lambda $
with no sources, the
![]() $C^{\star }$
-algebra
$C^{\star }$
-algebra
![]() $C^{\star }(\Lambda )$
is separable, nuclear, unital, and satisfies the universal coefficient theorem. Furthermore, we have shown in Proposition 4.6 that, given a complete bipartite graph
$C^{\star }(\Lambda )$
is separable, nuclear, unital, and satisfies the universal coefficient theorem. Furthermore, we have shown in Proposition 4.6 that, given a complete bipartite graph
![]() $\kappa = \kappa (\alpha , \beta )$
with
$\kappa = \kappa (\alpha , \beta )$
with
![]() $\alpha , \beta \geq 3$
, the
$\alpha , \beta \geq 3$
, the
![]() $C^{\star }$
-algebra
$C^{\star }$
-algebra
![]() $C^{\star }(\kappa )$
associated to its
$C^{\star }(\kappa )$
associated to its
![]() $2$
-rank graph is simple and purely infinite. Hence, we can deduce the following result.
$2$
-rank graph is simple and purely infinite. Hence, we can deduce the following result.
Corollary 4.7. Consider the complete bipartite graph
![]() $\kappa = \kappa (\alpha ,\beta )$
for
$\kappa = \kappa (\alpha ,\beta )$
for
![]() $\alpha ,\beta \geq 3$
, with corresponding
$\alpha ,\beta \geq 3$
, with corresponding
![]() $2$
-rank graph
$2$
-rank graph
![]() $\Lambda (\kappa )$
. Then the isomorphism class of the associated
$\Lambda (\kappa )$
. Then the isomorphism class of the associated
![]() $C^{\star }$
-algebra
$C^{\star }$
-algebra
![]() $C^{\star }(\Lambda (\kappa ))$
is completely determined by the K-groups
$C^{\star }(\Lambda (\kappa ))$
is completely determined by the K-groups
![]() $K_0 (C^{\star }(\kappa )) = K_1 (C^{\star }(\kappa ))$
and the position of the class of the identity in
$K_0 (C^{\star }(\kappa )) = K_1 (C^{\star }(\kappa ))$
and the position of the class of the identity in
![]() $K_0(C^{\star }(\kappa ))$
.
$K_0(C^{\star }(\kappa ))$
.
5 Unpointed tiles
There is an alternative way we could have defined the adjacency matrices above, giving rise to a different
![]() $2$
-rank graph structure.
$2$
-rank graph structure.
Define an unpointed tile system
![]() $(G,U,V,\mathcal {S}')$
in the same way as in Definition 2.4, but replacing
$(G,U,V,\mathcal {S}')$
in the same way as in Definition 2.4, but replacing
![]() $\mathcal {S}=\mathcal {S}(G)$
with the set of unpointed tiles
$\mathcal {S}=\mathcal {S}(G)$
with the set of unpointed tiles
![]() $\mathcal {S}'=\mathcal {S}'(G)$
. We show that analogues of the results in Section 3 also hold for unpointed tile systems.
$\mathcal {S}'=\mathcal {S}'(G)$
. We show that analogues of the results in Section 3 also hold for unpointed tile systems.
Definition 5.1. Let
![]() $(G, U, V, \mathcal {S}')$
be an unpointed tile system, and let
$(G, U, V, \mathcal {S}')$
be an unpointed tile system, and let
![]() $A', B' \in \mathcal {S}'$
be unpointed tiles, that is, equivalence classes of some pointed tiles
$A', B' \in \mathcal {S}'$
be unpointed tiles, that is, equivalence classes of some pointed tiles
![]() $A, B \in \mathcal {S}$
(see Definition 2.3). Recall the matrices
$A, B \in \mathcal {S}$
(see Definition 2.3). Recall the matrices
![]() $M_1,M_2$
from Definition 3.1. We define functions
$M_1,M_2$
from Definition 3.1. We define functions
![]() $M^{\prime }_1,M^{\prime }_2:\mathcal {S}' \times \mathcal {S}' \rightarrow \lbrace 0,1\rbrace $
as follows:
$M^{\prime }_1,M^{\prime }_2:\mathcal {S}' \times \mathcal {S}' \rightarrow \lbrace 0,1\rbrace $
as follows:
 $$ \begin{align*} \begin{array}{r} M^{\prime}_1(A',B') = \left\{ \begin{array}{@{}l} 1 \quad \text{if}\ M_1(A_\bullet ,B_\bullet) = 1,\ \text{for some}\ A_\bullet \sim A,\ B_\bullet \sim B, \\ 0 \quad \text{otherwise,} \end{array} \right.\\ \text{}\\ M^{\prime}_2(A',B') = \left\{ \begin{array}{@{}l} 1 \quad \text{if}\ M_2(A_\bullet ,B_\bullet) = 1,\ \text{for some}\ A_\bullet \sim A, B_\bullet \sim B, \\ 0 \quad \text{otherwise.} \end{array} \right. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{r} M^{\prime}_1(A',B') = \left\{ \begin{array}{@{}l} 1 \quad \text{if}\ M_1(A_\bullet ,B_\bullet) = 1,\ \text{for some}\ A_\bullet \sim A,\ B_\bullet \sim B, \\ 0 \quad \text{otherwise,} \end{array} \right.\\ \text{}\\ M^{\prime}_2(A',B') = \left\{ \begin{array}{@{}l} 1 \quad \text{if}\ M_2(A_\bullet ,B_\bullet) = 1,\ \text{for some}\ A_\bullet \sim A, B_\bullet \sim B, \\ 0 \quad \text{otherwise.} \end{array} \right. \end{array} \end{align*} $$
We define adjacency matrices
![]() $M^{\prime }_1$
,
$M^{\prime }_1$
,
![]() $M^{\prime }_2$
accordingly.
$M^{\prime }_2$
accordingly.
Proposition 5.2. Consider the complete bipartite graph
![]() $\kappa = \kappa (\alpha ,\beta )$
on
$\kappa = \kappa (\alpha ,\beta )$
on
![]() $\alpha \geq 2$
white and
$\alpha \geq 2$
white and
![]() $\beta \geq 2$
black vertices, and let
$\beta \geq 2$
black vertices, and let
![]() $(\kappa , U, V, \mathcal {S}'(\kappa ))$
be an unpointed tile system. Then the corresponding adjacency matrices
$(\kappa , U, V, \mathcal {S}'(\kappa ))$
be an unpointed tile system. Then the corresponding adjacency matrices
![]() $M^{\prime }_1$
and
$M^{\prime }_1$
and
![]() $M^{\prime }_2$
commute, and
$M^{\prime }_2$
commute, and
![]() $(\kappa , U, V, \mathcal {S}'(\kappa ))$
has the UCE property. Hence,
$(\kappa , U, V, \mathcal {S}'(\kappa ))$
has the UCE property. Hence,
![]() $(\kappa ,U,V,\mathcal {S}'(\kappa ))$
has a
$(\kappa ,U,V,\mathcal {S}'(\kappa ))$
has a
![]() $2$
-rank graph structure.
$2$
-rank graph structure.
Proof. Given two unpointed tiles
![]() $A',B' \in \mathcal {S}'(\kappa )$
, consider their respective sets of pointed tiles
$A',B' \in \mathcal {S}'(\kappa )$
, consider their respective sets of pointed tiles
![]() $\mathcal {A},\mathcal {B} \in \mathcal {S}(\kappa )$
as defined in Definition 5.1. Notice that
$\mathcal {A},\mathcal {B} \in \mathcal {S}(\kappa )$
as defined in Definition 5.1. Notice that
![]() $M^{\prime }_1(A',B') = 1$
if and only if, for every
$M^{\prime }_1(A',B') = 1$
if and only if, for every
![]() $A_\bullet \in \mathcal {A}$
, we can find some
$A_\bullet \in \mathcal {A}$
, we can find some
![]() $B_\bullet \in \mathcal {B}$
such that
$B_\bullet \in \mathcal {B}$
such that
![]() $M_1 (A_\bullet ,B_\bullet ) = 1$
. The same is true for
$M_1 (A_\bullet ,B_\bullet ) = 1$
. The same is true for
![]() $M^{\prime }_2$
. Write
$M^{\prime }_2$
. Write
![]() $A' = ( u_i^1, v_j^1, u_i^2, v_j^2 )$
, and define sets
$A' = ( u_i^1, v_j^1, u_i^2, v_j^2 )$
, and define sets
Then
![]() $X_A$
contains precisely those tiles of the form
$X_A$
contains precisely those tiles of the form
![]() $( u_k^1, v_j^1, u_k^2, v_j^2)$
, where
$( u_k^1, v_j^1, u_k^2, v_j^2)$
, where
![]() $k \neq i$
, and
$k \neq i$
, and
![]() $Y_A$
only those of the form
$Y_A$
only those of the form
![]() $( u_i^1, v_l^1, u_i^2, v_l^2)$
, where
$( u_i^1, v_l^1, u_i^2, v_l^2)$
, where
![]() $l \neq j$
. The proof then proceeds in a similar fashion to that of Proposition 3.3, and the
$l \neq j$
. The proof then proceeds in a similar fashion to that of Proposition 3.3, and the
![]() $2$
-rank graph structure follows immediately from [Reference Kumjian and Pask6, Section 6] as in Theorem 3.5.
$2$
-rank graph structure follows immediately from [Reference Kumjian and Pask6, Section 6] as in Theorem 3.5.
We write
![]() $\Lambda '(\kappa )$
for the
$\Lambda '(\kappa )$
for the
![]() $2$
-rank graph induced by the adjacency matrices
$2$
-rank graph induced by the adjacency matrices
![]() $M^{\prime }_1$
and
$M^{\prime }_1$
and
![]() $M^{\prime }_2$
. It is not difficult to verify that
$M^{\prime }_2$
. It is not difficult to verify that
![]() $\Lambda '(\kappa )$
is row-finite, with a finite vertex set and no sources. Hence, we can apply Theorem 3.8, and derive the following result.
$\Lambda '(\kappa )$
is row-finite, with a finite vertex set and no sources. Hence, we can apply Theorem 3.8, and derive the following result.
Theorem 5.3 (K-groups for unpointed tile systems)
Let
![]() $a,b \geq 0$
, and let
$a,b \geq 0$
, and let
![]() ${\kappa (a+2,b+2)}$
be the complete bipartite graph on
${\kappa (a+2,b+2)}$
be the complete bipartite graph on
![]() $a+2$
white and
$a+2$
white and
![]() $b+2$
black vertices. Again, without loss of generality, we can assume that
$b+2$
black vertices. Again, without loss of generality, we can assume that
![]() $a\leq b$
. Write
$a\leq b$
. Write
![]() $C^{\star }(\kappa ) := C^{\star }(\Lambda '(\kappa ))$
. Then, for
$C^{\star }(\kappa ) := C^{\star }(\Lambda '(\kappa ))$
. Then, for
![]() $\epsilon = 0,1$
, we have the following assertions.
$\epsilon = 0,1$
, we have the following assertions.
-
(1) If
 $a=b=0$
, then
$a=b=0$
, then
 $K_\epsilon (C^{\star }(\kappa (a+2,b+2)))=K_\epsilon (C^{\star }(\kappa (2,2))) \cong \mathbb {Z}^2$
.
$K_\epsilon (C^{\star }(\kappa (a+2,b+2)))=K_\epsilon (C^{\star }(\kappa (2,2))) \cong \mathbb {Z}^2$
. -
(2) If
 $a=0$
and
$a=0$
and
 $b \geq 1$
, then
$b \geq 1$
, then  $$ \begin{align*} K_\epsilon(C^{\star}(\kappa(a+2,b+2))) \cong ( \mathbb{Z}/2)^b\oplus ( \mathbb{Z}/(2b)). \end{align*} $$
$$ \begin{align*} K_\epsilon(C^{\star}(\kappa(a+2,b+2))) \cong ( \mathbb{Z}/2)^b\oplus ( \mathbb{Z}/(2b)). \end{align*} $$
-
(3) If
 $a,b \geq 1$
, then where
$a,b \geq 1$
, then where $$ \begin{align*} K_\epsilon(C^{\star}(\kappa(a+2,b+2))) \cong ( \mathbb{Z}/2)^{(a+1)(b+1)-1}\oplus ( \mathbb{Z}/2g), \end{align*} $$
$$ \begin{align*} K_\epsilon(C^{\star}(\kappa(a+2,b+2))) \cong ( \mathbb{Z}/2)^{(a+1)(b+1)-1}\oplus ( \mathbb{Z}/2g), \end{align*} $$
 $g := \gcd (a, b)$
.
$g := \gcd (a, b)$
.
Proof. Again, we start by proving (3) as the first two cases follow. Write
![]() $\alpha := a+2$
,
$\alpha := a+2$
,
![]() $\beta := b+2$
, and let
$\beta := b+2$
, and let
![]() $\alpha , \beta \geq 3$
. For
$\alpha , \beta \geq 3$
. For
![]() $1 \leq i \leq \alpha $
,
$1 \leq i \leq \alpha $
,
![]() $1 \leq j \leq \beta $
, write
$1 \leq j \leq \beta $
, write
![]() $A_{ij}'$
for the unpointed tile
$A_{ij}'$
for the unpointed tile
![]() $( u_i^1, v_j^1, u_i^2, v_j^2 ) \in \mathcal {S}'(\kappa )$
. Then
$( u_i^1, v_j^1, u_i^2, v_j^2 ) \in \mathcal {S}'(\kappa )$
. Then
 $$ \begin{align} \operatorname{\mathrm{coker}} &= \operatorname{\mathrm{coker}}(\mathbf{1}-(M_1')^T, \mathbf{1}-(M_2')^T )\nonumber\\ &= \bigg\langle A_{ij}' \in \mathcal{S}'(\kappa) \bigg\vert\, A_{ij}' = \sum_{T' \in \mathcal{S}'(\kappa)} M_1'(A_{ij}',T') \cdot T' = \sum_{T' \in \mathcal{S}'(\kappa)} M_2'(A_{ij}',T')\cdot T' \bigg\rangle. \end{align} $$
$$ \begin{align} \operatorname{\mathrm{coker}} &= \operatorname{\mathrm{coker}}(\mathbf{1}-(M_1')^T, \mathbf{1}-(M_2')^T )\nonumber\\ &= \bigg\langle A_{ij}' \in \mathcal{S}'(\kappa) \bigg\vert\, A_{ij}' = \sum_{T' \in \mathcal{S}'(\kappa)} M_1'(A_{ij}',T') \cdot T' = \sum_{T' \in \mathcal{S}'(\kappa)} M_2'(A_{ij}',T')\cdot T' \bigg\rangle. \end{align} $$
Fix
![]() $p \in \lbrace 1,\ldots , \alpha \rbrace $
,
$p \in \lbrace 1,\ldots , \alpha \rbrace $
,
![]() $q \in \lbrace 1,\ldots , \beta \rbrace $
, and notice that:
$q \in \lbrace 1,\ldots , \beta \rbrace $
, and notice that:
-
•
 $M^{\prime }_1(A_{pq}', T') = 1$
if and only if
$M^{\prime }_1(A_{pq}', T') = 1$
if and only if
 $T' = A_{iq}'$
for some
$T' = A_{iq}'$
for some
 $i \neq p$
;
$i \neq p$
; -
•
 $M^{\prime }_2(A_{pq}', T') = 1$
if and only if
$M^{\prime }_2(A_{pq}', T') = 1$
if and only if
 $T' = A_{pj}'$
for some
$T' = A_{pj}'$
for some
 $j \neq q$
.
$j \neq q$
.
Hence, the relations of (5-1) are equivalent to
![]() $A_{pq}' = \sum _{i \neq p} A_{iq}' = \sum _{j \neq q} A_{pj}'$
. Define
$A_{pq}' = \sum _{i \neq p} A_{iq}' = \sum _{j \neq q} A_{pj}'$
. Define
 $$ \begin{align*} J_{pq} := \bigg(\sum_{i=2}^{\alpha} A_{iq}'\bigg) - A_{pq}' \quad \text{and}\quad I_{pq} := \bigg(\sum_{j=2}^{\beta} A_{pj}'\bigg) - A_{pq}' \end{align*} $$
$$ \begin{align*} J_{pq} := \bigg(\sum_{i=2}^{\alpha} A_{iq}'\bigg) - A_{pq}' \quad \text{and}\quad I_{pq} := \bigg(\sum_{j=2}^{\beta} A_{pj}'\bigg) - A_{pq}' \end{align*} $$
for
![]() $p, q \geq 2$
. Then
$p, q \geq 2$
. Then
 $$ \begin{align*} 2J_{pq} &= 2\bigg(\sum_{i=2}^{\alpha} A_{iq}'\bigg) - 2A_{pq}' \\ &= 2(A_{2q}' + \cdots + A_{\alpha q}' - A_{pq}') + A_{1q}' - A_{1q}' \\ &= (A_{1q}' + A_{2q}' + \cdots + A_{\alpha q}' - A_{pq}') + (-A_{1q}' + A_{2q}' + \cdots + A_{\alpha q}') - A_{pq}' \\ &= A_{pq}' + 0 - A_{pq}' = 0, \end{align*} $$
$$ \begin{align*} 2J_{pq} &= 2\bigg(\sum_{i=2}^{\alpha} A_{iq}'\bigg) - 2A_{pq}' \\ &= 2(A_{2q}' + \cdots + A_{\alpha q}' - A_{pq}') + A_{1q}' - A_{1q}' \\ &= (A_{1q}' + A_{2q}' + \cdots + A_{\alpha q}' - A_{pq}') + (-A_{1q}' + A_{2q}' + \cdots + A_{\alpha q}') - A_{pq}' \\ &= A_{pq}' + 0 - A_{pq}' = 0, \end{align*} $$
and, similarly,
![]() $2I_{pq} = 0$
. Now
$2I_{pq} = 0$
. Now
![]() $J_{pq} = 0$
or
$J_{pq} = 0$
or
![]() $I_{pq} = 0$
only if
$I_{pq} = 0$
only if
![]() $A_{pq}' = A_{1q}'$
or
$A_{pq}' = A_{1q}'$
or
![]() $A_{pq}' = A_{p1}'$
, respectively. But, since
$A_{pq}' = A_{p1}'$
, respectively. But, since
![]() $\alpha , \beta \geq 3$
, these equivalences are not relations listed at (5-1), and so
$\alpha , \beta \geq 3$
, these equivalences are not relations listed at (5-1), and so
![]() $\operatorname {\mathrm {ord}}(J_{pq}) = \operatorname {\mathrm {ord}}(I_{pq}) = 2$
. Notice that we can write each
$\operatorname {\mathrm {ord}}(J_{pq}) = \operatorname {\mathrm {ord}}(I_{pq}) = 2$
. Notice that we can write each
![]() $A_{1q}'$
and
$A_{1q}'$
and
![]() $A_{p1}'$
in terms of the other
$A_{p1}'$
in terms of the other
![]() $A_{ij}'$
for
$A_{ij}'$
for
![]() $p,q \geq 2$
; hence, we can remove these from the list of generators by a sequence of Tietze transformations.
$p,q \geq 2$
; hence, we can remove these from the list of generators by a sequence of Tietze transformations.
Also notice that
![]() $A_{2q}' = J_{2q} - \sum _{i=3}^\alpha A_{iq}'$
. Proceeding inductively, we can write each
$A_{2q}' = J_{2q} - \sum _{i=3}^\alpha A_{iq}'$
. Proceeding inductively, we can write each
![]() $A_{pq}'$
in terms of the
$A_{pq}'$
in terms of the
![]() $J_{iq}$
and the
$J_{iq}$
and the
![]() $A_{iq}'$
for
$A_{iq}'$
for
![]() $i> p$
. Similarly, we can express each
$i> p$
. Similarly, we can express each
![]() $A_{pq}'$
in terms of the
$A_{pq}'$
in terms of the
![]() $I_{pj}$
and the
$I_{pj}$
and the
![]() $A_{pj}'$
for
$A_{pj}'$
for
![]() $j> q$
. Hence, we can rewrite the generators of
$j> q$
. Hence, we can rewrite the generators of
![]() $\operatorname {\mathrm {coker}}$
as
$\operatorname {\mathrm {coker}}$
as
![]() $A_{11}'$
,
$A_{11}'$
,
![]() $I_{pq}$
,
$I_{pq}$
,
![]() $J_{pq}$
for
$J_{pq}$
for
![]() $p,q \geq 2$
. But
$p,q \geq 2$
. But
![]() $A_{11}' = -(A_{p1}'+J_{p1}) = -(A_{1q}'+I_{1q})$
for all
$A_{11}' = -(A_{p1}'+J_{p1}) = -(A_{1q}'+I_{1q})$
for all
![]() $p,q \geq 2$
, so
$p,q \geq 2$
, so
 $$ \begin{align*} (\alpha - 2)A_{11}' = -\sum_{i=3}^{\alpha} (A_{i1}' + J_{i1}) = -\bigg( J_{21} + \sum_{i=3}^\alpha J_{i1}\bigg ), \end{align*} $$
$$ \begin{align*} (\alpha - 2)A_{11}' = -\sum_{i=3}^{\alpha} (A_{i1}' + J_{i1}) = -\bigg( J_{21} + \sum_{i=3}^\alpha J_{i1}\bigg ), \end{align*} $$
and
![]() $2(\alpha - 2)A_{11}' = 0$
. Similarly,
$2(\alpha - 2)A_{11}' = 0$
. Similarly,
![]() $2(\beta - 2)A_{11}' = 0$
, and, hence,
$2(\beta - 2)A_{11}' = 0$
, and, hence,
![]() $2gA_{11}' = 0$
, where
$2gA_{11}' = 0$
, where
![]() $g:= \gcd (\alpha -2,\beta -2)$
.
$g:= \gcd (\alpha -2,\beta -2)$
.
Observe that, since
![]() $I_{pq}$
is defined in terms of the
$I_{pq}$
is defined in terms of the
![]() $A_{pj}'$
, and each
$A_{pj}'$
, and each
![]() $A_{pj}'$
can be written in terms of the
$A_{pj}'$
can be written in terms of the
![]() $J_{ij}$
, we can remove the
$J_{ij}$
, we can remove the
![]() $I_{pq}$
from the list of generators of
$I_{pq}$
from the list of generators of
![]() $\operatorname {\mathrm {coker}}$
. Finally, we can rewrite (5-1) as
$\operatorname {\mathrm {coker}}$
. Finally, we can rewrite (5-1) as
 $$ \begin{align*} \operatorname{\mathrm{coker}} &= \langle J_{2q}, J_{p2}, J_{pq}, A_{11}' \mid 2J_{2q} = 2J_{p2} = 2J_{pq} = 2gA_{11}' = 0, \\ &\qquad \text{ for } 3 \leq p \leq \alpha, 3 \leq q \leq \beta \rangle, \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{coker}} &= \langle J_{2q}, J_{p2}, J_{pq}, A_{11}' \mid 2J_{2q} = 2J_{p2} = 2J_{pq} = 2gA_{11}' = 0, \\ &\qquad \text{ for } 3 \leq p \leq \alpha, 3 \leq q \leq \beta \rangle, \end{align*} $$
and, after substituting
![]() $a = \alpha - 2$
,
$a = \alpha - 2$
,
![]() $b = \beta - 2$
, this gives a presentation for
$b = \beta - 2$
, this gives a presentation for
![]() $(\mathbb {Z}/2)^{(a+1)(b+1)-1}\oplus (\mathbb {Z}/2g)$
. There is no torsion-free part, so this proves (3). If
$(\mathbb {Z}/2)^{(a+1)(b+1)-1}\oplus (\mathbb {Z}/2g)$
. There is no torsion-free part, so this proves (3). If
![]() $\alpha = 2$
, then
$\alpha = 2$
, then
![]() $A_{1q}' = A_{2q}'$
for all
$A_{1q}' = A_{2q}'$
for all
![]() $1 \leq q \leq \beta $
, so we can write
$1 \leq q \leq \beta $
, so we can write
 $$ \begin{align*} \operatorname{\mathrm{coker}} = \bigg\langle A_{1q}' \bigg\vert\, A_{1q}' = \sum_{j\neq q} A_{1j}', \text{ for } 1 \leq q \leq \beta \bigg\rangle. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{coker}} = \bigg\langle A_{1q}' \bigg\vert\, A_{1q}' = \sum_{j\neq q} A_{1j}', \text{ for } 1 \leq q \leq \beta \bigg\rangle. \end{align*} $$
We adjust the proof above accordingly to obtain the result of (2). Finally, in case (1), where
![]() $\alpha = \beta = 2$
, we have
$\alpha = \beta = 2$
, we have
![]() $A_{11}' = A_{12}' = A_{21}' = A_{22}'$
with no further relations, so that
$A_{11}' = A_{12}' = A_{21}' = A_{22}'$
with no further relations, so that
![]() $\operatorname {\mathrm {coker}} = \langle A_{11}' \rangle \cong \mathbb {Z}$
, and the result follows from Theorem 3.8.
$\operatorname {\mathrm {coker}} = \langle A_{11}' \rangle \cong \mathbb {Z}$
, and the result follows from Theorem 3.8.
Theorem 5.4. Let
![]() $\alpha , \beta \geq 3$
, let
$\alpha , \beta \geq 3$
, let
![]() $\kappa = \kappa (\alpha , \beta )$
be the complete bipartite graph on
$\kappa = \kappa (\alpha , \beta )$
be the complete bipartite graph on
![]() $\alpha $
white and
$\alpha $
white and
![]() $\beta $
black vertices, and write
$\beta $
black vertices, and write
![]() $g := \gcd (\alpha - 2, \beta - 2)$
. Then the order of the class of the identity
$g := \gcd (\alpha - 2, \beta - 2)$
. Then the order of the class of the identity
![]() $[\mathbf {1}]$
in
$[\mathbf {1}]$
in
![]() $K_0(C^{\star }(\Lambda '(\kappa )))$
is equal to g if g is odd, and
$K_0(C^{\star }(\Lambda '(\kappa )))$
is equal to g if g is odd, and
![]() $g/2$
if g is even.
$g/2$
if g is even.
Proof. We use the same notation as in the proof of Theorem 5.3. As with Theorem 3.12, we know that the order of
![]() $[\mathbf {1}]$
in
$[\mathbf {1}]$
in
![]() $K_0(C^{\star }(\kappa ))$
is equal to the order of the sum of all tiles
$K_0(C^{\star }(\kappa ))$
is equal to the order of the sum of all tiles
![]() $A_{ij}'$
. We write
$A_{ij}'$
. We write
![]() $\Sigma $
for this sum.
$\Sigma $
for this sum.
We have
![]() $A_{pq}' = \sum _{i \neq p} A_{iq}' = \sum _{j \neq q} A_{pj}'$
, and so
$A_{pq}' = \sum _{i \neq p} A_{iq}' = \sum _{j \neq q} A_{pj}'$
, and so
![]() $\Sigma = (\alpha - 1)\Sigma = (\beta - 1)\Sigma $
. From this, it follows that
$\Sigma = (\alpha - 1)\Sigma = (\beta - 1)\Sigma $
. From this, it follows that
![]() $g\Sigma = 0$
. We also have
$g\Sigma = 0$
. We also have
![]() $A_{pq}' = \sum _{i \neq p} \sum _{j \neq q} A_{ij}'$
, so
$A_{pq}' = \sum _{i \neq p} \sum _{j \neq q} A_{ij}'$
, so
 $$ \begin{align*} \Sigma = A_{pq}' + \sum_{i \neq p} A_{iq}' + \sum_{j \neq q} A_{pj}' + \sum_{i \neq p} \sum_{j \neq q} A_{ij}' = 4A_{pq}' \end{align*} $$
$$ \begin{align*} \Sigma = A_{pq}' + \sum_{i \neq p} A_{iq}' + \sum_{j \neq q} A_{pj}' + \sum_{i \neq p} \sum_{j \neq q} A_{ij}' = 4A_{pq}' \end{align*} $$
for any fixed
![]() $p,q$
. But
$p,q$
. But
![]() $2gA_{pq}' = 0$
, and so, if
$2gA_{pq}' = 0$
, and so, if
![]() $g=2h$
for some integer h, then
$g=2h$
for some integer h, then
![]() $h\Sigma = 4hA_{pq}' = 0$
, and we are done.
$h\Sigma = 4hA_{pq}' = 0$
, and we are done.
The proof of the next proposition is analogous to that of Proposition 4.6.
Proposition 5.5. Consider the complete bipartite graph
![]() $\kappa = \kappa (\alpha ,\beta )$
for
$\kappa = \kappa (\alpha ,\beta )$
for
![]() $\alpha ,\beta \geq 3$
, and the associated
$\alpha ,\beta \geq 3$
, and the associated
![]() $2$
-rank graph
$2$
-rank graph
![]() $\Lambda '(\kappa )$
. Then the isomorphism class of the universal
$\Lambda '(\kappa )$
. Then the isomorphism class of the universal
![]() $C^{\star }$
-algebra
$C^{\star }$
-algebra
![]() $C^{\star }(\Lambda '(\kappa ))$
is completely determined by its K-theory and the position of the class of the identity in
$C^{\star }(\Lambda '(\kappa ))$
is completely determined by its K-theory and the position of the class of the identity in
![]() $K_0(C^{\star }(\Lambda '(\kappa )))$
.
$K_0(C^{\star }(\Lambda '(\kappa )))$
.
6 The homology of a tile complex
Theorem 6.1. Let
![]() $\kappa = \kappa (\alpha ,\beta )$
be the complete bipartite graph on
$\kappa = \kappa (\alpha ,\beta )$
be the complete bipartite graph on
![]() $\alpha \geq 2$
white and
$\alpha \geq 2$
white and
![]() $\beta \geq 2$
black vertices, let
$\beta \geq 2$
black vertices, let
![]() $(\kappa , U, V, \mathcal {S}'(\kappa ))$
be an unpointed tile system, and let
$(\kappa , U, V, \mathcal {S}'(\kappa ))$
be an unpointed tile system, and let
![]() $TC(\kappa )$
be its associated tile complex. Then the homology groups of
$TC(\kappa )$
be its associated tile complex. Then the homology groups of
![]() $TC(\kappa )$
are given by
$TC(\kappa )$
are given by
 $$ \begin{align*} H_n(TC(\kappa)) \cong \begin{cases} 0 & \text{ for }n = 0, \\ \mathbb{Z}^{\alpha + \beta - 2} & \text{ for } n = 1, \\ \mathbb{Z}^{(\alpha - 1)(\beta - 1)} & \text{ for } n = 2, \\ 0 & \text{ for } n \geq 3. \end{cases} \end{align*} $$
$$ \begin{align*} H_n(TC(\kappa)) \cong \begin{cases} 0 & \text{ for }n = 0, \\ \mathbb{Z}^{\alpha + \beta - 2} & \text{ for } n = 1, \\ \mathbb{Z}^{(\alpha - 1)(\beta - 1)} & \text{ for } n = 2, \\ 0 & \text{ for } n \geq 3. \end{cases} \end{align*} $$
Proof. As
![]() $TC(\kappa )$
is a path-connected, two-dimensional CW-complex by construction,
$TC(\kappa )$
is a path-connected, two-dimensional CW-complex by construction,
![]() $H_n(TC(\kappa )) \cong 0$
for
$H_n(TC(\kappa )) \cong 0$
for
![]() $n=0$
and
$n=0$
and
![]() $n \geq 3$
.
$n \geq 3$
.
The proof is based on that of [Reference Norledge, Thomas and Vdovina7, Proposition 3]. The boundary of each square in
![]() $TC(\kappa )$
is given by an element of
$TC(\kappa )$
is given by an element of
![]() $\mathcal {S}'(\kappa )$
; write these elements as
$\mathcal {S}'(\kappa )$
; write these elements as
![]() $(u_i^1,v_j^1,u_i^2,v_j^2)$
. By construction,
$(u_i^1,v_j^1,u_i^2,v_j^2)$
. By construction,
![]() $TC(\kappa )$
has four vertices: each is the origin of all directed edges labelled
$TC(\kappa )$
has four vertices: each is the origin of all directed edges labelled
![]() $u_i^1$
,
$u_i^1$
,
![]() $v_j^1$
,
$v_j^1$
,
![]() $u_i^2$
and
$u_i^2$
and
![]() $v_j^2$
. Each tile is homotopy equivalent to a point; pick tile
$v_j^2$
. Each tile is homotopy equivalent to a point; pick tile
![]() $(u_1^1,v_1^1,u_1^2,v_1^2)$
and contract it, thereby identifying the four vertices. Call the resulting tile complex
$(u_1^1,v_1^1,u_1^2,v_1^2)$
and contract it, thereby identifying the four vertices. Call the resulting tile complex
![]() $TC_1(\kappa )$
. This is a two-dimensional CW-complex whose edges are loops, and whose
$TC_1(\kappa )$
. This is a two-dimensional CW-complex whose edges are loops, and whose
![]() $2$
-cells comprise for
$2$
-cells comprise for
![]() $2 \leq i \leq \alpha $
,
$2 \leq i \leq \alpha $
,
![]() $2 \leq j \leq \beta $
$2 \leq j \leq \beta $
-
•
 $(\alpha -1)(\beta -1)$
-many unpointed tiles
$(\alpha -1)(\beta -1)$
-many unpointed tiles
 $A_{ij}'= (u_i^1,v_j^1,u_i^2,v_j^2)$
;
$A_{ij}'= (u_i^1,v_j^1,u_i^2,v_j^2)$
; -
•
 $(\alpha -1)$
-many
$(\alpha -1)$
-many
 $2$
-gons
$2$
-gons
 $X_i'$
with boundaries described analogously by
$X_i'$
with boundaries described analogously by
 $(u_i^1,u_i^2)$
;
$(u_i^1,u_i^2)$
; -
•
 $(\beta -1)$
-many
$(\beta -1)$
-many
 $2$
-gons
$2$
-gons
 $Y_j'$
with boundaries described by
$Y_j'$
with boundaries described by
 $(v_j^1,v_j^2)$
.
$(v_j^1,v_j^2)$
.
Consider the chain complex associated to
![]() $TC_1(\kappa )$
:
$TC_1(\kappa )$
:
Since
![]() $TC_1(\kappa )$
is two-dimensional and has one vertex, this boils down to
$TC_1(\kappa )$
is two-dimensional and has one vertex, this boils down to
and so
![]() $H_1(TC_1(\kappa )) \cong C_1 / \operatorname {\mathrm {im}}(\partial _2)$
and
$H_1(TC_1(\kappa )) \cong C_1 / \operatorname {\mathrm {im}}(\partial _2)$
and
![]() $H_2(TC_1(\kappa )) \cong \ker (\partial _2)$
. We have
$H_2(TC_1(\kappa )) \cong \ker (\partial _2)$
. We have
![]() $\partial _2(A_{ij}') = u_i^1 + v_j^1 + u_i^2 + v_j^2$
,
$\partial _2(A_{ij}') = u_i^1 + v_j^1 + u_i^2 + v_j^2$
,
![]() $\partial _2(X_i') = u_i^1 + u_i^2$
, and
$\partial _2(X_i') = u_i^1 + u_i^2$
, and
![]() $\partial _2(Y_j') = v_j^1 + v_j^2$
. Clearly
$\partial _2(Y_j') = v_j^1 + v_j^2$
. Clearly
![]() $\ker (\partial _2)$
is generated by
$\ker (\partial _2)$
is generated by
![]() $\lbrace A_{ij}' - X_i' - Y_j' \mid 2 \leq i \leq \alpha , 2 \leq j \leq \beta \rbrace $
, which implies that
$\lbrace A_{ij}' - X_i' - Y_j' \mid 2 \leq i \leq \alpha , 2 \leq j \leq \beta \rbrace $
, which implies that
![]() $\ker (\partial _2) \cong \mathbb {Z}^{(\alpha - 1 )( \beta - 1)}$
.
$\ker (\partial _2) \cong \mathbb {Z}^{(\alpha - 1 )( \beta - 1)}$
.
Similarly, an Abelian group presentation for
![]() $H_1(TC_1(\kappa ))$
is given by
$H_1(TC_1(\kappa ))$
is given by
 $$ \begin{align*} H_1(TC_1(\kappa))\cong \langle &u_i^1,v_j^1,u_i^2,v_j^2 \vert\, u_i^1 + v_j^1 + u_i^2 + v_j^2 = u_i^1 + u_i^2 \\ &= v_j^1 + v_j^2 = 0 \text{ for } 2 \leq i \leq \alpha, 2 \leq j \leq \beta \rangle, \end{align*} $$
$$ \begin{align*} H_1(TC_1(\kappa))\cong \langle &u_i^1,v_j^1,u_i^2,v_j^2 \vert\, u_i^1 + v_j^1 + u_i^2 + v_j^2 = u_i^1 + u_i^2 \\ &= v_j^1 + v_j^2 = 0 \text{ for } 2 \leq i \leq \alpha, 2 \leq j \leq \beta \rangle, \end{align*} $$
which, after substituting
![]() $u_i^2 = -u_i^1$
and
$u_i^2 = -u_i^1$
and
![]() $v_j^2 = -v_j^1$
, gives
$v_j^2 = -v_j^1$
, gives
This is a presentation for
![]() $\mathbb {Z}^{\alpha + \beta - 2}$
, and, since
$\mathbb {Z}^{\alpha + \beta - 2}$
, and, since
![]() $TC_1(\kappa )$
is homotopy equivalent to
$TC_1(\kappa )$
is homotopy equivalent to
![]() $TC(\kappa )$
, we are done.
$TC(\kappa )$
, we are done.
7 Pointed and unpointed
 $2t$
-gon systems
$2t$
-gon systems
In this section we suggest generalisations of the methods above for constructing
![]() $C^{\star }$
-algebras associated to
$C^{\star }$
-algebras associated to
![]() $2t$
-gon systems, both for even and arbitrary
$2t$
-gon systems, both for even and arbitrary
![]() $t \geq 1$
.
$t \geq 1$
.
When
![]() $t=2$
, we have an innate idea of what it means for two
$t=2$
, we have an innate idea of what it means for two
![]() $2t$
-gons to be ‘stackable’ – functions we called horizontal and vertical adjacency in Definition 3.1. We extend this notion to all even
$2t$
-gons to be ‘stackable’ – functions we called horizontal and vertical adjacency in Definition 3.1. We extend this notion to all even
![]() $t \geq 2$
in as natural a way as possible. The following definition directly generalises those at the beginning of Section 2.
$t \geq 2$
in as natural a way as possible. The following definition directly generalises those at the beginning of Section 2.
Definition 7.1. Let G be a connected bipartite graph on
![]() $\alpha $
white and
$\alpha $
white and
![]() $\beta $
black vertices. Let U, V be sets with
$\beta $
black vertices. Let U, V be sets with
![]() $|U| = 2t\alpha $
,
$|U| = 2t\alpha $
,
![]() $|V| = 2t\beta $
, gifted with fixed-point-free involutions
$|V| = 2t\beta $
, gifted with fixed-point-free involutions
![]() $u \mapsto \bar {u}$
,
$u \mapsto \bar {u}$
,
![]() $v \mapsto \bar {v}$
, respectively. Using U and V, construct the
$v \mapsto \bar {v}$
, respectively. Using U and V, construct the
![]() $2t$
-polyhedron
$2t$
-polyhedron
![]() $P(G)$
from Theorem 2.2, which comprises
$P(G)$
from Theorem 2.2, which comprises
![]() $2t$
-gons
$2t$
-gons
![]() $A_e = [ u_p^1,v_q^1,\ldots , u_p^t,v_q^t ]$
and has G as its link at each vertex. Write
$A_e = [ u_p^1,v_q^1,\ldots , u_p^t,v_q^t ]$
and has G as its link at each vertex. Write
![]() $\mathcal {S}'(G) := \lbrace A_e \mid e \in E(G)\rbrace $
for the set of
$\mathcal {S}'(G) := \lbrace A_e \mid e \in E(G)\rbrace $
for the set of
![]() $2t$
-gons comprising
$2t$
-gons comprising
![]() $P(G)$
. We call elements of
$P(G)$
. We call elements of
![]() $\mathcal {S}_t'(G)$
unpointed
$\mathcal {S}_t'(G)$
unpointed
![]() $2t$
-gons, and denote them by
$2t$
-gons, and denote them by
![]() $A_e = ( x_1,y_1,\ldots , x_t,y_t)$
.
$A_e = ( x_1,y_1,\ldots , x_t,y_t)$
.
Analogously to Section 2, we write
![]() $[ x_1,y_1,\ldots , x_t,y_t ]$
for a pointed
$[ x_1,y_1,\ldots , x_t,y_t ]$
for a pointed
![]() $2t$
-gon, that is, a
$2t$
-gon, that is, a
![]() $2t$
-gon labelled anticlockwise and starting from a distinguished basepoint by the sequence
$2t$
-gon labelled anticlockwise and starting from a distinguished basepoint by the sequence
![]() $x_1, y_1, \ldots , x_t, y_t$
, for some
$x_1, y_1, \ldots , x_t, y_t$
, for some
![]() $x_i \in U$
,
$x_i \in U$
,
![]() $y_i \in V$
. Write
$y_i \in V$
. Write
![]() $\mathcal {S}_t=\mathcal {S}_t(G)$
for the set of
$\mathcal {S}_t=\mathcal {S}_t(G)$
for the set of
![]() $2t\alpha \beta $
pointed
$2t\alpha \beta $
pointed
![]() $2t$
-gons. We call the tuple
$2t$
-gons. We call the tuple
![]() $(G,U,V,\mathcal {S}_t)$
a
$(G,U,V,\mathcal {S}_t)$
a
![]() $2t$
-gon system. Similarly, we call the tuple
$2t$
-gon system. Similarly, we call the tuple
![]() $(G,U,V,\mathcal {S}_t')$
an unpointed
$(G,U,V,\mathcal {S}_t')$
an unpointed
![]() $2t$
-gon system.
$2t$
-gon system.
Consider the adjacency matrices
![]() $M_1$
and
$M_1$
and
![]() $M_2$
from Definition 3.1. We can view two pointed tiles (
$M_2$
from Definition 3.1. We can view two pointed tiles (
![]() $4$
-gons)
$4$
-gons)
![]() $A=[x_1,y_1,x_2,y_2]$
and B as being horizontally adjacent, that is,
$A=[x_1,y_1,x_2,y_2]$
and B as being horizontally adjacent, that is,
![]() $M_1(A,B)=1$
, if and only if, after reflecting A through an axis connecting the midpoints of
$M_1(A,B)=1$
, if and only if, after reflecting A through an axis connecting the midpoints of
![]() $x_1$
and
$x_1$
and
![]() $x_2$
, and then replacing
$x_2$
, and then replacing
![]() $x_1$
,
$x_1$
,
![]() $x_2$
by some
$x_2$
by some
![]() $x_1' \neq x_1$
,
$x_1' \neq x_1$
,
![]() $x_2' \neq x_2$
respectively, we can obtain B. Likewise, if and only if we can obtain B by reflecting A through an axis joining the midpoints of the y edges, and then changing the labels of those edges, do we say that A and B are vertically adjacent.
$x_2' \neq x_2$
respectively, we can obtain B. Likewise, if and only if we can obtain B by reflecting A through an axis joining the midpoints of the y edges, and then changing the labels of those edges, do we say that A and B are vertically adjacent.
Definition 7.2. Let t be an even integer, let
![]() $(G,U,V,\mathcal {S}_t)$
be a
$(G,U,V,\mathcal {S}_t)$
be a
![]() $2t$
-gon system, and let
$2t$
-gon system, and let
![]() $A = [ x_1,y_1,\ldots ,x_t,y_t] \in \mathcal {S}_t$
be a pointed
$A = [ x_1,y_1,\ldots ,x_t,y_t] \in \mathcal {S}_t$
be a pointed
![]() $2t$
-gon.
$2t$
-gon.
Reflect A through an axis joining the midpoints of the sides labelled
![]() $x_1$
and
$x_1$
and
![]() $x_{(t/2)+1}$
to obtain a new pointed
$x_{(t/2)+1}$
to obtain a new pointed
![]() $2t$
-gon
$2t$
-gon
![]() $[ \bar {x}_1, \bar {y}_t, \bar {x}_t, \bar {y}_{t-1}, \ldots , \bar {x}_2, \bar {y}_1]$
. A pointed
$[ \bar {x}_1, \bar {y}_t, \bar {x}_t, \bar {y}_{t-1}, \ldots , \bar {x}_2, \bar {y}_1]$
. A pointed
![]() $2t$
-gon
$2t$
-gon
![]() $B \in \mathcal {S}_t$
is V-adjacent to A whenever
$B \in \mathcal {S}_t$
is V-adjacent to A whenever
![]() $B = [ \bar {x}_1', \bar {y}_t, \bar {x}_t', \bar {y}_{t-1}, \ldots , \bar {x}_2', \bar {y}_1 ]$
for some
$B = [ \bar {x}_1', \bar {y}_t, \bar {x}_t', \bar {y}_{t-1}, \ldots , \bar {x}_2', \bar {y}_1 ]$
for some
![]() $x_i' \neq x_i$
.
$x_i' \neq x_i$
.
Similarly, reflect A so that
![]() $x_1 \mapsto \bar {x}_{(t/2)+1}$
; we obtain a new pointed
$x_1 \mapsto \bar {x}_{(t/2)+1}$
; we obtain a new pointed
![]() $2t$
-gon
$2t$
-gon
We say that a pointed
![]() $2t$
-gon
$2t$
-gon
![]() $B \in \mathcal {S}_t$
is U-adjacent to A if B is of the form (7-1), but with all elements
$B \in \mathcal {S}_t$
is U-adjacent to A if B is of the form (7-1), but with all elements
![]() $y_i$
replaced with some
$y_i$
replaced with some
![]() $y_i' \neq y_i$
(Figure 9).
$y_i' \neq y_i$
(Figure 9).

Figure 9
U-, V-adjacency: Consider the pointed octagons
![]() $A = [ x_1,y_1,\ldots ,x_4,y_4]$
,
$A = [ x_1,y_1,\ldots ,x_4,y_4]$
,
![]() $B = [ \bar {x}_1', \bar {y}_4, \ldots ,\bar {x}_2', \bar {y}_1]$
, and
$B = [ \bar {x}_1', \bar {y}_4, \ldots ,\bar {x}_2', \bar {y}_1]$
, and
![]() $C = [\bar {x}_3, \bar {y}_2', \ldots ,\bar {x}_4, \bar {y}_3']$
in
$C = [\bar {x}_3, \bar {y}_2', \ldots ,\bar {x}_4, \bar {y}_3']$
in
![]() $\mathcal {S}_4$
. We say that A and B are V-adjacent, and A and C are U-adjacent. There is a unique octagon
$\mathcal {S}_4$
. We say that A and B are V-adjacent, and A and C are U-adjacent. There is a unique octagon
![]() $D = [x_3',y_3', \ldots , x_2', y_2']$
that is both U-adjacent to B and V-adjacent to C.
$D = [x_3',y_3', \ldots , x_2', y_2']$
that is both U-adjacent to B and V-adjacent to C.
We define the U- and V-adjacency matrices,
![]() $M_U$
and
$M_U$
and
![]() $M_V$
, respectively, to be the
$M_V$
, respectively, to be the
![]() $2t\alpha \beta \times 2t\alpha \beta $
matrices with
$2t\alpha \beta \times 2t\alpha \beta $
matrices with
![]() $AB$
th entry
$AB$
th entry
![]() $1$
if A and B are U-adjacent (respectively, V-adjacent), and
$1$
if A and B are U-adjacent (respectively, V-adjacent), and
![]() $0$
otherwise.
$0$
otherwise.
Proposition 7.3. Let t be even, and
![]() $(\kappa , U, V, \mathcal {S}_t(\kappa ))$
be a
$(\kappa , U, V, \mathcal {S}_t(\kappa ))$
be a
![]() $2t$
-gon system with adjacency matrices
$2t$
-gon system with adjacency matrices
![]() $M_U$
,
$M_U$
,
![]() $M_V$
. Then these matrices commute, and
$M_V$
. Then these matrices commute, and
![]() $(\kappa , U, V, \mathcal {S}_t(\kappa ))$
has the UCE property. Hence,
$(\kappa , U, V, \mathcal {S}_t(\kappa ))$
has the UCE property. Hence,
![]() $(\kappa ,U,V,\mathcal {S}_t(\kappa ))$
has a
$(\kappa ,U,V,\mathcal {S}_t(\kappa ))$
has a
![]() $2$
-rank graph structure.
$2$
-rank graph structure.
Proof. Consider the pointed
![]() $2t$
-gon
$2t$
-gon
![]() $A = [ u_i^1,v_j^1,\ldots ,u_i^t,v_j^t] \in \mathcal {S}_t(\kappa )$
; those
$A = [ u_i^1,v_j^1,\ldots ,u_i^t,v_j^t] \in \mathcal {S}_t(\kappa )$
; those
![]() $2t$
-gons corresponding to its reflections and rotations are treated similarly. Then a pointed
$2t$
-gons corresponding to its reflections and rotations are treated similarly. Then a pointed
![]() $2t$
-gon B is V-adjacent to A if and only if
$2t$
-gon B is V-adjacent to A if and only if
![]() $B = [ \bar {u}_k^1, \bar {v}_j^t, \ldots , \bar {u}_k^2, \bar {v}_j^1 ]$
for some
$B = [ \bar {u}_k^1, \bar {v}_j^t, \ldots , \bar {u}_k^2, \bar {v}_j^1 ]$
for some
![]() $k \neq i$
. Suppose B is such a
$k \neq i$
. Suppose B is such a
![]() $2t$
-gon V-adjacent to A; then a pointed
$2t$
-gon V-adjacent to A; then a pointed
![]() $2t$
-gon D is U-adjacent to B if and only if
$2t$
-gon D is U-adjacent to B if and only if
for some
![]() $l \neq j$
. Likewise, C is U-adjacent to A if and only if
$l \neq j$
. Likewise, C is U-adjacent to A if and only if
for some
![]() $l \neq j$
. Clearly, if C is such a
$l \neq j$
. Clearly, if C is such a
![]() $2t$
-gon, then D is V-adjacent to C if and only if it is of the form (7-2). Exactly one such D exists in
$2t$
-gon, then D is V-adjacent to C if and only if it is of the form (7-2). Exactly one such D exists in
![]() $\mathcal {S}_t(\kappa )$
; hence,
$\mathcal {S}_t(\kappa )$
; hence,
![]() $M_U$
and
$M_U$
and
![]() $M_V$
commute. Then
$M_V$
commute. Then
![]() $(\kappa , U, V, \mathcal {S}_t(\kappa ))$
has the UCE property, and the
$(\kappa , U, V, \mathcal {S}_t(\kappa ))$
has the UCE property, and the
![]() $2$
-rank graph structure follows from [Reference Kumjian and Pask6, Section 6].
$2$
-rank graph structure follows from [Reference Kumjian and Pask6, Section 6].
Recall the
![]() $2$
-rank graph
$2$
-rank graph
![]() $\Lambda (\kappa )$
induced from a tile system and its adjacency matrices
$\Lambda (\kappa )$
induced from a tile system and its adjacency matrices
![]() $M_1$
,
$M_1$
,
![]() $M_2$
in Section 3, and recall its associated universal
$M_2$
in Section 3, and recall its associated universal
![]() $C^{\star }$
-algebra
$C^{\star }$
-algebra
![]() $C^{\star }(\Lambda )$
from Definition 3.7. We similarly write
$C^{\star }(\Lambda )$
from Definition 3.7. We similarly write
![]() $\Lambda _t(\kappa )$
for the
$\Lambda _t(\kappa )$
for the
![]() $2$
-rank graph induced from the U- and V-adjacency matrices
$2$
-rank graph induced from the U- and V-adjacency matrices
![]() $M_U$
and
$M_U$
and
![]() $M_V$
, and observe that
$M_V$
, and observe that
![]() $\Lambda _t(\kappa )$
is row-finite, with a finite vertex set and no sources. Hence, from Theorem 3.8 we can deduce the following theorem.
$\Lambda _t(\kappa )$
is row-finite, with a finite vertex set and no sources. Hence, from Theorem 3.8 we can deduce the following theorem.
Theorem 7.4 (K-groups for pointed
 $2t$
-gon systems, t even)
$2t$
-gon systems, t even)
Let
![]() $\alpha , \beta \geq 2$
, let
$\alpha , \beta \geq 2$
, let
![]() $t \geq 2$
be even, and let
$t \geq 2$
be even, and let
![]() $\kappa = \kappa (\alpha , \beta )$
be the complete bipartite graph on
$\kappa = \kappa (\alpha , \beta )$
be the complete bipartite graph on
![]() $\alpha $
white and
$\alpha $
white and
![]() $\beta $
black vertices. Then
$\beta $
black vertices. Then
for
![]() $\epsilon = 0,1$
.
$\epsilon = 0,1$
.
Proof. Fix t and assume, without loss of generality, that
![]() $\alpha \leq \beta $
. Analogously to the proof of Theorem 3.10, we denote the pointed
$\alpha \leq \beta $
. Analogously to the proof of Theorem 3.10, we denote the pointed
![]() $2t$
-gons in
$2t$
-gons in
![]() $\mathcal {S}_t(\kappa )$
as follows:
$\mathcal {S}_t(\kappa )$
as follows:
-
•
 $(A_r)_{ij} = [u_i^r, v_j^r, \ldots , u_i^t, v_j^t, u_i^1, v_j^1, \ldots , u_i^{r-1}, v_j^{r-1} ]$
;
$(A_r)_{ij} = [u_i^r, v_j^r, \ldots , u_i^t, v_j^t, u_i^1, v_j^1, \ldots , u_i^{r-1}, v_j^{r-1} ]$
; -
•
 $(B_r)_{ij} = [ \bar {u}_i^r, \bar {v}_j^{r-1}, \ldots , \bar {u}_i^1, \bar {v}_j^t, \ldots , \bar {u}_i^{r+1}, \bar {v}_j^r ]$
;
$(B_r)_{ij} = [ \bar {u}_i^r, \bar {v}_j^{r-1}, \ldots , \bar {u}_i^1, \bar {v}_j^t, \ldots , \bar {u}_i^{r+1}, \bar {v}_j^r ]$
; -
•
 $(C_r)_{ij} = [ \bar {u}_i^{(t/2)+r}, \bar {v}_j^{(t/2)+r-1}, \ldots , \bar {u}_i^1, \bar {v}_j^t, \ldots , \bar {u}_i^{(t/2)+r+1}, \bar {v}_j^{(t/2)+r} ]$
;
$(C_r)_{ij} = [ \bar {u}_i^{(t/2)+r}, \bar {v}_j^{(t/2)+r-1}, \ldots , \bar {u}_i^1, \bar {v}_j^t, \ldots , \bar {u}_i^{(t/2)+r+1}, \bar {v}_j^{(t/2)+r} ]$
; -
•
 $(D_r)_{ij} = [ u_i^{(t/2)+r}, v_j^{(t/2)+r}, \ldots , u_i^t, v_j^t, u_i^1, v_j^1, \ldots , u_i^{(t/2)+r-1}, v_j^{(t/2)+r-1} ]$
$(D_r)_{ij} = [ u_i^{(t/2)+r}, v_j^{(t/2)+r}, \ldots , u_i^t, v_j^t, u_i^1, v_j^1, \ldots , u_i^{(t/2)+r-1}, v_j^{(t/2)+r-1} ]$
for
![]() $1 \leq i \leq \alpha $
,
$1 \leq i \leq \alpha $
,
![]() $1 \leq j \leq \beta $
,
$1 \leq j \leq \beta $
,
![]() $1 \leq r \leq t/2$
. Here, the addition in the subscript indices is defined modulo t. Note that each
$1 \leq r \leq t/2$
. Here, the addition in the subscript indices is defined modulo t. Note that each
![]() $S \in \mathcal {S}_t(\kappa )$
takes one of the above forms. Then
$S \in \mathcal {S}_t(\kappa )$
takes one of the above forms. Then
 $$ \begin{align*} \operatorname{\mathrm{coker}} ( \mathbf{1}-M_U^T, \mathbf{1}-M_V^T) = \bigg\langle &(A_r)_{pq}, (B_r)_{pq}, (C_r)_{pq}, (D_r)_{pq} \bigg\vert\, \\ &(A_r)_{pq} = \sum_{i \neq p} (B_r)_{iq} = \sum_{j \neq q} (C_r)_{pj}, \\ &(B_r)_{pq} = \sum_{i \neq p} (A_r)_{iq} = \sum_{j \neq q} (D_r)_{pj}, \\ &(C_r)_{pq} = \sum_{i \neq p} (D_r)_{iq} = \sum_{j \neq q} (A_r)_{pj}, \\ &(D_r)_{pq} = \sum_{i \neq p} (C_r)_{iq} = \sum_{j \neq q} (B_r)_{pj}, \\[-3pt] &\text{for }1 \leq p \leq \alpha, 1 \leq q \leq \beta, \text{ and }1 \leq r \leq t/2 \bigg\rangle. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{coker}} ( \mathbf{1}-M_U^T, \mathbf{1}-M_V^T) = \bigg\langle &(A_r)_{pq}, (B_r)_{pq}, (C_r)_{pq}, (D_r)_{pq} \bigg\vert\, \\ &(A_r)_{pq} = \sum_{i \neq p} (B_r)_{iq} = \sum_{j \neq q} (C_r)_{pj}, \\ &(B_r)_{pq} = \sum_{i \neq p} (A_r)_{iq} = \sum_{j \neq q} (D_r)_{pj}, \\ &(C_r)_{pq} = \sum_{i \neq p} (D_r)_{iq} = \sum_{j \neq q} (A_r)_{pj}, \\ &(D_r)_{pq} = \sum_{i \neq p} (C_r)_{iq} = \sum_{j \neq q} (B_r)_{pj}, \\[-3pt] &\text{for }1 \leq p \leq \alpha, 1 \leq q \leq \beta, \text{ and }1 \leq r \leq t/2 \bigg\rangle. \end{align*} $$
But, comparing this to (3-1), we see this is precisely a presentation for the direct sum of
![]() $t/2$
copies of
$t/2$
copies of
![]() $\operatorname {\mathrm {coker}}( I-M_1^T, I-M_2^T)$
as in Theorem 3.10, and the result follows.
$\operatorname {\mathrm {coker}}( I-M_1^T, I-M_2^T)$
as in Theorem 3.10, and the result follows.
Theorem 7.5. Let
![]() $\alpha , \beta \geq 3$
, let
$\alpha , \beta \geq 3$
, let
![]() $t \geq 2$
be even, and let
$t \geq 2$
be even, and let
![]() $\kappa = \kappa (\alpha , \beta )$
be the complete bipartite graph on
$\kappa = \kappa (\alpha , \beta )$
be the complete bipartite graph on
![]() $\alpha $
white and
$\alpha $
white and
![]() $\beta $
black vertices. Then the order of the class of the identity
$\beta $
black vertices. Then the order of the class of the identity
![]() $[\mathbf {1}]$
in
$[\mathbf {1}]$
in
![]() $K_0(C^{\star }(\Lambda _t(\kappa )))$
is equal to
$K_0(C^{\star }(\Lambda _t(\kappa )))$
is equal to
![]() $g := \gcd (\alpha - 2, \beta - 2)$
.
$g := \gcd (\alpha - 2, \beta - 2)$
.
Furthermore, the isomorphism class of
![]() $C^{\star }(\Lambda _t(\kappa ))$
is completely determined by the K-groups from Theorem 7.4 and the order of
$C^{\star }(\Lambda _t(\kappa ))$
is completely determined by the K-groups from Theorem 7.4 and the order of
![]() $[\mathbf {1}]$
in
$[\mathbf {1}]$
in
![]() $K_0$
.
$K_0$
.
Proof. The result follows from Theorems 3.12 and 7.4, and considerations similar to those in the proof of Proposition 4.6.
If we extend the concept of U- and V-adjacency from Definition 7.2 in the obvious way, we can obtain a generalisation of Section 5 for unpointed
![]() $2t$
-gon systems of complete bipartite graphs. Write
$2t$
-gon systems of complete bipartite graphs. Write
![]() $\Lambda _t'(\kappa )$
for the induced
$\Lambda _t'(\kappa )$
for the induced
![]() $2$
-rank graph. We realise that the proof of Theorem 5.3 does not depend on the number of sides
$2$
-rank graph. We realise that the proof of Theorem 5.3 does not depend on the number of sides
![]() $2t$
of the
$2t$
of the
![]() $2t$
-gons; nor do the K-groups associated with
$2t$
-gons; nor do the K-groups associated with
![]() $\Lambda _t'(\kappa )$
.
$\Lambda _t'(\kappa )$
.
Corollary 7.6 (to Theorem 5.3: K-groups for unpointed
 $2t$
-gon systems)
$2t$
-gon systems)
Let
![]() $\alpha ,\beta \geq 2$
, and let
$\alpha ,\beta \geq 2$
, and let
![]() $\kappa = \kappa (\alpha ,\beta )$
be the complete bipartite graph on
$\kappa = \kappa (\alpha ,\beta )$
be the complete bipartite graph on
![]() $\alpha $
white and
$\alpha $
white and
![]() $\beta $
black vertices. Then
$\beta $
black vertices. Then
for
![]() $\epsilon = 0,1$
, and all
$\epsilon = 0,1$
, and all
![]() $t \geq 1$
.
$t \geq 1$
.
Proposition 7.7. Let
![]() $\alpha , \beta \geq 3$
, let
$\alpha , \beta \geq 3$
, let
![]() $\kappa = \kappa (\alpha , \beta )$
be the complete bipartite graph, and write
$\kappa = \kappa (\alpha , \beta )$
be the complete bipartite graph, and write
![]() $g := \gcd (\alpha - 2, \beta - 2)$
. Then, for all
$g := \gcd (\alpha - 2, \beta - 2)$
. Then, for all
![]() $t \geq 1$
, the order of the class of the identity
$t \geq 1$
, the order of the class of the identity
![]() $[\mathbf {1}]$
in
$[\mathbf {1}]$
in
![]() $K_0(C^{\star }(\Lambda _t'(\kappa )))$
is equal to g if g is odd, and
$K_0(C^{\star }(\Lambda _t'(\kappa )))$
is equal to g if g is odd, and
![]() $g/2$
if g is even.
$g/2$
if g is even.
Furthermore, the isomorphism class of
![]() $C^{\star }(\Lambda _t'(\kappa ))$
is completely determined by the K-groups in Corollary 7.6 and the order of
$C^{\star }(\Lambda _t'(\kappa ))$
is completely determined by the K-groups in Corollary 7.6 and the order of
![]() $[\mathbf {1}]$
in
$[\mathbf {1}]$
in
![]() $K_0$
.
$K_0$
.
Corollary 7.8 (to Theorem 6.1)
Let
![]() $(\kappa , U, V, \mathcal {S}_t'(\kappa ))$
be an unpointed
$(\kappa , U, V, \mathcal {S}_t'(\kappa ))$
be an unpointed
![]() $2t$
-gon system, and let
$2t$
-gon system, and let
![]() $P(\kappa )$
be its associated
$P(\kappa )$
be its associated
![]() $2t$
-polyhedron. Then the homology groups of
$2t$
-polyhedron. Then the homology groups of
![]() $P(\kappa )$
do not depend on t, that is,
$P(\kappa )$
do not depend on t, that is,
 $$ \begin{align*} H_n(P(\kappa)) \cong \begin{cases} 0 & \text{ for }n = 0, \\ \mathbb{Z}^{\alpha + \beta - 2} & \text{ for } n = 1, \\ \mathbb{Z}^{(\alpha - 1)(\beta - 1)} & \text{ for } n = 2, \\ 0 & \text{ for } n \geq 3. \end{cases} \end{align*} $$
$$ \begin{align*} H_n(P(\kappa)) \cong \begin{cases} 0 & \text{ for }n = 0, \\ \mathbb{Z}^{\alpha + \beta - 2} & \text{ for } n = 1, \\ \mathbb{Z}^{(\alpha - 1)(\beta - 1)} & \text{ for } n = 2, \\ 0 & \text{ for } n \geq 3. \end{cases} \end{align*} $$
7.1 Questions on canonicality
Corollary 7.6 gives us a collection of K-groups corresponding to systems of
![]() $2t$
-gons with an arbitrary even number of sides
$2t$
-gons with an arbitrary even number of sides
![]() $2t$
, whereas in the pointed case, Theorem 7.4 insists on
$2t$
, whereas in the pointed case, Theorem 7.4 insists on
![]() $2t$
being divisible by
$2t$
being divisible by
![]() $4$
. This is due to how we define adjacency in each instance: in the
$4$
. This is due to how we define adjacency in each instance: in the
![]() $2t$
-polyhedron
$2t$
-polyhedron
![]() $P(\kappa )$
, each face is adjacent to every other, and since the number of faces is not dependent on t, nor are the U- and V-adjacency matrices in an unpointed
$P(\kappa )$
, each face is adjacent to every other, and since the number of faces is not dependent on t, nor are the U- and V-adjacency matrices in an unpointed
![]() $2t$
-gon system.
$2t$
-gon system.
Adjacency in the pointed case is more difficult to define canonically. When
![]() $t=2$
, and we are dealing with tiles, there is an obvious pair of adjacency functions. We extend these in Definition 7.2, thinking of two
$t=2$
, and we are dealing with tiles, there is an obvious pair of adjacency functions. We extend these in Definition 7.2, thinking of two
![]() $2t$
-gons as adjacent if we can reflect one horizontally or vertically in order to obtain the form of the other. This works since horizontal and vertical reflections commute, and so the
$2t$
-gons as adjacent if we can reflect one horizontally or vertically in order to obtain the form of the other. This works since horizontal and vertical reflections commute, and so the
![]() $2t$
-gon system has the UCE property. If t is not even, then there are no two distinct reflections of
$2t$
-gon system has the UCE property. If t is not even, then there are no two distinct reflections of
![]() $2t$
-gons which commute, and preserve the structure of pointed
$2t$
-gons which commute, and preserve the structure of pointed
![]() $2t$
-gons. We must pick the same two reflections for both adjacency functions, or else some combination of rotations and identity transformations. None of these options is a direct extension of our horizontal and vertical adjacency functions from Section 3, and so there is no natural choice.
$2t$
-gons. We must pick the same two reflections for both adjacency functions, or else some combination of rotations and identity transformations. None of these options is a direct extension of our horizontal and vertical adjacency functions from Section 3, and so there is no natural choice.
We suggest that the following definitions of U- and V-adjacency for pointed
![]() $2t$
-gons are the most intuitive for
$2t$
-gons are the most intuitive for
![]() $t \geq 3$
, based on the idea that adjacent
$t \geq 3$
, based on the idea that adjacent
![]() $2t$
-gons should have opposite orientations. They do not, however, generalise the tile systems from Sections 2–5, themselves being the most natural constructions when
$2t$
-gons should have opposite orientations. They do not, however, generalise the tile systems from Sections 2–5, themselves being the most natural constructions when
![]() $t=2$
. Because of this, the previous constructions are the main focus of this paper.
$t=2$
. Because of this, the previous constructions are the main focus of this paper.
Definition 7.9. Let
![]() $t \geq 1$
be a fixed arbitrary integer, let
$t \geq 1$
be a fixed arbitrary integer, let
![]() $(G,U,V,\mathcal {S}_t)$
be a
$(G,U,V,\mathcal {S}_t)$
be a
![]() $2t$
-gon system, and let
$2t$
-gon system, and let
![]() $A = [ x_1,y_1,\ldots ,x_t,y_t] \in \mathcal {S}_t$
be a pointed
$A = [ x_1,y_1,\ldots ,x_t,y_t] \in \mathcal {S}_t$
be a pointed
![]() $2t$
-gon.
$2t$
-gon.
A pointed
![]() $2t$
-gon
$2t$
-gon
![]() $B \in \mathcal {S}_t$
is
$B \in \mathcal {S}_t$
is
![]() $V^*$
-adjacent to A if and only if
$V^*$
-adjacent to A if and only if
![]() $B = [\bar {x}_1', \bar {y}_t, \ldots , \bar {x}_2', \bar {y}_1]$
for some
$B = [\bar {x}_1', \bar {y}_t, \ldots , \bar {x}_2', \bar {y}_1]$
for some
![]() $x_i' \neq x_i$
.
$x_i' \neq x_i$
.
Similarly, we say that a pointed
![]() $2t$
-gon
$2t$
-gon
![]() $C \in \mathcal {S}_t$
is
$C \in \mathcal {S}_t$
is
![]() $U^*$
-adjacent to A if and only if
$U^*$
-adjacent to A if and only if
![]() $C = [ \bar {x}_1, \bar {y}_t', \ldots , \bar {x}_2, \bar {y}_1' ]$
for some
$C = [ \bar {x}_1, \bar {y}_t', \ldots , \bar {x}_2, \bar {y}_1' ]$
for some
![]() $y_i' \neq y_i$
. We define the
$y_i' \neq y_i$
. We define the
![]() $U^*$
- and
$U^*$
- and
![]() $V^*$
-adjacency matrices
$V^*$
-adjacency matrices
![]() $M_U^*$
and
$M_U^*$
and
![]() $M_V^*$
, respectively, as above.
$M_V^*$
, respectively, as above.
The proof of the following proposition is almost identical to that of Proposition 7.3, together with Proposition 3.5. From this, along with Theorem 3.8, we can deduce Theorem 7.11.
Proposition 7.10. Let
![]() $(\kappa , U, V, \mathcal {S}_t(\kappa ))$
be a
$(\kappa , U, V, \mathcal {S}_t(\kappa ))$
be a
![]() $2t$
-gon system with adjacency matrices
$2t$
-gon system with adjacency matrices
![]() $M_U^*$
,
$M_U^*$
,
![]() $M_V^*$
. Then
$M_V^*$
. Then
![]() $(\kappa , U, V, \mathcal {S}_t(\kappa ))$
induces a
$(\kappa , U, V, \mathcal {S}_t(\kappa ))$
induces a
![]() $2$
-rank graph
$2$
-rank graph
![]() $\Lambda _t^*(\kappa )$
, which is row-finite, with a finite vertex set and no sources.
$\Lambda _t^*(\kappa )$
, which is row-finite, with a finite vertex set and no sources.
Theorem 7.11 (K-groups for pointed
 $2t$
-gon systems, t arbitrary)
$2t$
-gon systems, t arbitrary)
Let
![]() $a,b \geq 0$
, let
$a,b \geq 0$
, let
![]() $t \geq 1$
, and let
$t \geq 1$
, and let
![]() $\kappa = \kappa (a+2, b+2)$
be the complete bipartite graph on
$\kappa = \kappa (a+2, b+2)$
be the complete bipartite graph on
![]() $a+2$
white and
$a+2$
white and
![]() $b+2$
black vertices. Without loss of generality, we assume that
$b+2$
black vertices. Without loss of generality, we assume that
![]() $a \leq b$
. Then, for
$a \leq b$
. Then, for
![]() $\epsilon = 0,1$
, we have the following assertions.
$\epsilon = 0,1$
, we have the following assertions.
-
(1) If
 $a=b=0$
, then
$a=b=0$
, then
 $K_\epsilon (C^{\star } (\Lambda _t^*(\kappa ) )) \cong \mathbb {Z}^{4t}$
.
$K_\epsilon (C^{\star } (\Lambda _t^*(\kappa ) )) \cong \mathbb {Z}^{4t}$
. -
(2) If
 $b \geq 1$
and
$b \geq 1$
and
 $a,b$
are coprime, then
$a,b$
are coprime, then
 $K_\epsilon (C^{\star } (\Lambda _t^*(\kappa ) )) \cong \mathbb {Z}^{2t(a+1)(b+1)}$
.
$K_\epsilon (C^{\star } (\Lambda _t^*(\kappa ) )) \cong \mathbb {Z}^{2t(a+1)(b+1)}$
. -
(3) If
 $b \geq 1$
and
$b \geq 1$
and
 $a,b$
are not coprime, then where
$a,b$
are not coprime, then where $$ \begin{align*} K_\epsilon (C^{\star} (\Lambda_t^*(\kappa) )) \cong \mathbb{Z}^{2t(a+1)(b+1)} \oplus (\mathbb{Z}/g)^t, \end{align*} $$
$$ \begin{align*} K_\epsilon (C^{\star} (\Lambda_t^*(\kappa) )) \cong \mathbb{Z}^{2t(a+1)(b+1)} \oplus (\mathbb{Z}/g)^t, \end{align*} $$
 $g := \gcd (a,b)$
.
$g := \gcd (a,b)$
.
Proof. The proof follows the same lines as those of Theorems 3.10, 5.3, and 7.4. Write
![]() $\alpha := a+2$
,
$\alpha := a+2$
,
![]() $\beta := b+2$
, and let
$\beta := b+2$
, and let
![]() $\beta \geq 3$
. We denote the pointed
$\beta \geq 3$
. We denote the pointed
![]() $2t$
-gons in
$2t$
-gons in
![]() $\mathcal {S}_t(\kappa )$
by
$\mathcal {S}_t(\kappa )$
by
-
•
 $(A_r)_{ij} := [u_i^r, v_j^r, \ldots , u_i^t, v_j^t, u_i^1, v_j^1, \ldots , u_i^{r-1}, v_j^{r-1} ]$
,
$(A_r)_{ij} := [u_i^r, v_j^r, \ldots , u_i^t, v_j^t, u_i^1, v_j^1, \ldots , u_i^{r-1}, v_j^{r-1} ]$
, -
•
 $(B_r)_{ij} := [ \bar {u}_i^r, \bar {v}_j^{r-1}, \ldots , \bar {u}_i^1, \bar {v}_j^t, \ldots , \bar {u}_i^{r+1}, \bar {v}_j^r ]$
$(B_r)_{ij} := [ \bar {u}_i^r, \bar {v}_j^{r-1}, \ldots , \bar {u}_i^1, \bar {v}_j^t, \ldots , \bar {u}_i^{r+1}, \bar {v}_j^r ]$
for
![]() $1 \leq i \leq \alpha $
,
$1 \leq i \leq \alpha $
,
![]() $1 \leq j \leq \beta $
,
$1 \leq j \leq \beta $
,
![]() $1 \leq r \leq t$
, and with addition in superscript indices defined modulo t. Observe that each
$1 \leq r \leq t$
, and with addition in superscript indices defined modulo t. Observe that each
![]() $S \in \mathcal {S}_t(\kappa )$
is either of the form
$S \in \mathcal {S}_t(\kappa )$
is either of the form
![]() $(A_r)_{ij}$
or
$(A_r)_{ij}$
or
![]() $(B_r)_{ij}$
. Then
$(B_r)_{ij}$
. Then
 $$ \begin{align*} \operatorname{\mathrm{coker}}= \bigg\langle &(A_r)_{pq}, (B_r)_{pq} \bigg \vert \\[-2pt] &(A_r)_{pq} = \sum_{i \neq p} (B_r)_{iq} = \sum_{j \neq q} (B_r)_{pj},\\[-2pt] &(B_r)_{pq} = \sum_{i \neq p} (A_r)_{iq} = \sum_{j \neq q} (A_r)_{pj},\\[-2pt] &\text{for } 1 \leq p \leq \alpha, 1 \leq q \leq \beta, \text{ and } 1 \leq r \leq t \bigg\rangle, \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{coker}}= \bigg\langle &(A_r)_{pq}, (B_r)_{pq} \bigg \vert \\[-2pt] &(A_r)_{pq} = \sum_{i \neq p} (B_r)_{iq} = \sum_{j \neq q} (B_r)_{pj},\\[-2pt] &(B_r)_{pq} = \sum_{i \neq p} (A_r)_{iq} = \sum_{j \neq q} (A_r)_{pj},\\[-2pt] &\text{for } 1 \leq p \leq \alpha, 1 \leq q \leq \beta, \text{ and } 1 \leq r \leq t \bigg\rangle, \end{align*} $$
where
![]() $\operatorname {\mathrm {coker}} := \operatorname {\mathrm {coker}}( \mathbf {1} - (M_U^*)^T, \mathbf {1} - (M_V^*)^T )$
. As in the proof of Theorem 3.10, define
$\operatorname {\mathrm {coker}} := \operatorname {\mathrm {coker}}( \mathbf {1} - (M_U^*)^T, \mathbf {1} - (M_V^*)^T )$
. As in the proof of Theorem 3.10, define
![]() $(J_r)_q := \sum _{i=1}^\alpha (A_r)_{iq}$
, and
$(J_r)_q := \sum _{i=1}^\alpha (A_r)_{iq}$
, and
![]() $(I_r)_p := \sum _{j=1}^\beta (A_r)_{pj}$
. Through a sequence of Tietze transformations, and using some observations from previous proofs, we see that the above presentation, and hence
$(I_r)_p := \sum _{j=1}^\beta (A_r)_{pj}$
. Through a sequence of Tietze transformations, and using some observations from previous proofs, we see that the above presentation, and hence
![]() $\operatorname {\mathrm {coker}}$
, is equivalent to
$\operatorname {\mathrm {coker}}$
, is equivalent to
 $$ \begin{align*} \bigg\langle (A_r)_{pq} \bigg \vert\, (A_r)_{pq} &= \sum_{i \neq p} \sum_{k \neq i} (A_r)_{kq} = \sum_{j \neq q} \sum_{l \neq j} (A_r)_{pl}, \sum_{i \neq p} (A_r)_{iq} = \sum_{j \neq q} (A_r)_{pj} \bigg\rangle \\[-2pt] &= \bigg\langle (A_r)_{pq} \bigg \vert\, (\alpha - 2)(J_r)_q = (\beta - 2)(I_r)_p = 0, \sum_{i \neq p} (A_r)_{iq} = \sum_{j \neq q} (A_r)_{pj} \bigg\rangle \\[-2pt] &= \bigg\langle (A_r)_{pq} \bigg \vert\, (\alpha - 2)(J_r)_q = (\beta - 2)(I_r)_p = 0, (J_r)_q = (I_r)_p \text{ for all }p,q \bigg\rangle. \end{align*} $$
$$ \begin{align*} \bigg\langle (A_r)_{pq} \bigg \vert\, (A_r)_{pq} &= \sum_{i \neq p} \sum_{k \neq i} (A_r)_{kq} = \sum_{j \neq q} \sum_{l \neq j} (A_r)_{pl}, \sum_{i \neq p} (A_r)_{iq} = \sum_{j \neq q} (A_r)_{pj} \bigg\rangle \\[-2pt] &= \bigg\langle (A_r)_{pq} \bigg \vert\, (\alpha - 2)(J_r)_q = (\beta - 2)(I_r)_p = 0, \sum_{i \neq p} (A_r)_{iq} = \sum_{j \neq q} (A_r)_{pj} \bigg\rangle \\[-2pt] &= \bigg\langle (A_r)_{pq} \bigg \vert\, (\alpha - 2)(J_r)_q = (\beta - 2)(I_r)_p = 0, (J_r)_q = (I_r)_p \text{ for all }p,q \bigg\rangle. \end{align*} $$
We can rewrite each
![]() $(A_r)_{i1}$
and
$(A_r)_{i1}$
and
![]() $(A_r)_{1j}$
in terms of the other
$(A_r)_{1j}$
in terms of the other
![]() $(A_r)_{ij}$
, the
$(A_r)_{ij}$
, the
![]() $(J_r)_q$
, and the
$(J_r)_q$
, and the
![]() $(I_r)_p$
, and, hence, remove them from the list of generators. Then, since
$(I_r)_p$
, and, hence, remove them from the list of generators. Then, since
![]() $(J_r)_q = (I_r)_p$
for all
$(J_r)_q = (I_r)_p$
for all
![]() $1 \leq p \leq \alpha $
,
$1 \leq p \leq \alpha $
,
![]() $1 \leq q \leq \beta $
, we can remove all but one of these from the list of generators as well, leaving
$1 \leq q \leq \beta $
, we can remove all but one of these from the list of generators as well, leaving
 $$ \begin{align} \operatorname{\mathrm{coker}} &= \langle (A_r)_{pq}, (J_r)_1 \mid (\alpha - 2)(J_r)_1 = (\beta - 2)(J_r)_1 = 0, \nonumber\\ &\qquad \text{for }2 \leq p \leq \alpha, 2 \leq q \leq \beta, \text{ and }1 \leq r \leq t \rangle. \end{align} $$
$$ \begin{align} \operatorname{\mathrm{coker}} &= \langle (A_r)_{pq}, (J_r)_1 \mid (\alpha - 2)(J_r)_1 = (\beta - 2)(J_r)_1 = 0, \nonumber\\ &\qquad \text{for }2 \leq p \leq \alpha, 2 \leq q \leq \beta, \text{ and }1 \leq r \leq t \rangle. \end{align} $$
We substitute
![]() $a = \alpha -2$
,
$a = \alpha -2$
,
![]() $b = \beta - 2$
, and write
$b = \beta - 2$
, and write
![]() $g := \gcd (a,b)$
. Then (7-3) is a presentation of
$g := \gcd (a,b)$
. Then (7-3) is a presentation of
![]() $\mathbb {Z}^{t(a+1)(b+1)} \oplus (\mathbb {Z}/g)^t$
if
$\mathbb {Z}^{t(a+1)(b+1)} \oplus (\mathbb {Z}/g)^t$
if
![]() $g> 1$
, and
$g> 1$
, and
![]() $\mathbb {Z}^{t(a+1)(b+1)}$
otherwise. If
$\mathbb {Z}^{t(a+1)(b+1)}$
otherwise. If
![]() $\alpha = \beta = 2$
, then (7-3) gives a presentation of
$\alpha = \beta = 2$
, then (7-3) gives a presentation of
![]() $\mathbb {Z}^2$
. Together with Theorem 3.8, this gives the desired result.
$\mathbb {Z}^2$
. Together with Theorem 3.8, this gives the desired result.
Proposition 7.12. Let
![]() $\alpha , \beta \geq 3$
, and let
$\alpha , \beta \geq 3$
, and let
![]() $\kappa = \kappa (\alpha , \beta )$
be the complete bipartite graph on
$\kappa = \kappa (\alpha , \beta )$
be the complete bipartite graph on
![]() $\alpha $
white and
$\alpha $
white and
![]() $\beta $
black vertices. Then, for all
$\beta $
black vertices. Then, for all
![]() $t \geq 1$
, the order of the class of the identity
$t \geq 1$
, the order of the class of the identity
![]() $[\mathbf {1}]$
in
$[\mathbf {1}]$
in
![]() $K_0(C^{\star }(\Lambda _t^*(\kappa )))$
is equal to
$K_0(C^{\star }(\Lambda _t^*(\kappa )))$
is equal to
![]() $g := \gcd (\alpha -2,\beta -2)$
.
$g := \gcd (\alpha -2,\beta -2)$
.
Furthermore, the isomorphism class of
![]() $C^{\star }(\Lambda _t^*(\kappa ))$
is completely determined by the K-groups from Theorem 7.11 and the order of
$C^{\star }(\Lambda _t^*(\kappa ))$
is completely determined by the K-groups from Theorem 7.11 and the order of
![]() $[\mathbf {1}]$
in
$[\mathbf {1}]$
in
![]() $K_0$
.
$K_0$
.
Acknowledgements
The author wishes to acknowledge their advisor Alina Vdovina for introducing them to the subject and for her guidance throughout, and the referee for detailed and enlightening feedback. The author expresses their gratitude to Newcastle University for providing an excellent research environment.