Hostname: page-component-cb9f654ff-r5d9c Total loading time: 0 Render date: 2025-08-29T17:48:54.915Z Has data issue: false hasContentIssue false
  • English
  • Français

LOCAL COORDINATES FOR COMPLEX AND QUATERNIONIC HYPERBOLIC PAIRS

Part of: Real and complex geometry Smooth dynamical systems: general theory Special matrices Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  04 March 2021

KRISHNENDU GONGOPADHYAY Open the ORCID record for KRISHNENDU GONGOPADHYAY [Opens in a new window]  and
SAGAR B. KALANE
KRISHNENDU GONGOPADHYAY*
Affiliation:
Indian Institute of Science Education and Research (IISER) Mohali, Knowledge City, Sector 81, S.A.S. Nagar 140306, Punjab, India e-mail: krishnendu@iisermohali.ac.in
SAGAR B. KALANE
Affiliation:
Indian Institute of Science Education and Research (IISER) Pune, Dr. Homi Bhabha Road, Pashan, Pune 411008, India e-mail: sagark327@gmail.com
*
e-mail: krishnendug@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 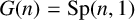$G(n)={\textrm {Sp}}(n,1)$ or 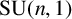${\textrm {SU}}(n,1)$. We classify conjugation orbits of generic pairs of loxodromic elements in 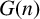$G(n)$. Such pairs, called ‘nonsingular’, were introduced by Gongopadhyay and Parsad for 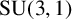${\textrm {SU}}(3,1)$. We extend this notion and classify 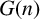$G(n)$-conjugation orbits of such elements in arbitrary dimension. For 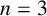$n=3$, they give a subspace that can be parametrized using a set of coordinates whose local dimension equals the dimension of the underlying group. We further construct twist-bend parameters to glue such representations and obtain local parametrization for generic representations of the fundamental group of a closed (genus 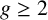$g \geq 2$) oriented surface into 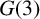$G(3)$.

Keywords

character varietycomplex hyperbolic spaceloxodromic elementsquaternionic hyperbolic spacesurface grouptraces

MSC classification

Primary: 37C15: Topological and differentiable equivalence, conjugacy, invariants, moduli, classification
Secondary: 51M10: Hyperbolic and elliptic geometries (general) and generalizations 15B57: Hermitian, skew-Hermitian, and related matrices 20E45: Conjugacy classes

Information

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 113 , Issue 1 , August 2022 , pp. 57 - 78
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Communicated by Ben Martin

K. Gongopadhyay acknowledges partial support from SERB-DST MATRICS project MTR/2017/000355. S. B. Kalane is supported by an IISER Pune Institute post doctoral fellowship.

References

Apanasov, B. N. and Kim, I., ‘Cartan’s angular invariant and deformations in symmetric spaces of rank 1’, Mat. Sb. 198(2) (2007), 3–28.Google Scholar
Cao, W., ‘Congruence classes of points in quaternionic hyperbolic space’, Geom. Dedicata 180 (2016), 203–228.10.1007/s10711-015-0099-zCrossRefGoogle Scholar
Chen, S. S. and Greenberg, L., ‘Hyperbolic spaces’, in: Contributions to Analysis, Collection of Papers Dedicated to Lipman Bers (Academic Press, New York–London, 1974), 49–87.Google Scholar
Cunha, H. and Gusevskii, N., ‘On the moduli space of quadruples of points in the boundary of complex hyperbolic space’, Transform. Groups 15(2) (2010), 261–283.10.1007/s00031-010-9086-5CrossRefGoogle Scholar
Cunha, H. and Gusevskii, N., ‘The moduli space of points in the boundary of complex hyperbolic space’, J. Geom. Anal. 22(1) (2012), 1–11.10.1007/s12220-010-9188-2CrossRefGoogle Scholar
Goldman, W. M., Complex Hyperbolic Geometry, Oxford Mathematical Monographs (Oxford Science, The Clarendon Press, Oxford University Press, New York, 1999).Google Scholar
Gongopadhyay, K., ‘The $z$ -classes of quaternionic hyperbolic isometries’, J. Group Theory 16(6) (2013), 941–964.10.1515/jgt-2013-0013CrossRefGoogle Scholar
Gongopadhyay, K. and Kalane, S. B., ‘Quaternionic hyperbolic Fenchel–Nielsen coordinates’, Geom. Dedicata 199(1) (2019), 247–271.10.1007/s10711-018-0347-0CrossRefGoogle Scholar
Gongopadhyay, K. and Kalane, S. B., ‘Conjugation orbits of semisimple pairs in rank one’, Forum Math. 31(5) (2019), 1097–1118.10.1515/forum-2018-0221CrossRefGoogle Scholar
Gongopadhyay, K. and Lawton, S., ‘Invariants of pairs in $\mathrm{SL}\ (4,\mathbb{C})$ and $\mathrm{SU}\ (3,1)$ ’, Proc. Amer. Math. Soc. 145(11) (2017), 4703–4715.10.1090/proc/13638CrossRefGoogle Scholar
Gongopadhyay, K. and Parsad, S., ‘Classification of quaternionic hyperbolic isometries’, Conform. Geom. Dyn. 17 (2013), 68–76.10.1090/S1088-4173-2013-00256-7CrossRefGoogle Scholar
Gongopadhyay, K. and Parsad, S., ‘On Fenchel–Nielsen coordinates of surface group representations into $\mathrm{SU}\ (3,1)$ ’, Math. Proc. Cambridge Philos. Soc. 165(1) (2018), 1–23.10.1017/S0305004117000159CrossRefGoogle Scholar
Gongopadhyay, K. and Parsad, S., ‘Conjugation orbits of loxodromic pairs in $\mathrm{SU}\ (n,1)$ ’, Bull. Sci. Math. 148 (2018), 14–32.10.1016/j.bulsci.2018.06.004CrossRefGoogle Scholar
Gou, G. and Jiang, Y., ‘The moduli space of points in the boundary of quaternionic hyperbolic space’, Osaka J. Math. 57(4) (2020), 827–846.Google Scholar
Korányi, A. and Reimann, H. M., ‘The complex cross ratio on the Heisenberg group’, Enseign. Math. (2) 33(3–4) (1987), 291–300.Google Scholar
Marché, J. and Will, P., ‘Configuration of flags and representations of surface groups in complex hyperbolic geometry’, Geom. Dedicata 156 (2012), 49–70.10.1007/s10711-011-9589-9CrossRefGoogle Scholar
Parker, J. R. and Platis, I. D., ‘Complex hyperbolic Fenchel–Nielsen coordinates’, Topology 47(2) (2008), 101–135.10.1016/j.top.2007.08.001CrossRefGoogle Scholar
Platis, I. D., ‘Cross-ratios and the Ptolemaean inequality in boundaries of symmetric spaces of rank 1’, Geom. Dedicata 169 (2014), 187–208.10.1007/s10711-013-9850-5CrossRefGoogle Scholar