Hostname: page-component-54dcc4c588-br6xx Total loading time: 0 Render date: 2025-09-12T03:35:17.369Z Has data issue: false hasContentIssue false
  • English
  • Français

TRIVIAL MAXIMAL 1-ORTHOGONAL SUBCATEGORIES FOR AUSLANDER 1-GORENSTEIN ALGEBRAS

Part of: Representation theory of rings and algebras Homological methods

Published online by Cambridge University Press:  28 February 2013

ZHAOYONG HUANG  and
XIAOJIN ZHANG
ZHAOYONG HUANG*
Affiliation:
Department of Mathematics, Nanjing University, Nanjing 210093, Jiangsu Province, PR China
XIAOJIN ZHANG
Affiliation:
College of Mathematics and Physics, Nanjing University of Information Science and Technology, Nanjing 210044, Jiangsu Province, PR China email xjzhang@nuist.edu.cn
*
✉huangzy@nju.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 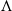$\Lambda $ be an Auslander 1-Gorenstein Artinian algebra with global dimension two. If 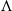$\Lambda $ admits a trivial maximal 1-orthogonal subcategory of 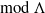$\text{mod } \Lambda $, then, for any indecomposable module 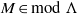$M\in \text{mod } \Lambda $, the projective dimension of 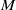$M$ is equal to one if and only if its injective dimension is also equal to one, and 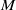$M$ is injective if the projective dimension of 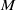$M$ is equal to two. In this case, we further get that 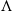$\Lambda $ is a tilted algebra.

Keywords

trivial maximal 1-orthogonal subcategoriesAuslander 1-Gorenstein algebrastilted algebrasindecomposable modulesprojective dimensioninjective dimension

MSC classification

Secondary: 16G10: Representations of Artinian rings 16E10: Homological dimension

Information

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 94 , Issue 1 , February 2013 , pp. 133 - 144
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Auslander, M., Reprensentation Dimension of Artin Algebras, Queen Mary College Math. Notes (Queen Mary College, London, 1971).Google Scholar
Auslander, M., ‘Functors and morphisms determined by objects’, in: Representation Theory of Algebras, Proc. Conf. Temple Univ. (Philadelphia, PA, 1976), Lecture Notes in Pure and Applied Mathematics, 37 (ed. Gordon, R.) (Dekker, New York, 1978), 1–244.Google Scholar
Auslander, M. and Reiten, I., ‘Representation theory of Artin algebras III: Almost split sequences’, Comm. Algebra 3 (1975), 239–294.CrossRefGoogle Scholar
Auslander, M. and Reiten, I., ‘Applications of contravariantly finite subcategories’, Adv. Math. 86 (1991), 111–152.CrossRefGoogle Scholar
Auslander, M. and Reiten, I., ‘$k$-Gorenstein algebras and syzygy modules’, J. Pure Appl. Algebra 92 (1994), 1–27.CrossRefGoogle Scholar
Auslander, M. and Reiten, I., ‘Syzygy modules for noetherian rings’, J. Algebra 183 (1996), 167–185.CrossRefGoogle Scholar
Bongartz, K. and Gabriel, P., ‘Covering spaces in representation-theory’, Invent. Math. 65 (1981/82), 331–378.CrossRefGoogle Scholar
Brenner, S., ‘A combinatorial characterization of finite Auslander-Reiten quivers’, in: Representation Theory I: Finite Dimensional Algebras (Ottawa, Ont., 1984), Lecture Notes in Mathematics, 1177 (Springer, Berlin, 1986), 13–49.CrossRefGoogle Scholar
Erdmann, K. and Holm, T., ‘Maximal $n$-orthogonal modules for selfinjective algebras’, Proc. Amer. Math. Soc. 136 (2008), 3069–3078.CrossRefGoogle Scholar
Fossum, R. M., Griffith, P. A. and Reiten, I., Trivial Extensions of Abelian Categories, Lecture Notes in Mathematics, 456 (Springer, Berlin, 1975).CrossRefGoogle Scholar
Gabriel, P., ‘The universal cover of a representation-finite algebra’, in: Representations of Algebras (Puebla, 1980), Lecture Notes in Mathematics, 903 (Springer, Berlin, 1981), 68–105.CrossRefGoogle Scholar
Geiss, C., Leclerc, B. and Schröer, J., ‘Rigid modules over preprojective algebras’, Invent. Math. 165 (2006), 589–632.CrossRefGoogle Scholar
Happel, D., Reiten, I. and Smal, S. O., Tilting in Abelian categories and Quasitilted Algebras, Memoirs of the American Mathematical Society, 575 (American Mathematical Society, Providence, RI, 1996).CrossRefGoogle Scholar
Huang, Z. Y. and Zhang, X. J., ‘The existence of maxmal $n$-orthogonal subcateries’, J. Algebra 321 (2009), 2829–2842.CrossRefGoogle Scholar
Huang, Z. Y. and Zhang, X. J., ‘Higher Auslander algebras admitting trivial maximal orthogonal subcategories’, J. Algebra 330 (2011), 375–387.CrossRefGoogle Scholar
Igusa, K. and Todorov, G., ‘A characterization of finite Auslander–Reiten quivers’, J. Algebra 89 (1984), 148–177.CrossRefGoogle Scholar
Iwanaga, Y. and Sato, H., ‘On Auslander’s $n$-Gorenstein rings’, J. Pure Appl. Algebra 106 (1996), 61–76.CrossRefGoogle Scholar
Iyama, O., ‘Higher-dimensional Auslander–Reiten theory on maximal orthogonal subcategories’, Adv. Math. 210 (2007), 22–50.CrossRefGoogle Scholar
Iyama, O., ‘Auslander correspondence’, Adv. Math. 210 (2007), 51–82.CrossRefGoogle Scholar
Iyama, O., ‘Cluster tilting for higher Auslander algebras’, Adv. Math. 226 (2011), 1–61.CrossRefGoogle Scholar
Keller, B. and Reiten, I., ‘Cluster-tilted algebras are Gorenstein and stably Calabi–Yau’, Adv. Math. 211 (2007), 123–151.CrossRefGoogle Scholar
Miyashita, Y., ‘Tilting modules of finite projective dimension’, Math. Z. 193 (1986), 113–146.CrossRefGoogle Scholar
Riedtmann, Chr., ‘Algebren, Darstellungsköcher, Überlagerungen, und zurück’, Comment. Math. Helv. 55 (1980), 199–224.CrossRefGoogle Scholar