Hostname: page-component-848d4c4894-ndmmz Total loading time: 0 Render date: 2024-06-02T04:00:33.548Z Has data issue: false hasContentIssue false
  • English
  • Français

UNIQUENESS OF SOLUTIONS TO SCHRÖDINGER EQUATIONS ON $H$-TYPE GROUPS

Part of: Abstract harmonic analysis Lie groups

Published online by Cambridge University Press:  07 August 2013

SALEM BEN SAÏD ,
SUNDARAM THANGAVELU  and
VENKU NAIDU DOGGA
SALEM BEN SAÏD*
Affiliation:
Institut Elie Cartan, Université de Lorraine, B.P. 239, 54506 Vandoeuvre-Les-Nancy, France
SUNDARAM THANGAVELU
Affiliation:
Department of Mathematics, Indian Institute of Science, Bangalore 560 012, India email veluma@math.iisc.ernet.invenku11@math.iisc.ernet.in
VENKU NAIDU DOGGA
Affiliation:
Department of Mathematics, Indian Institute of Science, Bangalore 560 012, India email veluma@math.iisc.ernet.invenku11@math.iisc.ernet.in
*
✉Salem.BenSaid@univ-lorraine.fr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper deals with the Schrödinger equation 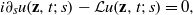$i{\partial }_{s} u(\mathbf{z} , t; s)- \mathcal{L} u(\mathbf{z} , t; s)= 0, $ where 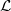$ \mathcal{L} $ is the sub-Laplacian on the Heisenberg group. Assume that the initial data 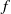$f$ satisfies 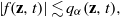$\vert f(\mathbf{z} , t)\vert \lesssim {q}_{\alpha } (\mathbf{z} , t), $ where 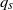${q}_{s} $ is the heat kernel associated to 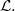$ \mathcal{L} . $ If in addition 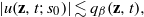$\vert u(\mathbf{z} , t; {s}_{0} )\vert \lesssim {q}_{\beta } (\mathbf{z} , t), $ for some 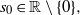${s}_{0} \in \mathbb{R} \setminus \{ 0\} , $ then we prove that 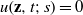$u(\mathbf{z} , t; s)= 0$ for all 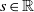$s\in \mathbb{R} $ whenever 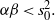$\alpha \beta \lt { s}_{0}^{2} . $ This result holds true in the more general context of 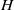$H$-type groups. We also prove an analogous result for the Grushin operator on 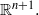${ \mathbb{R} }^{n+ 1} . $

Keywords

H-type groupssub-LaplacianSchrödinger equationheat kernelspherical harmonics

MSC classification

Secondary: 22E30: Analysis on real and complex Lie groups 43A80: Analysis on other specific Lie groups
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 95 , Issue 3 , December 2013 , pp. 297 - 314
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Berndt, J., Tricerri, F. and Vanhecke, L., Generalized Heisenberg Groups and Damek–Ricci Harmonic Spaces, Lecture Notes in Mathematics, 1598 (Springer, Berlin, 1995).CrossRefGoogle Scholar
Chanillo, S., ‘Uniqueness of solutions to Schrödinger equations on complex semi-simple Lie groups’, Proc. Indian Acad. Sci. Math. Sci. 117 (2007), 325–331.CrossRefGoogle Scholar
Cowling, M., Escauriaza, L., Kenig, C. E., Ponce, G. and Vega, L., ‘The Hardy uncertainty principle revisted’, Indiana Univ. Math. J. 59 (6) (2010), 2007–2026.CrossRefGoogle Scholar
Escauriaza, L., Kenig, C. E., Ponce, G. and Vega, L., ‘Hardy’s uncertainty principle, convexity and Schrödinger evolutions’, J. Eur. Math. Soc. (JEMS) 10 (2008), 883–907.Google Scholar
Escauriaza, L., Kenig, C. E., Ponce, G. and Vega, L., ‘Convexity of free solutions of Schrödinger equations with Gaussian decay’, Math. Res. Lett. 15 (2008), 957–971.CrossRefGoogle Scholar
Escauriaza, L., Kenig, C. E., Ponce, G. and Vega, L., ‘The sharp Hardy uncertainty principle for Schrödinger evolutions’, Duke Math. J. 155 (2010), 163–187.CrossRefGoogle Scholar
Escauriaza, L., Kenig, C. E., Ponce, G. and Vega, L., ‘Uncertainty principles of Morgan type and Schrödinger evolutions’, J. Lond. Math. Soc. (2) 83 (2011), 187–207.CrossRefGoogle Scholar
Ionescu, I. D. and Kenig, C. E., ‘Uniqueness properties of solutions of Schrödinger equations’, J. Funct. Anal. 232 (2006), 90–136.CrossRefGoogle Scholar
Kaplan, A., ‘Fundamental solutions for a class of hypoelliptic PDE generated by composition of quadratic forms’, Trans. Amer. Math. Soc. 258 (1980), 147–153.CrossRefGoogle Scholar
Kenig, C. E., Ponce, G. and Vega, L., ‘On the support of solutions of nonlinear Schrödinger equations’, Comm. Pure Appl. Math. 56 (2002), 1247–1262.CrossRefGoogle Scholar
Ludwig, J. and Müller, D., ‘Uniqueness of solutions to Schrödinger equations on 2-step nilpotent Lie groups’, 2012, arXiv:1207.4652.Google Scholar
Pasquale, A. and Sundari, M., ‘Uncertainty principles for the Schrödinger equation on Riemannian symmetric spaces of the noncompact type’, Ann. Inst. Fourier (Grenoble) 62 (2012), 859–886.CrossRefGoogle Scholar
Randall, J., ‘The heat kernel for generalized Heisenberg groups’, J. Geom. Anal. 6 (1996), 287–316.CrossRefGoogle Scholar
Ricci, F., ‘Commutative algebras of invariant functions on groups of Heisenberg type’, J. Lond. Math. Soc. 32 (1985), 265–271.CrossRefGoogle Scholar
Robbiano, L., ‘Unicité forte à l’infini pour KdV’, ESAIM Control Optim. Calc. Var. 8 (2002), 933–939.CrossRefGoogle Scholar
Thangavelu, S., Lectures on Hermite and Laguerre expansions, Mathematical Notes, 42 (Princeton University Press, Princeton, 1993).CrossRefGoogle Scholar
Thangavelu, S., An Introduction to the Uncertainty Principle. Hardy’s Theorem on Lie Groups, Progress in Mathematics, 217 (Birkhäuser, Boston, MA, 2004).CrossRefGoogle Scholar
Tuan, V.-K., ‘Uncertainty principles for the Hankel transform’, Integral Transforms Spec. Funct. 18 (2007), 369–381.CrossRefGoogle Scholar
Zhang, B.-Y., ‘Unique continuation for the Korteweg-de Vries equation’, SIAM J. Math. Anal. 23 (1992), 55–71.CrossRefGoogle Scholar