Article contents
WEIGHTED WEAK TYPE ENDPOINT ESTIMATES FOR THE COMPOSITIONS OF CALDERÓN–ZYGMUND OPERATORS
Published online by Cambridge University Press: 08 April 2019
Abstract
Let 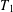 $T_{1}$,
$T_{1}$,  $T_{2}$ be two Calderón–Zygmund operators and
$T_{2}$ be two Calderón–Zygmund operators and 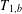 $T_{1,b}$ be the commutator of
$T_{1,b}$ be the commutator of 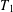 $T_{1}$ with symbol
$T_{1}$ with symbol 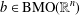 $b\in \text{BMO}(\mathbb{R}^{n})$. In this paper, by establishing new bilinear sparse dominations and a new weighted estimate for bilinear sparse operators, we prove that the composite operator
$b\in \text{BMO}(\mathbb{R}^{n})$. In this paper, by establishing new bilinear sparse dominations and a new weighted estimate for bilinear sparse operators, we prove that the composite operator 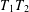 $T_{1}T_{2}$ satisfies the following estimate: for
$T_{1}T_{2}$ satisfies the following estimate: for 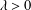 $\unicode[STIX]{x1D706}>0$ and weight
$\unicode[STIX]{x1D706}>0$ and weight  $w\in A_{1}(\mathbb{R}^{n})$,
$w\in A_{1}(\mathbb{R}^{n})$, 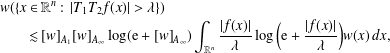 $$\begin{eqnarray}\displaystyle & & \displaystyle w(\{x\in \mathbb{R}^{n}:\,|T_{1}T_{2}f(x)|>\unicode[STIX]{x1D706}\})\nonumber\\ \displaystyle & & \displaystyle \qquad \lesssim [w]_{A_{1}}[w]_{A_{\infty }}\log (\text{e}+[w]_{A_{\infty }})\int _{\mathbb{R}^{n}}\frac{|f(x)|}{\unicode[STIX]{x1D706}}\log \bigg(\text{e}+\frac{|f(x)|}{\unicode[STIX]{x1D706}}\bigg)w(x)\,dx,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle w(\{x\in \mathbb{R}^{n}:\,|T_{1}T_{2}f(x)|>\unicode[STIX]{x1D706}\})\nonumber\\ \displaystyle & & \displaystyle \qquad \lesssim [w]_{A_{1}}[w]_{A_{\infty }}\log (\text{e}+[w]_{A_{\infty }})\int _{\mathbb{R}^{n}}\frac{|f(x)|}{\unicode[STIX]{x1D706}}\log \bigg(\text{e}+\frac{|f(x)|}{\unicode[STIX]{x1D706}}\bigg)w(x)\,dx,\nonumber\end{eqnarray}$$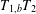 $T_{1,b}T_{2}$ satisfies
$T_{1,b}T_{2}$ satisfies 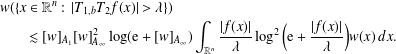 $$\begin{eqnarray}\displaystyle & & \displaystyle w(\{x\in \mathbb{R}^{n}:\,|T_{1,b}T_{2}f(x)|>\unicode[STIX]{x1D706}\})\nonumber\\ \displaystyle & & \displaystyle \qquad \lesssim [w]_{A_{1}}[w]_{A_{\infty }}^{2}\log (\text{e}+[w]_{A_{\infty }})\int _{\mathbb{R}^{n}}\frac{|f(x)|}{\unicode[STIX]{x1D706}}\log ^{2}\bigg(\text{e}+\frac{|f(x)|}{\unicode[STIX]{x1D706}}\bigg)w(x)\,dx.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle w(\{x\in \mathbb{R}^{n}:\,|T_{1,b}T_{2}f(x)|>\unicode[STIX]{x1D706}\})\nonumber\\ \displaystyle & & \displaystyle \qquad \lesssim [w]_{A_{1}}[w]_{A_{\infty }}^{2}\log (\text{e}+[w]_{A_{\infty }})\int _{\mathbb{R}^{n}}\frac{|f(x)|}{\unicode[STIX]{x1D706}}\log ^{2}\bigg(\text{e}+\frac{|f(x)|}{\unicode[STIX]{x1D706}}\bigg)w(x)\,dx.\nonumber\end{eqnarray}$$
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 109 , Issue 3 , December 2020 , pp. 320 - 339
- Copyright
- © 2019 Australian Mathematical Publishing Association Inc.
Footnotes
Communicated by C. Meaney
The research was supported by the NNSF of China under grant no. 11871108.
References
- 8
- Cited by


