No CrossRef data available.
Article contents
PETERZIL–STEINHORN SUBGROUPS AND 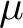 $\mu $-STABILIZERS IN ACF
$\mu $-STABILIZERS IN ACF
Published online by Cambridge University Press: 21 July 2021
Abstract
We consider G, a linear algebraic group defined over 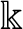 $\Bbbk $, an algebraically closed field (ACF). By considering
$\Bbbk $, an algebraically closed field (ACF). By considering 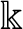 $\Bbbk $ as an embedded residue field of an algebraically closed valued field K, we can associate to it a compact G-space
$\Bbbk $ as an embedded residue field of an algebraically closed valued field K, we can associate to it a compact G-space 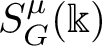 $S^\mu _G(\Bbbk )$ consisting of
$S^\mu _G(\Bbbk )$ consisting of 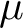 $\mu $-types on G. We show that for each
$\mu $-types on G. We show that for each  $p_\mu \in S^\mu _G(\Bbbk )$,
$p_\mu \in S^\mu _G(\Bbbk )$, 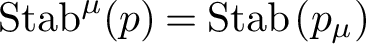 $\mathrm {Stab}^\mu (p)=\mathrm {Stab}\left (p_\mu \right )$ is a solvable infinite algebraic group when
$\mathrm {Stab}^\mu (p)=\mathrm {Stab}\left (p_\mu \right )$ is a solvable infinite algebraic group when 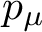 $p_\mu $ is centered at infinity and residually algebraic. Moreover, we give a description of the dimension of
$p_\mu $ is centered at infinity and residually algebraic. Moreover, we give a description of the dimension of 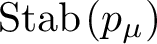 $\mathrm {Stab}\left (p_\mu \right )$ in terms of the dimension of p.
$\mathrm {Stab}\left (p_\mu \right )$ in terms of the dimension of p.
MSC classification
Primary:
14M17: Homogeneous spaces and generalizations
14L30: Group actions on varieties or schemes (quotients)
Secondary:
03C65: Models of other mathematical theories
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 22 , Issue 3 , May 2023 , pp. 1003 - 1022
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
Bump, D., Automorphic Forms and Representations, 55 (Cambridge University Press, Cambridge, 1997), xiv–574 https://doi.org/10.1017/CBO9780511609572.CrossRefGoogle Scholar
Halevi, Y., On stably pointed varieties and generically stable groups in ACVF. Ann. Pure Appl. Logic 170(2) (2019), 180–217.CrossRefGoogle Scholar
Hrushovski, E. and Kazhdan, D., Motivic Poisson summation, Mosc. Math. J. 9(3) (2009), 569–623, back matter.CrossRefGoogle Scholar
Hrushovski, E. and Loeser, F., Non-Archimedean Tame Topology and Stably Dominated Types (AM-192) (Princeton University Press, Princeton, NJ, 2016).Google Scholar
Hrushovski, E. and Rideau-Kikuchi, S., Valued fields, metastable groups, Selecta Math. (N.S.) 25(3) (2019), Art. 47, 58.Google Scholar
Kaplansky, I., Maximal fields with valuations, Duke Math. J. 9(2) (1942), 303–321.CrossRefGoogle Scholar
Peterzil, Y. and Starchenko, S., Topological groups,
 $\mu$
-types and their stabilizers, J. Eur. Math. Soc. (JEMS) 19(10) (2017), 2965–2995.CrossRefGoogle Scholar
$\mu$
-types and their stabilizers, J. Eur. Math. Soc. (JEMS) 19(10) (2017), 2965–2995.CrossRefGoogle Scholar
Peterzil, Y. and Starchenko, S., Algebraic and o-minimal flows on complex and real tori, Adv. Math. 333 (2018), 539–569.CrossRefGoogle Scholar
Peterzil, Y. and Steinhorn, C., Definable compactness and definable subgroups of o-minimal groups, J. Lond. Math. Soc. (2) 59(3) (1999), 769–786.CrossRefGoogle Scholar


