Article contents
ADJOINT FUNCTORS BETWEEN CATEGORIES OF HILBERT 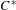 $C^{\ast }$ -MODULES
$C^{\ast }$ -MODULES
Published online by Cambridge University Press: 30 June 2016
Abstract
Let 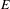 $E$ be a (right) Hilbert module over a
$E$ be a (right) Hilbert module over a 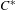 $C^{\ast }$ -algebra
$C^{\ast }$ -algebra  $A$ . If
$A$ . If 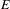 $E$ is equipped with a left action of a second
$E$ is equipped with a left action of a second 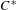 $C^{\ast }$ -algebra
$C^{\ast }$ -algebra 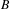 $B$ , then tensor product with
$B$ , then tensor product with 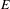 $E$ gives rise to a functor from the category of Hilbert
$E$ gives rise to a functor from the category of Hilbert 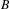 $B$ -modules to the category of Hilbert
$B$ -modules to the category of Hilbert  $A$ -modules. The purpose of this paper is to study adjunctions between functors of this sort. We shall introduce a new kind of adjunction relation, called a local adjunction, that is weaker than the standard concept from category theory. We shall give several examples, the most important of which is the functor of parabolic induction in the tempered representation theory of real reductive groups. Each local adjunction gives rise to an ordinary adjunction of functors between categories of Hilbert space representations. In this way we shall show that the parabolic induction functor has a simultaneous left and right adjoint, namely the parabolic restriction functor constructed in Clare et al. [Parabolic induction and restriction via
$A$ -modules. The purpose of this paper is to study adjunctions between functors of this sort. We shall introduce a new kind of adjunction relation, called a local adjunction, that is weaker than the standard concept from category theory. We shall give several examples, the most important of which is the functor of parabolic induction in the tempered representation theory of real reductive groups. Each local adjunction gives rise to an ordinary adjunction of functors between categories of Hilbert space representations. In this way we shall show that the parabolic induction functor has a simultaneous left and right adjoint, namely the parabolic restriction functor constructed in Clare et al. [Parabolic induction and restriction via 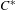 $C^{\ast }$ -algebras and Hilbert
$C^{\ast }$ -algebras and Hilbert 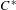 $C^{\ast }$ -modules, Compos. Math.FirstView (2016), 1–33, 2].
$C^{\ast }$ -modules, Compos. Math.FirstView (2016), 1–33, 2].
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 17 , Issue 2 , April 2018 , pp. 453 - 488
- Copyright
- © Cambridge University Press 2016
References
- 5
- Cited by

