Hostname: page-component-848d4c4894-wg55d Total loading time: 0 Render date: 2024-05-13T19:53:52.176Z Has data issue: false hasContentIssue false
  • English
  • Français

CATEGORICITY OF MODULAR AND SHIMURA CURVES

Part of: Arithmetic algebraic geometry Model theory

Published online by Cambridge University Press:  30 September 2015

Christopher Daw  and
Adam Harris
Christopher Daw
Affiliation:
Institut des Hautes Etudes Scientifiques, Le Bois-Marie 35, route de Chartres, 91440 Bures-sur-Yvette, France (c.daw@ihes.fr)
Adam Harris
Affiliation:
University of East Anglia, Norwich Research Park, Norwich, Norfolk, NR4 7TJ, UK (adam.harris@uea.ac.uk)
Get access Rights & Permissions [Opens in a new window]

Abstract

We describe a model-theoretic setting for the study of Shimura varieties, and study the interaction between model theory and arithmetic geometry in this setting. In particular, we show that the model-theoretic statement of a certain 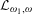${\mathcal{L}}_{\unicode[STIX]{x1D714}_{1},\unicode[STIX]{x1D714}}$-sentence having a unique model of cardinality 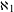$\aleph _{1}$ is equivalent to a condition regarding certain Galois representations associated with Hodge-generic points. We then show that for modular and Shimura curves this 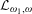${\mathcal{L}}_{\unicode[STIX]{x1D714}_{1},\unicode[STIX]{x1D714}}$-sentence has a unique model in every infinite cardinality. In the process, we prove a new characterisation of the special points on any Shimura variety.

Keywords

categoricitymodular curvesShimura varietiesopen image theorems

MSC classification

Primary: 03C35: Categoricity and completeness of theories 11G18: Arithmetic aspects of modular and Shimura varieties 03C10: Quantifier elimination, model completeness and related topics 11G05: Elliptic curves over global fields
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 16 , Issue 5 , November 2017 , pp. 1075 - 1101
Copyright
© Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baily, W. L. and Borel, A., Compactification of arithmetic quotients of bounded symmetric domains, Ann. of Math. (2) 84 (1966), 442–528.CrossRefGoogle Scholar
Bays, M., Hart, B., Hyttinen, T., Kesälä, M. and Kirby, J., Quasiminimal structures and excellence, Bull. LMS 46(1) (2014), 155–163.Google Scholar
Bays, M. and Zilber, B., Covers of multiplicative groups of algebraically closed fields of arbitrary characteristic, Bull. Lond. Math. Soc. 43(4) (2011), 689–702.CrossRefGoogle Scholar
Cadoret, A., An open adelic image theorem for abelian schemes, Int. Math. Res. Not. IMRN, 2014, to appear.CrossRefGoogle Scholar
Daw, C. and Orr, M., Heights of pre-special points of Shimura varieties, 2015, available on the first author’s web page.CrossRefGoogle Scholar
Keisler, H. J., On the quantifier ‘there exist uncountably many x’, Ann. Math. Log. 1 (1970), 1–91.CrossRefGoogle Scholar
Kirby, J., On quasiminimal excellent classes, J. Symbolic Logic 75(2) (2010), 551–564.CrossRefGoogle Scholar
Klingler, B. and Yafaev, A., The André–Oort conjecture, Ann. of Math. (3) 180 (2006), 867–925.Google Scholar
Lang, S., Elliptic functions: GTM 112, 2nd edn (Springer, New York, 1987).Google Scholar
Marker, D., Model Theory: An Introduction (Springer, New York, 2002).Google Scholar
Milne, J. S., Introduction to Shimura varieties, in Harmonic Analysis, the Trace Formula and Shimura Varieties, (ed. Arthur, J. and Kottwitz, R.), Lectures at the Summer School held at the Fields Institute, June 2–June 27, 2003, (The AMS and the Clay Mathematics Institute, Cambridge, MA, 2005).Google Scholar
Milne, J. S., Modular functions and modular forms, 2012, available at www.jmilne.org/math/CourseNotes/mf.Google Scholar
Gavrilovich, M., A remark on transitivity of Galois action on the set of uniquely divisible abelian extensions in …, K-Theory 38(2) (2008), 135–152.CrossRefGoogle Scholar
Ohta, M., On l-adic representations of Galois groups obtained from certain two dimensional abelian varieties, J. Fac. Sci. Univ. Tokyo 21 (1974), 299–308.Google Scholar
Pillay, A., Model theory, 2002, Lecture notes available on author’s web page.Google Scholar
Pink, R., A combination of the conjectures of Mordell–Lang and André–Oort, in Geometric Methods in Algebra and Number Theory,(ed. Bogomolov, F. and Tschinkel, Y.), Progress in Mathematics, Volume 253, pp. 251–282 (Birkhäuser, 2005).Google Scholar
Ribet, K. A., On l-adic representations attached to modular forms, Invent. Math. 28 (1975), 245–275.CrossRefGoogle Scholar
Serre, J.-P., Propriétés galoisiennes des points d’ordre fini des courbes elliptiques, Invent. Math. 15 (1972), 259–331.Google Scholar
Ullmo, E. and Yafaev, A., Mumford–Tate and generalized Shafarevich conjectures, Ann. Sci. Québec 37(2) (2013), 255–284.Google Scholar
Zilber, B., Covers of the multiplicative group of an algebraically closed field of characteristic zero, J. Lond. Math. Soc. (2) 74(1) (2006), 41–58.CrossRefGoogle Scholar
Zilber, B., Model theory, geometry and arithmetic of the universal cover of a semi-abelian variety, in Model Theory and Applications, Quad. Mat., Volume 11, pp. 427–458. (Aracne, Rome, 2002).Google Scholar