Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
COLLAS, BENJAMIN
2012.
ACTION OF A GROTHENDIECK–TEICHMÜLLER GROUP ON TORSION ELEMENTS OF FULL TEICHMÜLLER MODULAR GROUPS OF GENUS ONE.
International Journal of Number Theory,
Vol. 08,
Issue. 03,
p.
763.
Collas, Benjamin
2012.
Action of the Grothendieck-Teichmüller group on torsion elements of full Teichmüller modular groups in genus zero.
Journal de théorie des nombres de Bordeaux,
Vol. 24,
Issue. 3,
p.
605.
Furusho, Hidekazu
2023.
The ℓ-adic hypergeometric function and
associators.
Tunisian Journal of Mathematics,
Vol. 5,
Issue. 1,
p.
1.
Vidussi, Stefano
2025.
Higher incoherence of the automorphism groups of a free group.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
p.
1.

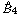 . A consequence is to represent a matrix specialization of the ‘equianharmonic’ parameter in terms of special values of the adelic beta function introduced and studied by Anderson and Ihara.
. A consequence is to represent a matrix specialization of the ‘equianharmonic’ parameter in terms of special values of the adelic beta function introduced and studied by Anderson and Ihara.