Article contents
ILL-POSEDNESS FOR THE COMPRESSIBLE NAVIER–STOKES EQUATIONS WITH THE VELOCITY IN 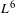 $L^{6}$ FRAMEWORK
$L^{6}$ FRAMEWORK
Published online by Cambridge University Press: 29 June 2017
Abstract
Ill-posedness for the compressible Navier–Stokes equations has been proved by Chen et al. [On the ill-posedness of the compressible Navier–Stokes equations in the critical Besov spaces, Revista Mat. Iberoam.31 (2015), 1375–1402] in critical Besov space 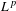 $L^{p}$
$L^{p}$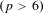 $(p>6)$ framework. In this paper, we prove ill-posedness with the initial data satisfying
$(p>6)$ framework. In this paper, we prove ill-posedness with the initial data satisfying 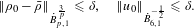 $$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D70C}_{0}-\bar{\unicode[STIX]{x1D70C}}\Vert _{{\dot{B}}_{p,1}^{\frac{3}{p}}}\leqslant \unicode[STIX]{x1D6FF},\quad \Vert u_{0}\Vert _{{\dot{B}}_{6,1}^{-\frac{1}{2}}}\leqslant \unicode[STIX]{x1D6FF}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D70C}_{0}-\bar{\unicode[STIX]{x1D70C}}\Vert _{{\dot{B}}_{p,1}^{\frac{3}{p}}}\leqslant \unicode[STIX]{x1D6FF},\quad \Vert u_{0}\Vert _{{\dot{B}}_{6,1}^{-\frac{1}{2}}}\leqslant \unicode[STIX]{x1D6FF}. & & \displaystyle \nonumber\end{eqnarray}$$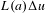 $L(a)\unicode[STIX]{x1D6E5}u$ instead of
$L(a)\unicode[STIX]{x1D6E5}u$ instead of 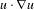 $u\cdot \unicode[STIX]{x1D6FB}u$ and construct a new decomposition of the density.
$u\cdot \unicode[STIX]{x1D6FB}u$ and construct a new decomposition of the density.
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 18 , Issue 4 , July 2019 , pp. 829 - 854
- Copyright
- © Cambridge University Press 2017
Footnotes
The original version of this article was submitted without an identified corresponding author. A notice detailing this has been published and the error rectified in the online PDF and HTML copies.
Author for correspondence.
References
An addendum has been issued for this article:
- 5
- Cited by
Linked content
Please note an has been issued for this article.

