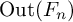1 Introduction
Throughout, X denotes either a separable geodesic Gromov hyperbolic space or the Teichmüller space of a closed orientable surface of genus at least two, which is equipped with the Teichmüller metric. G denotes a countable subgroup of
![]() $\operatorname {Isom}(X)$
containing a pair of independent hyperbolic isometries.Footnote 1 When X is a Gromov hyperbolic space, following Maher and Tiozzo [Reference Maher and TiozzoMT18], we call G a weakly hyperbolic group.
$\operatorname {Isom}(X)$
containing a pair of independent hyperbolic isometries.Footnote 1 When X is a Gromov hyperbolic space, following Maher and Tiozzo [Reference Maher and TiozzoMT18], we call G a weakly hyperbolic group.
![]() $\mu $
denotes a non-elementary probability measure on G, i.e., a measure on G such that the semigroup generated by the support of
$\mu $
denotes a non-elementary probability measure on G, i.e., a measure on G such that the semigroup generated by the support of
![]() $\mu $
contains independent hyperbolic isometries.
$\mu $
contains independent hyperbolic isometries.
![]() $\operatorname {\mathbb {P}}$
stands for the probability measure for random walks induced by
$\operatorname {\mathbb {P}}$
stands for the probability measure for random walks induced by
![]() $\mu $
. See section 2.3 for details.
$\mu $
. See section 2.3 for details.
Random walks on the isometry group of Gromov hyperbolic spaces or Teichmüller spaces have been studied in depth for several decades. For example, Kaimanovich investigated random walks on hyperbolic groups and semi-simple Lie groups in [Reference KaimanovichKai00], identifying the Poisson boundary with other natural boundaries such as the Gromov boundary or the Furstenberg boundary, under some moment and entropy conditions on the measure. See also [Reference LedrappierLed01] for the behavior of random walks on free groups with general conditions. A generalization to relatively hyperbolic groups was considered by Gautero and Mathéus in [Reference Gautero and MathéusGM12]. This was further generalized to weakly hyperbolic groups by Maher and Tiozzo in [Reference Maher and TiozzoMT18].
In the course of characterizing the Poisson boundary, Maher and Tiozzo observed the following phenomenon.
Theorem 1.1 [Reference Maher and TiozzoMT18, Theorem 1.2, 1.4]
Let
![]() $\omega $
be the random walk generated by
$\omega $
be the random walk generated by
![]() $\mu $
. Then there exists a constant
$\mu $
. Then there exists a constant
![]() $L>0$
such that
$L>0$
such that
for
![]() $\operatorname {\mathbb {P}}$
-almost every (a.e. in short) sample path
$\operatorname {\mathbb {P}}$
-almost every (a.e. in short) sample path
![]() $(\operatorname {\omega }_{n})$
. Moreover, the translation length
$(\operatorname {\omega }_{n})$
. Moreover, the translation length
![]() $\tau (\operatorname {\omega }_{n})$
of
$\tau (\operatorname {\omega }_{n})$
of
![]() $\operatorname {\omega }_{n}$
grows at least linearly; that is,
$\operatorname {\omega }_{n}$
grows at least linearly; that is,
for some constant
![]() $L'>0$
.
$L'>0$
.
Maher and Tiozzo proved these results for weakly hyperbolic groups, which implies the results for Teichmüller space thanks to the coarsely Lipschitz systole map from Teichmüller space to the curve complex. One can also refer to the earlier work of Ledrappier [Reference LedrappierLed01] that proves similar results with considerations on harmonic measures in the case of free groups.
If
![]() $\mu $
further has finite first moment, Kingman’s subadditive ergodic theorem provides a constant
$\mu $
further has finite first moment, Kingman’s subadditive ergodic theorem provides a constant
![]() $\lambda $
such that
$\lambda $
such that
![]() $\lim _{n \rightarrow \infty } d_{X}(x_{0}, \operatorname {\omega }_{n}x_{0})/n = \lambda $
for
$\lim _{n \rightarrow \infty } d_{X}(x_{0}, \operatorname {\omega }_{n}x_{0})/n = \lambda $
for
![]() $\operatorname {\mathbb {P}}$
-a.e.
$\operatorname {\mathbb {P}}$
-a.e.
![]() $(\operatorname {\omega }_{n})$
. Here,
$(\operatorname {\omega }_{n})$
. Here,
![]() $\lambda $
is called the escape rate or the drift of the random walk. One consequence of Theorem 1.1 is that the drift of a non-elementary random walk on weakly hyperbolic groups is strictly positive.
$\lambda $
is called the escape rate or the drift of the random walk. One consequence of Theorem 1.1 is that the drift of a non-elementary random walk on weakly hyperbolic groups is strictly positive.
As presented in Theorem 1.1, due to the lack of subadditivity, translation length is more difficult to investigate than displacement. Hence, although the growth of displacements is given almost surely, the growth of translation lengths is given in probability. Maher and Tiozzo also proved in [Reference Maher and TiozzoMT18] almost sure linear growth; that is,
when the support of
![]() $\mu $
is bounded. This relies on the exponential decay of shadows explained in [Reference MaherMah12].
$\mu $
is bounded. This relies on the exponential decay of shadows explained in [Reference MaherMah12].
Amongst weakly hyperbolic groups are mapping class groups and
![]() $\operatorname {Out}(F_{n})$
that act on the corresponding curve complexes or the complexes of free factors, respectively. We remark that before the work [Reference Maher and TiozzoMT18] of Maher and Tiozzo, Maher proved in [Reference MaherMah11] that random element of the mapping class group becomes pseudo-Anosov in probability.
$\operatorname {Out}(F_{n})$
that act on the corresponding curve complexes or the complexes of free factors, respectively. We remark that before the work [Reference Maher and TiozzoMT18] of Maher and Tiozzo, Maher proved in [Reference MaherMah11] that random element of the mapping class group becomes pseudo-Anosov in probability.
Previously known results about the growth of translation lengths rely on moment conditions that require
![]() $\mu $
to have bounded support, finite exponential moment or finite second moment. One of our purposes is to study the growth of translation lengths without any moment condition. With the finite first moment condition (so that the drift is available), one can describe this growth with greater precision. Our first main theorem is as follows.
$\mu $
to have bounded support, finite exponential moment or finite second moment. One of our purposes is to study the growth of translation lengths without any moment condition. With the finite first moment condition (so that the drift is available), one can describe this growth with greater precision. Our first main theorem is as follows.
Theorem A. Let G be a weakly hyperbolic group acting on a Gromov hyperbolic space X and let
![]() $\mu $
be a non-elementary probability measure on G. Then
$\mu $
be a non-elementary probability measure on G. Then
![]() $\operatorname {\mathbb {P}}$
-almost every sample path shows at least linear growth of translation lengths. More precisely, there exists a constant
$\operatorname {\mathbb {P}}$
-almost every sample path shows at least linear growth of translation lengths. More precisely, there exists a constant
![]() $\mathcal {L}>0$
such that for
$\mathcal {L}>0$
such that for
![]() $\operatorname {\mathbb {P}}$
-a.e.
$\operatorname {\mathbb {P}}$
-a.e.
![]() $(\operatorname {\omega }_{n})$
,
$(\operatorname {\omega }_{n})$
,
![]() $\tau (\operatorname {\omega }_{n}) \ge \mathcal {L}n$
for sufficiently large n.
$\tau (\operatorname {\omega }_{n}) \ge \mathcal {L}n$
for sufficiently large n.
Moreover, if
![]() $\mu $
further has finite first moment, then for
$\mu $
further has finite first moment, then for
![]() $\operatorname {\mathbb {P}}$
-a.e.
$\operatorname {\mathbb {P}}$
-a.e.
![]() $(\operatorname {\omega }_{n})$
, we have
$(\operatorname {\omega }_{n})$
, we have
where
![]() $\lambda $
is the drift of the random walk.
$\lambda $
is the drift of the random walk.
As a corollary, almost every sample path of non-elementary random walks on mapping class groups or
![]() $\operatorname {Out}(F_{n})$
becomes pseudo-Anosov or fully irreducible, respectively. Here, mapping class groups are acting on the curve complexes, and
$\operatorname {Out}(F_{n})$
becomes pseudo-Anosov or fully irreducible, respectively. Here, mapping class groups are acting on the curve complexes, and
![]() $\operatorname {Out}(F_{n})$
are acting on the complexes of free factors; see [Reference Masur and MinskyMM99], [Reference Masur and MinskyMM00], [Reference Bestvina and FeighnBF14]. In addition to full irreducibility, another notion that captures the loxodromic property of an outer automorphism is that of atoroidality. Using the action of
$\operatorname {Out}(F_{n})$
are acting on the complexes of free factors; see [Reference Masur and MinskyMM99], [Reference Masur and MinskyMM00], [Reference Bestvina and FeighnBF14]. In addition to full irreducibility, another notion that captures the loxodromic property of an outer automorphism is that of atoroidality. Using the action of
![]() $\operatorname {Out}(F_{n})$
on hyperbolic spaces such as Dowdall-Taylor’s co-surface graph [Reference Dowdall and TaylorDT17] or Brian Mann’s intersection graph [Reference MannMan14], one can even deduce the genericity of fully irreducible atoroidal outer automorphisms in
$\operatorname {Out}(F_{n})$
on hyperbolic spaces such as Dowdall-Taylor’s co-surface graph [Reference Dowdall and TaylorDT17] or Brian Mann’s intersection graph [Reference MannMan14], one can even deduce the genericity of fully irreducible atoroidal outer automorphisms in
![]() $\operatorname {Out}(F_{n})$
.
$\operatorname {Out}(F_{n})$
.
Corollary 1.2 (Eventually pseudo-Anosov behavior)
Let S be a closed orientable surface of genus at least 2 and
![]() $\operatorname {Mod}(S)$
be its mapping class group. Let
$\operatorname {Mod}(S)$
be its mapping class group. Let
![]() $\mu $
be a non-elementary measure on
$\mu $
be a non-elementary measure on
![]() $\operatorname {Mod}(S)$
. Then for
$\operatorname {Mod}(S)$
. Then for
![]() $\operatorname {\mathbb {P}}$
-a.e. sample path
$\operatorname {\mathbb {P}}$
-a.e. sample path
![]() $(\operatorname {\omega }_n)$
of the random walk generated by
$(\operatorname {\omega }_n)$
of the random walk generated by
![]() $\mu $
, there exists
$\mu $
, there exists
![]() $N> 0$
such that
$N> 0$
such that
![]() $\operatorname {\omega }_n$
is pseudo-Anosov for all
$\operatorname {\omega }_n$
is pseudo-Anosov for all
![]() $n> N$
.
$n> N$
.
Corollary 1.3 (Spectral theorem for
 $\operatorname {Mod}(S)$
on the curve complex)
$\operatorname {Mod}(S)$
on the curve complex)
Let S be a closed orientable surface of genus at least 2 and
![]() $\operatorname {Mod}(S)$
be its mapping class group. Let
$\operatorname {Mod}(S)$
be its mapping class group. Let
![]() $\mu $
be a non-elementary measure on
$\mu $
be a non-elementary measure on
![]() $\operatorname {Mod}(S)$
having finite first moment on the curve complex and let
$\operatorname {Mod}(S)$
having finite first moment on the curve complex and let
![]() $\lambda> 0$
be its drift. Then for
$\lambda> 0$
be its drift. Then for
![]() $\operatorname {\mathbb {P}}$
-a.e.
$\operatorname {\mathbb {P}}$
-a.e.
![]() $(\operatorname {\omega }_n)$
, we have
$(\operatorname {\omega }_n)$
, we have
We record a relevant work [Reference Erlandsson, Souto and TaoEST20] regarding the genericity of pseudo-Anosov elements in
![]() $\operatorname {Mod}(S)$
.
$\operatorname {Mod}(S)$
.
Recently, there has been a remarkable progress on the study of the large deviation principle for random walks. In [Reference Bounlanger, Mathieu, Sert and SistoBMSS22], Boulanger, Mathieu, Sert and Sisto showed the large deviation property of the displacement and translation length of non-elementary random walks on weakly hyperbolic groups under finite exponential moment condition. Also investigated are the properties of the deviation function. Their result is related to the large deviation principle of spectral radii of some random matrix products; see [Reference Aoun and SertAS21] for this perspective.
Recently, Gouëzel proved the exponential error bounds for non-elementary random walks on Gromov hyperbolic spaces without moment condition in [Reference GouëzelGou22]. His strategy shares the philosophy of pivoting described in the present article, but his aim differs from ours. A similar technique appears in [Reference Haïssinsky, Mathieu and MüllerHMM18], where the authors aim to deal with surface groups and central limit theorems.
Meanwhile, mapping class groups also act on Teichmüller spaces equipped with the Teichmüller metric, which are not Gromov hyperbolic in general ([Reference Masur and WolfMW95], [Reference LenzhenLen08], [Reference MasurMas75], [Reference McCarthy and PapadopoulosMP89], [Reference IvanovIva02]). Thus, random walks on Teichmüller spaces are of independent interest. Kaimanovich and Masur [Reference Kaimanovich and MasurKM96] proposed a way to investigate random walks on Teichmüller spaces and related them with their Poisson boundary. Meanwhile, Dahmani and Horbez proved in [Reference Dahmani and HorbezDH18] the spectral theorem for mapping class groups with respect to the Teichmüller metric under finite second moment condition. Their strategy is to lift the deviation of random paths on the curve complex to Teichmüller setting. In [Reference Baik, Choi and KimBCK22], the authors applied these techniques to establish the spectral theorems for free subgroups of
![]() $\operatorname {Mod}(S)$
generated by two multitwists under finite second moment condition.
$\operatorname {Mod}(S)$
generated by two multitwists under finite second moment condition.
Our next main theorem generalizes the result of Dahmani and Horbez in [Reference Dahmani and HorbezDH18].
Theorem B. Let S be a closed orientable surface of genus at least 2. Let
![]() $G=\operatorname {Mod}(S)$
be its mapping class group,
$G=\operatorname {Mod}(S)$
be its mapping class group,
![]() $X=\operatorname {\mathcal {T}}(S)$
be its Teichmüller space equipped with the Teichmüller metric, and
$X=\operatorname {\mathcal {T}}(S)$
be its Teichmüller space equipped with the Teichmüller metric, and
![]() $\mu $
be a non-elementary probability measure on
$\mu $
be a non-elementary probability measure on
![]() $\operatorname {Mod}(S)$
. Then
$\operatorname {Mod}(S)$
. Then
![]() $\operatorname {\mathbb {P}}$
-a.e. sample path shows at least linear growth of translation lengths. More precisely, there exists a constant
$\operatorname {\mathbb {P}}$
-a.e. sample path shows at least linear growth of translation lengths. More precisely, there exists a constant
![]() $\mathcal {L}>0$
such that for
$\mathcal {L}>0$
such that for
![]() $\operatorname {\mathbb {P}}$
-a.e.
$\operatorname {\mathbb {P}}$
-a.e.
![]() $(\operatorname {\omega }_{n})$
,
$(\operatorname {\omega }_{n})$
,
![]() $\tau (\operatorname {\omega }_{n}) \ge \mathcal {L}n$
for sufficiently large n.
$\tau (\operatorname {\omega }_{n}) \ge \mathcal {L}n$
for sufficiently large n.
Moreover, if
![]() $\mu $
further has finite first moment with respect to the Teichmüller metric, then for
$\mu $
further has finite first moment with respect to the Teichmüller metric, then for
![]() $\operatorname {\mathbb {P}}$
-a.e.
$\operatorname {\mathbb {P}}$
-a.e.
![]() $(\operatorname {\omega }_{n})$
, we have
$(\operatorname {\omega }_{n})$
, we have
where
![]() $\lambda>0$
is the drift.
$\lambda>0$
is the drift.
We remark that Theorem B implies the spectral theorem for Teichmüller spaces equipped with Thurston’s asymmetric Lipschitz metric. This is due to the result of Choi and Rafi in [Reference Choi and RafiCR07]: among the (marked) surfaces of the same injectivity radius, the distances with respect to the Teichmüller metric and the Thurston metric differ by a uniformly bounded amount.
Our methods are influenced by [Reference Maher and TiozzoMT18], where Maher and Tiozzo defined the notion of persistent joints that records the permanent depart of the random walk from the origin. We also make use of the boundary convergence of the random walk and the non-atomness of the limiting measure, which are established in [Reference Maher and TiozzoMT18]. Another approach to study the deviation of random walks was suggested by [Reference Mathieu and SistoMS20]. These traditional methods require finite second moment condition to deduce a deviation inequality that leads to the summable decay of shadows. A related result is the central limit theorem on hyperbolic groups established by Benoist and Quint in [Reference Benoist and QuintBQ16].
In contrast, apart from the boundary convergence, pivoting and probability estimation appearing in our methods rely purely on the elementary properties of Gromov products and fellow-traveling geodesics. As long as pivots are present in the sample path, the pivoting method works regardless of deviation from the escape rate. (See [Reference GouëzelGou22] for a similar idea.) In order to implement this idea on Teichmüller spaces, we utilize the fellow-traveling phenomena of certain Teichmüller geodesics due to Rafi [Reference RafiRaf14]. We remark that Duchin also investigated “thin triangles” in Teichmüller spaces in [Reference DuchinDuc05] to study the dynamics of random walks on Teichmüller spaces.
2 Preliminaries
2.1 Geometry of a Gromov hyperbolic space
Let
![]() $(X, d)$
be a metric space. Throughout, we fix a basepoint
$(X, d)$
be a metric space. Throughout, we fix a basepoint
![]() $x_{0}$
in X. The following notion is crucial to defining Gromov hyperbolicity.
$x_{0}$
in X. The following notion is crucial to defining Gromov hyperbolicity.
Definition 2.1 (Gromov product)
For
![]() $x, y, z \in X$
, the Gromov product
$x, y, z \in X$
, the Gromov product
![]() $(x, y)_{z}$
is defined by
$(x, y)_{z}$
is defined by
Definition 2.2 (Gromov hyperbolic space)
A metric space
![]() $(X, d)$
is said to be Gromov hyperbolic if it satisfies the following property for some
$(X, d)$
is said to be Gromov hyperbolic if it satisfies the following property for some
![]() $\delta> 0$
:
$\delta> 0$
:
Property 2.3. For any
![]() $x, y, z,w\in X$
, we have
$x, y, z,w\in X$
, we have
For details on the properties of Gromov hyperbolic spaces, see [Reference GromovGro87] and [Reference Bridson and HaefligerBH99]. In sections 2 and 3, we assume that
![]() $(X, d)$
is a separable, geodesic, Gromov hyperbolic space.
$(X, d)$
is a separable, geodesic, Gromov hyperbolic space.
We now consider the Gromov boundary
![]() $\partial X$
of X in terms of the Gromov product. We regard that a sequence
$\partial X$
of X in terms of the Gromov product. We regard that a sequence
![]() $(x_n)_{n \in \operatorname {\mathbb {N}}}$
in X is converging to a point at infinity if
$(x_n)_{n \in \operatorname {\mathbb {N}}}$
in X is converging to a point at infinity if
![]() $(x_n, x_m)_{x_0} \to \infty $
as
$(x_n, x_m)_{x_0} \to \infty $
as
![]() $\min \{m, n\} \to \infty $
. Furthermore, two such sequences
$\min \{m, n\} \to \infty $
. Furthermore, two such sequences
![]() $(x_n), (y_n)$
will be considered as converging to the same point at infinity if
$(x_n), (y_n)$
will be considered as converging to the same point at infinity if
![]() $(x_n, y_n)_{x_0} \to \infty $
as
$(x_n, y_n)_{x_0} \to \infty $
as
![]() $n \to \infty $
. In this case, we regard
$n \to \infty $
. In this case, we regard
![]() $(x_n)$
and
$(x_n)$
and
![]() $(y_n)$
to be equivalent and denote
$(y_n)$
to be equivalent and denote
![]() $(x_n) \sim (y_n)$
. In this point of view, the Gromov boundary is defined as follows:
$(x_n) \sim (y_n)$
. In this point of view, the Gromov boundary is defined as follows:
 $$ \begin{align*}\partial X := \left\lbrace (x_n) \in X^{\operatorname{\mathbb{N}}} : \lim_{\min\{m, n\} \to \infty}(x_n, x_m)_{x_0} \to \infty \right\rbrace / \sim.\end{align*} $$
$$ \begin{align*}\partial X := \left\lbrace (x_n) \in X^{\operatorname{\mathbb{N}}} : \lim_{\min\{m, n\} \to \infty}(x_n, x_m)_{x_0} \to \infty \right\rbrace / \sim.\end{align*} $$
The Gromov product defined above can be extended to the Gromov boundary by setting
One can interpret the Gromov product
![]() $(x, y)_{z}$
as a crude distance from z to the geodesic connecting x and y. Having this in mind, we have the following useful lemma.
$(x, y)_{z}$
as a crude distance from z to the geodesic connecting x and y. Having this in mind, we have the following useful lemma.
Lemma 2.4. Let
![]() $n \ge 1$
and
$n \ge 1$
and
![]() $x_{0}, \ldots , x_{n}$
be points in X. Suppose that
$x_{0}, \ldots , x_{n}$
be points in X. Suppose that
for
![]() $i = 1, \ldots , n-2$
. Then
$i = 1, \ldots , n-2$
. Then
-
(1)
 $|(x_{i}, x_{k})_{x_{j}} - (x_{j-1}, x_{j+1})_{x_{j}}| \le 2\delta $
for
$|(x_{i}, x_{k})_{x_{j}} - (x_{j-1}, x_{j+1})_{x_{j}}| \le 2\delta $
for
 $0 \le i < j < k \le n$
, and
$0 \le i < j < k \le n$
, and -
(2)
 $$ \begin{align*} \left| \left(\sum_{i=0}^{n-1} d(x_{i}, x_{i+1}) - 2 \sum_{i=1}^{n-1} (x_{i-1}, x_{i+1})_{x_{i}} \right) - d(x_{0}, x_{n}) \right| \le 2(n-1) \delta. \end{align*} $$
$$ \begin{align*} \left| \left(\sum_{i=0}^{n-1} d(x_{i}, x_{i+1}) - 2 \sum_{i=1}^{n-1} (x_{i-1}, x_{i+1})_{x_{i}} \right) - d(x_{0}, x_{n}) \right| \le 2(n-1) \delta. \end{align*} $$
Proof. We prove (1) and (2) by induction on n. For
![]() $n = 1$
, (1) is void and (2) holds automatically.
$n = 1$
, (1) is void and (2) holds automatically.
Let us now assume (1) and (2) for
![]() $n =m\ge 1$
and prove them for
$n =m\ge 1$
and prove them for
![]() $n=m+1$
. We claim that
$n=m+1$
. We claim that
for
![]() $0 \le i < j < k \le m+1$
concludes (1) for
$0 \le i < j < k \le m+1$
concludes (1) for
![]() $n=m+1$
. Indeed, given a triple
$n=m+1$
. Indeed, given a triple
![]() $(i, j, k)$
, Inequality 2.2 and Inequality 2.3 (with i replaced with
$(i, j, k)$
, Inequality 2.2 and Inequality 2.3 (with i replaced with
![]() $j-1$
) lead to the inequality in (1).
$j-1$
) lead to the inequality in (1).
The nontrivial case for Inequality 2.2 is when
![]() $i < j-1$
. Since
$i < j-1$
. Since
![]() $0 \le i < j-1 < j \le m$
in this case, Inequality 2.2 for
$0 \le i < j-1 < j \le m$
in this case, Inequality 2.2 for
![]() $n=m$
implies
$n=m$
implies
Moreover, since
![]() $1 \le j-1 < j < k \le m+1$
, Inequality 2.3 for
$1 \le j-1 < j < k \le m+1$
, Inequality 2.3 for
![]() $n=m$
implies
$n=m$
implies
Combining them, we have
 $$ \begin{align}\begin{aligned} (x_{i}, x_{j-1})_{x_{j}} &= d(x_{j-1}, x_{j}) - (x_{i}, x_{j})_{x_{j-1}} &\\ &\ge d(x_{j-1}, x_{j}) - (x_{j-2}, x_{j})_{x_{j-1}} - \delta &(\because \textrm{ Inequality}\ 2.4) \\ &>(x_{j-1}, x_{j+1})_{x_{j}} +2 \delta & (\because\ \textrm{Inequality}\ 2.1) \\ &\ge (x_{j-1}, x_{k})_{x_{j}} + \delta. & (\because\ \textrm{Inequality}\ 2.5) \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} (x_{i}, x_{j-1})_{x_{j}} &= d(x_{j-1}, x_{j}) - (x_{i}, x_{j})_{x_{j-1}} &\\ &\ge d(x_{j-1}, x_{j}) - (x_{j-2}, x_{j})_{x_{j-1}} - \delta &(\because \textrm{ Inequality}\ 2.4) \\ &>(x_{j-1}, x_{j+1})_{x_{j}} +2 \delta & (\because\ \textrm{Inequality}\ 2.1) \\ &\ge (x_{j-1}, x_{k})_{x_{j}} + \delta. & (\because\ \textrm{Inequality}\ 2.5) \end{aligned}\end{align} $$
Now Property 2.3 reads
and
If
![]() $\min \{(x_{j-1}, x_{i})_{x_{j}}, (x_{i}, x_{k})_{x_{j}}\} = (x_{j-1}, x_{i})_{x_{j}}$
then Inequality 2.6 and 2.8 imply
$\min \{(x_{j-1}, x_{i})_{x_{j}}, (x_{i}, x_{k})_{x_{j}}\} = (x_{j-1}, x_{i})_{x_{j}}$
then Inequality 2.6 and 2.8 imply
a contradiction. Hence,
![]() $\min \{(x_{j-1}, x_{i})_{x_{j}}, (x_{i}, x_{j})_{x_{j}}\} = (x_{i}, x_{k})_{x_{j}}$
, and Inequality 2.8 reads
$\min \{(x_{j-1}, x_{i})_{x_{j}}, (x_{i}, x_{j})_{x_{j}}\} = (x_{i}, x_{k})_{x_{j}}$
, and Inequality 2.8 reads
Inequality 2.7 and 2.9 lead to Inequality 2.2. Inequality 2.3 is deduced in a similar manner.
For (2), we have
 $$ \begin{align*}\begin{aligned} &\left| \left(\sum_{i=0}^{m} d(x_{i}, x_{i+1}) - 2 \sum_{i=1}^{m} (x_{i-1}, x_{i+1})_{x_{i}} \right) - d(x_{0}, x_{m+1}) \right| \\ &\le \left| \left(\sum_{i=0}^{m-1} d(x_{i}, x_{i+1}) - 2 \sum_{i=1}^{m-1} (x_{i-1}, x_{i+1})_{x_{i}} \right) - d(x_{0}, x_{m}) \right|\\ & \quad + \left| d(x_{0}, x_{m}) + d(x_{m}, x_{m+1}) - d(x_{0}, x_{m+1}) - 2(x_{m-1}, x_{m+1})_{x_{m}}\right| \\ &\le 2(m-1) \delta + 2 |(x_{0} ,x_{m+1})_{x_{m}} - (x_{m-1}, x_{m+1})_{x_{m}}| \le 2m \delta. \\[-17pt] \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} &\left| \left(\sum_{i=0}^{m} d(x_{i}, x_{i+1}) - 2 \sum_{i=1}^{m} (x_{i-1}, x_{i+1})_{x_{i}} \right) - d(x_{0}, x_{m+1}) \right| \\ &\le \left| \left(\sum_{i=0}^{m-1} d(x_{i}, x_{i+1}) - 2 \sum_{i=1}^{m-1} (x_{i-1}, x_{i+1})_{x_{i}} \right) - d(x_{0}, x_{m}) \right|\\ & \quad + \left| d(x_{0}, x_{m}) + d(x_{m}, x_{m+1}) - d(x_{0}, x_{m+1}) - 2(x_{m-1}, x_{m+1})_{x_{m}}\right| \\ &\le 2(m-1) \delta + 2 |(x_{0} ,x_{m+1})_{x_{m}} - (x_{m-1}, x_{m+1})_{x_{m}}| \le 2m \delta. \\[-17pt] \end{aligned} \end{align*} $$
We now define the shadows of a point in terms of the Gromov product.
Definition 2.5 (Shadow)
For
![]() $x_0, x \in X$
and
$x_0, x \in X$
and
![]() $R> 0$
, the shadow
$R> 0$
, the shadow
![]() $S_{x_0}(x, R)$
is defined by
$S_{x_0}(x, R)$
is defined by
Intuitively, the shadow is a set of points
![]() $y \in X$
that the geodesic segment connecting
$y \in X$
that the geodesic segment connecting
![]() $x_0$
and y is of distance at most R from x up to an additive constant. See Figure 1.
$x_0$
and y is of distance at most R from x up to an additive constant. See Figure 1.

Figure 1 Shadow of x with respect to
![]() $x_{0}$
.
$x_{0}$
.
2.2 Isometries of a Gromov hyperbolic space
We mainly consider the group
![]() $\operatorname {Isom}(X)$
of isometries
$\operatorname {Isom}(X)$
of isometries
![]() $X \to X$
. Isometries of Gromov hyperbolic spaces are classified into the following categories.
$X \to X$
. Isometries of Gromov hyperbolic spaces are classified into the following categories.
Proposition 2.6 (Classification of isometries)
For
![]() $g \in \operatorname {Isom}(X)$
, one of the following holds.
$g \in \operatorname {Isom}(X)$
, one of the following holds.
-
(1) g is elliptic (i.e.,
 $\{g^nx : n \in \operatorname {\mathbb {Z}}\}$
is bounded for any
$\{g^nx : n \in \operatorname {\mathbb {Z}}\}$
is bounded for any
 $x \in X$
);
$x \in X$
); -
(2) g is parabolic (i.e., g is not elliptic and has exactly one fixed point in
 $\partial X$
); or
$\partial X$
); or -
(3) g is hyperbolic (i.e., g is not elliptic and has exactly two fixed points in
 $\partial X$
).
$\partial X$
).
In particular, when g is hyperbolic, its action shows a source-sink dynamics; one fixed point in
![]() $\partial X$
is the attracting point while the other is the repelling point.
$\partial X$
is the attracting point while the other is the repelling point.
One quantity representing the dynamics of an isometry is its translation length.
Definition 2.7 (Translation length)
For
![]() $g \in \operatorname {Isom}(X)$
, its translation length
$g \in \operatorname {Isom}(X)$
, its translation length
![]() $\tau (g)$
is
$\tau (g)$
is
for any
![]() $x \in X$
.
$x \in X$
.
Note that Lemma 2.4 gives the following corollary. (cf. [Reference Maher and TiozzoMT18, Proposition 5.8])
Corollary 2.8. For
![]() $g \in \operatorname {Isom}(X)$
, if g and
$g \in \operatorname {Isom}(X)$
, if g and
![]() $x_0 \in X$
satisfy
$x_0 \in X$
satisfy
then we have
2.3 Random walks
We define a bi-infinite random walk on a group by adopting the convention in [Reference Maher and TiozzoMT18].
For a countable group G, let
![]() $\mu : G \to [0, 1]$
be a probability measure on G. Then the product space
$\mu : G \to [0, 1]$
be a probability measure on G. Then the product space
![]() $(G^{\operatorname {\mathbb {Z}}},\ \mu ^{\operatorname {\mathbb {Z}}})$
forms the step space consisting of bi-infinite step paths. To obtain random walks, we consider the map
$(G^{\operatorname {\mathbb {Z}}},\ \mu ^{\operatorname {\mathbb {Z}}})$
forms the step space consisting of bi-infinite step paths. To obtain random walks, we consider the map
![]() $G^{\operatorname {\mathbb {Z}}} \to G^{\operatorname {\mathbb {Z}}}$
,
$G^{\operatorname {\mathbb {Z}}} \to G^{\operatorname {\mathbb {Z}}}$
,
![]() $(g_n) \mapsto (\operatorname {\omega }_n)$
so that
$(g_n) \mapsto (\operatorname {\omega }_n)$
so that
![]() $\operatorname {\omega }_0$
is the identity and
$\operatorname {\omega }_0$
is the identity and
![]() $\operatorname {\omega }_{n-1}^{-1}\operatorname {\omega }_n = g_n$
for all n. In other words, we set
$\operatorname {\omega }_{n-1}^{-1}\operatorname {\omega }_n = g_n$
for all n. In other words, we set
 $$ \begin{align*}\operatorname{\omega}_n = \begin{cases} g_1 \cdots g_n &, n> 0\\ id &, n = 0\\ g_0^{-1}g_{-1}^{-1} \cdots g_{n+1}^{-1} &, n < 0. \end{cases}\end{align*} $$
$$ \begin{align*}\operatorname{\omega}_n = \begin{cases} g_1 \cdots g_n &, n> 0\\ id &, n = 0\\ g_0^{-1}g_{-1}^{-1} \cdots g_{n+1}^{-1} &, n < 0. \end{cases}\end{align*} $$
Via this map,
![]() $(G^{\operatorname {\mathbb {Z}}},\ \mu ^{\operatorname {\mathbb {Z}}})$
induces the probability space
$(G^{\operatorname {\mathbb {Z}}},\ \mu ^{\operatorname {\mathbb {Z}}})$
induces the probability space
![]() $(\Omega , \operatorname {\mathbb {P}})$
, where
$(\Omega , \operatorname {\mathbb {P}})$
, where
![]() $\Omega $
denotes the space of sample paths for random walks.
$\Omega $
denotes the space of sample paths for random walks.
We often need to estimate the distance or the Gromov product among the translates of
![]() $x_{0}$
by isometries. In this situation, bringing a particular point to the basepoint can ease notation and computation. For example, consider isometries w, g and
$x_{0}$
by isometries. In this situation, bringing a particular point to the basepoint can ease notation and computation. For example, consider isometries w, g and
![]() $ h$
. Then
$ h$
. Then
![]() $(wg x_{0},\ wh x_{0})_{wx_{0}}$
can also be computed by
$(wg x_{0},\ wh x_{0})_{wx_{0}}$
can also be computed by
![]() $(gx_{0},\ hx_{0})_{x_{0}}$
, which does not depend on w. In particular, when w are words at step n and g, h are the next steps, then this reduction helps unify the cases.
$(gx_{0},\ hx_{0})_{x_{0}}$
, which does not depend on w. In particular, when w are words at step n and g, h are the next steps, then this reduction helps unify the cases.
In this philosophy, we keep the following notations throughout the paper: for a path
![]() $\vec {w} = (w_{1}, \ldots , w_{n})$
, we write
$\vec {w} = (w_{1}, \ldots , w_{n})$
, we write
Morally, this amounts to shifting the basepoint to
![]() $x_{n}$
and observing the phenomena relative to step n. One can readily observe the following equalities:
$x_{n}$
and observing the phenomena relative to step n. One can readily observe the following equalities:
-
(1)
 $x_{0 \rightarrow n} = x_{n} = w_{n}x_{0}$
,
$x_{0 \rightarrow n} = x_{n} = w_{n}x_{0}$
,
 $x_{n \rightarrow 0} = w_{n}^{-1} x_{0}$
,
$x_{n \rightarrow 0} = w_{n}^{-1} x_{0}$
,
 $x_{n \rightarrow n} = x_{0}$
.
$x_{n \rightarrow n} = x_{0}$
. -
(2)
 $d(x_{n}, x_{m}) = d(x_{k \rightarrow n}, x_{k \rightarrow m}) = d(x_{0}, x_{n \rightarrow m}) = d(x_{0}, x_{m \rightarrow n})$
.
$d(x_{n}, x_{m}) = d(x_{k \rightarrow n}, x_{k \rightarrow m}) = d(x_{0}, x_{n \rightarrow m}) = d(x_{0}, x_{m \rightarrow n})$
. -
(3)
 $(x_{n}, x_{m})_{x_{k}} = (x_{k \rightarrow n}, x_{k \rightarrow m})_{x_{0}}$
.
$(x_{n}, x_{m})_{x_{k}} = (x_{k \rightarrow n}, x_{k \rightarrow m})_{x_{0}}$
.
3 Random walks on hyperbolic spaces
3.1 Ingredients for persistent joints
In this section,
![]() $(X, d)$
is a separable geodesic Gromov hyperbolic space,
$(X, d)$
is a separable geodesic Gromov hyperbolic space,
![]() $G \le \operatorname {Isom}(X)$
is a weakly hyperbolic group, and
$G \le \operatorname {Isom}(X)$
is a weakly hyperbolic group, and
![]() $\mu : G \to [0, 1]$
is a non-elementary probability measure. As in section 2.3,
$\mu : G \to [0, 1]$
is a non-elementary probability measure. As in section 2.3,
![]() $\mu $
induces the probability space
$\mu $
induces the probability space
![]() $(\Omega , \operatorname {\mathbb {P}})$
for random walks.
$(\Omega , \operatorname {\mathbb {P}})$
for random walks.
We recall some facts proved in [Reference Maher and TiozzoMT18]. First of all, Maher and Tiozzo proved in [Reference Maher and TiozzoMT18, Theorem 1.1] that almost every sample path
![]() $\operatorname {\omega }_n x_0$
converges to a point
$\operatorname {\omega }_n x_0$
converges to a point
![]() $\operatorname {\omega }_+$
in
$\operatorname {\omega }_+$
in
![]() $\partial X$
. This induces the hitting measure
$\partial X$
. This induces the hitting measure
![]() $\nu $
on
$\nu $
on
![]() $\partial X$
by
$\partial X$
by
for Borel sets
![]() $S \subseteq \partial X$
. Maher and Tiozzo also showed that
$S \subseteq \partial X$
. Maher and Tiozzo also showed that
![]() $\nu $
is the unique
$\nu $
is the unique
![]() $\mu $
-stationary probability measure on
$\mu $
-stationary probability measure on
![]() $\partial X$
and is non-atomic. We also borrow the notation
$\partial X$
and is non-atomic. We also borrow the notation
Proposition 3.1. [Reference Maher and TiozzoMT18, Proposition 5.1]
For each subset U of X, we also define
Similarly, we define
![]() $H_x^{-}(U) := \operatorname {\mathbb {P}}(\operatorname {\omega }_{n}x \in U \mbox { for some } n \le 0)$
. Then the above proposition holds analogously.
$H_x^{-}(U) := \operatorname {\mathbb {P}}(\operatorname {\omega }_{n}x \in U \mbox { for some } n \le 0)$
. Then the above proposition holds analogously.
Proposition 3.2 [Reference Maher and TiozzoMT18, Proposition 5.2]
We have
Let
![]() $R_{1}>0$
be such that
$R_{1}>0$
be such that
![]() $ \sup _{S \in Sh(x_{0}, R_{1})} H_{x_{0}}^{\pm }(S) < 0.01$
.
$ \sup _{S \in Sh(x_{0}, R_{1})} H_{x_{0}}^{\pm }(S) < 0.01$
.
Meanwhile, since
![]() $\mu $
is assumed to be non-elementary, there exist two independent hyperbolic isometries
$\mu $
is assumed to be non-elementary, there exist two independent hyperbolic isometries
![]() $w_{+}, w_{-}$
in
$w_{+}, w_{-}$
in
![]() $\langle \langle \operatorname {supp} \mu \rangle \rangle $
, the subsemigroup generated by the support of
$\langle \langle \operatorname {supp} \mu \rangle \rangle $
, the subsemigroup generated by the support of
![]() $\mu $
. Their independence implies the following:
$\mu $
. Their independence implies the following:
![]() $\{(w_{1}^{n} x_{0}, w_{2}^{m} x_{0})_{x_{0}}\}_{m, n> 0}$
is bounded, say by
$\{(w_{1}^{n} x_{0}, w_{2}^{m} x_{0})_{x_{0}}\}_{m, n> 0}$
is bounded, say by
![]() $R_{2}>0$
, for
$R_{2}>0$
, for
See Figure 2. We now fix
![]() $R = 1000(R_{1} + R_{2} + \delta +1)$
. Note that the bound
$R = 1000(R_{1} + R_{2} + \delta +1)$
. Note that the bound
![]() $R_{2}$
for
$R_{2}$
for
![]() $\{(w_{1}^{n} x_{0}, w_{2}^{m} x_{0})_{x_{0}}\}_{m, n> 0}$
still works if we replace
$\{(w_{1}^{n} x_{0}, w_{2}^{m} x_{0})_{x_{0}}\}_{m, n> 0}$
still works if we replace
![]() $w_{+}$
and
$w_{+}$
and
![]() $w_{-}$
with their positive powers. By taking suitable powers of
$w_{-}$
with their positive powers. By taking suitable powers of
![]() $w_{\pm }$
if necessary, we can assume that:
$w_{\pm }$
if necessary, we can assume that:
-
(1)
 $w_{+}, w_{-} \in \operatorname {supp} \mu ^{L}$
for the same power L (i.e.,
$w_{+}, w_{-} \in \operatorname {supp} \mu ^{L}$
for the same power L (i.e.,
 $w_{+} = a_{1} \cdots a_{L}$
and
$w_{+} = a_{1} \cdots a_{L}$
and
 $w_{-} = b_{1} \cdots b_{L}$
for some isometries
$w_{-} = b_{1} \cdots b_{L}$
for some isometries
 $a_{i}, b_{i} \in \operatorname {supp} \mu $
), and
$a_{i}, b_{i} \in \operatorname {supp} \mu $
), and -
(2)
 $d(x_{0}, w_{+} x_{0}), d(x_{0}, w_{-}x_{0})> 100R$
.
$d(x_{0}, w_{+} x_{0}), d(x_{0}, w_{-}x_{0})> 100R$
.

Figure 2 Choice of R and
![]() $w_{\pm }$
. Here,
$w_{\pm }$
. Here,
![]() $P_+$
and
$P_+$
and
![]() $P_+'$
are attracting points and
$P_+'$
are attracting points and
![]() $P_-$
and
$P_-$
and
![]() $P_-'$
are repelling points of w and
$P_-'$
are repelling points of w and
![]() $w'$
, respectively.
$w'$
, respectively.
For convenience, we fix the following notations:
 $$ \begin{align*}\begin{aligned} p_{+} &= \mu(a_{1}) \cdots \mu(a_{L}) , \\ p_{-} &= \mu(b_{1}) \cdots \mu(b_{L}), \\ P &= \max\left(\frac{p_{+}}{p_{+}+ p_{-}}, \frac{p_{-}}{p_{+} + p_{-}}\right). \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} p_{+} &= \mu(a_{1}) \cdots \mu(a_{L}) , \\ p_{-} &= \mu(b_{1}) \cdots \mu(b_{L}), \\ P &= \max\left(\frac{p_{+}}{p_{+}+ p_{-}}, \frac{p_{-}}{p_{+} + p_{-}}\right). \end{aligned} \end{align*} $$
3.2 Persistent joints
We define a random variable
![]() $\chi _{k}(\operatorname {\omega })$
that witnesses persistent joints at position
$\chi _{k}(\operatorname {\omega })$
that witnesses persistent joints at position
![]() $3kL$
, which is a slight variation of the one defined by Maher and Tiozzo in [Reference Maher and TiozzoMT18, Section 5.2]. See also Figure 3.
$3kL$
, which is a slight variation of the one defined by Maher and Tiozzo in [Reference Maher and TiozzoMT18, Section 5.2]. See also Figure 3.
Definition 3.3 (Persistent joint)
For a sample path
![]() $\operatorname {\omega } = (\operatorname {\omega }_n)$
with the step sequence
$\operatorname {\omega } = (\operatorname {\omega }_n)$
with the step sequence
![]() $(g_n) = (\operatorname {\omega }_{n-1}^{-1}\operatorname {\omega }_n)$
, we define a random variable
$(g_n) = (\operatorname {\omega }_{n-1}^{-1}\operatorname {\omega }_n)$
, we define a random variable
![]() $\chi _k(\operatorname {\omega })$
as follows.
$\chi _k(\operatorname {\omega })$
as follows.
![]() $\chi _{k}(\operatorname {\omega }) = 1$
if
$\chi _{k}(\operatorname {\omega }) = 1$
if
-
(1)
 $$ \begin{align*} (g_{3(k-1)L + 1}, \ldots, g_{3kL})= \left\{ \begin{array}{c} (b_{1}, \ldots, b_{L}, a_{1}, \ldots, a_{L}, b_{1}, \ldots, b_{L}) \\ \textrm{or} \\ (b_{1}, \ldots, b_{L}, b_{1}, \ldots, b_{L}, b_{1}, \ldots, b_{L})\end{array} \right., \end{align*} $$
$$ \begin{align*} (g_{3(k-1)L + 1}, \ldots, g_{3kL})= \left\{ \begin{array}{c} (b_{1}, \ldots, b_{L}, a_{1}, \ldots, a_{L}, b_{1}, \ldots, b_{L}) \\ \textrm{or} \\ (b_{1}, \ldots, b_{L}, b_{1}, \ldots, b_{L}, b_{1}, \ldots, b_{L})\end{array} \right., \end{align*} $$
-
(2)
 $x_{n} \in S_{x_{(3k - 2)L}} (x_{3(k-1)L}, 0.9R)$
for all integers
$x_{n} \in S_{x_{(3k - 2)L}} (x_{3(k-1)L}, 0.9R)$
for all integers
 $n \le 3(k-1)L$
, and
$n \le 3(k-1)L$
, and -
(3)
 $x_{n} \in S_{x_{(3k-1)L} }(x_{3kL}, 0.9R)$
for all integers
$x_{n} \in S_{x_{(3k-1)L} }(x_{3kL}, 0.9R)$
for all integers
 $n \ge 3kL$
$n \ge 3kL$
where
![]() $x_n = \operatorname {\omega }_n x_0$
. Otherwise,
$x_n = \operatorname {\omega }_n x_0$
. Otherwise,
![]() $\chi _{k}(\operatorname {\omega })=0$
.
$\chi _{k}(\operatorname {\omega })=0$
.

Figure 3 Description of a persistent joint.
We first observe that
![]() $\operatorname {\mathbb {E}}(\chi _{1}(\operatorname {\omega }))> 0$
. The probability for condition (1) is
$\operatorname {\mathbb {E}}(\chi _{1}(\operatorname {\omega }))> 0$
. The probability for condition (1) is
![]() $(p_{+} + p_{-}) p_{-}^{2} \neq 0$
. Given (1) as the prior condition, (2) and (3) become independent events. (2) holds if the shifted random walk
$(p_{+} + p_{-}) p_{-}^{2} \neq 0$
. Given (1) as the prior condition, (2) and (3) become independent events. (2) holds if the shifted random walk
![]() $T^{3(k-1)L}\operatorname {\omega }$
does not hit
$T^{3(k-1)L}\operatorname {\omega }$
does not hit
![]() $S_{x_0}(w_-x_0, d(x_{0}, w_{-}x_{0}) - 0.9R)$
in negative time. Indeed, we have
$S_{x_0}(w_-x_0, d(x_{0}, w_{-}x_{0}) - 0.9R)$
in negative time. Indeed, we have
 $$ \begin{align*}\begin{aligned} &g_{3(k-1) L}^{-1} \cdots g_{n+1}^{-1} x_{0} \notin S_{x_{0}} (w_{-}x_{0}, d(x_{0}, w_{-} x_{0}) - 0.9R) \\ \Leftrightarrow &\operatorname{\omega}_{n} x_{0} \notin S_{\operatorname{\omega}_{3(k-1) L} x_{0}} (\operatorname{\omega}_{3(k-1)L} w_{-} x_{0}, d(x_{0}, w_{-} x_{0}) -0.9R) \\ \Leftrightarrow & \operatorname{\omega}_{n} x_{0} \in S_{\operatorname{\omega}_{(3k-2) L} x_{0}} (\operatorname{\omega}_{3(k-1)L} x_{0}, 0.9R) \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} &g_{3(k-1) L}^{-1} \cdots g_{n+1}^{-1} x_{0} \notin S_{x_{0}} (w_{-}x_{0}, d(x_{0}, w_{-} x_{0}) - 0.9R) \\ \Leftrightarrow &\operatorname{\omega}_{n} x_{0} \notin S_{\operatorname{\omega}_{3(k-1) L} x_{0}} (\operatorname{\omega}_{3(k-1)L} w_{-} x_{0}, d(x_{0}, w_{-} x_{0}) -0.9R) \\ \Leftrightarrow & \operatorname{\omega}_{n} x_{0} \in S_{\operatorname{\omega}_{(3k-2) L} x_{0}} (\operatorname{\omega}_{3(k-1)L} x_{0}, 0.9R) \end{aligned} \end{align*} $$
for
![]() $n < 3(k-1) L$
. Here, the last inequality follows from the equality
$n < 3(k-1) L$
. Here, the last inequality follows from the equality
for
![]() $p \in X$
and
$p \in X$
and
![]() $y = \operatorname {\omega }_{3(k-1)L} x_{0}$
,
$y = \operatorname {\omega }_{3(k-1)L} x_{0}$
,
![]() $z = \operatorname {\omega }_{3(k-1)L} w_{-} x_{0} = \operatorname {\omega }_{(3k-2)L} x_{0}$
. Thus, the probability for condition (2) is at least
$z = \operatorname {\omega }_{3(k-1)L} w_{-} x_{0} = \operatorname {\omega }_{(3k-2)L} x_{0}$
. Thus, the probability for condition (2) is at least
Similarly, the probability for condition (3) is at least
Overall, we have
Note also that
![]() $\chi _{k}(\operatorname {\omega }) = \chi _{1}(T^{3(k-1)L} \operatorname {\omega })$
. We invoke a variant of Kingman’s subadditive ergodic theorem.
$\chi _{k}(\operatorname {\omega }) = \chi _{1}(T^{3(k-1)L} \operatorname {\omega })$
. We invoke a variant of Kingman’s subadditive ergodic theorem.
Theorem 3.4 [Reference WoessWoe00, (8.10) Theorem]
Let
![]() $(\Omega , \operatorname {\mathbb {P}})$
be a probability space and
$(\Omega , \operatorname {\mathbb {P}})$
be a probability space and
![]() $U : \Omega \rightarrow \Omega $
be a measure-preserving transformation. If
$U : \Omega \rightarrow \Omega $
be a measure-preserving transformation. If
![]() $W_{n}$
is a non-negative real-valued random variable on
$W_{n}$
is a non-negative real-valued random variable on
![]() $\Omega $
satisfying the subadditivity
$\Omega $
satisfying the subadditivity
![]() $W_{n+m} \le W_{n} + W_{m} \circ U^{n}$
for all
$W_{n+m} \le W_{n} + W_{m} \circ U^{n}$
for all
![]() $m, n \in \operatorname {\mathbb {N}}$
, and
$m, n \in \operatorname {\mathbb {N}}$
, and
![]() $W_{1}$
has finite first moment, then there is a U-invariant random variable
$W_{1}$
has finite first moment, then there is a U-invariant random variable
![]() $W_{\infty }$
such that
$W_{\infty }$
such that
almost surely and in
![]() $L^{1}(\Omega , \operatorname {\mathbb {P}})$
. If U is ergodic in addition, then
$L^{1}(\Omega , \operatorname {\mathbb {P}})$
. If U is ergodic in addition, then
![]() $W_{\infty }$
is constant a.e.
$W_{\infty }$
is constant a.e.
We define
![]() $W_{n} = \sum _{k=1}^{n} \chi _{k}(\operatorname {\omega })$
. Then
$W_{n} = \sum _{k=1}^{n} \chi _{k}(\operatorname {\omega })$
. Then
![]() $W_{n+m} = W_{n} + W_{m} \circ T^{3Ln}$
holds. Since
$W_{n+m} = W_{n} + W_{m} \circ T^{3Ln}$
holds. Since
![]() $W_{1}$
is bounded, it has finite first moment. Applying Theorem 3.4, we get almost everywhere convergence of
$W_{1}$
is bounded, it has finite first moment. Applying Theorem 3.4, we get almost everywhere convergence of
![]() $\frac {1}{n} W_{n}$
to an a.e. constant
$\frac {1}{n} W_{n}$
to an a.e. constant
![]() $W_{\infty }$
. Since
$W_{\infty }$
. Since
![]() $\mathbb {E}(W_{1}) = \eta> 0$
, we have
$\mathbb {E}(W_{1}) = \eta> 0$
, we have
![]() $W_{\infty } = \eta $
a.e.
$W_{\infty } = \eta $
a.e.
We now consider a modified version of
![]() $W_{n}$
. Given positive integers
$W_{n}$
. Given positive integers
![]() $m \le n$
, we say that
$m \le n$
, we say that
![]() $\mathcal {N} = \{n_{1}< \cdots < n_{k}\}\subseteq 3L\operatorname {\mathbb {Z}}$
is an
$\mathcal {N} = \{n_{1}< \cdots < n_{k}\}\subseteq 3L\operatorname {\mathbb {Z}}$
is an
![]() $(m, n)$
-set of pivots for a finite path
$(m, n)$
-set of pivots for a finite path
![]() $\vec {w} = (w_{1}, \ldots , w_{n})$
if the following hold:
$\vec {w} = (w_{1}, \ldots , w_{n})$
if the following hold:
-
(1)
 $\mathcal {N} \subseteq \{1, \ldots , m\}$
;
$\mathcal {N} \subseteq \{1, \ldots , m\}$
; -
(2) for each
 $i=1, \ldots , k$
,
$i=1, \ldots , k$
,  $$ \begin{align*} (g_{n_{i} - 3L + 1}, \ldots, g_{n_{i}})= \left\{ \begin{array}{c} (b_{1}, \ldots, b_{L}, a_{1}, \ldots, a_{L}, b_{1}, \ldots, b_{L}) \\ \textrm{or} \\ (b_{1}, \ldots, b_{L}, b_{1}, \ldots, b_{L}, b_{1}, \ldots, b_{L})\end{array} \right., \end{align*} $$
$$ \begin{align*} (g_{n_{i} - 3L + 1}, \ldots, g_{n_{i}})= \left\{ \begin{array}{c} (b_{1}, \ldots, b_{L}, a_{1}, \ldots, a_{L}, b_{1}, \ldots, b_{L}) \\ \textrm{or} \\ (b_{1}, \ldots, b_{L}, b_{1}, \ldots, b_{L}, b_{1}, \ldots, b_{L})\end{array} \right., \end{align*} $$
-
(3) for each
 $i=1, \ldots , k$
,
$i=1, \ldots , k$
,
 $x_{j} \in S_{x_{n_{i} - 2L}} (x_{n_{i} - 3L}, 0.9R)$
for
$x_{j} \in S_{x_{n_{i} - 2L}} (x_{n_{i} - 3L}, 0.9R)$
for
 $n_{i-1} - L \le j \le n_{i} - 3L$
, and
$n_{i-1} - L \le j \le n_{i} - 3L$
, and -
(4) for each
 $i=1, \ldots , k$
,
$i=1, \ldots , k$
,
 $x_{j} \in S_{x_{n_{i} - L}}(x_{n_{i}}, 0.9R)$
for
$x_{j} \in S_{x_{n_{i} - L}}(x_{n_{i}}, 0.9R)$
for
 $n_{i} \le j \le n_{i+1}-2L$
.
$n_{i} \le j \le n_{i+1}-2L$
.
(For convenience, we set
![]() $n_{0} = L$
and
$n_{0} = L$
and
![]() $n_{k+1} = n+2L$
.) Note that if
$n_{k+1} = n+2L$
.) Note that if
![]() $\mathcal {N}$
and
$\mathcal {N}$
and
![]() $\mathcal {N}'$
are
$\mathcal {N}'$
are
![]() $(m, n)$
-sets of pivots for
$(m, n)$
-sets of pivots for
![]() $\vec {w} = (w_{1}, \ldots , w_{n})$
, then so is their union. Thus, we can associate each finite path
$\vec {w} = (w_{1}, \ldots , w_{n})$
, then so is their union. Thus, we can associate each finite path
![]() $\vec {w} = (w_{1}, \ldots , w_{n})$
with its maximal
$\vec {w} = (w_{1}, \ldots , w_{n})$
with its maximal
![]() $(m, n)$
-set of pivots
$(m, n)$
-set of pivots
![]() $\mathcal {N}(\vec {w}) = \mathcal {N}_{m, n}(\vec {w})$
. We also define
$\mathcal {N}(\vec {w}) = \mathcal {N}_{m, n}(\vec {w})$
. We also define
Note that
![]() $\#\mathcal {N}_{n, n}(\operatorname {\omega }_1, \ldots , \operatorname {\omega }_n) \ge W_{\lfloor n/3L\rfloor }(\operatorname {\omega }_1, \ldots , \operatorname {\omega }_n)$
for each n and
$\#\mathcal {N}_{n, n}(\operatorname {\omega }_1, \ldots , \operatorname {\omega }_n) \ge W_{\lfloor n/3L\rfloor }(\operatorname {\omega }_1, \ldots , \operatorname {\omega }_n)$
for each n and
![]() $W_{\lfloor n/3L \rfloor } (\operatorname {\omega })\ge \eta \lfloor n/3L\rfloor \ge \frac {\eta n}{ 6L}+1$
eventually holds for a.e. sample path
$W_{\lfloor n/3L \rfloor } (\operatorname {\omega })\ge \eta \lfloor n/3L\rfloor \ge \frac {\eta n}{ 6L}+1$
eventually holds for a.e. sample path
![]() $\operatorname {\omega }$
. Consequently,
$\operatorname {\omega }$
. Consequently,
![]() $(\operatorname {\omega }_{1}, \ldots , \operatorname {\omega }_{n}) \in F_{n}$
eventually holds for a.e.
$(\operatorname {\omega }_{1}, \ldots , \operatorname {\omega }_{n}) \in F_{n}$
eventually holds for a.e.
![]() $\operatorname {\omega }$
.
$\operatorname {\omega }$
.
Let us now fix a finite path
![]() $\vec {w} = (w_{1}, \ldots , w_{n})$
with
$\vec {w} = (w_{1}, \ldots , w_{n})$
with
![]() $\mathcal {N}_{n, n}(\vec {w}) = \{n_{1} < \ldots < n_{k}\}$
. For convenience, we define the following for
$\mathcal {N}_{n, n}(\vec {w}) = \{n_{1} < \ldots < n_{k}\}$
. For convenience, we define the following for
![]() $i=1, \ldots , k$
:
$i=1, \ldots , k$
:
 $$ \begin{align}\begin{aligned} A_{i}'(\vec{w})&:= n_i(\vec{w}) - 3L, \\ \alpha^{\prime}_{i}(\vec{w}) &:= n_i(\vec{w}) - 2L,\\ \beta^{\prime}_{i}(\vec{w}) &:= n_i(\vec{w}) - L,\\ B^{\prime}_{i}(\vec{w}) &:= n_{i}(\vec{w}). \end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} A_{i}'(\vec{w})&:= n_i(\vec{w}) - 3L, \\ \alpha^{\prime}_{i}(\vec{w}) &:= n_i(\vec{w}) - 2L,\\ \beta^{\prime}_{i}(\vec{w}) &:= n_i(\vec{w}) - L,\\ B^{\prime}_{i}(\vec{w}) &:= n_{i}(\vec{w}). \end{aligned} \end{align} $$
We also let
![]() $\beta ^{\prime }_{0}(\vec {w}) = B^{\prime }_{0}(\vec {w}) := 0$
and
$\beta ^{\prime }_{0}(\vec {w}) = B^{\prime }_{0}(\vec {w}) := 0$
and
![]() $\alpha ^{\prime }_{k+1}(\vec {w}) = A^{\prime }_{k+1}(\vec {w}) := n$
. The following lemma allows us to calculate the distances among
$\alpha ^{\prime }_{k+1}(\vec {w}) = A^{\prime }_{k+1}(\vec {w}) := n$
. The following lemma allows us to calculate the distances among
![]() $x_{j}$
.
$x_{j}$
.
Lemma 3.5. We have the following:
-
(1)
 $d(x_{\beta ^{\prime }_{i-1}}, x_{\alpha ^{\prime }_{i}})> 99R$
for each
$d(x_{\beta ^{\prime }_{i-1}}, x_{\alpha ^{\prime }_{i}})> 99R$
for each
 $i=1, \ldots , k+1$
;
$i=1, \ldots , k+1$
; -
(2)
 $(x_{\alpha ^{\prime }_{i} \rightarrow \beta ^{\prime }_{i-1}}, w_{\pm }x_0)_{x_{0}} < 0.6R$
for each
$(x_{\alpha ^{\prime }_{i} \rightarrow \beta ^{\prime }_{i-1}}, w_{\pm }x_0)_{x_{0}} < 0.6R$
for each
 $i=1, \ldots , k$
, and
$i=1, \ldots , k$
, and -
(3)
 $(x_{\beta ^{\prime }_{i} \rightarrow \alpha ^{\prime }_{i+1}}, w_{\pm }^{-1}x_0)_{x_{0}} < 0.6R$
for each
$(x_{\beta ^{\prime }_{i} \rightarrow \alpha ^{\prime }_{i+1}}, w_{\pm }^{-1}x_0)_{x_{0}} < 0.6R$
for each
 $i=1, \ldots , k$
.
$i=1, \ldots , k$
.
Proof. Let us discuss (1). For
![]() $2 \le i \le k+1$
, we have
$2 \le i \le k+1$
, we have
Since
![]() $(x_{\alpha ^{\prime }_{i}}, x_{B^{\prime }_{i-1}})_{x_{\beta ^{\prime }_{i-1}}} \le d(x_{\alpha ^{\prime }_{i}}, x_{\beta ^{\prime }_{i-1}})$
, we deduce the desired conclusion. Similar discussion on
$(x_{\alpha ^{\prime }_{i}}, x_{B^{\prime }_{i-1}})_{x_{\beta ^{\prime }_{i-1}}} \le d(x_{\alpha ^{\prime }_{i}}, x_{\beta ^{\prime }_{i-1}})$
, we deduce the desired conclusion. Similar discussion on
![]() $(x_{\beta ^{\prime }_{i-1}}, x_{A^{\prime }_{i}})_{x_{\alpha ^{\prime }_{i}}}$
for
$(x_{\beta ^{\prime }_{i-1}}, x_{A^{\prime }_{i}})_{x_{\alpha ^{\prime }_{i}}}$
for
![]() $1 \le i \le k$
handles the remaining case:
$1 \le i \le k$
handles the remaining case:
For (2), we invoke Property 2.3:
Here,
![]() $(w_{-}^{-1} x_{0}, x_{\alpha ^{\prime }_{i} \rightarrow \beta ^{\prime }_{i-1}})_{x_{0}} = (x_{\alpha ^{\prime }_{i} \rightarrow A^{\prime }_{i}}, x_{\alpha ^{\prime }_{i} \rightarrow \beta ^{\prime }_{i-1}})_{x_{0}}> 99 R$
was proven in Inequality 3.2. Hence, we deduce
$(w_{-}^{-1} x_{0}, x_{\alpha ^{\prime }_{i} \rightarrow \beta ^{\prime }_{i-1}})_{x_{0}} = (x_{\alpha ^{\prime }_{i} \rightarrow A^{\prime }_{i}}, x_{\alpha ^{\prime }_{i} \rightarrow \beta ^{\prime }_{i-1}})_{x_{0}}> 99 R$
was proven in Inequality 3.2. Hence, we deduce
![]() $(x_{\alpha ^{\prime }_{i} \rightarrow \beta ^{\prime }_{i-1}}, w_{\pm } x_{0})_{x_{0}} < 0.5R+\delta < 0.6R$
. (3) is argued similarly.
$(x_{\alpha ^{\prime }_{i} \rightarrow \beta ^{\prime }_{i-1}}, w_{\pm } x_{0})_{x_{0}} < 0.5R+\delta < 0.6R$
. (3) is argued similarly.
Corollary 3.6. Let
for
![]() $i = 1, \ldots , k$
and
$i = 1, \ldots , k$
and
![]() $y_{0} = x_{0}$
,
$y_{0} = x_{0}$
,
![]() $y_{2k+1} = x_{n}$
. Then we have
$y_{2k+1} = x_{n}$
. Then we have
for all
![]() $0 \le i \le j \le l\le 2k+1$
.
$0 \le i \le j \le l\le 2k+1$
.
Proof. The first item of Lemma 3.5 tells us that
![]() $d(y_{2i}, y_{2i+1})> 99R$
for
$d(y_{2i}, y_{2i+1})> 99R$
for
![]() $i = 0, \ldots , k$
. Moreover,
$i = 0, \ldots , k$
. Moreover,
![]() $d(y_{2i-1}, y_{2i}) = d(x_{0}, w_{\pm } x_{0}) \ge 100R$
for
$d(y_{2i-1}, y_{2i}) = d(x_{0}, w_{\pm } x_{0}) \ge 100R$
for
![]() $i = 1, \ldots , k$
. Finally, (2) and (3) of Lemma 3.5 read that
$i = 1, \ldots , k$
. Finally, (2) and (3) of Lemma 3.5 read that
![]() $(y_{i-1}, y_{i+1})_{y_{i}} < 0.6R$
for
$(y_{i-1}, y_{i+1})_{y_{i}} < 0.6R$
for
![]() $i = 1, \ldots , 2k$
and
$i = 1, \ldots , 2k$
and
for
![]() $i=1, \ldots , 2k-1$
. We can then apply Lemma 2.4 and conclude
$i=1, \ldots , 2k-1$
. We can then apply Lemma 2.4 and conclude
for
![]() $0 \le i < j < l \le 2k+1$
. Moreover, this implies
$0 \le i < j < l \le 2k+1$
. Moreover, this implies
for
![]() $0 \le i \le j < 2k+1$
, which leads to the second conclusion.
$0 \le i \le j < 2k+1$
, which leads to the second conclusion.
We now define constants
![]() $D, M$
and set
$D, M$
and set
![]() $G_{n}$
such that
$G_{n}$
such that
 $$ \begin{align*}\begin{aligned} D &:= R\eta / L, \\ M &> 1+10R + 2d(x_{0}, w_{+} x_{0}) + 2d(x_{0}, w_{-}x_{0})+4L,\\ G_{n} &:= \left\{ \vec{w} \in F_n : \tau(w_{n}) \le \left(2D-\frac{2\eta}{M}\right)n\right\}. \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} D &:= R\eta / L, \\ M &> 1+10R + 2d(x_{0}, w_{+} x_{0}) + 2d(x_{0}, w_{-}x_{0})+4L,\\ G_{n} &:= \left\{ \vec{w} \in F_n : \tau(w_{n}) \le \left(2D-\frac{2\eta}{M}\right)n\right\}. \end{aligned} \end{align*} $$
Furthermore, for
![]() $\vec {w} \in F_{n}$
and
$\vec {w} \in F_{n}$
and
![]() $Q> 0$
, we define
$Q> 0$
, we define
 $$ \begin{align*} \begin{aligned} \mathcal{N}_{f}(\vec{w}; Q) &= \left\{ n_{i} \in \mathcal{N}(\vec{w}) : d(x_{0}, x_{\beta_{i}'}) \le \frac{1}{2} d(x_{0}, x_{n}) -(D+Q\eta/M)n \right\},\\ \mathcal{N}_{b}(\vec{w};Q) &= \left\{ n_{i} \in \mathcal{N}(\vec{w}): d(x_{n}, x_{\alpha_{i}'}) \le \frac{1}{2} d(x_{0}, x_{n}) - (D+Q\eta/M)n\right\},\\ \mathcal{N}_{0}(\vec{w};Q) &= \mathcal{N}(\vec{w})\setminus \left[\mathcal{N}_{f}(\vec{w};Q) \cup \mathcal{N}_{b}(\vec{w};Q)\right]. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathcal{N}_{f}(\vec{w}; Q) &= \left\{ n_{i} \in \mathcal{N}(\vec{w}) : d(x_{0}, x_{\beta_{i}'}) \le \frac{1}{2} d(x_{0}, x_{n}) -(D+Q\eta/M)n \right\},\\ \mathcal{N}_{b}(\vec{w};Q) &= \left\{ n_{i} \in \mathcal{N}(\vec{w}): d(x_{n}, x_{\alpha_{i}'}) \le \frac{1}{2} d(x_{0}, x_{n}) - (D+Q\eta/M)n\right\},\\ \mathcal{N}_{0}(\vec{w};Q) &= \mathcal{N}(\vec{w})\setminus \left[\mathcal{N}_{f}(\vec{w};Q) \cup \mathcal{N}_{b}(\vec{w};Q)\right]. \end{aligned} \end{align*} $$
We observe the following estimation of
![]() $\mathcal {N}_{f}$
and
$\mathcal {N}_{f}$
and
![]() $\mathcal {N}_{b}$
.
$\mathcal {N}_{b}$
.
Lemma 3.7. For
![]() $n>10L/\eta $
, if
$n>10L/\eta $
, if
![]() $\vec {w} \in F_{n}$
and
$\vec {w} \in F_{n}$
and
![]() $Q \le 1$
, then
$Q \le 1$
, then
holds.
Proof. Suppose not. Then
![]() $\mathcal {N}_{0}(\vec {w};Q)$
contains at least
$\mathcal {N}_{0}(\vec {w};Q)$
contains at least
![]() $\frac {\eta n}{15L}+1$
indices. By setting
$\frac {\eta n}{15L}+1$
indices. By setting
![]() $i = 1$
and increasing j, Corollary 3.6 implies that
$i = 1$
and increasing j, Corollary 3.6 implies that
![]() $d(x_{0}, x_{\beta _{j}^{\prime }})$
increases as j increases. Similarly, by setting
$d(x_{0}, x_{\beta _{j}^{\prime }})$
increases as j increases. Similarly, by setting
![]() $j = N+1$
and decreasing i, we realize that
$j = N+1$
and decreasing i, we realize that
![]() $d(x_{\alpha _{i}}, x_{n})$
increases as i decreases. Consequently, we may take t,
$d(x_{\alpha _{i}}, x_{n})$
increases as i decreases. Consequently, we may take t,
![]() $t'$
such that
$t'$
such that
Again, using Corollary 3.6, we deduce that
Recall that
![]() $R>1000>Q$
,
$R>1000>Q$
,
![]() $M>L$
,
$M>L$
,
![]() $D ={R \eta \over L}$
and
$D ={R \eta \over L}$
and
![]() $\frac {2\eta n}{L}\ge 20$
. Then Corollary 3.6 implies that
$\frac {2\eta n}{L}\ge 20$
. Then Corollary 3.6 implies that
 $$ \begin{align*}\begin{aligned} d(x_{0}, x_{n}) & \ge d(x_{0}, x_{\beta_{t}^{\prime}}) + d(x_{\beta_{t}^{\prime}}, x_{\alpha_{t^{\prime}}^{\prime}}) + d(x_{\alpha_{t^{\prime}}^{\prime}}, x_{n}) - 4.4R\\ & \ge d(x_{0}, x_{n}) - 2Dn - \frac{2Q\eta n}{M} + \frac{6 R \eta n}{L} - 4.4R\\ & \ge d(x_{0}, x_{n}) - \frac{2R \eta n}{L} -\frac{2R \eta n}{L} + \frac{6R \eta n}{L}- 4.4R> d(x_{0}, x_{n}), \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} d(x_{0}, x_{n}) & \ge d(x_{0}, x_{\beta_{t}^{\prime}}) + d(x_{\beta_{t}^{\prime}}, x_{\alpha_{t^{\prime}}^{\prime}}) + d(x_{\alpha_{t^{\prime}}^{\prime}}, x_{n}) - 4.4R\\ & \ge d(x_{0}, x_{n}) - 2Dn - \frac{2Q\eta n}{M} + \frac{6 R \eta n}{L} - 4.4R\\ & \ge d(x_{0}, x_{n}) - \frac{2R \eta n}{L} -\frac{2R \eta n}{L} + \frac{6R \eta n}{L}- 4.4R> d(x_{0}, x_{n}), \end{aligned} \end{align*} $$
wich is a contradiction.
From this lemma, it follows that
 $$ \begin{align*}\begin{aligned} F_{n, f}(Q) & := \left\{ \vec{w} \in F_{n} : |\mathcal{N}_{f}(\vec{w};Q)| \ge \frac{\eta n}{20 LM^{2}} \right\},\\ F_{n, b}(Q) & := \left\{ \vec{w} \in F_n : |\mathcal{N}_{b}(\vec{w};Q)| \ge \frac{\eta n}{20LM^{2}} \right\} \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} F_{n, f}(Q) & := \left\{ \vec{w} \in F_{n} : |\mathcal{N}_{f}(\vec{w};Q)| \ge \frac{\eta n}{20 LM^{2}} \right\},\\ F_{n, b}(Q) & := \left\{ \vec{w} \in F_n : |\mathcal{N}_{b}(\vec{w};Q)| \ge \frac{\eta n}{20LM^{2}} \right\} \end{aligned} \end{align*} $$
cover entire
![]() $F_{n}$
for
$F_{n}$
for
![]() $Q\le 1$
and large enough n. We also define
$Q\le 1$
and large enough n. We also define
For each
![]() $\vec {w} \in F_{n, f}(Q)$
(
$\vec {w} \in F_{n, f}(Q)$
(
![]() $\vec {w} \in F_{n, b}(Q)$
, resp.), we fix an integer
$\vec {w} \in F_{n, b}(Q)$
, resp.), we fix an integer
![]() $N=N(\vec {w})$
between
$N=N(\vec {w})$
between
![]() $\frac {\eta n}{50 M^{2}L}$
and
$\frac {\eta n}{50 M^{2}L}$
and
![]() $\frac {\eta n}{20 M^{2} L}$
. Then we pick pivot indices
$\frac {\eta n}{20 M^{2} L}$
. Then we pick pivot indices
![]() $p_{1}(\vec {w})<\ldots < p_{N}(\vec {w})$
from
$p_{1}(\vec {w})<\ldots < p_{N}(\vec {w})$
from
![]() $\mathcal {N}_{f}$
(
$\mathcal {N}_{f}$
(
![]() $\mathcal {N}_{b}$
, resp.). We introduce a notation:
$\mathcal {N}_{b}$
, resp.). We introduce a notation:
 $$ \begin{align*} \begin{aligned} A_{i}(\vec{w})&:= p_i(\vec{w}) - 3L, \\ \alpha_{i}(\vec{w}) &:= p_i(\vec{w}) - 2L,\\ \beta_{i}(\vec{w}) &:= p_i(\vec{w}) - L,\\ B_{i}(\vec{w}) &:= p_{i}(\vec{w}). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} A_{i}(\vec{w})&:= p_i(\vec{w}) - 3L, \\ \alpha_{i}(\vec{w}) &:= p_i(\vec{w}) - 2L,\\ \beta_{i}(\vec{w}) &:= p_i(\vec{w}) - L,\\ B_{i}(\vec{w}) &:= p_{i}(\vec{w}). \end{aligned} \end{align*} $$
For convenience, we also let
![]() $\beta _{0}(\vec {w}) = B_{0}(\vec {w}) := 0$
and
$\beta _{0}(\vec {w}) = B_{0}(\vec {w}) := 0$
and
![]() $\alpha _{N+1}(\vec {w}) = A_{N+1}(\vec {w}) := n$
. Recalling Figure 3,
$\alpha _{N+1}(\vec {w}) = A_{N+1}(\vec {w}) := n$
. Recalling Figure 3,
![]() $A_i$
,
$A_i$
,
![]() $\alpha _i$
,
$\alpha _i$
,
![]() $\beta _i$
,
$\beta _i$
,
![]() $B_i$
are described as in Figure 4
$B_i$
are described as in Figure 4

Figure 4 Choice of
![]() $A_i$
,
$A_i$
,
![]() $\alpha _i$
,
$\alpha _i$
,
![]() $\beta _i$
,
$\beta _i$
,
![]() $B_i$
.
$B_i$
.
For each choice of
![]() $\sigma \in \{0, 1\}^{N}$
, we now define the pivoted word
$\sigma \in \{0, 1\}^{N}$
, we now define the pivoted word
![]() $\vec {w}^{\sigma }$
by declaring the steps
$\vec {w}^{\sigma }$
by declaring the steps
![]() $\{g_{i}^{\sigma }\}$
as follows. In plain words, we modify the type of joints that are marked by
$\{g_{i}^{\sigma }\}$
as follows. In plain words, we modify the type of joints that are marked by
![]() $\sigma $
only. For
$\sigma $
only. For
![]() $\sigma (i) = 1$
, we set
$\sigma (i) = 1$
, we set
 $$ \begin{align*} (g^{\sigma}_{\alpha_i + 1}, \ldots, g^{\sigma}_{\beta_i}) := \begin{cases} (a_1, \ldots, a_L) &\mbox{if } (g_{\alpha_i + 1}, \ldots, g_{\beta_i}) = (b_1, \ldots, b_L)\\ (b_1, \ldots, b_L) &\mbox{if } (g_{\alpha_i + 1}, \ldots, g_{\beta_i}) = (a_1, \ldots, a_L). \end{cases} \end{align*} $$
$$ \begin{align*} (g^{\sigma}_{\alpha_i + 1}, \ldots, g^{\sigma}_{\beta_i}) := \begin{cases} (a_1, \ldots, a_L) &\mbox{if } (g_{\alpha_i + 1}, \ldots, g_{\beta_i}) = (b_1, \ldots, b_L)\\ (b_1, \ldots, b_L) &\mbox{if } (g_{\alpha_i + 1}, \ldots, g_{\beta_i}) = (a_1, \ldots, a_L). \end{cases} \end{align*} $$
Other steps remain unchanged. For
![]() $\vec {w}^{\sigma } = (w_i^{\sigma })$
, we similarly denote
$\vec {w}^{\sigma } = (w_i^{\sigma })$
, we similarly denote
![]() $w_{n}^{\sigma } x_{0}$
by
$w_{n}^{\sigma } x_{0}$
by
![]() $x_{n}^{\sigma }$
and
$x_{n}^{\sigma }$
and
![]() $(w_{n}^{\sigma })^{-1} w_{m}^{\sigma } x_{0}$
by
$(w_{n}^{\sigma })^{-1} w_{m}^{\sigma } x_{0}$
by
![]() $x_{n \rightarrow m}^{\sigma }$
. Then we observe
$x_{n \rightarrow m}^{\sigma }$
. Then we observe
By definition, we have
Clearly,
![]() $\vec {w}^{\sigma } \neq \vec {w}^{\sigma '}$
for
$\vec {w}^{\sigma } \neq \vec {w}^{\sigma '}$
for
![]() $\sigma \neq \sigma '$
. Finally, note that
$\sigma \neq \sigma '$
. Finally, note that
![]() $\mathcal {N}(\vec {w}) = \mathcal {N}(\vec {w}^{\sigma })$
for
$\mathcal {N}(\vec {w}) = \mathcal {N}(\vec {w}^{\sigma })$
for
![]() $ \sigma \in \{0, 1\}^{N}$
, while a priori
$ \sigma \in \{0, 1\}^{N}$
, while a priori
![]() $\mathcal {N}_{f}(\vec {w})$
and
$\mathcal {N}_{f}(\vec {w})$
and
![]() $\mathcal {N}_{f}(\vec {w}^{\sigma })$
may not coincide.
$\mathcal {N}_{f}(\vec {w}^{\sigma })$
may not coincide.
The proof of Lemma 3.5 and Corollary 3.6 also apply here, so we omit the proof.
Lemma 3.8. We have the following.
-
(1)
 $d(x_{\beta _{i-1}'}^{\sigma }, x_{\alpha _{i}'}^{\sigma })> 99R$
for each
$d(x_{\beta _{i-1}'}^{\sigma }, x_{\alpha _{i}'}^{\sigma })> 99R$
for each
 $1 \le i\le k+1$
.
$1 \le i\le k+1$
. -
(2)
 $(x_{\alpha _{i}' \rightarrow \beta _{i-1}'}^{\sigma }, w_{\pm }x_0)_{x_{0}} < 0.6R$
for each i.
$(x_{\alpha _{i}' \rightarrow \beta _{i-1}'}^{\sigma }, w_{\pm }x_0)_{x_{0}} < 0.6R$
for each i. -
(3)
 $(x_{\beta _{i}' \rightarrow \alpha _{i+1}'}^{\sigma }, w_{\pm }^{-1}x_0)_{x_{0}} < 0.6R$
for each i.
$(x_{\beta _{i}' \rightarrow \alpha _{i+1}'}^{\sigma }, w_{\pm }^{-1}x_0)_{x_{0}} < 0.6R$
for each i.
Corollary 3.9. Let
for
![]() $i = 1, \ldots , k$
and
$i = 1, \ldots , k$
and
![]() $y_{0} = x_{0}$
,
$y_{0} = x_{0}$
,
![]() $y_{2k+1} = x_{n}$
. Then
$y_{2k+1} = x_{n}$
. Then
![]() $(y_{i}, y_{l})_{y_{j}} \le 0.8R$
and
$(y_{i}, y_{l})_{y_{j}} \le 0.8R$
and
![]() $d(y_{i}, y_{j}) \le d(y_{i}, y_{l}) - 95(l-j)R$
for all
$d(y_{i}, y_{j}) \le d(y_{i}, y_{l}) - 95(l-j)R$
for all
![]() $0 \le i < j < l\le 2N+1$
.
$0 \le i < j < l\le 2N+1$
.
Now we have all ingredients ready.
Lemma 3.10. Let
![]() $Q \ge 0.9$
and
$Q \ge 0.9$
and
![]() $n \ge 40 M R/\eta $
. For each
$n \ge 40 M R/\eta $
. For each
![]() $\vec {w} \in F_{n, f}(Q)$
and
$\vec {w} \in F_{n, f}(Q)$
and
![]() $\sigma \neq \kappa \in \{0, 1\}^{N}$
, if
$\sigma \neq \kappa \in \{0, 1\}^{N}$
, if
![]() $\tau (w_{n}^{\kappa }) \le \left (2D -2\eta /M\right )n$
, then
$\tau (w_{n}^{\kappa }) \le \left (2D -2\eta /M\right )n$
, then
![]() $\tau (w_{n}^{\sigma }) \ge (2D +\eta /M)n$
.
$\tau (w_{n}^{\sigma }) \ge (2D +\eta /M)n$
.
Proof. We first establish a bound on
![]() $d(x_{0}, x_{n}^{\sigma })$
. Note that this part does not require any assumption on
$d(x_{0}, x_{n}^{\sigma })$
. Note that this part does not require any assumption on
![]() $\tau (w_{n}^{\kappa })$
.
$\tau (w_{n}^{\kappa })$
.
Claim 3.11. We have
and for each
![]() $i = 1, \cdots , N$
,
$i = 1, \cdots , N$
,
 $$ \begin{align*} \begin{aligned} |d(x_n^{\kappa}, x_{\alpha_{i}'}^{\kappa}) - d(x_n^{\sigma}, x_{\alpha_{i}'}^{\sigma})|& \le {\eta n \over 40M}, \\ |d(x_0, x_{\beta_{i}'}^{\kappa}) - d(x_0, x_{\beta_{i}'}^{\sigma})|& \le {\eta n \over 40M}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} |d(x_n^{\kappa}, x_{\alpha_{i}'}^{\kappa}) - d(x_n^{\sigma}, x_{\alpha_{i}'}^{\sigma})|& \le {\eta n \over 40M}, \\ |d(x_0, x_{\beta_{i}'}^{\kappa}) - d(x_0, x_{\beta_{i}'}^{\sigma})|& \le {\eta n \over 40M}. \end{aligned} \end{align*} $$
Proof of the Claim
By Lemma 2.4, we have
 $$ \begin{align*}\begin{aligned} d(x_{0}, x_{n}^{\sigma}) &\ge \sum_{i=1}^{N+1} d(x_{\beta_{i-1}}^{\sigma}, x_{\alpha_{i}}^{\sigma}) + \sum_{i=1}^{N} d(x_{\alpha_{i}}^{\sigma}, x_{\beta_{i}}^{\sigma}) \\ & \quad - 2 \sum_{i=1}^{N} (x_{\beta_{i}}^{\sigma}, x_{\beta_{i-1}}^{\sigma})_{x_{\alpha_{i}}^{\sigma}} - 2 \sum_{i=1}^{N} (x_{\alpha_{i}}^{\sigma}, x_{\alpha_{i+1}}^{\sigma})_{x_{\beta_{i}}^{\sigma}} - 2 \cdot 2N \cdot \delta \\ & \ge \sum_{i=1}^{N+1} d(x_{\beta_{i-1}}^{\sigma}, x_{\alpha_{i}}^{\sigma}) = \sum_{i=1}^{N+1} d(x_{\beta_{i-1}}^{\kappa}, x_{\alpha_{i}}^{\kappa}). \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} d(x_{0}, x_{n}^{\sigma}) &\ge \sum_{i=1}^{N+1} d(x_{\beta_{i-1}}^{\sigma}, x_{\alpha_{i}}^{\sigma}) + \sum_{i=1}^{N} d(x_{\alpha_{i}}^{\sigma}, x_{\beta_{i}}^{\sigma}) \\ & \quad - 2 \sum_{i=1}^{N} (x_{\beta_{i}}^{\sigma}, x_{\beta_{i-1}}^{\sigma})_{x_{\alpha_{i}}^{\sigma}} - 2 \sum_{i=1}^{N} (x_{\alpha_{i}}^{\sigma}, x_{\alpha_{i+1}}^{\sigma})_{x_{\beta_{i}}^{\sigma}} - 2 \cdot 2N \cdot \delta \\ & \ge \sum_{i=1}^{N+1} d(x_{\beta_{i-1}}^{\sigma}, x_{\alpha_{i}}^{\sigma}) = \sum_{i=1}^{N+1} d(x_{\beta_{i-1}}^{\kappa}, x_{\alpha_{i}}^{\kappa}). \end{aligned} \end{align*} $$
Recall also that
![]() $d(x_{\alpha _{i}}^{\kappa }, x_{\beta _{i}}^{\kappa })$
is either
$d(x_{\alpha _{i}}^{\kappa }, x_{\beta _{i}}^{\kappa })$
is either
![]() $d(x_0, w_{+} x_0)$
or
$d(x_0, w_{+} x_0)$
or
![]() $d(x_0, w_{-} x_0)$
, which are both smaller than
$d(x_0, w_{-} x_0)$
, which are both smaller than
![]() $M/2$
. Since N is chosen to be less than
$M/2$
. Since N is chosen to be less than
![]() $\frac {\eta n}{20M^2L}$
, we have
$\frac {\eta n}{20M^2L}$
, we have
 $$ \begin{align*}\begin{aligned} d(x_0, x_n^{\sigma}) &\ge \sum_{i=1}^{N+1} d(x_{\beta_{i-1}}^{\kappa}, x_{\alpha_{i}}^{\kappa}) + \sum_{i=1}^{N} d(x_{\alpha_{i}}^{\kappa}, x_{\beta_{i}}^{\kappa}) - 0.5M \cdot \frac{\eta n}{20 M^{2} L}\\ & \ge d(x_{0}, x_{n}^{\kappa}) - \frac{\eta n}{40ML} \\ &\ge d(x_{0}, x_{n}^{\kappa}) - \frac{\eta n}{40M}. \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} d(x_0, x_n^{\sigma}) &\ge \sum_{i=1}^{N+1} d(x_{\beta_{i-1}}^{\kappa}, x_{\alpha_{i}}^{\kappa}) + \sum_{i=1}^{N} d(x_{\alpha_{i}}^{\kappa}, x_{\beta_{i}}^{\kappa}) - 0.5M \cdot \frac{\eta n}{20 M^{2} L}\\ & \ge d(x_{0}, x_{n}^{\kappa}) - \frac{\eta n}{40ML} \\ &\ge d(x_{0}, x_{n}^{\kappa}) - \frac{\eta n}{40M}. \end{aligned} \end{align*} $$
A symmetric argument shows that
![]() $d(x_{0}, x_{n}^{\sigma }) \le d(x_{0}, x_{n}^{\kappa }) + \eta n/40M$
. Similar arguments involving partial sums give the remaining results.
$d(x_{0}, x_{n}^{\sigma }) \le d(x_{0}, x_{n}^{\kappa }) + \eta n/40M$
. Similar arguments involving partial sums give the remaining results.
Now suppose
![]() $\tau (w_n^{\kappa }) \le (2D - 2\eta /M)n$
. We observe the following:
$\tau (w_n^{\kappa }) \le (2D - 2\eta /M)n$
. We observe the following:
Claim 3.12.
Proof of the Claim
Recall that
![]() $M> L$
,
$M> L$
,
![]() $R>1+3\delta $
and
$R>1+3\delta $
and
![]() $n> 40 M R/\eta $
. This implies
$n> 40 M R/\eta $
. This implies
![]() $1/40 M < R/L$
, and consequently,
$1/40 M < R/L$
, and consequently,
Now suppose that Inequality 3.3 does not hold. This implies
 $$ \begin{align*}\begin{aligned} d(x_{0}, x_{n}^{\kappa}) - 2(x_{n}^{\kappa}, x_{n \rightarrow 0}^{\kappa})_{x_{0}} &\ge \left[d(x_{0}, x_{n}) - \frac{\eta n}{40 M}\right]- 2(x_{n}^{\kappa}, x_{n \rightarrow 0}^{\kappa})_{x_{0}} & (\because\ \textrm{Claim}\ 3.11)\\ &> 2Dn - \frac{\eta n}{40 M} > \frac{\eta n}{40 M}> 3\delta. \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} d(x_{0}, x_{n}^{\kappa}) - 2(x_{n}^{\kappa}, x_{n \rightarrow 0}^{\kappa})_{x_{0}} &\ge \left[d(x_{0}, x_{n}) - \frac{\eta n}{40 M}\right]- 2(x_{n}^{\kappa}, x_{n \rightarrow 0}^{\kappa})_{x_{0}} & (\because\ \textrm{Claim}\ 3.11)\\ &> 2Dn - \frac{\eta n}{40 M} > \frac{\eta n}{40 M}> 3\delta. \end{aligned} \end{align*} $$
Then from Corollary 2.8, we have
This contradicts the assumption that
![]() $\tau (w_n^{\kappa }) \le (2D - 2\eta /M)n$
.
$\tau (w_n^{\kappa }) \le (2D - 2\eta /M)n$
.
Fixing
![]() $\sigma \in \{0, 1\}^{N}$
other than
$\sigma \in \{0, 1\}^{N}$
other than
![]() $\kappa $
, we now estimate the Gromov products among four points
$\kappa $
, we now estimate the Gromov products among four points
![]() $x_n^{\kappa }, x_n^{\sigma }, x_{n \to 0}^{\kappa },$
and
$x_n^{\kappa }, x_n^{\sigma }, x_{n \to 0}^{\kappa },$
and
![]() $x_{n \to 0}^{\sigma }$
based at
$x_{n \to 0}^{\sigma }$
based at
![]() $x_0$
. See Figure 5.
$x_0$
. See Figure 5.

Figure 5 Four segments in the pivoting process and the Gromov products.
Claim 3.13. We have
Proof of the Claim
Since
![]() $\vec {w} \in F_{n, f}$
,
$\vec {w} \in F_{n, f}$
,
![]() $B_{N}=p_{N}$
belongs to
$B_{N}=p_{N}$
belongs to
![]() $\mathcal {N}_{f}(\vec {w})$
. Note that the steps
$\mathcal {N}_{f}(\vec {w})$
. Note that the steps
![]() $(g_{i})_{i}$
of
$(g_{i})_{i}$
of
![]() $\vec {w}$
after
$\vec {w}$
after
![]() $\beta _{N}$
are not altered by the pivoting; thus, we have
$\beta _{N}$
are not altered by the pivoting; thus, we have
Moreover, Claim 3.11 and
![]() $p_{N} \in \mathcal {N}_{f}(\vec {w})$
imply
$p_{N} \in \mathcal {N}_{f}(\vec {w})$
imply
 $$ \begin{align*}\begin{aligned} d(x_{n \rightarrow 0}^{\kappa}, x_{n \rightarrow \beta_{N}}^{\kappa}) &= d(x_{0}^{\kappa}, x_{\beta_{N}}^{\kappa} )\le d(x_{0}, x_{\beta_{N}}) + \frac{\eta n}{40 M} \\ &\le \frac{1}{2} d(x_{0}, x_{n}) - (D + Q \eta / M) n + \frac{\eta n}{40 M}. \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} d(x_{n \rightarrow 0}^{\kappa}, x_{n \rightarrow \beta_{N}}^{\kappa}) &= d(x_{0}^{\kappa}, x_{\beta_{N}}^{\kappa} )\le d(x_{0}, x_{\beta_{N}}) + \frac{\eta n}{40 M} \\ &\le \frac{1}{2} d(x_{0}, x_{n}) - (D + Q \eta / M) n + \frac{\eta n}{40 M}. \end{aligned} \end{align*} $$
The same upper bound also applies to
![]() $d(x_{n \rightarrow 0}^{\sigma }, x_{n \rightarrow \beta _{N}}^{\sigma })$
. Hence,
$d(x_{n \rightarrow 0}^{\sigma }, x_{n \rightarrow \beta _{N}}^{\sigma })$
. Hence,
 $$ \begin{align*} \begin{aligned} d(x_{n \rightarrow 0}^{\kappa}, x_{n\rightarrow 0}^{\sigma}) &\le d(x_{n \rightarrow 0}^{\kappa}, x_{n \rightarrow \beta_{N}}^{\kappa}) + d(x_{n \rightarrow \beta_{N}}^{\kappa}, x_{n \rightarrow \beta_{N}}^{\sigma}) + d(x_{n \rightarrow \beta_{N}}^{\sigma}, x_{n \rightarrow 0}^{\sigma}) \\ &\le 2 \cdot \left(\frac{1}{2} d(x_{0}, x_{n}) - (D + Q \eta /M) n + \frac{\eta n}{40M}\right). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} d(x_{n \rightarrow 0}^{\kappa}, x_{n\rightarrow 0}^{\sigma}) &\le d(x_{n \rightarrow 0}^{\kappa}, x_{n \rightarrow \beta_{N}}^{\kappa}) + d(x_{n \rightarrow \beta_{N}}^{\kappa}, x_{n \rightarrow \beta_{N}}^{\sigma}) + d(x_{n \rightarrow \beta_{N}}^{\sigma}, x_{n \rightarrow 0}^{\sigma}) \\ &\le 2 \cdot \left(\frac{1}{2} d(x_{0}, x_{n}) - (D + Q \eta /M) n + \frac{\eta n}{40M}\right). \end{aligned} \end{align*} $$
This inequality and Claim 3.11 together yield
 $$ \begin{align*} \begin{aligned} (x_{n \rightarrow 0}^{\kappa}, x_{n \rightarrow 0}^{\sigma})_{x_{0}} &\ge \frac{1}{2} [d(x_{0}, x_{n}^{\kappa}) + d(x_{0}, x_{n}^{\sigma})] - \left(\frac{1}{2} d(x_{0}, x_{n}) - (D + Q \eta /M) n + \frac{\eta n}{40M}\right) \\ &\ge d(x_{0}, x_{n}) - \frac{\eta n}{40 M} - \left(\frac{1}{2} d(x_{0}, x_{n}) - (D + Q \eta /M) n + \frac{\eta n}{40M}\right) \\ &\ge \frac{1}{2} d(x_{0}, x_{n}) + Dn + \left( \frac{0.9 \eta}{M} - \frac{\eta}{20 M} \right) n. \\[-22pt] \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} (x_{n \rightarrow 0}^{\kappa}, x_{n \rightarrow 0}^{\sigma})_{x_{0}} &\ge \frac{1}{2} [d(x_{0}, x_{n}^{\kappa}) + d(x_{0}, x_{n}^{\sigma})] - \left(\frac{1}{2} d(x_{0}, x_{n}) - (D + Q \eta /M) n + \frac{\eta n}{40M}\right) \\ &\ge d(x_{0}, x_{n}) - \frac{\eta n}{40 M} - \left(\frac{1}{2} d(x_{0}, x_{n}) - (D + Q \eta /M) n + \frac{\eta n}{40M}\right) \\ &\ge \frac{1}{2} d(x_{0}, x_{n}) + Dn + \left( \frac{0.9 \eta}{M} - \frac{\eta}{20 M} \right) n. \\[-22pt] \end{aligned} \end{align*} $$
In contrast, we get the following inequality.
Claim 3.14. We have
Proof of the Claim
To see this, let l be the minimum among
![]() $\{1, \ldots , N\}$
such that
$\{1, \ldots , N\}$
such that
![]() $\sigma (l) \neq \kappa (l)$
. We let
$\sigma (l) \neq \kappa (l)$
. We let
Then Corollary 3.9 tells us that
![]() $d(y_{i-1}, y_{i})> 99R$
for
$d(y_{i-1}, y_{i})> 99R$
for
![]() $i = 1, \ldots , 4$
and
$i = 1, \ldots , 4$
and
![]() $(y_{0}, y_{2})_{y_{1}}, (y_{2}, y_{4})_{y_{3}} < 0.8R$
. We also have
$(y_{0}, y_{2})_{y_{1}}, (y_{2}, y_{4})_{y_{3}} < 0.8R$
. We also have
![]() $(y_{1}, y_{3})_{y_{2}} = (w_{+} x_{0}, w_{-}x_{0})_{x_{0}} \le R_{1} <0.5R$
. Hence, we have
$(y_{1}, y_{3})_{y_{2}} = (w_{+} x_{0}, w_{-}x_{0})_{x_{0}} \le R_{1} <0.5R$
. Hence, we have
for
![]() $i=1, 2$
. We then apply Lemma 2.4 and deduce
$i=1, 2$
. We then apply Lemma 2.4 and deduce
![]() $(y_{0}, y_{4})_{y_{2}} < 0.5R + 2\delta < 0.6R$
. This implies
$(y_{0}, y_{4})_{y_{2}} < 0.5R + 2\delta < 0.6R$
. This implies
 $$ \begin{align}\begin{aligned} 2(x^{\kappa}_{n}, x_{n}^{\sigma})_{x_{0}} &= d(x_{0}, y_{0}) + d(x_{0}, y_{4}) - d(y_{0}, y_{4}) \\ &\le \big(d(x_{0}, y_{2}) + d(y_{2}, y_{0}) \big)+ \big(d(x_{0}, y_{2}) + d(y_{2}, y_{4}) \big) \\ & \quad - \big(d(y_{0}, y_{2}) + d(y_{2}, y_{4}) - 2(y_{0}, y_{4})_{y_{2}}\big) \\ &\le 2d(x_{0}, y_{2}) + 2 \cdot 0.6R. \end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} 2(x^{\kappa}_{n}, x_{n}^{\sigma})_{x_{0}} &= d(x_{0}, y_{0}) + d(x_{0}, y_{4}) - d(y_{0}, y_{4}) \\ &\le \big(d(x_{0}, y_{2}) + d(y_{2}, y_{0}) \big)+ \big(d(x_{0}, y_{2}) + d(y_{2}, y_{4}) \big) \\ & \quad - \big(d(y_{0}, y_{2}) + d(y_{2}, y_{4}) - 2(y_{0}, y_{4})_{y_{2}}\big) \\ &\le 2d(x_{0}, y_{2}) + 2 \cdot 0.6R. \end{aligned} \end{align} $$
Meanwhile, the distance from
![]() $x_{0}$
and
$x_{0}$
and
![]() $y_{2} = x_{\alpha _{l}}^{\kappa }$
is estimated as follows:
$y_{2} = x_{\alpha _{l}}^{\kappa }$
is estimated as follows:
 $$ \begin{align*}\begin{aligned} d(x_{0}, x_{\alpha_{l}}^{\kappa}) &\le d(x_{0}, x_{\beta_{N}}^{\kappa}) & (\because\ \textrm{Corollary}\ 3.9)\\ &\le d(x_{0}, x_{\beta_{N}}) + \frac{\eta n}{40 M} & (\because\ \textrm{Claim}\ 3.11)\\ &\le \frac{1}{2} d(x_{0}, x_{n}) - \left( D + \frac{Q \eta}{M} \right) n + \frac{\eta n}{40M} & \left(p_{N} \in \mathcal{N}_{f}(\vec{w})\right). \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} d(x_{0}, x_{\alpha_{l}}^{\kappa}) &\le d(x_{0}, x_{\beta_{N}}^{\kappa}) & (\because\ \textrm{Corollary}\ 3.9)\\ &\le d(x_{0}, x_{\beta_{N}}) + \frac{\eta n}{40 M} & (\because\ \textrm{Claim}\ 3.11)\\ &\le \frac{1}{2} d(x_{0}, x_{n}) - \left( D + \frac{Q \eta}{M} \right) n + \frac{\eta n}{40M} & \left(p_{N} \in \mathcal{N}_{f}(\vec{w})\right). \end{aligned} \end{align*} $$
By plugging this into Inequality 3.7, we obtain
 $$ \begin{align*}\begin{aligned} (x^{\kappa}_{n}, x_{n}^{\sigma})_{x_{0}}& \le \frac{1}{2} d(x_{0}, x_{n}) - \left( D + \frac{Q \eta}{M} \right)n + \frac{ \eta n}{40 M} + 0.6 R \\ &\le \frac{1}{2} d(x_{0}, x_{n}) - \left( D + \frac{0.9 \eta}{M} \right) n + \frac{0.05 \eta n}{M} + \frac{0.02n\eta}{M} \\ &\le \frac{1}{2} d(x_{0}, x_{n}) - \left( D + \frac{0.8 \eta}{M} \right) n \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} (x^{\kappa}_{n}, x_{n}^{\sigma})_{x_{0}}& \le \frac{1}{2} d(x_{0}, x_{n}) - \left( D + \frac{Q \eta}{M} \right)n + \frac{ \eta n}{40 M} + 0.6 R \\ &\le \frac{1}{2} d(x_{0}, x_{n}) - \left( D + \frac{0.9 \eta}{M} \right) n + \frac{0.05 \eta n}{M} + \frac{0.02n\eta}{M} \\ &\le \frac{1}{2} d(x_{0}, x_{n}) - \left( D + \frac{0.8 \eta}{M} \right) n \end{aligned} \end{align*} $$
for
![]() $n> 40R M/\eta $
, as desired.
$n> 40R M/\eta $
, as desired.
Now let us finish the proof of Lemma 3.10. If we have
 $$ \begin{align} (x_{n}^{\sigma}, x_{n \rightarrow 0}^{\sigma})_{x_{0}} \ge \frac{1}{2} d(x_{0}, x_{n}) - \left(D + \frac{0.7 \eta }{M} \right)n, \end{align} $$
$$ \begin{align} (x_{n}^{\sigma}, x_{n \rightarrow 0}^{\sigma})_{x_{0}} \ge \frac{1}{2} d(x_{0}, x_{n}) - \left(D + \frac{0.7 \eta }{M} \right)n, \end{align} $$
then we have
 $$ \begin{align*}\begin{aligned}(x_{n}^{\kappa}, x_{n}^{\sigma})_{x_{0}} &\ge \min \{ (x_{n}^{\kappa}, x_{n \rightarrow 0}^{\kappa})_{x_{0}}, (x_{n\rightarrow 0}^{\kappa}, x_{n}^{\sigma})_{x_{0}} \} - \delta & (\because\ \textrm{Property}\ 2.3) \\&\ge \min \left\{ \begin{array}{c} (x_{n}^{\kappa}, x_{n \rightarrow 0}^{\kappa})_{x_{0}}, (x_{n \rightarrow 0}^{\kappa}, x_{n \rightarrow 0}^{\sigma})_{x_{0}}, \\(x_{n \rightarrow 0}^{\sigma}, x_{n}^{\sigma})_{x_{0}} \end{array}\right\} - 2\delta & (\because\ \textrm{Property}\ 2.3)\\&\ge \frac{1}{2} d(x_{0}, x_{n}) - \left(D + \frac{0.7 \eta}{M} \right)n - 2\delta & \left(\because \begin{array}{c} \textrm{Claim}\ 3.12,\\ \textrm{ Claim}\ 3.13 \end{array}\right)\\&> \frac{1}{2} d(x_{0}, x_{n}) - \left(D + \frac{0.8 \eta }{M} \right)n . & (\because\ \textrm{Inequality}\ 3.4)\end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned}(x_{n}^{\kappa}, x_{n}^{\sigma})_{x_{0}} &\ge \min \{ (x_{n}^{\kappa}, x_{n \rightarrow 0}^{\kappa})_{x_{0}}, (x_{n\rightarrow 0}^{\kappa}, x_{n}^{\sigma})_{x_{0}} \} - \delta & (\because\ \textrm{Property}\ 2.3) \\&\ge \min \left\{ \begin{array}{c} (x_{n}^{\kappa}, x_{n \rightarrow 0}^{\kappa})_{x_{0}}, (x_{n \rightarrow 0}^{\kappa}, x_{n \rightarrow 0}^{\sigma})_{x_{0}}, \\(x_{n \rightarrow 0}^{\sigma}, x_{n}^{\sigma})_{x_{0}} \end{array}\right\} - 2\delta & (\because\ \textrm{Property}\ 2.3)\\&\ge \frac{1}{2} d(x_{0}, x_{n}) - \left(D + \frac{0.7 \eta}{M} \right)n - 2\delta & \left(\because \begin{array}{c} \textrm{Claim}\ 3.12,\\ \textrm{ Claim}\ 3.13 \end{array}\right)\\&> \frac{1}{2} d(x_{0}, x_{n}) - \left(D + \frac{0.8 \eta }{M} \right)n . & (\because\ \textrm{Inequality}\ 3.4)\end{aligned} \end{align*} $$
This contradicts Claim 3.14. Therefore, Inequality 3.8 does not hold and
 $$ \begin{align*}\begin{aligned} d(x_{0}, x_{n}^{\sigma}) - 2(x_{n}^{\sigma}, x_{n \rightarrow 0}^{\sigma})_{x_{0}} &\ge \left[d(x_{0}, x_{n}) - \frac{\eta n}{40 M}\right] - 2(x_{n}^{\sigma}, x_{n \rightarrow 0}^{\sigma})_{x_{0}}\\ &\ge 2\left( D + \frac{0.7 \eta}{M} \right)n - \frac{\eta n}{40 M} \\ &\ge \left(2D + \eta/M\right) n + 3\delta> 3\delta. & (\because\ \textrm{Inequality}\ 3.4) \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} d(x_{0}, x_{n}^{\sigma}) - 2(x_{n}^{\sigma}, x_{n \rightarrow 0}^{\sigma})_{x_{0}} &\ge \left[d(x_{0}, x_{n}) - \frac{\eta n}{40 M}\right] - 2(x_{n}^{\sigma}, x_{n \rightarrow 0}^{\sigma})_{x_{0}}\\ &\ge 2\left( D + \frac{0.7 \eta}{M} \right)n - \frac{\eta n}{40 M} \\ &\ge \left(2D + \eta/M\right) n + 3\delta> 3\delta. & (\because\ \textrm{Inequality}\ 3.4) \end{aligned} \end{align*} $$
Then Corollary 2.8 tells us that
![]() $\tau (\operatorname {\omega }_{n}^{\sigma }) \ge \left (2D + \eta /M\right ) n$
.
$\tau (\operatorname {\omega }_{n}^{\sigma }) \ge \left (2D + \eta /M\right ) n$
.
In particular, for
![]() $\vec {w} \in G_{n, f}(Q)$
,
$\vec {w} \in G_{n, f}(Q)$
,
![]() $\vec {w}^{\sigma } \notin G_{n}$
for any nontrivial
$\vec {w}^{\sigma } \notin G_{n}$
for any nontrivial
![]() $\sigma $
. Similar discussion holds for
$\sigma $
. Similar discussion holds for
![]() $F_{n, b}$
and
$F_{n, b}$
and
![]() $G_{n, b}$
.
$G_{n, b}$
.
In the following crucial observation, we finally set the optimal value for Q and
![]() $N(\vec {w})$
.
$N(\vec {w})$
.
Lemma 3.15. Let
![]() $Q=1$
and
$Q=1$
and
![]() $n \ge 40 RM/\eta $
. Suppose that
$n \ge 40 RM/\eta $
. Suppose that
![]() $\vec {w}, \vec {w}' \in G_{n, f}(Q=1)$
and the numbers of pivots
$\vec {w}, \vec {w}' \in G_{n, f}(Q=1)$
and the numbers of pivots
![]() $N(\vec {w})$
,
$N(\vec {w})$
,
![]() $N(\vec {w}')$
are
$N(\vec {w}')$
are
![]() $\lfloor \frac {\eta n}{40 M^{2}L}\rfloor $
. Then for
$\lfloor \frac {\eta n}{40 M^{2}L}\rfloor $
. Then for
![]() $\sigma , \sigma ' \in \{0, 1\}^{N}$
,
$\sigma , \sigma ' \in \{0, 1\}^{N}$
,
![]() $\vec {w}^{\sigma } = \vec {w}^{\prime \sigma '}$
if and only if
$\vec {w}^{\sigma } = \vec {w}^{\prime \sigma '}$
if and only if
![]() $\vec {w}= \vec {w}'$
and
$\vec {w}= \vec {w}'$
and
![]() $\sigma = \sigma '$
.
$\sigma = \sigma '$
.
Proof. Let
![]() $\vec {v} = \vec {w}^{\sigma } = \vec {w}^{\prime \sigma '}$
. The key idea here is to change the roles of
$\vec {v} = \vec {w}^{\sigma } = \vec {w}^{\prime \sigma '}$
. The key idea here is to change the roles of
![]() $\vec {w}$
,
$\vec {w}$
,
![]() $\vec {w}'$
and
$\vec {w}'$
and
![]() $\vec {v}$
. First note that
$\vec {v}$
. First note that
Moreover, for each
![]() $n_{i} \in \mathscr {N}_{f} (\vec {w}; Q=1)$
, we have
$n_{i} \in \mathscr {N}_{f} (\vec {w}; Q=1)$
, we have
 $$ \begin{align*}\begin{aligned} d(x_{0}, x_{\beta_{i}}^{\sigma})&\le d(x_{0}, x_{\beta_{i}}) + \frac{\eta n}{40M} & (\because\ \textrm{Claim}\ 3.11) \\ &\le \frac{1}{2} d(x_{0}, x_{n})+ \frac{\eta n}{40M}- \left(D + \frac{\eta}{M}\right)n & \left(\because p_{i} \in \mathcal{N}_{f}(\vec{w}; Q = 1)\right) \\ &\le \frac{1}{2} d(x_{0}, x_{n}^{\sigma}) + \frac{3\eta n}{80M} - \left(D + \frac{\eta}{M}\right)n & (\because \textrm{Claim}\ 3.11)\\ &\le \frac{1}{2} d(x_{0}, x_{n}^{\sigma})- \left(D + \frac{0.9\eta}{M}\right)n. \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} d(x_{0}, x_{\beta_{i}}^{\sigma})&\le d(x_{0}, x_{\beta_{i}}) + \frac{\eta n}{40M} & (\because\ \textrm{Claim}\ 3.11) \\ &\le \frac{1}{2} d(x_{0}, x_{n})+ \frac{\eta n}{40M}- \left(D + \frac{\eta}{M}\right)n & \left(\because p_{i} \in \mathcal{N}_{f}(\vec{w}; Q = 1)\right) \\ &\le \frac{1}{2} d(x_{0}, x_{n}^{\sigma}) + \frac{3\eta n}{80M} - \left(D + \frac{\eta}{M}\right)n & (\because \textrm{Claim}\ 3.11)\\ &\le \frac{1}{2} d(x_{0}, x_{n}^{\sigma})- \left(D + \frac{0.9\eta}{M}\right)n. \end{aligned} \end{align*} $$
This implies
![]() $n_{i} \in \mathcal {N}_{f}(\vec {v}; Q = 0.9)$
. It follows that
$n_{i} \in \mathcal {N}_{f}(\vec {v}; Q = 0.9)$
. It follows that
Similarly,
![]() $\mathcal {N}_{f}(\vec {w}'; Q=1) \subseteq \mathcal {N}_{f} (\vec {v}; Q=0.9)$
.
$\mathcal {N}_{f}(\vec {w}'; Q=1) \subseteq \mathcal {N}_{f} (\vec {v}; Q=0.9)$
.
Thus, we are able to pick forward pivots
![]() $p_{i}(\vec {w})$
and
$p_{i}(\vec {w})$
and
![]() $p^{\prime }_{i}(\vec {w}')$
of
$p^{\prime }_{i}(\vec {w}')$
of
![]() $\vec {w}$
and
$\vec {w}$
and
![]() $\vec {w}'$
altogether for
$\vec {w}'$
altogether for
![]() $\vec {v}$
. (This will give
$\vec {v}$
. (This will give
![]() $N(\vec {v}) \le \frac {\eta n}{20 M^{2}L}$
, which is legitimate.) Then Lemma 3.10 applied to
$N(\vec {v}) \le \frac {\eta n}{20 M^{2}L}$
, which is legitimate.) Then Lemma 3.10 applied to
![]() $\vec {v} \in F_{n, f}(Q=0.9)$
yields a contradiction with
$\vec {v} \in F_{n, f}(Q=0.9)$
yields a contradiction with
![]() $\vec {w}, \vec {w}' \in G_{n}$
unless
$\vec {w}, \vec {w}' \in G_{n}$
unless
![]() $\sigma = \sigma '$
.
$\sigma = \sigma '$
.
Similar discussion also holds for
![]() $G_{n, b}$
.
$G_{n, b}$
.
3.3 Translation lengths of random isometries
We now prove the first main theorem:
Theorem A. Let G be a weakly hyperbolic group acting on a Gromov hyperbolic space X and let
![]() $\mu $
be a non-elementary probability measure on G. Then
$\mu $
be a non-elementary probability measure on G. Then
![]() $\operatorname {\mathbb {P}}$
-almost every sample path shows at least linear growth of translation lengths. More precisely, there exists a constant
$\operatorname {\mathbb {P}}$
-almost every sample path shows at least linear growth of translation lengths. More precisely, there exists a constant
![]() $\mathcal {L}>0$
such that for
$\mathcal {L}>0$
such that for
![]() $\operatorname {\mathbb {P}}$
-a.e.
$\operatorname {\mathbb {P}}$
-a.e.
![]() $(\operatorname {\omega }_{n})$
,
$(\operatorname {\omega }_{n})$
,
![]() $\tau (\operatorname {\omega }_{n}) \ge \mathcal {L}n$
for sufficiently large n.
$\tau (\operatorname {\omega }_{n}) \ge \mathcal {L}n$
for sufficiently large n.
Moreover, if
![]() $\mu $
further has finite first moment, then for
$\mu $
further has finite first moment, then for
![]() $\operatorname {\mathbb {P}}$
-a.e.
$\operatorname {\mathbb {P}}$
-a.e.
![]() $(\operatorname {\omega }_{n})$
, we have
$(\operatorname {\omega }_{n})$
, we have
where
![]() $\lambda $
is the drift of the random walk.
$\lambda $
is the drift of the random walk.
Proof. Let
![]() $n \ge 40 RM / \eta $
. By Lemma 3.7,
$n \ge 40 RM / \eta $
. By Lemma 3.7,
![]() $F_{n, f}(Q=1)$
and
$F_{n, f}(Q=1)$
and
![]() $F_{n, b}(Q=1)$
cover entire
$F_{n, b}(Q=1)$
cover entire
![]() $F_{n}$
. Consequently,
$F_{n}$
. Consequently,
![]() $G_{n, f}(Q=1)$
and
$G_{n, f}(Q=1)$
and
![]() $G_{n, b}(Q=1)$
cover
$G_{n, b}(Q=1)$
cover
![]() $G_{n}$
.
$G_{n}$
.
As in Lemma 3.15, we let
![]() $N(\vec {w})=\lfloor \frac {\eta n}{40 M^{2} L} \rfloor $
for each
$N(\vec {w})=\lfloor \frac {\eta n}{40 M^{2} L} \rfloor $
for each
![]() $\vec {w} \in G_{n, f}(Q=1)$
. Let
$\vec {w} \in G_{n, f}(Q=1)$
. Let
![]() $\mathcal {C}(\vec {w}) := \{ \vec {w}^{\sigma } : \sigma \in \{0, 1\}^{N}\}$
. Lemma 3.15 asserts that
$\mathcal {C}(\vec {w}) := \{ \vec {w}^{\sigma } : \sigma \in \{0, 1\}^{N}\}$
. Lemma 3.15 asserts that
![]() $\mathcal {C}(\vec {w})$
and
$\mathcal {C}(\vec {w})$
and
![]() $\mathcal {C}(\vec {w}')$
are disjoint for distinct elements
$\mathcal {C}(\vec {w}')$
are disjoint for distinct elements
![]() $\vec {w}, \vec {w}' \in G_{n, f}(Q=1)$
. Moreover, for each
$\vec {w}, \vec {w}' \in G_{n, f}(Q=1)$
. Moreover, for each
![]() $\vec {w} \in G_{n, f}(Q=1)$
, the conditional probability of
$\vec {w} \in G_{n, f}(Q=1)$
, the conditional probability of
![]() $\vec {w}$
in
$\vec {w}$
in
![]() $\mathcal {C}(\vec {w})$
is bounded by
$\mathcal {C}(\vec {w})$
is bounded by
![]() $P^{N}$
. Indeed, elements
$P^{N}$
. Indeed, elements
![]() $\vec {v} = (v_{i})_{i=1}^{n}$
in
$\vec {v} = (v_{i})_{i=1}^{n}$
in
![]() $\mathcal {C}(\vec {w})$
are determined by N independent choices at pivotal times, with probability
$\mathcal {C}(\vec {w})$
are determined by N independent choices at pivotal times, with probability
![]() $p_{+}$
for
$p_{+}$
for
![]() $(v_{\alpha _{i} + (j-1)}^{-1} v_{\alpha _{i} + j})_{j=1}^{L} = (a_{1}, \ldots , a_{n})$
and with probability
$(v_{\alpha _{i} + (j-1)}^{-1} v_{\alpha _{i} + j})_{j=1}^{L} = (a_{1}, \ldots , a_{n})$
and with probability
![]() $p_{-}$
for
$p_{-}$
for
![]() $(v_{\alpha _{i} + (j-1)}^{-1} v_{\alpha _{i} + j})_{j=1}^{L} = (b_{1}, \ldots , b_{n})$
. Since
$(v_{\alpha _{i} + (j-1)}^{-1} v_{\alpha _{i} + j})_{j=1}^{L} = (b_{1}, \ldots , b_{n})$
. Since
![]() $\vec {w}$
corresponds to a single outcome, its probability is at most
$\vec {w}$
corresponds to a single outcome, its probability is at most
![]() $P^{N}$
.
$P^{N}$
.
This implies that
 $$ \begin{align*}\begin{aligned} \operatorname{\mathbb{P}}((\omega_{i})_{i=1}^{n} \in G_{n, f}(Q=1)) & = \sum_{w \in G_{n, f}(Q=1)} \operatorname{\mathbb{P}}((\omega_{i})_{i=1}^{n} = \vec{w})\\ & \le P^{N} \sum_{w \in G_{n, f}(Q=1)} \operatorname{\mathbb{P}}((\omega_{i})_{i=1}^{n} \in \mathcal{C}(\vec{w})) \\ & \le P^{N}, \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} \operatorname{\mathbb{P}}((\omega_{i})_{i=1}^{n} \in G_{n, f}(Q=1)) & = \sum_{w \in G_{n, f}(Q=1)} \operatorname{\mathbb{P}}((\omega_{i})_{i=1}^{n} = \vec{w})\\ & \le P^{N} \sum_{w \in G_{n, f}(Q=1)} \operatorname{\mathbb{P}}((\omega_{i})_{i=1}^{n} \in \mathcal{C}(\vec{w})) \\ & \le P^{N}, \end{aligned}\end{align*} $$
where the disjointness of
![]() $\mathcal {C}(\vec {w})$
was used at the end. Similarly, we have
$\mathcal {C}(\vec {w})$
was used at the end. Similarly, we have
Then the Borel-Cantelli lemma guarantees that
![]() $\mathbb {P}$
-a.e. sample path
$\mathbb {P}$
-a.e. sample path
![]() $\operatorname {\omega }$
avoids
$\operatorname {\omega }$
avoids
![]() $G_{n}$
eventually. Pictorially, we have Figure 6.
$G_{n}$
eventually. Pictorially, we have Figure 6.

Figure 6 Schematic for
![]() $F_{n}$
and
$F_{n}$
and
![]() $G_{n}$
. Each colored region corresponds to
$G_{n}$
. Each colored region corresponds to
![]() $\{\operatorname {\omega } : (\operatorname {\omega }_{i})_{i=1}^{k} \in F_{k}$
for
$\{\operatorname {\omega } : (\operatorname {\omega }_{i})_{i=1}^{k} \in F_{k}$
for
![]() $k \ge n$
,
$k \ge n$
,
![]() $(\operatorname {\omega }_{i})_{i=1}^{n} = \vec {w} \in G_{n}\}$
and is copied inside
$(\operatorname {\omega }_{i})_{i=1}^{n} = \vec {w} \in G_{n}\}$
and is copied inside
![]() $\{\operatorname {\omega } : (\operatorname {\omega }_{i})_{i=1}^{k} \in F_{k}$
for
$\{\operatorname {\omega } : (\operatorname {\omega }_{i})_{i=1}^{k} \in F_{k}$
for
![]() $k \ge n\}$
by pivoting (hatched regions). Copies of distinct words in
$k \ge n\}$
by pivoting (hatched regions). Copies of distinct words in
![]() $G_{n}$
(colored in distinct colors) are disjoint. The sum of the measures of colored regions is bounded. Note that
$G_{n}$
(colored in distinct colors) are disjoint. The sum of the measures of colored regions is bounded. Note that
![]() $\{\operatorname {\omega } : (\operatorname {\omega }_{i})_{i=1}^{k} \notin F_{k}$
for some
$\{\operatorname {\omega } : (\operatorname {\omega }_{i})_{i=1}^{k} \notin F_{k}$
for some
![]() $k \ge n\}$
decreases to a measure zero set.
$k \ge n\}$
decreases to a measure zero set.
For those paths, if
![]() $\tau (\operatorname {\omega }_n) \le {1.5R \eta n \over L} < (2D - 2\eta /M)n$
happens infinitely often, then
$\tau (\operatorname {\omega }_n) \le {1.5R \eta n \over L} < (2D - 2\eta /M)n$
happens infinitely often, then
![]() $(\operatorname {\omega }_1, \ldots , \operatorname {\omega }_{n})$
should avoid
$(\operatorname {\omega }_1, \ldots , \operatorname {\omega }_{n})$
should avoid
![]() $F_n$
infinitely often. However, as mentioned before, almost every sample path avoids
$F_n$
infinitely often. However, as mentioned before, almost every sample path avoids
![]() $F_{n}$
eventually. Consequently,
$F_{n}$
eventually. Consequently,
![]() $\tau (\operatorname {\omega }_n) \ge {1.5R \eta n \over L}$
eventually holds for
$\tau (\operatorname {\omega }_n) \ge {1.5R \eta n \over L}$
eventually holds for
![]() $\operatorname {\mathbb {P}}$
-a.e.
$\operatorname {\mathbb {P}}$
-a.e.
![]() $(\operatorname {\omega }_n)$
.
$(\operatorname {\omega }_n)$
.
Now let us prove the second assertion. When
![]() $\mu $
has finite first moment, there exists a constant
$\mu $
has finite first moment, there exists a constant
![]() $0<\lambda < +\infty $
, called drift, satisfying that
$0<\lambda < +\infty $
, called drift, satisfying that
![]() $\lambda = \lim _{k \to \infty } {1 \over k}d(x_0, \operatorname {\omega }_k x_0)$
for
$\lambda = \lim _{k \to \infty } {1 \over k}d(x_0, \operatorname {\omega }_k x_0)$
for
![]() $\operatorname {\mathbb {P}}$
-a.e.
$\operatorname {\mathbb {P}}$
-a.e.
![]() $(\operatorname {\omega }_k)$
. Set a threshold
$(\operatorname {\omega }_k)$
. Set a threshold
![]() $0 < \epsilon <1$
. We slightly modify the definition of
$0 < \epsilon <1$
. We slightly modify the definition of
![]() $F_{n}$
and
$F_{n}$
and
![]() $G_{n}$
as follows:
$G_{n}$
as follows:
 $$ \begin{align*}\begin{aligned} F_{n} & := \left\{ \vec{w} : \begin{matrix} \# \mathcal{N}_{\lfloor \epsilon n/7 \rfloor, n}(\vec{w}) \ge {\eta \epsilon n \over 24L}, \,\,d(x_{0}, w_{n} x_{0}) \ge \left(1-\frac{\epsilon}{1000}\right) \lambda n,\\ d(x_{0}, w_{\lfloor \epsilon n / 7\rfloor} x_{0}) \le \frac{\epsilon \lambda n}{6} \end{matrix} \right\}\\ G_{n} & := \left\{ \vec{w} \in F_{n}: \tau(w_{n}) \le \left(2D - \frac{2\eta}{M} \right) n \right\}. \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} F_{n} & := \left\{ \vec{w} : \begin{matrix} \# \mathcal{N}_{\lfloor \epsilon n/7 \rfloor, n}(\vec{w}) \ge {\eta \epsilon n \over 24L}, \,\,d(x_{0}, w_{n} x_{0}) \ge \left(1-\frac{\epsilon}{1000}\right) \lambda n,\\ d(x_{0}, w_{\lfloor \epsilon n / 7\rfloor} x_{0}) \le \frac{\epsilon \lambda n}{6} \end{matrix} \right\}\\ G_{n} & := \left\{ \vec{w} \in F_{n}: \tau(w_{n}) \le \left(2D - \frac{2\eta}{M} \right) n \right\}. \end{aligned}\end{align*} $$
We again invoke the subadditive ergodic theorem. Theorem 3.4 asserts that for a.e. path
![]() $\operatorname {\omega }$
, there exists some
$\operatorname {\omega }$
, there exists some
![]() $t(\operatorname {\omega })$
such that for all
$t(\operatorname {\omega })$
such that for all
![]() $i> t(\operatorname {\omega })$
,
$i> t(\operatorname {\omega })$
,
-
(1)
 $W_{i} \ge 0.999\eta i$
,
$W_{i} \ge 0.999\eta i$
, -
(2)
 $d(x_{0}, \operatorname {\omega }_{i} x_{0}) \ge ( 1- \epsilon /1000) \lambda i$
,
$d(x_{0}, \operatorname {\omega }_{i} x_{0}) \ge ( 1- \epsilon /1000) \lambda i$
, -
(3)
 $d(x_{0}, \operatorname {\omega }_{i} x_{0}) \le 1.001 \lambda i$
.
$d(x_{0}, \operatorname {\omega }_{i} x_{0}) \le 1.001 \lambda i$
.
Note also that
![]() $\#N_{i, j}(\operatorname {\omega }) \ge W_{\lfloor i/ 3L \rfloor }$
for any
$\#N_{i, j}(\operatorname {\omega }) \ge W_{\lfloor i/ 3L \rfloor }$
for any
![]() $i \le j$
. Considering this, such path
$i \le j$
. Considering this, such path
![]() $\operatorname {\omega }$
will be contained in
$\operatorname {\omega }$
will be contained in
![]() $F_{n}$
for
$F_{n}$
for
![]() $n \ge 1000 (L+1)t(\operatorname {\omega })/\epsilon $
.
$n \ge 1000 (L+1)t(\operatorname {\omega })/\epsilon $
.
This time, we set
 $$ \begin{align*}\begin{aligned} D &:= 0.5(1 - \epsilon/2), \\ M &> 1 + 10R + 2d(x_{0}, w_{+} x_{0}) + 2d(x_{0}, w_{-} x_{0}) + 4L + \frac{2000 \eta}{\lambda \epsilon} + {2000\eta \over \epsilon} + {2000 \over \epsilon}. \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} D &:= 0.5(1 - \epsilon/2), \\ M &> 1 + 10R + 2d(x_{0}, w_{+} x_{0}) + 2d(x_{0}, w_{-} x_{0}) + 4L + \frac{2000 \eta}{\lambda \epsilon} + {2000\eta \over \epsilon} + {2000 \over \epsilon}. \end{aligned} \end{align*} $$
Note that Inequality 3.4 still holds. Considering this, Lemma 3.8, Lemma 3.10 and Lemma 3.15 also hold with the same proofs. The only missing step is Lemma 3.7. We now claim that
![]() $F_{n, f}(D, Q=1) = F_{n}$
. If
$F_{n, f}(D, Q=1) = F_{n}$
. If
![]() $\vec {w} \in F_{n}$
, then
$\vec {w} \in F_{n}$
, then
 $$ \begin{align} \begin{aligned} d(x_{0}, w_{\lfloor \epsilon n / 7 \rfloor}x_{0} ) & \le \frac{\epsilon \lambda n}{6} \\ & \le \frac{1}{2}\left(1-\frac{\epsilon}{1000}\right) \lambda n - \left( \frac{1}{2} (1-\epsilon/2) \lambda + \eta \cdot \frac{\epsilon\lambda}{2000 \eta}\right)n \\ & \le\frac{1}{2} d(x_{0}, w_{n}x_{0}) - \left(D + \frac{\eta}{M} \right)n. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} d(x_{0}, w_{\lfloor \epsilon n / 7 \rfloor}x_{0} ) & \le \frac{\epsilon \lambda n}{6} \\ & \le \frac{1}{2}\left(1-\frac{\epsilon}{1000}\right) \lambda n - \left( \frac{1}{2} (1-\epsilon/2) \lambda + \eta \cdot \frac{\epsilon\lambda}{2000 \eta}\right)n \\ & \le\frac{1}{2} d(x_{0}, w_{n}x_{0}) - \left(D + \frac{\eta}{M} \right)n. \end{aligned} \end{align} $$
Let us denote
![]() $\mathcal {N}_{\lfloor \epsilon n/7 \rfloor , n} (\vec {w})= \{n_{1} < \ldots < n_{k}\}$
. We have
$\mathcal {N}_{\lfloor \epsilon n/7 \rfloor , n} (\vec {w})= \{n_{1} < \ldots < n_{k}\}$
. We have
![]() $k \ge \eta \epsilon n / 24 L$
(since
$k \ge \eta \epsilon n / 24 L$
(since
![]() $\vec {w} \in F_{n}$
) and
$\vec {w} \in F_{n}$
) and
![]() $\mathcal {N}_{\lfloor \epsilon n/7 \rfloor , n}(\vec {w}) \subseteq \mathcal {N}_{\lfloor \epsilon n/7 \rfloor , \lfloor \epsilon n/7 \rfloor }(\vec {w})$
. Let
$\mathcal {N}_{\lfloor \epsilon n/7 \rfloor , n}(\vec {w}) \subseteq \mathcal {N}_{\lfloor \epsilon n/7 \rfloor , \lfloor \epsilon n/7 \rfloor }(\vec {w})$
. Let
for
![]() $i=1, \ldots , k$
and
$i=1, \ldots , k$
and
![]() $y_{2k+1} = x_{\lfloor \epsilon n / 7 \rfloor }$
. Then, Corollary 3.6 tells us that
$y_{2k+1} = x_{\lfloor \epsilon n / 7 \rfloor }$
. Then, Corollary 3.6 tells us that
for each
![]() $n_{i} \in \mathcal {N}_{\lfloor \epsilon n/7 \rfloor , n}$
. Hence, these joints contribute to
$n_{i} \in \mathcal {N}_{\lfloor \epsilon n/7 \rfloor , n}$
. Hence, these joints contribute to
![]() $\mathcal {N}_f(\vec {w})$
. We then have
$\mathcal {N}_f(\vec {w})$
. We then have
![]() $\vec {w} \in F_{n, f}$
because
$\vec {w} \in F_{n, f}$
because
Given that the lemmata still holds true, the previous argument to deduce that almost every path
![]() $\operatorname {\omega }$
does not fall into
$\operatorname {\omega }$
does not fall into
![]() $G_{n}$
infinitely often. Note also that
$G_{n}$
infinitely often. Note also that
Together with the observation that a.e. path does not avoid
![]() $F_{n}$
infinitely often, we deduce that
$F_{n}$
infinitely often, we deduce that
![]() $\liminf \frac {1}{n}\tau (\operatorname {\omega }_{n}) \ge (1-\epsilon ) \lambda $
almost surely. By setting
$\liminf \frac {1}{n}\tau (\operatorname {\omega }_{n}) \ge (1-\epsilon ) \lambda $
almost surely. By setting
![]() $\epsilon = 1/k$
and taking intersection of those events for
$\epsilon = 1/k$
and taking intersection of those events for
![]() $k \in \operatorname {\mathbb {Z}}_{>1}$
, we deduce that
$k \in \operatorname {\mathbb {Z}}_{>1}$
, we deduce that
![]() $\liminf \frac {1}{n} \tau (\operatorname {\omega }_{n}) \ge \lambda $
almost surely. Since
$\liminf \frac {1}{n} \tau (\operatorname {\omega }_{n}) \ge \lambda $
almost surely. Since
![]() $\frac {1}{n} \tau (\operatorname {\omega }_{n}) \le \frac {1}{n}d(x_{0}, \operatorname {\omega }_{n} x_{0})$
and the latter one converges to
$\frac {1}{n} \tau (\operatorname {\omega }_{n}) \le \frac {1}{n}d(x_{0}, \operatorname {\omega }_{n} x_{0})$
and the latter one converges to
![]() $\lambda $
a.s., we finally conclude that
$\lambda $
a.s., we finally conclude that
![]() $\frac {1}{n} \tau (\operatorname {\omega }_{n}) \rightarrow \lambda $
a.s.
$\frac {1}{n} \tau (\operatorname {\omega }_{n}) \rightarrow \lambda $
a.s.
4 Teichmüller space and its geometry
4.1 Basic notions
In this section, we investigate the geometry of the Teichmüller space
![]() $(X, d)$
equipped with the Teichmüller metric. Let S be a closed orientable surface of genus at least 2. Its Teichmüller space is the space of equivalence classes
$(X, d)$
equipped with the Teichmüller metric. Let S be a closed orientable surface of genus at least 2. Its Teichmüller space is the space of equivalence classes
![]() $[(f, \Sigma )]$
of an orientation preserving homeomorphism
$[(f, \Sigma )]$
of an orientation preserving homeomorphism
![]() $f : S \to \Sigma $
to a hyperbolic surface
$f : S \to \Sigma $
to a hyperbolic surface
![]() $\Sigma $
, where
$\Sigma $
, where
![]() $(f, \Sigma )$
and
$(f, \Sigma )$
and
![]() $(g, \Sigma ')$
are equivalent if there is an isometry
$(g, \Sigma ')$
are equivalent if there is an isometry
![]() $i : \Sigma \to \Sigma '$
so that
$i : \Sigma \to \Sigma '$
so that
![]() $i \circ f$
is homotopic to g. The Teichmüller space admits a metric d called the Teichmüller metric defined by
$i \circ f$
is homotopic to g. The Teichmüller space admits a metric d called the Teichmüller metric defined by
![]() $d([(f, \Sigma )], [(g, \Sigma ')]) = {1 \over 2} \inf _{\varphi } \log K_{\varphi }$
, where the infimum is taken over quasiconformal homeomorphisms
$d([(f, \Sigma )], [(g, \Sigma ')]) = {1 \over 2} \inf _{\varphi } \log K_{\varphi }$
, where the infimum is taken over quasiconformal homeomorphisms
![]() $\varphi $
with
$\varphi $
with
![]() $f = \varphi \circ g$
up to homotopy and
$f = \varphi \circ g$
up to homotopy and
![]() $K_{\varphi }$
is its quasiconformal constant. Then the mapping class group
$K_{\varphi }$
is its quasiconformal constant. Then the mapping class group
![]() $\operatorname {Mod}(S)$
of the surface acts isometrically on its Teichmüller space
$\operatorname {Mod}(S)$
of the surface acts isometrically on its Teichmüller space
![]() $X = \mathcal {T}(S)$
. We denote
$X = \mathcal {T}(S)$
. We denote
![]() $G = \operatorname {Mod}(S)$
for the rest of the paper. For details on the Teichmüller geometry, see [Reference HubbardHub06], [Reference PapadopoulosPap07], [Reference Imayoshi and TaniguchiIT92].
$G = \operatorname {Mod}(S)$
for the rest of the paper. For details on the Teichmüller geometry, see [Reference HubbardHub06], [Reference PapadopoulosPap07], [Reference Imayoshi and TaniguchiIT92].
We recall the notion of the extremal length of a curve.
Definition 4.1 (Extremal length)
For a point
![]() $x \in X$
in the Teichmüller space and an isotopy class
$x \in X$
in the Teichmüller space and an isotopy class
![]() $\alpha $
of simple closed curves on the underlying surface S, the extremal length is defined as
$\alpha $
of simple closed curves on the underlying surface S, the extremal length is defined as
 $$ \begin{align*}Ext_x(\alpha):= \sup_{\sigma \in [x]} {l_{\sigma}^2(\alpha) \over \mbox{area}(\sigma)}.\end{align*} $$
$$ \begin{align*}Ext_x(\alpha):= \sup_{\sigma \in [x]} {l_{\sigma}^2(\alpha) \over \mbox{area}(\sigma)}.\end{align*} $$
Here,
![]() $\sigma $
is a Riemannian metric in the conformal class x and
$\sigma $
is a Riemannian metric in the conformal class x and
![]() $l_{\sigma }(\alpha )$
is the length of
$l_{\sigma }(\alpha )$
is the length of
![]() $\alpha $
measured by
$\alpha $
measured by
![]() $\sigma $
.
$\sigma $
.
Kerckhoff [Reference KerckhoffKer80] characterized the Teichmüller metric in terms of the extremal length:
 $$ \begin{align*}d(x, y) = {1 \over 2} \log \sup_{\alpha \in \mathcal{C}_0(S)} {Ext_y (\alpha) \over Ext_x(\alpha)},\end{align*} $$
$$ \begin{align*}d(x, y) = {1 \over 2} \log \sup_{\alpha \in \mathcal{C}_0(S)} {Ext_y (\alpha) \over Ext_x(\alpha)},\end{align*} $$
where
![]() $\mathcal {C}_0(S)$
is a space of isotopy classes of essential simple closed curves on S.
$\mathcal {C}_0(S)$
is a space of isotopy classes of essential simple closed curves on S.
We denote the
![]() $\epsilon $
-thick part of the Teichmüller space X by
$\epsilon $
-thick part of the Teichmüller space X by
![]() $X_{\ge \epsilon }$
. That is,
$X_{\ge \epsilon }$
. That is,
![]() $X_{\ge \epsilon }$
consists of surfaces whose shortest extremal length is at least
$X_{\ge \epsilon }$
consists of surfaces whose shortest extremal length is at least
![]() $\epsilon $
. From Kerckhoff’s formula,
$\epsilon $
. From Kerckhoff’s formula,
![]() $x \in X_{\ge \epsilon }$
implies
$x \in X_{\ge \epsilon }$
implies
![]() $y \in X_{\ge \epsilon '}$
where
$y \in X_{\ge \epsilon '}$
where
![]() $\epsilon ' = \epsilon e^{-2d(x, y)}$
.
$\epsilon ' = \epsilon e^{-2d(x, y)}$
.
A geodesic segment on X refers to an isometric embedding
![]() $\Gamma : I=[a,b] \rightarrow X$
of a closed interval
$\Gamma : I=[a,b] \rightarrow X$
of a closed interval
![]() $[a, b]$
into X (i.e.,
$[a, b]$
into X (i.e.,
![]() $d_{X}(\Gamma (t_{1}), \Gamma (t_{2})) =|t_{1}-t_{2}|$
for all
$d_{X}(\Gamma (t_{1}), \Gamma (t_{2})) =|t_{1}-t_{2}|$
for all
![]() $t_{1}, t_{2} \in I$
). We make an abuse of notation: the image
$t_{1}, t_{2} \in I$
). We make an abuse of notation: the image
![]() $\Gamma ([a, b])$
of
$\Gamma ([a, b])$
of
![]() $\Gamma $
is also called the geodesic segment connecting
$\Gamma $
is also called the geodesic segment connecting
![]() $\Gamma (a)$
and
$\Gamma (a)$
and
![]() $\Gamma (b)$
and denoted by
$\Gamma (b)$
and denoted by
![]() $[\Gamma (a), \Gamma (b)]$
. Note that for each
$[\Gamma (a), \Gamma (b)]$
. Note that for each
![]() $x, y \in X$
,
$x, y \in X$
,
![]() $[x, y]$
uniquely exists by Teichmüller’s theorem. We say that a segment
$[x, y]$
uniquely exists by Teichmüller’s theorem. We say that a segment
![]() $\Gamma ' : J=[c, d]\rightarrow X$
is a subsegment of
$\Gamma ' : J=[c, d]\rightarrow X$
is a subsegment of
![]() $\Gamma : I=[a, b] \rightarrow X$
if
$\Gamma : I=[a, b] \rightarrow X$
if
![]() $\Gamma |_{J} = \Gamma '$
. In this situation, we also say that
$\Gamma |_{J} = \Gamma '$
. In this situation, we also say that
![]() $[\Gamma '(c), \Gamma '(d)]$
is a subsegment of
$[\Gamma '(c), \Gamma '(d)]$
is a subsegment of
![]() $[\Gamma (a), \Gamma (b)]$
. For
$[\Gamma (a), \Gamma (b)]$
. For
![]() $\epsilon> 0$
, we also call a segment
$\epsilon> 0$
, we also call a segment
![]() $\epsilon $
-thick if it is contained in the
$\epsilon $
-thick if it is contained in the
![]() $\epsilon $
-thick part.
$\epsilon $
-thick part.
For subsets
![]() $A, B \subseteq X$
and
$A, B \subseteq X$
and
![]() $R> 0$
, we define
$R> 0$
, we define
 $$ \begin{align*} \begin{aligned} N_{R}(A) &:= \{y \in X : \textrm{there exists}\,\, x \in A \,\,\textrm{such that}\,\, d(x, y) < R\},\\ d(A, B) &:= \inf\{ d(x, y) : x \in A,\,\, y \in B\},\mbox{ and}\\ d_{H}(A, B) & := \inf\{R> 0: A \subseteq N_{R}(B)\,\,\textrm{and}\,\, B \subseteq N_{R}(A) \}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} N_{R}(A) &:= \{y \in X : \textrm{there exists}\,\, x \in A \,\,\textrm{such that}\,\, d(x, y) < R\},\\ d(A, B) &:= \inf\{ d(x, y) : x \in A,\,\, y \in B\},\mbox{ and}\\ d_{H}(A, B) & := \inf\{R> 0: A \subseteq N_{R}(B)\,\,\textrm{and}\,\, B \subseteq N_{R}(A) \}. \end{aligned} \end{align*} $$
4.2 Curve complex
We temporarily digress to the relationship between the Teichmüller geometry and the curve complex. The payback for this is Theorem 4.3, which guarantees the existence of persistent joints.
The curve complex
![]() $Y = Y(S)$
of a surface S is a simplicial complex whose vertices are isotopy classes of essential simple closed curves and each
$Y = Y(S)$
of a surface S is a simplicial complex whose vertices are isotopy classes of essential simple closed curves and each
![]() $(k+1)$
-simplex corresponds to
$(k+1)$
-simplex corresponds to
![]() $k+1$
vertices represented by disjoint simple closed curves. The curve complex was first introduced by Harvey [Reference HarveyHar81], and it endows with a natural metric that each edge has a length
$k+1$
vertices represented by disjoint simple closed curves. The curve complex was first introduced by Harvey [Reference HarveyHar81], and it endows with a natural metric that each edge has a length
![]() $1$
.
$1$
.
There exists a projection
![]() $\pi : X \rightarrow Y$
from Teichmüller space to the curve complex that associates each surface
$\pi : X \rightarrow Y$
from Teichmüller space to the curve complex that associates each surface
![]() $x \in X$
with the curve
$x \in X$
with the curve
![]() $\pi (x)$
with the shortest extremal length. Masur and Minsky [Reference Masur and MinskyMM99] showed that
$\pi (x)$
with the shortest extremal length. Masur and Minsky [Reference Masur and MinskyMM99] showed that
![]() $\pi $
is coarsely
$\pi $
is coarsely
![]() $\operatorname {Mod}(S)$
-equivariant and coarsely Lipschitz. That is, there exists a constant
$\operatorname {Mod}(S)$
-equivariant and coarsely Lipschitz. That is, there exists a constant
![]() $A> 0$
such that
$A> 0$
such that
for each
![]() $x, y \in X$
and
$x, y \in X$
and
![]() $g \in \operatorname {Mod}(S)$
. Furthermore, there exists a constant
$g \in \operatorname {Mod}(S)$
. Furthermore, there exists a constant
![]() $K> 0$
such that every geodesic
$K> 0$
such that every geodesic
![]() $\gamma $
in the Teichmüller space X descends to a K-quasi-geodesic
$\gamma $
in the Teichmüller space X descends to a K-quasi-geodesic
![]() $\pi \circ \gamma $
in the curve complex
$\pi \circ \gamma $
in the curve complex
![]() $Y(S)$
up to reparametrization. Finally, since
$Y(S)$
up to reparametrization. Finally, since
![]() $Y(S)$
is Gromov hyperbolic, the following assertions hold for some
$Y(S)$
is Gromov hyperbolic, the following assertions hold for some
![]() $A'> 0$
.
$A'> 0$
.
-
(1) If
 $\gamma $
,
$\gamma $
,
 $\eta $
are K-quasi-geodesics with the same endpoints, then
$\eta $
are K-quasi-geodesics with the same endpoints, then
 $d_{H}(\gamma , \eta ) < A'$
.
$d_{H}(\gamma , \eta ) < A'$
. -
(2) Given
 $x, y, z\in Y(S)$
,
$x, y, z\in Y(S)$
,
 $d(y, [x, z]) \ge d(x, y) - (y, z)_{x} - A'$
.
$d(y, [x, z]) \ge d(x, y) - (y, z)_{x} - A'$
.
Thurston [Reference ThurstonThu88] compactified the Teichmüller space by introducing
![]() $\mathcal {PMF}$
, the projective space of measured foliations, as the boundary of the Teichmüller space. Pseudo-Anosov maps exhibit source-sink dynamics on this compactified Teichmüller space as follows. Let
$\mathcal {PMF}$
, the projective space of measured foliations, as the boundary of the Teichmüller space. Pseudo-Anosov maps exhibit source-sink dynamics on this compactified Teichmüller space as follows. Let
![]() $\mathcal {UE} \subseteq \mathcal {PMF}$
be the set of uniquely ergodic measured foliations. Then for each pseudo-Anosov
$\mathcal {UE} \subseteq \mathcal {PMF}$
be the set of uniquely ergodic measured foliations. Then for each pseudo-Anosov
![]() $\phi $
, there exists distinct foliations
$\phi $
, there exists distinct foliations
![]() $\phi ^{+\infty }, \phi ^{-\infty } \in \mathcal {UE}$
such that
$\phi ^{+\infty }, \phi ^{-\infty } \in \mathcal {UE}$
such that
![]() $\lim _{n \rightarrow +\infty } \phi ^{ \pm n} x = \phi ^{\pm \infty }$
for any
$\lim _{n \rightarrow +\infty } \phi ^{ \pm n} x = \phi ^{\pm \infty }$
for any
![]() $x \in X$
.
$x \in X$
.
Moreover, Kaimanovich and Masur [Reference Kaimanovich and MasurKM96] proved the boundary convergence of random walks on the Teichmüller space. More precisely, for non-elementary random walks on mapping class groups, almost every orbit on the Teichmüller space converges to
![]() $\mathcal {UE} \subset \mathcal {PMF}$
, the space of uniquely ergodic measured foliations.
$\mathcal {UE} \subset \mathcal {PMF}$
, the space of uniquely ergodic measured foliations.
Klarreich [Reference KlarreichKla22] and Hamenstädt [Reference HamenstädtHam06] also proved that the boundary of the curve complex can be identified with
![]() $\widetilde {\mathcal {MIN}}$
, the space of equivalence classes of minimal topological foliations. As such, we can define a map
$\widetilde {\mathcal {MIN}}$
, the space of equivalence classes of minimal topological foliations. As such, we can define a map
![]() $\pi _{\infty } : \operatorname {\mathcal {UE}}\to \widetilde {\mathcal {MIN}}$
which forgets the measure structure and quotients by topological equivalence. This map
$\pi _{\infty } : \operatorname {\mathcal {UE}}\to \widetilde {\mathcal {MIN}}$
which forgets the measure structure and quotients by topological equivalence. This map
![]() $\pi _{\infty }$
is injective, and further, if a sequence
$\pi _{\infty }$
is injective, and further, if a sequence
![]() $x_{n} \in X$
converges to a point
$x_{n} \in X$
converges to a point
![]() $x_{\infty } \in \operatorname {\mathcal {UE}}$
, then the corresponding
$x_{\infty } \in \operatorname {\mathcal {UE}}$
, then the corresponding
![]() $\pi (x_{n})$
converges to a point
$\pi (x_{n})$
converges to a point
![]() $\pi _{\infty }(x_{\infty })$
.
$\pi _{\infty }(x_{\infty })$
.
We now observe that two sequences on Teichmüller space diverge from each other if they are heading to distinct uniquely ergodic foliations.
Proposition 4.2. Let
![]() $\phi $
be a pseudo-Anosov mapping class and
$\phi $
be a pseudo-Anosov mapping class and
![]() $\{z_{k}\}_{k \ge 0}$
be a sequence in X that converges to a uniquely ergodic foliation
$\{z_{k}\}_{k \ge 0}$
be a sequence in X that converges to a uniquely ergodic foliation
![]() $\xi $
other than
$\xi $
other than
![]() $\phi ^{+\infty }$
. Then for each
$\phi ^{+\infty }$
. Then for each
![]() $C>0$
, there exists
$C>0$
, there exists
![]() $F=F(C, \phi , \{z_{k}\}_{k})>0$
such that
$F=F(C, \phi , \{z_{k}\}_{k})>0$
such that
![]() $d(\phi ^{m} x_{0}, [x_{0}, z_{k}])> C$
for all
$d(\phi ^{m} x_{0}, [x_{0}, z_{k}])> C$
for all
![]() $k \ge 0$
and
$k \ge 0$
and
![]() $m \ge F$
.
$m \ge F$
.
Proof. Since
![]() $\{z_{k}\}_{k}$
and
$\{z_{k}\}_{k}$
and
![]() $\{\phi ^{n}x_{0}\}_{n}$
are both heading to points in
$\{\phi ^{n}x_{0}\}_{n}$
are both heading to points in
![]() $\operatorname {\mathcal {UE}}$
, we can descend them to the curve complex;
$\operatorname {\mathcal {UE}}$
, we can descend them to the curve complex;
![]() $\pi (z_{k}) \rightarrow \pi _{\infty }(\xi )$
and
$\pi (z_{k}) \rightarrow \pi _{\infty }(\xi )$
and
![]() $\pi (\phi ^{n}x_{0}) \rightarrow \pi _{\infty }(\phi ^{+\infty })$
. Since
$\pi (\phi ^{n}x_{0}) \rightarrow \pi _{\infty }(\phi ^{+\infty })$
. Since
![]() $\xi $
and
$\xi $
and
![]() $\phi ^{+\infty }$
are distinct, we have
$\phi ^{+\infty }$
are distinct, we have
Take F such that
for any
![]() $m \ge F$
. Suppose to the contrary that
$m \ge F$
. Suppose to the contrary that
![]() $d(\phi ^{m} x_{0}, [x_{0}, z_{k}]) \le C$
for some
$d(\phi ^{m} x_{0}, [x_{0}, z_{k}]) \le C$
for some
![]() $m \ge F$
and
$m \ge F$
and
![]() $k \ge 0$
. Let
$k \ge 0$
. Let
![]() $x^{\dagger } \in [x_{0}, z_{k}]$
be the closest point to
$x^{\dagger } \in [x_{0}, z_{k}]$
be the closest point to
![]() $\phi ^{m}x_{0}$
.
$\phi ^{m}x_{0}$
.
Note that
![]() $[\pi (x_{0}), \pi (z_{k})]$
and
$[\pi (x_{0}), \pi (z_{k})]$
and
![]() $\pi ([x_{0}, z_{k}])$
are (unparametrized) K-quasi-geodesics on
$\pi ([x_{0}, z_{k}])$
are (unparametrized) K-quasi-geodesics on
![]() $Y(S)$
with the same endpoints. Hence, we have
$Y(S)$
with the same endpoints. Hence, we have
Moreover, since the projection
![]() $\pi $
is coarsely Lipschitz, we have
$\pi $
is coarsely Lipschitz, we have
Combining these yields
 $$ \begin{align*}\begin{aligned} d([\pi(x_{0}), \pi(z_{k})], \pi(\phi^{m}x_{0})) &\le d_{H}([\pi(x_{0}), \pi(z_{k})], \pi([x_{0}, z_{k}])) + d(\pi(x^{\dagger}), \pi(\phi^{m}x_{0})) \\ &\le A' + A (C+ 1). \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} d([\pi(x_{0}), \pi(z_{k})], \pi(\phi^{m}x_{0})) &\le d_{H}([\pi(x_{0}), \pi(z_{k})], \pi([x_{0}, z_{k}])) + d(\pi(x^{\dagger}), \pi(\phi^{m}x_{0})) \\ &\le A' + A (C+ 1). \end{aligned} \end{align*} $$
Meanwhile, we also have
 $$ \begin{align*}\begin{aligned} d([\pi(x_{0}), \pi(z_{k})], \pi(\phi^{m}x_{0})) &\ge d(\pi(x_{0}), \pi(\phi^{m}x_{0})) - (\pi(\phi^{m}x_{0}), \pi(z_{k}))_{\pi(x_{0})} - A' \\ &> (P + 2A' + A (C + 1))- P - A'\\ &= A' + A(C+ 1), \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} d([\pi(x_{0}), \pi(z_{k})], \pi(\phi^{m}x_{0})) &\ge d(\pi(x_{0}), \pi(\phi^{m}x_{0})) - (\pi(\phi^{m}x_{0}), \pi(z_{k}))_{\pi(x_{0})} - A' \\ &> (P + 2A' + A (C + 1))- P - A'\\ &= A' + A(C+ 1), \end{aligned} \end{align*} $$
a contradiction.
Proposition 4.2 leads to the following probabilistic observation. Recall that
![]() $\operatorname {\omega }$
is a non-elementary random walk on the mapping class group.
$\operatorname {\omega }$
is a non-elementary random walk on the mapping class group.
Theorem 4.3. Let
![]() $\phi $
be a pseudo-Anosov mapping class. Then for each
$\phi $
be a pseudo-Anosov mapping class. Then for each
![]() $C>0$
, there exists a constant
$C>0$
, there exists a constant
![]() $F = F(C, \phi )> 0$
such that
$F = F(C, \phi )> 0$
such that
 $$ \begin{align*} \operatorname{\mathbb{P}}\left( (\operatorname{\omega}_{n})_{n \in \operatorname{\mathbb{Z}}} : \begin{array}{c} \exists m, n \in \operatorname{\mathbb{Z}}\ \text{such that}\ |m| \ge F\ \text{and} \\ d(\phi^{m} x_{0}, [x_{0}, \operatorname{\omega}_{n} x_{0}]) <C \end{array}\right) < 1. \end{align*} $$
$$ \begin{align*} \operatorname{\mathbb{P}}\left( (\operatorname{\omega}_{n})_{n \in \operatorname{\mathbb{Z}}} : \begin{array}{c} \exists m, n \in \operatorname{\mathbb{Z}}\ \text{such that}\ |m| \ge F\ \text{and} \\ d(\phi^{m} x_{0}, [x_{0}, \operatorname{\omega}_{n} x_{0}]) <C \end{array}\right) < 1. \end{align*} $$
Proof. Suppose not. Then for each N, for almost every sample path
![]() $\operatorname {\omega } =(\operatorname {\omega }_{i})_{i}$
there exists
$\operatorname {\omega } =(\operatorname {\omega }_{i})_{i}$
there exists
![]() $m, n \in \operatorname {\mathbb {Z}}$
such that
$m, n \in \operatorname {\mathbb {Z}}$
such that
![]() $|m| \ge N$
and
$|m| \ge N$
and
![]() $d(\phi ^{m} x_{0}, [x_{0}, \operatorname {\omega }_{n} x_{0}]) <C$
. Taking intersection of these events, we deduce that
$d(\phi ^{m} x_{0}, [x_{0}, \operatorname {\omega }_{n} x_{0}]) <C$
. Taking intersection of these events, we deduce that
 $$ \begin{align} \operatorname{\mathbb{P}}\left( \mathcal{E} := \left\{(\operatorname{\omega}_{n})_{n \in \operatorname{\mathbb{Z}}} : \begin{array}{c} \exists (n_{i}), (m_{i})\ \textrm{such that}\ \lim_{i \rightarrow \infty} |m_{i}| = +\infty\ \textrm{and} \\ d(\phi^{m_{i}} x_{0}, [x_{0}, \operatorname{\omega}_{n_{i}}x_{0}]) < C\end{array}\right\}\right) =1. \end{align} $$
$$ \begin{align} \operatorname{\mathbb{P}}\left( \mathcal{E} := \left\{(\operatorname{\omega}_{n})_{n \in \operatorname{\mathbb{Z}}} : \begin{array}{c} \exists (n_{i}), (m_{i})\ \textrm{such that}\ \lim_{i \rightarrow \infty} |m_{i}| = +\infty\ \textrm{and} \\ d(\phi^{m_{i}} x_{0}, [x_{0}, \operatorname{\omega}_{n_{i}}x_{0}]) < C\end{array}\right\}\right) =1. \end{align} $$
Meanwhile, recall the result of Kaimanovich and Masur that a.e. path
![]() $\operatorname {\omega }$
have boundary points
$\operatorname {\omega }$
have boundary points
![]() $\xi ^{+}(\operatorname {\omega }), \xi ^{-}(\operatorname {\omega }) \in \operatorname {\mathcal {UE}}$
such that
$\xi ^{+}(\operatorname {\omega }), \xi ^{-}(\operatorname {\omega }) \in \operatorname {\mathcal {UE}}$
such that
![]() $\lim _{n \rightarrow \pm \infty } \operatorname {\omega }_{n} x_{0} = \xi ^{\pm }(\operatorname {\omega })$
. Since the forward and the backward stationary measure does not have atoms, we have
$\lim _{n \rightarrow \pm \infty } \operatorname {\omega }_{n} x_{0} = \xi ^{\pm }(\operatorname {\omega })$
. Since the forward and the backward stationary measure does not have atoms, we have
Finally, Proposition 4.2 tells us that
![]() $\mathcal {E} \cap \mathcal {E}' = \emptyset $
. This implies that
$\mathcal {E} \cap \mathcal {E}' = \emptyset $
. This implies that
![]() $\operatorname {\mathbb {P}}(\mathcal {E} \cup \mathcal {E}') = \operatorname {\mathbb {P}}(\mathcal {E}) + \operatorname {\mathbb {P}}(\mathcal {E}') = 2> 1$
, a contradiction.
$\operatorname {\mathbb {P}}(\mathcal {E} \cup \mathcal {E}') = \operatorname {\mathbb {P}}(\mathcal {E}) + \operatorname {\mathbb {P}}(\mathcal {E}') = 2> 1$
, a contradiction.
4.3 Fellow traveling
Let
![]() $\gamma : [0, L] \rightarrow X$
and
$\gamma : [0, L] \rightarrow X$
and
![]() $\gamma ' : [0, L'] \rightarrow X$
be paths on X. We say that
$\gamma ' : [0, L'] \rightarrow X$
be paths on X. We say that
![]() $\gamma $
and
$\gamma $
and
![]() $\gamma '\ \epsilon $
-fellow travel if
$\gamma '\ \epsilon $
-fellow travel if
![]() $d(\gamma (kL), \gamma '(kL')) < \epsilon $
for each
$d(\gamma (kL), \gamma '(kL')) < \epsilon $
for each
![]() $0 \le k \le 1$
. We remark that we always stick to the arclength parametrization when discussing geodesics on X. The following is a direct observation.
$0 \le k \le 1$
. We remark that we always stick to the arclength parametrization when discussing geodesics on X. The following is a direct observation.
Lemma 4.4. Let
![]() $\gamma ^{(i)} : [0, L_{i}] \rightarrow X$
be arcs on X for
$\gamma ^{(i)} : [0, L_{i}] \rightarrow X$
be arcs on X for
![]() $i = 1, 2, 3$
. Suppose that
$i = 1, 2, 3$
. Suppose that
![]() $\gamma ^{(1)}$
and
$\gamma ^{(1)}$
and
![]() $\gamma ^{(2)}\ \epsilon $
-fellow travel, and
$\gamma ^{(2)}\ \epsilon $
-fellow travel, and
![]() $\gamma ^{(2)}$
and
$\gamma ^{(2)}$
and
![]() $\gamma ^{(3)}\ \epsilon '$
-fellow travel. Then
$\gamma ^{(3)}\ \epsilon '$
-fellow travel. Then
-
(1)
 $\gamma ^{(1)}|_{[kL_{1}, k'L_{1}]}$
and
$\gamma ^{(1)}|_{[kL_{1}, k'L_{1}]}$
and
 $\gamma ^{(2)}|_{[kL_{2}, k'L_{2}]}\ \epsilon $
-fellow travel for each
$\gamma ^{(2)}|_{[kL_{2}, k'L_{2}]}\ \epsilon $
-fellow travel for each
 $0 \le k \le k'\le 1$
. In particular, any initial (terminal, resp.) subarc of
$0 \le k \le k'\le 1$
. In particular, any initial (terminal, resp.) subarc of
 $\gamma _{1}\ \epsilon $
-fellow travel with an initial (terminal, resp.) subarc of
$\gamma _{1}\ \epsilon $
-fellow travel with an initial (terminal, resp.) subarc of
 $\gamma _{2}$
.
$\gamma _{2}$
. -
(2)
 $\gamma _{1}$
and
$\gamma _{1}$
and
 $\gamma _{3}\ (\epsilon +\epsilon ')$
-fellow travel.
$\gamma _{3}\ (\epsilon +\epsilon ')$
-fellow travel.
In Gromov hyperbolic spaces, two geodesics fellow travel if their endpoints are pairwise near. In contrast, such geodesics in Teichmüller spaces need not fellow travel since Teichmüller spaces are not Gromov hyperbolic in general. Indeed, Rafi [Reference RafiRaf14] presented examples of pairs of geodesics whose endpoints are pairwise near while they are not fellow traveling with a uniform constant. Nonetheless, Rafi also proved the fellow traveling phenomenon of geodesics with near endpoints, given that the endpoints are lying on an
![]() $\epsilon $
-thick part.
$\epsilon $
-thick part.
Theorem 4.5 [Reference RafiRaf14, Theorem 7.1]
There exists a constant
![]() $\mathscr {B}_{0}(\epsilon )$
satisfying the following. For
$\mathscr {B}_{0}(\epsilon )$
satisfying the following. For
![]() $x, x', y, y'\in X_{\ge \epsilon }$
such that
$x, x', y, y'\in X_{\ge \epsilon }$
such that
![]() $[x, y]$
and
$[x, y]$
and
![]() $[x', y']\ \mathscr {B}_{0}(\epsilon )$
-fellow travel.
$[x', y']\ \mathscr {B}_{0}(\epsilon )$
-fellow travel.
From this, one can also see the following.
Corollary 4.6. For each
![]() $C>0$
, there exists a constant
$C>0$
, there exists a constant
![]() $\mathscr {B}(\epsilon , C)> C$
satisfying the following. For all
$\mathscr {B}(\epsilon , C)> C$
satisfying the following. For all
![]() $x, y \in X_{\ge \epsilon }$
and all
$x, y \in X_{\ge \epsilon }$
and all
![]() $x', y' \in X$
such that
$x', y' \in X$
such that
![]() $[x, y]$
and
$[x, y]$
and
![]() $[x', y']\ \mathscr {B}(\epsilon , C)$
-fellow travel.
$[x', y']\ \mathscr {B}(\epsilon , C)$
-fellow travel.
Proof. Let
![]() $\{x_{t}\}$
(
$\{x_{t}\}$
(
![]() $\{y_{t}\}$
, resp.) be a segment connecting x and
$\{y_{t}\}$
, resp.) be a segment connecting x and
![]() $x'$
(y and
$x'$
(y and
![]() $y'$
, resp.) with speed less than 1 and
$y'$
, resp.) with speed less than 1 and
![]() $x_{0} = x$
,
$x_{0} = x$
,
![]() $x_{C} = x'$
,
$x_{C} = x'$
,
![]() $y_{0}= y$
and
$y_{0}= y$
and
![]() $y_{C} = y'$
. Then each of
$y_{C} = y'$
. Then each of
![]() $x_{t}$
,
$x_{t}$
,
![]() $y_{t}$
is
$y_{t}$
is
![]() $\epsilon e^{-2t}$
-thick. Thus,
$\epsilon e^{-2t}$
-thick. Thus,
![]() $[x_{t}, y_{t}]$
and
$[x_{t}, y_{t}]$
and
![]() $[x_{t+1}, y_{t+1}]\ \mathscr {B}_{0}(\epsilon e^{-2(t+1)})$
-fellow travel. This implies that
$[x_{t+1}, y_{t+1}]\ \mathscr {B}_{0}(\epsilon e^{-2(t+1)})$
-fellow travel. This implies that
![]() $[x, y]$
and
$[x, y]$
and
![]() $[x', y']\ (\sum _{t=1}^{\lceil C \rceil } \mathscr {B}_{0}(\epsilon e^{-2t}))$
-fellow travel.
$[x', y']\ (\sum _{t=1}^{\lceil C \rceil } \mathscr {B}_{0}(\epsilon e^{-2t}))$
-fellow travel.
Rafi also proved that geodesic triangles in a thick part of the Teichmüller space are thin.
Theorem 4.7 [Reference RafiRaf14, Theorem 8.1]
There exist constants
![]() $\mathscr {C}_{0}(\epsilon )$
and
$\mathscr {C}_{0}(\epsilon )$
and
![]() $\mathscr {D}_{0}(\epsilon )$
such that the following holds. Let
$\mathscr {D}_{0}(\epsilon )$
such that the following holds. Let
![]() $x, y, z \in X_{\ge \epsilon }$
and suppose that the geodesic
$x, y, z \in X_{\ge \epsilon }$
and suppose that the geodesic
![]() $[x, y]$
contains a segment
$[x, y]$
contains a segment
![]() $\gamma \subseteq X_{\ge \epsilon }$
of length at least
$\gamma \subseteq X_{\ge \epsilon }$
of length at least
![]() $\mathscr {C}_{0}(\epsilon )$
. Then there exists a point
$\mathscr {C}_{0}(\epsilon )$
. Then there exists a point
![]() $w\in \gamma $
such that
$w\in \gamma $
such that
From now on, we fix a point
![]() $x_0 \in X$
as the basepoint. Since the random walk
$x_0 \in X$
as the basepoint. Since the random walk
![]() $\operatorname {\omega }$
is generated by a non-elementary probability measure
$\operatorname {\omega }$
is generated by a non-elementary probability measure
![]() $\mu $
, there exist two independent pseudo-Anosovs
$\mu $
, there exist two independent pseudo-Anosovs
![]() $\phi _{+}$
,
$\phi _{+}$
,
![]() $\phi _{-}$
in
$\phi _{-}$
in
![]() $\langle \langle \operatorname {supp} \mu \rangle \rangle $
, the subsemigroup generated by the support of
$\langle \langle \operatorname {supp} \mu \rangle \rangle $
, the subsemigroup generated by the support of
![]() $\mu $
. By taking suitable powers, we may assume that they are made of equal numbers of elements in
$\mu $
. By taking suitable powers, we may assume that they are made of equal numbers of elements in
![]() $\operatorname {supp} \mu $
.
$\operatorname {supp} \mu $
.
Let
![]() $\Gamma (\phi _{\pm })$
be the invariant axis of
$\Gamma (\phi _{\pm })$
be the invariant axis of
![]() $\phi _{\pm }$
on X, respectively. We fix points
$\phi _{\pm }$
on X, respectively. We fix points
![]() $y_{+} \in \Gamma (\phi _{+})$
and
$y_{+} \in \Gamma (\phi _{+})$
and
![]() $y_{-} \in \Gamma (\phi _{-})$
. We also let
$y_{-} \in \Gamma (\phi _{-})$
. We also let
![]() $\tau _{\pm }$
be the translation length of
$\tau _{\pm }$
be the translation length of
![]() $\phi _{\pm }$
on X, respectively.
$\phi _{\pm }$
on X, respectively.
Lemma 4.8. There exists
![]() $\mathscr {M}, \epsilon> 0$
such that the following holds. Let
$\mathscr {M}, \epsilon> 0$
such that the following holds. Let
![]() $\phi \in \{\phi _{+}, \phi _{-}\}$
and
$\phi \in \{\phi _{+}, \phi _{-}\}$
and
![]() $n \le m$
. Then
$n \le m$
. Then
-
(1)
 $[\phi ^{n} x_{0}, \phi ^{m} x_{0}]$
is
$[\phi ^{n} x_{0}, \phi ^{m} x_{0}]$
is
 $\epsilon $
-thick, and
$\epsilon $
-thick, and -
(2)
 $\{\phi ^{i} x_{0} : n \le i \le m\}$
is contained in the
$\{\phi ^{i} x_{0} : n \le i \le m\}$
is contained in the
 $\mathscr {M}$
-neighborhood of
$\mathscr {M}$
-neighborhood of
 $[\phi ^{n} x_{0}, \phi ^{m} x_{0}]$
.
$[\phi ^{n} x_{0}, \phi ^{m} x_{0}]$
.
Proof. Let us discuss the case for
![]() $\phi = \phi _{+}$
. Let
$\phi = \phi _{+}$
. Let
![]() $\epsilon _{0}> 0$
be such that
$\epsilon _{0}> 0$
be such that
![]() $x_{0}, y_{+}$
are
$x_{0}, y_{+}$
are
![]() $\epsilon _{0}$
-thick.
$\epsilon _{0}$
-thick.
First,
![]() $\{\phi _{+}^{i} x_{0} : n \le i \le m \}$
and
$\{\phi _{+}^{i} x_{0} : n \le i \le m \}$
and
![]() $\{\phi _{+}^{i} y_{+} : n \le i \le m\}$
are within Hausdorff distance
$\{\phi _{+}^{i} y_{+} : n \le i \le m\}$
are within Hausdorff distance
![]() $d(x_{0}, y_{+})$
. Moreover,
$d(x_{0}, y_{+})$
. Moreover,
![]() $\{\phi _{+}^{i} y_{+} : n \le i \le m\}$
periodically appear on the Teichmüller geodesic
$\{\phi _{+}^{i} y_{+} : n \le i \le m\}$
periodically appear on the Teichmüller geodesic
![]() $[\phi _{+}^{n} y_{+}, \phi _{+}^{m} y_{+}]$
with period
$[\phi _{+}^{n} y_{+}, \phi _{+}^{m} y_{+}]$
with period
![]() $\tau _{+}$
. Hence, they are within Hausdorff distance
$\tau _{+}$
. Hence, they are within Hausdorff distance
![]() $\tau _{+}$
, and
$\tau _{+}$
, and
![]() $[\phi _{+}^{n} y_{+}, \phi _{+}^{m} y_{+}]$
is
$[\phi _{+}^{n} y_{+}, \phi _{+}^{m} y_{+}]$
is
![]() $\epsilon _{0} e^{-2\tau _{+}}$
-thick.
$\epsilon _{0} e^{-2\tau _{+}}$
-thick.
Finally, note that
![]() $\phi _{+}^{n} y_{+}, \phi _{+}^{m} y_{+}$
are
$\phi _{+}^{n} y_{+}, \phi _{+}^{m} y_{+}$
are
![]() $\epsilon _{0}$
-thick and
$\epsilon _{0}$
-thick and
![]() $d(\phi _{+}^{n} y_{+}, \phi _{+}^{n} x_{0}), d(\phi _{+}^{m} y_{+}, \phi _{+}^{m} x_{0}) < d(x_{0}, y_{+})$
. Corollary 4.6 then tells us that the Hausdorff distance between
$d(\phi _{+}^{n} y_{+}, \phi _{+}^{n} x_{0}), d(\phi _{+}^{m} y_{+}, \phi _{+}^{m} x_{0}) < d(x_{0}, y_{+})$
. Corollary 4.6 then tells us that the Hausdorff distance between
![]() $[\phi _{+}^{n} y_{+}, \phi _{+}^{m} y_{+}]$
and
$[\phi _{+}^{n} y_{+}, \phi _{+}^{m} y_{+}]$
and
![]() $[\phi _{+}^{n} x_{0}, \phi _{+}^{m} x_{0}]$
is bounded by
$[\phi _{+}^{n} x_{0}, \phi _{+}^{m} x_{0}]$
is bounded by
![]() $\mathscr {B}(\epsilon _{0}, d(x_{0}, y_{+}))$
.
$\mathscr {B}(\epsilon _{0}, d(x_{0}, y_{+}))$
.
Remark 4.9. We have actually proved something stronger, namely, that the Hausdorff distance between
![]() $[\phi ^{n} x_{0}, \phi ^{m} x_{0}]$
and
$[\phi ^{n} x_{0}, \phi ^{m} x_{0}]$
and
![]() $\{\phi ^{i} x_{0} : n \le i \le m\}$
is bounded by
$\{\phi ^{i} x_{0} : n \le i \le m\}$
is bounded by
![]() $\mathscr {M}$
. We stick to the weaker conclusion as in Lemma 4.8 since it still holds true after replacing
$\mathscr {M}$
. We stick to the weaker conclusion as in Lemma 4.8 since it still holds true after replacing
![]() $\phi _{\pm }$
with their powers.
$\phi _{\pm }$
with their powers.
Lemma 4.10. For each
![]() $C> 0$
, there exists a constant
$C> 0$
, there exists a constant
![]() $\mathscr {G}(C)>0$
such that
$\mathscr {G}(C)>0$
such that
![]() $d(\phi _{+}^{k} y_{+}, \phi _{-}^{m} y_{-}) \le C$
implies
$d(\phi _{+}^{k} y_{+}, \phi _{-}^{m} y_{-}) \le C$
implies
![]() $\max (|k|, |m|) \le \mathscr {G}(C)$
.
$\max (|k|, |m|) \le \mathscr {G}(C)$
.
Proof. Suppose not. Without loss of generality, for each
![]() $i \in \operatorname {\mathbb {Z}}_{> 0}$
, let
$i \in \operatorname {\mathbb {Z}}_{> 0}$
, let
![]() $k_{i}, m_{i} \in \operatorname {\mathbb {Z}}$
be such that
$k_{i}, m_{i} \in \operatorname {\mathbb {Z}}$
be such that
![]() $|k_{i}|> i$
and
$|k_{i}|> i$
and
![]() $d(\phi _{+}^{k_{i}} y_{+}, \phi _{-}^{m_{i}} y_{-})\le C$
. Note that
$d(\phi _{+}^{k_{i}} y_{+}, \phi _{-}^{m_{i}} y_{-})\le C$
. Note that
tends to infinity. Since
![]() $d(\phi _{+}^{k_{i}}y_{+}, \phi _{-}^{m_{i}}y_{-}) < C$
,
$d(\phi _{+}^{k_{i}}y_{+}, \phi _{-}^{m_{i}}y_{-}) < C$
,
![]() $d(x_{0}, \phi _{-}^{m_{i}} y_{-})$
also tends to infinity. Possibly after passing to subsequences, this implies that
$d(x_{0}, \phi _{-}^{m_{i}} y_{-})$
also tends to infinity. Possibly after passing to subsequences, this implies that
![]() $\phi _{+}^{k_{i}} y_{+}$
approaches an endpoint of
$\phi _{+}^{k_{i}} y_{+}$
approaches an endpoint of
![]() $\Gamma (\phi _{+})$
and
$\Gamma (\phi _{+})$
and
![]() $\phi _{-}^{m_{i}} y_{-}$
approaches an endpoint of
$\phi _{-}^{m_{i}} y_{-}$
approaches an endpoint of
![]() $\Gamma (\phi _{-})$
. Since
$\Gamma (\phi _{-})$
. Since
![]() $d(\phi _{+}^{k_{i}}y_+, \phi _{-}^{m_{i}}y_- )$
is bounded, this implies that those endpoints are identical ([Reference Kaimanovich and MasurKM96, Lemma 1.4.2]); this contradicts the independence of
$d(\phi _{+}^{k_{i}}y_+, \phi _{-}^{m_{i}}y_- )$
is bounded, this implies that those endpoints are identical ([Reference Kaimanovich and MasurKM96, Lemma 1.4.2]); this contradicts the independence of
![]() $\phi _{+}$
and
$\phi _{+}$
and
![]() $\phi _{-}$
.
$\phi _{-}$
.
Lemma 4.11. There exists
![]() $C_{Grom}>0$
such that the following holds. For any pair of distinct elements
$C_{Grom}>0$
such that the following holds. For any pair of distinct elements
![]() $\phi , \psi $
of
$\phi , \psi $
of
![]() $\{\phi _{+}, \phi _{+}^{-1}, \phi _{-}, \phi _{-}^{-1}\}$
and
$\{\phi _{+}, \phi _{+}^{-1}, \phi _{-}, \phi _{-}^{-1}\}$
and
![]() $m, n \ge 0$
, we have
$m, n \ge 0$
, we have
![]() $(\phi ^{n} x_{0}, \psi ^{m} x_{0})_{x_{0}} < C_{Grom}$
.
$(\phi ^{n} x_{0}, \psi ^{m} x_{0})_{x_{0}} < C_{Grom}$
.
Proof. Let
![]() $\mathscr {M}, \epsilon> 0$
be as in Lemma 4.8 and let
$\mathscr {M}, \epsilon> 0$
be as in Lemma 4.8 and let
![]() $\mathscr {C}_{0}(\epsilon ), \mathscr {D}_{0}(\epsilon )$
be as in Theorem 4.7. Finally, let
$\mathscr {C}_{0}(\epsilon ), \mathscr {D}_{0}(\epsilon )$
be as in Theorem 4.7. Finally, let
![]() $\mathscr {G} = \mathscr {G}(\mathscr {D}_{0}(\epsilon ) + 2\mathscr {M})$
be as in Lemma 4.10.
$\mathscr {G} = \mathscr {G}(\mathscr {D}_{0}(\epsilon ) + 2\mathscr {M})$
be as in Lemma 4.10.
When
![]() $\phi = \psi ^{-1}$
, the conclusion follows from the fact that
$\phi = \psi ^{-1}$
, the conclusion follows from the fact that
![]() $\phi _{+}$
,
$\phi _{+}$
,
![]() $\phi _{-}$
have positive translation lengths. In particular, we have
$\phi _{-}$
have positive translation lengths. In particular, we have
for any integers
![]() $m, n \in \operatorname {\mathbb {Z}}$
. This leads to
$m, n \in \operatorname {\mathbb {Z}}$
. This leads to
for
![]() $m, n \ge 0$
.
$m, n \ge 0$
.
Let us now fix
![]() $m, n \in \operatorname {\mathbb {Z}}$
and estimate
$m, n \in \operatorname {\mathbb {Z}}$
and estimate
![]() $(\phi _{+}^{m} x_{0}, \phi _{-}^{n} x_{0})_{x_{0}}$
. If
$(\phi _{+}^{m} x_{0}, \phi _{-}^{n} x_{0})_{x_{0}}$
. If
![]() $d(x_{0}, \phi _{+}^{m} x_{0})$
is smaller than
$d(x_{0}, \phi _{+}^{m} x_{0})$
is smaller than
![]() $\mathscr {G} \tau _{+} + 2d(x_{0}, y_{+}) + \mathscr {M} + 1 + \mathscr {C}_{0}(\epsilon )$
, so is the Gromov product. If not, we take the subsegment
$\mathscr {G} \tau _{+} + 2d(x_{0}, y_{+}) + \mathscr {M} + 1 + \mathscr {C}_{0}(\epsilon )$
, so is the Gromov product. If not, we take the subsegment
![]() $\eta $
of
$\eta $
of
![]() $[x_{0}, \phi _{+}^{m} x_{0}]$
with length
$[x_{0}, \phi _{+}^{m} x_{0}]$
with length
![]() $\mathscr {C}_{0}(\epsilon )$
such that
$\mathscr {C}_{0}(\epsilon )$
such that
![]() $d(x_{0}, \eta ) = \mathscr {G} \tau _{+} + 2d(x_{0}, y_{+}) + \mathscr {M} + 1$
. By Theorem 4.7, either
$d(x_{0}, \eta ) = \mathscr {G} \tau _{+} + 2d(x_{0}, y_{+}) + \mathscr {M} + 1$
. By Theorem 4.7, either
![]() $[x_{0}, \phi _{-}^{n} x_{0}]$
or
$[x_{0}, \phi _{-}^{n} x_{0}]$
or
![]() $[\phi _{+}^{m} x_{0}, \phi _{-}^{n} x_{0}]$
intersects the
$[\phi _{+}^{m} x_{0}, \phi _{-}^{n} x_{0}]$
intersects the
![]() $\mathscr {D}_{0}(\epsilon )$
-neighborhood of
$\mathscr {D}_{0}(\epsilon )$
-neighborhood of
![]() $\eta $
.
$\eta $
.
In the former case, let
![]() $p \in [x_{0}, \phi _{-}^{n} x_{0}]$
and
$p \in [x_{0}, \phi _{-}^{n} x_{0}]$
and
![]() $q \in \eta $
be such that
$q \in \eta $
be such that
![]() $d(p, q) \le \mathscr {D}_{0}(\epsilon )$
. By Lemma 4.8, there exists
$d(p, q) \le \mathscr {D}_{0}(\epsilon )$
. By Lemma 4.8, there exists
![]() $m', n'$
such that
$m', n'$
such that
![]() $\phi _{+}^{m'} x_{0} \in N_{\mathscr {M}}(p)$
and
$\phi _{+}^{m'} x_{0} \in N_{\mathscr {M}}(p)$
and
![]() $\phi _{-}^{n'} x_{0} \in N_{\mathscr {M}}(q)$
. Then we have
$\phi _{-}^{n'} x_{0} \in N_{\mathscr {M}}(q)$
. Then we have
![]() $d(\phi _{+}^{m'} x_{0}, \phi _{-}^{n'} x_{0}) \le \mathscr {D}_0(\epsilon ) + 2 \mathscr {M}$
for some
$d(\phi _{+}^{m'} x_{0}, \phi _{-}^{n'} x_{0}) \le \mathscr {D}_0(\epsilon ) + 2 \mathscr {M}$
for some
![]() $m', n' \in \operatorname {\mathbb {Z}}$
such that
$m', n' \in \operatorname {\mathbb {Z}}$
such that
![]() $d(x_{0}, \phi _{+}^{m'} x_{0}) \ge d(x_{0}, \eta ) - \mathscr {M}> \mathscr {G} \tau _{+} + 2d(x_{0}, y_{+})$
. This contradicts Lemma 4.10.
$d(x_{0}, \phi _{+}^{m'} x_{0}) \ge d(x_{0}, \eta ) - \mathscr {M}> \mathscr {G} \tau _{+} + 2d(x_{0}, y_{+})$
. This contradicts Lemma 4.10.
Hence, the latter case holds: there exists
![]() $p \in [\phi _{+}^{m} x_{0}, \phi _{-}^{n} x_{0}]$
that belongs to the
$p \in [\phi _{+}^{m} x_{0}, \phi _{-}^{n} x_{0}]$
that belongs to the
![]() $\mathscr {D}_{0}(\epsilon )$
-neighborhood of
$\mathscr {D}_{0}(\epsilon )$
-neighborhood of
![]() $\eta $
. This implies that
$\eta $
. This implies that
 $$ \begin{align*}\begin{aligned} 2(\phi_{+}^{m} x_{0}, \phi_{-}^{n} x_{0})_{x_{0}} &= [d(x_{0}, \phi_{+}^{m} x_{0}) - d(\phi_{+}^{m} x_{0}, p)] + [d(x_{0}, \phi_{-}^{n} x_{0}) - d(p, \phi_{-}^{n} x_{0})]\\ & \le 2d(x_{0}, p) \le 2d(x_{0}, \eta) + 2\operatorname{diam}(\eta) + 2\mathscr{D}_{0}(\epsilon). \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} 2(\phi_{+}^{m} x_{0}, \phi_{-}^{n} x_{0})_{x_{0}} &= [d(x_{0}, \phi_{+}^{m} x_{0}) - d(\phi_{+}^{m} x_{0}, p)] + [d(x_{0}, \phi_{-}^{n} x_{0}) - d(p, \phi_{-}^{n} x_{0})]\\ & \le 2d(x_{0}, p) \le 2d(x_{0}, \eta) + 2\operatorname{diam}(\eta) + 2\mathscr{D}_{0}(\epsilon). \end{aligned} \end{align*} $$
In conclusion, we have
![]() $(\phi _{+}^{m} x_{0}, \phi _{-}^{n} x_{0})_{x_{0}} \le \mathscr {G} \tau _{+} + 2d(x_{0}, y_{+}) + \mathscr {C}_{0}(\epsilon ) + \mathscr {D}_{0}(\epsilon ) + \mathscr {M} + 1$
.
$(\phi _{+}^{m} x_{0}, \phi _{-}^{n} x_{0})_{x_{0}} \le \mathscr {G} \tau _{+} + 2d(x_{0}, y_{+}) + \mathscr {C}_{0}(\epsilon ) + \mathscr {D}_{0}(\epsilon ) + \mathscr {M} + 1$
.
4.4 Witnessing
Recall that G stands for the mapping class group of the underlying surface.
Definition 4.12. Let
![]() $D>0$
,
$D>0$
,
![]() $\gamma $
,
$\gamma $
,
![]() $\gamma '$
be paths on X. We say that
$\gamma '$
be paths on X. We say that
![]() $\gamma $
is D-witnessed by
$\gamma $
is D-witnessed by
![]() $\gamma '$
if there exists a subsegment
$\gamma '$
if there exists a subsegment
![]() $\eta $
of
$\eta $
of
![]() $\gamma $
that D-fellow travels with
$\gamma $
that D-fellow travels with
![]() $\gamma '$
. Here, if
$\gamma '$
. Here, if
![]() $\gamma $
and
$\gamma $
and
![]() $\gamma '$
share the beginning point (ending point, resp.), we additionally require
$\gamma '$
share the beginning point (ending point, resp.), we additionally require
![]() $\eta $
to begin at (end at, resp.) that shared point.
$\eta $
to begin at (end at, resp.) that shared point.
For
![]() $w, w' \in G$
, we say that
$w, w' \in G$
, we say that
-
• w is D-witnessed by
 $\gamma '$
if
$\gamma '$
if
 $[x_{0}, w x_{0}]$
is D-witnessed by
$[x_{0}, w x_{0}]$
is D-witnessed by
 $\gamma '$
;
$\gamma '$
; -
•
 $\gamma $
is D-witnessed by
$\gamma $
is D-witnessed by
 $w'$
if
$w'$
if
 $\gamma $
is D-witnessed by
$\gamma $
is D-witnessed by
 $[x_{0}, w'x_{0}]$
, and
$[x_{0}, w'x_{0}]$
, and -
• w is D-witnessed by
 $w'$
if
$w'$
if
 $[x_{0}, w x_{0}]$
is D-witnessed by
$[x_{0}, w x_{0}]$
is D-witnessed by
 $[x_{0}, w'x_{0}]$
.
$[x_{0}, w'x_{0}]$
.
We also define
 $$ \begin{align*} \begin{aligned} \mathcal{C}_{D}(\phi \rightarrow 0) &:= \{w \in G: w\,\,\textrm{is}\ D\textrm{-witnessed by}\,\,\phi \},\\ \mathcal{C}_{D}(0 \rightarrow \phi) &:= \{w \in G : w^{-1}\,\textrm{is}\ D\textrm{-witnessed by}\,\,\phi^{-1} \},\\ \mathcal{C}_{D}(\phi \rightarrow \psi) &:= \mathcal{C}_{D}(\phi \rightarrow 0) \cap \mathcal{C}_{D}(0 \rightarrow \psi). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathcal{C}_{D}(\phi \rightarrow 0) &:= \{w \in G: w\,\,\textrm{is}\ D\textrm{-witnessed by}\,\,\phi \},\\ \mathcal{C}_{D}(0 \rightarrow \phi) &:= \{w \in G : w^{-1}\,\textrm{is}\ D\textrm{-witnessed by}\,\,\phi^{-1} \},\\ \mathcal{C}_{D}(\phi \rightarrow \psi) &:= \mathcal{C}_{D}(\phi \rightarrow 0) \cap \mathcal{C}_{D}(0 \rightarrow \psi). \end{aligned} \end{align*} $$
The following lemma will tell us that sample paths are witnessed by
![]() $\phi _{\pm }$
for a definite probability.
$\phi _{\pm }$
for a definite probability.
Lemma 4.13. For each
![]() $F>0$
, there exists
$F>0$
, there exists
![]() $\mathscr {F} = \mathscr {F}(F)$
such that the following holds.
$\mathscr {F} = \mathscr {F}(F)$
such that the following holds.
Let
![]() $\phi \in \{\phi _{+}, \phi _{+}^{-1}, \phi _{-}, \phi _{-}^{-1}\}$
and
$\phi \in \{\phi _{+}, \phi _{+}^{-1}, \phi _{-}, \phi _{-}^{-1}\}$
and
![]() $w \in G$
. If
$w \in G$
. If
![]() $d(\phi ^{F} x_{0}, [x_{0}, wx_{0}])> \mathscr {C}_{0}(\epsilon ) + \mathscr {D}_{0}(\epsilon ) + \mathscr {M}$
, then
$d(\phi ^{F} x_{0}, [x_{0}, wx_{0}])> \mathscr {C}_{0}(\epsilon ) + \mathscr {D}_{0}(\epsilon ) + \mathscr {M}$
, then
![]() $\phi ^{-m} w$
is
$\phi ^{-m} w$
is
![]() $\mathscr {F}$
-witnessed by
$\mathscr {F}$
-witnessed by
![]() $\phi ^{-m}$
for every
$\phi ^{-m}$
for every
![]() $m \ge 0$
.
$m \ge 0$
.
Proof. Let
![]() $K_{1}>0$
be such that
$K_{1}>0$
be such that
![]() $d(x_{0}, \phi ^{i} x_{0})> \mathscr {M} + \mathscr {C}_{0}(\epsilon )$
for each
$d(x_{0}, \phi ^{i} x_{0})> \mathscr {M} + \mathscr {C}_{0}(\epsilon )$
for each
![]() $\phi \in \{\phi _{+}, \phi _{+}^{-1}, \phi _{-}, \phi _{-}^{-1}\}$
and
$\phi \in \{\phi _{+}, \phi _{+}^{-1}, \phi _{-}, \phi _{-}^{-1}\}$
and
![]() $i \ge K_{1}$
. Then, let
$i \ge K_{1}$
. Then, let
![]() $K_{2}>0$
be such that
$K_{2}>0$
be such that
![]() $d(x_{0}, \phi ^{i} x_{0}) \le K_{2}$
for each
$d(x_{0}, \phi ^{i} x_{0}) \le K_{2}$
for each
![]() $\phi \in \{\phi _{+}, \phi _{+}^{-1}, \phi _{-}, \phi _{-}^{-1}\}$
and
$\phi \in \{\phi _{+}, \phi _{+}^{-1}, \phi _{-}, \phi _{-}^{-1}\}$
and
![]() $0 \le i \le F+K_{1}$
. We then take
$0 \le i \le F+K_{1}$
. We then take
Note that for any
![]() $x, y, z \in X$
,
$x, y, z \in X$
,
![]() $[x, y]$
is
$[x, y]$
is
![]() $d(x, z)$
-witnessed by
$d(x, z)$
-witnessed by
![]() $[x, z]$
. Since
$[x, z]$
. Since
![]() $\mathscr {F} \ge K_{2}$
,
$\mathscr {F} \ge K_{2}$
,
![]() $\phi ^{-m} w$
is
$\phi ^{-m} w$
is
![]() $\mathscr {F}$
-witnessed by
$\mathscr {F}$
-witnessed by
![]() $\phi ^{-m}$
for
$\phi ^{-m}$
for
![]() $0 \le m \le F+K_{1}$
.
$0 \le m \le F+K_{1}$
.
Let us now consider the case of
![]() $m> F+K_{1}$
. Let y be a point on
$m> F+K_{1}$
. Let y be a point on
![]() $[\phi ^{-m} x_{0}, x_{0}]$
that lies in the
$[\phi ^{-m} x_{0}, x_{0}]$
that lies in the
![]() $\mathscr {M}$
-neighborhood of
$\mathscr {M}$
-neighborhood of
![]() $\phi ^{F-m} x_{0}$
. Note that
$\phi ^{F-m} x_{0}$
. Note that
![]() $d(y, x_{0}) \ge d(\phi ^{m-F} x_{0}, x_{0}) - \mathscr {M} \ge \mathscr {C}_{0}(\epsilon )$
. Hence, we can take a subsegment
$d(y, x_{0}) \ge d(\phi ^{m-F} x_{0}, x_{0}) - \mathscr {M} \ge \mathscr {C}_{0}(\epsilon )$
. Hence, we can take a subsegment
![]() $\eta = [y, y']$
of
$\eta = [y, y']$
of
![]() $[\phi ^{-m} x_{0}, x_{0}]$
such that
$[\phi ^{-m} x_{0}, x_{0}]$
such that
![]() $d(y, y') = \mathscr {C}_{0}(\epsilon )$
.
$d(y, y') = \mathscr {C}_{0}(\epsilon )$
.
By Theorem 4.7, either
![]() $[\phi ^{-m}w x_{0}, x_{0}]$
or
$[\phi ^{-m}w x_{0}, x_{0}]$
or
![]() $[\phi ^{-m} w x_{0}, \phi ^{-m} x_{0}]$
intersects the
$[\phi ^{-m} w x_{0}, \phi ^{-m} x_{0}]$
intersects the
![]() $\mathscr {D}_{0}(\epsilon )$
-neighborhood of
$\mathscr {D}_{0}(\epsilon )$
-neighborhood of
![]() $\eta $
. If
$\eta $
. If
![]() $d([\phi ^{-m} w x_{0}, \phi ^{-m} x_{0}], \eta ) < \mathscr {D}_{0}(\epsilon )$
, then we deduce
$d([\phi ^{-m} w x_{0}, \phi ^{-m} x_{0}], \eta ) < \mathscr {D}_{0}(\epsilon )$
, then we deduce
![]() $d(\phi ^{F-m} x_{0}, [\phi ^{-m} w x_{0}, \phi ^{-m} x_{0}]) < \mathscr {D}_{0}(\epsilon )+ \mathscr {M} + \mathscr {C}_{0}(\epsilon )$
. This is equivalent to
$d(\phi ^{F-m} x_{0}, [\phi ^{-m} w x_{0}, \phi ^{-m} x_{0}]) < \mathscr {D}_{0}(\epsilon )+ \mathscr {M} + \mathscr {C}_{0}(\epsilon )$
. This is equivalent to
![]() $d(\phi ^{F} x_{0}, [x_{0}, wx_{0}]) < \mathscr {C}_{0}(\epsilon ) + \mathscr {D}_{0}(\epsilon ) + \mathscr {M}$
, which contradicts the assumption.
$d(\phi ^{F} x_{0}, [x_{0}, wx_{0}]) < \mathscr {C}_{0}(\epsilon ) + \mathscr {D}_{0}(\epsilon ) + \mathscr {M}$
, which contradicts the assumption.
Hence,
![]() $[\phi ^{-m} w x_{0}, x_{0}]$
contains a point p that lies in the
$[\phi ^{-m} w x_{0}, x_{0}]$
contains a point p that lies in the
![]() $\mathscr {D}_{0}(\epsilon )$
-neighborhood of
$\mathscr {D}_{0}(\epsilon )$
-neighborhood of
![]() $\eta $
. Note that
$\eta $
. Note that
 $$ \begin{align*} \begin{aligned} d(p, \phi^{-m} x_{0}) & \le d(p, \eta) + \operatorname{diam}(\eta) + \mathscr{M} + d(\phi^{F-m} x_{0}, \phi^{-m} x_{0}) \\ & \le \mathscr{C}_{0}(\epsilon) + \mathscr{D}_{0}(\epsilon) + \mathscr{M} + K_{2}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} d(p, \phi^{-m} x_{0}) & \le d(p, \eta) + \operatorname{diam}(\eta) + \mathscr{M} + d(\phi^{F-m} x_{0}, \phi^{-m} x_{0}) \\ & \le \mathscr{C}_{0}(\epsilon) + \mathscr{D}_{0}(\epsilon) + \mathscr{M} + K_{2}. \end{aligned} \end{align*} $$
Then
![]() $[p, x_{0}]$
and
$[p, x_{0}]$
and
![]() $[\phi ^{-1}x_{0}, x_{0}]\ \mathscr {B}(\epsilon , \mathscr {C}_{0}(\epsilon ) + \mathscr {D}_{0}(\epsilon ) + \mathscr {M} + K_{2})$
-fellow travel as desired.
$[\phi ^{-1}x_{0}, x_{0}]\ \mathscr {B}(\epsilon , \mathscr {C}_{0}(\epsilon ) + \mathscr {D}_{0}(\epsilon ) + \mathscr {M} + K_{2})$
-fellow travel as desired.
Corollary 4.14. There exists
![]() $\mathscr {F}> 0$
such that for
$\mathscr {F}> 0$
such that for
![]() $\phi \in \{\phi _{+}, \phi _{-}\}$
, we have
$\phi \in \{\phi _{+}, \phi _{-}\}$
, we have
Proof. Let
![]() $F = F(\mathscr {C}_{0}(\epsilon ) + \mathscr {D}_{0}(\epsilon ) + \mathscr {M}, \phi )$
be as in Theorem 4.3 and
$F = F(\mathscr {C}_{0}(\epsilon ) + \mathscr {D}_{0}(\epsilon ) + \mathscr {M}, \phi )$
be as in Theorem 4.3 and
![]() $\mathscr {F} = \mathscr {F}(F)$
be as in Lemma 4.13. We consider the event
$\mathscr {F} = \mathscr {F}(F)$
be as in Lemma 4.13. We consider the event
![]() $\mathcal {E}$
of sample paths
$\mathcal {E}$
of sample paths
![]() $\operatorname {\omega } = (\operatorname {\omega }_{n})_{n}$
such that
$\operatorname {\omega } = (\operatorname {\omega }_{n})_{n}$
such that
for all
![]() $n \in \operatorname {\mathbb {Z}}$
. Then
$n \in \operatorname {\mathbb {Z}}$
. Then
![]() $\operatorname {\mathbb {P}}(\mathcal {E})>0$
thanks to Theorem 4.3. Moreover, Lemma 4.13 implies that for
$\operatorname {\mathbb {P}}(\mathcal {E})>0$
thanks to Theorem 4.3. Moreover, Lemma 4.13 implies that for
![]() $\operatorname {\omega } \in \mathcal {E}$
,
$\operatorname {\omega } \in \mathcal {E}$
,
![]() $\phi ^{m} \operatorname {\omega }_{n}$
is
$\phi ^{m} \operatorname {\omega }_{n}$
is
![]() $\mathscr {F}$
-witnessed by
$\mathscr {F}$
-witnessed by
![]() $\phi ^{m}$
for each
$\phi ^{m}$
for each
![]() $m \in \operatorname {\mathbb {Z}}$
, as desired.
$m \in \operatorname {\mathbb {Z}}$
, as desired.
We now fix some constants. As the base case, we set
 $$ \begin{align*} \begin{aligned} \mathscr{D}_{1} &:= \mathscr{D}_{0}(\epsilon) + \mathscr{B}(\epsilon, \mathscr{C}_{0}(\epsilon) + \mathscr{D}_{0}(\epsilon) + \mathscr{M}) + \mathscr{F}, \\ \epsilon_{1} &:= \epsilon e^{-2\mathscr{D}_{1}}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathscr{D}_{1} &:= \mathscr{D}_{0}(\epsilon) + \mathscr{B}(\epsilon, \mathscr{C}_{0}(\epsilon) + \mathscr{D}_{0}(\epsilon) + \mathscr{M}) + \mathscr{F}, \\ \epsilon_{1} &:= \epsilon e^{-2\mathscr{D}_{1}}. \end{aligned} \end{align*} $$
Now given
![]() $\mathscr {D}_{j}$
and
$\mathscr {D}_{j}$
and
![]() $\epsilon _{j}$
, we define
$\epsilon _{j}$
, we define
 $$ \begin{align}\begin{aligned} \mathscr{D}_{j+1} & := \mathscr{D}_{j} + \mathscr{B}(\epsilon, 4\mathscr{D}_{j} + 2C_{Grom} + 5\mathscr{C}_{0}(\epsilon_{j}) + 5\mathscr{D}_{0}(\epsilon_{j}) + 2), \\ \epsilon_{j+1} &:= \epsilon e^{-2\mathscr{D}_{j+1}}. \end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} \mathscr{D}_{j+1} & := \mathscr{D}_{j} + \mathscr{B}(\epsilon, 4\mathscr{D}_{j} + 2C_{Grom} + 5\mathscr{C}_{0}(\epsilon_{j}) + 5\mathscr{D}_{0}(\epsilon_{j}) + 2), \\ \epsilon_{j+1} &:= \epsilon e^{-2\mathscr{D}_{j+1}}. \end{aligned} \end{align} $$
Note that the constants
![]() $\epsilon , \mathscr {M}, \mathscr {F}, C_{Grom}$
remain the same even if we replace
$\epsilon , \mathscr {M}, \mathscr {F}, C_{Grom}$
remain the same even if we replace
![]() $\phi _{+}$
,
$\phi _{+}$
,
![]() $\phi _{-}$
with their powers. Hence, by employing sufficiently large powers of
$\phi _{-}$
with their powers. Hence, by employing sufficiently large powers of
![]() $\phi _{\pm }$
if necessary, we may assume
$\phi _{\pm }$
if necessary, we may assume
for
![]() $j = 1, \ldots , 6$
. Finally, we set
$j = 1, \ldots , 6$
. Finally, we set
Lemma 4.15. For any
![]() $\phi \in \{\phi _{+}, \phi _{+}^{-1}, \phi _{-}, \phi _{-}^{-1}\}$
and
$\phi \in \{\phi _{+}, \phi _{+}^{-1}, \phi _{-}, \phi _{-}^{-1}\}$
and
![]() $n>0$
,
$n>0$
,
![]() $\phi ^{n}$
belongs to
$\phi ^{n}$
belongs to
![]() $\mathcal {C}_{\mathscr {D}_{1}}(\phi \rightarrow \phi )$
.
$\mathcal {C}_{\mathscr {D}_{1}}(\phi \rightarrow \phi )$
.
Proof. By Lemma 4.8, we have
![]() $p \in [x_{0}, \phi ^{n} x_{0}]$
such that
$p \in [x_{0}, \phi ^{n} x_{0}]$
such that
Since
![]() $x_{0}$
and
$x_{0}$
and
![]() $\phi x_{0}$
are
$\phi x_{0}$
are
![]() $\epsilon $
-thick, Corollary 4.6 tells us that
$\epsilon $
-thick, Corollary 4.6 tells us that
![]() $[x_{0}, p]$
and
$[x_{0}, p]$
and
![]() $[x_{0}, \phi x_{0}]\ \mathscr {B}(\epsilon , \mathscr {C}_{0}(\epsilon ) + \mathscr {D}_{0}(\epsilon ) + \mathscr {M})$
-fellow travel. By a similar reason, there exists
$[x_{0}, \phi x_{0}]\ \mathscr {B}(\epsilon , \mathscr {C}_{0}(\epsilon ) + \mathscr {D}_{0}(\epsilon ) + \mathscr {M})$
-fellow travel. By a similar reason, there exists
![]() $q \in [x_{0}, \phi ^{n} x_{0}]$
such that
$q \in [x_{0}, \phi ^{n} x_{0}]$
such that
![]() $[q, \phi ^{n} x_{0}]$
and
$[q, \phi ^{n} x_{0}]$
and
![]() $[\phi ^{n-1} x_{0}, \phi ^{n} x_{0}]\ \mathscr {B}(\epsilon , \mathscr {C}_{0}(\epsilon ) + \mathscr {D}_{0}(\epsilon ) + \mathscr {M})$
-fellow travel.
$[\phi ^{n-1} x_{0}, \phi ^{n} x_{0}]\ \mathscr {B}(\epsilon , \mathscr {C}_{0}(\epsilon ) + \mathscr {D}_{0}(\epsilon ) + \mathscr {M})$
-fellow travel.
Remark 4.16. We will observe that if
![]() $\phi , \psi \in \{\phi _{+}, \phi _{+}^{-1}, \phi _{-}, \phi _{-}^{-1}\}$
are distinct, then
$\phi , \psi \in \{\phi _{+}, \phi _{+}^{-1}, \phi _{-}, \phi _{-}^{-1}\}$
are distinct, then
![]() $\mathcal {C}_{\mathscr {D}_{5}}(\phi \rightarrow 0) \cap \mathcal {C}_{\mathscr {D}_{5}}(\psi \rightarrow 0) = \emptyset $
.
$\mathcal {C}_{\mathscr {D}_{5}}(\phi \rightarrow 0) \cap \mathcal {C}_{\mathscr {D}_{5}}(\psi \rightarrow 0) = \emptyset $
.
We can now discuss the concatenation of witnessed mapping classes.
Definition 4.17. Let
![]() $\phi _{i}, \psi _i \in \{\phi _{+}, \phi _{+}^{-1}, \phi _{-}, \phi _{-}^{-1}\}$
. We say that the sequences
$\phi _{i}, \psi _i \in \{\phi _{+}, \phi _{+}^{-1}, \phi _{-}, \phi _{-}^{-1}\}$
. We say that the sequences
![]() $(\phi _{i})_{i}$
and
$(\phi _{i})_{i}$
and
![]() $(\psi _{i})_{i}$
are repulsive if
$(\psi _{i})_{i}$
are repulsive if
![]() $\phi _{i+1} \neq \psi _{i}^{-1}$
for each i.
$\phi _{i+1} \neq \psi _{i}^{-1}$
for each i.
Given repulsive sequences
![]() $(\phi _{i})_{i}$
and
$(\phi _{i})_{i}$
and
![]() $(\psi _{i})_{i}$
, we say that a sequence
$(\psi _{i})_{i}$
, we say that a sequence
![]() $(g_{i})_{i=1}^{n} \subseteq G$
is D-marked with
$(g_{i})_{i=1}^{n} \subseteq G$
is D-marked with
![]() $(\phi _{i})_{i=2}^{n}$
and
$(\phi _{i})_{i=2}^{n}$
and
![]() $(\psi _{i})_{i=1}^{n-1}$
if
$(\psi _{i})_{i=1}^{n-1}$
if
-
(1)
 $g_{1} \in \mathcal {C}_{D}(0 \rightarrow \psi _{1})$
,
$g_{1} \in \mathcal {C}_{D}(0 \rightarrow \psi _{1})$
, -
(2)
 $g_{i} \in \mathcal {C}_{D}(\phi _{i} \rightarrow \psi _{i})$
for
$g_{i} \in \mathcal {C}_{D}(\phi _{i} \rightarrow \psi _{i})$
for
 $i=2, \ldots , n-1$
,
$i=2, \ldots , n-1$
, -
(3)
 $g_{n} \in \mathcal {C}_{D}(\phi _{n} \rightarrow 0)$
.
$g_{n} \in \mathcal {C}_{D}(\phi _{n} \rightarrow 0)$
.
If
![]() $(g_{i})$
additionally satisfies that
$(g_{i})$
additionally satisfies that
![]() $g_{1} \in \mathcal {C}_{D}(\phi _{1} \rightarrow \psi _{1})$
, then we say that
$g_{1} \in \mathcal {C}_{D}(\phi _{1} \rightarrow \psi _{1})$
, then we say that
![]() $(g_{i})_{i=1}^{n}$
is D-strongly marked with
$(g_{i})_{i=1}^{n}$
is D-strongly marked with
![]() $(\phi _{i})_{i=1}^{n}$
and
$(\phi _{i})_{i=1}^{n}$
and
![]() $(\psi _{i})_{i=1}^{n-1}$
.
$(\psi _{i})_{i=1}^{n-1}$
.
Lemma 4.18. For each
![]() $j = 1, \ldots , 5$
, we have the following.
$j = 1, \ldots , 5$
, we have the following.
Let
![]() $(\phi _{i})_{i}$
,
$(\phi _{i})_{i}$
,
![]() $(\psi _{i})_{i}$
be repulsive sequences and
$(\psi _{i})_{i}$
be repulsive sequences and
![]() $(g_{i})_{i=1}^{n}$
be a sequence that is
$(g_{i})_{i=1}^{n}$
be a sequence that is
![]() $\mathscr {D}_{j}$
-marked with
$\mathscr {D}_{j}$
-marked with
![]() $(\phi _{i})_{i=2}^{n}, (\psi _{i})_{i=1}^{n-1}$
. Let also
$(\phi _{i})_{i=2}^{n}, (\psi _{i})_{i=1}^{n-1}$
. Let also
![]() $w: = g_{1} \cdots g_{n}$
. Then w is
$w: = g_{1} \cdots g_{n}$
. Then w is
![]() $\mathscr {D}_{j+1}$
-witnessed by
$\mathscr {D}_{j+1}$
-witnessed by
![]() $[g_{1} \psi _{1}^{-1} x_{0}, g_{1}x_{0}]$
. If, moreover,
$[g_{1} \psi _{1}^{-1} x_{0}, g_{1}x_{0}]$
. If, moreover,
![]() $(g_{i})_{i}$
is
$(g_{i})_{i}$
is
![]() $\mathscr {D}_{j}$
-strongly marked with
$\mathscr {D}_{j}$
-strongly marked with
![]() $(\phi _{i})_{i=1}^{n}$
,
$(\phi _{i})_{i=1}^{n}$
,
![]() $(\psi _{i})_{i=1}^{n-1}$
, then w is
$(\psi _{i})_{i=1}^{n-1}$
, then w is
![]() $\mathscr {D}_{j+1}$
-witnessed by
$\mathscr {D}_{j+1}$
-witnessed by
![]() $\phi _{1}$
.
$\phi _{1}$
.
Proof. Let
![]() $C_{Grom}$
be the constant obtained from Lemma 4.11 and let
$C_{Grom}$
be the constant obtained from Lemma 4.11 and let
![]() $K = \mathscr {C}_{0}(\epsilon _{j}) + \mathscr {D}_{0}(\epsilon _{j}) + 2\mathscr {D}_{j} + C_{Grom} + 1$
. Recall that we have assumed in Condition 4.3 that
$K = \mathscr {C}_{0}(\epsilon _{j}) + \mathscr {D}_{0}(\epsilon _{j}) + 2\mathscr {D}_{j} + C_{Grom} + 1$
. Recall that we have assumed in Condition 4.3 that
![]() $d(x_{0}, \phi ^{\pm } x_{0}) \ge 2K + 2\mathscr {D}_{j+1}$
.
$d(x_{0}, \phi ^{\pm } x_{0}) \ge 2K + 2\mathscr {D}_{j+1}$
.
We induct on the number of segments. For
![]() $n=1$
, the conclusion follows from Lemma 4.13 since
$n=1$
, the conclusion follows from Lemma 4.13 since
![]() $\mathscr {D}_{j} \le \mathscr {D}_{j+1}$
.
$\mathscr {D}_{j} \le \mathscr {D}_{j+1}$
.
Now suppose that the theorem holds for
![]() $(g_{2}, \ldots , g_{n})$
. By induction hypothesis, there exists
$(g_{2}, \ldots , g_{n})$
. By induction hypothesis, there exists
![]() $q_{2} \in [g_{1} x_{0}, wx_{0}]$
such that
$q_{2} \in [g_{1} x_{0}, wx_{0}]$
such that
![]() $[g_{1} x_{0}, q_{2}]$
and
$[g_{1} x_{0}, q_{2}]$
and
![]() $[g_{1} x_{0}, g_{1} \phi _{2} x_{0}]\ \mathscr {D}_{j+1}$
-fellow travel. Note that the length of
$[g_{1} x_{0}, g_{1} \phi _{2} x_{0}]\ \mathscr {D}_{j+1}$
-fellow travel. Note that the length of
![]() $[g_{1} x_{0}, q_{2}]$
is at least
$[g_{1} x_{0}, q_{2}]$
is at least
![]() $d(x_{0}, \phi _{2} x_{0}) - 2\mathscr {D}_{j+1} \ge 2K$
.
$d(x_{0}, \phi _{2} x_{0}) - 2\mathscr {D}_{j+1} \ge 2K$
.
There exists
![]() $q_{1} \in [x_{0}, g_{1} x_{0}]$
such that
$q_{1} \in [x_{0}, g_{1} x_{0}]$
such that
![]() $[g_{1} x_{0}, q_{1}]$
and
$[g_{1} x_{0}, q_{1}]$
and
![]() $[g_{1} x_{0}, g_{1} \psi _1^{-1} x_{0}]\ \mathscr {D}_{j}$
-fellow travel. Then
$[g_{1} x_{0}, g_{1} \psi _1^{-1} x_{0}]\ \mathscr {D}_{j}$
-fellow travel. Then
![]() $[g_{1} x_{0}, q_{1}]$
is
$[g_{1} x_{0}, q_{1}]$
is
![]() $\epsilon _{j}$
-thick and its length is at least
$\epsilon _{j}$
-thick and its length is at least
![]() $d(x_{0}, \psi _1^{-1} x_{0}) - 2\mathscr {D}_{j} \ge 2K$
.
$d(x_{0}, \psi _1^{-1} x_{0}) - 2\mathscr {D}_{j} \ge 2K$
.
Let
![]() $\eta = [y, y']$
be the subsegment of
$\eta = [y, y']$
be the subsegment of
![]() $[q_{1}, g_{1} x_{0}] \subseteq [x_{0}, g_{1} x_{0}]$
such that
$[q_{1}, g_{1} x_{0}] \subseteq [x_{0}, g_{1} x_{0}]$
such that
![]() $d(y, y') = \mathscr {C}_{0}(\epsilon _{j})$
and
$d(y, y') = \mathscr {C}_{0}(\epsilon _{j})$
and
![]() $d(y', g_{1} x_{0}) = K$
. By Theorem 4.7, at least one of
$d(y', g_{1} x_{0}) = K$
. By Theorem 4.7, at least one of
![]() $[x_{0}, wx_{0}]$
and
$[x_{0}, wx_{0}]$
and
![]() $[g_{1} x_{0}, wx_{0}]$
intersects the
$[g_{1} x_{0}, wx_{0}]$
intersects the
![]() $\mathscr {D}_{0}(\epsilon _{j})$
-neighborhood of
$\mathscr {D}_{0}(\epsilon _{j})$
-neighborhood of
![]() $\eta $
.
$\eta $
.
Suppose that there exists a point
![]() $p \in [g_{1} x_{0}, wx_{0}]$
that belongs to the
$p \in [g_{1} x_{0}, wx_{0}]$
that belongs to the
![]() $\mathscr {D}_{0}(\epsilon _{j})$
-neighborhood of
$\mathscr {D}_{0}(\epsilon _{j})$
-neighborhood of
![]() $\eta $
. We then have
$\eta $
. We then have
 $$ \begin{align*}\begin{aligned} d(g_{1} x_{0}, p) &\le d(g_{1} x_{0}, \eta) + \operatorname{diam}(\eta) + \mathscr{D}_{0}(\epsilon_{j})\\[1pt] &= K+ \mathscr{C}_{0}(\epsilon_{j}) + \mathscr{D}_{0}(\epsilon_{j}) \\[1pt] &< 2K\le d(g_{1} x_{0}, q_{2}). \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} d(g_{1} x_{0}, p) &\le d(g_{1} x_{0}, \eta) + \operatorname{diam}(\eta) + \mathscr{D}_{0}(\epsilon_{j})\\[1pt] &= K+ \mathscr{C}_{0}(\epsilon_{j}) + \mathscr{D}_{0}(\epsilon_{j}) \\[1pt] &< 2K\le d(g_{1} x_{0}, q_{2}). \end{aligned} \end{align*} $$
Hence,
![]() $d(g_{1}\psi _{1}^{-1}x_{0}, g_{1} \phi _{2} x_{0})$
is at most
$d(g_{1}\psi _{1}^{-1}x_{0}, g_{1} \phi _{2} x_{0})$
is at most
 $$ \begin{align}\begin{aligned} & \le d(g_{1} \psi_{1}^{-1} x_{0}, q_{1}) + d(q_{1}, y) + d(y, p) + d(p, q_{2}) + d(q_{2}, g_{1}\phi_{2} x_{0}) \\[1pt] &= d(g_{1} \psi_{1}^{-1} x_{0}, q_{1}) + [d(q_{1}, g_{1} x_{0}) - d(y, g_{1} x_{0})] + d(y, p) \\[1pt] & \quad + [ d(g_{1} x_{0}, q_{2}) - d(g_{1} x_{0}, p)] + d(q_{2}, g_{1} \phi_{2} x_{0}) \\[1pt] &\le d(g_{1} \psi_{1}^{-1} x_{0}, q_{1}) + [d(q_{1}, g_{1} \psi_{1}^{-1} x_{0}) + d(g_{1} \phi_{1}^{-1} x_{0}, g_{1} x_{0})] - d(y, g_{1} x_{0}) + d(y, p) \\ & \quad + [d(g_{1} x_{0}, g_{1} \phi_{2} x_{0}) + d(g_{1}\phi_{2} x_{0}, q_{2})] - d(g_{1} x_{0}, p) + d(q_{2}, g_{1} \phi_{2} x_{0}) \\ & \le d(g_{1} \phi_{1}^{-1} x_{0}, g_{1} x_{0}) + d(g_{1} x_{0}, g_{1} \phi_{2} x_{0}) - 2d(y, g_{1} x_{0}) \\ & \quad + 2d(y, p) + 2d(q_{1}, g_{1}\psi_{1}^{-1} x_{0}) + 2d(q_{2}, g_{1} \phi_{2} x_{0}) \\ &\le d(g_{1} \phi_{1}^{-1} x_{0}, g_{1} x_{0}) + d(g_{1} x_{0}, g_{1} \phi_{2} x_{0}) - 2[K - \mathscr{D}_{0}(\epsilon_{j}) - \mathscr{C}_{0}(\epsilon_{j}) - 2\mathscr{D}_{j}]. \end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} & \le d(g_{1} \psi_{1}^{-1} x_{0}, q_{1}) + d(q_{1}, y) + d(y, p) + d(p, q_{2}) + d(q_{2}, g_{1}\phi_{2} x_{0}) \\[1pt] &= d(g_{1} \psi_{1}^{-1} x_{0}, q_{1}) + [d(q_{1}, g_{1} x_{0}) - d(y, g_{1} x_{0})] + d(y, p) \\[1pt] & \quad + [ d(g_{1} x_{0}, q_{2}) - d(g_{1} x_{0}, p)] + d(q_{2}, g_{1} \phi_{2} x_{0}) \\[1pt] &\le d(g_{1} \psi_{1}^{-1} x_{0}, q_{1}) + [d(q_{1}, g_{1} \psi_{1}^{-1} x_{0}) + d(g_{1} \phi_{1}^{-1} x_{0}, g_{1} x_{0})] - d(y, g_{1} x_{0}) + d(y, p) \\ & \quad + [d(g_{1} x_{0}, g_{1} \phi_{2} x_{0}) + d(g_{1}\phi_{2} x_{0}, q_{2})] - d(g_{1} x_{0}, p) + d(q_{2}, g_{1} \phi_{2} x_{0}) \\ & \le d(g_{1} \phi_{1}^{-1} x_{0}, g_{1} x_{0}) + d(g_{1} x_{0}, g_{1} \phi_{2} x_{0}) - 2d(y, g_{1} x_{0}) \\ & \quad + 2d(y, p) + 2d(q_{1}, g_{1}\psi_{1}^{-1} x_{0}) + 2d(q_{2}, g_{1} \phi_{2} x_{0}) \\ &\le d(g_{1} \phi_{1}^{-1} x_{0}, g_{1} x_{0}) + d(g_{1} x_{0}, g_{1} \phi_{2} x_{0}) - 2[K - \mathscr{D}_{0}(\epsilon_{j}) - \mathscr{C}_{0}(\epsilon_{j}) - 2\mathscr{D}_{j}]. \end{aligned} \end{align} $$
This implies that
![]() $(\phi _{2} x_{0}, \psi _{1}^{-1} x_{0})_{x_{0}}> C_{Grom}$
, a contradiction.
$(\phi _{2} x_{0}, \psi _{1}^{-1} x_{0})_{x_{0}}> C_{Grom}$
, a contradiction.
Hence, we instead obtain a point
![]() $p \in [x_{0}, wx_{0}]$
that belongs to the
$p \in [x_{0}, wx_{0}]$
that belongs to the
![]() $\mathscr {D}_{0}(\epsilon _{j})$
-neighborhood of
$\mathscr {D}_{0}(\epsilon _{j})$
-neighborhood of
![]() $\eta $
. Then p is within distance
$\eta $
. Then p is within distance
![]() $\mathscr {D}_{0}(\epsilon _{j}) + \mathscr {C}_{0}(\epsilon _{j}) + K$
from
$\mathscr {D}_{0}(\epsilon _{j}) + \mathscr {C}_{0}(\epsilon _{j}) + K$
from
![]() $g_{1} x_{0}$
. Then Corollary 4.6 tells us that
$g_{1} x_{0}$
. Then Corollary 4.6 tells us that
![]() $[x_{0}, g_{1} x_{0}]$
and
$[x_{0}, g_{1} x_{0}]$
and
![]() $[x_{0}, p]\ \mathscr {B}(\epsilon , 2K)$
-fellow travel. Since
$[x_{0}, p]\ \mathscr {B}(\epsilon , 2K)$
-fellow travel. Since
![]() $[g_{1}\psi _{1}^{-1} x_{0}, g_{1} x_{0}]\ \mathscr {D}_{j}$
-fellow travel with a terminal subsegment of
$[g_{1}\psi _{1}^{-1} x_{0}, g_{1} x_{0}]\ \mathscr {D}_{j}$
-fellow travel with a terminal subsegment of
![]() $[x_{0}, g_{1} x_{0}]$
, we conclude that
$[x_{0}, g_{1} x_{0}]$
, we conclude that
![]() $[g_{1} \psi _{1}^{-1}x_{0}, g_{1} x_{0}]$
and a terminal subsegment of
$[g_{1} \psi _{1}^{-1}x_{0}, g_{1} x_{0}]$
and a terminal subsegment of
![]() $[x_{0}, p]\ \mathscr {D}_{j+1}$
-fellow travel. This establishes the first item.
$[x_{0}, p]\ \mathscr {D}_{j+1}$
-fellow travel. This establishes the first item.
If
![]() $[x_{0}, \phi _{1} x_{0}]\ \mathscr {D}_{j}$
-fellow travel with an initial subsegment of
$[x_{0}, \phi _{1} x_{0}]\ \mathscr {D}_{j}$
-fellow travel with an initial subsegment of
![]() $[x_{0}, g_{1} x_{0}]$
, we also conclude that an initial subsegment of
$[x_{0}, g_{1} x_{0}]$
, we also conclude that an initial subsegment of
![]() $[x_{0}, p]$
and
$[x_{0}, p]$
and
![]() $[x_{0}, \phi _{1}x_{0}]\ \mathscr {D}_{j+1}$
-fellow travel. This establishes the second item.
$[x_{0}, \phi _{1}x_{0}]\ \mathscr {D}_{j+1}$
-fellow travel. This establishes the second item.
Several corollaries of Lemma 4.18 follow.
Corollary 4.19. Let
![]() $\phi _{1}, \phi _{2} \in \{\phi _{+}, \phi _{+}^{-1}, \phi _{-}, \phi _{-}^{-1}\}$
and
$\phi _{1}, \phi _{2} \in \{\phi _{+}, \phi _{+}^{-1}, \phi _{-}, \phi _{-}^{-1}\}$
and
![]() $v\in G$
. Suppose v is
$v\in G$
. Suppose v is
![]() $\mathscr {D}_{5}$
-witnessed by
$\mathscr {D}_{5}$
-witnessed by
![]() $\phi _{1}$
and
$\phi _{1}$
and
![]() $\phi _{2}$
. Then
$\phi _{2}$
. Then
![]() $\phi _{1} = \phi _{2}$
.
$\phi _{1} = \phi _{2}$
.
Proof. Suppose not (i.e.,
![]() $\phi _{1} \neq \phi _{2}$
). This implies that the sequence
$\phi _{1} \neq \phi _{2}$
). This implies that the sequence
![]() $(v^{-1}, v)$
is
$(v^{-1}, v)$
is
![]() $\mathscr {D}_{5}$
-marked with
$\mathscr {D}_{5}$
-marked with
![]() $\phi _{1}$
,
$\phi _{1}$
,
![]() $\phi _{2}$
, which are repulsive. Lemma 4.18 then implies that
$\phi _{2}$
, which are repulsive. Lemma 4.18 then implies that
![]() $[x_{0}, x_{0}] = \{x_{0}\}$
is
$[x_{0}, x_{0}] = \{x_{0}\}$
is
![]() $\mathscr {D}_{6}$
-witnessed by
$\mathscr {D}_{6}$
-witnessed by
![]() $[v^{-1}\phi _{2}^{-1}x_{0}, v^{-1}x_{0}]$
, which is impossible since
$[v^{-1}\phi _{2}^{-1}x_{0}, v^{-1}x_{0}]$
, which is impossible since
![]() $d(x_{0}, \phi _{2} x_{0})> 2\mathscr {D}_{6}$
.
$d(x_{0}, \phi _{2} x_{0})> 2\mathscr {D}_{6}$
.
Corollary 4.20. Let
![]() $1\le j \le 4$
,
$1\le j \le 4$
,
![]() $(\phi _{i})$
,
$(\phi _{i})$
,
![]() $(\psi _{i})$
be repulsive sequences and
$(\psi _{i})$
be repulsive sequences and
![]() $(g_{i})_{i=1}^{n}$
be a sequence that is
$(g_{i})_{i=1}^{n}$
be a sequence that is
![]() $\mathscr {D}_{j}$
-marked with
$\mathscr {D}_{j}$
-marked with
![]() $(\phi _{i})_{i=2}^{n}$
and
$(\phi _{i})_{i=2}^{n}$
and
![]() $(\psi _{i})_{i=1}^{n-1}$
. Let
$(\psi _{i})_{i=1}^{n-1}$
. Let
![]() $w = g_{1} \cdots g_{n}$
and
$w = g_{1} \cdots g_{n}$
and
![]() $i \in \{1, \ldots , n-1\}$
. Then
$i \in \{1, \ldots , n-1\}$
. Then
-
(1)
 $[x_{0}, w x_{0}]$
is
$[x_{0}, w x_{0}]$
is
 $\mathscr {D}_{j+2}$
-witnessed by
$\mathscr {D}_{j+2}$
-witnessed by
 $[g_{1} \cdots g_{i} x_{0}, g_{1} \cdots g_{i} \phi _{i+1} x_{0}]$
;
$[g_{1} \cdots g_{i} x_{0}, g_{1} \cdots g_{i} \phi _{i+1} x_{0}]$
; -
(2)
 $[x_{0}, wx_{0}]$
is
$[x_{0}, wx_{0}]$
is
 $\mathscr {D}_{j+2}$
-witnessed by
$\mathscr {D}_{j+2}$
-witnessed by
 $[g_{1} \cdots g_{i} \psi _{i}^{-1} x_{0}, g_{1} \cdots g_{i} x_{0}]$
; and
$[g_{1} \cdots g_{i} \psi _{i}^{-1} x_{0}, g_{1} \cdots g_{i} x_{0}]$
; and -
(3)
 $d(x_{0}, wx_{0}) \ge d(x_{0}, g_{1} \cdots g_{i} x_{0}) + d(x_{0}, g_{i+1} \cdots g_{n} x_{0}) - \mathscr {D}_{j+2}$
.
$d(x_{0}, wx_{0}) \ge d(x_{0}, g_{1} \cdots g_{i} x_{0}) + d(x_{0}, g_{i+1} \cdots g_{n} x_{0}) - \mathscr {D}_{j+2}$
.
Proof. Note that
![]() $(g_{i+1}, \ldots , g_{n})$
is
$(g_{i+1}, \ldots , g_{n})$
is
![]() $\mathscr {D}_{j}$
-strongly marked with
$\mathscr {D}_{j}$
-strongly marked with
![]() $(\phi _{i+j})_{j=1}^{n-i}$
,
$(\phi _{i+j})_{j=1}^{n-i}$
,
![]() $(\psi _{i+j})_{j=1}^{n-i-1}$
and
$(\psi _{i+j})_{j=1}^{n-i-1}$
and
![]() $(g_{i}^{-1}, \ldots , g_{1}^{-1})$
is
$(g_{i}^{-1}, \ldots , g_{1}^{-1})$
is
![]() $\mathscr {D}_{j}$
-strongly marked with
$\mathscr {D}_{j}$
-strongly marked with
![]() $(\psi _{i+1-j}^{-1})_{j=1}^{i}$
,
$(\psi _{i+1-j}^{-1})_{j=1}^{i}$
,
![]() $(\phi _{i+1-j}^{-1})_{j=1}^{i-1}$
. Thus, by Lemma 4.18,
$(\phi _{i+1-j}^{-1})_{j=1}^{i-1}$
. Thus, by Lemma 4.18,
![]() $g_{i+1} \cdots g_{n}$
is
$g_{i+1} \cdots g_{n}$
is
![]() $\mathscr {D}_{j+1}$
-witnessed by
$\mathscr {D}_{j+1}$
-witnessed by
![]() $\phi _{i+1}$
and
$\phi _{i+1}$
and
![]() $g_{i}^{-1} \cdots g_{1}^{-1}$
is
$g_{i}^{-1} \cdots g_{1}^{-1}$
is
![]() $\mathscr {D}_{j+1}$
-witnessed by
$\mathscr {D}_{j+1}$
-witnessed by
![]() $\psi _{i}^{-1}$
. In other words,
$\psi _{i}^{-1}$
. In other words,
![]() $(g_{1} \cdots g_{i}, g_{i+1} \cdots g_{n})$
is
$(g_{1} \cdots g_{i}, g_{i+1} \cdots g_{n})$
is
![]() $\mathscr {D}_{j+1}$
-marked with
$\mathscr {D}_{j+1}$
-marked with
![]() $\phi _{i+1}$
,
$\phi _{i+1}$
,
![]() $\psi _{i}$
. We then apply Lemma 4.18 again to deduce the conclusion.
$\psi _{i}$
. We then apply Lemma 4.18 again to deduce the conclusion.
The next corollary plays the role of Lemma 2.4 on the Teichmüller space.
Corollary 4.21. Let
![]() $1\le j \le 4$
,
$1\le j \le 4$
,
![]() $(\phi _{i})_{i=2}^{n}$
,
$(\phi _{i})_{i=2}^{n}$
,
![]() $(\psi _{i})_{i=1}^{n-1}$
be repulsive sequences,
$(\psi _{i})_{i=1}^{n-1}$
be repulsive sequences,
![]() $(g_{i})_{i=1}^{n}$
be a step sequence
$(g_{i})_{i=1}^{n}$
be a step sequence
![]() $\mathscr {D}_{j}$
-marked with
$\mathscr {D}_{j}$
-marked with
![]() $(\phi _{i})$
,
$(\phi _{i})$
,
![]() $(\psi _{i})$
, and
$(\psi _{i})$
, and
![]() $1=t_{0} < t_{1} < \cdots < t_{k}=n$
. Then
$1=t_{0} < t_{1} < \cdots < t_{k}=n$
. Then
 $$ \begin{align*} \left|d(x_{0}, g_{1} \cdots g_{n} x_{0}) - \sum_{i=1}^{k} d(x_{0}, g_{t_{i-1}+1} \cdots g_{t_{i}} x_{0}) \right| \le (k-1)\mathscr{D}_{j+2} \end{align*} $$
$$ \begin{align*} \left|d(x_{0}, g_{1} \cdots g_{n} x_{0}) - \sum_{i=1}^{k} d(x_{0}, g_{t_{i-1}+1} \cdots g_{t_{i}} x_{0}) \right| \le (k-1)\mathscr{D}_{j+2} \end{align*} $$
holds.
Proof. Note that a subsequence of a step sequence marked with repulsive sequences is again marked by the corresponding repulsive subsequences. Thus, using induction on k, it suffices to prove the result for
![]() $k=2$
. Then Corollary 4.20 applies.
$k=2$
. Then Corollary 4.20 applies.
4.5 Translation lengths of mapping classes
So far, we observed that the directions witnessed by repulsive sequences of mapping classes are persistent in the final geodesic. Our next aim is to relate these recorded directions with the translation length of w and analyze the effect of pivoting.
Lemma 4.22. Let
![]() $h_{1}, h_{2} \in G$
and
$h_{1}, h_{2} \in G$
and
![]() $\phi , \psi _{1}, \psi _{2} \in \{\phi _{+}, \phi _{+}^{-1}, \phi _{-}, \phi _{-}^{-1}\}$
be such that the following hold:
$\phi , \psi _{1}, \psi _{2} \in \{\phi _{+}, \phi _{+}^{-1}, \phi _{-}, \phi _{-}^{-1}\}$
be such that the following hold:
-
•
 $d(x_{0}, h_{1} x_{0}) \ge d(x_{0}, h_{2} x_{0}) + Z$
,
$d(x_{0}, h_{1} x_{0}) \ge d(x_{0}, h_{2} x_{0}) + Z$
, -
•
 $h_{1}^{-1}$
is
$h_{1}^{-1}$
is
 $\mathscr {D}_{3}$
-witnessed by
$\mathscr {D}_{3}$
-witnessed by
 $\phi $
, and
$\phi $
, and -
•
 $\psi _{1} \neq \psi _{2}$
.
$\psi _{1} \neq \psi _{2}$
.
Then the following hold:
-
(1)
 $h_{1}^{-1} h_{2} \psi _{i}$
is
$h_{1}^{-1} h_{2} \psi _{i}$
is
 $\mathscr {D}_{4}$
-witnessed by
$\mathscr {D}_{4}$
-witnessed by
 $\phi $
for each
$\phi $
for each
 $i=1, 2$
.
$i=1, 2$
. -
(2) If
 $\psi _{1}^{-1} h_{2}^{-1} h_{1}$
is not
$\psi _{1}^{-1} h_{2}^{-1} h_{1}$
is not
 $\mathscr {D}_{2}$
-witnessed by
$\mathscr {D}_{2}$
-witnessed by
 $\psi _{1}^{-1}$
, then
$\psi _{1}^{-1}$
, then
 $\psi _{2}^{-1} h_{2}^{-1} h_{1}$
is
$\psi _{2}^{-1} h_{2}^{-1} h_{1}$
is
 $\mathscr {D}_{2}$
-witnessed by
$\mathscr {D}_{2}$
-witnessed by
 $\psi _{2}^{-1}$
.
$\psi _{2}^{-1}$
. -
(3) If
 $\psi _{2}^{-1} h_{2}^{-1} h_{1}$
is not
$\psi _{2}^{-1} h_{2}^{-1} h_{1}$
is not
 $\mathscr {D}_{2}$
-witnessed by
$\mathscr {D}_{2}$
-witnessed by
 $\psi _{2}^{-1}$
, then
$\psi _{2}^{-1}$
, then
 $\psi _{1}^{-1} h_{2}^{-1} h_{1}$
is
$\psi _{1}^{-1} h_{2}^{-1} h_{1}$
is
 $\mathscr {D}_{2}$
-witnessed by
$\mathscr {D}_{2}$
-witnessed by
 $\psi _{1}^{-1}$
.
$\psi _{1}^{-1}$
.
Proof. Let us first establish (1). The assumption tells us that
![]() $[h_{1}x_{0}, x_{0}]$
contains an initial subsegment
$[h_{1}x_{0}, x_{0}]$
contains an initial subsegment
![]() $[h_{1}x_{0}, q_{1}]$
that
$[h_{1}x_{0}, q_{1}]$
that
![]() $\mathscr {D}_{3}$
-fellow travels with
$\mathscr {D}_{3}$
-fellow travels with
![]() $[h_{1}x_{0}, h_{1}\phi x_{0}]$
. This implies that
$[h_{1}x_{0}, h_{1}\phi x_{0}]$
. This implies that
![]() $[h_{1} x_{0}, q_{1}]$
is
$[h_{1} x_{0}, q_{1}]$
is
![]() $\epsilon _{3}$
-thick. Moreover, the length of
$\epsilon _{3}$
-thick. Moreover, the length of
![]() $[h_{1}x_{0}, q_{1}]$
is at least
$[h_{1}x_{0}, q_{1}]$
is at least
![]() $d(x_{0}, \phi x_{0}) - \mathscr {D}_{3} \ge \mathscr {C}_{0}(\epsilon _{3})$
and at most
$d(x_{0}, \phi x_{0}) - \mathscr {D}_{3} \ge \mathscr {C}_{0}(\epsilon _{3})$
and at most
![]() $d(x_{0}, \phi x_{0}) + \mathscr {D}_{3}$
.
$d(x_{0}, \phi x_{0}) + \mathscr {D}_{3}$
.
Let
![]() $\eta = [y, q_{1}]$
be the subsegment of
$\eta = [y, q_{1}]$
be the subsegment of
![]() $[h_{1}x_{0}, q_{1}] \subseteq [h_{1}x_{0}, x_{0}]$
such that
$[h_{1}x_{0}, q_{1}] \subseteq [h_{1}x_{0}, x_{0}]$
such that
![]() $d(y, q_{1}) = \mathscr {C}_{0}(\epsilon _{3})$
. By Theorem 4.7, at least one of
$d(y, q_{1}) = \mathscr {C}_{0}(\epsilon _{3})$
. By Theorem 4.7, at least one of
![]() $[h_{1} x_{0}, h_{2}\psi _{i} x_{0}]$
and
$[h_{1} x_{0}, h_{2}\psi _{i} x_{0}]$
and
![]() $[h_{2}\psi _{i} x_{0}, x_{0}]$
intersects the
$[h_{2}\psi _{i} x_{0}, x_{0}]$
intersects the
![]() $\mathscr {D}_{0}(\epsilon _{3})$
-neighborhood of
$\mathscr {D}_{0}(\epsilon _{3})$
-neighborhood of
![]() $\eta $
.
$\eta $
.
If there exists a point
![]() $p \in [h_{2}\psi _{i} x_{0}, x_{0}]$
that belongs to the
$p \in [h_{2}\psi _{i} x_{0}, x_{0}]$
that belongs to the
![]() $\mathscr {D}_{0}(\epsilon _{3})$
-neighborhood of
$\mathscr {D}_{0}(\epsilon _{3})$
-neighborhood of
![]() $\eta $
, we have
$\eta $
, we have
 $$ \begin{align*} \begin{aligned} d(x_{0}, h_{2} x_{0}) &\ge d(x_{0}, h_{2}\psi_{i} x_{0}) - d(h_{2} x_{0}, h_{2}\psi_{i} x_{0}) \\ &\ge d(x_{0}, p) - d(x_{0}, \psi_{i} x_{0}) \\ &\ge d(x_{0}, \eta) - \operatorname{diam}(\eta) - \mathscr{D}_{0}(\epsilon_{3}) - d(x_{0}, \psi_{i} x_{0}) \\ &\ge d(x_{0}, h_{1} x_{0}) - [d(x_{0}, \phi x_{0}) + \mathscr{D}_{3}] -\mathscr{C}_{0}(\epsilon_{3}) -\mathscr{D}_{0}(\epsilon_{3}) - d(x_{0}, \psi_{i} x_{0}). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} d(x_{0}, h_{2} x_{0}) &\ge d(x_{0}, h_{2}\psi_{i} x_{0}) - d(h_{2} x_{0}, h_{2}\psi_{i} x_{0}) \\ &\ge d(x_{0}, p) - d(x_{0}, \psi_{i} x_{0}) \\ &\ge d(x_{0}, \eta) - \operatorname{diam}(\eta) - \mathscr{D}_{0}(\epsilon_{3}) - d(x_{0}, \psi_{i} x_{0}) \\ &\ge d(x_{0}, h_{1} x_{0}) - [d(x_{0}, \phi x_{0}) + \mathscr{D}_{3}] -\mathscr{C}_{0}(\epsilon_{3}) -\mathscr{D}_{0}(\epsilon_{3}) - d(x_{0}, \psi_{i} x_{0}). \end{aligned} \end{align*} $$
This contradicts the assumption that
![]() $d(x_{0}, h_{1} x_{0}) \ge d(x_{0}, h_{2} x_{0}) + Z$
.
$d(x_{0}, h_{1} x_{0}) \ge d(x_{0}, h_{2} x_{0}) + Z$
.
Hence,
![]() $[h_{1} x_{0}, h_{2}\psi _{i} x_{0}]$
contains a point p that belongs to the
$[h_{1} x_{0}, h_{2}\psi _{i} x_{0}]$
contains a point p that belongs to the
![]() $\mathscr {D}_{0}(\epsilon _{3})$
-neighborhood of
$\mathscr {D}_{0}(\epsilon _{3})$
-neighborhood of
![]() $\eta $
. Then
$\eta $
. Then
 $$ \begin{align*}\begin{aligned} d(p, h_{1} \phi x_{0}) &\le d(p, \eta) + \operatorname{diam}(\eta) + d(q_{1}, h_{1} \phi x_{0}) \\ &\le \mathscr{D}_{0}(\epsilon_{3}) + \mathscr{C}_{0}(\epsilon_{3}) + \mathscr{D}_{3} \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} d(p, h_{1} \phi x_{0}) &\le d(p, \eta) + \operatorname{diam}(\eta) + d(q_{1}, h_{1} \phi x_{0}) \\ &\le \mathscr{D}_{0}(\epsilon_{3}) + \mathscr{C}_{0}(\epsilon_{3}) + \mathscr{D}_{3} \end{aligned} \end{align*} $$
and
![]() $[h_{1} x_{0}, p]\ \mathscr {D}_{4}$
-fellow travels with
$[h_{1} x_{0}, p]\ \mathscr {D}_{4}$
-fellow travels with
![]() $[h_{1}x_0, h_{1}\phi x_{0}]$
.
$[h_{1}x_0, h_{1}\phi x_{0}]$
.
Let us now establish (2). Let
![]() $K = 2\mathscr {C}_{0}(\epsilon ) + 2\mathscr {D}_{0}(\epsilon ) + C_{Grom}$
. Recall that
$K = 2\mathscr {C}_{0}(\epsilon ) + 2\mathscr {D}_{0}(\epsilon ) + C_{Grom}$
. Recall that
![]() $[h_{2} x_{0}, h_{2} \psi _{1} x_{0}]$
is an
$[h_{2} x_{0}, h_{2} \psi _{1} x_{0}]$
is an
![]() $\epsilon $
-thick geodesic whose length is at least
$\epsilon $
-thick geodesic whose length is at least
![]() $\mathscr {C}_{0}(\epsilon ) + K$
.
$\mathscr {C}_{0}(\epsilon ) + K$
.
Let
![]() $\eta = [y, y']$
be the subsegment of
$\eta = [y, y']$
be the subsegment of
![]() $[h_{2} x_{0}, h_{2}\psi _{1} x_{0}]$
with
$[h_{2} x_{0}, h_{2}\psi _{1} x_{0}]$
with
![]() $d(y, y') = \mathscr {C}_{0}(\epsilon )$
and
$d(y, y') = \mathscr {C}_{0}(\epsilon )$
and
![]() $d(h_{2}x_{0}, y) = K$
. By Theorem 4.7, either
$d(h_{2}x_{0}, y) = K$
. By Theorem 4.7, either
![]() $[h_{1}x_{0}, h_{2}\psi _{1} x_{0}]$
or
$[h_{1}x_{0}, h_{2}\psi _{1} x_{0}]$
or
![]() $[h_{1} x_{0}, h_{2}x_{0}]$
intersects the
$[h_{1} x_{0}, h_{2}x_{0}]$
intersects the
![]() $\mathscr {D}_{0}(\epsilon )$
-neighborhood of
$\mathscr {D}_{0}(\epsilon )$
-neighborhood of
![]() $\eta $
. If there exists a point
$\eta $
. If there exists a point
![]() $p \in [h_{1}x_{0}, h_{2}\psi _{1} x_{0}]$
that belongs to
$p \in [h_{1}x_{0}, h_{2}\psi _{1} x_{0}]$
that belongs to
![]() $N_{\mathscr {D}_{0}(\epsilon )}(\eta )$
, then
$N_{\mathscr {D}_{0}(\epsilon )}(\eta )$
, then
![]() $d(p, h_{2} x_{0}) \le \mathscr {C}_{0}(\epsilon ) + \mathscr {D}_{0}(\epsilon ) + K$
. This implies that
$d(p, h_{2} x_{0}) \le \mathscr {C}_{0}(\epsilon ) + \mathscr {D}_{0}(\epsilon ) + K$
. This implies that
![]() $[p, h_{2}\psi _{1} x_{0}]$
and
$[p, h_{2}\psi _{1} x_{0}]$
and
![]() $[h_{2} x_{0}, h_{2}\psi _{1} x_{0}]\ \mathscr {D}_{2}$
-fellow travel, which contradicts the assumption. Hence, we instead have a point
$[h_{2} x_{0}, h_{2}\psi _{1} x_{0}]\ \mathscr {D}_{2}$
-fellow travel, which contradicts the assumption. Hence, we instead have a point
![]() $p \in [h_{1}x_{0}, h_{2}x_{0}]$
that belongs to
$p \in [h_{1}x_{0}, h_{2}x_{0}]$
that belongs to
![]() $N_{\mathscr {D}_{0}(\epsilon )}(\eta )$
.
$N_{\mathscr {D}_{0}(\epsilon )}(\eta )$
.
We now consider a subsegment
![]() $\eta ' = [z, z']$
of
$\eta ' = [z, z']$
of
![]() $[h_{2}x_{0}, h_{2} \psi _{2} x_{0}]$
with
$[h_{2}x_{0}, h_{2} \psi _{2} x_{0}]$
with
![]() $d(z, z') = \mathscr {C}_{0}(\epsilon )$
and
$d(z, z') = \mathscr {C}_{0}(\epsilon )$
and
![]() $d(h_{2}x_{0}, z) = K$
. By Theorem 4.7, either
$d(h_{2}x_{0}, z) = K$
. By Theorem 4.7, either
![]() $[h_{1}x_{0}, h_{2} \psi _{2} x_{0}]$
or
$[h_{1}x_{0}, h_{2} \psi _{2} x_{0}]$
or
![]() $[h_{1}x_{0}, h_{2}x_{0}]$
intersects the
$[h_{1}x_{0}, h_{2}x_{0}]$
intersects the
![]() $\mathscr {D}_{0}(\epsilon )$
-neighborhood of
$\mathscr {D}_{0}(\epsilon )$
-neighborhood of
![]() $\eta $
.
$\eta $
.
Suppose that there exists a point
![]() $q \in [h_{1} x_{0}, h_{2}x_{0}]$
that belongs to
$q \in [h_{1} x_{0}, h_{2}x_{0}]$
that belongs to
![]() $N_{\mathscr {D}_{0}(\epsilon )}(\eta ')$
. Then from the inequalities
$N_{\mathscr {D}_{0}(\epsilon )}(\eta ')$
. Then from the inequalities
 $$ \begin{align*}\begin{aligned} |d(h_{2}x_{0}, p) - d(h_{2}x_{0}, y)| &\le \operatorname{diam}(\eta) + \mathscr{D}_{0}(\epsilon), \\ |d(h_{2}x_{0}, q) - d(h_{2}x_{0}, z)| &\le \operatorname{diam}(\eta') + \mathscr{D}_{0}(\epsilon) \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} |d(h_{2}x_{0}, p) - d(h_{2}x_{0}, y)| &\le \operatorname{diam}(\eta) + \mathscr{D}_{0}(\epsilon), \\ |d(h_{2}x_{0}, q) - d(h_{2}x_{0}, z)| &\le \operatorname{diam}(\eta') + \mathscr{D}_{0}(\epsilon) \end{aligned} \end{align*} $$
and the fact that
![]() $h_{2} x_{0}, p, q$
are on the same geodesic, we have
$h_{2} x_{0}, p, q$
are on the same geodesic, we have
 $$ \begin{align*}\begin{aligned} d(p, q) &= |d(h_{2} x_{0}, p) - d(h_{2} x_{0}, q)|\\ &\le \operatorname{diam}(\eta) + \operatorname{diam}(\eta') + 2\mathscr{D}_{0}(\epsilon). \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} d(p, q) &= |d(h_{2} x_{0}, p) - d(h_{2} x_{0}, q)|\\ &\le \operatorname{diam}(\eta) + \operatorname{diam}(\eta') + 2\mathscr{D}_{0}(\epsilon). \end{aligned} \end{align*} $$
This in turn implies
 $$ \begin{align*}\begin{aligned} d(h_{2} \psi_{1} x_{0}, h_{2} \psi_{2} x_{0}) &\le d(h_{2} \psi_{1} x_{0}, y) + d(y, p) + d(p, q) + d(q, z) + d(z, h_{2} \psi_{2} x_{0}) \\ &\le [d(h_{2} x_{0}, h_{2} \psi_{1} x_{0}) - K] + [\mathscr{C}_{0}(\epsilon) + \mathscr{D}_{0}(\epsilon)] + [2\mathscr{C}_{0}(\epsilon) + 2 \mathscr{D}_{0}(\epsilon)] \\ & \quad+ [\mathscr{C}_{0}(\epsilon) + \mathscr{D}_{0}(\epsilon)] + [d(h_{2} x_{0}, h_{2} \psi_{2} x_{0}) - K] \\ &\le d(h_{2} x_{0}, h_{2}\psi_{1} x_{0}) + d(h_{2} x_{0}, h_{2} \psi_{2} x_{0}) - 2C_{Grom}. \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} d(h_{2} \psi_{1} x_{0}, h_{2} \psi_{2} x_{0}) &\le d(h_{2} \psi_{1} x_{0}, y) + d(y, p) + d(p, q) + d(q, z) + d(z, h_{2} \psi_{2} x_{0}) \\ &\le [d(h_{2} x_{0}, h_{2} \psi_{1} x_{0}) - K] + [\mathscr{C}_{0}(\epsilon) + \mathscr{D}_{0}(\epsilon)] + [2\mathscr{C}_{0}(\epsilon) + 2 \mathscr{D}_{0}(\epsilon)] \\ & \quad+ [\mathscr{C}_{0}(\epsilon) + \mathscr{D}_{0}(\epsilon)] + [d(h_{2} x_{0}, h_{2} \psi_{2} x_{0}) - K] \\ &\le d(h_{2} x_{0}, h_{2}\psi_{1} x_{0}) + d(h_{2} x_{0}, h_{2} \psi_{2} x_{0}) - 2C_{Grom}. \end{aligned} \end{align*} $$
This contradicts the fact that
![]() $(\psi _{1} x_{0}, \psi _{2} x_{0})_{x_{0}} < C_{Grom}$
.
$(\psi _{1} x_{0}, \psi _{2} x_{0})_{x_{0}} < C_{Grom}$
.
Hence, we instead have a point
![]() $q \in [h_{1}x_{0}, h_{2} \psi _{2} x_{0}]$
that is within distance
$q \in [h_{1}x_{0}, h_{2} \psi _{2} x_{0}]$
that is within distance
![]() $\mathscr {D}_{0}(\epsilon )$
from
$\mathscr {D}_{0}(\epsilon )$
from
![]() $\eta $
. Then we have
$\eta $
. Then we have
Corollary 4.6 then tells us that
![]() $[q, h_{2}\psi _{2} x_{0}]$
and
$[q, h_{2}\psi _{2} x_{0}]$
and
![]() $[h_{2} x_{0}, h_{2} \psi _{2} x_{0}]\ \mathscr {D}_{2}$
-fellow travel as desired.
$[h_{2} x_{0}, h_{2} \psi _{2} x_{0}]\ \mathscr {D}_{2}$
-fellow travel as desired.
(3) is deduced from a similar argument.
5 Random walks on Teichmüller space
In this section, we adapt the proof of Theorem A to deal with Teichmüller space. Before delving into details, we briefly sketch our plan. We will define persistent joints in sample paths and pivot the path at those joints as in section 3. (See Figure 5.) The basic philosophy of section 3 was using Property 2.3 for hyperbolic spaces. More precisely, we applied Property 2.3 to the Gromov products
to conclude that
![]() $(x_{n}^{\sigma }, x_{n\rightarrow 0}^{\sigma })_{x_{0}}$
is small enough. This led to the lower bound on
$(x_{n}^{\sigma }, x_{n\rightarrow 0}^{\sigma })_{x_{0}}$
is small enough. This led to the lower bound on
![]() $\tau (w_{n}^{\sigma })$
.
$\tau (w_{n}^{\sigma })$
.
Our aim is to copy this phenomenon to the Teichmüller space X. However, several issues arise due to the fact that X is not Gromov hyperbolic:
-
• Property 2.3 among the Gromov products may not hold;
-
• small
 $(x_{n}^{\sigma }, x_{n \rightarrow 0}^{\sigma })_{x_{0}}$
may not lead to large translation length of
$(x_{n}^{\sigma }, x_{n \rightarrow 0}^{\sigma })_{x_{0}}$
may not lead to large translation length of
 $w_{n}^{\sigma }$
.
$w_{n}^{\sigma }$
.
In order to overcome these difficulties, we copy the following property of Gromov hyperbolicity: for a geodesic triangle with vertices x, y and z, the edge
![]() $[x, y]$
fellow travels with either
$[x, y]$
fellow travels with either
![]() $[x, z]$
or
$[x, z]$
or
![]() $[z, x]$
. Thanks to Rafi’s theorems (Corollary 4.6 and Theorem 4.7), we can partially guarantee such a phenomenon among certain Teichmüller geodesics witnessed by pseudo-Anosov mapping classes.
$[z, x]$
. Thanks to Rafi’s theorems (Corollary 4.6 and Theorem 4.7), we can partially guarantee such a phenomenon among certain Teichmüller geodesics witnessed by pseudo-Anosov mapping classes.
We now begin our discussion. Recall that
![]() $\mu $
is a non-elementary probability measure on the mapping class group G. We have fixed two independent pseudo-Anosov mapping classes
$\mu $
is a non-elementary probability measure on the mapping class group G. We have fixed two independent pseudo-Anosov mapping classes
![]() $\phi _{+}$
,
$\phi _{+}$
,
![]() $\phi _{-}$
in
$\phi _{-}$
in
![]() $\operatorname {supp} \mu ^{L}$
for some
$\operatorname {supp} \mu ^{L}$
for some
![]() $L>0$
. Here,
$L>0$
. Here,
![]() $\phi _{\pm }$
are associated with constants
$\phi _{\pm }$
are associated with constants
![]() $\epsilon , \mathscr {M}, C_{Grom}$
and
$\epsilon , \mathscr {M}, C_{Grom}$
and
![]() $\mathscr {F}$
that satisfy Lemma 4.8, Lemma 4.11 and Corollary 4.14. We have also defined constants
$\mathscr {F}$
that satisfy Lemma 4.8, Lemma 4.11 and Corollary 4.14. We have also defined constants
![]() $\mathscr {D}_{j}, \epsilon _{j}$
as in Display 4.2 and assumed Inequality 4.3.
$\mathscr {D}_{j}, \epsilon _{j}$
as in Display 4.2 and assumed Inequality 4.3.
Let
![]() $a_{i}, b_{i} \in \operatorname {supp} \mu $
be the letters for
$a_{i}, b_{i} \in \operatorname {supp} \mu $
be the letters for
![]() $\phi _{\pm }$
satisfying
$\phi _{\pm }$
satisfying
![]() $\phi _{+}= b_{1} \cdots b_{L}$
and
$\phi _{+}= b_{1} \cdots b_{L}$
and
![]() $\phi _{-}= a_{1} \cdots a_{L}$
. As before, we fix the following notations:
$\phi _{-}= a_{1} \cdots a_{L}$
. As before, we fix the following notations:
 $$ \begin{align*}\begin{aligned} p_{+} &= \mu(a_{1}) \cdots \mu(a_{L}) , \\ p_{-} &= \mu(b_{1}) \cdots \mu(b_{L}), \\ P &= \max\left(\frac{p_{+}}{p_{+}+ p_{-}}, \frac{p_{-}}{p_{+} + p_{-}}\right). \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} p_{+} &= \mu(a_{1}) \cdots \mu(a_{L}) , \\ p_{-} &= \mu(b_{1}) \cdots \mu(b_{L}), \\ P &= \max\left(\frac{p_{+}}{p_{+}+ p_{-}}, \frac{p_{-}}{p_{+} + p_{-}}\right). \end{aligned} \end{align*} $$
This time, we define
![]() $\chi _{k}(\omega )$
as follows.
$\chi _{k}(\omega )$
as follows.
![]() $\chi _{k}(\omega ) = 1$
if
$\chi _{k}(\omega ) = 1$
if
-
(1)
 $$ \begin{align*} (g_{3(k-1)L + 1}, \ldots, g_{3kL})= \left\{ \begin{array}{c} (b_{1}, \ldots, b_{L}, a_{1}, \ldots, a_{L}, b_{1}, \ldots, b_{L}) \\ \textrm{or} \\ (b_{1}, \ldots, b_{L}, b_{1}, \ldots, b_{L}, b_{1}, \ldots, b_{L})\end{array} \right., \end{align*} $$
$$ \begin{align*} (g_{3(k-1)L + 1}, \ldots, g_{3kL})= \left\{ \begin{array}{c} (b_{1}, \ldots, b_{L}, a_{1}, \ldots, a_{L}, b_{1}, \ldots, b_{L}) \\ \textrm{or} \\ (b_{1}, \ldots, b_{L}, b_{1}, \ldots, b_{L}, b_{1}, \ldots, b_{L})\end{array} \right., \end{align*} $$
-
(2)
 $[x_{0}, x_{(3k-2)L \rightarrow n}]$
is
$[x_{0}, x_{(3k-2)L \rightarrow n}]$
is
 $\mathscr {D}_{1}$
-witnessed by
$\mathscr {D}_{1}$
-witnessed by
 $\phi _{+}^{-1}$
for
$\phi _{+}^{-1}$
for
 $n \le 3(k-1)L$
, and
$n \le 3(k-1)L$
, and -
(3)
 $[x_{0}, x_{(3k-1)L \rightarrow n}]$
is
$[x_{0}, x_{(3k-1)L \rightarrow n}]$
is
 $\mathscr {D}_{1}$
-witnessed by
$\mathscr {D}_{1}$
-witnessed by
 $\phi _{+}$
for
$\phi _{+}$
for
 $n \ge 3kL$
,
$n \ge 3kL$
,
and
![]() $\chi _{k}(\operatorname {\omega })=0$
otherwise.
$\chi _{k}(\operatorname {\omega })=0$
otherwise.
We first observe that
![]() $\operatorname {\mathbb {E}}(\chi _{1}(\operatorname {\omega }))> 0$
. The probability for condition (1) is
$\operatorname {\mathbb {E}}(\chi _{1}(\operatorname {\omega }))> 0$
. The probability for condition (1) is
![]() $(p_{+} + p_{-}) p_{-}^{2} \neq 0$
. Given (1) as the prior condition, (2) and (3) become independent events. Moreover, since
$(p_{+} + p_{-}) p_{-}^{2} \neq 0$
. Given (1) as the prior condition, (2) and (3) become independent events. Moreover, since
![]() $\mathscr {F} \le \mathscr {D}_{1}$
, Corollary 4.14 tells us that (2) and (3) hold for nonzero probability. Hence, we conclude that
$\mathscr {F} \le \mathscr {D}_{1}$
, Corollary 4.14 tells us that (2) and (3) hold for nonzero probability. Hence, we conclude that
![]() $\eta := \operatorname {\mathbb {P}}(\chi _{1}(\operatorname {\omega }) =1) \neq 0$
.
$\eta := \operatorname {\mathbb {P}}(\chi _{1}(\operatorname {\omega }) =1) \neq 0$
.
Note that
![]() $\chi _{k}(\operatorname {\omega }) = \chi _{1}(T^{3(k-1)L} \operatorname {\omega })$
. We define
$\chi _{k}(\operatorname {\omega }) = \chi _{1}(T^{3(k-1)L} \operatorname {\omega })$
. We define
![]() $W_{n} = \sum _{k=1}^{n} \chi _{k}(\operatorname {\omega })$
. Then
$W_{n} = \sum _{k=1}^{n} \chi _{k}(\operatorname {\omega })$
. Then
![]() $W_{n+m} = W_{n} + W_{m} \circ T^{3Ln}$
holds. Since
$W_{n+m} = W_{n} + W_{m} \circ T^{3Ln}$
holds. Since
![]() $W_{1}$
is bounded, it has finite first moment. Applying Theorem 3.4, we get almost everywhere convergence of
$W_{1}$
is bounded, it has finite first moment. Applying Theorem 3.4, we get almost everywhere convergence of
![]() $\frac {1}{n} W_{n}$
to an a.e. constant variable
$\frac {1}{n} W_{n}$
to an a.e. constant variable
![]() $W_{\infty }$
. Since
$W_{\infty }$
. Since
![]() $\mathbb {E}(\frac {1}{n} W_{n}) = \eta> 0$
, we have
$\mathbb {E}(\frac {1}{n} W_{n}) = \eta> 0$
, we have
![]() $W_{\infty } = \eta $
a.e.
$W_{\infty } = \eta $
a.e.
We also consider a modified version of
![]() $W_{n}$
as in section 3. Given positive integers
$W_{n}$
as in section 3. Given positive integers
![]() $n \le m$
, we say that
$n \le m$
, we say that
![]() $\mathcal {N}_{m, n} = \{n_1 < \cdots < n_k\} \subseteq 3L\operatorname {\mathbb {Z}}$
is an
$\mathcal {N}_{m, n} = \{n_1 < \cdots < n_k\} \subseteq 3L\operatorname {\mathbb {Z}}$
is an
![]() $(m, n)$
-set of pivots for
$(m, n)$
-set of pivots for
![]() $\vec {w} = (w_{1}, \cdots , w_{m})$
if the following holds:
$\vec {w} = (w_{1}, \cdots , w_{m})$
if the following holds:
-
(1)
 $\mathcal {N}_{m, n} \subseteq \{1, \ldots , n\}$
;
$\mathcal {N}_{m, n} \subseteq \{1, \ldots , n\}$
; -
(2) for each i,
 $$ \begin{align*} \left(g_{n_{i}-3L+1}, \ldots, g_{n_{i}}\right)= \left\{ \begin{array}{c} \left(b_{1}, \ldots, b_{L}, a_{1}, \ldots, a_{L}, b_{1}, \ldots, b_{L}\right) \\ \textrm{or, } \\ \left(b_{1}, \ldots, b_{L}, b_{1}, \ldots, b_{L}, b_{1}, \ldots, b_{L}\right)\end{array} \right., \end{align*} $$
$$ \begin{align*} \left(g_{n_{i}-3L+1}, \ldots, g_{n_{i}}\right)= \left\{ \begin{array}{c} \left(b_{1}, \ldots, b_{L}, a_{1}, \ldots, a_{L}, b_{1}, \ldots, b_{L}\right) \\ \textrm{or, } \\ \left(b_{1}, \ldots, b_{L}, b_{1}, \ldots, b_{L}, b_{1}, \ldots, b_{L}\right)\end{array} \right., \end{align*} $$
-
(3) for each i,
 $[x_{0}, x_{n_{i} - 2L\rightarrow j}]$
is
$[x_{0}, x_{n_{i} - 2L\rightarrow j}]$
is
 $\mathscr {D}_{1}$
-witnessed by
$\mathscr {D}_{1}$
-witnessed by
 $\phi _{+}^{-1}$
for
$\phi _{+}^{-1}$
for
 $n_{i-1} - L \le j \le n_{i} - 3L$
, and
$n_{i-1} - L \le j \le n_{i} - 3L$
, and -
(4) for each i,
 $[x_{0}, x_{n_{i} - L\rightarrow j}]$
is
$[x_{0}, x_{n_{i} - L\rightarrow j}]$
is
 $\mathscr {D}_{1}$
-witnessed by
$\mathscr {D}_{1}$
-witnessed by
 $\phi _{+}$
for
$\phi _{+}$
for
 $n_{i} \le j \le n_{i+1} - 2L$
.
$n_{i} \le j \le n_{i+1} - 2L$
.
For convenience, we set
![]() $n_{0} = L$
and
$n_{0} = L$
and
![]() $n_{k+1} = m+2L$
.
$n_{k+1} = m+2L$
.
As before, we denote the maximal
![]() $(m, n)$
-set of pivots of
$(m, n)$
-set of pivots of
![]() $\vec {w}$
by
$\vec {w}$
by
![]() $\mathcal {N}(\vec {w}) = \mathcal {N}_{m, n}(\vec {w})$
, whose cardinality is denoted by
$\mathcal {N}(\vec {w}) = \mathcal {N}_{m, n}(\vec {w})$
, whose cardinality is denoted by
![]() $W_{n}^{m}$
. Note that
$W_{n}^{m}$
. Note that
![]() $W_{n}^{n} \ge W_{\lfloor n/3L \rfloor }$
always holds.
$W_{n}^{n} \ge W_{\lfloor n/3L \rfloor }$
always holds.
Now given a finite path
![]() $\vec {w} = (w_{1}, \ldots , w_{n})$
with
$\vec {w} = (w_{1}, \ldots , w_{n})$
with
![]() $\mathcal {N}_{n, n}(\vec {w}) = \{n_{1} < \ldots < n_{k}\}$
, we define the following:
$\mathcal {N}_{n, n}(\vec {w}) = \{n_{1} < \ldots < n_{k}\}$
, we define the following:
 $$ \begin{align*}\begin{aligned} A_{i}'(\vec{w}) &:= n_{i}(\vec{w}) - 3L,\\ \alpha_{i}'(\vec{w}) &:= n_{i}(\vec{w}) - 2L,\\ \beta_{i}'(\vec{w}) &:= n_{i}(\vec{w}) - L, \\ B_{i}'(\vec{w}) &= n_{i}(\vec{w}). \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} A_{i}'(\vec{w}) &:= n_{i}(\vec{w}) - 3L,\\ \alpha_{i}'(\vec{w}) &:= n_{i}(\vec{w}) - 2L,\\ \beta_{i}'(\vec{w}) &:= n_{i}(\vec{w}) - L, \\ B_{i}'(\vec{w}) &= n_{i}(\vec{w}). \end{aligned} \end{align*} $$
Next, we set
for
![]() $i=1, \ldots , k$
and
$i=1, \ldots , k$
and
![]() $h_{0}' = id$
,
$h_{0}' = id$
,
![]() $h_{2k+1}' = w_{n}$
. We can now discuss an analogue of Lemma 3.5:
$h_{2k+1}' = w_{n}$
. We can now discuss an analogue of Lemma 3.5:
Lemma 5.1. The sequence
![]() $(h_{i-1}^{\prime -1} h_{i}')_{i=1}^{2k+1}$
is
$(h_{i-1}^{\prime -1} h_{i}')_{i=1}^{2k+1}$
is
![]() $\mathscr {D}_{1}$
-marked with repulsive sequences
$\mathscr {D}_{1}$
-marked with repulsive sequences
where
![]() $\phi _{i}' := h_{2i-1}^{\prime -1} h_{2i}'$
is either
$\phi _{i}' := h_{2i-1}^{\prime -1} h_{2i}'$
is either
![]() $\phi _{+}$
or
$\phi _{+}$
or
![]() $\phi _{-}$
. We also have
$\phi _{-}$
. We also have
![]() $h_{i}^{\prime -1} h_{j} \in \mathcal {C}_{\mathscr {D}_{2}}(\psi \rightarrow \psi ')$
for
$h_{i}^{\prime -1} h_{j} \in \mathcal {C}_{\mathscr {D}_{2}}(\psi \rightarrow \psi ')$
for
![]() $0 \le i < j \le 2k+1$
, where
$0 \le i < j \le 2k+1$
, where
 $$ \begin{align*} \psi = \left\{ \begin{array}{cc} \phi_{+} & i\ \textrm{is odd} \\ \phi_{i/2}' & i\ \textrm{is even} \end{array} \right.,\quad\psi' = \left\{ \begin{array}{cc} \phi_{(i+1)/2}' & i\ \textrm{is odd} \\ \phi_{+} & i\ \textrm{is even} \end{array} \right.. \end{align*} $$
$$ \begin{align*} \psi = \left\{ \begin{array}{cc} \phi_{+} & i\ \textrm{is odd} \\ \phi_{i/2}' & i\ \textrm{is even} \end{array} \right.,\quad\psi' = \left\{ \begin{array}{cc} \phi_{(i+1)/2}' & i\ \textrm{is odd} \\ \phi_{+} & i\ \textrm{is even} \end{array} \right.. \end{align*} $$
Here, we set
![]() $\phi _{0}' = \phi _{k+1}' = id$
for convenience.
$\phi _{0}' = \phi _{k+1}' = id$
for convenience.
Moreover, we have
for each
![]() $0 \le i \le j \le l \le 2k+1$
.
$0 \le i \le j \le l \le 2k+1$
.
Proof. For each
![]() $i = 1, \ldots , k$
,
$i = 1, \ldots , k$
,
![]() $h_{2i-1}^{\prime -1} h_{2i}' = w_{\alpha _{i}'(\vec {w})}^{-1} w_{\beta _{i}'(\vec {w})} = \phi _{i}'$
for some
$h_{2i-1}^{\prime -1} h_{2i}' = w_{\alpha _{i}'(\vec {w})}^{-1} w_{\beta _{i}'(\vec {w})} = \phi _{i}'$
for some
![]() $\phi _{i}' \in \{\phi _{+}, \phi _{-}\}$
. Lemma 4.15 then tells us that
$\phi _{i}' \in \{\phi _{+}, \phi _{-}\}$
. Lemma 4.15 then tells us that
![]() $h_{2i-1}^{\prime -1} h_{2i}' \in \mathcal {C}_{\mathscr {D}_{1}}(\phi _{i}' \rightarrow \phi _{i}')$
.
$h_{2i-1}^{\prime -1} h_{2i}' \in \mathcal {C}_{\mathscr {D}_{1}}(\phi _{i}' \rightarrow \phi _{i}')$
.
Moreover, for each
![]() $i=2, \ldots , k$
, Condition (3) and (4) for an
$i=2, \ldots , k$
, Condition (3) and (4) for an
![]() $(m,n)$
-set of pivots tell us that
$(m,n)$
-set of pivots tell us that
-
(1)
 $[x_{0}, x_{n_{i} - 2L\rightarrow n_{i-1} - L}] = [x_{0}, x_{\alpha _{i}'(\vec {w})\rightarrow \beta _{i-1}'(\vec {w})}]$
is
$[x_{0}, x_{n_{i} - 2L\rightarrow n_{i-1} - L}] = [x_{0}, x_{\alpha _{i}'(\vec {w})\rightarrow \beta _{i-1}'(\vec {w})}]$
is
 $\mathscr {D}_{1}$
-witnessed by
$\mathscr {D}_{1}$
-witnessed by
 $\phi _{+}^{-1}$
, and
$\phi _{+}^{-1}$
, and -
(2)
 $[x_{0}, x_{n_{i-1} - L\rightarrow n_{i} - 2L}] = [x_{0}, x_{\beta _{i-1}'(\vec {w})\rightarrow \alpha _{i}'(\vec {w})}]$
is
$[x_{0}, x_{n_{i-1} - L\rightarrow n_{i} - 2L}] = [x_{0}, x_{\beta _{i-1}'(\vec {w})\rightarrow \alpha _{i}'(\vec {w})}]$
is
 $\mathscr {D}_{1}$
-witnessed by
$\mathscr {D}_{1}$
-witnessed by
 $\phi _{+}$
.
$\phi _{+}$
.
This means that
![]() $h_{2i-2}^{\prime -1} h_{2i-1}' = w_{\beta _{i-1}'(\vec {w})}^{-1} w_{\alpha _{i}'(\vec {w})}$
belongs to
$h_{2i-2}^{\prime -1} h_{2i-1}' = w_{\beta _{i-1}'(\vec {w})}^{-1} w_{\alpha _{i}'(\vec {w})}$
belongs to
![]() $\mathcal {C}_{\mathscr {D}_{1}}(\phi _{+} \rightarrow \phi _{+})$
. Similarly, we observe
$\mathcal {C}_{\mathscr {D}_{1}}(\phi _{+} \rightarrow \phi _{+})$
. Similarly, we observe
![]() $h_{1}' \in \mathcal {C}_{\mathscr {D}_{1}}(0 \rightarrow \phi _{+})$
and
$h_{1}' \in \mathcal {C}_{\mathscr {D}_{1}}(0 \rightarrow \phi _{+})$
and
![]() $h_{2k+1}' \in \mathcal {C}_{\mathscr {D}_{1}}(\phi _{+}\rightarrow 0)$
. Since
$h_{2k+1}' \in \mathcal {C}_{\mathscr {D}_{1}}(\phi _{+}\rightarrow 0)$
. Since
![]() $\phi _{i}'$
is either
$\phi _{i}'$
is either
![]() $\phi _{+}$
or
$\phi _{+}$
or
![]() $\phi _{-}$
,
$\phi _{-}$
,
![]() $\phi _{i}'$
and
$\phi _{i}'$
and
![]() $\phi _{+}^{-1}$
are distinct for each i. This concludes that
$\phi _{+}^{-1}$
are distinct for each i. This concludes that
![]() $(h_{i-1}^{\prime -1} h_{i}')_{i=1}^{2k+1}$
is
$(h_{i-1}^{\prime -1} h_{i}')_{i=1}^{2k+1}$
is
![]() $\mathscr {D}_{1}$
-marked with repulsive sequences
$\mathscr {D}_{1}$
-marked with repulsive sequences
Lemma 4.18 then tells us that
![]() $h_{i}^{\prime -1} h_{j} \in \mathcal {C}_{\mathscr {D}_{2}} (\psi \rightarrow \psi ')$
for each pair
$h_{i}^{\prime -1} h_{j} \in \mathcal {C}_{\mathscr {D}_{2}} (\psi \rightarrow \psi ')$
for each pair
![]() $(i, j)$
and the corresponding
$(i, j)$
and the corresponding
![]() $\psi $
,
$\psi $
,
![]() $\psi '$
. Moreover, Corollary 4.20 implies Inequality 5.1 for each triple
$\psi '$
. Moreover, Corollary 4.20 implies Inequality 5.1 for each triple
![]() $(i, j, l)$
.
$(i, j, l)$
.
Finally, for each
![]() $i = 2, \ldots , 2k+1$
,
$i = 2, \ldots , 2k+1$
,
![]() $h_{i-1}^{\prime -1} h_{i}'$
is
$h_{i-1}^{\prime -1} h_{i}'$
is
![]() $\mathscr {D}_{1}$
-witnessed by either
$\mathscr {D}_{1}$
-witnessed by either
![]() $\phi _{+}$
or
$\phi _{+}$
or
![]() $\phi _{-}$
. Moreover,
$\phi _{-}$
. Moreover,
![]() $h_{1}^{\prime -1}$
is
$h_{1}^{\prime -1}$
is
![]() $\mathscr {D}_{1}$
-witnessed by
$\mathscr {D}_{1}$
-witnessed by
![]() $\phi _{+}^{-1}$
. Hence, for
$\phi _{+}^{-1}$
. Hence, for
![]() $i = 1, \ldots , 2k+1$
, we have
$i = 1, \ldots , 2k+1$
, we have
We now set
 $$ \begin{align*}\begin{aligned} M&>1000(1 + L + L/\mathscr{D}_{3} + \mathscr{D}_{3} + Z),\\ &D =10\eta/M,\quad 0.9 \le Q \le 1, \\ \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} M&>1000(1 + L + L/\mathscr{D}_{3} + \mathscr{D}_{3} + Z),\\ &D =10\eta/M,\quad 0.9 \le Q \le 1, \\ \end{aligned} \end{align*} $$
and
 $$ \begin{align*}\begin{aligned} F_{n} &:=\left\{ \vec{w} = (w_{1}, \cdots, w_{n}) : W_{n}^{n} \ge \frac{\eta n}{6L}+1\right\}, \\ G_{n}&:= \left\{ \vec{w} \in F_{n}: \tau(w_{n}) \le \left(2D-\frac{2\eta}{M}\right)n\right\}. \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} F_{n} &:=\left\{ \vec{w} = (w_{1}, \cdots, w_{n}) : W_{n}^{n} \ge \frac{\eta n}{6L}+1\right\}, \\ G_{n}&:= \left\{ \vec{w} \in F_{n}: \tau(w_{n}) \le \left(2D-\frac{2\eta}{M}\right)n\right\}. \end{aligned} \end{align*} $$
As before, for
![]() $\vec {w} \in F_{n}$
and
$\vec {w} \in F_{n}$
and
![]() $Q> 0$
, we also define
$Q> 0$
, we also define
 $$ \begin{align*}\begin{aligned} \mathcal{N}_{f}(\vec{w};Q) &:= \left\{ s \in \mathcal{N}(\vec{w}) : d(x_{0}, x_{s - L}) \le \frac{1}{2} d(x_{0}, x_{n}) -(D+Q\eta/M)n \right\},\\ \mathcal{N}_{b}(\vec{w};Q) &= \left\{ s \in \mathcal{N}(\vec{w}): d(x_{n}, x_{s - 2L}) \le \frac{1}{2} d(x_{0}, x_{n}) - (D+Q\eta/M)n\right\},\\ \mathcal{N}_{0}(\vec{w};Q) &:= \mathcal{N}(\vec{w})\setminus (\mathcal{N}_{f}(\vec{w};Q) \cup \mathcal{N}_{b}(\vec{w};Q)). \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} \mathcal{N}_{f}(\vec{w};Q) &:= \left\{ s \in \mathcal{N}(\vec{w}) : d(x_{0}, x_{s - L}) \le \frac{1}{2} d(x_{0}, x_{n}) -(D+Q\eta/M)n \right\},\\ \mathcal{N}_{b}(\vec{w};Q) &= \left\{ s \in \mathcal{N}(\vec{w}): d(x_{n}, x_{s - 2L}) \le \frac{1}{2} d(x_{0}, x_{n}) - (D+Q\eta/M)n\right\},\\ \mathcal{N}_{0}(\vec{w};Q) &:= \mathcal{N}(\vec{w})\setminus (\mathcal{N}_{f}(\vec{w};Q) \cup \mathcal{N}_{b}(\vec{w};Q)). \end{aligned} \end{align*} $$
Lemma 5.2. For sufficiently large n, if
![]() $\vec {w} \in F_{n}$
and
$\vec {w} \in F_{n}$
and
![]() $Q \le 1$
, then
$Q \le 1$
, then
holds.
Proof. If not, we have
![]() $|\mathcal {N}_{0}(\vec {w}; Q)| \ge \frac {\eta n}{15 L}+1$
. As in the proof of Lemma 3.7, we can take
$|\mathcal {N}_{0}(\vec {w}; Q)| \ge \frac {\eta n}{15 L}+1$
. As in the proof of Lemma 3.7, we can take
![]() $t, t'$
such that
$t, t'$
such that
![]() $\mathcal {N}_{0}(\vec {w}; Q) = \{n_{t}, n_{t+1}, \ldots , n_{t'}\}$
. Using Inequality 5.1 and 5.2, we obtain
$\mathcal {N}_{0}(\vec {w}; Q) = \{n_{t}, n_{t+1}, \ldots , n_{t'}\}$
. Using Inequality 5.1 and 5.2, we obtain
for large enough n. Moreover, since
![]() $n_{t} \notin \mathcal {N}_{f}(\vec {w};Q)$
and
$n_{t} \notin \mathcal {N}_{f}(\vec {w};Q)$
and
![]() $n_{t'} \notin \mathcal {N}_{b}(\vec {w};Q)$
, we have
$n_{t'} \notin \mathcal {N}_{b}(\vec {w};Q)$
, we have
Combining these inequalities, we obtain
 $$ \begin{align*}\begin{aligned} d(x_{0}, x_{n}) &\ge d(x_{0}, x_{\beta_{t}^{\prime}}) + d(x_{\beta_{t}^{\prime}}, x_{\alpha_{t^{\prime}}^{\prime}}) + d(x_{\alpha_{t^{\prime}}^{\prime}}, x_{n}) - 4\mathscr{D}_{3} \\ &\ge 2\left(\frac{1}{2} d(x_{0}, x_{n}) - (D + Q\eta / M)n\right) + \frac{60\eta n}{M} \\ &\ge d(x_{0}, x_{n}) + \frac{\eta n}{M}, \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} d(x_{0}, x_{n}) &\ge d(x_{0}, x_{\beta_{t}^{\prime}}) + d(x_{\beta_{t}^{\prime}}, x_{\alpha_{t^{\prime}}^{\prime}}) + d(x_{\alpha_{t^{\prime}}^{\prime}}, x_{n}) - 4\mathscr{D}_{3} \\ &\ge 2\left(\frac{1}{2} d(x_{0}, x_{n}) - (D + Q\eta / M)n\right) + \frac{60\eta n}{M} \\ &\ge d(x_{0}, x_{n}) + \frac{\eta n}{M}, \end{aligned} \end{align*} $$
a contradiction.
Thus, when
![]() $Q \le 1$
,
$Q \le 1$
,
 $$ \begin{align*}\begin{aligned} F_{n, f}(Q) & := \left\{ \vec{w} \in F_{n} : |\mathcal{N}_{f}(\vec{w}; Q)| \ge \frac{\eta n}{20 L} \right\},\\ F_{n, b}(Q) & := \left\{\vec{w} \in F_n : |\mathcal{N}_{b}(\vec{w}; Q)| \ge \frac{\eta n}{20L} \right\} \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} F_{n, f}(Q) & := \left\{ \vec{w} \in F_{n} : |\mathcal{N}_{f}(\vec{w}; Q)| \ge \frac{\eta n}{20 L} \right\},\\ F_{n, b}(Q) & := \left\{\vec{w} \in F_n : |\mathcal{N}_{b}(\vec{w}; Q)| \ge \frac{\eta n}{20L} \right\} \end{aligned} \end{align*} $$
cover entire
![]() $F_{n}$
. We also define
$F_{n}$
. We also define
From now on, we will focus on
![]() $\vec {w} \in F_{n, f}(Q)$
; the argument for
$\vec {w} \in F_{n, f}(Q)$
; the argument for
![]() $\vec {w} \in F_{n, b}(Q)$
is analogous.
$\vec {w} \in F_{n, b}(Q)$
is analogous.
For each
![]() $\vec {w} \in F_{n, f}(Q)$
, we fix an integer
$\vec {w} \in F_{n, f}(Q)$
, we fix an integer
![]() $N =N(\vec {w})$
between
$N =N(\vec {w})$
between
![]() $\frac {\eta n}{50M^{2} L}$
and
$\frac {\eta n}{50M^{2} L}$
and
![]() $\frac {\eta n}{20M^{2}L}$
as before and pick pivot indices
$\frac {\eta n}{20M^{2}L}$
as before and pick pivot indices
![]() $p_{1}(\vec {w}), \ldots , p_{N}(\vec {w})$
from
$p_{1}(\vec {w}), \ldots , p_{N}(\vec {w})$
from
![]() $\mathcal {N}_{f}(\vec {w}; Q)$
. We also bring the previous notation
$\mathcal {N}_{f}(\vec {w}; Q)$
. We also bring the previous notation
 $$ \begin{align*} \begin{aligned} A_{i}(\vec{w}) &:= p_{i}(\vec{w}) - 3L,\\ \alpha_{i}(\vec{w}) &:= p_{i}(\vec{w}) - 2L,\\ \beta_{i}(\vec{w}) &:= p_{i}(\vec{w}) - L,\\ B_{i} (\vec{w}) &:= p_{i}(\vec{w}). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} A_{i}(\vec{w}) &:= p_{i}(\vec{w}) - 3L,\\ \alpha_{i}(\vec{w}) &:= p_{i}(\vec{w}) - 2L,\\ \beta_{i}(\vec{w}) &:= p_{i}(\vec{w}) - L,\\ B_{i} (\vec{w}) &:= p_{i}(\vec{w}). \end{aligned} \end{align*} $$
We also let
![]() $\beta _{0}(\vec {w}) = B_{0}(\vec {w}) := 0$
,
$\beta _{0}(\vec {w}) = B_{0}(\vec {w}) := 0$
,
![]() $\alpha _{N+1}(\vec {w}) = A_{N+1}(\vec {w}) := n$
,
$\alpha _{N+1}(\vec {w}) = A_{N+1}(\vec {w}) := n$
,
for
![]() $i=1, \ldots , N$
and
$i=1, \ldots , N$
and
![]() $h_{0} = id$
,
$h_{0} = id$
,
![]() $h_{2k+1} = w_{n}$
. Since
$h_{2k+1} = w_{n}$
. Since
![]() $(\alpha _{i})_{i}$
,
$(\alpha _{i})_{i}$
,
![]() $(\beta _{i})_{i}$
are subsequences of
$(\beta _{i})_{i}$
are subsequences of
![]() $(\alpha _{i}')_{i}$
and
$(\alpha _{i}')_{i}$
and
![]() $(\beta _{i}')_{i}$
, respectively, the marking information from Lemma 5.1 and Lemma 4.18 tells us the following.
$(\beta _{i}')_{i}$
, respectively, the marking information from Lemma 5.1 and Lemma 4.18 tells us the following.
Lemma 5.3. The sequence
![]() $(h_{i-1}^{-1} h_{i})_{i=1}^{2k+1}$
is
$(h_{i-1}^{-1} h_{i})_{i=1}^{2k+1}$
is
![]() $\mathscr {D}_{2}$
-marked with repulsive sequences
$\mathscr {D}_{2}$
-marked with repulsive sequences
where
![]() $\phi _{i} = h_{2i-1}^{-1} h_{2i}$
is either
$\phi _{i} = h_{2i-1}^{-1} h_{2i}$
is either
![]() $\phi _{+}$
or
$\phi _{+}$
or
![]() $\phi _{-}$
. Moreover, we have
$\phi _{-}$
. Moreover, we have
for each
![]() $0 \le i \le j \le l \le 2k+1$
.
$0 \le i \le j \le l \le 2k+1$
.
For each choice
![]() $\sigma \in \{0, 1\}^{N}$
, we define the pivoted
$\sigma \in \{0, 1\}^{N}$
, we define the pivoted
![]() $\vec {w}^{\sigma }$
as before: we modify the type of joints that are marked by
$\vec {w}^{\sigma }$
as before: we modify the type of joints that are marked by
![]() $\sigma $
only. Precisely speaking, the step sequences
$\sigma $
only. Precisely speaking, the step sequences
![]() $(g_{i})_{i}$
and
$(g_{i})_{i}$
and
![]() $(g_{i}^{\sigma })_{i}$
for
$(g_{i}^{\sigma })_{i}$
for
![]() $\vec {w}$
and
$\vec {w}$
and
![]() $\vec {w}^{\sigma }$
coincide except at
$\vec {w}^{\sigma }$
coincide except at
![]() $\alpha _{j} + 1 \le i \le \beta _{j}$
for some j such that
$\alpha _{j} + 1 \le i \le \beta _{j}$
for some j such that
![]() $\sigma (j) = 1$
. For
$\sigma (j) = 1$
. For
![]() $\sigma (j) = 1$
, we set
$\sigma (j) = 1$
, we set
 $$ \begin{align*} (g^{\sigma}_{\alpha_j + 1}, \ldots, g^{\sigma}_{\beta_j}) := \begin{cases} (a_1, \ldots, a_L) &\mbox{if } (g_{\alpha_j + 1}, \ldots, g_{\beta_j}) = (b_1, \ldots, b_L)\\ (b_1, \ldots, b_L) &\mbox{if } (g_{\alpha_j + 1}, \ldots, g_{\beta_j}) = (a_1, \ldots, a_L). \end{cases} \end{align*} $$
$$ \begin{align*} (g^{\sigma}_{\alpha_j + 1}, \ldots, g^{\sigma}_{\beta_j}) := \begin{cases} (a_1, \ldots, a_L) &\mbox{if } (g_{\alpha_j + 1}, \ldots, g_{\beta_j}) = (b_1, \ldots, b_L)\\ (b_1, \ldots, b_L) &\mbox{if } (g_{\alpha_j + 1}, \ldots, g_{\beta_j}) = (a_1, \ldots, a_L). \end{cases} \end{align*} $$
Other steps remain unchanged. Now, for
we have the following observation:
Lemma 5.4. The sequence
![]() $((h_{i-1}^{\sigma })^{-1} h_{i}^{\sigma })_{i=1}^{2k+1}$
is
$((h_{i-1}^{\sigma })^{-1} h_{i}^{\sigma })_{i=1}^{2k+1}$
is
![]() $\mathscr {D}_{2}$
-marked with repulsive sequences
$\mathscr {D}_{2}$
-marked with repulsive sequences
where
![]() $\phi _{i}^{\sigma } \in \{\phi _{+}, \phi _{-}\}$
and
$\phi _{i}^{\sigma } \in \{\phi _{+}, \phi _{-}\}$
and
![]() $\phi _{i}^{\sigma } = \phi _{i}$
if and only if
$\phi _{i}^{\sigma } = \phi _{i}$
if and only if
![]() $\sigma (i) = 0$
. Moreover, we have
$\sigma (i) = 0$
. Moreover, we have
for each
![]() $0 \le i \le j \le l \le 2k+1$
.
$0 \le i \le j \le l \le 2k+1$
.
Proof. Since
![]() $g_{i} = g_{i}^{\sigma }$
for all i except for
$g_{i} = g_{i}^{\sigma }$
for all i except for
![]() $\alpha _{j+1} \le i \le \beta _{j}$
where
$\alpha _{j+1} \le i \le \beta _{j}$
where
![]() $\sigma (j) = 1$
. In particular, we have
$\sigma (j) = 1$
. In particular, we have
![]() $w_{\beta _{i-1}'(\vec {w}) \rightarrow \alpha _{i}'(\vec {w})}^{\sigma } \in \mathcal {C}_{\mathscr {D}_{1}}(\phi _{+} \rightarrow \phi _{+})$
for various i. Moreover,
$w_{\beta _{i-1}'(\vec {w}) \rightarrow \alpha _{i}'(\vec {w})}^{\sigma } \in \mathcal {C}_{\mathscr {D}_{1}}(\phi _{+} \rightarrow \phi _{+})$
for various i. Moreover,
![]() $w_{\alpha _{i}'(\vec {w}) \rightarrow \beta _{i}'(\vec {w})}^{\sigma } = (\phi _{i}^{\prime \sigma })^{F+1}\in \mathcal {C}_{\mathscr {D}_{1}}(\phi _{i}' \rightarrow \phi _{i}')$
for some
$w_{\alpha _{i}'(\vec {w}) \rightarrow \beta _{i}'(\vec {w})}^{\sigma } = (\phi _{i}^{\prime \sigma })^{F+1}\in \mathcal {C}_{\mathscr {D}_{1}}(\phi _{i}' \rightarrow \phi _{i}')$
for some
![]() $\phi _{i}^{\prime \sigma } \in \{\phi _{+}, \phi _{-}\}$
. Then we have the marking information as in Lemma 5.1 (with constant
$\phi _{i}^{\prime \sigma } \in \{\phi _{+}, \phi _{-}\}$
. Then we have the marking information as in Lemma 5.1 (with constant
![]() $\mathscr {D}_{1}$
), and the marking information as in Lemma 5.3 (with constant
$\mathscr {D}_{1}$
), and the marking information as in Lemma 5.3 (with constant
![]() $\mathscr {D}_{2}$
) by taking subsequences. Finally,
$\mathscr {D}_{2}$
) by taking subsequences. Finally,
![]() $\phi _{i}^{\prime \sigma } \neq \phi _{i}'$
if and only if
$\phi _{i}^{\prime \sigma } \neq \phi _{i}'$
if and only if
![]() $p_{i}'$
is chosen as a pivot index
$p_{i}'$
is chosen as a pivot index
![]() $p_{j}$
such that
$p_{j}$
such that
![]() $\sigma (j) = 1$
. This leads to the condition when
$\sigma (j) = 1$
. This leads to the condition when
![]() $\phi _{i}^{\sigma }$
equals
$\phi _{i}^{\sigma }$
equals
![]() $\phi _{i}$
.
$\phi _{i}$
.
We now prove an analogy of Lemma 3.10 for sufficiently large n in a different way, in the case of the Teichmüller space.
Lemma 5.5. Suppose that
![]() $n \ge (Z + 2 \mathscr {D}_{6})M/\eta $
. If
$n \ge (Z + 2 \mathscr {D}_{6})M/\eta $
. If
![]() $\kappa \neq \sigma \in \{0, 1\}^{N}$
and
$\kappa \neq \sigma \in \{0, 1\}^{N}$
and
![]() $\tau (w_{n}^{\kappa }) \le (2D - 2\eta /M)n$
, then
$\tau (w_{n}^{\kappa }) \le (2D - 2\eta /M)n$
, then
Proof. We first need the result of Claim 3.11. Lemma 5.1 tells us that
 $$ \begin{align*}\begin{aligned} \left|d(x_{0}, x_{n}^{\sigma}) - \left(\sum_{i=1}^{N+1} d(x_{\beta_{i-1}}^{\sigma}, x_{\alpha_{i}}^{\sigma}) +\sum_{i=1}^{N} d(x_{\alpha_{i}}^{\sigma}, x_{\beta_{i}}^{\sigma})\right) \right| \le 2N \mathscr{D}_{3}, \\ \left|d(x_{0}, x_{n}^{\kappa}) - \left(\sum_{i=1}^{N+1} d(x_{\beta_{i-1}}^{\kappa}, x_{\alpha_{i}}^{\kappa}) + \sum_{i=1}^{N} d(x_{\alpha_{i}}^{\kappa}, x_{\beta_{i}}^{\kappa})\right) \right| \le 2N \mathscr{D}_{3}. \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} \left|d(x_{0}, x_{n}^{\sigma}) - \left(\sum_{i=1}^{N+1} d(x_{\beta_{i-1}}^{\sigma}, x_{\alpha_{i}}^{\sigma}) +\sum_{i=1}^{N} d(x_{\alpha_{i}}^{\sigma}, x_{\beta_{i}}^{\sigma})\right) \right| \le 2N \mathscr{D}_{3}, \\ \left|d(x_{0}, x_{n}^{\kappa}) - \left(\sum_{i=1}^{N+1} d(x_{\beta_{i-1}}^{\kappa}, x_{\alpha_{i}}^{\kappa}) + \sum_{i=1}^{N} d(x_{\alpha_{i}}^{\kappa}, x_{\beta_{i}}^{\kappa})\right) \right| \le 2N \mathscr{D}_{3}. \end{aligned} \end{align*} $$
Recall that
-
(1)
 $d(x_{\beta _{i-1}}^{\kappa }, x_{\alpha _{i}}^{\kappa }) = d(x_{\beta _{i-1}}^{\sigma }, x_{\alpha _{i}}^{\sigma })$
for all i,
$d(x_{\beta _{i-1}}^{\kappa }, x_{\alpha _{i}}^{\kappa }) = d(x_{\beta _{i-1}}^{\sigma }, x_{\alpha _{i}}^{\sigma })$
for all i, -
(2)
 $d(x_{\alpha _{i}}^{\kappa }, x_{\beta _{i}}^{\kappa }) = d(x_{\alpha _{i}}^{\sigma }, x_{\beta _{i}}^{\sigma })$
for i such that
$d(x_{\alpha _{i}}^{\kappa }, x_{\beta _{i}}^{\kappa }) = d(x_{\alpha _{i}}^{\sigma }, x_{\beta _{i}}^{\sigma })$
for i such that
 $\sigma (i) = 0$
, and
$\sigma (i) = 0$
, and -
(3)
 $|d(x_{\alpha _{i}}^{\kappa }, x_{\beta _{i}}^{\kappa }) - d(x_{\alpha _{i}}^{\sigma }, x_{\beta _{i}}^{\sigma })| \le Z$
.
$|d(x_{\alpha _{i}}^{\kappa }, x_{\beta _{i}}^{\kappa }) - d(x_{\alpha _{i}}^{\sigma }, x_{\beta _{i}}^{\sigma })| \le Z$
.
From these, we deduce that
For similar reasons, we also get
 $$ \begin{align*} \begin{aligned} |d(x_n, x_{\alpha_{i}'}^{\kappa}) - d(x_n, x_{\alpha_{i}'}^{\sigma})|& \le {\eta n \over 40M}, \\ |d(x_0, x_{\beta_{i}'}^{\kappa}) - d(x_0, x_{\beta_{i}'}^{\sigma})|& \le {\eta n \over 40M} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} |d(x_n, x_{\alpha_{i}'}^{\kappa}) - d(x_n, x_{\alpha_{i}'}^{\sigma})|& \le {\eta n \over 40M}, \\ |d(x_0, x_{\beta_{i}'}^{\kappa}) - d(x_0, x_{\beta_{i}'}^{\sigma})|& \le {\eta n \over 40M} \end{aligned} \end{align*} $$
for
![]() $i=1, \cdots , N$
by considering partial sums.
$i=1, \cdots , N$
by considering partial sums.
Among the indices at which
![]() $\sigma $
and
$\sigma $
and
![]() $\kappa $
differ, let i and j be the first and the last ones, respectively. We then have
$\kappa $
differ, let i and j be the first and the last ones, respectively. We then have
 $$ \begin{align} \begin{aligned} d(x_{0}, x_{\alpha(i)}^{\kappa}) + d(x_{0}, x_{\beta(j)}^{\kappa}) &\le d(x_{0}, x_{\alpha(i)}) + d(x_{0}, x_{\beta(j)}) + \frac{\eta n}{20 M} \\ &\le d(x_{0}, x_{n}) - 2(D + Q \eta / M)n + \frac{\eta n}{20 M} \\ &\le d(x_{0}, x_{n}^{\kappa}) - 2(D + 0.9 \eta /M) n \\ &\le d(x_{0}, x_{n}^{\kappa}) - Z \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} d(x_{0}, x_{\alpha(i)}^{\kappa}) + d(x_{0}, x_{\beta(j)}^{\kappa}) &\le d(x_{0}, x_{\alpha(i)}) + d(x_{0}, x_{\beta(j)}) + \frac{\eta n}{20 M} \\ &\le d(x_{0}, x_{n}) - 2(D + Q \eta / M)n + \frac{\eta n}{20 M} \\ &\le d(x_{0}, x_{n}^{\kappa}) - 2(D + 0.9 \eta /M) n \\ &\le d(x_{0}, x_{n}^{\kappa}) - Z \end{aligned} \end{align} $$
for large enough n. We similarly have
Now Inequality 5.7 implies
 $$ \begin{align*}\begin{aligned} d(x_0, x^{\kappa}_{n \to \beta(j)}) & \ge d(x_0, x^{\kappa}_n) - d(x_0, x^{\kappa}_{\beta(j)}) \\ & \ge d(x_0, x^{\kappa}_{\alpha(i)}) + Z. \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} d(x_0, x^{\kappa}_{n \to \beta(j)}) & \ge d(x_0, x^{\kappa}_n) - d(x_0, x^{\kappa}_{\beta(j)}) \\ & \ge d(x_0, x^{\kappa}_{\alpha(i)}) + Z. \end{aligned} \end{align*} $$
Moreover,
![]() $w_{\beta (j) \rightarrow n}^{\kappa }$
is
$w_{\beta (j) \rightarrow n}^{\kappa }$
is
![]() $\mathscr {D}_{2}$
-witnessed by
$\mathscr {D}_{2}$
-witnessed by
![]() $\phi _{+}$
. Lemma 4.22 then tells us that
$\phi _{+}$
. Lemma 4.22 then tells us that
![]() $w_{\beta (j) \rightarrow n}^{\kappa } w_{0 \rightarrow \alpha (i)}^{\kappa } \phi _{\pm }$
is
$w_{\beta (j) \rightarrow n}^{\kappa } w_{0 \rightarrow \alpha (i)}^{\kappa } \phi _{\pm }$
is
![]() $\mathscr {D}_{4}$
-witnessed by
$\mathscr {D}_{4}$
-witnessed by
![]() $\phi _{+}$
. Also note that
$\phi _{+}$
. Also note that
![]() $w_{\beta (j) \rightarrow n}^{\kappa } = w_{\beta (j) \rightarrow n}^{\sigma }$
and
$w_{\beta (j) \rightarrow n}^{\kappa } = w_{\beta (j) \rightarrow n}^{\sigma }$
and
![]() $w_{0 \rightarrow \alpha (i)}^{\kappa } = w_{0 \rightarrow \alpha (i)}^{\sigma }$
.
$w_{0 \rightarrow \alpha (i)}^{\kappa } = w_{0 \rightarrow \alpha (i)}^{\sigma }$
.
At this moment, if
![]() $(\phi _{i}^{\kappa })^{-1} w_{\alpha (i) \rightarrow 0}^{\kappa } w_{n \rightarrow \beta (j)}^{\kappa }$
is
$(\phi _{i}^{\kappa })^{-1} w_{\alpha (i) \rightarrow 0}^{\kappa } w_{n \rightarrow \beta (j)}^{\kappa }$
is
![]() $\mathscr {D}_{2}$
-witnessed by
$\mathscr {D}_{2}$
-witnessed by
![]() $(\phi _{i}^{\kappa })^{-1}$
, then
$(\phi _{i}^{\kappa })^{-1}$
, then
 $$ \begin{align*}\begin{aligned} & \quad \,\,(w_{\beta(j) \rightarrow n}^{\kappa} w_{0 \rightarrow \beta(i)}^{\kappa}\quad \,,w_{\beta(i) \rightarrow \beta(j)}^{\kappa}\, ,w_{\beta(j) \rightarrow n}^{\kappa} w_{0 \rightarrow \beta(i)}^{\kappa}\quad \, , \operatorname{\omega}_{\beta(i) \rightarrow \beta(j)}^{\kappa}\, ,\ldots) \\ &= (w_{\beta(j) \rightarrow n}^{\kappa} w_{0 \rightarrow \alpha(i)}^{\kappa} \phi_{i}^{\kappa}, w_{\beta(i) \rightarrow \beta(j)}^{\kappa}\, ,w_{\beta(j) \rightarrow n}^{\kappa} w_{0 \rightarrow \alpha(i)}^{\kappa} \phi_{i}^{\kappa}, w_{\beta(i) \rightarrow \beta(j)}^{\kappa}\, , \ldots) \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} & \quad \,\,(w_{\beta(j) \rightarrow n}^{\kappa} w_{0 \rightarrow \beta(i)}^{\kappa}\quad \,,w_{\beta(i) \rightarrow \beta(j)}^{\kappa}\, ,w_{\beta(j) \rightarrow n}^{\kappa} w_{0 \rightarrow \beta(i)}^{\kappa}\quad \, , \operatorname{\omega}_{\beta(i) \rightarrow \beta(j)}^{\kappa}\, ,\ldots) \\ &= (w_{\beta(j) \rightarrow n}^{\kappa} w_{0 \rightarrow \alpha(i)}^{\kappa} \phi_{i}^{\kappa}, w_{\beta(i) \rightarrow \beta(j)}^{\kappa}\, ,w_{\beta(j) \rightarrow n}^{\kappa} w_{0 \rightarrow \alpha(i)}^{\kappa} \phi_{i}^{\kappa}, w_{\beta(i) \rightarrow \beta(j)}^{\kappa}\, , \ldots) \end{aligned} \end{align*} $$
is
![]() $\mathscr {D}_{4}$
-marked with repulsive sequences
$\mathscr {D}_{4}$
-marked with repulsive sequences
Corollary 4.21 then tells us that
![]() $(v^{i}x_{0}, v^{k} x_{0})_{v^{j} x_{0}} \le \mathscr {D}_{6}$
for
$(v^{i}x_{0}, v^{k} x_{0})_{v^{j} x_{0}} \le \mathscr {D}_{6}$
for
![]() $v=w_{\beta (j) \rightarrow n}^{\kappa }w_{0 \rightarrow \beta (j)}^{\kappa }$
and
$v=w_{\beta (j) \rightarrow n}^{\kappa }w_{0 \rightarrow \beta (j)}^{\kappa }$
and
![]() $i < j < k$
. This implies
$i < j < k$
. This implies
 $$ \begin{align*} \begin{aligned} \tau(w_{n}^{\kappa}) &= \tau((w_{\beta(j)}^{\kappa})^{-1} w_{n}^{\kappa} w_{\beta(j)}^{\kappa}) \\ &= \lim_{m \rightarrow \infty} \frac{1}{m} d(x_{0}, v^{m} x_{0}) \ge d(x_{0}, vx_{0}) - 2\mathscr{D}_{6} \\ &\ge d(x_{0}, w_{\beta(j) \rightarrow n}^{\kappa} x_{0}) - d(w_{\beta(j) \rightarrow n}^{\kappa}w_{0 \rightarrow \beta(j)}^{\kappa} x_{0}, w_{\beta(j) \rightarrow n}^{\kappa} x_{0}) - 2\mathscr{D}_{6}\\ &\ge d(x_{0}, x_{n}^{\kappa}) - 2d(x_{0}, x_{\beta(j)}^{\kappa}) - 2\mathscr{D}_{6} \\ &\ge 2(D+ 0.95 \eta/M) n - 2\mathscr{D}_{6}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \tau(w_{n}^{\kappa}) &= \tau((w_{\beta(j)}^{\kappa})^{-1} w_{n}^{\kappa} w_{\beta(j)}^{\kappa}) \\ &= \lim_{m \rightarrow \infty} \frac{1}{m} d(x_{0}, v^{m} x_{0}) \ge d(x_{0}, vx_{0}) - 2\mathscr{D}_{6} \\ &\ge d(x_{0}, w_{\beta(j) \rightarrow n}^{\kappa} x_{0}) - d(w_{\beta(j) \rightarrow n}^{\kappa}w_{0 \rightarrow \beta(j)}^{\kappa} x_{0}, w_{\beta(j) \rightarrow n}^{\kappa} x_{0}) - 2\mathscr{D}_{6}\\ &\ge d(x_{0}, x_{n}^{\kappa}) - 2d(x_{0}, x_{\beta(j)}^{\kappa}) - 2\mathscr{D}_{6} \\ &\ge 2(D+ 0.95 \eta/M) n - 2\mathscr{D}_{6}, \end{aligned} \end{align*} $$
which contradicts the fact that
![]() $\tau (w_{n}^{\kappa }) \le (2D - 2\eta /M) n$
.
$\tau (w_{n}^{\kappa }) \le (2D - 2\eta /M) n$
.
Hence,
![]() $(\phi _{i}^{\kappa })^{-1} w_{\alpha (i) \rightarrow 0}^{\kappa } w_{n \rightarrow \beta (j)}^{\kappa }$
is not
$(\phi _{i}^{\kappa })^{-1} w_{\alpha (i) \rightarrow 0}^{\kappa } w_{n \rightarrow \beta (j)}^{\kappa }$
is not
![]() $\mathscr {D}_{2}$
-witnessed by
$\mathscr {D}_{2}$
-witnessed by
![]() $(\phi _{i}^{\kappa })^{-1}$
. Instead, by Lemma 4.22,
$(\phi _{i}^{\kappa })^{-1}$
. Instead, by Lemma 4.22,
![]() $(\phi _{i}^{\sigma })^{-1} w_{\alpha (i) \rightarrow 0}^{\kappa } w_{n \rightarrow \beta (j)}^{\kappa }$
is
$(\phi _{i}^{\sigma })^{-1} w_{\alpha (i) \rightarrow 0}^{\kappa } w_{n \rightarrow \beta (j)}^{\kappa }$
is
![]() $\mathscr {D}_{2}$
-witnessed by
$\mathscr {D}_{2}$
-witnessed by
![]() $(\phi _{i}^{\sigma })^{-1}$
. Then the above argument tells us that
$(\phi _{i}^{\sigma })^{-1}$
. Then the above argument tells us that
![]() $\tau (w_{n}^{\sigma }) \ge (2D + 0.9\eta /M) n$
.
$\tau (w_{n}^{\sigma }) \ge (2D + 0.9\eta /M) n$
.
In particular, for
![]() $\vec {w} \in G_{n, f}(Q)$
,
$\vec {w} \in G_{n, f}(Q)$
,
![]() $\vec {w}^{\sigma } \notin G_{n}$
for any nontrivial
$\vec {w}^{\sigma } \notin G_{n}$
for any nontrivial
![]() $\sigma $
. We now observe an analogue of Lemma 3.15.
$\sigma $
. We now observe an analogue of Lemma 3.15.
Lemma 5.6. Let
![]() $Q=1$
and n be a sufficiently large integer. Suppose that
$Q=1$
and n be a sufficiently large integer. Suppose that
![]() $\vec {w}, \vec {w}' \in G_{n, f}(Q=1)$
and the number of pivots
$\vec {w}, \vec {w}' \in G_{n, f}(Q=1)$
and the number of pivots
![]() $N(\vec {w})$
,
$N(\vec {w})$
,
![]() $N(\vec {w}')$
are
$N(\vec {w}')$
are
![]() $\lfloor \frac {\eta n}{40 M^{2}L}\rfloor $
. Then for
$\lfloor \frac {\eta n}{40 M^{2}L}\rfloor $
. Then for
![]() $\sigma , \sigma ' \in \{0, 1\}^{N}$
,
$\sigma , \sigma ' \in \{0, 1\}^{N}$
,
![]() $\vec {w}^{\sigma } = \vec {w}^{\prime \sigma '}$
if and only if
$\vec {w}^{\sigma } = \vec {w}^{\prime \sigma '}$
if and only if
![]() $\vec {w}= \vec {w}'$
and
$\vec {w}= \vec {w}'$
and
![]() $\sigma = \sigma '$
.
$\sigma = \sigma '$
.
Proof. Let
![]() $\vec {v} = \vec {w}^{\sigma } = \vec {w}^{\prime \sigma '}$
. As before, note that
$\vec {v} = \vec {w}^{\sigma } = \vec {w}^{\prime \sigma '}$
. As before, note that
Moreover, for each
![]() $n_{i} \in \mathcal {N}_{f}(\vec {w}; Q=1)$
, we have
$n_{i} \in \mathcal {N}_{f}(\vec {w}; Q=1)$
, we have
 $$ \begin{align*}\begin{aligned} d(x_{0}, x_{\beta_{i}'}^{\sigma})&\le d(x_{0}, x_{\beta_{i}'}) + \frac{\eta n}{40M}\\ &\le \frac{1}{2} d(x_{0}, x_{n})+ \frac{\eta n}{40M}- \left(D + \frac{\eta}{M}\right)n \\ &\le \frac{1}{2} d(x_{0}, x_{n}^{\sigma}) + \frac{3\eta n}{80M} - \left(D + \frac{\eta}{M}\right)n\\ &\le \frac{1}{2} d(x_{0}, x_{n}^{\sigma})- \left(D + \frac{0.9\eta}{M}\right)n \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} d(x_{0}, x_{\beta_{i}'}^{\sigma})&\le d(x_{0}, x_{\beta_{i}'}) + \frac{\eta n}{40M}\\ &\le \frac{1}{2} d(x_{0}, x_{n})+ \frac{\eta n}{40M}- \left(D + \frac{\eta}{M}\right)n \\ &\le \frac{1}{2} d(x_{0}, x_{n}^{\sigma}) + \frac{3\eta n}{80M} - \left(D + \frac{\eta}{M}\right)n\\ &\le \frac{1}{2} d(x_{0}, x_{n}^{\sigma})- \left(D + \frac{0.9\eta}{M}\right)n \end{aligned} \end{align*} $$
from Claim 3.11. Thus,
![]() $n_{i} \in \mathcal {N}_{f}(\vec {v}; Q = 0.9)$
. It follows that
$n_{i} \in \mathcal {N}_{f}(\vec {v}; Q = 0.9)$
. It follows that
Similarly,
![]() $\mathcal {N}_{f}(\vec {w}'; Q=1) \subseteq \mathcal {N}_{f} (\vec {v}; Q=0.9)$
.
$\mathcal {N}_{f}(\vec {w}'; Q=1) \subseteq \mathcal {N}_{f} (\vec {v}; Q=0.9)$
.
Thus, we are able to pick forward pivots
![]() $p_{i}(\vec {w})$
and
$p_{i}(\vec {w})$
and
![]() $p^{\prime }_{i}(\vec {w}')$
of
$p^{\prime }_{i}(\vec {w}')$
of
![]() $\vec {w}$
and
$\vec {w}$
and
![]() $\vec {w}'$
altogether for
$\vec {w}'$
altogether for
![]() $\vec {v}$
. (This will give
$\vec {v}$
. (This will give
![]() $N(\vec {v}) \le \frac {\eta n}{20 M^{2}L}$
, so we are safe.) Then Lemma 5.5 applied to
$N(\vec {v}) \le \frac {\eta n}{20 M^{2}L}$
, so we are safe.) Then Lemma 5.5 applied to
![]() $\vec {v} \in F_{n, f}(Q=0.9)$
yields a contradiction with
$\vec {v} \in F_{n, f}(Q=0.9)$
yields a contradiction with
![]() $\vec {w}, \vec {w}' \in G_{n}$
unless
$\vec {w}, \vec {w}' \in G_{n}$
unless
![]() $\sigma = \sigma '$
.
$\sigma = \sigma '$
.
We are now ready to prove the second main theorem, Theorem B:
Theorem B. Let S be a closed orientable surface of genus at least 2. Let
![]() $G=\operatorname {Mod}(S)$
be its mapping class group,
$G=\operatorname {Mod}(S)$
be its mapping class group,
![]() $X=\operatorname {\mathcal {T}}(S)$
be its Teichmüller space equipped with the Teichmüller metric, and
$X=\operatorname {\mathcal {T}}(S)$
be its Teichmüller space equipped with the Teichmüller metric, and
![]() $\mu $
be a non-elementary probability measure on
$\mu $
be a non-elementary probability measure on
![]() $\operatorname {Mod}(S)$
. Then
$\operatorname {Mod}(S)$
. Then
![]() $\operatorname {\mathbb {P}}$
-a.e. sample path shows at least linear growth of translation lengths. More precisely, there exists a constant
$\operatorname {\mathbb {P}}$
-a.e. sample path shows at least linear growth of translation lengths. More precisely, there exists a constant
![]() $\mathcal {L}>0$
such that for
$\mathcal {L}>0$
such that for
![]() $\operatorname {\mathbb {P}}$
-a.e.
$\operatorname {\mathbb {P}}$
-a.e.
![]() $(\operatorname {\omega }_{n})$
,
$(\operatorname {\omega }_{n})$
,
![]() $\tau (\operatorname {\omega }_{n}) \ge \mathcal {L}n$
for sufficiently large n.
$\tau (\operatorname {\omega }_{n}) \ge \mathcal {L}n$
for sufficiently large n.
Moreover, if
![]() $\mu $
further has finite first moment with respect to the Teichmüller metric, then for
$\mu $
further has finite first moment with respect to the Teichmüller metric, then for
![]() $\operatorname {\mathbb {P}}$
-a.e.
$\operatorname {\mathbb {P}}$
-a.e.
![]() $(\operatorname {\omega }_{n})$
, we have
$(\operatorname {\omega }_{n})$
, we have
where
![]() $\lambda>0$
is the drift.
$\lambda>0$
is the drift.
Proof. Lemma 5.6 tells us that
![]() $\operatorname {\mathbb {P}}((\operatorname {\omega }_{i})_{i=1}^{n} \in G_{n, f}(Q=1)) \le P^{n}$
for sufficiently large n. Similarly, we obtain
$\operatorname {\mathbb {P}}((\operatorname {\omega }_{i})_{i=1}^{n} \in G_{n, f}(Q=1)) \le P^{n}$
for sufficiently large n. Similarly, we obtain
![]() $\operatorname {\mathbb {P}}((\operatorname {\omega }_{i})_{i=1}^{n} \in G_{n, b}(Q=1)) \le P^{n}$
. Since
$\operatorname {\mathbb {P}}((\operatorname {\omega }_{i})_{i=1}^{n} \in G_{n, b}(Q=1)) \le P^{n}$
. Since
![]() $G_{n, f}(Q=1) \cup G_{n, b}(Q=1) = G_{n}$
, we deduce that
$G_{n, f}(Q=1) \cup G_{n, b}(Q=1) = G_{n}$
, we deduce that
![]() $\operatorname {\mathbb {P}}((\operatorname {\omega }_i)_{i=1}^n \in G_{n}) \le 2P^{n}$
for sufficiently large n. Thus, by the Borel-Cantelli lemma, almost every path avoids
$\operatorname {\mathbb {P}}((\operatorname {\omega }_i)_{i=1}^n \in G_{n}) \le 2P^{n}$
for sufficiently large n. Thus, by the Borel-Cantelli lemma, almost every path avoids
![]() $G_{n}$
eventually. If
$G_{n}$
eventually. If
![]() $\operatorname {\omega }$
avoids
$\operatorname {\omega }$
avoids
![]() $G_{n}$
eventually but
$G_{n}$
eventually but
![]() $\tau (\operatorname {\omega }_{n}) \le (2D - 2\eta /M) n$
infinitely often, then
$\tau (\operatorname {\omega }_{n}) \le (2D - 2\eta /M) n$
infinitely often, then
![]() $\operatorname {\omega }_{n}$
avoids
$\operatorname {\omega }_{n}$
avoids
![]() $F_{n}$
infinitely often. However, since
$F_{n}$
infinitely often. However, since
![]() $W_{n}^{n} \ge W_{\lfloor n/3L\rfloor }$
, the subadditive ergodic theorem implies that such path constitutes a measure zero set.
$W_{n}^{n} \ge W_{\lfloor n/3L\rfloor }$
, the subadditive ergodic theorem implies that such path constitutes a measure zero set.
We now investigate the second assertion of Theorem B. When
![]() $\mu $
has finite first moment, the drift
$\mu $
has finite first moment, the drift
![]() $\lambda $
of the random walk
$\lambda $
of the random walk
![]() $\operatorname {\omega }$
is finite and strictly positive. Here, the strict positivity of
$\operatorname {\omega }$
is finite and strictly positive. Here, the strict positivity of
![]() $\lambda $
follows from the nontriviality of the Poisson boundary of non-elementary random walks on Teichmüller space (cf. [Reference Kaimanovich and MasurKM96, Theorem 2.3.2]). As in the proof of the second assertion of Theorem A, we define the following set for
$\lambda $
follows from the nontriviality of the Poisson boundary of non-elementary random walks on Teichmüller space (cf. [Reference Kaimanovich and MasurKM96, Theorem 2.3.2]). As in the proof of the second assertion of Theorem A, we define the following set for
![]() $0<\epsilon < 1$
and
$0<\epsilon < 1$
and
![]() $D = 0.5(1-\epsilon /2)\lambda $
:
$D = 0.5(1-\epsilon /2)\lambda $
:
 $$ \begin{align*}\begin{aligned} F_{n} & := \left\{ \vec{w} : \begin{matrix} \# \mathcal{N}_{\lfloor \epsilon n/7 \rfloor, n}(\vec{w}) \ge {\eta \epsilon n \over 24L}, \,\,d(x_{0}, w_{n} x_{0}) \ge \left(1-\frac{\epsilon}{1000}\right) \lambda n,\\ d(x_{0}, w_{\lfloor \epsilon n / 7\rfloor} x_{0}) \le \frac{\epsilon \lambda n}{6} \end{matrix} \right\}\\ G_{n} & := \left\{ \vec{w} \in F_{n}: \tau(w_{n}) \le \left(2D - \frac{2\eta}{M} \right) n \right\}. \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} F_{n} & := \left\{ \vec{w} : \begin{matrix} \# \mathcal{N}_{\lfloor \epsilon n/7 \rfloor, n}(\vec{w}) \ge {\eta \epsilon n \over 24L}, \,\,d(x_{0}, w_{n} x_{0}) \ge \left(1-\frac{\epsilon}{1000}\right) \lambda n,\\ d(x_{0}, w_{\lfloor \epsilon n / 7\rfloor} x_{0}) \le \frac{\epsilon \lambda n}{6} \end{matrix} \right\}\\ G_{n} & := \left\{ \vec{w} \in F_{n}: \tau(w_{n}) \le \left(2D - \frac{2\eta}{M} \right) n \right\}. \end{aligned}\end{align*} $$
By the subadditive ergodic theorem, a.e. sample path
![]() $\operatorname {\omega }$
belongs to
$\operatorname {\omega }$
belongs to
![]() $F_{n}$
for all sufficiently large n. We then require
$F_{n}$
for all sufficiently large n. We then require
![]() $M> \frac {2000 \eta }{\lambda \epsilon } + {2000\eta \over \epsilon } + {2000 \over \epsilon } + 1$
and
$M> \frac {2000 \eta }{\lambda \epsilon } + {2000\eta \over \epsilon } + {2000 \over \epsilon } + 1$
and
![]() $0.9 \le Q \le 1$
. Given
$0.9 \le Q \le 1$
. Given
![]() $\vec {w} \in F_{n}$
, we observe as before that
$\vec {w} \in F_{n}$
, we observe as before that
for each
![]() $n_{i} \in \mathcal {N}_{\lfloor \epsilon n/7 \rfloor , n} (\vec {w})$
. This implies that
$n_{i} \in \mathcal {N}_{\lfloor \epsilon n/7 \rfloor , n} (\vec {w})$
. This implies that
![]() $\mathcal {N}_{\lfloor \epsilon n/7 \rfloor , n} (\vec {w}) \subseteq \mathcal {N}_{f}(\vec {w})$
and
$\mathcal {N}_{\lfloor \epsilon n/7 \rfloor , n} (\vec {w}) \subseteq \mathcal {N}_{f}(\vec {w})$
and
![]() $\vec {w} \in F_{n, f}$
. In other words,
$\vec {w} \in F_{n, f}$
. In other words,
![]() $F_{n, f}$
already covers
$F_{n, f}$
already covers
![]() $F_{n}$
, which is stronger than what we hope in Lemma 5.2.
$F_{n}$
, which is stronger than what we hope in Lemma 5.2.
Given this, Lemma 5.3, Lemma 5.5 and Lemma 5.6 still hold true. Using them, we deduce that almost every path
![]() $\operatorname {\omega }$
does not fall into
$\operatorname {\omega }$
does not fall into
![]() $G_{n}(Q=1)$
infinitely often. Note also that
$G_{n}(Q=1)$
infinitely often. Note also that
Together with the observation that a.e. path does not avoid
![]() $F_{n}$
infinitely often, we deduce that
$F_{n}$
infinitely often, we deduce that
![]() $\liminf \frac {1}{n}\tau (\operatorname {\omega } _{n}) \ge (1-\epsilon ) \lambda $
almost surely, as desired.
$\liminf \frac {1}{n}\tau (\operatorname {\omega } _{n}) \ge (1-\epsilon ) \lambda $
almost surely, as desired.
Acknowledgements
We truly appreciate Çağri Sert for fruitful conversations. We also thank the anonymous referee for valuable comments.
The first and second authors were partially supported by Samsung Science & Technology Foundation grant No. SSTF-BA1702-01.
Competing Interests
The authors have no competing interest to declare.