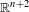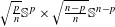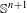Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Székelyhidi, Gábor
2020.
Uniqueness of some Calabi–Yau metrics on $${\mathbf {C}}^{{n}}$$.
Geometric and Functional Analysis,
Vol. 30,
Issue. 4,
p.
1152.
Chen, Letian
2023.
Rotational symmetry of solutions of mean curvature flow coming out of a double cone II.
Calculus of Variations and Partial Differential Equations,
Vol. 62,
Issue. 2,
Agudelo, Oscar
and
Rizzi, Matteo
2025.
The Jacobi operator of some special minimal hypersurfaces.
Annali di Matematica Pura ed Applicata (1923 -),
Vol. 204,
Issue. 4,
p.
1493.