Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-16T02:21:07.442Z Has data issue: false hasContentIssue false
  • English
  • Français

NON-COMMUTATIVE LOCALIZATIONS OF ADDITIVE CATEGORIES AND WEIGHT STRUCTURES

Part of: (Co)homology theory Rings and algebras arising under various constructions Conditions on elements Homological algebra Cycles and subschemes Abelian categories Homological methods $K$-theory in geometry

Published online by Cambridge University Press:  24 May 2016

Mikhail V. Bondarko Open the ORCID record for Mikhail V. Bondarko [Opens in a new window]  and
Vladimir A. Sosnilo
Mikhail V. Bondarko
Affiliation:
St. Petersburg State University, Mathematics and Mechanics, St. Petersburg, Russian Federation (mbondarko@hotmail.com)
Vladimir A. Sosnilo
Affiliation:
St. Petersburg State University, Mathematics and Mechanics, St. Petersburg, Russian Federation (mbondarko@hotmail.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we demonstrate that non-commutative localizations of arbitrary additive categories (generalizing those defined by Cohn in the setting of rings) are closely (and naturally) related to weight structures. Localizing an arbitrary triangulated category 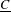$\text{}\underline{C}$ by a set $S$ of morphisms in the heart 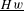$\text{}\underline{Hw}$ of a weight structure 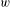$w$ on it one obtains a triangulated category endowed with a weight structure 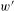$w^{\prime }$. The heart of 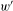$w^{\prime }$ is a certain version of the Karoubi envelope of the non-commutative localization 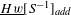$\text{}\underline{Hw}[S^{-1}]_{\mathit{add}}$ (of 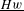$\text{}\underline{Hw}$ by $S$). The functor 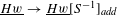$\text{}\underline{Hw}\rightarrow \text{}\underline{Hw}[S^{-1}]_{\mathit{add}}$ is the natural categorical version of Cohn’s localization of a ring, i.e., it is universal among additive functors that make all elements of $S$ invertible. For any additive category 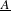$\text{}\underline{A}$, taking 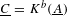$\text{}\underline{C}=K^{b}(\text{}\underline{A})$ we obtain a very efficient tool for computing 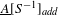$\text{}\underline{A}[S^{-1}]_{\mathit{add}}$; using it, we generalize the calculations of Gerasimov and Malcolmson (made for rings only). We also prove that 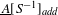$\text{}\underline{A}[S^{-1}]_{\mathit{add}}$ coincides with the ‘abstract’ localization 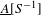$\text{}\underline{A}[S^{-1}]$ (as constructed by Gabriel and Zisman) if $S$ contains all identity morphisms of 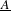$\text{}\underline{A}$ and is closed with respect to direct sums. We apply our results to certain categories of birational motives 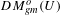$DM_{gm}^{o}(U)$ (generalizing those defined by Kahn and Sujatha). We define 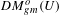$DM_{gm}^{o}(U)$ for an arbitrary 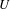$U$ as a certain localization of 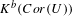$K^{b}(Cor(U))$ and obtain a weight structure for it. When 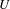$U$ is the spectrum of a perfect field, the weight structure obtained this way is compatible with the corresponding Chow and Gersten weight structures defined by the first author in previous papers. For a general 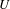$U$ the result is completely new. The existence of the corresponding adjacent$t$-structure is also a new result over a general base scheme; its heart is a certain category of birational sheaves with transfers over 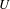$U$.

Keywords

category theoryhomological algebraK-theorynon-commutative localizationstriangulated categoriesweight structuresbirational motivest-structuresalgebraic geometry

MSC classification

Primary: 18E35: Localization of categories 16S85: Rings of fractions and localizations 14C15: (Equivariant) Chow groups and rings; motives
Secondary: 18E30: Derived categories, triangulated categories 18E05: Preadditive, additive categories 14F42: Motivic cohomology; motivic homotopy theory 19E15: Algebraic cycles and motivic cohomology 16U20: Ore rings, multiplicative sets, Ore localization 18G35: Chain complexes 16E20: Grothendieck groups, $K$-theory, etc.
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 17 , Issue 4 , September 2018 , pp. 785 - 821
Copyright
© Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Theorem 0.1 and Theorem 4.2.3 were proven under support of the Russian Science Foundation grant no. 14-21-00035. The research was also supported by RFBR grant no. 15-01-03034-a. Besides, the first author was supported by RFBR (grants no. 14-01-00393-a) and by Dmitry Zimin’s Foundation ‘Dynasty’; the second author was supported by the Chebyshev Laboratory (Department of Mathematics and Mechanics, St. Petersburg State University), by JSC ‘Gazprom Neft’, and by the Saint-Petersburg State University research grant no. 38.37.208.2016.

References

Balmer, P. and Schlichting, M., Idempotent completion of triangulated categories, J. Algebra 236(2) (2001), 819–834.Google Scholar
Beilinson, A., Bernstein, J. and Deligne, P., Faisceaux pervers, Asterisque 100 (1982), 5–171.Google Scholar
Bondarko, M. V., Differential graded motives: weight complex, weight filtrations and spectral sequences for realizations; Voevodsky vs. Hanamura, J. Inst. Math. Jussieu v.8(1) (2009), 39–97. see also arXiv:math.AG/0601713.Google Scholar
Bondarko, M. V., Weight structures vs. t-structures; weight filtrations, spectral sequences, and complexes (for motives and in general), J. K-theory 6(03) (2010), 387–504. see also arXiv:0704.4003.Google Scholar
Bondarko, M. V., Motivically functorial coniveau spectral sequences; direct summands of cohomology of function fields, Doc. Math. (2010), 33–117. see also arXiv:0812.2672.Google Scholar
Bondarko, M. V., $\mathbb{Z}[\frac{1}{p}]$ -motivic resolution of singularities, Compos. Math. 147(5) (2011), 1434–1446.Google Scholar
Bondarko, M. V., Gersten weight structures for motivic homotopy categories; direct summands of cohomology of function fields and coniveau spectral sequences, Preprint, 2013, arXiv:1312.7493.Google Scholar
Bondarko, M. V., Weights for relative motives: relation with mixed complexes of sheaves, Int. Math. Res. Not. IMRN 2014(17) (2014), 4715–4767, see also arXiv:1007.4543.Google Scholar
Bondarko, M. V. and Ivanov, M. A., On Chow weight structures for cdh-motives with integral coefficients, Algebra i Analiz 27 (2015), 14–40, see also arXiv:1506.00631.Google Scholar
Cisinski, D.-C., the answer http://mathoverflow.net/questions/44047/localizing-an-arbitrary-additive-category/44155#44155.Google Scholar
Cisinski, D.-C. and Deglise, F., Triangulated categories of mixed motives, Preprint, 2009, arXiv:0912.2110v3.pdf.Google Scholar
Cohn, P. M., Free Rings and Their Relations, 2nd ed. (Academic Press, London & New York, 1985). xxii + 588 pp.Google Scholar
Dwyer, W. G., Noncommutative localization in homotopy theory, in Non-commutative Localization in Algebra and Topology, London Mathematical Society Lecture Note Series, Volume 330, pp. 24–39 (Cambridge University Press, Cambridge, 2006).Google Scholar
Fornasiero, M., Projective version of Malcolmson’s criterion, Ann. Univ. Ferrara, Sci. Mat. 48(1) (2002), 119–131.Google Scholar
Gabriel, P. and Zisman, M., Calculus of Fractions and Homotopy Theory, Ergebnisse der Mathematik und ihrer Grenzgebiete, Volume 35 (Springer-Verlag New York, Inc., New York, 1967).Google Scholar
Gerasimov, V.N., Localization in associative rings, Siberian Math. Zh. 23–6 (1982), 36–54. (Russian).Google Scholar
Hébert, D., Structures de poids á la Bondarko sur les motifs de Beilinson, Compos. Math. 147(5) (2011), 1447–1462.Google Scholar
Ivorra, F., Réalisation l-adique des motifs triangulés géométriques. I, Doc. Math. 12 (2007), 607–671.Google Scholar
Kahn, B. and Sujatha, R., (with appendices by Jean-Louis Colliot-Thélène and Ofer Gabber), Birational geometry and localization of categories, Documenta Mathematica, Extra Volume: Alexander S. Merkurjev’s Sixtieth Birthday, 277–334, 2015.Google Scholar
Kahn, B. and Sujatha, R., Birational motives, I: pure birational motives, Preprint, 2009, arXiv:0902.4902v5.pdf.Google Scholar
Kahn, B. and Sujatha, R., Birational motives, II: triangulated birational motives, Preprint, 2015, arXiv:1506.08385.Google Scholar
Malcolmson, P., Construction of Universal Matrix Localizations, Lecture Notes in Mathematics, Volume 951, pp. 117–132 (Springer, Berlin, Heidelberg, 1982).Google Scholar
Neeman, A., Triangulated Categories, Annals of Mathematics Studies, Volume 148 (Princeton University Press, Princeton, 2001). viii+449 pp.Google Scholar
Neeman, A. and Ranicki, A., Noncommutative localisation in algebraic K-theory I, Geom. Topol. 8 (2004), 1385–1425.Google Scholar
Pauksztello, D., Compact cochain objects in triangulated categories and co-t-structures, Cent. Eur. J. Math. 6(1) (2008), 25–42.Google Scholar
Positselski, L., Mixed Artin-Tate motives with finite coefficients, Mosc. Math. J. 11(2) (2011), 317–402.Google Scholar
Schofield, A. H., Representation of Rings Over Skew Fields, London Mathematical Society Lecture Note Series, Volume 92 (Cambridge University Press, Cambridge, 1985). xii+223 pp.Google Scholar
Sosnilo, V.A., Weight structures in localizations (revisited) and the weight lifting property, Preprint, 2015, arXiv:1510.03403.Google Scholar
Voevodsky, V., Triangulated categories of motives over a field, in Cycles, Transfers and Motivic Homology Theories (ed. Voevodsky, V., Suslin, A. and Friedlander, E.), Annals of Mathematical Studies, Volume 143, pp. 188–238 (Princeton University Press, Princeton, 2000).Google Scholar
Wildeshaus, J., Chow motives without projectivity, Compos. Math. 145(5) (2009), 1196–1226.Google Scholar