Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Jäger, Tobias
and
Koropecki, Andres
2017.
Poincaré Theory for Decomposable Cofrontiers.
Annales Henri Poincaré,
Vol. 18,
Issue. 1,
p.
85.
Guihéneuf, Pierre-Antoine
and
Koropecki, Andres
2017.
Stability of the rotation set of area-preserving toral homeomorphisms.
Nonlinearity,
Vol. 30,
Issue. 3,
p.
1089.
PASSEGGI, ALEJANDRO
and
SAMBARINO, MARTÍN
2020.
Deviations in the Franks–Misiurewicz conjecture.
Ergodic Theory and Dynamical Systems,
Vol. 40,
Issue. 9,
p.
2533.
Conejeros, Jonathan
and
Tal, Fábio Armando
2020.
Existence of non-contractible periodic orbits for homeomorphisms of the open annulus.
Mathematische Zeitschrift,
Vol. 294,
Issue. 3-4,
p.
1413.
Jäger, Tobias
Koropecki, Andres
and
Tal, Fabio Armando
2021.
On the onset of diffusion in the kicked Harper model.
Communications in Mathematical Physics,
Vol. 383,
Issue. 2,
p.
953.
Bowden, Jonathan
Hensel, Sebastian
Mann, Kathryn
Militon, Emmanuel
and
Webb, Richard
2022.
Rotation sets and actions on curves.
Advances in Mathematics,
Vol. 408,
Issue. ,
p.
108579.
Le Calvez, Patrice
2022.
Conservative surface homeomorphisms with finitely many periodic points.
Journal of Fixed Point Theory and Applications,
Vol. 24,
Issue. 2,
SILVA SALOMÃO, GUILHERME
and
TAL, FABIO ARMANDO
2022.
Non-existence of sublinear diffusion for a class of torus homeomorphisms.
Ergodic Theory and Dynamical Systems,
Vol. 42,
Issue. 4,
p.
1517.
Addas-Zanata, Salvador
and
Koropecki, Andres
2022.
Homotopically unbounded disks for generic surface diffeomorphisms.
Transactions of the American Mathematical Society,
Vol. 375,
Issue. 8,
p.
5859.
QIN, WEN-XIN
SHEN, BAI-NIAN
SUN, YI-LIN
and
ZHOU, TONG
2023.
Zero entropy and stable rotation sets for monotone recurrence relations.
Ergodic Theory and Dynamical Systems,
Vol. 43,
Issue. 5,
p.
1737.
Nunes, Pollyanna Vicente
and
Tal, Fábio Armando
2023.
Transitivity and the existence of horseshoes on the 2-torus.
Nonlinearity,
Vol. 36,
Issue. 1,
p.
199.
Briane, Marc
and
Hervé, Loïc
2023.
Fine asymptotic expansion of the ODE's flow.
Journal of Differential Equations,
Vol. 373,
Issue. ,
p.
327.
Liu, Xiao-Chuan
and
Tal, Fábio Armando
2024.
On non-contractible periodic orbits and bounded deviations.
Nonlinearity,
Vol. 37,
Issue. 7,
p.
075007.
Guihéneuf, Pierre‐Antoine
and
Militon, Emmanuel
2024.
Parabolic isometries of the fine curve graph of the torus.
Proceedings of the London Mathematical Society,
Vol. 129,
Issue. 2,
Briane, Marc
and
Casado-Díaz, Juan
2024.
A New Divergence-Curl Result for Measures. Application to the Two-Dimensional ODE’s Flow.
SIAM Journal on Mathematical Analysis,
Vol. 56,
Issue. 5,
p.
6398.
Briane, Marc
2025.
Asymptotic properties of integrable ODEs flows under a min-max condition.
Journal of Differential Equations,
Vol. 430,
Issue. ,
p.
113181.
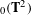 $_{0}(\mathbf{T}^{2})$ by their rotation set
$_{0}(\mathbf{T}^{2})$ by their rotation set  $\unicode[STIX]{x1D70C}$, according to wether
$\unicode[STIX]{x1D70C}$, according to wether  $\unicode[STIX]{x1D70C}$ is a point, a segment or a set with nonempty interior. A recent classification of nonwandering elements in Homeo
$\unicode[STIX]{x1D70C}$ is a point, a segment or a set with nonempty interior. A recent classification of nonwandering elements in Homeo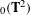 $_{0}(\mathbf{T}^{2})$ by Koropecki and Tal was given in (Invent. Math.196 (2014), 339–381), according to the intrinsic underlying ambient space where the dynamics takes place: planar, annular and strictly toral maps. We study the link between these two classifications, showing that, even abroad the nonwandering setting, annular maps are characterized by rotation sets which are rational segments. Also, we obtain information on the sublinear diffusion of orbits in the—not very well understood—case that
$_{0}(\mathbf{T}^{2})$ by Koropecki and Tal was given in (Invent. Math.196 (2014), 339–381), according to the intrinsic underlying ambient space where the dynamics takes place: planar, annular and strictly toral maps. We study the link between these two classifications, showing that, even abroad the nonwandering setting, annular maps are characterized by rotation sets which are rational segments. Also, we obtain information on the sublinear diffusion of orbits in the—not very well understood—case that  $\unicode[STIX]{x1D70C}$ has nonempty interior.
$\unicode[STIX]{x1D70C}$ has nonempty interior.
