Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
MILLER, JASON
SHEFFIELD, SCOTT
and
WERNER, WENDELIN
2017.
CLE PERCOLATIONS.
Forum of Mathematics, Pi,
Vol. 5,
Issue. ,
Miller, Jason
and
Werner, Wendelin
2018.
Connection Probabilities for Conformal Loop Ensembles.
Communications in Mathematical Physics,
Vol. 362,
Issue. 2,
p.
415.
Lupu, Titus
and
Werner, Wendelin
2018.
The random pseudo-metric on a graph defined via the zero-set of the Gaussian free field on its metric graph.
Probability Theory and Related Fields,
Vol. 171,
Issue. 3-4,
p.
775.
Aru, Juhan
and
Sepúlveda, Avelio
2018.
Two-valued local sets of the 2D continuum Gaussian free field: connectivity, labels, and induced metrics.
Electronic Journal of Probability,
Vol. 23,
Issue. none,
Sepúlveda, Avelio
2019.
On thin local sets of the Gaussian free field.
Annales de l'Institut Henri Poincaré, Probabilités et Statistiques,
Vol. 55,
Issue. 3,
Benoist, Stéphane
and
Hongler, Clément
2019.
The scaling limit of critical Ising interfaces is $\mathrm{CLE}_{3}$.
The Annals of Probability,
Vol. 47,
Issue. 4,
Qian, Wei
2019.
Conditioning a Brownian loop-soup cluster on a portion of its boundary.
Annales de l'Institut Henri Poincaré, Probabilités et Statistiques,
Vol. 55,
Issue. 1,
Aru, Juhan
Lupu, Titus
and
Sepúlveda, Avelio
2020.
The First Passage Sets of the 2D Gaussian Free Field: Convergence and Isomorphisms.
Communications in Mathematical Physics,
Vol. 375,
Issue. 3,
p.
1885.
Berestycki, Nathanaël
Powell, Ellen
and
Ray, Gourab
2020.
A characterisation of the Gaussian free field.
Probability Theory and Related Fields,
Vol. 176,
Issue. 3-4,
p.
1259.
Aru, Juhan
Powell, Ellen
and
Sepúlveda, Avelio
2020.
Liouville measure as a multiplicative cascade via level sets of the Gaussian free field.
Annales de l'Institut Fourier,
Vol. 70,
Issue. 1,
p.
205.
Werner, Wendelin
2021.
In and Out of Equilibrium 3: Celebrating Vladas Sidoravicius.
Vol. 77,
Issue. ,
p.
797.
Aru, Juhan
Lupu, Titus
and
Sepúlveda, Avelio
2022.
Extremal distance and conformal radius of a CLE4 loop.
The Annals of Probability,
Vol. 50,
Issue. 2,
Schoug, Lukas
Sepúlveda, Avelio
and
Viklund, Fredrik
2022.
Dimensions of Two-Valued Sets via Imaginary Chaos.
International Mathematics Research Notices,
Vol. 2022,
Issue. 5,
p.
3219.
Aru, Juhan
Papon, Léonie
and
Powell, Ellen
2023.
Thick points of the planar GFF are totally disconnected for all γ≠0.
Electronic Journal of Probability,
Vol. 28,
Issue. none,
Berestycki, Nathanaël
Lis, Marcin
and
Qian, Wei
2023.
Free boundary dimers: random walk representation and scaling limit.
Probability Theory and Related Fields,
Vol. 186,
Issue. 3-4,
p.
735.
Lehmkuehler, Matthis
2023.
The trunks of CLE(4) explorations.
The Annals of Applied Probability,
Vol. 33,
Issue. 5,
Holden, Nina
and
Lehmkuehler, Matthis
2024.
Liouville quantum gravity weighted by conformal loop ensemble nesting statistics.
Probability and Mathematical Physics,
Vol. 5,
Issue. 4,
p.
847.
Wan, Guoyang
Hu, Yaocong
Liu, Bingyou
Bai, Shoujun
Xing, Kaisheng
and
Tao, Xiuwen
2024.
A 6DOF pose measurement method for metal casts object based on stereo vision sensor.
Sensor Review,
Vol. 44,
Issue. 1,
p.
22.
Duminil‐Copin, Hugo
Lis, Marcin
and
Qian, Wei
2025.
Conformal invariance of double random currents I: Identification of the limit.
Proceedings of the London Mathematical Society,
Vol. 130,
Issue. 1,
Aru, Juhan
Garban, Christophe
and
Sepúlveda, Avelio
2025.
Percolation for 2D Classical Heisenberg Model and Exit Sets of Vector Valued GFF.
Communications in Mathematical Physics,
Vol. 406,
Issue. 2,
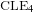 $\text{CLE}_{4}$ and its variants. More specifically, we consider bounded-type thin local sets (BTLS), where thin means that the local set is small in size, and bounded type means that the harmonic function describing the mean value of the field away from the local set is bounded by some deterministic constant. We show that a local set is a BTLS if and only if it is contained in some nested version of the
$\text{CLE}_{4}$ and its variants. More specifically, we consider bounded-type thin local sets (BTLS), where thin means that the local set is small in size, and bounded type means that the harmonic function describing the mean value of the field away from the local set is bounded by some deterministic constant. We show that a local set is a BTLS if and only if it is contained in some nested version of the 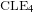 $\text{CLE}_{4}$ carpet, and prove that all BTLS are necessarily connected to the boundary of the domain. We also construct all possible BTLS for which the corresponding harmonic function takes only two prescribed values and show that all these sets (and this includes the case of
$\text{CLE}_{4}$ carpet, and prove that all BTLS are necessarily connected to the boundary of the domain. We also construct all possible BTLS for which the corresponding harmonic function takes only two prescribed values and show that all these sets (and this includes the case of 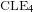 $\text{CLE}_{4}$) are in fact measurable functions of the GFF.
$\text{CLE}_{4}$) are in fact measurable functions of the GFF.