Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Guàrdia, Jordi
Montes, Jesús
and
Nart, Enric
2015.
Higher Newton polygons and integral bases.
Journal of Number Theory,
Vol. 147,
Issue. ,
p.
549.
Milstead, Jonathan
Pauli, Sebastian
and
Sinclair, Brian
2015.
Collaborative Mathematics and Statistics Research.
Vol. 109,
Issue. ,
p.
101.
Poteaux, Adrien
and
Rybowicz, Marc
2015.
Improving Complexity Bounds for the Computation of Puiseux Series over Finite Fields.
p.
299.
Bauch, Jens-Dietrich
2015.
Genus computation of global function fields.
Journal of Symbolic Computation,
Vol. 66,
Issue. ,
p.
8.
Bauch, Jens-Dietrich
2016.
Computation of integral bases.
Journal of Number Theory,
Vol. 165,
Issue. ,
p.
382.
Neiger, Vincent
Rosenkilde, Johan
and
Schost, Éric
2017.
Fast Computation of the Roots of Polynomials Over the Ring of Power Series.
p.
349.
Bauch, Jens-Dietrich
and
Nguyen Tran, Ha Thanh
2019.
Computation of triangular integral bases.
The Open Book Series,
Vol. 2,
Issue. 1,
p.
69.
Rojas, J. Maurice
and
Zhu, Yuyu
2020.
A complexity chasm for solving sparse polynomial equations over
p
-adic fields
.
ACM Communications in Computer Algebra,
Vol. 54,
Issue. 3,
p.
86.
Poteaux, Adrien
and
Weimann, Martin
2021.
Computing Puiseux series: a fast divide and conquer algorithm.
Annales Henri Lebesgue,
Vol. 4,
Issue. ,
p.
1061.
Rojas, J. Maurice
and
Zhu, Yuyu
2021.
A Complexity Chasm for Solving Univariate Sparse Polynomial Equations Over p-adic Fields.
p.
337.
Rojas, J. Maurice
and
Zhu, Yuyu
2022.
Root repulsion and faster solving for very sparse polynomials over p-adic fields.
Journal of Number Theory,
Vol. 241,
Issue. ,
p.
655.
Kyng, Madeleine
2022.
Computing zeta functions of algebraic curves using Harvey’s trace formula.
Research in Number Theory,
Vol. 8,
Issue. 4,
Poteaux, Adrien
and
Weimann, Martin
2022.
A quasi-linear irreducibility test in $$\mathbb{K}[[x]][y]$$.
computational complexity,
Vol. 31,
Issue. 1,
Poteaux, Adrien
and
Weimann, Martin
2022.
Local Polynomial Factorisation.
p.
149.
Poteaux, Adrien
and
Weimann, Martin
2024.
Computer Algebra in Scientific Computing.
Vol. 14938,
Issue. ,
p.
292.
Alberich-Carramiñana, Maria
Guàrdia, Jordi
Nart, Enric
Poteaux, Adrien
Roé, Joaquim
and
Weimann, Martin
2025.
Polynomial Factorization Over Henselian Fields.
Foundations of Computational Mathematics,
Vol. 25,
Issue. 2,
p.
631.
van der Hoeven, Joris
and
Lecerf, Grégoire
2025.
Plane curve germs and contact factorization.
Applicable Algebra in Engineering, Communication and Computing,
Vol. 36,
Issue. 1,
p.
5.
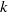 $k$ be a locally compact complete field with respect to a discrete valuation
$k$ be a locally compact complete field with respect to a discrete valuation  $v$ . Let
$v$ . Let 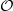 $ \mathcal{O} $ be the valuation ring,
$ \mathcal{O} $ be the valuation ring, 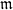 $\mathfrak{m}$ the maximal ideal and
$\mathfrak{m}$ the maximal ideal and 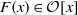 $F(x)\in \mathcal{O} [x] $ a monic separable polynomial of degree
$F(x)\in \mathcal{O} [x] $ a monic separable polynomial of degree  $n$ . Let
$n$ . Let 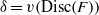 $\delta = v(\mathrm{Disc} (F))$ . The Montes algorithm computes an OM factorization of
$\delta = v(\mathrm{Disc} (F))$ . The Montes algorithm computes an OM factorization of 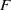 $F$ . The single-factor lifting algorithm derives from this data a factorization of
$F$ . The single-factor lifting algorithm derives from this data a factorization of 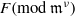 $F(\mathrm{mod~} {\mathfrak{m}}^{\nu } )$ , for a prescribed precision
$F(\mathrm{mod~} {\mathfrak{m}}^{\nu } )$ , for a prescribed precision  $\nu $ . In this paper we find a new estimate for the complexity of the Montes algorithm, leading to an estimation of
$\nu $ . In this paper we find a new estimate for the complexity of the Montes algorithm, leading to an estimation of 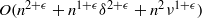 $O({n}^{2+ \epsilon } + {n}^{1+ \epsilon } {\delta }^{2+ \epsilon } + {n}^{2} {\nu }^{1+ \epsilon } )$ word operations for the complexity of the computation of a factorization of
$O({n}^{2+ \epsilon } + {n}^{1+ \epsilon } {\delta }^{2+ \epsilon } + {n}^{2} {\nu }^{1+ \epsilon } )$ word operations for the complexity of the computation of a factorization of 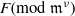 $F(\mathrm{mod~} {\mathfrak{m}}^{\nu } )$ , assuming that the residue field of
$F(\mathrm{mod~} {\mathfrak{m}}^{\nu } )$ , assuming that the residue field of 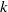 $k$ is small.
$k$ is small.
